A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration
Abstract
1. Introduction
2. Materials and Methods
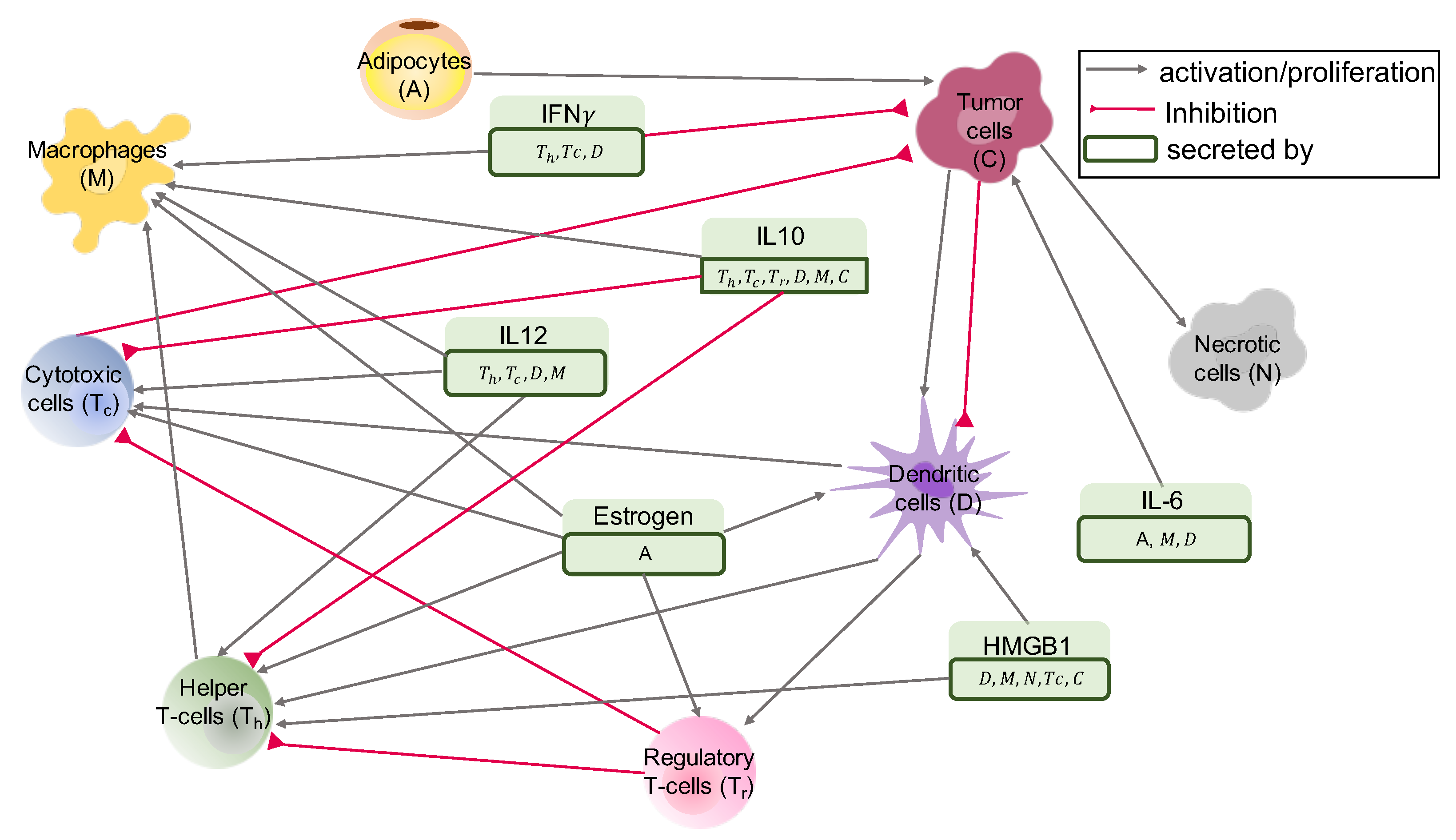
2.1. Interaction Network of Cells and Molecules—ODE Model
2.1.1. T-Cells
CD4+ Helper T-Cells ()
Cytotoxic T-Cells ()
Regulatory T-Cells ()
Naive T-Cells ()
2.1.2. Dendritic Cells (D)
2.1.3. Macrophages (M)
2.1.4. Cancer Cells (C)
2.1.5. Cancer Associated Adipocytes (A)
2.1.6. Necrotic Cells (N)
2.1.7. Molecules
HMGB1 (H)
IL-12 ()
IL-10 ()
Estrogen (E)
IFN- ()
IL-6 ()
2.2. Data of the Model
2.2.1. Breast Cancer Patients’ Data
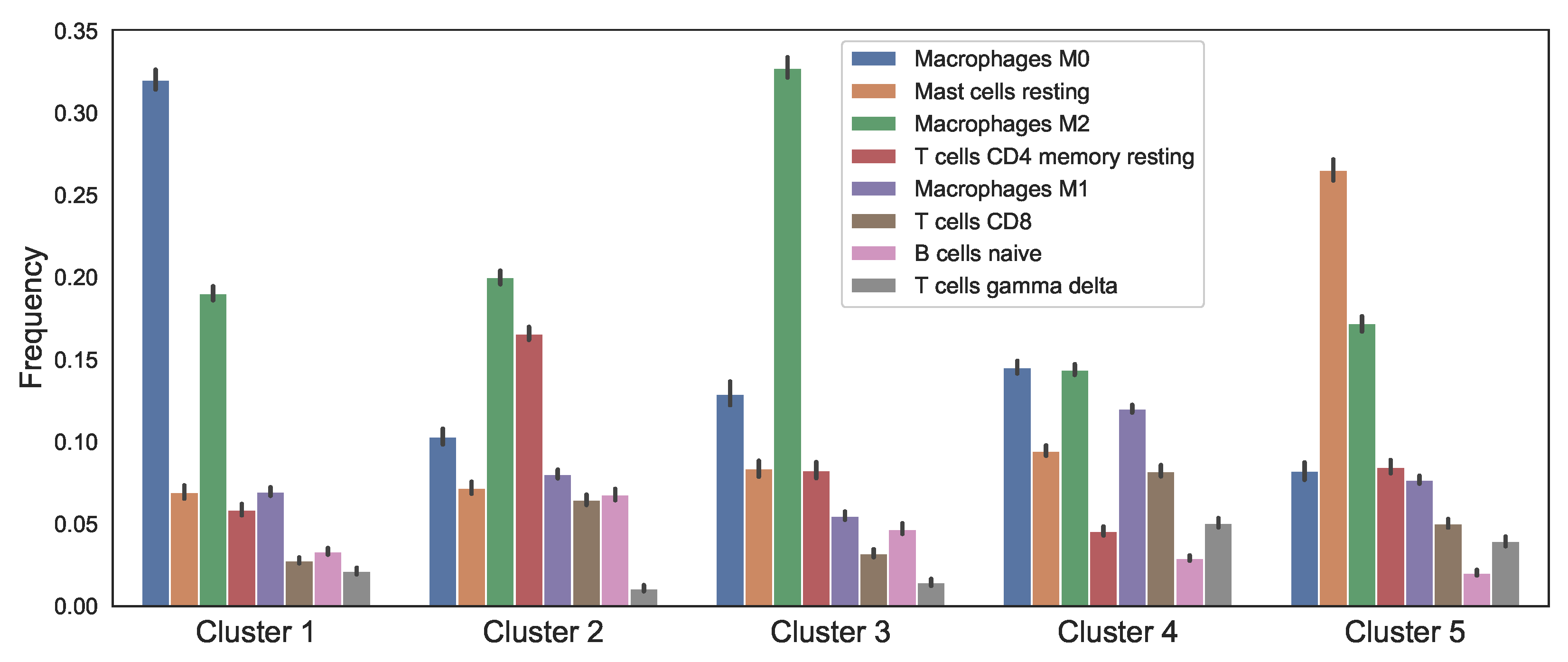
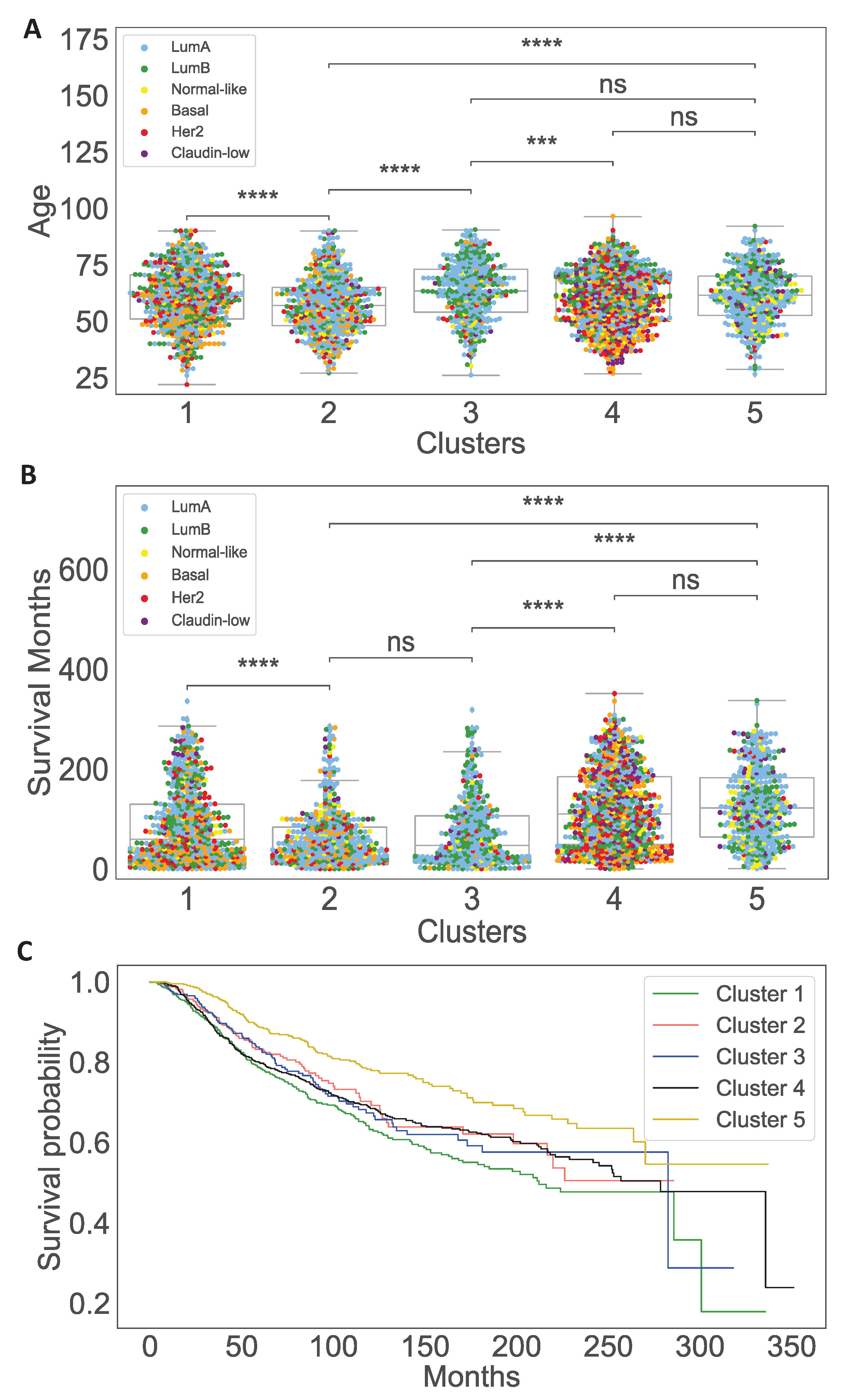
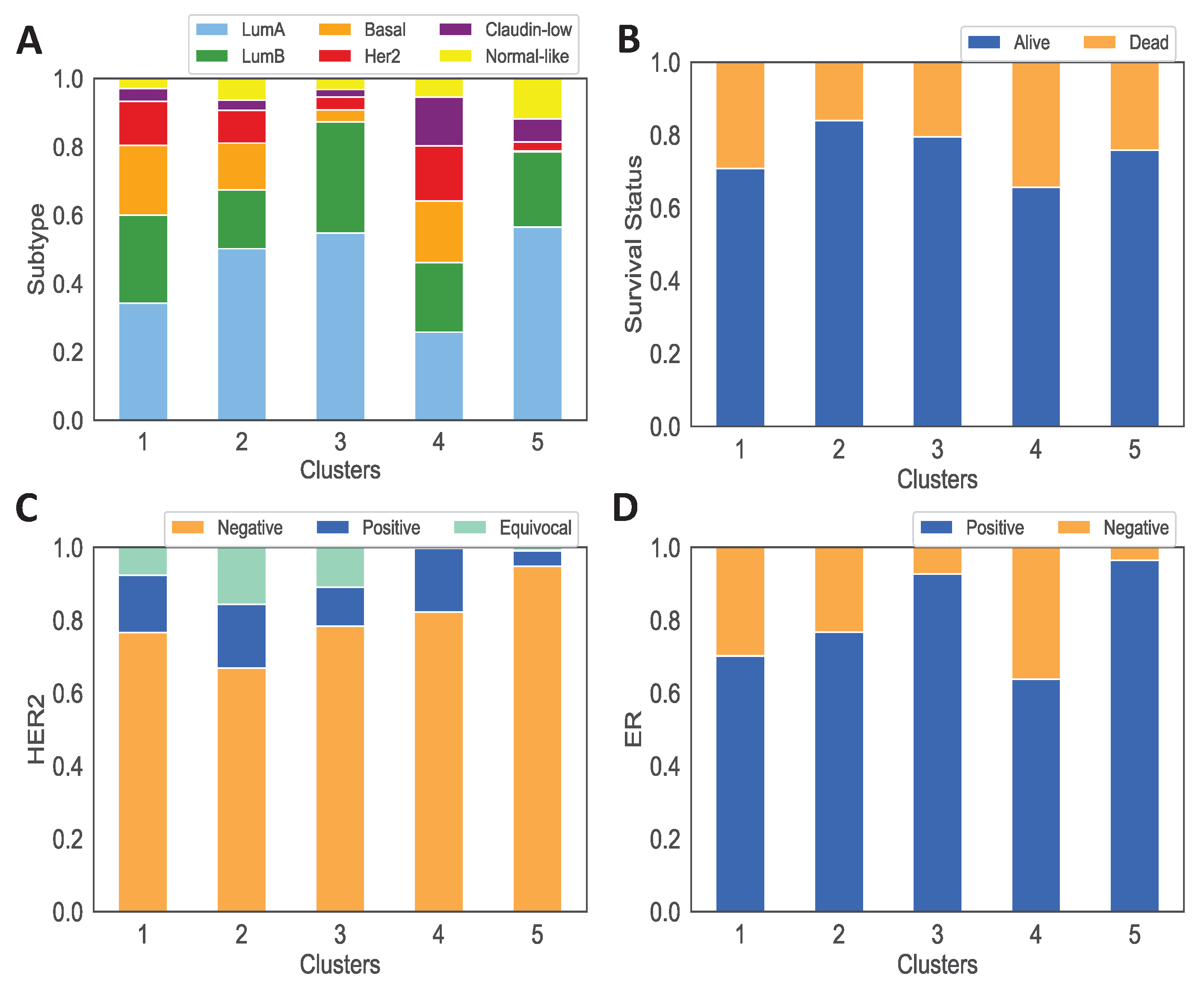
2.2.2. Patient Data Analysis
2.2.3. Parameter Estimation
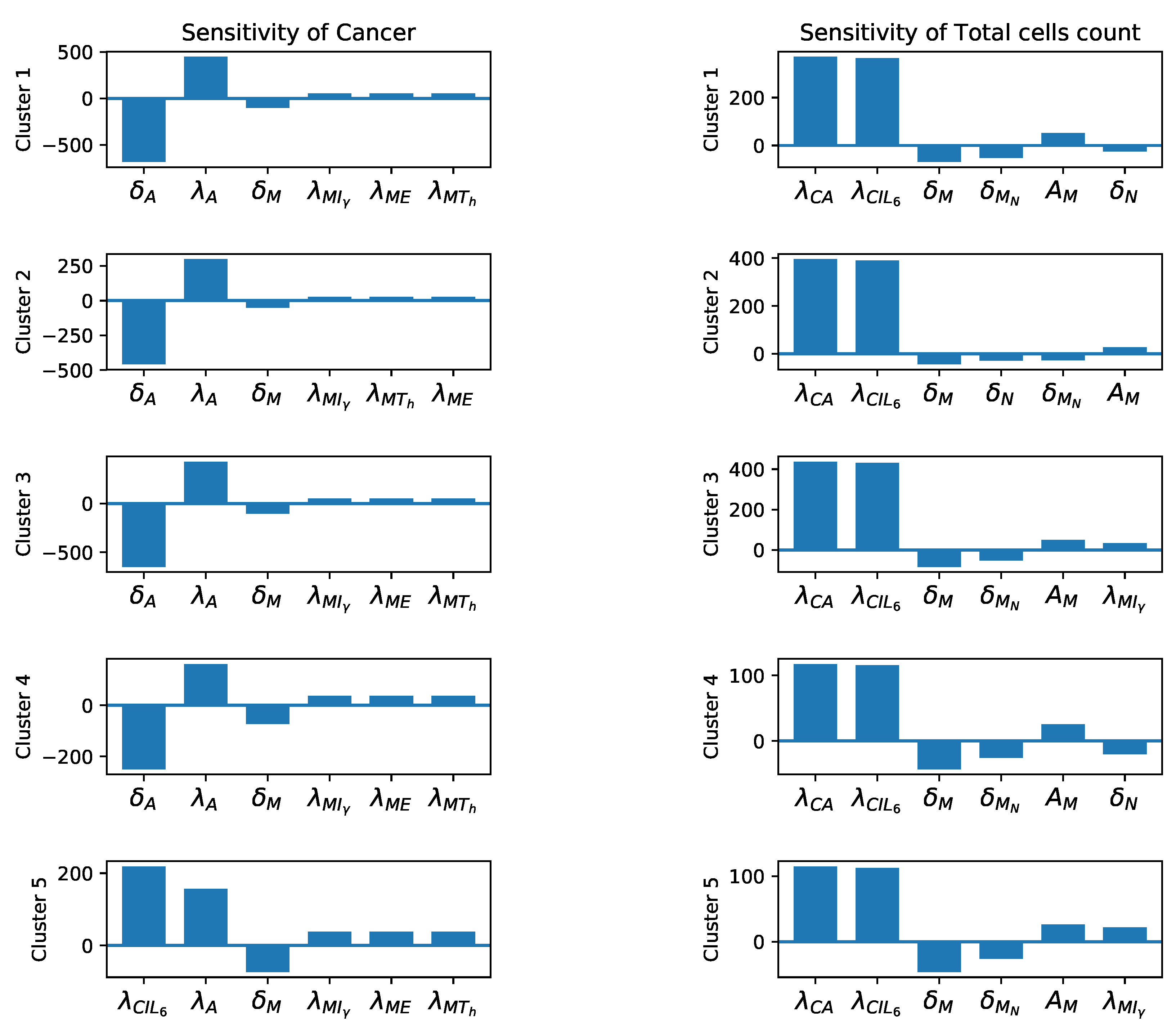
2.2.4. Sensitivity Analysis
- First, we define a local sensitivity measure for each parameter in the neighborhood as
- Second, we found weights for the aforementioned neighborhoods. Scaling each assumption provides us with a new set of parameters. The weights were then determined by calculating the distance of each resulting parameter set to a fixed base parameter set. We assigned higher weights to the parameters that were closer to the base values. We denote each weight by for and corresponding to the parameter and its neighborhood, respectively.
- Finally, we obtained the global sensitivity level to each parameter by
3. Results
3.1. Data Analysis of the Clusters
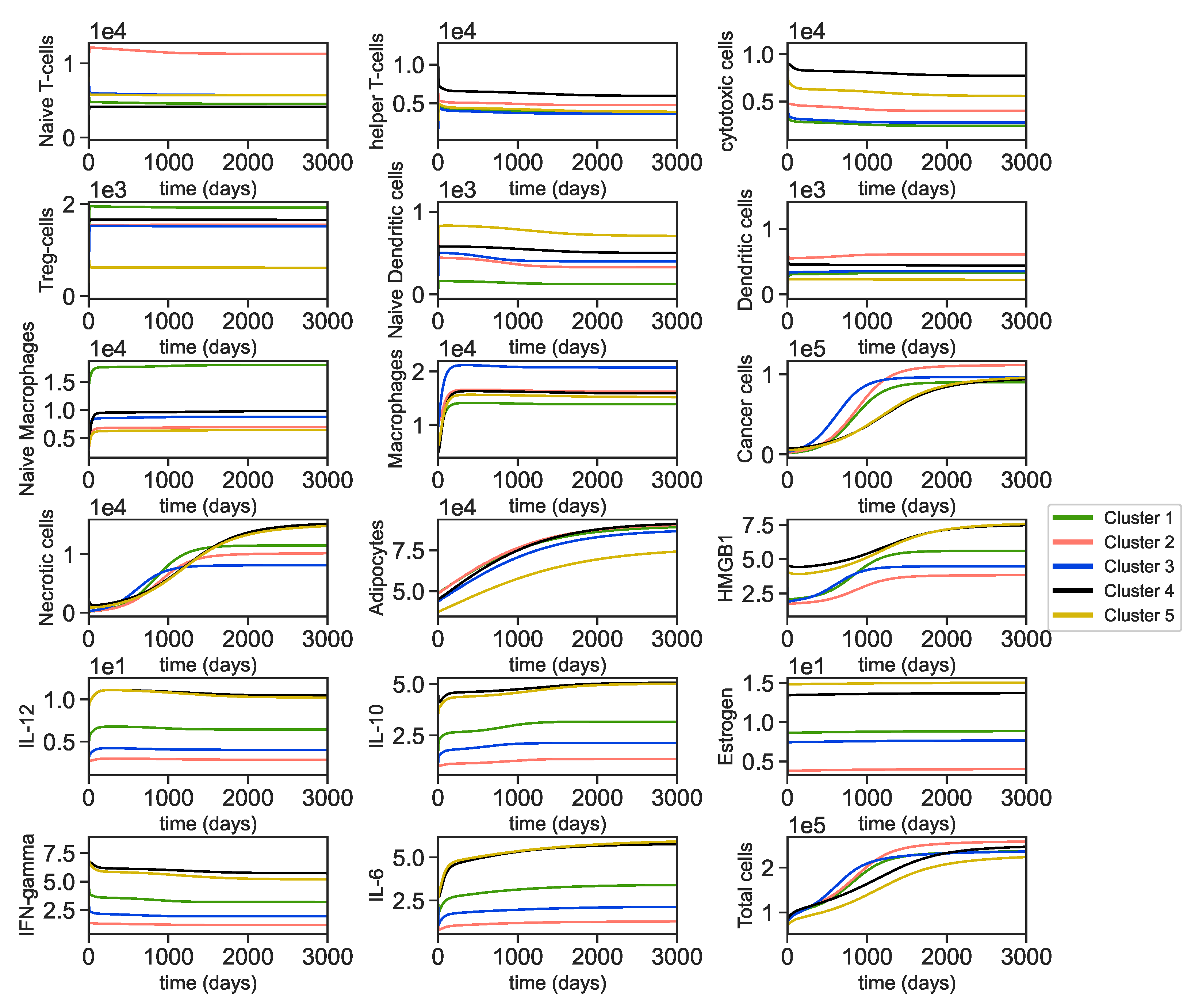
3.2. Dynamics of the Breast Cancer Microenvironment
3.3. Sensitivity Analysis
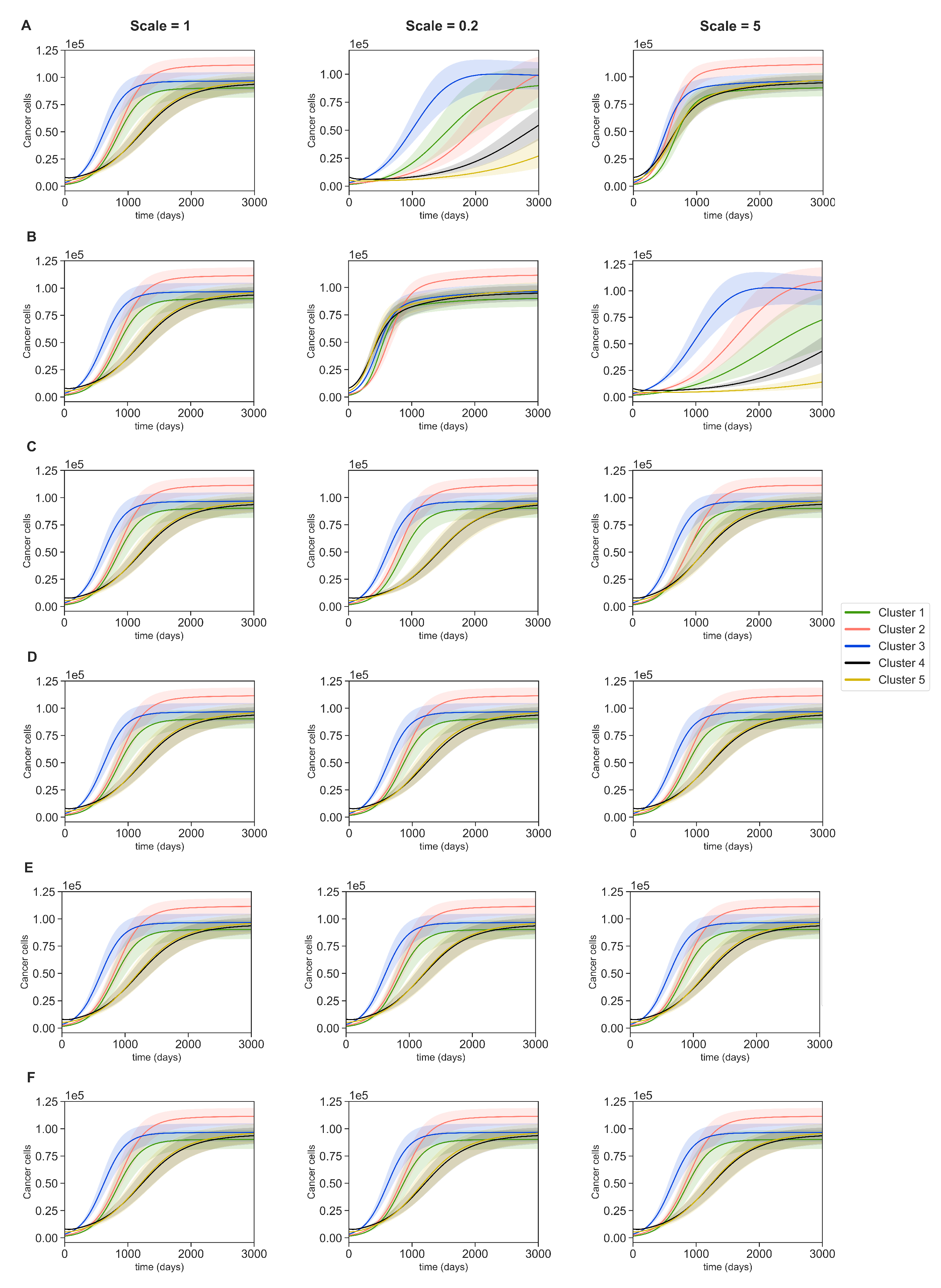
3.4. Dynamics with Varying Assumptions
3.5. Dynamics with Different Initial Conditions
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TCGA | The Cancer Genome Atlas |
| METABRIC | Molecular Taxonomy of Breast Cancer International Consortium |
| HMGB1 | High mobility group box-1 |
| LumA | Luminal A |
| LumB | Luminal B |
| TNBC | Triple negative breast cancer |
| IFN- | Interferon gamma |
| HER2 | Human epidermal growth factor 2 |
| ER | Estrogen receptor |
| DAMP | Damage-associated molecular pattern |
| UCSC | University of Santa Cruz |
Appendix A. Derivation of Sample Parameters
Appendix A.1. Steady State and Additional Assumptions
Appendix A.2. Non-Dimensionalization
Appendix A.3. Parameter Values
| Parameter | Value | Reference | Parameter | Value | Reference |
|---|---|---|---|---|---|
| [71] | 18 | [71,121] | |||
| 0.231 | [71] | 4.16 | [122] | ||
| 0.406 | [71] | 1.07 | [71] | ||
| 0.406 | [71] | 4.62 | [71] | ||
| 0.277 | [71] | 128 | [123] | ||
| 0.0198 | [71] | 33.3 | [71] | ||
| [125] |
| Parameter | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 |
|---|---|---|---|---|---|
Appendix A.4. Dynamics with Varying Initial Conditions
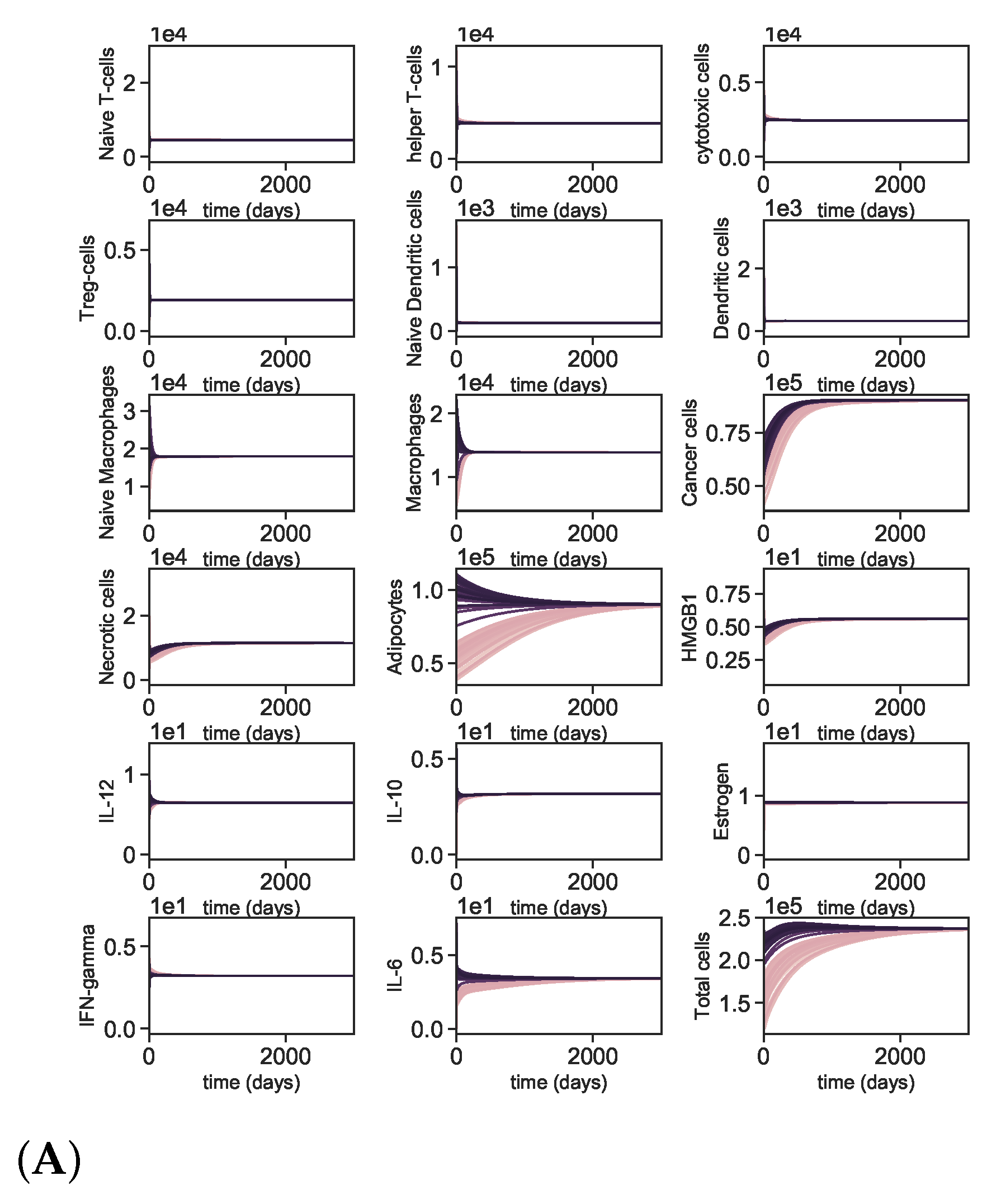
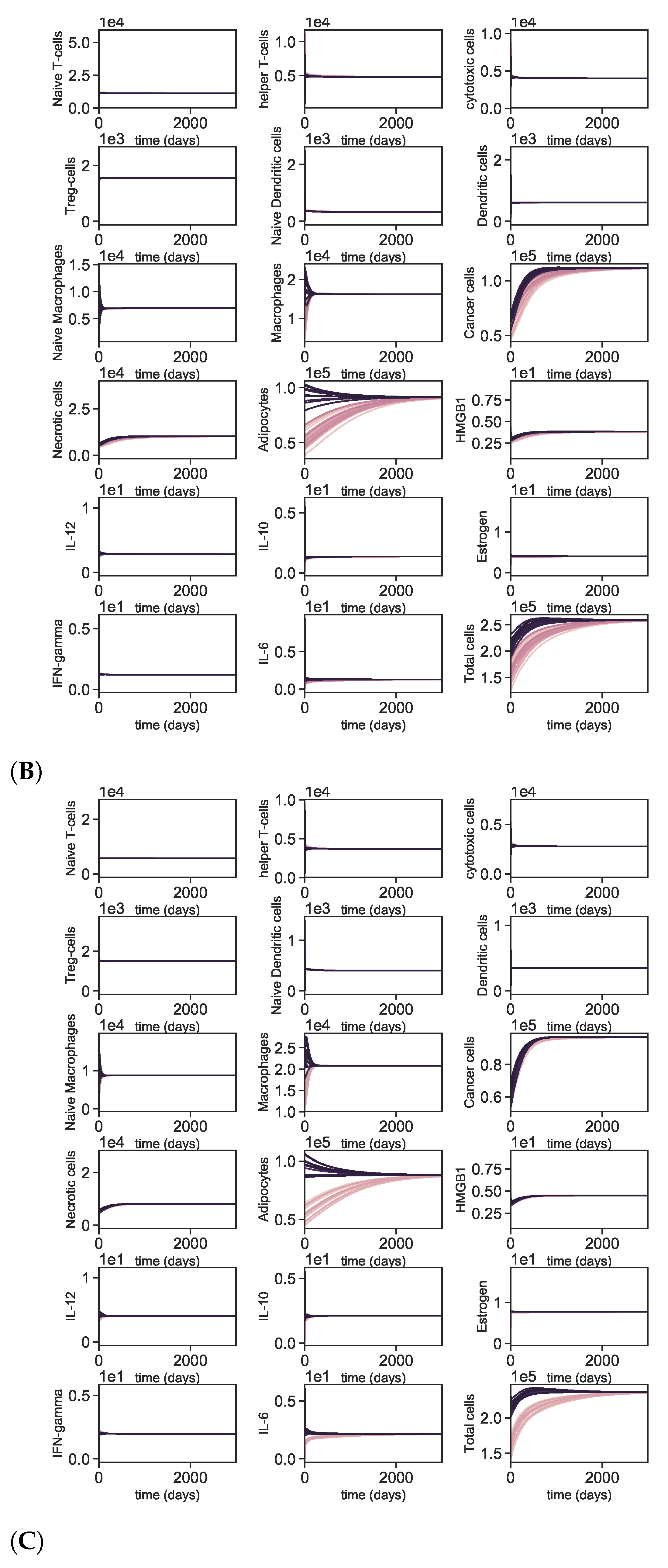
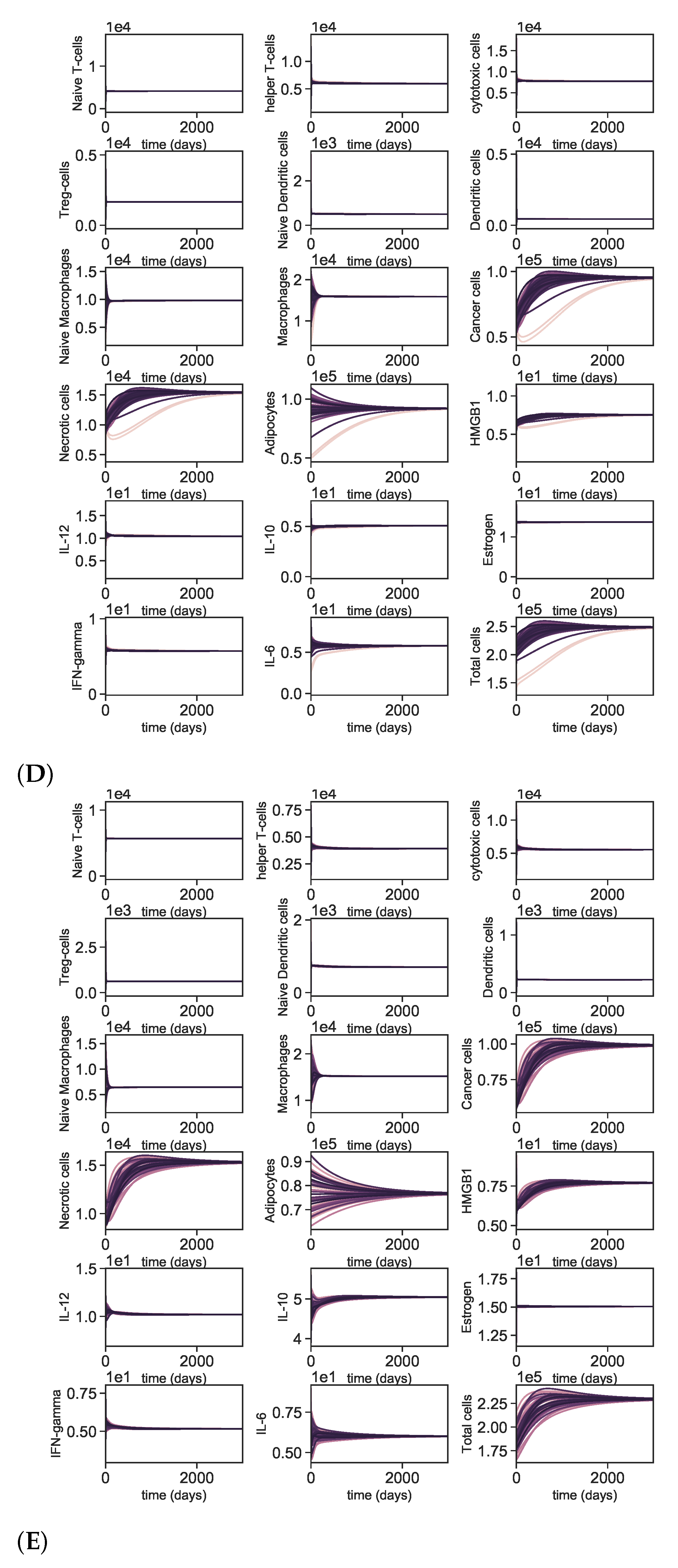
Appendix A.5. Dynamics of the Tumor Microenvironment with Cross-Cluster Initial Conditions
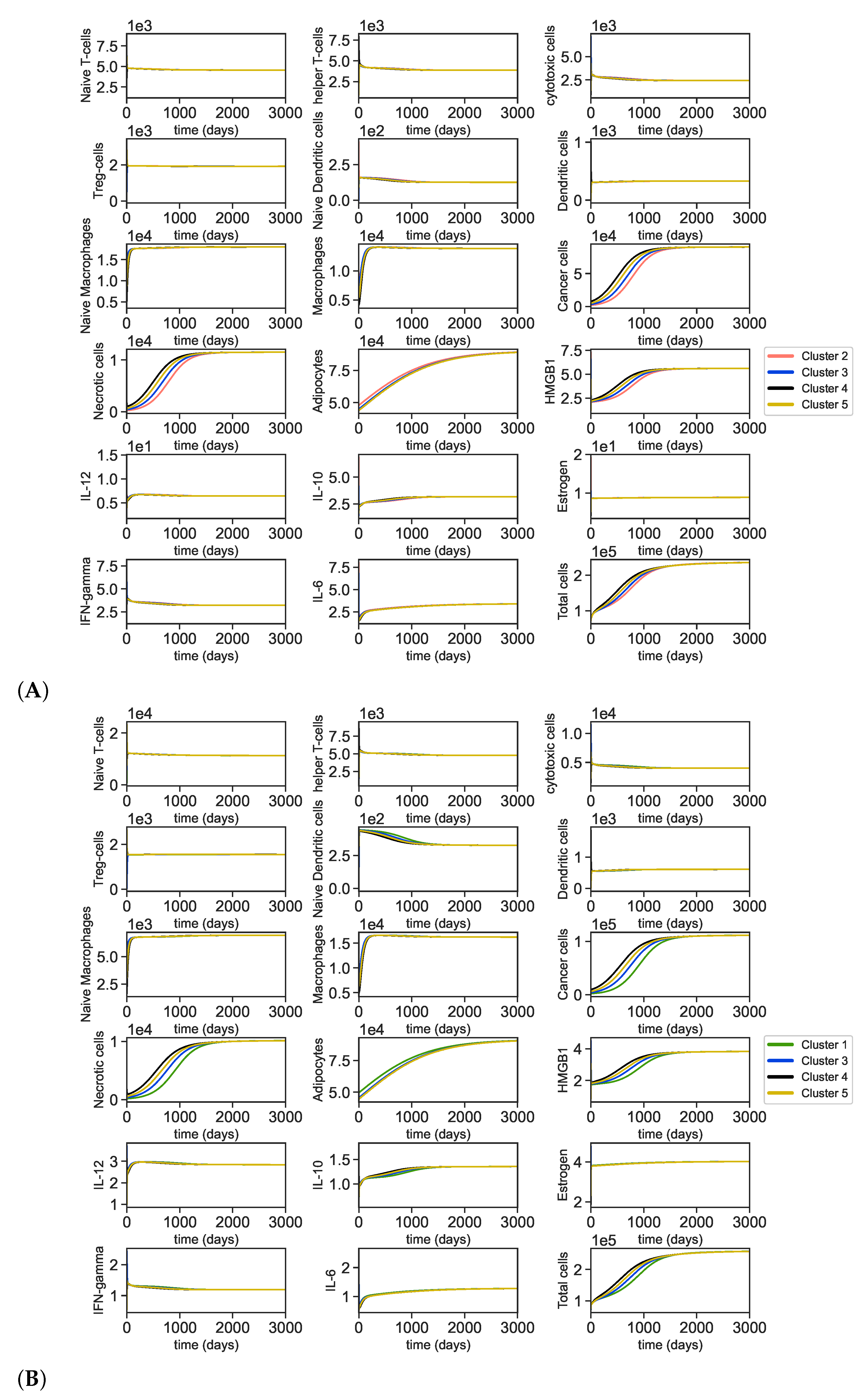
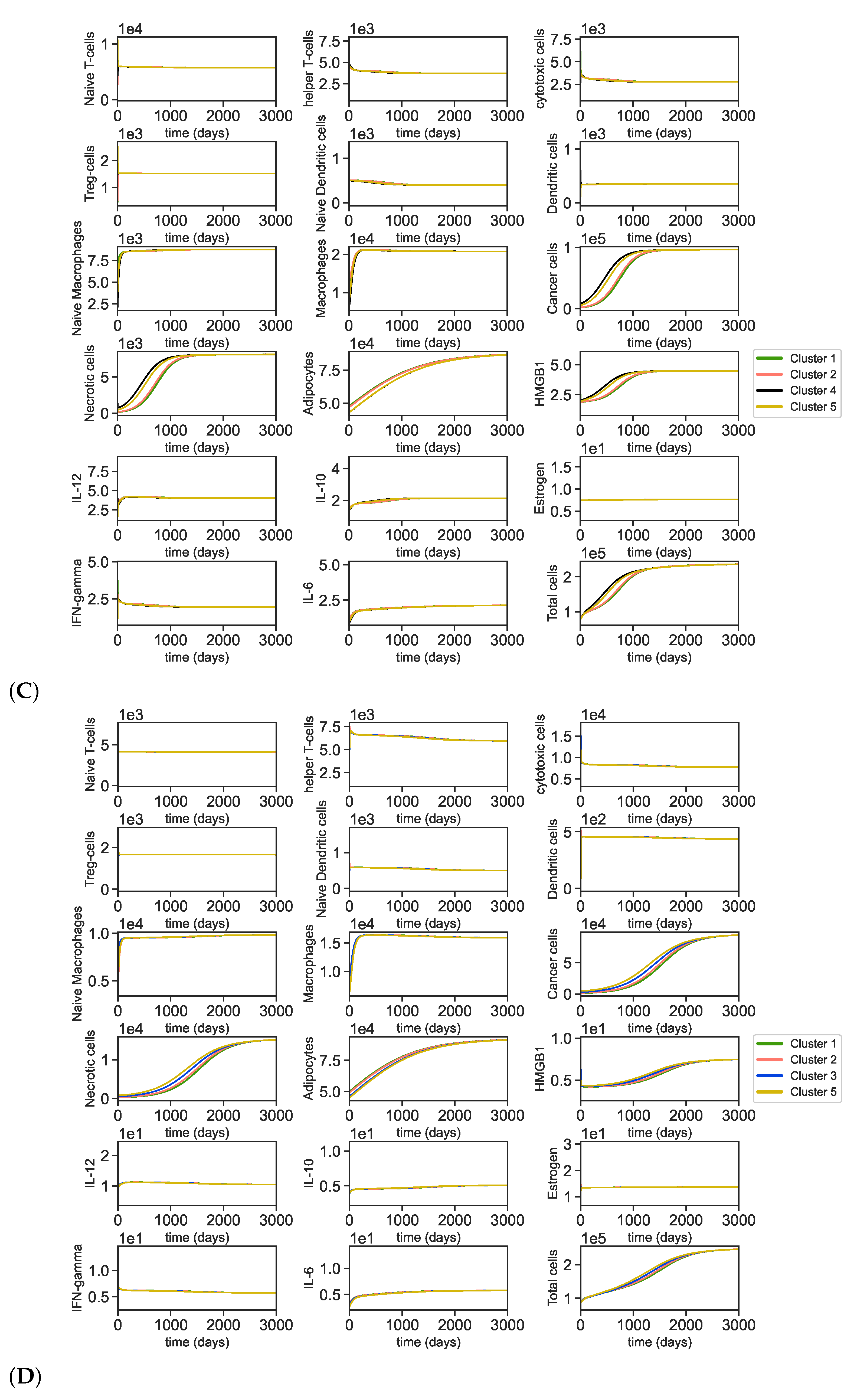
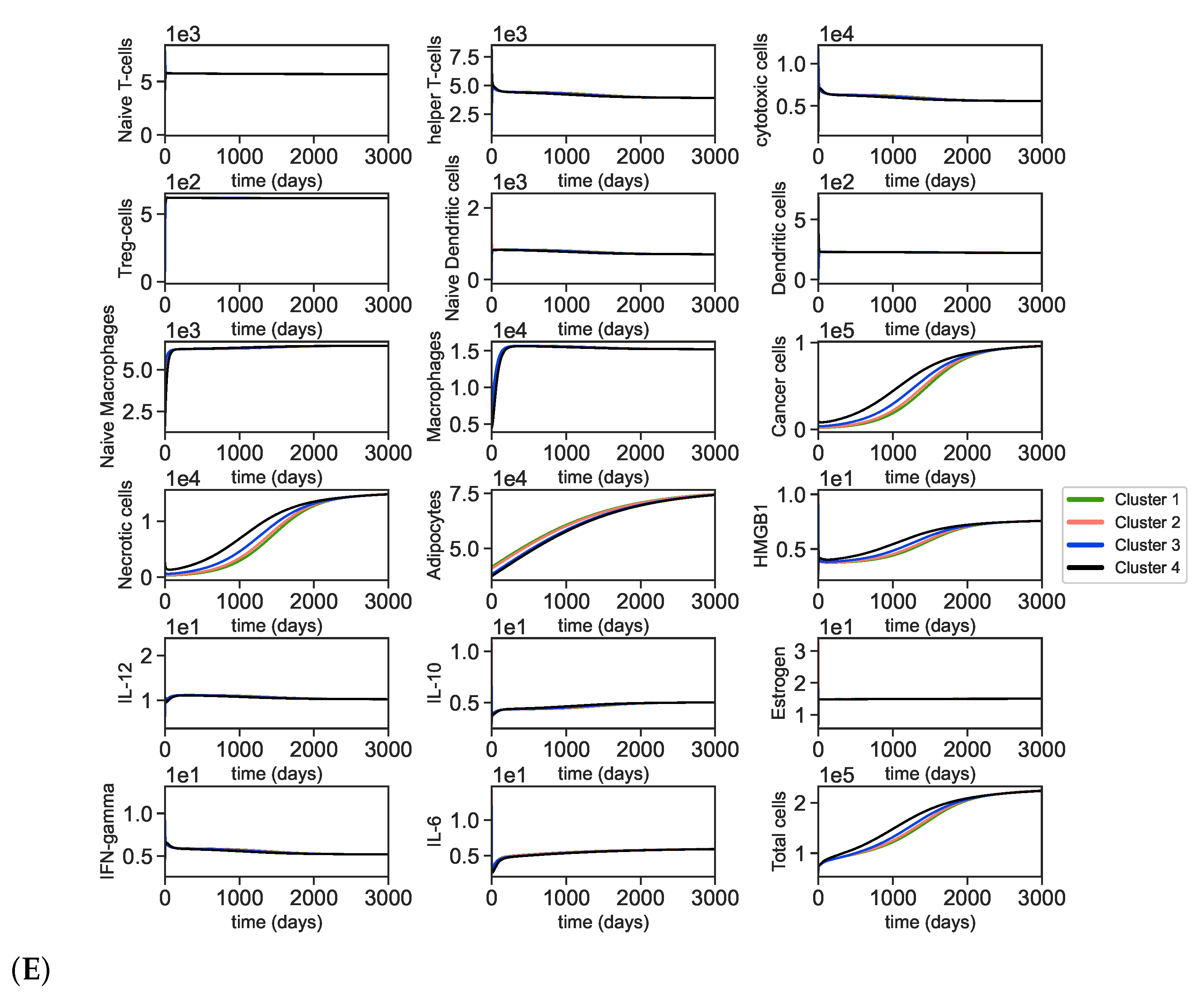
Appendix A.6. Bifurcation and Lyapunov Exponent for the Cancer ODE

Appendix A.7. Positivity
References
- About Breast Cancer. Available online: https://www.cancer.org/cancer/breast-cancer/about/how-common-is-breast-cancer.html (accessed on 20 May 2021).
- Harbeck, N.; Penault-Llorca, F.; Cortes, J.; Gnant, M.; Houssami, N.; Poortmans, P.; Ruddy, K.; Tsang, J.; Cardoso, F. Breast cancer. Nat. Rev. Dis. Prim. 2019, 5, 66. [Google Scholar] [CrossRef] [PubMed]
- Engstrøm, M.J.; Opdahl, S.; Hagen, A.I.; Romundstad, P.R.; Akslen, L.A.; Haugen, O.A.; Vatten, L.J.; Bofin, A.M. Molecular subtypes, histopathological grade and survival in a historic cohort of breast cancer patients. Breast Cancer Res. Treat. 2013, 140, 463–473. [Google Scholar] [CrossRef]
- Venkitaraman, R. Triple-negative/basal-like breast cancer: Clinical, pathologic and molecular features. Expert Rev. Anticancer Ther. 2010, 10, 199–207. [Google Scholar] [CrossRef]
- Bai, X.; Ni, J.; Beretov, J.; Graham, P.; Li, Y. Cancer stem cell in breast cancer therapeutic resistance. Cancer Treat. Rev. 2018, 69, 152–163. [Google Scholar] [CrossRef]
- Masoud, V.; Pagès, G. Targeted therapies in breast cancer: New challenges to fight against resistance. World J. Clin. Oncol. 2017, 8, 120. [Google Scholar] [CrossRef] [PubMed]
- Vagia, E.; Mahalingam, D.; Cristofanilli, M. The Landscape of Targeted Therapies in TNBC. Cancers 2020, 12, 916. [Google Scholar] [CrossRef]
- Nedeljković, M.; Damjanović, A. Mechanisms of Chemotherapy Resistance in Triple-Negative Breast Cancer—How We Can Rise to the Challenge. Cells 2019, 8, 957. [Google Scholar] [CrossRef]
- Kim, C.; Gao, R.; Sei, E.; Brandt, R.; Hartman, J.; Hatschek, T.; Crosetto, N.; Foukakis, T.; Navin, N.E. Chemoresistance Evolution in Triple-Negative Breast Cancer Delineated by Single-Cell Sequencing. Cell 2018, 173, 879–893.e13. [Google Scholar] [CrossRef]
- Place, A.E.; Jin Huh, S.; Polyak, K. The microenvironment in breast cancer progression: Biology and implications for treatment. Breast Cancer Res. 2011, 13, 1–11. [Google Scholar] [CrossRef]
- Korkaya, H.; Liu, S.; Wicha, M.S. Breast cancer stem cells, cytokine networks, and the tumor microenvironment. J. Clin. Investig. 2011, 121, 3804–3809. [Google Scholar] [CrossRef] [PubMed]
- Soysal, S.D.; Tzankov, A.; Muenst, S.E. Role of the Tumor Microenvironment in Breast Cancer. Pathobiology 2015, 82, 142–152. [Google Scholar] [CrossRef]
- Mittal, S.; Brown, N.J.; Holen, I. The breast tumor microenvironment: Role in cancer development, progression and response to therapy. Expert Rev. Mol. Diagn. 2018, 18, 227–243. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Dai, Y. Tumor microenvironment and therapeutic response. Cancer Lett. 2017, 387, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Palucka, K.; Banchereau, J. Cancer immunotherapy via dendritic cells. Nat. Rev. Cancer 2012, 12, 265–277. [Google Scholar] [CrossRef]
- Palucka, K.; Coussens, L.M.; O’Shaughnessy, J. Dendritic cells, inflammation, and breast cancer. Cancer J. (Sudbury, Mass.) 2013, 19, 511–516. [Google Scholar] [CrossRef]
- Tran Janco, J.M.; Lamichhane, P.; Karyampudi, L.; Knutson, K.L. Tumor-Infiltrating Dendritic Cells in Cancer Pathogenesis. J. Immunol. 2015, 194, 2985–2991. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Jiang, A. Dendritic Cells and CD8 T Cell Immunity in Tumor Microenvironment. Front. Immunol. 2018, 9, 3059. [Google Scholar] [CrossRef]
- Segovia-Mendoza, M.; Morales-Montor, J. Immune Tumor Microenvironment in Breast Cancer and the Participation of Estrogen and Its Receptors in Cancer Physiopathology. Front. Immunol. 2019, 10, 348. [Google Scholar] [CrossRef]
- Melssen, M.; Slingluff, C.L. Vaccines Targeting Helper T Cells for Cancer Immunotherapy. Curr. Opin. Immunol. 2017, 47, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Ni, L.; Lu, J. Interferon gamma in cancer immunotherapy. Cancer Med. 2018, 7, 4509–4516. [Google Scholar] [CrossRef]
- Moon, B.I.; Kim, T.H.; Seoh, J.Y. Functional Modulation of Regulatory T Cells by IL-2. PLoS ONE 2015, 10, e0141864. [Google Scholar] [CrossRef]
- Lai, X.; Stiff, A.; Duggan, M.; Wesolowski, R.; Carson, W.E.; Friedman, A. Modeling combination therapy for breast cancer with BET and immune checkpoint inhibitors. Proc. Natl. Acad. Sci. USA 2018, 115, 5534–5539. [Google Scholar] [CrossRef]
- Obeid, E.; Nanda, R.; Fu, Y.X.; Olopade, O.I. The role of tumor-associated macrophages in breast cancer progression (review). Int. J. Oncol. 2013, 43, 5–12. [Google Scholar] [CrossRef]
- Bingle, L.; Brown, N.J.; Lewis, C.E. The role of tumour-associated macrophages in tumour progression: Implications for new anticancer therapies. J. Pathol. 2002, 196, 254–265. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.; Provenzano, E.; Dawson, S.J.; Blows, F.; Liu, B.; Shah, M.; Earl, H.; Poole, C.; Hiller, L.; Dunn, J.; et al. Association between CD8+ T-cell infiltration and breast cancer survival in 12 439 patients. Ann. Oncol. 2014, 25, 1536–1543. [Google Scholar] [CrossRef]
- Ali, H.R.; Chlon, L.; Pharoah, P.D.P.; Markowetz, F.; Caldas, C. Patterns of Immune Infiltration in Breast Cancer and Their Clinical Implications: A Gene-Expression-Based Retrospective Study. PLoS Med. 2016, 13, e1002194. [Google Scholar] [CrossRef]
- Wang, Z.K.; Yang, B.; Liu, H.; Hu, Y.; Yang, J.L.; Wu, L.L.; Zhou, Z.H.; Jiao, S.C. Regulatory T cells increase in breast cancer and in stage IV breast cancer. Cancer Immunol. Immunother. 2012, 61, 911–916. [Google Scholar] [CrossRef]
- Shahriyari, L.; Komarova, N.L. Symmetric vs. asymmetric stem cell divisions: An adaptation against cancer? PLoS ONE 2013, 8, e76195. [Google Scholar] [CrossRef]
- Butner, J.D.; Wang, Z.; Elganainy, D.; Al Feghali, K.A.; Plodinec, M.; Calin, G.A.; Dogra, P.; Nizzero, S.; Ruiz-Ramírez, J.; Martin, G.V.; et al. A mathematical model for the quantification of a patient’s sensitivity to checkpoint inhibitors and long-term tumour burden. Nat. Biomed. Eng. 2021, 5, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Shahriyari, L.; Komarova, N.L. The role of the bi-compartmental stem cell niche in delaying cancer. Phys. Biol. 2015, 12, 055001. [Google Scholar] [CrossRef] [PubMed]
- Shahriyari, L. Cell dynamics in tumour environment after treatments. J. R. Soc. Interface 2017, 14, 20160977. [Google Scholar] [CrossRef] [PubMed]
- Chamseddine, I.M.; Rejniak, K.A. Hybrid modeling frameworks of tumor development and treatment. Wiley Interdiscip. Rev. Syst. Biol. Med. 2019, 12, e1461. [Google Scholar] [CrossRef] [PubMed]
- McKenna, M.T.; Weis, J.A.; Barnes, S.L.; Tyson, D.R.; Miga, M.I.; Quaranta, V.; Yankeelov, T.E. A Predictive Mathematical Modeling Approach for the Study of Doxorubicin Treatment in Triple Negative Breast Cancer. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef]
- Shahriyari, L.; Mahdipour-Shirayeh, A. Modeling dynamics of mutants in heterogeneous stem cell niche. Phys. Biol. 2017, 14, 016004. [Google Scholar] [CrossRef] [PubMed]
- Mehdizadeh, R.; Shariatpanahi, S.P.; Goliaei, B.; Peyvandi, S.; Rüegg, C. Dormant tumor cell vaccination: A mathematical model of immunological dormancy in triple-negative breast cancer. Cancers 2021, 13, 245. [Google Scholar] [CrossRef]
- Budithi, A.; Su, S.; Kirshtein, A.; Shahriyari, L. Data driven mathematical model of FOLFIRI treatment for colon cancer. Cancers 2021, 13, 2632. [Google Scholar] [CrossRef]
- Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Atangana, A. A fractional mathematical model of breast cancer competition model. Chaos Solitons Fractals 2019, 127, 38–54. [Google Scholar] [CrossRef]
- Wodarz, D.; Komarova, N. Dynamics of Cancer: Mathematical Foundations of Oncology; World Scientific Publishing Company: Singapore, 2014. [Google Scholar]
- Chakrabarti, A.; Verbridge, S.; Stroock, A.D.; Fischbach, C.; Varner, J.D. Multiscale models of breast cancer progression. Ann. Biomed. Eng. 2012, 40, 2488–2500. [Google Scholar] [CrossRef]
- Abernathy, K.; Abernathy, Z.; Baxter, A.; Stevens, M. Global dynamics of a breast cancer competition model. Differ. Equ. Dyn. Syst. 2020, 28, 791–805. [Google Scholar] [CrossRef]
- Knútsdóttir, H.; Pálsson, E.; Edelstein-Keshet, L. Mathematical model of macrophage-facilitated breast cancer cells invasion. J. Theor. Biol. 2014, 357, 184–199. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, A.M.; Bloom, M.J.; Godfrey, W.; Syed, A.K.; Ekrut, D.A.; Ehrlich, L.I.; Yankeelov, T.E.; Sorace, A.G. Mathematical modelling of trastuzumab-induced immune response in an in vivo murine model of HER2+ breast cancer. Math. Med. Biol. A J. IMA 2019, 36, 381–410. [Google Scholar] [CrossRef] [PubMed]
- Roe-Dale, R.; Isaacson, D.; Kupferschmid, M. A Mathematical Model of Breast Cancer Treatment with CMF and Doxorubicin. Bull. Math. Biol. 2011, 73, 585–608. [Google Scholar] [CrossRef]
- Wei, H.C. Mathematical modeling of tumor growth: The MCF-7 breast cancer cell line. Math. Biosci. Eng. 2019, 16, 6512–6535. [Google Scholar] [CrossRef]
- Johnston, M.D.; Edwards, C.M.; Bodmer, W.F.; Maini, P.K.; Chapman, S.J. Mathematical modeling of cell population dynamics in the colonic crypt and in colorectal cancer. Proc. Natl. Acad. Sci. USA 2007, 104, 4008–4013. [Google Scholar] [CrossRef]
- Lewin, T.D.; Byrne, H.M.; Maini, P.K.; Caudell, J.J.; Moros, E.G.; Enderling, H. The importance of dead material within a tumour on the dynamics in response to radiotherapy. Phys. Med. Biol. 2020, 65, 015007. [Google Scholar] [CrossRef]
- Lewin, T.D.; Maini, P.K.; Moros, E.G.; Enderling, H.; Byrne, H.M. A three phase model to investigate the effects of dead material on the growth of avascular tumours. Math. Model. Nat. Phenom. 2020, 15, 22. [Google Scholar] [CrossRef]
- Friedman, A.; Hao, W. The Role of Exosomes in Pancreatic Cancer Microenvironment. Bull. Math. Biol. 2018, 80, 1111–1133. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Crouser, E.D.; Friedman, A. Mathematical model of sarcoidosis. Proc. Natl. Acad. Sci. USA 2014, 111, 16065–16070. [Google Scholar] [CrossRef]
- Enderling, H.; Chaplain, M.A.J.; Anderson, A.R.A.; Vaidya, J.S. A mathematical model of breast cancer development, local treatment and recurrence. J. Theor. Biol. 2007, 246, 245–259. [Google Scholar] [CrossRef]
- Anderson, A.R.; Chaplain, M.A.; Newman, E.L.; Steele, R.J.; Thompson, A.M. Mathematical modelling of tumour invasion and metastasis. J. Theor. Med. 2000, 2, 129–154. [Google Scholar] [CrossRef]
- Dumitriu, I.E.; Baruah, P.; Valentinis, B.; Voll, R.E.; Herrmann, M.; Nawroth, P.P.; Arnold, B.; Bianchi, M.E.; Manfredi, A.A.; Rovere-Querini, P. Release of High Mobility Group Box 1 by Dendritic Cells Controls T Cell Activation via the Receptor for Advanced Glycation End Products. J. Immunol. 2005, 174, 7506–7515. [Google Scholar] [CrossRef]
- Bell, R.B.; Feng, Z.; Bifulco, C.B.; Leidner, R.; Weinberg, A.; Fox, B.A. 15-Immunotherapy. In Oral, Head and Neck Oncology and Reconstructive Surgery; Elsevier: Amsterdam, The Netherlands, 2018; pp. 314–340. [Google Scholar]
- Wang, K.; Vella, A.T. Regulatory T Cells and Cancer: A Two-Sided Story. Immunol. Investig. 2016, 45, 797–812. [Google Scholar] [CrossRef]
- Mohammad, I.; Starskaia, I.; Nagy, T.; Guo, J.; Yatkin, E.; Väänänen, K.; Watford, W.T.; Chen, Z. Estrogen receptor α contributes to T cell mediated autoimmune inflammation by promoting T cell activation and proliferation. Sci. Signal. 2018, 11. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Shurin, G.V.; Peiyuan, Z.; Shurin, M.R. Dendritic cells in the cancer microenvironment. J. Cancer 2013, 4, 36–44. [Google Scholar] [CrossRef]
- Luo, C.Y.; Wang, L.; Sun, C.; Li, D.J. Estrogen enhances the functions of CD4+CD25+Foxp3+ regulatory T cells that suppress osteoclast differentiation and bone resorption in vitro. Cell. Mol. Immunol. 2011, 8, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Kang, R.; Zeh, H.J.; Lotze, M.T. High-mobility Group Box 1 [HMGB1] and Cancer. Biochim. Biophys. Acta 2010, 1799, 131–140. [Google Scholar] [CrossRef]
- Lee, S.Y.; Ju, M.K.; Jeon, H.M.; Jeong, E.K.; Lee, Y.J.; Kim, C.H.; Park, H.G.; Han, S.I.; Kang, H.S. Regulation of Tumor Progression by Programmed Necrosis. Oxidative Med. Cell. Longev. 2018, 2018, 3537471. [Google Scholar] [CrossRef]
- Apetoh, L.; Ghiringhelli, F.; Tesniere, A.; Criollo, A.; Ortiz, C.; Lidereau, R.; Mariette, C.; Chaput, N.; Mira, J.P.; Delaloge, S.; et al. The interaction between HMGB1 and TLR4 dictates the outcome of anticancer chemotherapy and radiotherapy. Immunol. Rev. 2007, 220, 47–59. [Google Scholar] [CrossRef]
- Aras, S.; Zaidi, M.R. TAMeless traitors: Macrophages in cancer progression and metastasis. Br. J. Cancer 2017, 117, 1583–1591. [Google Scholar] [CrossRef] [PubMed]
- Sica, A.; Saccani, A.; Mantovani, A. Tumor-associated macrophages: A molecular perspective. Int. Immunopharmacol. 2002, 2, 1045–1054. [Google Scholar] [CrossRef]
- Tariq, M.; Zhang, J.; Liang, G.; Ding, L.; He, Q.; Yang, B. Macrophage Polarization: Anti-Cancer Strategies to Target Tumor-Associated Macrophage in Breast Cancer. J. Cell. Biochem. 2017, 118, 2484–2501. [Google Scholar] [CrossRef] [PubMed]
- Chanmee, T.; Ontong, P.; Konno, K.; Itano, N. Tumor-Associated Macrophages as Major Players in the Tumor Microenvironment. Cancers 2014, 6, 1670–1690. [Google Scholar] [CrossRef]
- Wu, Q.; Li, B.; Li, Z.; Li, J.; Sun, S.; Sun, S. Cancer-associated adipocytes: Key players in breast cancer progression. J. Hematol. Oncol. 2019, 12, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Keller, E.T.; Garfield, D.H.; Shen, K.; Wang, J. Stroma Cells in Tumor Microenvironment and Breast Cancer. Cancer Metastasis Rev. 2013, 32, 303–315. [Google Scholar] [CrossRef]
- Chu, D.T.; Phuong, T.N.T.; Tien, N.L.B.; Tran, D.K.; Nguyen, T.T.; Thanh, V.V.; Quang, T.L.; Minh, L.B.; Pham, V.H.; Ngoc, V.T.N.; et al. The Effects of Adipocytes on the Regulation of Breast Cancer in the Tumor Microenvironment: An Update. Cells 2019, 8, 857. [Google Scholar] [CrossRef]
- Neel, J.C.; Humbert, L.; Lebrun, J.J. The dual role of TGFβ in human cancer: From tumor suppression to cancer metastasis. Int. Sch. Res. Not. 2012, 2012, 381428. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Y.; Attané, C.; Milhas, D.; Dirat, B.; Dauvillier, S.; Guerard, A.; Gilhodes, J.; Lazar, I.; Alet, N.; Laurent, V.; et al. Mammary adipocytes stimulate breast cancer invasion through metabolic remodeling of tumor cells. JCI Insight 2017, 2, e87489. [Google Scholar] [CrossRef]
- Kirshtein, A.; Akbarinejad, S.; Hao, W.; Le, T.; Su, S.; Aronow, R.A.; Shahriyari, L. Data Driven Mathematical Model of Colon Cancer Progression. J. Clin. Med. 2020, 9, 3947. [Google Scholar] [CrossRef]
- Rubartelli, A.; Lotze, M.T. Inside, outside, upside down: Damage-associated molecular-pattern molecules (DAMPs) and redox. Trends Immunol. 2007, 28, 429–436. [Google Scholar] [CrossRef]
- Li, G.; Liang, X.; Lotze, M.T. HMGB1: The Central Cytokine for All Lymphoid Cells. Front. Immunol. 2013, 4, 68. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y. HMGB1 in inflammation and cancer. J. Hematol. Oncol. 2020, 13, 116. [Google Scholar] [CrossRef]
- Bonaldi, T.; Talamo, F.; Scaffidi, P.; Ferrera, D.; Porto, A.; Bachi, A.; Rubartelli, A.; Agresti, A.; Bianchi, M.E. Monocytic cells hyperacetylate chromatin protein HMGB1 to redirect it towards secretion. EMBO J. 2003, 22, 5551–5560. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Shi, Y.; Kang, R.; Li, T.; Xiao, W.; Wang, H.; Xiao, X. Hydrogen peroxide stimulates macrophages and monocytes to actively release HMGB1. J. Leukoc. Biol. 2007, 81, 741–747. [Google Scholar] [CrossRef]
- Semino, C.; Angelini, G.; Poggi, A.; Rubartelli, A. NK/iDC interaction results in IL-18 secretion by DCs at the synaptic cleft followed by NK cell activation and release of the DC maturation factor HMGB1. Blood 2005, 106, 609–616. [Google Scholar] [CrossRef] [PubMed]
- Gougeon, M.L.; Bras, M. Natural killer cells, dendritic cells, and the alarmin high-mobility group box 1 protein: A dangerous trio in HIV-1 infection? Curr. Opin. HIV AIDS 2011, 6, 364–372. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, H.; Cheng, Y.; Jiang, X.; Zhu, J.; Jin, T. Double roles of macrophages in human neuroimmune diseases and their animal models. Mediat. Inflamm. 2016, 2016, 8489251. [Google Scholar] [CrossRef]
- Hart, A.L.; Al-Hassi, H.O.; Rigby, R.J.; Bell, S.J.; Emmanuel, A.V.; Knight, S.C.; Kamm, M.A.; Stagg, A.J. Characteristics of intestinal dendritic cells in inflammatory bowel diseases. Gastroenterology 2005, 129, 50–65. [Google Scholar] [CrossRef]
- Iwasaki, A.; Kelsall, B.L. Freshly isolated Peyer’s patch, but not spleen, dendritic cells produce interleukin 10 and induce the differentiation of T helper type 2 cells. J. Exp. Med. 1999, 190, 229–240. [Google Scholar] [CrossRef]
- Couper, K.N.; Blount, D.G.; Riley, E.M. IL-10: The master regulator of immunity to infection. J. Immunol. 2008, 180, 5771–5777. [Google Scholar] [CrossRef] [PubMed]
- Trinchieri, G. Interleukin-10 production by effector T cells: Th1 cells show self control. J. Exp. Med. 2007, 204, 239–243. [Google Scholar] [CrossRef]
- Mufudza, C.; Sorofa, W.; Chiyaka, E.T. Assessing the Effects of Estrogen on the Dynamics of Breast Cancer. Comput. Math. Methods Med. 2012, 2012, e473572. [Google Scholar] [CrossRef]
- Simpson, E.R. Sources of estrogen and their importance. J. Steroid Biochem. Mol. Biol. 2003, 86, 225–230. [Google Scholar] [CrossRef]
- Nakaya, M.; Tachibana, H.; Yamada, K. Effect of estrogens on the interferon-γ producing cell population of mouse splenocytes. Biosci. Biotechnol. Biochem. 2006, 70, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Clark, R.K.; McDonnell, P.C.; Young, P.R.; White, R.F.; Barone, F.C.; Feuerstein, G.Z. Tumor necrosis factor-alpha expression in ischemic neurons. Stroke 1994, 25, 1481–1488. [Google Scholar] [CrossRef] [PubMed]
- Newman, A.M.; Steen, C.B.; Liu, C.L.; Gentles, A.J.; Chaudhuri, A.A.; Scherer, F.; Khodadoust, M.S.; Esfahani, M.S.; Luca, B.A.; Steiner, D.; et al. Determining cell type abundance and expression from bulk tissues with digital cytometry. Nat. Biotechnol. 2019, 37, 773–782. [Google Scholar] [CrossRef] [PubMed]
- Le, T.; Aronow, R.A.; Kirshtein, A.; Shahriyari, L. A review of digital cytometry methods: Estimating the relative abundance of cell types in a bulk of cells. Brief. Bioinform. 2021, 22, bbaa219. [Google Scholar] [CrossRef]
- Su, S.; Akbarinejad, S.; Shahriyari, L. Immune classification of clear cell renal cell carcinoma. Sci. Rep. 2021, 11, 4338. [Google Scholar] [CrossRef] [PubMed]
- Le, T.; Su, S.; Shahriyari, L. Immune classification of osteosarcoma. Math. Biosci. Eng. 2021, 18, 1879–1897. [Google Scholar] [CrossRef]
- The Cancer Genome Atlas Network. Comprehensive molecular portraits of human breast tumours. Nature 2012, 490, 61–70. [Google Scholar] [CrossRef]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef]
- Cerami, E.; Gao, J.; Dogrusoz, U.; Gross, B.E.; Sumer, S.O.; Aksoy, B.A.; Jacobsen, A.; Byrne, C.J.; Heuer, M.L.; Larsson, E.; et al. The cBio Cancer Genomics Portal: An Open Platform for Exploring Multidimensional Cancer Genomics Data: Figure 1. Cancer Discov. 2012, 2, 401–404. [Google Scholar] [CrossRef] [PubMed]
- Goldman, M.J.; Craft, B.; Hastie, M.; Repečka, K.; McDade, F.; Kamath, A.; Banerjee, A.; Luo, Y.; Rogers, D.; Brooks, A.N.; et al. Visualizing and interpreting cancer genomics data via the Xena platform. Nat. Biotechnol. 2020, 38, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Friedman, A. Interaction of Tumor with Its Micro-environment: A Mathematical Model. Bull. Math. Biol. 2010, 72, 1029–1068. [Google Scholar] [CrossRef] [PubMed]
- Heiss, F.; Winschel, V. Likelihood approximation by numerical integration on sparse grids. J. Econom. 2008, 144, 62–80. [Google Scholar] [CrossRef]
- Gerstner, T.; Griebel, M. Numerical integration using sparse grids. Numer. Algorithms 1998, 18, 209–232. [Google Scholar] [CrossRef]
- Punt, J. Chapter 4—Adaptive Immunity: T Cells and Cytokines. In Cancer Immunotherapy, 2nd ed.; Prendergast, G.C., Jaffee, E.M., Eds.; Academic Press: San Diego, CA, USA, 2013; pp. 41–53. [Google Scholar]
- Qiu, S.Q.; Waaijer, S.J.; Zwager, M.C.; de Vries, E.G.; van der Vegt, B.; Schröder, C.P. Tumor-associated macrophages in breast cancer: Innocent bystander or important player? Cancer Treat. Rev. 2018, 70, 178–189. [Google Scholar] [CrossRef]
- Keegan, T.H.; DeRouen, M.C.; Press, D.J.; Kurian, A.W.; Clarke, C.A. Occurrence of breast cancer subtypes in adolescent and young adult women. Breast Cancer Res. 2012, 14, R55. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.M.J.; Mills, G.B.; Ram, P.T. Cancer Systems Biology: A peek into the future of patient care? Nat. Rev. Clin. Oncol. 2014, 11, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Bekisz, S.; Geris, L. Cancer modeling: From mechanistic to data-driven approaches, and from fundamental insights to clinical applications. J. Comput. Sci. 2020, 46, 101198. [Google Scholar] [CrossRef]
- Heymann, M.F.; Heymann, D. Immune environment and osteosarcoma. In Osteosarcoma-Biology, Behavior and Mechanisms; InTech: London, UK, 2017; pp. 105–120. [Google Scholar]
- Griguolo, G.; Pascual, T.; Dieci, M.V.; Guarneri, V.; Prat, A. Interaction of host immunity with HER2-targeted treatment and tumor heterogeneity in HER2-positive breast cancer. J. ImmunoTherapy Cancer 2019, 7, 1–14. [Google Scholar] [CrossRef]
- Le, T.; Su, S.; Kirshtein, A.; Shahriyari, L. Data-Driven Mathematical Model of Osteosarcoma. Cancers 2021, 13, 2367. [Google Scholar] [CrossRef]
- Asano, Y.; Kashiwagi, S.; Goto, W.; Kurata, K.; Noda, S.; Takashima, T.; Onoda, N.; Tanaka, S.; Ohsawa, M.; Hirakawa, K. Tumour-infiltrating CD8 to FOXP3 lymphocyte ratio in predicting treatment responses to neoadjuvant chemotherapy of aggressive breast cancer. Br. J. Surg. 2016, 103, 845–854. [Google Scholar] [CrossRef]
- Yasuda, K.; Nirei, T.; Sunami, E.; Nagawa, H.; Kitayama, J. Density of CD4 (+) and CD8 (+) T lymphocytes in biopsy samples can be a predictor of pathological response to chemoradiotherapy (CRT) for rectal cancer. Radiat. Oncol. 2011, 6, 1–6. [Google Scholar] [CrossRef]
- Riemann, D.; Hase, S.; Fischer, K.; Seliger, B. Granulocyte-to-dendritic cell-ratio as marker for the immune monitoring in patients with renal cell carcinoma. Clin. Transl. Med. 2014, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]
- García-Tuñón, I.; Ricote, M.; Ruiz, A.; Fraile, B.; Paniagua, R.; Royuela, M. Influence of IFN-gamma and its receptors in human breast cancer. BMC Cancer 2007, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Gooch, J.L.; Herrera, R.E.; Yee, D. The role of p21 in interferon gamma-mediated growth inhibition of human breast cancer cells. Cell Growth Differ. Mol. Biol. J. Am. Assoc. Cancer Res. 2000, 11, 335–342. [Google Scholar]
- Ning, Y.; Riggins, R.; Mulla, J.; Chung, H.; Zwart, A.; Clarke, R. Interferon gamma restores breast cancer sensitivity to Fulvestrant by regulating STAT1, IRF1, NFkB, BCL2 family members and signaling to a caspase-dependent apoptosis. Mol Cancer Ther 2010, 9, 1274–1285. [Google Scholar] [CrossRef]
- Kopreski, M.S.; Lipton, A.; Harvey, H.A.; Kumar, R. Growth inhibition of breast cancer cell lines by combinations of anti-P185HER2 monoclonal antibody and cytokines. Anticancer Res. 1996, 16, 433–436. [Google Scholar]
- Bhat, P.; Leggatt, G.; Waterhouse, N.; Frazer, I.H. Interferon-γ derived from cytotoxic lymphocytes directly enhances their motility and cytotoxicity. Cell Death Dis. 2017, 8, e2836. [Google Scholar] [CrossRef]
- Zhao, Q.; Tong, L.; He, N.; Feng, G.; Leng, L.; Sun, W.; Xu, Y.; Wang, Y.; Xiang, R.; Li, Z. IFN-γ mediates graft-versus-breast cancer effects via enhancing cytotoxic T lymphocyte activity. Exp. Ther. Med. 2014, 8, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Chen, X.; He, Q.; Gimple, R.C.; Liao, Y.; Wang, L.; Wu, R.; Xie, Q.; Rich, J.N.; Shen, K.; et al. Adipocytes promote breast tumorigenesis through TAZ-dependent secretion of Resistin. Proc. Natl. Acad. Sci. USA 2020, 117, 33295–33304. [Google Scholar] [CrossRef]
- Voss, A.; Voss, J. A fast numerical algorithm for the estimation of diffusion model parameters. J. Math. Psychol. 2008, 52, 1–9. [Google Scholar] [CrossRef]
- Parra-Rojas, C.; Hernandez-Vargas, E.A. PDEparams: Parameter fitting toolbox for partial differential equations in python. Bioinformatics 2020, 36, 2618–2619. [Google Scholar] [CrossRef]
- Vyshemirsky, V.; Girolami, M. BioBayes: A software package for Bayesian inference in systems biology. Bioinformatics 2008, 24, 1933–1934. [Google Scholar] [CrossRef]
- Xun, X.; Cao, J.; Mallick, B.; Maity, A.; Carroll, R.J. Parameter estimation of partial differential equation models. J. Am. Stat. Assoc. 2013, 108, 1009–1020. [Google Scholar] [CrossRef] [PubMed]
- Zandarashvili, L.; Sahu, D.; Lee, K.; Lee, Y.S.; Singh, P.; Rajarathnam, K.; Iwahara, J. Real-time Kinetics of High-mobility Group Box 1 (HMGB1) Oxidation in Extracellular Fluids Studied by in Situ Protein NMR Spectroscopy. J. Biol. Chem. 2013, 288, 11621–11627. [Google Scholar] [CrossRef] [PubMed]
- Valley, C.C.; Solodin, N.M.; Powers, G.L.; Ellison, S.J.; Alarid, E.T. Temporal variation in estrogen receptor-? protein turnover in the presence of estrogen. J. Mol. Endocrinol. 2008, 40, 2334. [Google Scholar] [CrossRef][Green Version]
- Lee, S.M.; Suen, Y.; Chang, L.; Bruner, V.; Qian, J.; Indes, J.; Knoppel, E.; van de Ven, C.; Cairo, M.S. Decreased interleukin-12 (IL-12) from activated cord versus adult peripheral blood mononuclear cells and upregulation of interferon- gamma, natural killer, and lymphokine-activated killer activity by IL- 12 in cord blood mononuclear cells. Blood 1996, 88, 945–954. [Google Scholar] [CrossRef]
- Scherer, P.E. The many secret lives of adipocytes: Implications for diabetes. Diabetologia 2019, 62, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Strawford, A.; Antelo, F.; Christiansen, M.; Hellerstein, M. Adipose tissue triglyceride turnover, de novo lipogenesis, and cell proliferation in humans measured with 2H2O. Am. J. Physiol.-Endocrinol. Metab. 2004, 286, E577–E588. [Google Scholar] [CrossRef]
- Ryu, E.B.; Chang, J.M.; Seo, M.; Kim, S.A.; Lim, J.H.; Moon, W.K. Tumour volume doubling time of molecular breast cancer subtypes assessed by serial breast ultrasound. Eur. Radiol. 2014, 24, 2227–2235. [Google Scholar] [CrossRef]
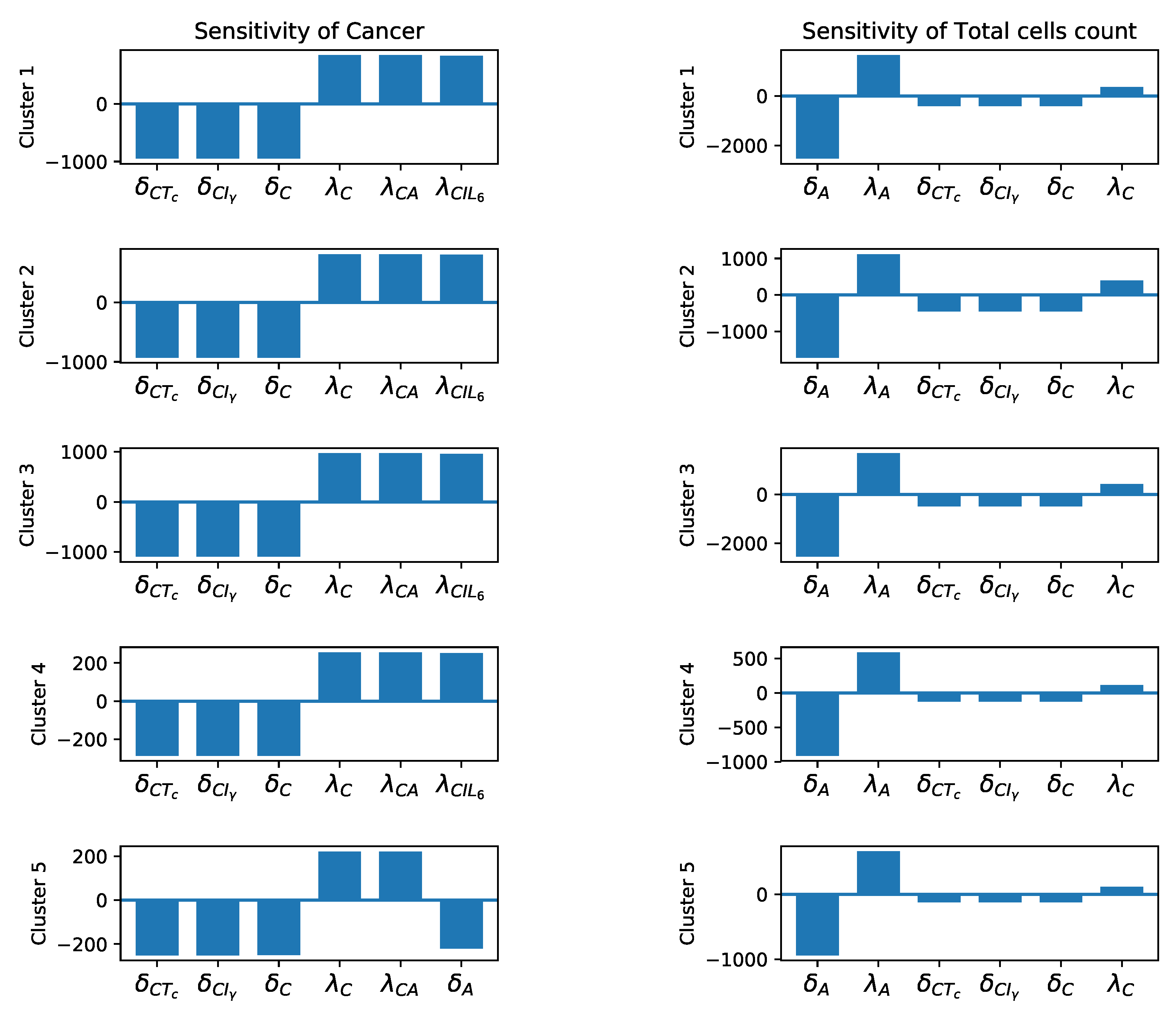
| Variable | Name | Data Used |
|---|---|---|
| Naive T-cells | Combination of CD4 naive and memory resting T-cells and resting NK cells | |
| Helper T-cells | Combination of memory activated CD4 T-cells and follicular helper T-cells | |
| Cytotoxic cells | Combination of CD8 T-cells and activated NK cells | |
| Regulatory T-cells | Regulatory T-cells | |
| Naive dendritic cells | Naive dendritic cells | |
| D | Activated dendritic cells | Activated dendritic cells |
| Naive Macrophages | Combination of Macrophages M0 and Monocytes | |
| M | Macrophages | Combination of M1 and M2 Macrophages |
| C | Cancer cells | Estimated |
| N | Necrotic cells | Estimated |
| A | Cancer Associated Adipocytes | Assumed to be twice the total number of immune cells |
| H | HMGB1 | HMGB1 gene expression |
| IL-12 | IL12A and IL12B gene expressions | |
| IL-10 | IL10 gene expression | |
| E | Estrogen | ESR1 and ESR2 gene expressions |
| IFN- | IFNG gene expressions | |
| IL-6 | IL6 gene expression |
| Cluster | D | M | C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
| Cluster | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
| Clusters | Without Scaling | Scale = 0.2 | Scale = 5 |
|---|---|---|---|
| Cluster 1 | |||
| Cluster 2 | |||
| Cluster 3 | |||
| Cluster 4 | |||
| Cluster 5 |
| Cluster | Without Scaling | Scale = 0.2 | Scale = 5 |
|---|---|---|---|
| Cluster 1 | |||
| Cluster 2 | |||
| Cluster 3 | |||
| Cluster 4 | |||
| Cluster 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad Mirzaei, N.; Su, S.; Sofia, D.; Hegarty, M.; Abdel-Rahman, M.H.; Asadpoure, A.; Cebulla, C.M.; Chang, Y.H.; Hao, W.; Jackson, P.R.; et al. A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration. J. Pers. Med. 2021, 11, 1031. https://doi.org/10.3390/jpm11101031
Mohammad Mirzaei N, Su S, Sofia D, Hegarty M, Abdel-Rahman MH, Asadpoure A, Cebulla CM, Chang YH, Hao W, Jackson PR, et al. A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration. Journal of Personalized Medicine. 2021; 11(10):1031. https://doi.org/10.3390/jpm11101031
Chicago/Turabian StyleMohammad Mirzaei, Navid, Sumeyye Su, Dilruba Sofia, Maura Hegarty, Mohamed H. Abdel-Rahman, Alireza Asadpoure, Colleen M. Cebulla, Young Hwan Chang, Wenrui Hao, Pamela R. Jackson, and et al. 2021. "A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration" Journal of Personalized Medicine 11, no. 10: 1031. https://doi.org/10.3390/jpm11101031
APA StyleMohammad Mirzaei, N., Su, S., Sofia, D., Hegarty, M., Abdel-Rahman, M. H., Asadpoure, A., Cebulla, C. M., Chang, Y. H., Hao, W., Jackson, P. R., Lee, A. V., Stover, D. G., Tatarova, Z., Zervantonakis, I. K., & Shahriyari, L. (2021). A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration. Journal of Personalized Medicine, 11(10), 1031. https://doi.org/10.3390/jpm11101031






