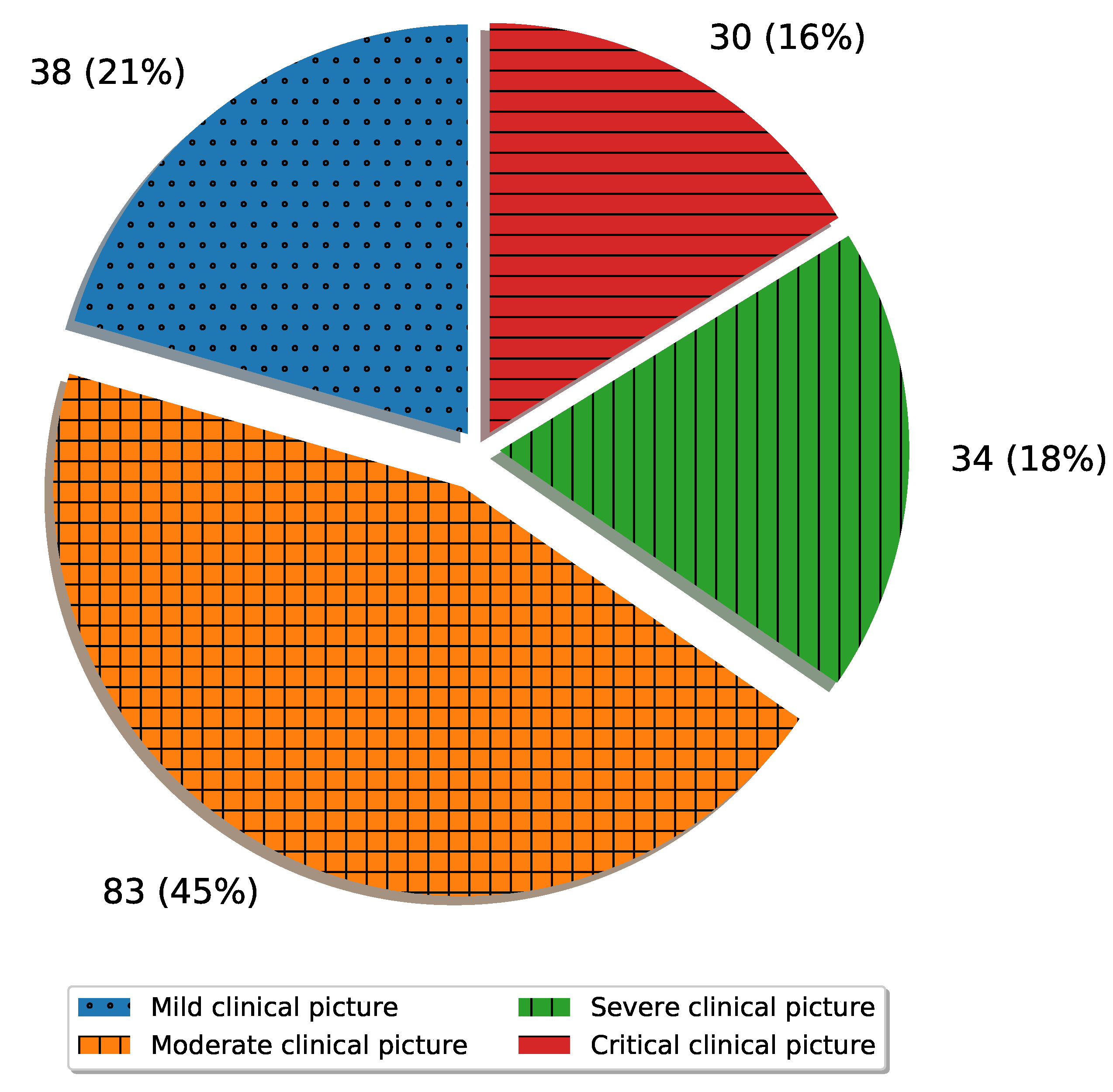
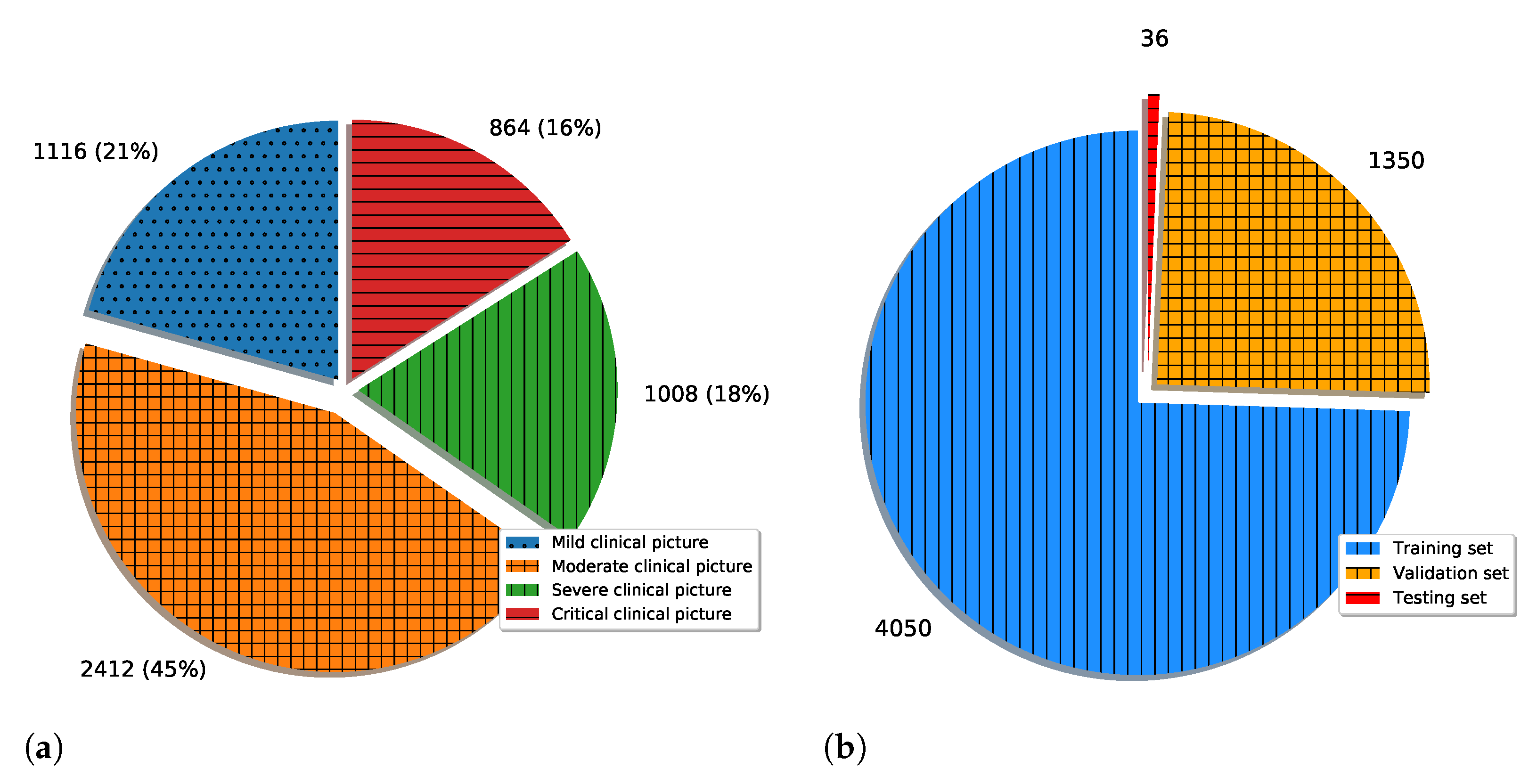
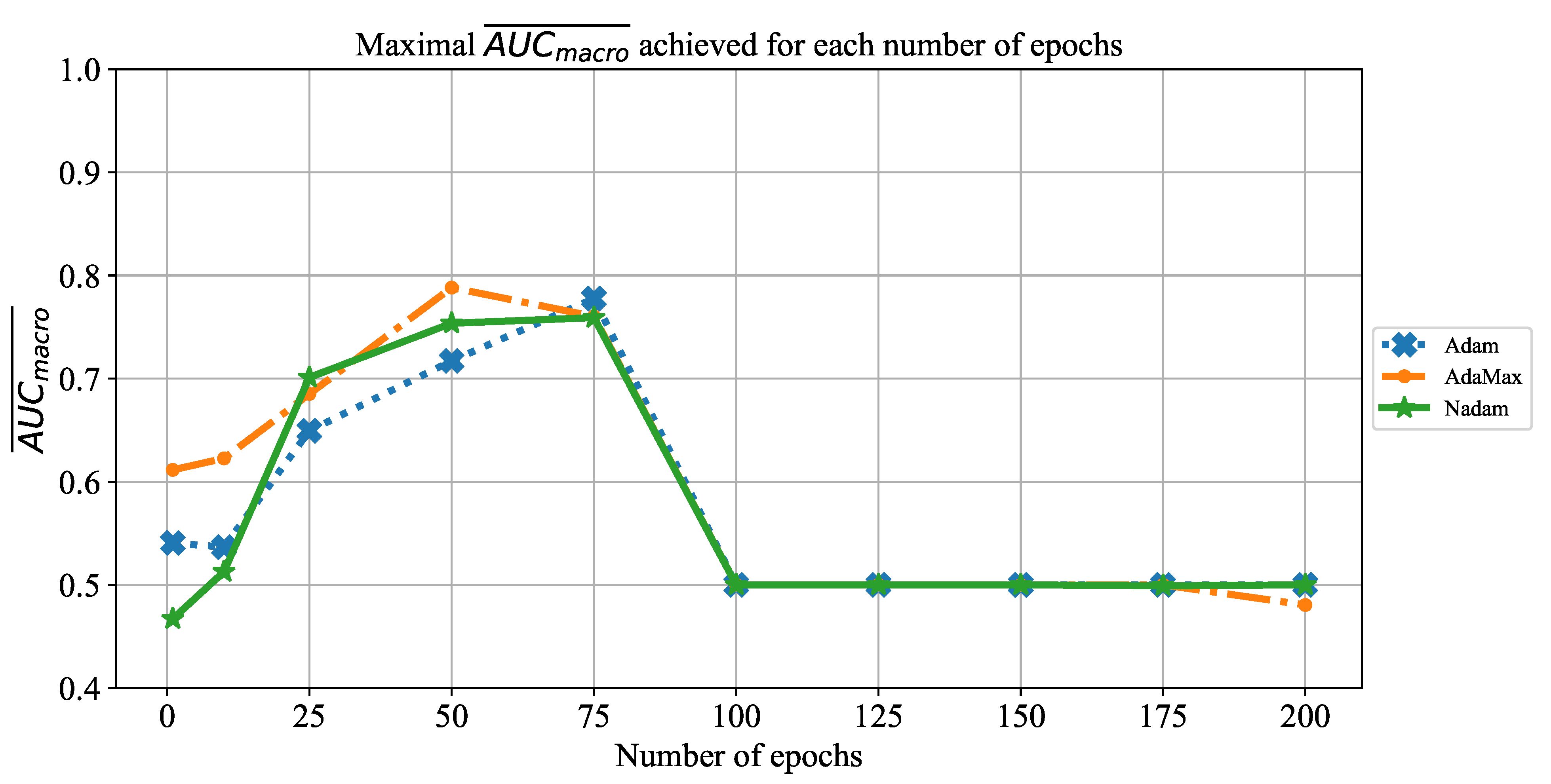
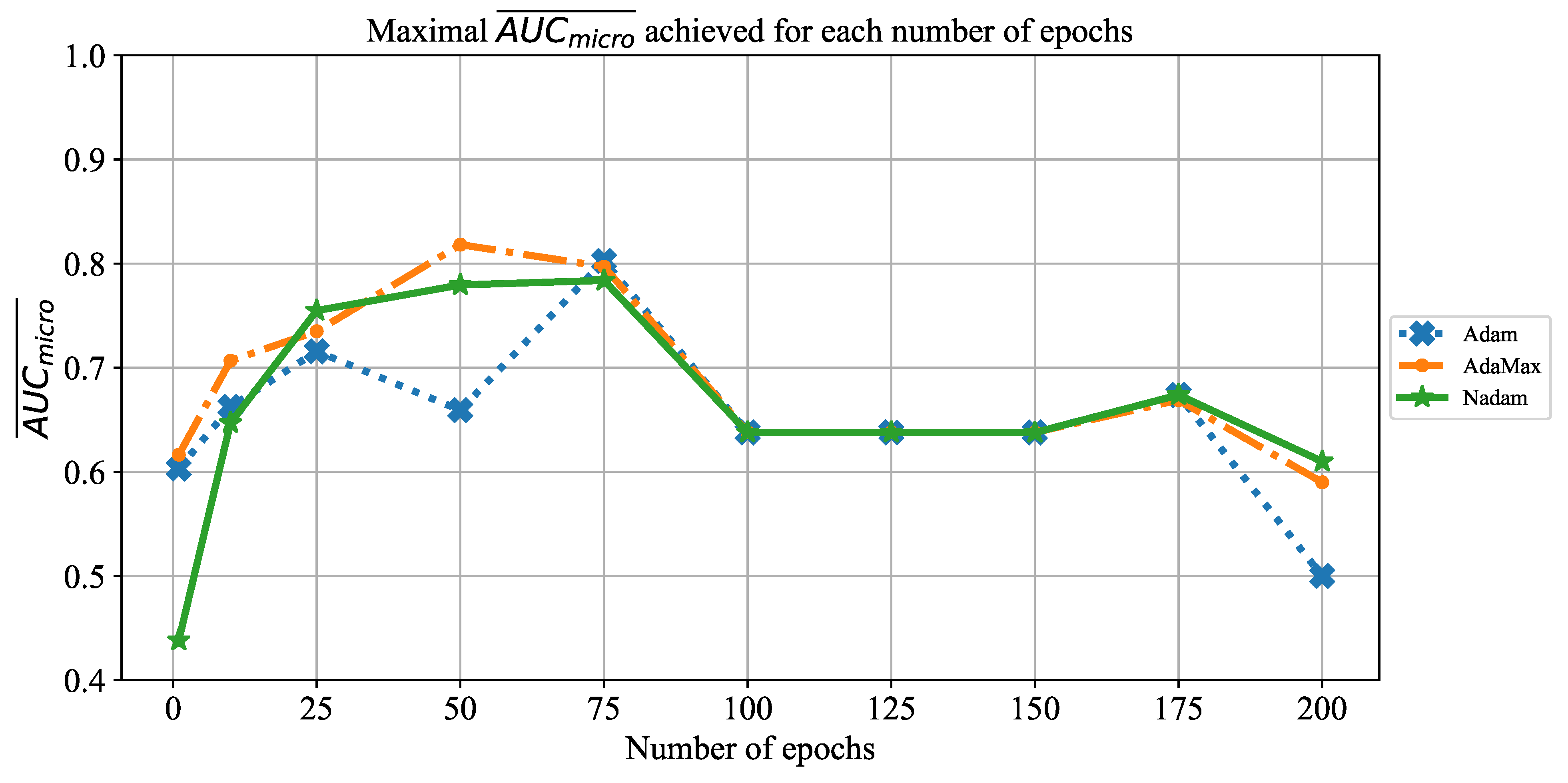
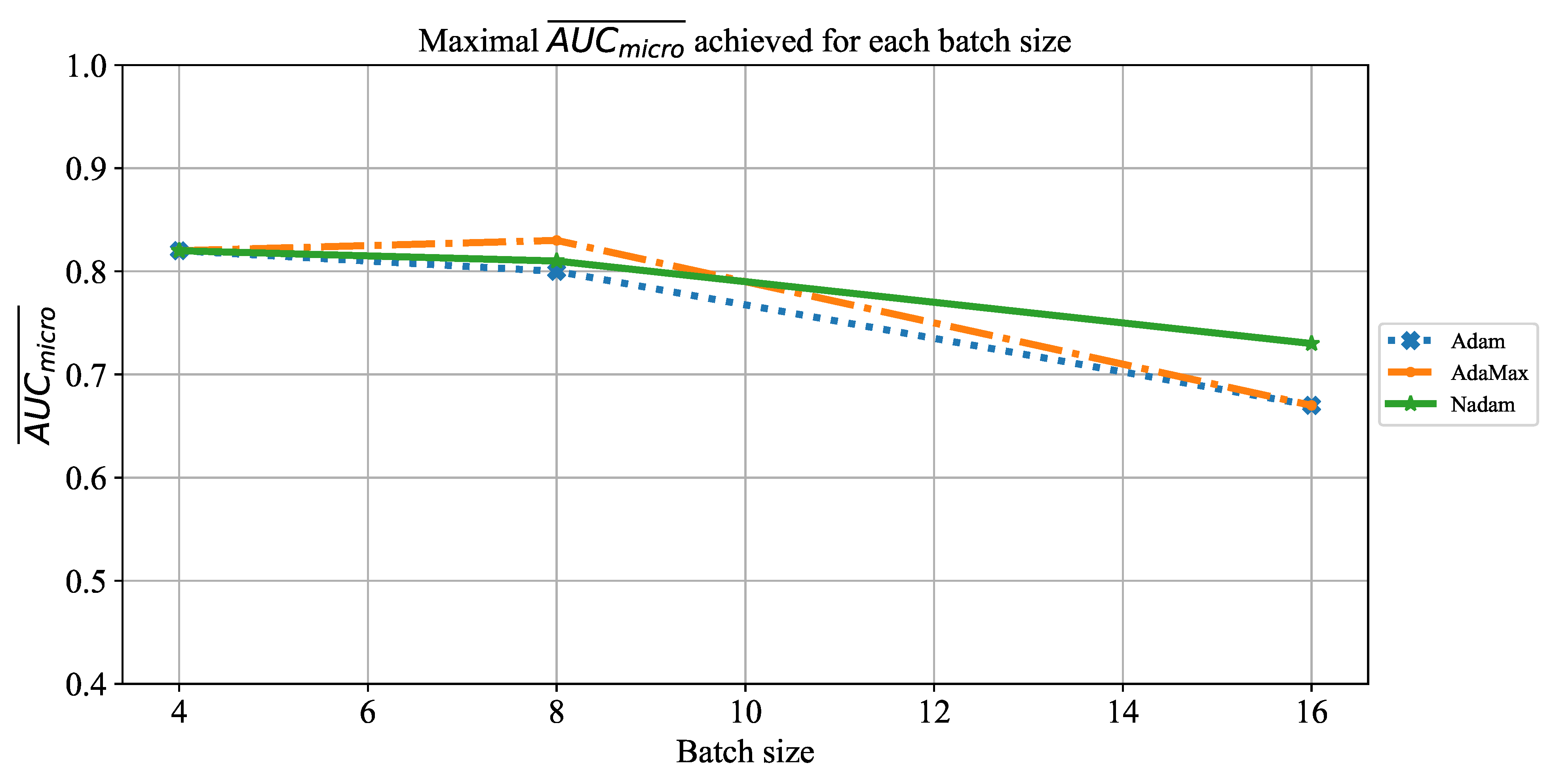
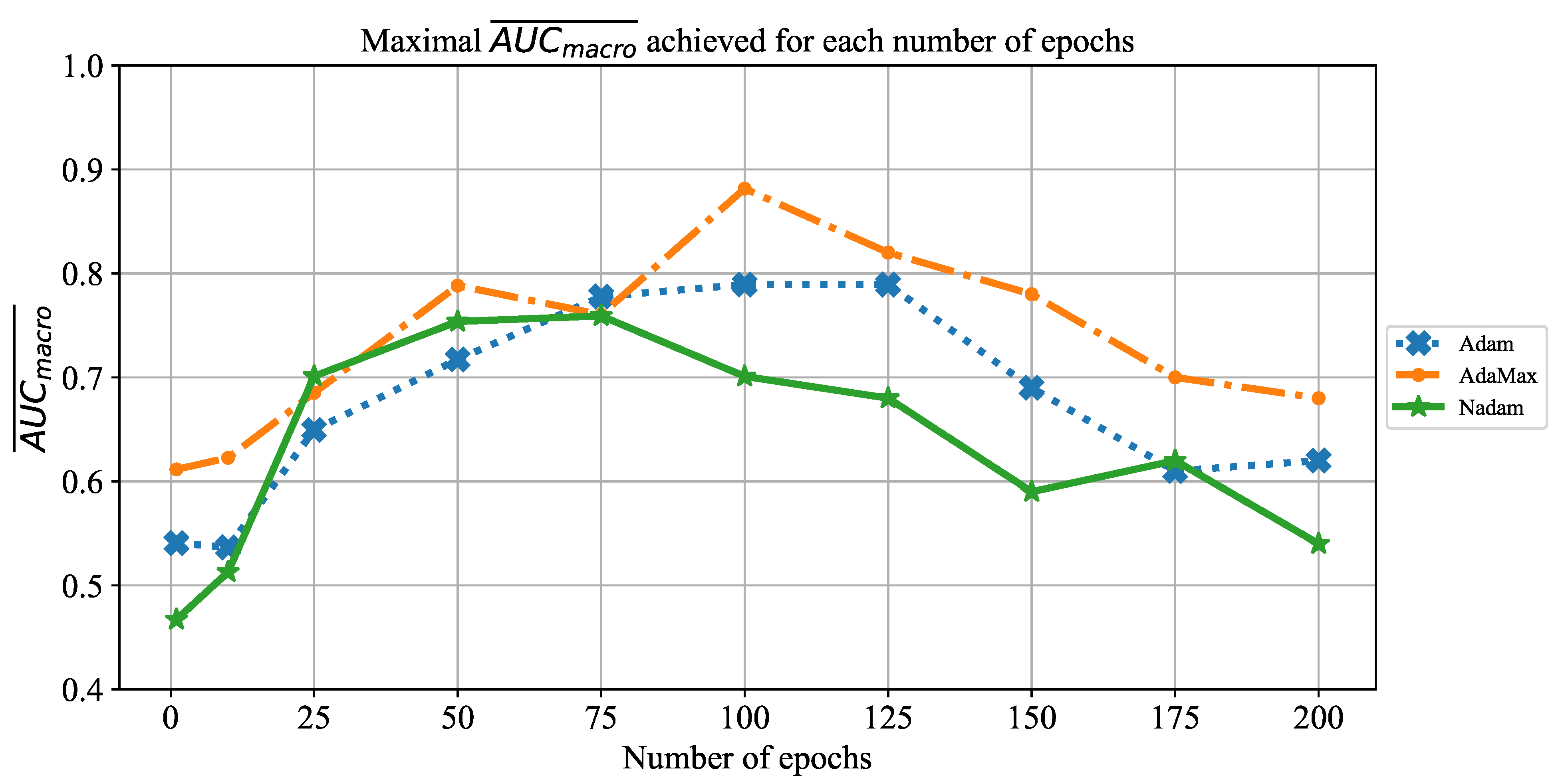
1. Introduction
The Coronavirus disease 2019 (COVID-19) caused by Severe Acute Respiratory Syndrome virus 2 (SARS-CoV-2) is a viral, respiratory lung disease [
1]. The spread of COVID-19 has been rapid, and it has affected the daily lives of millions across the globe. The dangers it poses are well-known [
2], with the most important ones being its relatively high severity and mortality rate [
3] and the strain it exhibits on the healthcare systems of countries worldwide [
4,
5]. Another problematic characteristic that COVID-19 exhibits is a wide variation in severity across the patients, which can cause issues for healthcare workers who wish to determine an appropriate individual treatment plan [
6]. Early determination of the severity of COVID-19 may be vital in securing the needed resources—such as planning the location for hospitalization of the patient or respiratory aids in case they may be necessary. There is a dire need for systems that will allow for the strain put on the resources of the healthcare systems, as well as healthcare workers, by allowing easier classification of patient case severity in early stages of hospitalization. Artificial intelligence (AI) techniques have already been proven to be a useful tool in the fight against COVID-19 [
7,
8], so the possibility exists of them being applied in this area as well. Existence of such algorithms may lower the strain on the potentially scarce resources, by allowing early planning and allocation. Additionally, they may provide decision support to overworked healthcare professionals.
Internet of Medical Things (IoMT) is a medical paradigm that allows for integration of modern technologies in the existing healthcare system [
9]. The algorithms developed as a part of the presented research can be made available to health professionals using IoMT [
10]. Models obtained using the described methodology can be integrated inside a pipeline system in which an X-ray image will automatically be processed using the developed models, and the predicted class of the patient whose image has been obtained will immediately be delivered to the medical professional examining the X-ray. Such automated diagnosis methods have already been applied in many studies, such as in histopathology [
11], neurological disorders [
12], urology [
13], and retinology [
14]. All the researchers agree that not only can such AI-based support systems provide an extremely precise diagnosis, but can also be integrated in automatic systems to provide assistance to medical experts in determining the correct diagnosis. The obtained models are suited for such an approach. While the training of the models is slow due to the backpropagation process, the classification (using forward propagation) is fast and computationally moderate [
15,
16], allowing for easy integration into existing in-hospital systems.
The machine learning diagnostic approach has been successfully applied to X-ray images a number of times in the past. For example, Lujan–Garcia et al. (2020) [
17] demonstrated the application of CNNs for the detection of pneumonia using chest X-ray images using Xception CNN, which was pre-trained using a ImageNet dataset for initial values. The evaluation was performed using precision, recall, F1 score, and AUROC, with the achieved scores being 0.84, 0.99, 0.91, and 0.97, respectively. Kieu et al. (2020) [
18] demonstrated the Multi-CNN approach to the detection of abnormalities on the chest X-ray images. The approach presented in the paper demonstrates the use of multiple CNNs to determine the class of the input image, with the hybrid system presented achieving an accuracy of
. Bullock et al. (2019) [
19] presented XNet—a CNN solution designed for medical, X-ray image segmentation. The presented solution is suitable for small datasets, and achieves high scores (
accuracy, F1 score of 0.92 and AUC of 0.98) on the used dataset. Takemiya et al. (2019) [
20] demonstrated the use of R-CNNs (Region with Convolutional Neural Network) in the detection of pulmonary nodules from the images of chest X-ray images. The proposed method utilizes the Selective Search algorithm to determine the potential candidate regions of chest X-rays and applied the CNN to classify the selected regions into two classes—nodule opacities and non-nodule opacities. The presented approach achieved high classification accuracy. Another example is by Stirenko et al. (2018) [
21], in which the authors applied the deep learning, CNN approach to the X-ray images of patients with tuberculosis. The CNN is applied to a small and non-balanced dataset with the goal of segmentation of chest X-ray images, allowing for classification of images with higher precision in comparison to non-segmented images. In combination with data augmentation techniques, the achieved results are better. Authors conclude that data augmentation and segmentation, combined with dataset stratification and removal of outliers, may provide better results in cases of small, poorly balanced datasets.
There was research that utilized transfer learning methodologies in order to recognize respiratory diseases from chest X-ray images. In [
22], the authors proposed a transfer learning approach in order to recognize pneumonia from X-ray images. The proposed approach, based on utilization of ImageNet weights has resulted with high accuracy of pneumonia recognition (
). Another transfer learning approach has been implemented for pneumonia detection in [
23]. By utilizing such an approach, a highly accurate multi-class classification can be achieved, with accuracy ranging from
to
.
Wong et al. [
24] (2020) noted that radiographic findings do indicate positivity in COVID-19 patients, the conclusions of which are further supported by Orsi et al. [
25] (2020) and Cozzi et al. [
26] (2020). Borghesi and Maroldi [
27] (2020) defined a scoring system for X-ray COVID-19 monitoring, concluding that there is a definite possibility of determining the severity of the disease through the observation of X-ray images. Research has been done in the application of AI in the detection of COVID-19 in patients. Recently, classification of patients for preliminary diagnosis has been done from cough samples. Authors Imran et al. [
28] (2020) applied and implemented this into an app, called AI4COVID-19.
Bragazzi et al. [
29] (2020) demonstrated the possible uses of information and communication technologies, artificial intelligence, and big data in order to handle the large amount of data that may be generated by the ongoing pandemic. Further reviews and comparisons of mathematical modeling, artificial intelligence, and datasets for the prediction were done by multiple authors, such as Mohamadou et al. [
30] (2020), Raza [
31] (2020), and Adly et al. [
32] 2020. All aforementioned authors concluded the possibility of application of AI in the current and possibly forthcoming pandemics. Most promise in AI applications being applied in this field has been shown in the field of epidemiological spread. Zheng et al. [
33] (2020) applied a hybrid model for a 14-day period prediction, Hazarika et al. [
34] (2020) applied wavelet-coupled random vector functional neural networks, while Car et al. [
35] (2020) applied a multilayer perceptron neural network for the goal of regressing the epidemiology curve components. Ye et al. [
36] (2020) demonstrated a
-Satellite, AI-driven system for risk assessment at a community level. Authors demonstrate the usability of such a system in combat against COVID-19, as a system that displays risk index and the number of cases among all larger locations across the United States. Authors in [
37] have proposed a method for forecasting the impact of COVID-19 on stock prices. The approach based on stationary wavelet transform and bidirectional long short-term memory has shown high estimation performances.
Still, a large amount of work was also done in the image classification and detection of COVID-19 in patients. Wang et al. [
38] (2020) demonstrated the use of high-complexity convolutional neural networks in the application of COVID-19 diagnosis. Their COVID-Net custom architecture reached high sensitivity scores (above 90%) in the detection of the COVID-19 in comparison to other infections and a normal lung state. Narin et al. [
39] (2020) also demonstrated a high-quality solution using deep convolutional neural networks on X-ray images. Through the application of five different architectures (ResNet50, ResNet101, ResNet152, Inception V3, and Inception-ResNetV2) high scores were achieved (accuracy 95% or higher) by the authors. Ozturk et al. [
40] (2020) developed a classification network for classifying the inflammation, named DarkCovidNet. DarkCovidNet reached an impressive score in binary classification at 98.08% in the case of binary classification, but a significantly lower score for 87.02% for multi-label classification. In the presented case, a multi-label classification was conducted with the aim of differentiating X-ray images of the lungs of healthy patients, patients with COVID-19, and patients with pneumonia. Abdulaal et al. [
41] (2020) demonstrated the AI-based prognostic model of COVID-19, achieving accuracy levels of 86.25% and AUC ROC 90.12% for UK patients.
There have been studies proposing a transfer-learning approach to COVID-19 diagnosis from X-ray images of the chest. The study presented in [
42] used pre-trained CNNs in order to automatically recognize COVID-19 infection. Such an approach has enabled high classification performances with an accuracy level of up to
. The research presented in [
43] proposed a similar approach in order to differentiate pneumonia from COVID-19 infection. Transfer learning has enabled higher classification accuracy with utilization of simpler CNN architecture, such as VGG-16.
While a lot of work suggests that neural networks may be used for the detection of COVID-19 infection, there is an apparent lack of work that tests the possibility of finding the severity of COVID-19 through patients’ lung X-rays. Such an approach would allow for automatic detection and prediction of case severity, allowing healthcare professionals to determine the appropriate approach and to leverage available resources in the treatment of that individual patient. Development of an AI basis for such a novel system is the goal of this paper. From a literature overview, it can be noticed that all presented research has been based on a binary classification of X-ray images (infected/not infected) or differentiating COVID-19 infection and other respiratory diseases.
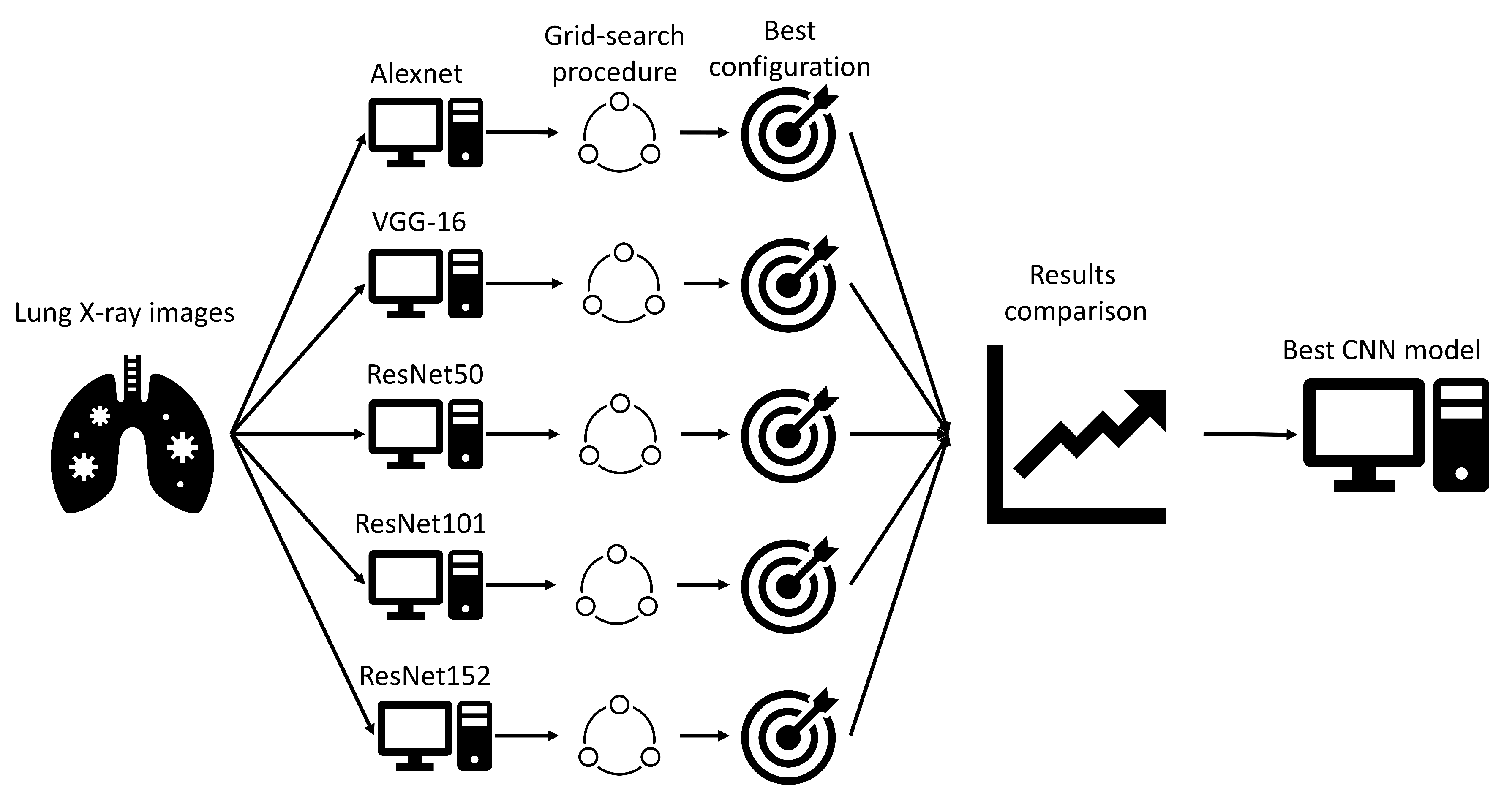
To summarize the novelty, this article, unlike the articles presented in the literature review, deals with a multi-class classification of X-ray images of positive COVID-19 patients with the aim of estimating the clinical picture. All the examples have used a large number of images (larger than 1000) in the training and testing processes of the neural network. While the number of COVID-19 patients is high, data collection, especially in countries with lower quality healthcare systems, may be problematic due to the strain exhibited by the coronavirus. Because of this, it is important to test the possibility of algorithm development combined with data augmentation operations, which is the secondary goal of the presented research.
According to presented facts and the literature overview, the following questions arise:
Is it possible to utilize CNN in order to classify COVID-19 patients according to X-ray images of lungs?
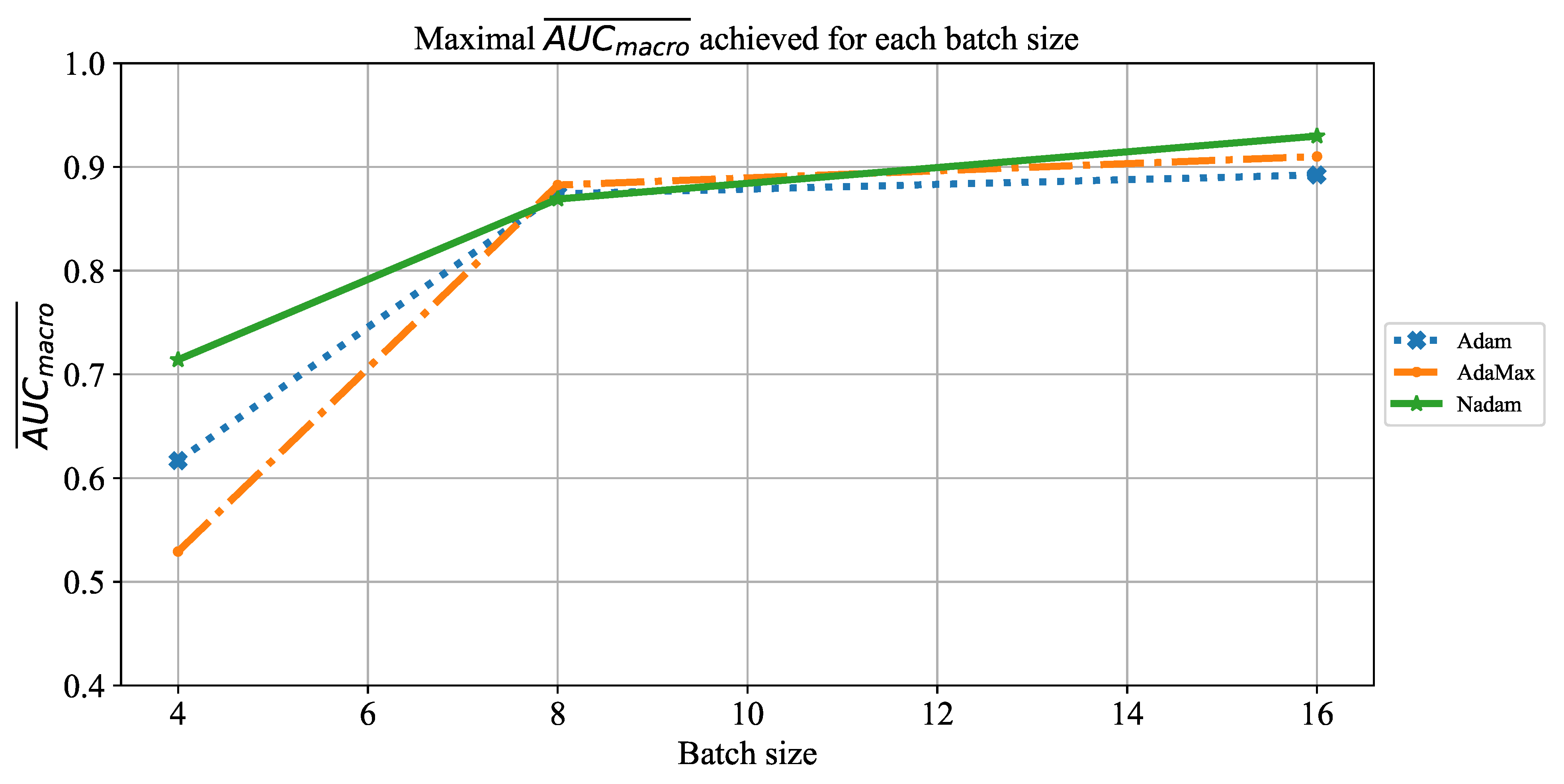
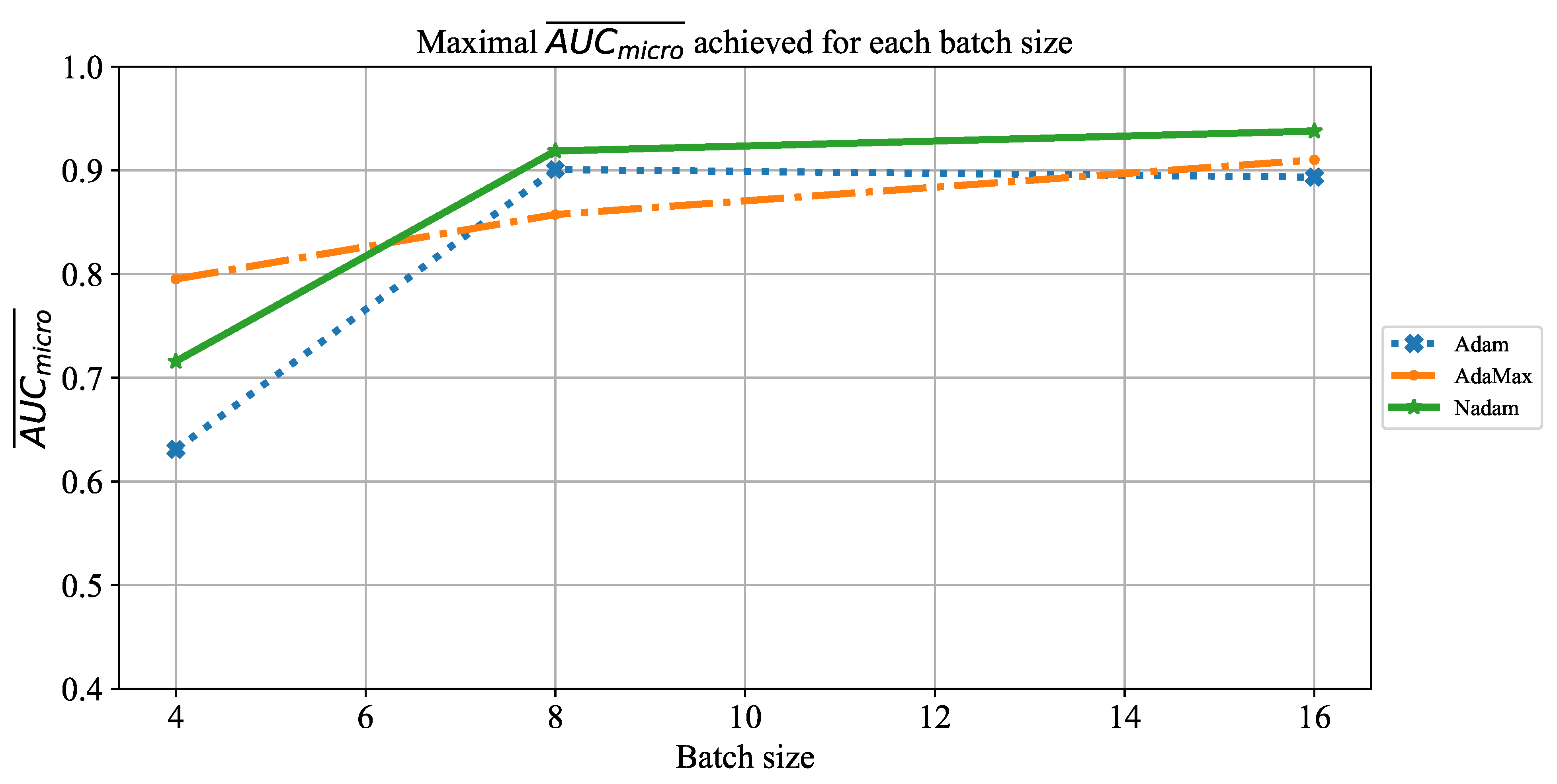
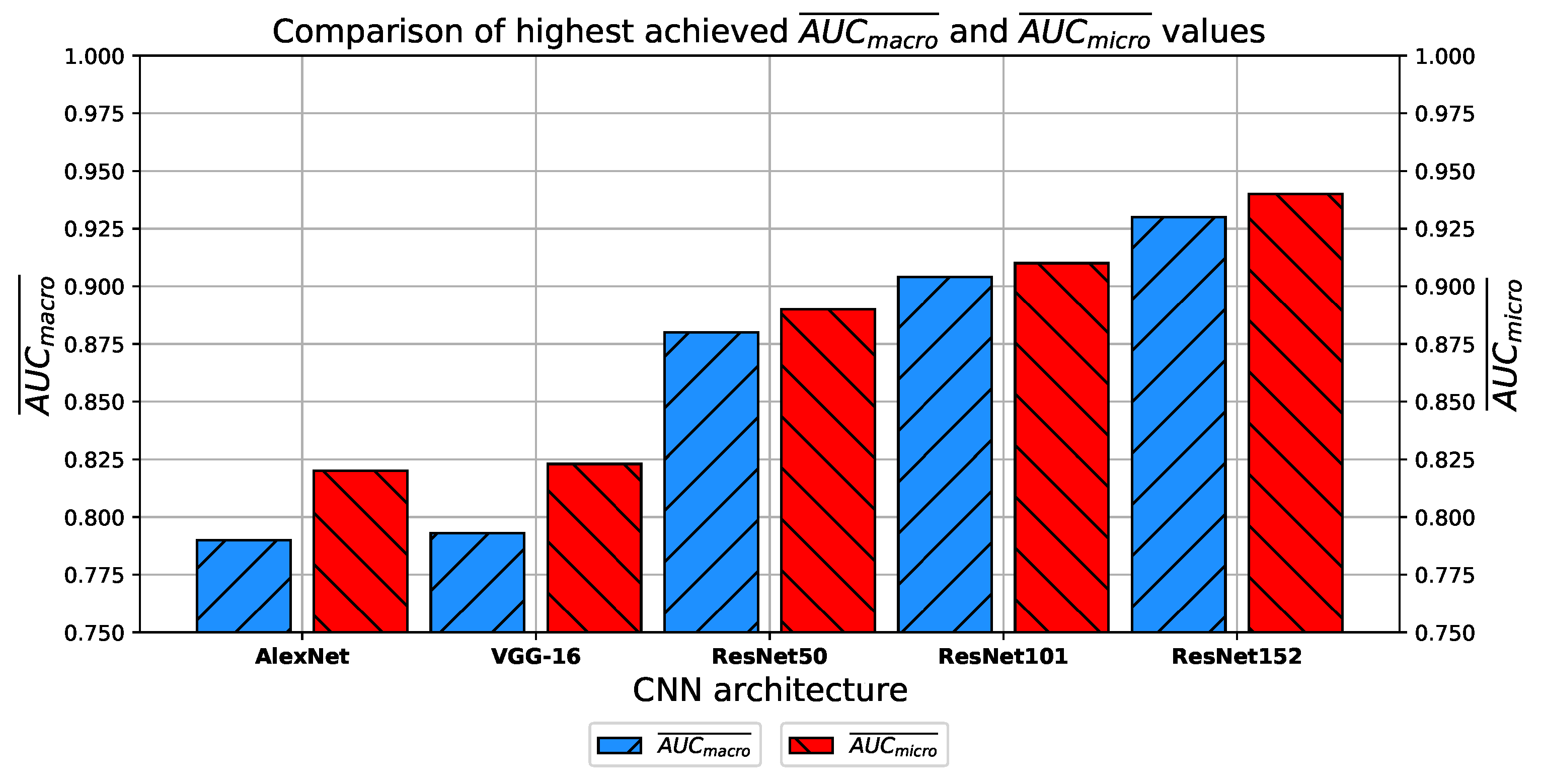
Which CNN architecture achieves the highest classification performance?
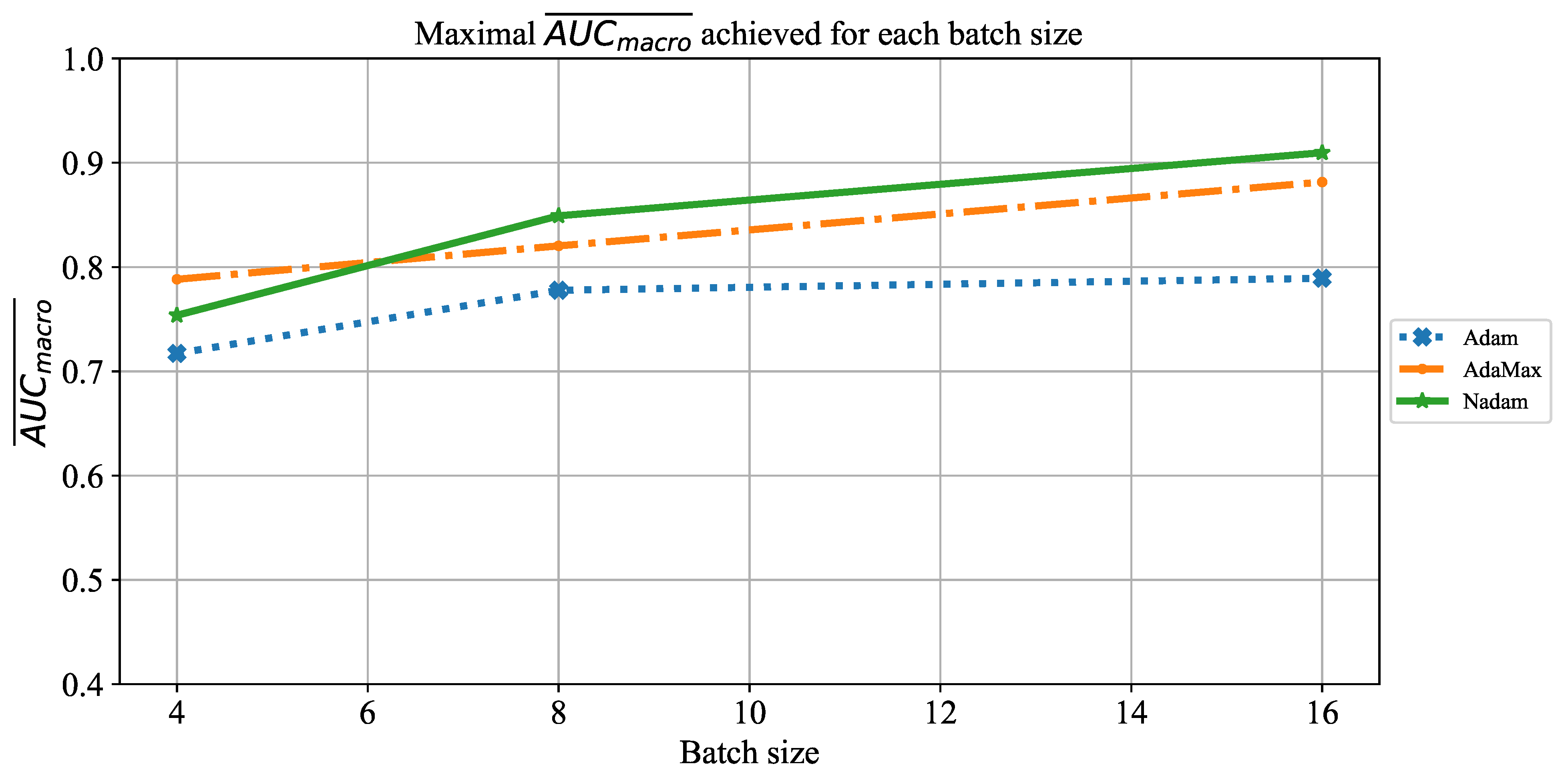
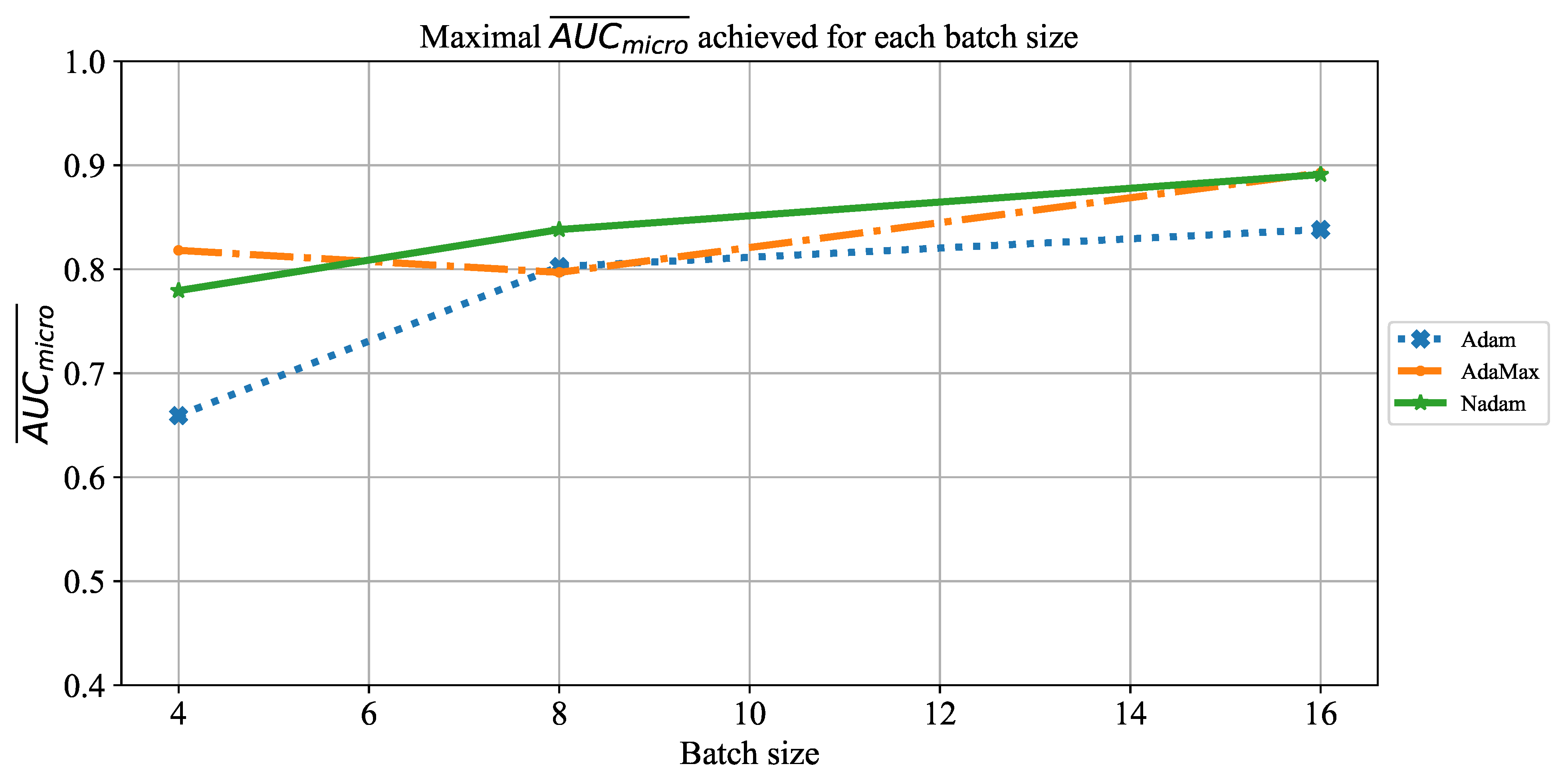
Which are the best-performing configurations in regards to the solver, number of iterations, and batch size?
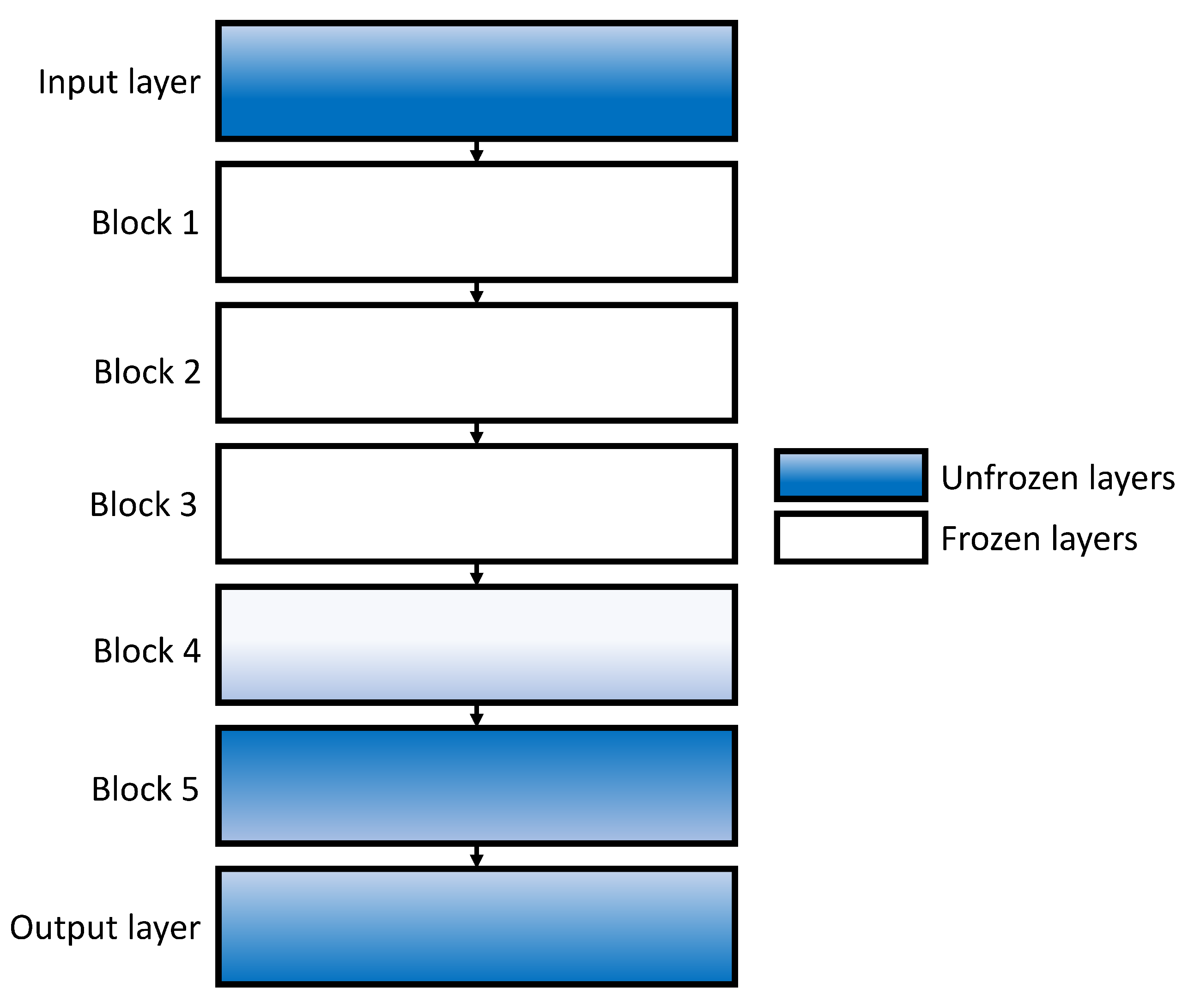
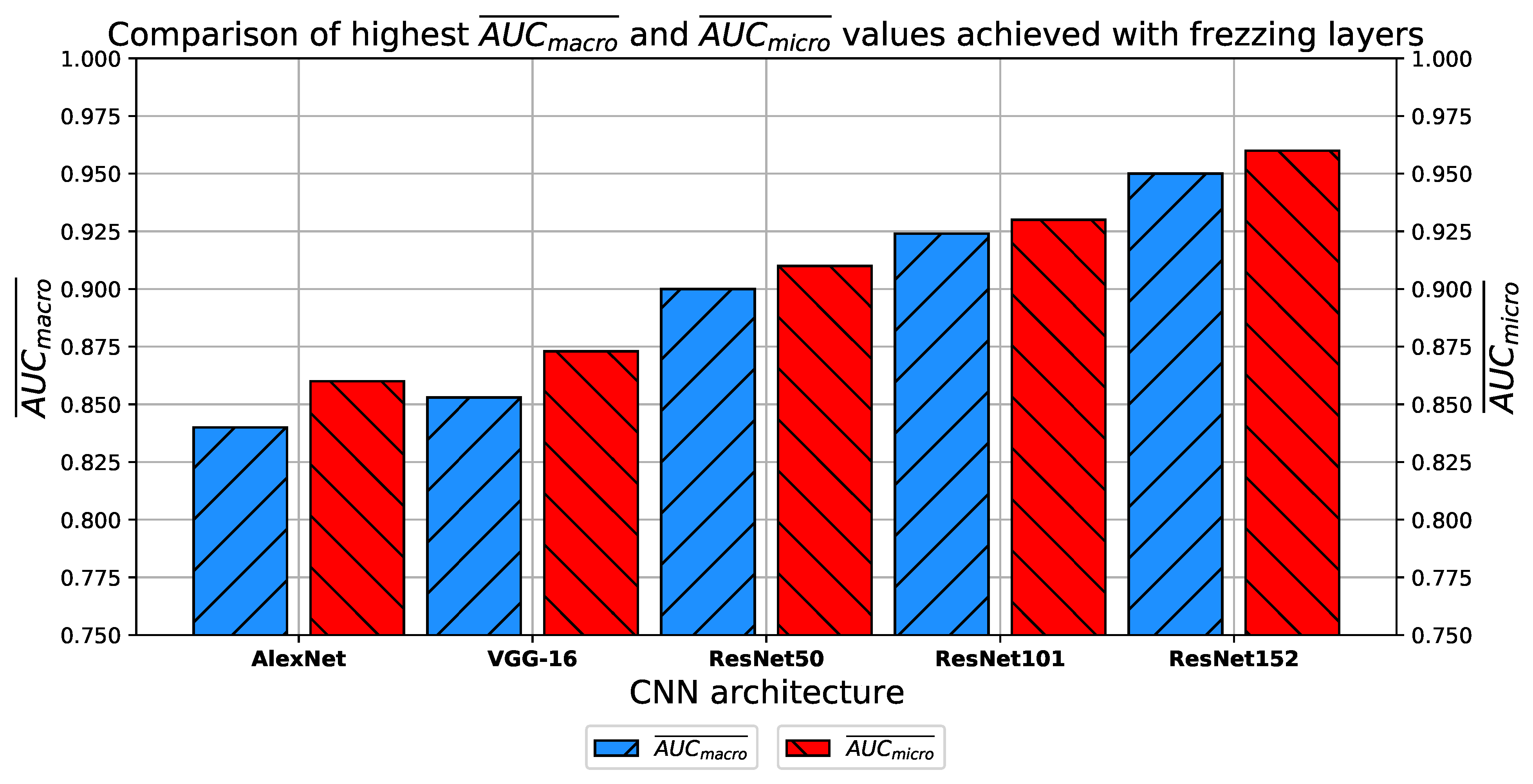
How do transfer learning and layer freezing influence the performances of the best configurations?
3. Description of Used Convolutional Neural Networks
In this subsection, an overview of CNN-based methods for image classification will be presented. The CNNs used in this research are, in fact, standard CNN architectures widely used for solving various computer vision and image recognition problems [
48]. Such an algorithm, alongside its variations, is widely used for various tasks of medical image recognition [
49]. For the case of this research, four different CNN architectures were used, and they are:
AlexNet,
VGG-16, and
ResNet.
All of the above-listed CNN architectures have predefined layers and activation functions, while other hyper-parameters, such as batch size, solver, and number of epochs could be varied. The above-listed architectures were chosen due to the history of their high classification performances in similar problems. It has been shown that ResNet architectures have achieved high classification performances when used for multi-class classification of X-ray chest images [
50]. Furthermore, ResNet architectures were used in various tasks of medical data classification ranging from tumor classification [
51,
52], trough recognition of respiratory diseases [
53], to fracture diagnosis [
54,
55].
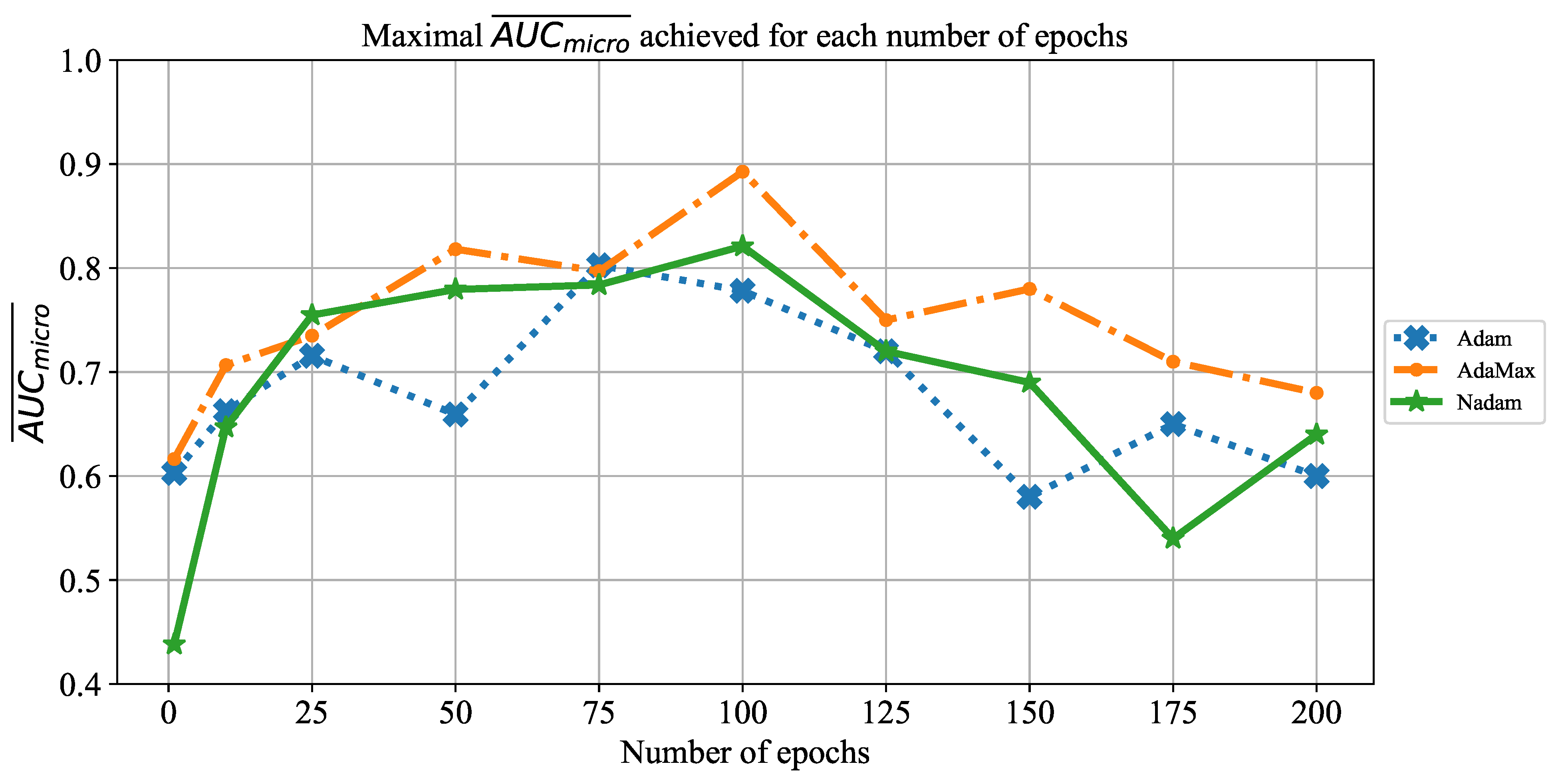
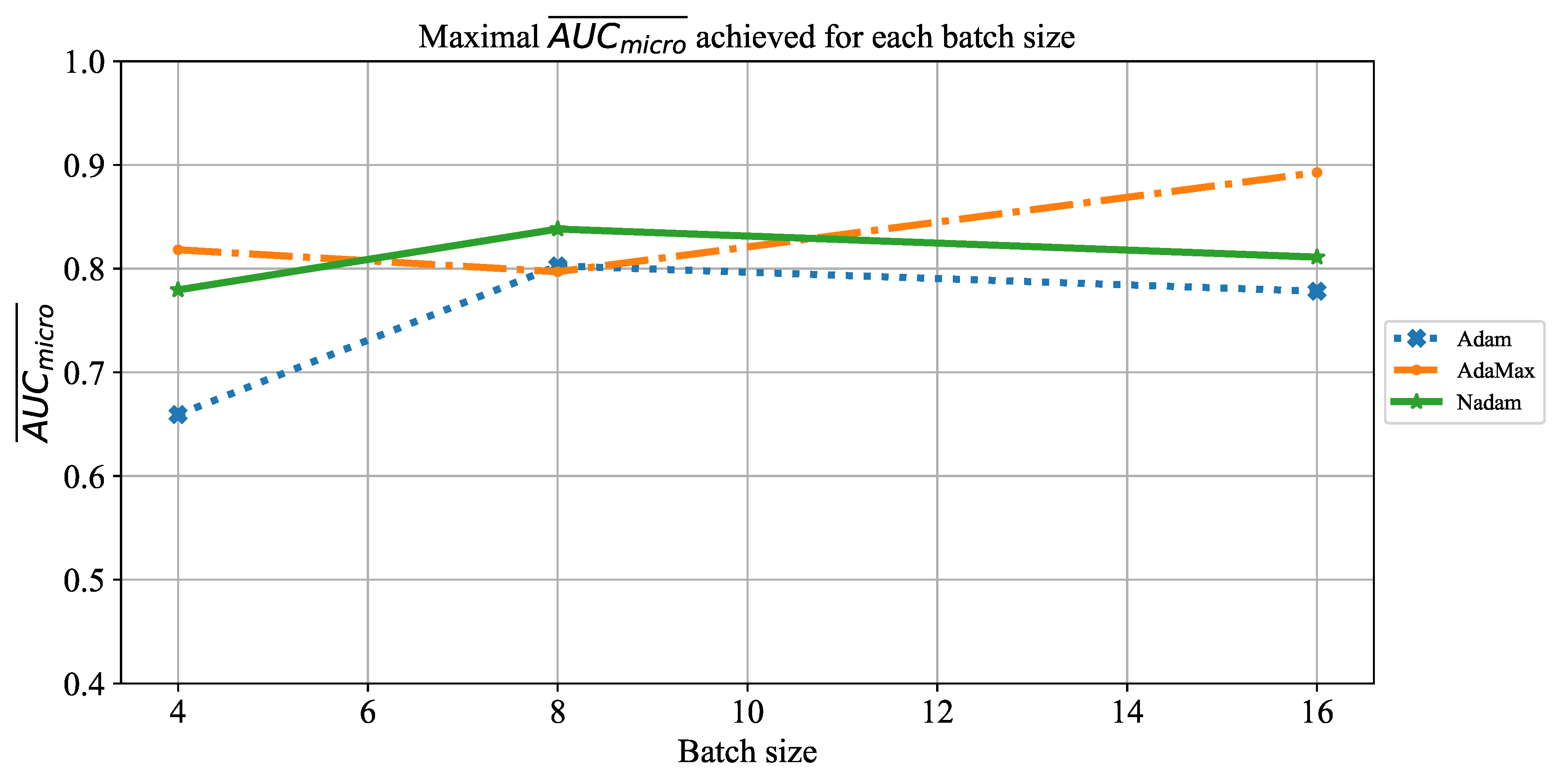
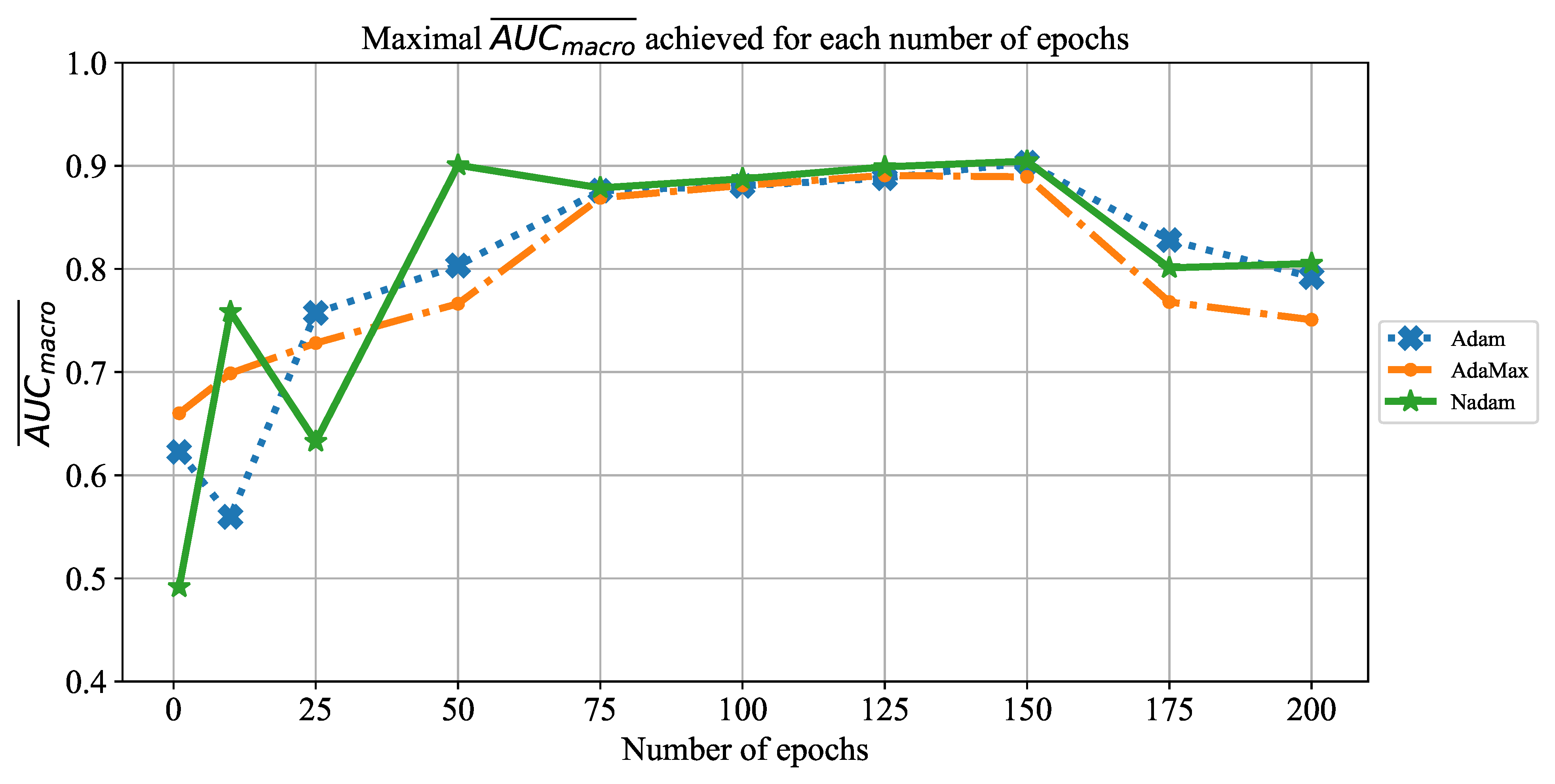
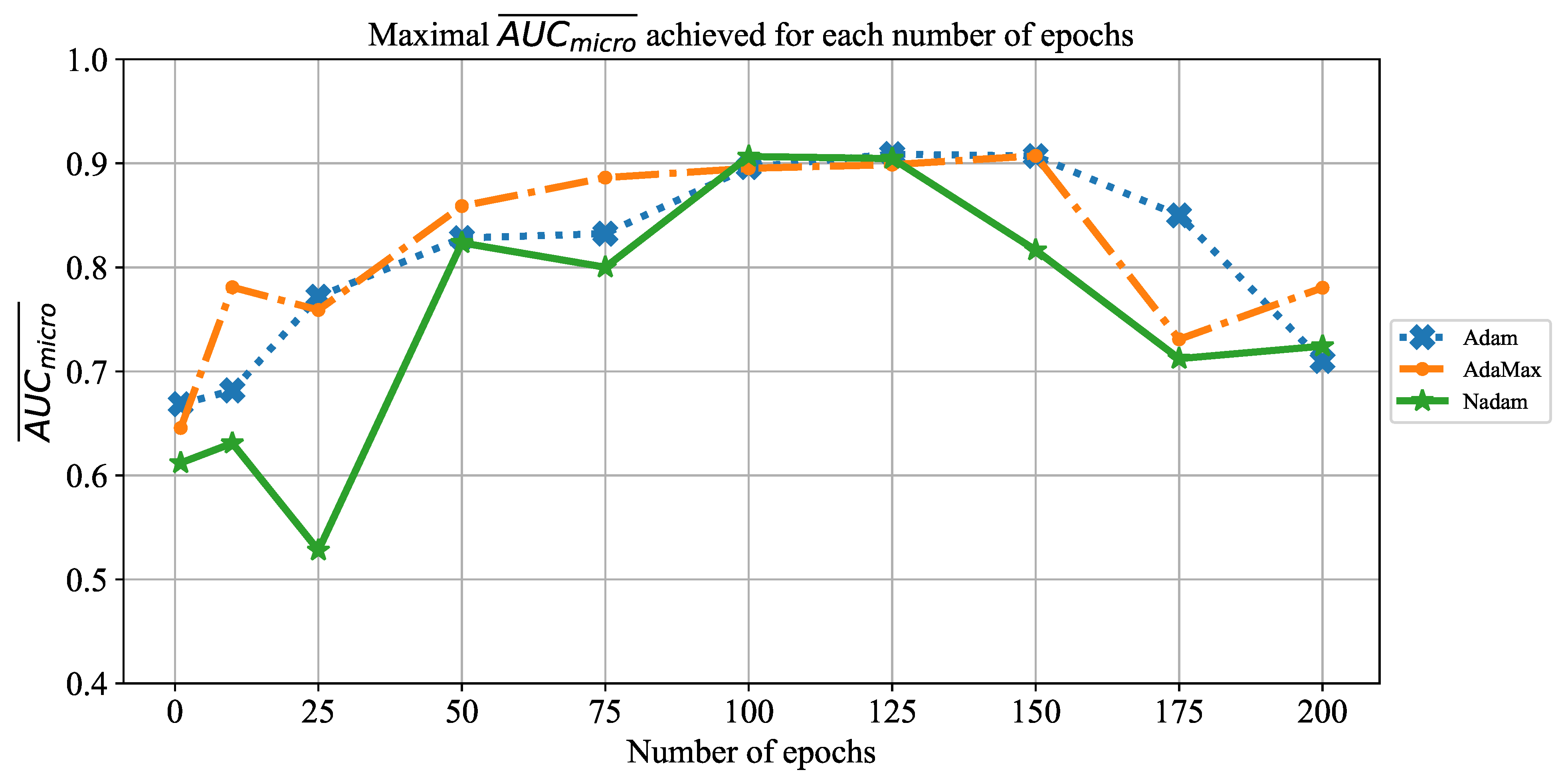
Extensive searches for the optimal solution through the hyper-parameter space can also be called the grid-search procedure. Variations of hyper-parameters used during the grid-search procedure for CNN-based models are presented in
Table 1.
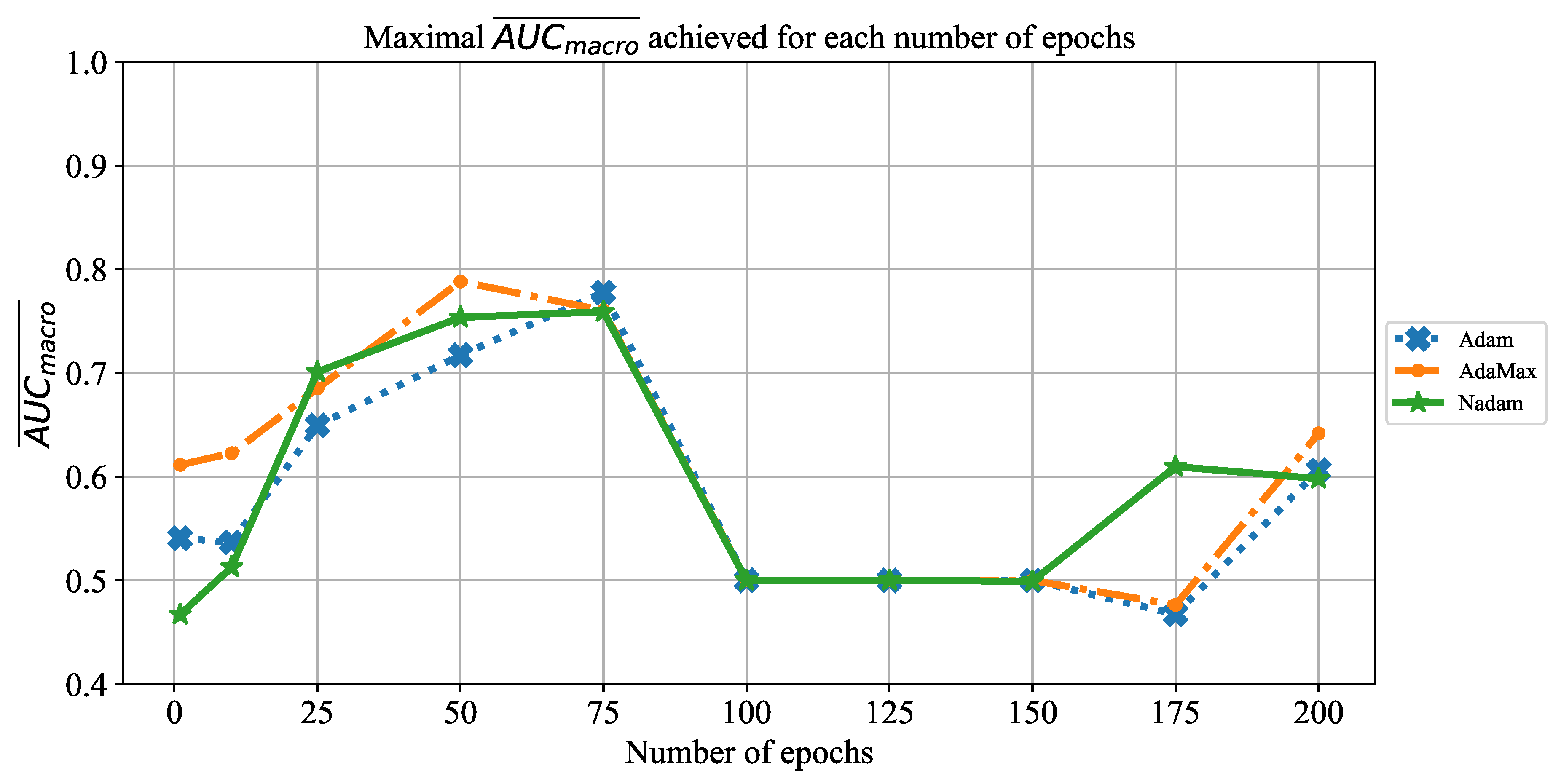
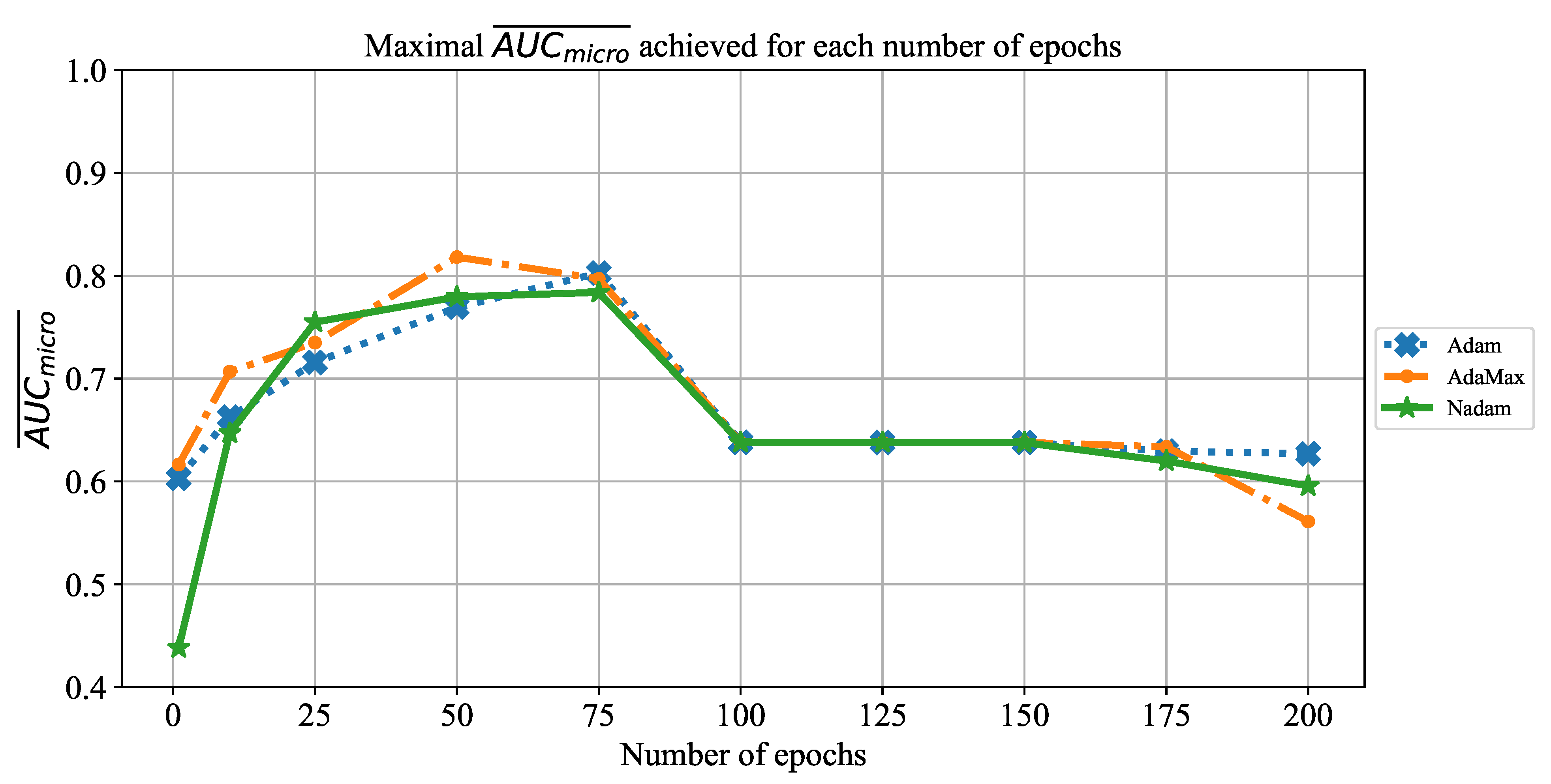
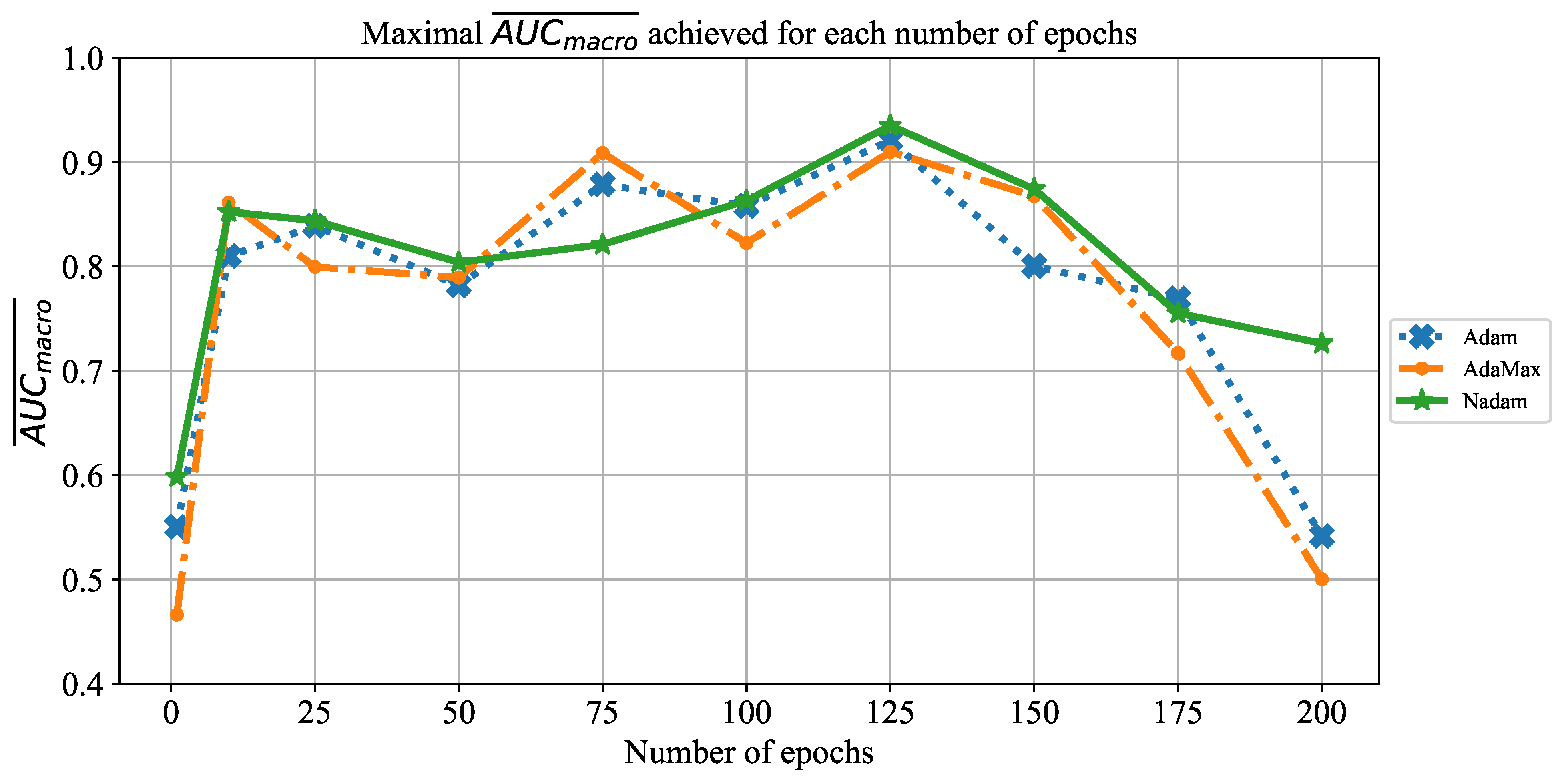
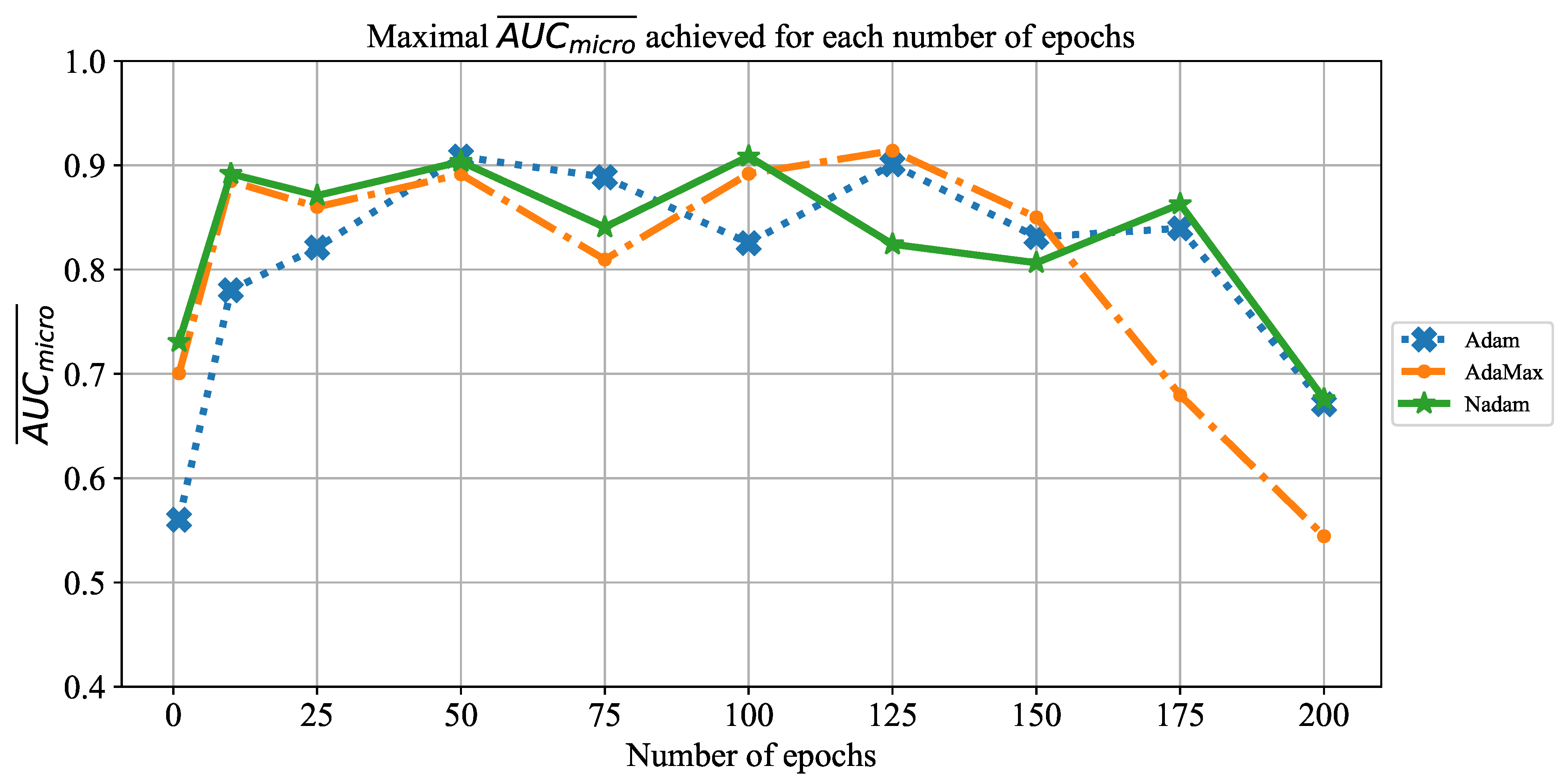
In order to determine the influence of overfitting, the number of epochs were varied with the aim of determining the number with the highest performances on the test dataset. With respect to theoretical knowledge, it can be defined that when training with a large number of epochs, the model is often over-fitted. For this reason, it is necessary to find the optimal number of training epochs [
15]. Solvers used in this research were selected due to their performance on multiple multi-label datasets [
59]. In the following paragraphs, a brief description and mathematical models will be provided for each solver.
Adam Solver
The Adam optimization algorithm represents one of the most-used algorithms for tasks of image recognition and computer vision. By using the Adam optimizer, weights are updated by following [
56]:
where
is defined as:
and
is defined as:
is defined as a running average of the gradients, and it can be described with:
Furthermore,
is defined as the running average of squared gradients, or:
G can be defined with:
where
represents a cost function. Parameters of the Adam solver used in this research are presented in
Table 2.
AdaMax Solver
AdaMax solver follows the logic similar to the Adam solver—in this case, the weights update was performed as [
58]:
where
is defined as:
Furthermore,
can be defined as:
and
is defined as:
As it is in the case of the Adam solver, parameters used in this research are presented in
Table 2.
Nadam Solver
The third optimizer used in this research in Nadam. As with the AdaMax algorithm, Nadam is also based on Adam. Weights in these case updates are as [
58]:
where
is defined with:
and
are defined as:
and
As it is in the case of the Adam and AdaMax optimizers, the parameters of the Nadam solver are presented in
Table 2.
The presented parameters will be used for training the CNNs, and the classification performances of all trained models will be evaluated by using the testing data set. In the following paragraphs, a brief overview of the used CNN architectures will be presented.
3.1. AlexNet
AlexNet represents one of the classical CNN architectures that are used for various tasks of image recognition and computer vision. This architecture is one of the first CNNs that are based on deeper configuration [
60]. AlexNet won the ImageNet competition in 2012. The success of such a deep architecture has introduced a trend for designing even deeper CNNs that can be noticed today [
61]. AlexNet is based on a configuration of nine layers, where the first five layers are convolutional and pooling layers, and the last four are fully connected layers [
62]. The detailed description of AlexNet architecture in provided in
Table 3.
3.2. VGG-16
The described trend of deeper CNN configuration resulted in improvements of the original AlexNet architecture. One of such architectures is VGG-16, presented in the following year. VGG-16 represents a deeper version of AlexNet, where the nine-layer configuration is replaced with a 16-layer configuration, from which the name is derived [
63]. A main advantage of VGG-16 is the introduction of smaller kernels in convolutional layers, in comparison with AlexNet [
64]. The detailed description of VGG-16 layers is provided in
Table 4.
3.3. ResNet
According to the presented networks, the trend of designing deeper networks can be noticed [
65]. This approach can be utilized to a certain level, due to the vanishing gradient problem [
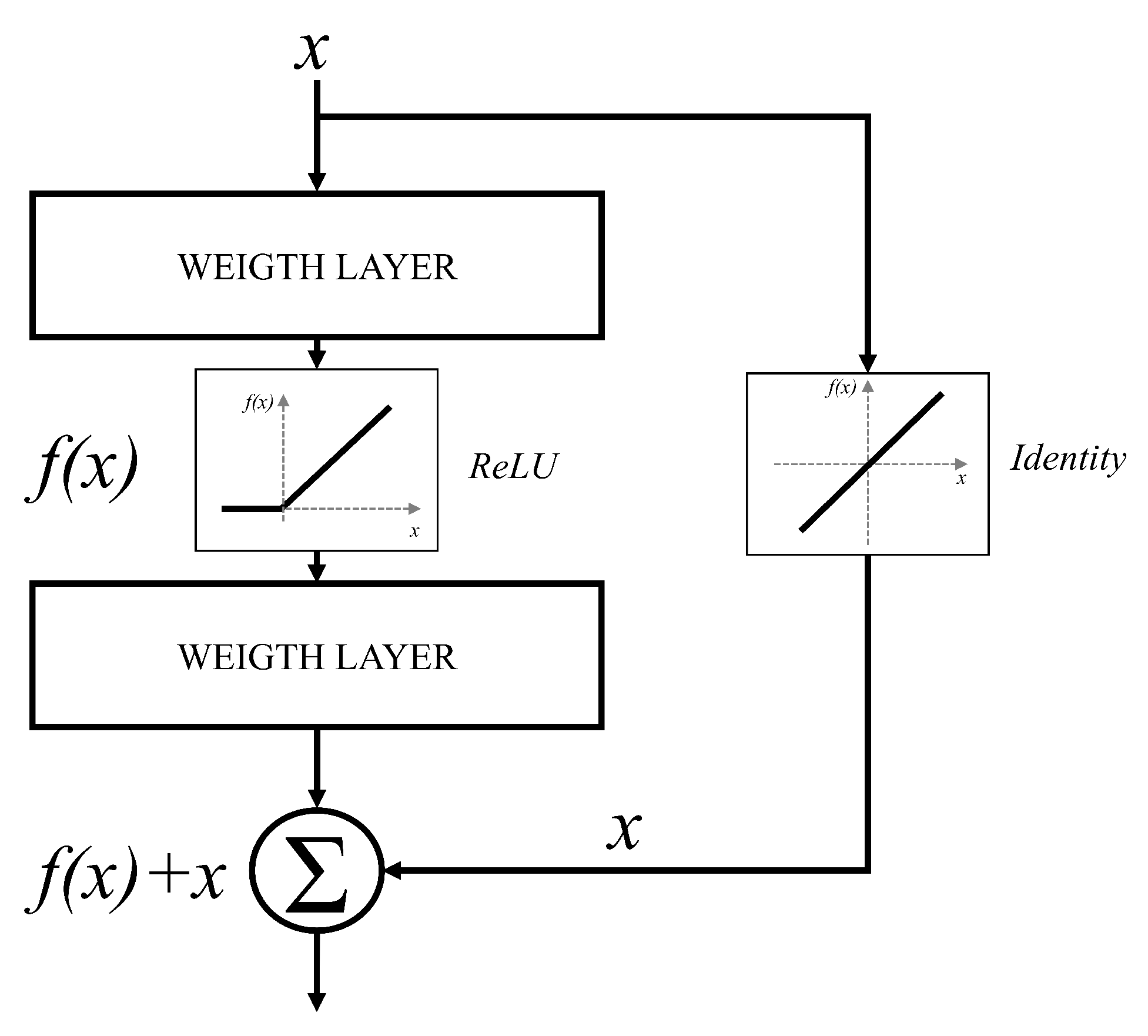
66]. It can be noticed that deeper configurations will have no significant improvements in terms of classification performances. Furthermore, in some cases, deeper CNNs can show lower classification performances than CNNs designed with a smaller number of layers. For these reasons, an approach based on residual blocks is proposed. The residual block represents a variation of a CNN layer, where a layer is bypassed with an identity connection [
67]. The block scheme of such an approach is presented in
Figure 5.
By using the presented residual approach, significantly deeper networks could be used without the vanishing gradient problem. This characteristic is a consequence of identity bypass utilization because identity layers do not influence the CNN training procedure [
68]. For these reasons, deeper CNNs designed with a residual block will not produce the higher error in comparison with shallower architectures. In other words, by stacking residual layers, significantly deeper architectures could be designed. For the case of this research, three different architectures based on the residual block will be used, and these are: ResNet50 [
69], ResNet101 [
70], and ResNet152 [
71]. The aforementioned architectures are pre-defined ResNet architectures that are mainly used for image recognition and computer vision problems which require deeper CNN configurations.