Local Disease-Free Survival Rate (LSR) Application to Personalize Radiation Therapy Treatments in Breast Cancer Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Cultures and Radiation Treatments
2.2. Clonogenic Survival Assay, Dose Response Curves, and Alfa and Beta Parameter Calculations
2.3. Local Disease-Free Survival Rate (LSR) Model
2.4. Statistical Analysis
3. Results
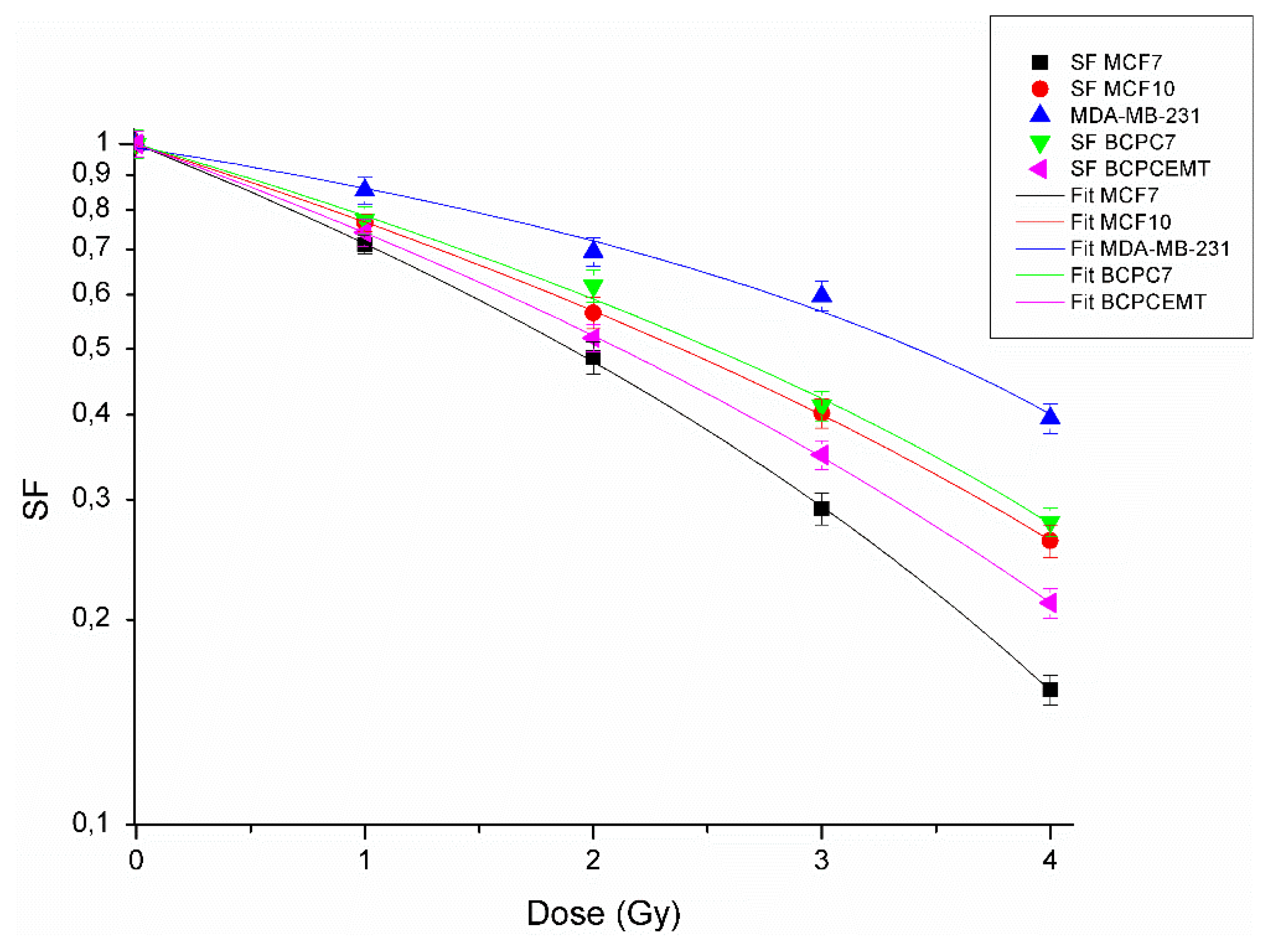
3.1. Radiobiological Characterization of Breast Cancer(BC) Cell Lines and Primary Cultures
3.2. Experimental LSR
4. Discussion
- -
- dose per fraction to achieve controlled death of cancer cells;
- -
- the intrinsic radiosensitivity values and ;
- -
- k, which represents tumor clonogens;
- -
- or the doubling time.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef]
- Chen, H.H.W.; Kuo, M.T. Improving radiotherapy in cancer treatment: Promises and challenges. Oncotarget 2017, 8, 62742–62758. [Google Scholar] [CrossRef]
- Forte, G.I.; Minafra, L.; Bravatà, V.; Cammarata, F.P.; Lamia, D.; Pisciotta, P.; Cirrone, G.A.P.; Cuttone, G.; Gilardi, M.C.; Russo, G. Radiogenomics: The utility in patient selection. Transl. Cancer Res. 2017, 65, S852–S874. [Google Scholar] [CrossRef]
- Baskar, R.; Lee, K.A.; Yeo, R.; Yeoh, K.W. Cancer and radiation therapy: Current advances and future directions. Int. J. Med. Sci. 2012, 9, 193–199. [Google Scholar] [CrossRef]
- Calvaruso, M.; Pucci, G.; Musso, R.; Bravatà, V.; Cammarata, F.P.; Russo, G.; Forte, G.I.; Minafra, L. Nutraceutical Compounds as Sensitizers for Cancer Treatment in Radiation Therapy. Int. J. Mol. Sci. 2019, 20, 5267. [Google Scholar] [CrossRef]
- Jalali, R.; Singh, S.; Budrukkar, A. Techniques of tumour bed boost irradiation in breast conserving therapy: Current evidence and suggested guidelines. Acta Oncol. 2007, 46, 879–892. [Google Scholar] [CrossRef]
- Smith, B.D.; Bellon, J.R.; Blitzblau, R.; Freedman, G.; Haffty, B.; Hahn, C.; Halberg, F.; Hoffman, K.; Horst, K.; Moran, J.; et al. Radiation therapy for the whole breast: Executive summary of an American Society for Radiation Oncology (ASTRO) evidence-based guideline. Pract. Radiat. Oncol. 2018, 8, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Hon, J.D.; Singh, B.; Sahin, A.; Du, G.; Wang, J.; Wang, V.Y.; Deng, F.M.; Zhang, D.Y.; Monaco, M.E.; Lee, P. Breast cancer molecular subtypes: From TNBC to QNBC. Am. J. Cancer Res. 2016, 6, 1864–1872. [Google Scholar] [PubMed]
- Alluri, P.; Newman, L.A. Basal-like and triple-negative breast cancers: Searching for positives among many negatives. Surg. Oncol. Clin. N. Am. 2014, 23, 567–577. [Google Scholar] [CrossRef] [PubMed]
- Burstein, M.D.; Tsimelzon, A.; Poage, G.M.; Covington, K.R.; Contreras, A.; Fuqua, S.A.; Savage, M.I.; Osborne, C.K.; Hilsenbeck, S.G.; Chang, J.C.; et al. Comprehensive genomic analysis identifies novel subtypes and targets of triple-negative breast cancer. Clin. Cancer Res. 2015, 21, 1688–1698. [Google Scholar] [CrossRef]
- Lebert, J.M.; Lester, R.; Powell, E.; Seal, M.; McCarthy, J. Advances in the systemic treatment of triple-negative breast cancer. Curr. Oncol. 2018, 25 (Suppl. 1), S142–S150. [Google Scholar] [CrossRef]
- Xia, L.Y.; Hu, Q.L.; Zhang, J.; Xu, W.Y.; Li, X.S. Survival outcomes of neoadjuvant versus adjuvant chemotherapy in triple-negative breast cancer: A meta-analysis of 36,480 cases. World J. Surg. Oncol. 2020, 18, 129. [Google Scholar] [CrossRef]
- Dent, R.; Trudeau, M.; Pritchard, K.I.; Hanna, W.M.; Kahn, H.K.; Sawka, C.A.; Lickley, L.A.; Rawlinson, E.; Sun, P.; Narod, S.A. Triple-negative breast cancer: Clinical features and patterns of recurrence. Clin. Cancer Res. 2007, 13 Pt 1, 4429–4434. [Google Scholar] [CrossRef]
- Voduc, K.D.; Cheang, M.C.; Tyldesley, S.; Gelmon, K.; Nielsen, T.O.; Kennecke, H. Breast cancer subtypes and the risk of local and regional relapse. J. Clin. Oncol. 2010, 28, 1684–1691. [Google Scholar] [CrossRef] [PubMed]
- Sioshansi, S.; Huber, K.E.; Wazer, D.E. The implications of breast cancer molecular phenotype for radiation oncology. Front. Oncol. 2011, 1, 12. [Google Scholar] [CrossRef]
- Steward, L.; Conant, L.; Gao, F.; Margenthaler, J.A. Predictive factors and patterns of recurrence in patients with triple negative breast cancer. Ann. Surg. Oncol. 2014, 21, 2165–2171. [Google Scholar] [CrossRef]
- Gonçalves, H., Jr.; Guerra, M.R.; Duarte Cintra, J.R.; Fayer, V.A.; Brum, I.V.; Bustamante Teixeira, M.T. Survival Study of Triple-Negative and Non-Triple-Negative Breast Cancer in a Brazilian Cohort. Clin. Med. Insights Oncol. 2018, 12, 1179554918790563. [Google Scholar] [CrossRef] [PubMed]
- Steward, L.T.; Gao, F.; Taylor, M.A.; Margenthaler, J.A. Impact of radiation therapy on survival in patients with triple-negative breast cancer. Oncol. Lett. 2014, 7, 548–552. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xia, F.; Luo, J.; Ma, J.; Yang, Z.; Zhang, L.; Feng, Y.; Shao, Z.; Yu, X.; Guo, X. Postmastectomy radiotherapy reduces locoregional and disease recurrence in patients with stage II-III triple-negative breast cancer treated with neoadjuvant chemotherapy and mastectomy. Onco Targets Ther. 2018, 11, 1973–1980. [Google Scholar] [CrossRef]
- Bravatà, V.; Cammarata, F.P.; Minafra, L.; Musso, R.; Pucci, G.; Spada, M.; Fazio, I.; Russo, G.; Forte, G.I. Gene Expression Profiles Induced by High-dose Ionizing Radiation in MDA-MB-231 Triple-negative Breast Cancer Cell Line. Cancer Genom. Proteom. 2019, 16, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen, C.M.; Oei, A.L.; Crezee, J.; Bel, A.; Franken, N.A.P.; Stalpers, L.J.A.; Kok, H.P. The alpha and beta of tumours: A review of parameters of the linear-quadratic model, derived from clinical radiotherapy studies. Radiat. Oncol. 2018, 13, 96. [Google Scholar] [CrossRef]
- McMahon, S.J. The linear quadratic model: Usage, interpretation and challenges. Phys. Med. Biol. 2018, 64, 01TR01. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.S.; White, J.; Li, X.A. Is α/β for breast cancer really low? Radiother. Oncol. 2011, 100, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.S.; Pajonk, F.; McCloskey, S.; Low, D.A.; Kupelian, P.; Steinberg, M.; Sheng, K. Radioresistance of the breast tumor is highly correlated to its level of cancer stem cell and its clinical implication for breast irradiation. Radiother. Oncol. 2017, 124, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Minafra, L.; Porcino, N.; Bravatà, V.; Gaglio, D.; Bonanomi, M.; Amore, E.; Cammarata, F.P.; Russo, G.; Militello, C.; Savoca, G.; et al. Radiosensitizing effect of curcumin-loaded lipid nanoparticles in breast cancer cells. Sci. Rep. 2019, 9, 11134. [Google Scholar] [CrossRef]
- Minafra, L.; Norata, R.; Bravatà, V.; Viola, M.; Lupo, C.; Gelfi, C.; Messa, C. Unmasking epithelial-mesenchymal transition in a breast cancer primary culture: A study report. BMC Res. Notes 2012, 5, 343. [Google Scholar] [CrossRef][Green Version]
- Minafra, L.; Bravatà, V.; Cammarata, F.P.; Russo, G.; Gilardi, M.C.; Forte, G.I. Radiation Gene-expression Signatures in Primary Breast Cancer Cells. Anticancer Res. 2018, 38, 2707–2715. [Google Scholar]
- Cammarata, F.P.; Torrisi, F.; Forte, G.I.; Minafra, L.; Bravatà, V.; Pisciotta, P.; Savoca, G.; Calvaruso, M.; Petringa, G.; Cirrone, G.A.P.; et al. Proton Therapy and Src Family Kinase Inhibitor Combined Treatments on U87 Human Glioblastoma Multiforme Cell Line. Int. J. Mol. Sci. 2019, 20, 4745. [Google Scholar] [CrossRef]
- Haviland, J.S.; Owen, J.R.; Dewar, J.A.; Agrawal, R.K.; Barrett, J.; Barrett-Lee, P.J.; Dobbs, H.J.; Hopwood, P.; Lawton, P.A.; Magee, B.J.; et al. The UK Standardisation of Breast Radiotherapy (START) trials of radiotherapy hypofractionation for treatment of early breast cancer: 10-year follow-up results of two randomised controlled trials. Lancet Oncol. 2013, 14, 1086–1094. [Google Scholar] [CrossRef]
- Dale, R.G. Radiobiological assessment of permanent implants using tumor repopulation factors in linear-quadratic model. Br. J. Radiol. 1989, 62, 241–244. [Google Scholar] [CrossRef]
- Joiner, M.; van der Kogel, A. Basic Clinical Radiobiology, 4th ed.; Hodder Arnold (UK Company): London, UK, 2009. [Google Scholar]
- Minafra, L.; Bravatà, V.; Russo, G.; Forte, G.I.; Cammarata, F.P.; Ripamonti, M.; Candiano, G.; Cervello, M.; Giallongo, A.; Perconti, G.; et al. Gene Expression Profiling of MCF10A Breast Epithelial Cells Exposed to IOERT. Anticancer Res. 2015, 35, 3223–3234. [Google Scholar] [PubMed]
- Minafra, L.; Bravatà, V.; Forte, G.I.; Cammarata, F.P.; Gilardi, M.C.; Messa, C. Gene expression profiling of epithelial-mesenchymal transition in primary breast cancer cell culture. Anticancer Res. 2014, 34, 2173–2183. [Google Scholar] [PubMed]
- Quon, H.; McNutt, T.; Lee, J.; Bowers, M.; Jiang, W.; Lakshminarayanan, P.; Cheng, Z.; Han, P.; Hui, X.; Shah, V.; et al. Needs and Challenges for Radiation Oncology in the Era of Precision Medicine. Int. J. Radiat. Oncol. Biol. Phys. 2019, 103, 809–817. [Google Scholar] [CrossRef] [PubMed]
- Turashvili, G.; Brogi, E. Tumor Heterogeneity in Breast Cancer. Front. Med. 2017, 4, 227. [Google Scholar] [CrossRef]
- Lee, J.S.; Yost, S.E.; Yuan, Y. Neoadjuvant Treatment for Triple Negative Breast Cancer: Recent Progresses and Challenges. Cancers 2020, 12, 1404. [Google Scholar] [CrossRef]
- Tai, A.; Liu, F.; Gore, E.; Li, X.A. An analysis of tumor control probability of stereotactic body radiation therapy for lung cancer with a regrowth model. Phys. Med. Biol. 2016, 61, 3903–3913. [Google Scholar] [CrossRef]
- Nahum, A.; Sanchez, B. Tumour control probability modelling: Basic principles and applications in treatment planning. Phys. Med. 2001, 17, 13–23. [Google Scholar]
- Carlone, M.C.; Warkentin, B.; Stavrev, P.; Fallone, B.G. Fundamental form of a population TCP model in the limit of large heterogeneity. Med. Phys. 2006, 33, 1634–1642. [Google Scholar] [CrossRef]
- Moran, M.S.; Truong, P.T. Hypofractionated radiation treatment for breast cancer: The time is now. Breast J. 2020, 26, 47–54. [Google Scholar] [CrossRef]
- Chan, C.W.H.; Law, B.M.H.; So, W.K.W.; Chow, K.M.; Waye, M.M.Y. Novel Strategies on Personalized Medicine for Breast Cancer Treatment: An Update. Int. J. Mol. Sci. 2017, 18, 2423. [Google Scholar] [CrossRef]
- Bravatà, V.; Cava, C.; Minafra, L.; Cammarata, F.P.; Russo, G.; Gilardi, M.C.; Castiglioni, I.; Forte, G.I. Radiation-Induced Gene Expression Changes in High and Low Grade Breast Cancer Cell Types. Int. J. Mol. Sci. 2018, 19, 1084. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Mahajan, R.; Ghoshal, S.; Yadav, B.S.; Rai, B. Hypofractionated radiotherapy in carcinoma breast: What we have achieved? J. Cancer Res. Ther. 2015, 11, 259–263. [Google Scholar] [CrossRef]
- Cammarata, F.P.; Forte, G.I.; Broggi, G.; Bravatà, V.; Minafra, L.; Pisciotta, P.; Calvaruso, M.; Tringali, R.; Tomasello, B.; Torrisi, F.; et al. Molecular Investigation on a Triple Negative Breast Cancer Xenograft Model Exposed to Proton Beams. Int. J. Mol. Sci. 2020, 21, 6337. [Google Scholar] [CrossRef]

| BC Cells | α (Gy−1) | β (Gy−2) | α/β (Gy) |
|---|---|---|---|
| MCF7 | 0.012 | 0.003 | 6.47 ± 0.52 |
| MCF10A | 0.007 | 0.002 | 9.83 ± 0.87 |
| MDA-MB-231 | 0.034 | 0.010 | 3.79 ± 2.24 |
| BcPc7 | 0.022 | 0.006 | 7.00 ± 1.63 |
| BcPcEMT | 0.008 | 0.002 | 8.83 ± 0.64 |
| BC Cells | Dose (Gy) [k exp] | Dose (Gy) [k = 36] | Dose (Gy) [k = 14.5] |
|---|---|---|---|
| MCF7 | 1.5 | ||
| MCF10A | 2.0 | ||
| MDA-MB-231 | 1.8 | ||
| BcPc7 | 2.8 | ||
| BcPcEMT | 2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savoca, G.; Calvaruso, M.; Minafra, L.; Bravatà, V.; Cammarata, F.P.; Iacoviello, G.; Abbate, B.; Evangelista, G.; Spada, M.; Forte, G.I.; et al. Local Disease-Free Survival Rate (LSR) Application to Personalize Radiation Therapy Treatments in Breast Cancer Models. J. Pers. Med. 2020, 10, 177. https://doi.org/10.3390/jpm10040177
Savoca G, Calvaruso M, Minafra L, Bravatà V, Cammarata FP, Iacoviello G, Abbate B, Evangelista G, Spada M, Forte GI, et al. Local Disease-Free Survival Rate (LSR) Application to Personalize Radiation Therapy Treatments in Breast Cancer Models. Journal of Personalized Medicine. 2020; 10(4):177. https://doi.org/10.3390/jpm10040177
Chicago/Turabian StyleSavoca, Gaetano, Marco Calvaruso, Luigi Minafra, Valentina Bravatà, Francesco Paolo Cammarata, Giuseppina Iacoviello, Boris Abbate, Giovanna Evangelista, Massimiliano Spada, Giusi Irma Forte, and et al. 2020. "Local Disease-Free Survival Rate (LSR) Application to Personalize Radiation Therapy Treatments in Breast Cancer Models" Journal of Personalized Medicine 10, no. 4: 177. https://doi.org/10.3390/jpm10040177
APA StyleSavoca, G., Calvaruso, M., Minafra, L., Bravatà, V., Cammarata, F. P., Iacoviello, G., Abbate, B., Evangelista, G., Spada, M., Forte, G. I., & Russo, G. (2020). Local Disease-Free Survival Rate (LSR) Application to Personalize Radiation Therapy Treatments in Breast Cancer Models. Journal of Personalized Medicine, 10(4), 177. https://doi.org/10.3390/jpm10040177











