Predicting Pulmonary Function Testing from Quantified Computed Tomography Using Machine Learning Algorithms in Patients with COPD
Abstract
1. Introduction
2. Methods
2.1. Subjects
2.2. Lung Function Testing
2.3. Computerized Tomography Examinations
2.4. Image Analysis
2.5. Model Training and Evaluation
2.6. Model Evaluation and Statistical Analysis
3. Results
3.1. Data Mining
3.2. Model Comparison in Prediction Performance
3.3. Absolute and Relative Errors of Prediction Models
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| COPD | chronic obstructive pulmonary disease |
| FEV1 | forced expiratory volume at one second |
| kNN | k-nearest neighbour |
| MRE | mean relative error |
| qCT | quantified computed tomography |
| RV | residual volume |
| TLC | total lung capacity |
| VC | vital capacity |
References
- Vogelmeier, C.F.; Criner, G.J.; Martinez, F.J.; Anzueto, A.; Barnes, P.J.; Bourbeau, J.; Celli, B.R.; Chen, R.; Decramer, M.; Fabbri, L.M.; et al. Global strategy for the diagnosis, management, and prevention of chronic obstructive lung disease 2017 report: Gold executive summary. Am. J. Respir. Crit. Care Med. 2017, 195, 577–582. [Google Scholar] [CrossRef] [PubMed]
- Muller, N.L.; Staples, C.A.; Miller, R.R.; Abboud, R.T. “Density mask”. An objective method to quantitate emphysema using computed tomography. Chest 1988, 94, 782–787. [Google Scholar]
- Gawlitza, J.; Trinkmann, F.; Scheffel, H.; Fischer, A.; Nance, J.W.; Henzler, C.; Vogler, N.; Saur, J.; Akin, I.; Borggrefe, M.; et al. Time to exhale: Additional value of expiratory chest CT in chronic obstructive pulmonary disease. Can. Respir. J. 2018, 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Han, M.K.; Kazerooni, E.A.; Lynch, D.A.; Liu, L.X.; Murray, S.; Curtis, J.L.; Criner, G.J.; Kim, V.; Bowler, R.P.; Hanania, N.A. Chronic obstructive pulmonary disease exacerbations in the COPDGene study: Associated radiologic phenotypes. Radiology 2011, 261, 274–282. [Google Scholar] [CrossRef] [PubMed]
- Grydeland, T.B.; Dirksen, A.; Coxson, H.O.; Eagan, T.M.; Thorsen, E.; Pillai, S.G.; Sharma, S.; Eide, G.E.; Gulsvik, A.; Bakke, P.S. Quantitative computed tomography measures of emphysema and airway wall thickness are related to respiratory symptoms. Am. J. Respir. Crit. Care Med. 2010, 181, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Ostridge, K.; Wilkinson, T.M. Present and future utility of computed tomography scanning in the assessment and management of COPD. Eur. Respir. J. 2016, 48, 216–228. [Google Scholar] [CrossRef] [PubMed]
- Haruna, A.; Muro, S.; Nakano, Y.; Ohara, T.; Hoshino, Y.; Ogawa, E.; Hirai, T.; Niimi, A.; Nishimura, K.; Chin, K.; et al. Ct scan findings of emphysema predict mortality in COPD. Chest 2010, 138, 635–640. [Google Scholar] [CrossRef] [PubMed]
- Johannessen, A.; Skorge, T.D.; Bottai, M.; Grydeland, T.B.; Nilsen, R.M.; Coxson, H.; Dirksen, A.; Omenaas, E.; Gulsvik, A.; Bakke, P. Mortality by level of emphysema and airway wall thickness. Am. J. Respir. Crit. Care Med. 2013, 187, 602–608. [Google Scholar] [CrossRef] [PubMed]
- Celli, B.R.; Decramer, M.; Wedzicha, J.A.; Wilson, K.C.; Agusti, A.A.; Criner, G.J.; MacNee, W.; Make, B.J.; Rennard, S.I.; Stockley, R.A.; et al. An official american thoracic society/european respiratory society statement: Research questions in COPD. Eur. Respir. Rev. 2015, 24, 159–172. [Google Scholar] [CrossRef] [PubMed]
- Parmar, C.; Grossmann, P.; Bussink, J.; Lambin, P.; Aerts, H.J. Machine learning methods for quantitative radiomic biomarkers. Sci. Rep. 2015, 5, 13087. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Chu, C.; Li, Y.; Lu, P.; Wang, W.; Liu, W.; Yu, L. The method and efficacy of support vector machine classifiers based on texture features and multi-resolution histogram from 18F-FDG PET-CT images for the evaluation of mediastinal lymph nodes in patients with lung cancer. Eur. J. Radiol. 2015, 84, 312–317. [Google Scholar] [CrossRef] [PubMed]
- Hoyte, L.C.; Al Sultan, A.S.; Finkelstein, S.; Boyko, M.; Fok, D.; Pordeli, P.; Horn, M.; Neweduk, A.; Yu, A.; Appireddy, R. Reliability of automated software to assign e-ASPECTS to CT scans for acute ischemic changes (s8. 006). Neurology 2017, 88, S8.006. [Google Scholar]
- Quanjer, P.H.; Stanojevic, S.; Cole, T.J.; Baur, X.; Hall, G.L.; Culver, B.H.; Enright, P.L.; Hankinson, J.L.; Ip, M.S.; Zheng, J.; et al. Multi-ethnic reference values for spirometry for the 3-95-yr age range: The global lung function 2012 equations. Eur. Respir. J. 2012, 40, 1324–1343. [Google Scholar] [CrossRef] [PubMed]
- Pellegrino, R.; Viegi, G.; Brusasco, V.; Crapo, R.O.; Burgos, F.; Casaburi, R.; Coates, A.; van der Grinten, C.P.; Gustafsson, P.; Hankinson, J.; et al. Interpretative strategies for lung function tests. Eur. Respir. J. 2005, 26, 948–968. [Google Scholar] [CrossRef]
- Weis, M.; Henzler, T.; Nance, J.W., Jr.; Haubenreisser, H.; Meyer, M.; Sudarski, S.; Schoenberg, S.O.; Neff, K.W.; Hagelstein, C. Radiation dose comparison between 70 kvp and 100 kvp with spectral beam shaping for non-contrast-enhanced pediatric chest computed tomography: A prospective randomized controlled study. Investig. Radiol. 2017, 52, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Haubenreisser, H.; Meyer, M.; Sudarski, S.; Allmendinger, T.; Schoenberg, S.O.; Henzler, T. Unenhanced third-generation dual-source chest CT using a tin filter for spectral shaping at 100 kvp. Eur. J. Radiol. 2015, 84, 1608–1613. [Google Scholar] [CrossRef] [PubMed]
- Gordic, S.; Morsbach, F.; Schmidt, B.; Allmendinger, T.; Flohr, T.; Husarik, D.; Baumueller, S.; Raupach, R.; Stolzmann, P.; Leschka, S.; et al. Ultralow-dose chest computed tomography for pulmonary nodule detection: First performance evaluation of single energy scanning with spectral shaping. Investig. Radiol. 2014, 49, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Gevenois, P.A.; de Maertelaer, V.; De Vuyst, P.; Zanen, J.; Yernault, J.C. Comparison of computed density and macroscopic morphometry in pulmonary emphysema. Am. J. Respir. Crit. Care Med. 1995, 152, 653–657. [Google Scholar] [CrossRef] [PubMed]
- Gevenois, P.A.; De Vuyst, P.; de Maertelaer, V.; Zanen, J.; Jacobovitz, D.; Cosio, M.G.; Yernault, J.C. Comparison of computed density and microscopic morphometry in pulmonary emphysema. Am. J. Respir. Crit. Care Med. 1996, 154, 187–192. [Google Scholar] [CrossRef] [PubMed]
- Madani, A.; Zanen, J.; de Maertelaer, V.; Gevenois, P.A. Pulmonary emphysema: Objective quantification at multi-detector row CT—Comparison with macroscopic and microscopic morphometry. Radiology 2006, 238, 1036–1043. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the IJCAI, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]
- Wong, T.-T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Shao, L.; Fan, X.; Cheng, N.; Wu, L.; Cheng, Y. Determination of minimum training sample size for microarray-based cancer outcome prediction–an empirical assessment. PLoS ONE 2013, 8, e68579. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Timmins, S.C.; Diba, C.; Farrow, C.E.; Schoeffel, R.E.; Berend, N.; Salome, C.M.; King, G.G. The relationship between airflow obstruction, emphysema extent, and small airways function in COPD. Chest 2012, 142, 312–319. [Google Scholar] [CrossRef]
- Schroeder, J.D.; McKenzie, A.S.; Zach, J.A.; Wilson, C.G.; Curran-Everett, D.; Stinson, D.S.; Newell, J.D., Jr.; Lynch, D.A. Relationships between airflow obstruction and quantitative CT measurements of emphysema, air trapping, and airways in subjects with and without chronic obstructive pulmonary disease. Am. J. Roentgenol. 2013, 201, W460–W470. [Google Scholar] [CrossRef] [PubMed]
- Lynch, D.A.; Austin, J.H.; Hogg, J.C.; Grenier, P.A.; Kauczor, H.U.; Bankier, A.A.; Barr, R.G.; Colby, T.V.; Galvin, J.R.; Gevenois, P.A.; et al. CT-definable subtypes of chronic obstructive pulmonary disease: A statement of the fleischner society. Radiology 2015, 277, 192–205. [Google Scholar] [CrossRef]
- Gawlitza, J.; Haubenreisser, H.; Henzler, T.; Akin, I.; Schönberg, S.; Borggrefe, M.; Trinkmann, F. Finding the right spot: Where to measure airway parameters in patients with COPD. Eur. J. Radiol. 2018, 104, 87–93. [Google Scholar] [CrossRef]
- Matsuoka, S.; Kurihara, Y.; Yagihashi, K.; Hoshino, M.; Nakajima, Y. Airway dimensions at inspiratory and expiratory multisection CT in chronic obstructive pulmonary disease: Correlation with airflow limitation. Radiology 2008, 248, 1042–1049. [Google Scholar] [CrossRef]
- Camiciottoli, G.; Bartolucci, M.; Maluccio, N.M.; Moroni, C.; Mascalchi, M.; Giuntini, C.; Pistolesi, M. Spirometrically gated high-resolution CT findings in COPD: Lung attenuation vs. lung function and dyspnea severity. Chest 2006, 129, 558–564. [Google Scholar] [CrossRef]
- Gu, S.; Leader, J.; Zheng, B.; Chen, Q.; Sciurba, F.; Kminski, N.; Gur, D.; Pu, J. Direct assessment of lung function in COPD using CT densitometric measures. Physiol. Meas. 2014, 35, 833–845. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.-P.; Sahiner, B.; Hadjiiski, L. Sample Size and Validation Issues on the Development of CAD Systems; International Congress Series; Elsevier: Amsterdam, The Netherlands, 2004; pp. 872–877. [Google Scholar]
- Fukunaga, K.; Hayes, R.R. Effects of sample size in classifier design. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 873–885. [Google Scholar] [CrossRef]
- Baldi, S.; Miniati, M.; Bellina, C.R.; Battolla, L.; Catapano, G.; Begliomini, E.; Giustini, D.; Giuntini, C. Relationship between extent of pulmonary emphysema by high-resolution computed tomography and lung elastic recoil in patients with chronic obstructive pulmonary disease. Am. J. Respir. Crit. Care Med. 2001, 164, 585–589. [Google Scholar] [CrossRef] [PubMed]
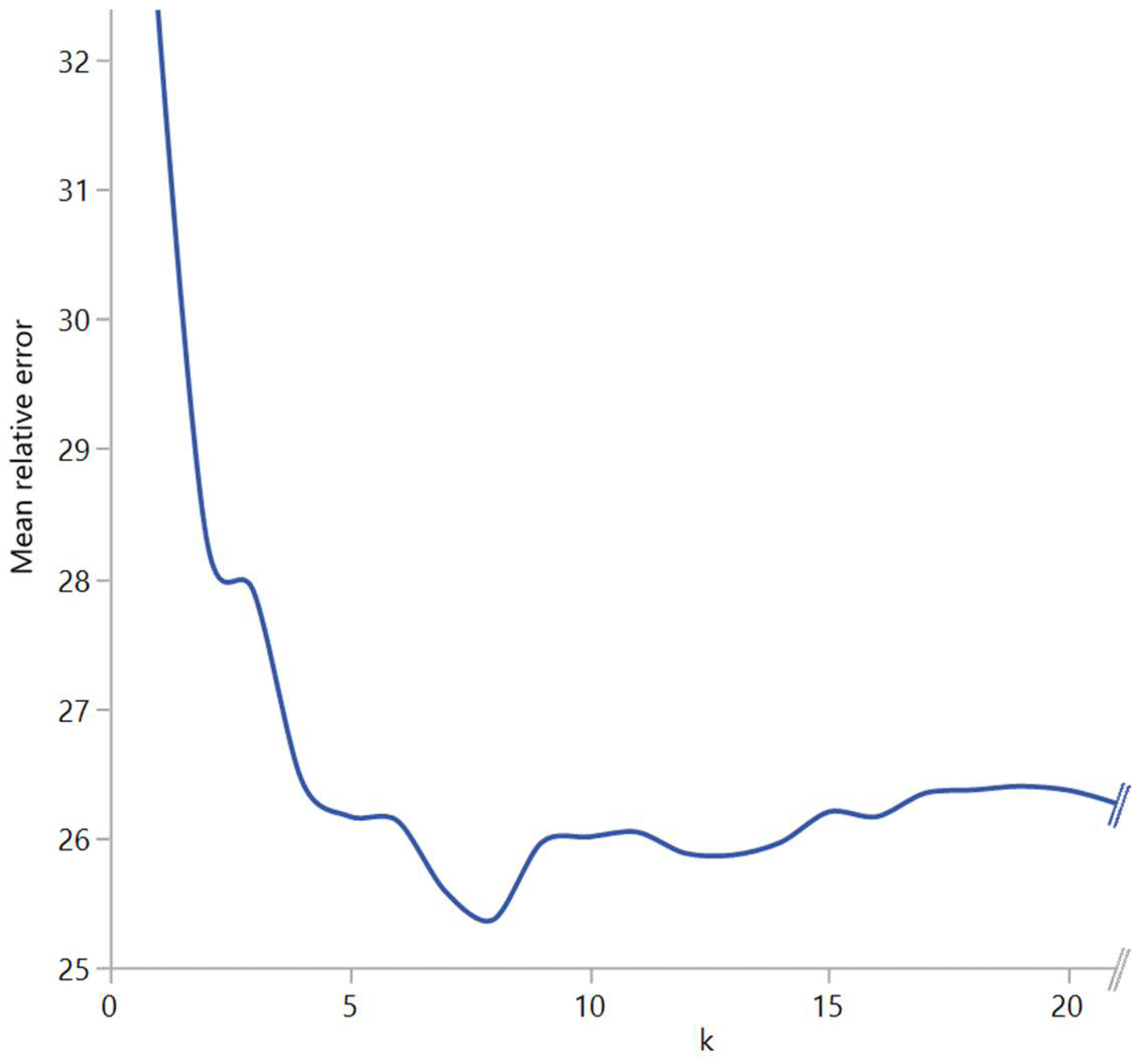
| ks and Degrees with Lowest Mean Relative Errors | ||
|---|---|---|
| k with Best MRE | Degree with Best MRE | |
| Inspiration %FEV1 | 23 | 1 |
| Inspiration %FEV1/VC | 14 | 1 |
| Inspiration RV/TLC | 13 | 2 |
| Expiration %FEV1 | 6 | 3 |
| Expiration %FEV1/VC | 13 | 2 |
| Expiration RV/TLC | 7 | 3 |
| Delta %FEV1 | 7 | 2 |
| Delta %FEV1/VC | 12 | 1 |
| Delta RV/TLC | 8 | 1 |
| Lung Function Values from Body Plethysmorgraphy and Predicted Lung Function Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured Values | Mean Prediction | Median Prediction | kNN | Polynomial Regression | Neural Network | XGBoost | p-Value | ||
| inspiration | %FEV1 | 56 ± 6 | 56 ± 0.3 | 48 ± 0.1 | 56 ± 6 | 55 ± 13 | 55 ± 13 | 56 ± 16 | 0.0024 |
| %FEV1/VC | 55 ± 7 | 56 ± 0.1 | 54 ± 0.1 | 55 ± 7 | 56 ± 7 | 56 ± 7 | 56 ± 10 | 0.732 | |
| RV/TLC | 59 ± 6 | 60 ± 0.2 | 61 ± 0.5 | 59 ± 6 | 60 ± 10 | 60 ± 11 | 59 ± 11 | 0.96 | |
| expiration | %FEV1 | 53 ± 12 | 56 ± 0.3 | 48 ± 0.1 | 53 ± 12 | 56 ± 14 | 55 ± 14 | 56 ± 16 | 0.0078 |
| %FEV1/VC | 55 ± 8 | 56 ± 0.1 | 54 ± 0.1 | 55 ± 8 | 56 ± 8 | 56 ± 8 | 56 ± 11 | 0.6 | |
| RV/TLC | 61 ± 9 | 60 ± 0.2 | 61 ± 0.5 | 61 ± 9 | 59 ± 11 | 59 ± 12 | 59 ± 12 | 0.7996 | |
| delta | %FEV1 | 56 ± 13 | 56 ± 0.3 | 48 ± 0.1 | 56 ± 13 | 56 ± 14 | 49 ± 27 | 56 ± 16 | 0.002 |
| %FEV1/VC | 55 ± 8 | 56 ± 0.1 | 54 ± 0.1 | 55 ± 8 | 56 ± 8 | 49 ± 25 | 56 ± 11 | 0.0005 | |
| RV/TLC | 59 ± 8 | 60 ± 0.2 | 61 ± 0.5 | 59 ± 8 | 59 ± 8 | 54 ± 26 | 58 ± 13 | 0.0522 | |
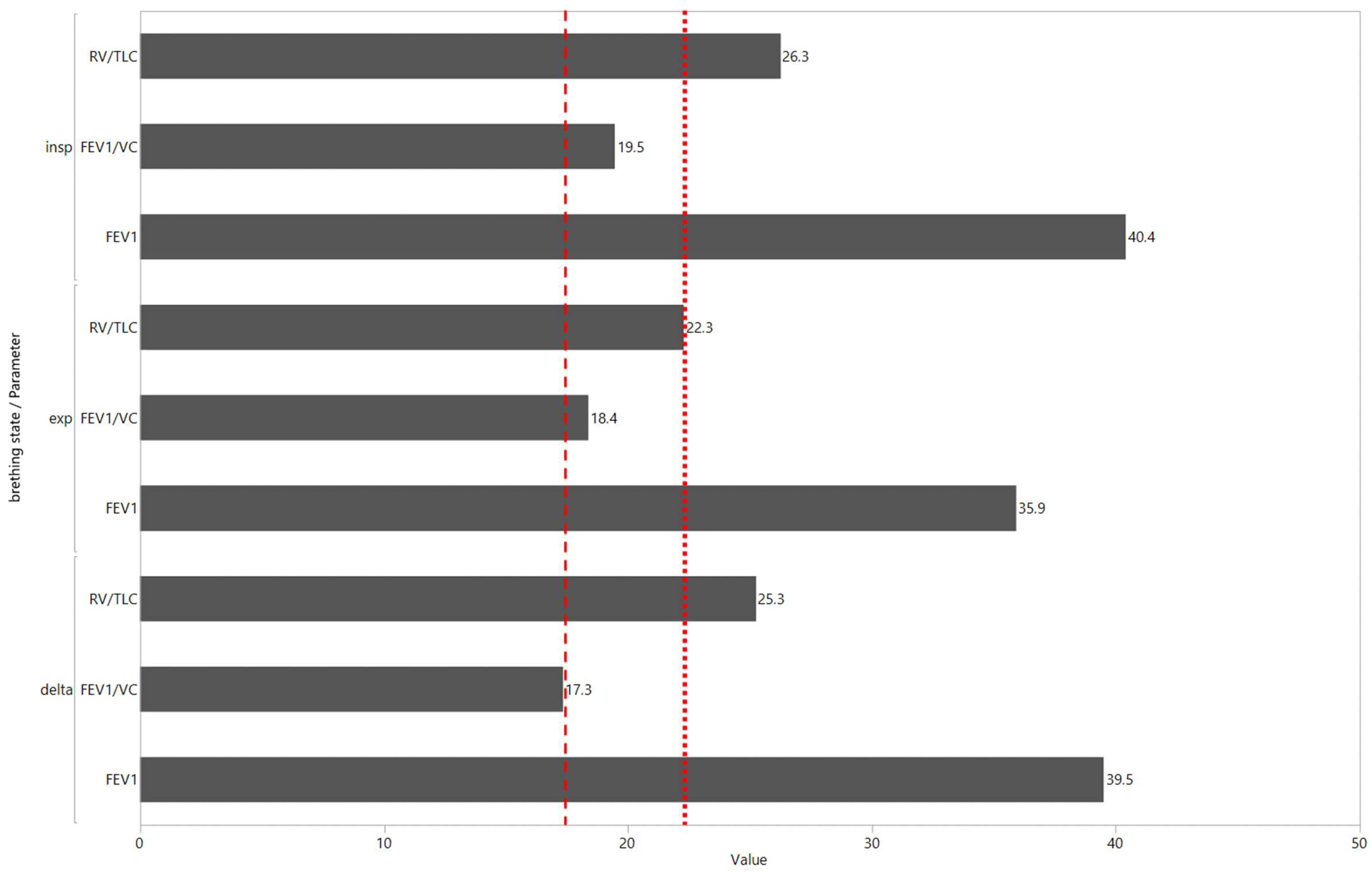
| Absolute and Relative Errors of Predicted Lung Function Values | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Prediction | Median Prediction | kNN | Polynomial Regression | Neural Network | XGBoost | ||||||||
| MAR | MRE | MAR | MRE | MAR | MRE | MAR | MRE | MAR | MRE | MAR | MRE | ||
| inspiration | %FEV1 | 21 ± 13 | 46 ± 43 | 20 ± 16 | 39 ± 6 | 19 ± 13 | 43 ± 39 | 19 ± 13 | 40 ± 37 | 20 ± 13 | 41 ± 34 | 22 ± 18 | 47 ± 50 |
| %FEV1/VC | 12 ± 8 | 22 ± 17 | 11 ± 8 | 21 ± 12 | 9 ± 8 | 17 ± 15 | 10 ± 7 | 19 ± 15 | 12 ± 8 | 22 ± 17 | 10 ± 8 | 19 ± 16 | |
| RV/TLC | 14 ± 10 | 30 ± 40 | 14 ± 10 | 31 ± 42 | 13 ± 9 | 28 ± 38 | 12 ± 8 | 26 ± 36 | 13 ± 9 | 27 ± 39 | 14 ± 12 | 31 ± 46 | |
| expiration | %FEV1 | 21 ± 13 | 46 ± 43 | 20 ± 16 | 39 ± 6 | 18 ± 15 | 36 ± 37 | 17 ± 13 | 36 ± 37 | 19 ± 14 | 41 ± 36 | 22 ± 16 | 46 ± 45 |
| %FEV1/VC | 12 ± 8 | 22 ± 17 | 11 ± 8 | 21 ± 12 | 9 ± 8 | 16 ± 14 | 10 ± 7 | 18 ± 15 | 12 ± 8 | 22 ± 17 | 10 ± 8 | 20 ± 17 | |
| RV/TLC | 14 ± 10 | 30 ± 40 | 14 ± 10 | 31 ± 42 | 11 ± 9 | 25 ± 31 | 11 ± 8 | 22 ± 28 | 11 ± 8 | 22 ± 25 | 12 ± 9 | 24 ± 26 | |
| delta | %FEV1 | 21 ± 13 | 46 ± 43 | 20 ± 16 | 39 ± 6 | 18 ± 15 | 39 ± 42 | 19 ± 15 | 40 ± 37 | 21 ± 19 | 38 ± 35 | 18 ± 15 | 40 ± 46 |
| %FEV1/VC | 12 ± 8 | 22 ± 17 | 11 ± 8 | 21 ± 12 | 9 ± 8 | 16 ± 14 | 9 ± 8 | 17 ± 15 | 20 ± 16 | 35 ± 25 | 9 ± 8 | 17 ± 16 | |
| RV/TLC | 14 ± 10 | 30 ± 40 | 14 ± 10 | 31 ± 42 | 12 ± 9 | 25 ± 30 | 12 ± 10 | 25 ± 30 | 26 ± 22 | 47 ± 49 | 14 ± 12 | 29 ± 34 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gawlitza, J.; Sturm, T.; Spohrer, K.; Henzler, T.; Akin, I.; Schönberg, S.; Borggrefe, M.; Haubenreisser, H.; Trinkmann, F. Predicting Pulmonary Function Testing from Quantified Computed Tomography Using Machine Learning Algorithms in Patients with COPD. Diagnostics 2019, 9, 33. https://doi.org/10.3390/diagnostics9010033
Gawlitza J, Sturm T, Spohrer K, Henzler T, Akin I, Schönberg S, Borggrefe M, Haubenreisser H, Trinkmann F. Predicting Pulmonary Function Testing from Quantified Computed Tomography Using Machine Learning Algorithms in Patients with COPD. Diagnostics. 2019; 9(1):33. https://doi.org/10.3390/diagnostics9010033
Chicago/Turabian StyleGawlitza, Joshua, Timo Sturm, Kai Spohrer, Thomas Henzler, Ibrahim Akin, Stefan Schönberg, Martin Borggrefe, Holger Haubenreisser, and Frederik Trinkmann. 2019. "Predicting Pulmonary Function Testing from Quantified Computed Tomography Using Machine Learning Algorithms in Patients with COPD" Diagnostics 9, no. 1: 33. https://doi.org/10.3390/diagnostics9010033
APA StyleGawlitza, J., Sturm, T., Spohrer, K., Henzler, T., Akin, I., Schönberg, S., Borggrefe, M., Haubenreisser, H., & Trinkmann, F. (2019). Predicting Pulmonary Function Testing from Quantified Computed Tomography Using Machine Learning Algorithms in Patients with COPD. Diagnostics, 9(1), 33. https://doi.org/10.3390/diagnostics9010033





