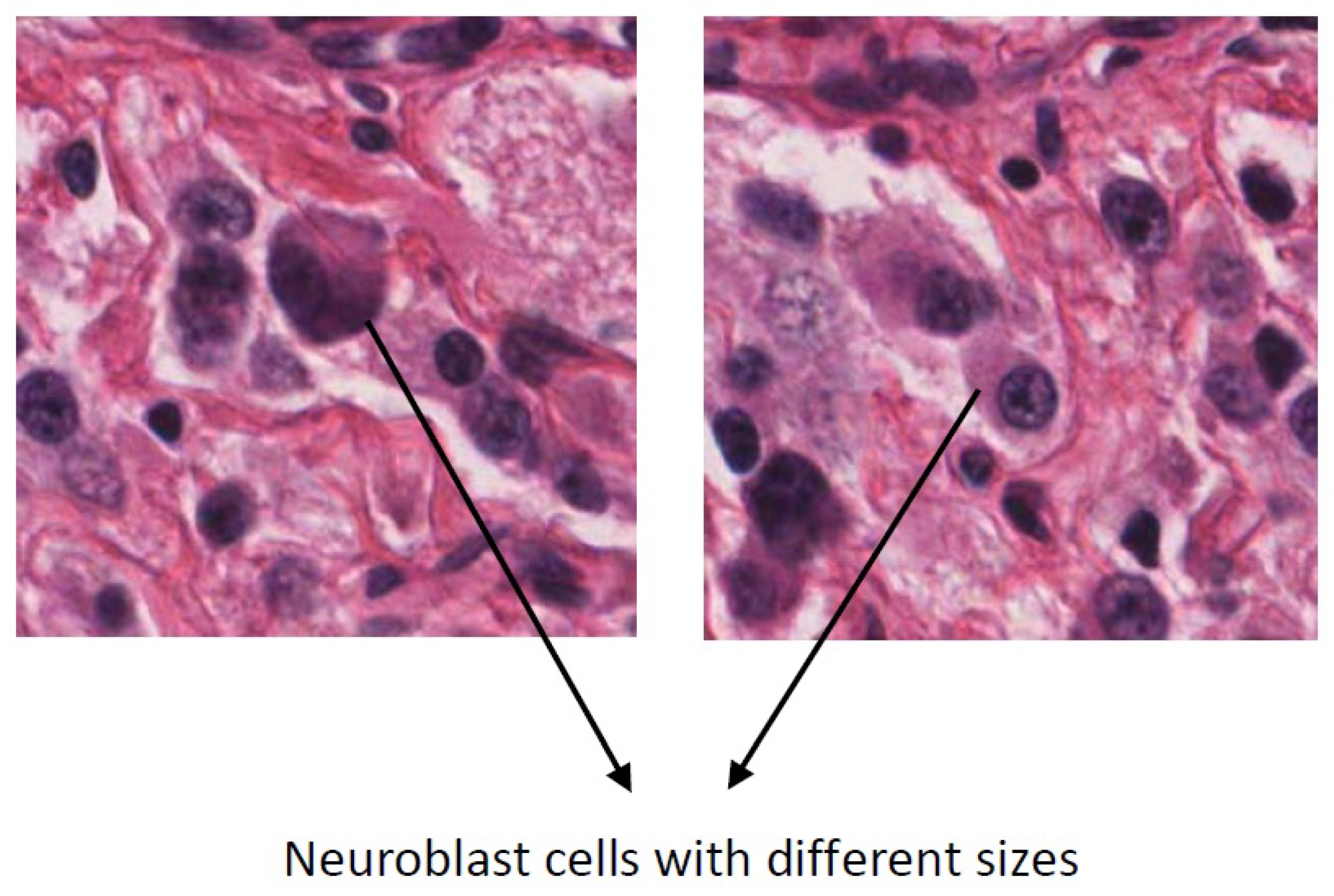
Figure 1.
High intra-class variation in the size of the neuroblast cells.
Figure 1.
High intra-class variation in the size of the neuroblast cells.
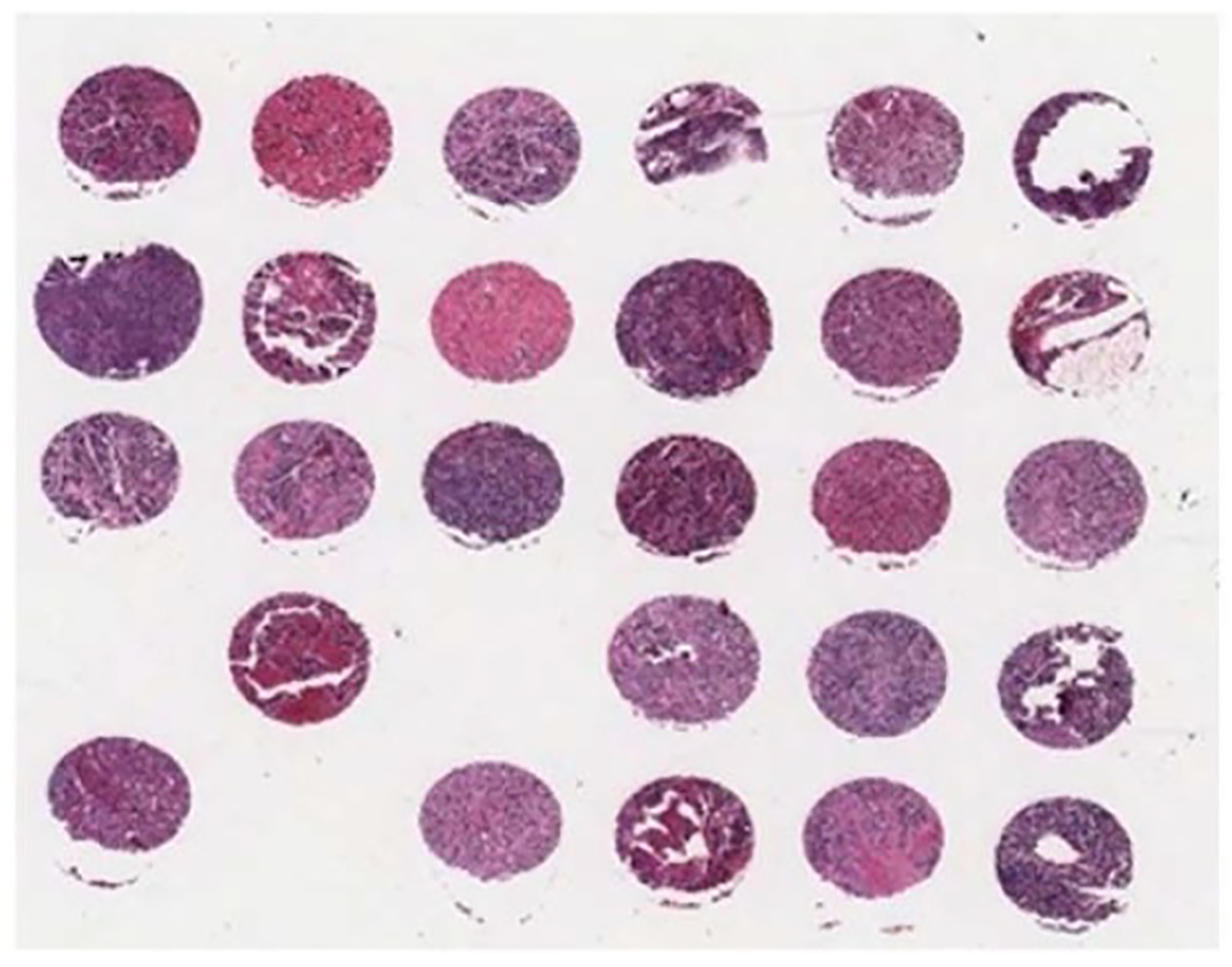
Figure 2.
A sample of tissue microarray (TMA) slide.
Figure 2.
A sample of tissue microarray (TMA) slide.
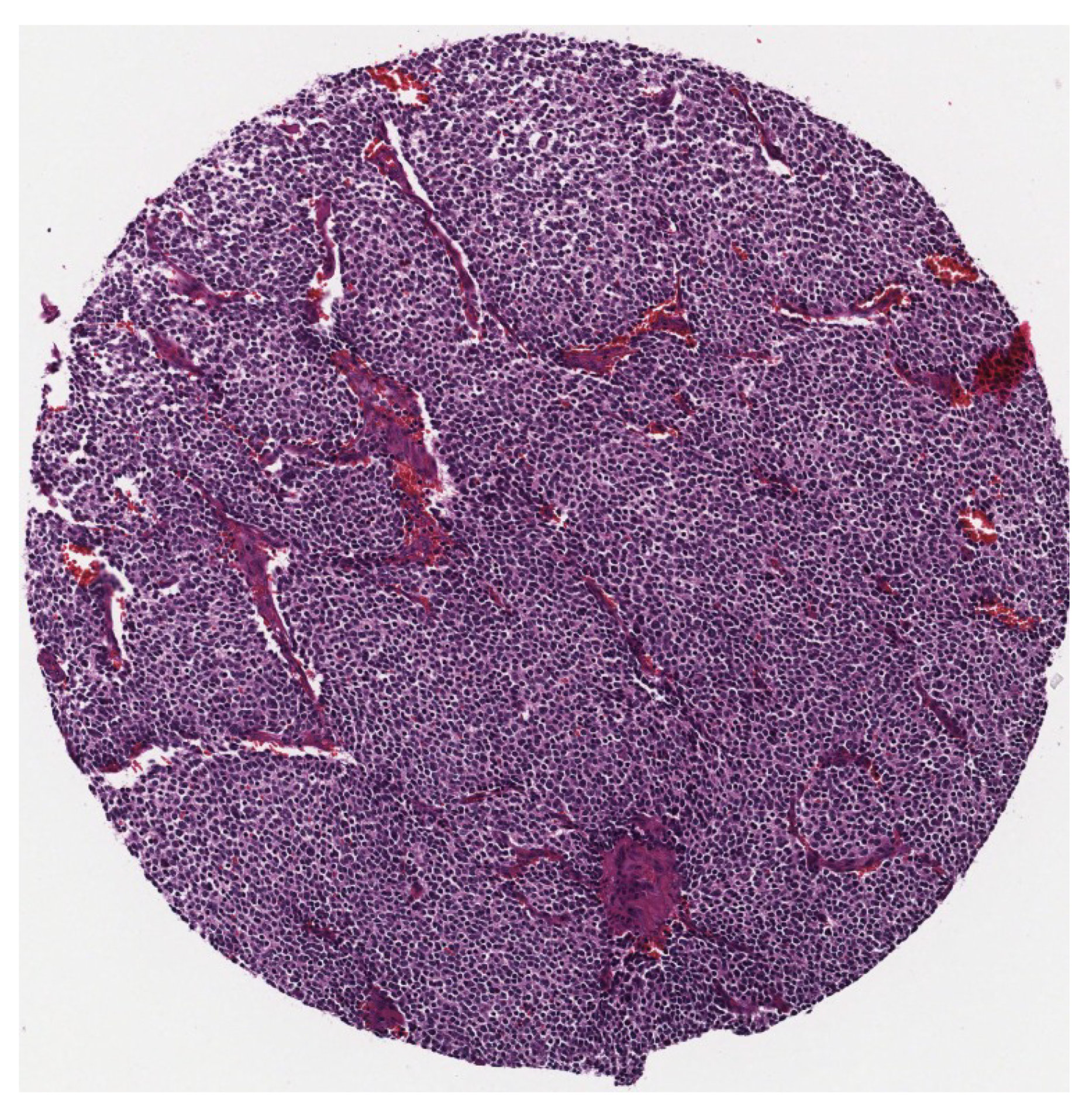
Figure 3.
A sample of a single tumour.
Figure 3.
A sample of a single tumour.
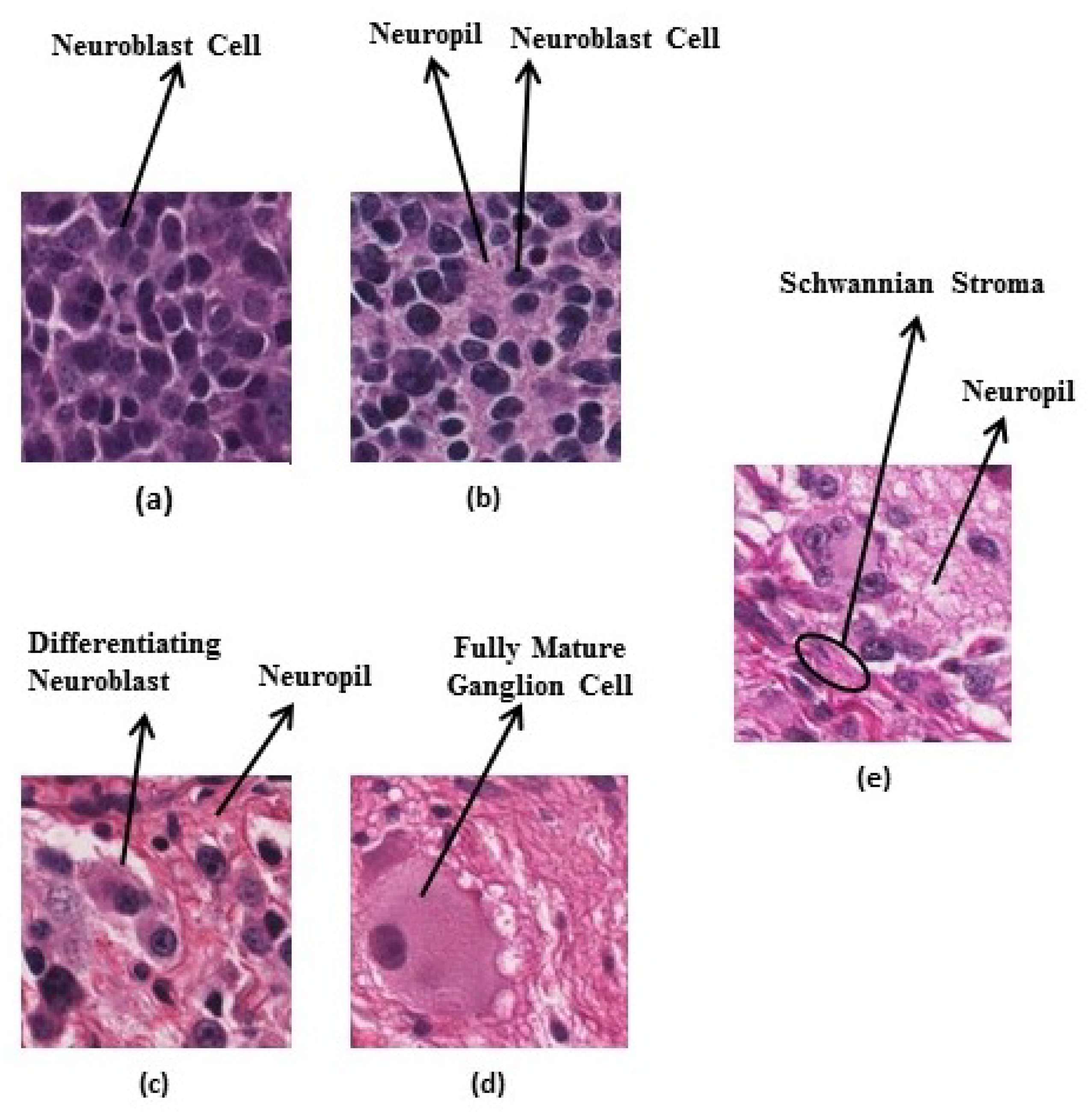
Figure 4.
Neuroblastic tumour categories: (a) undifferentiated neuroblastoma, (b) poorly-differentiated neuroblastoma, (c) differentiating neuroblastoma, (d) ganglioneuroma, and (e) ganglioneuroblastoma.
Figure 4.
Neuroblastic tumour categories: (a) undifferentiated neuroblastoma, (b) poorly-differentiated neuroblastoma, (c) differentiating neuroblastoma, (d) ganglioneuroma, and (e) ganglioneuroblastoma.
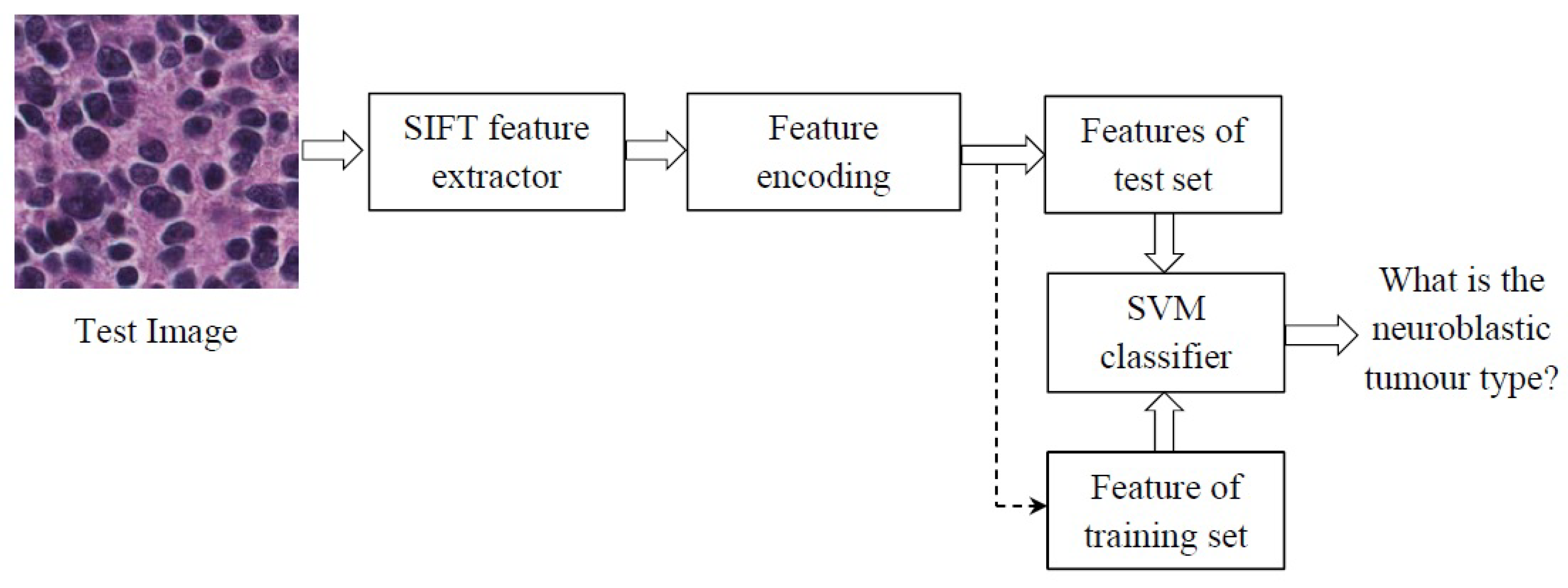
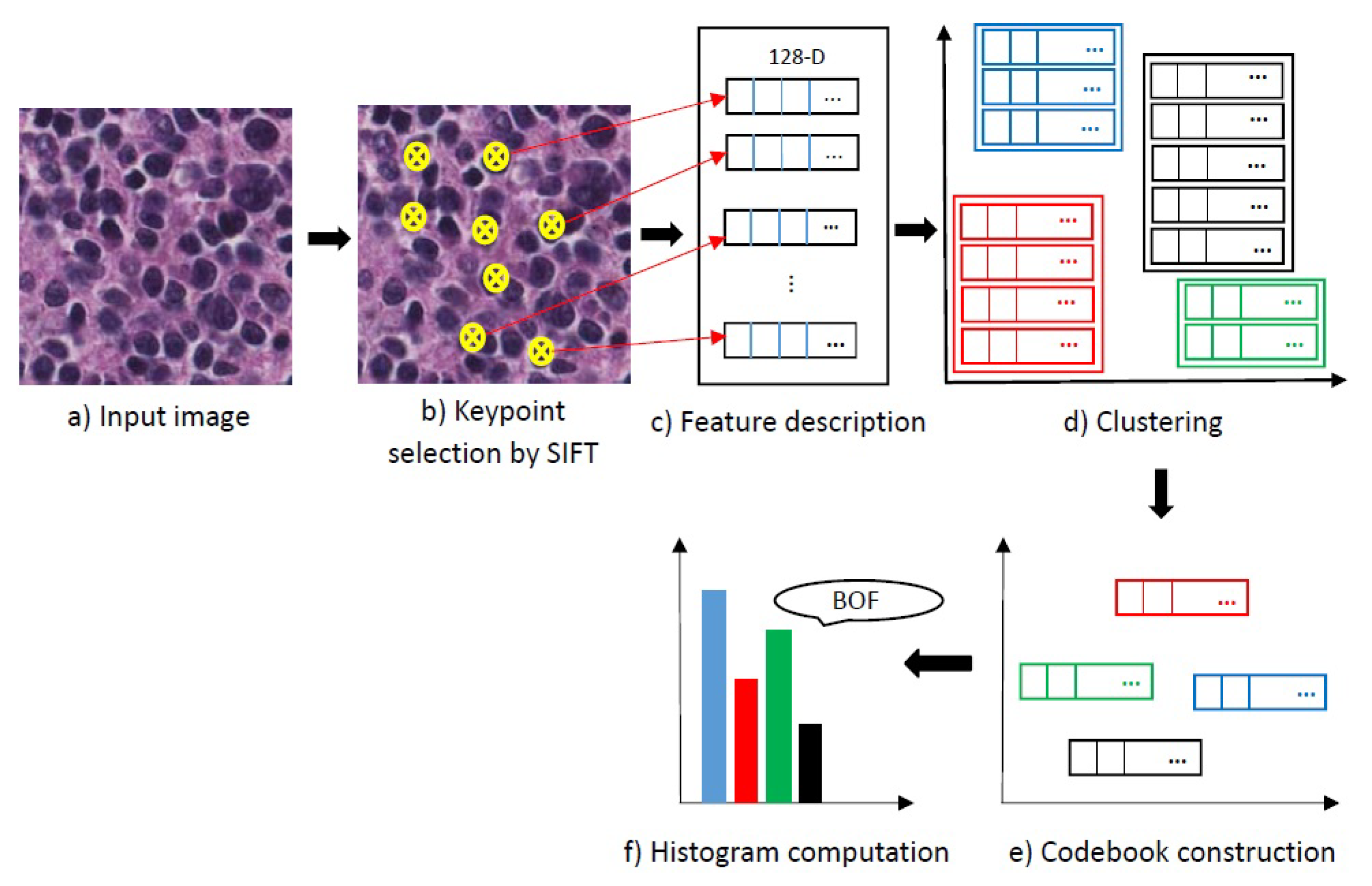
Figure 5.
The scheme of the proposed method. SIFT, Scale Invariant Feature Transform; SVM, Support Vector Machine.
Figure 5.
The scheme of the proposed method. SIFT, Scale Invariant Feature Transform; SVM, Support Vector Machine.
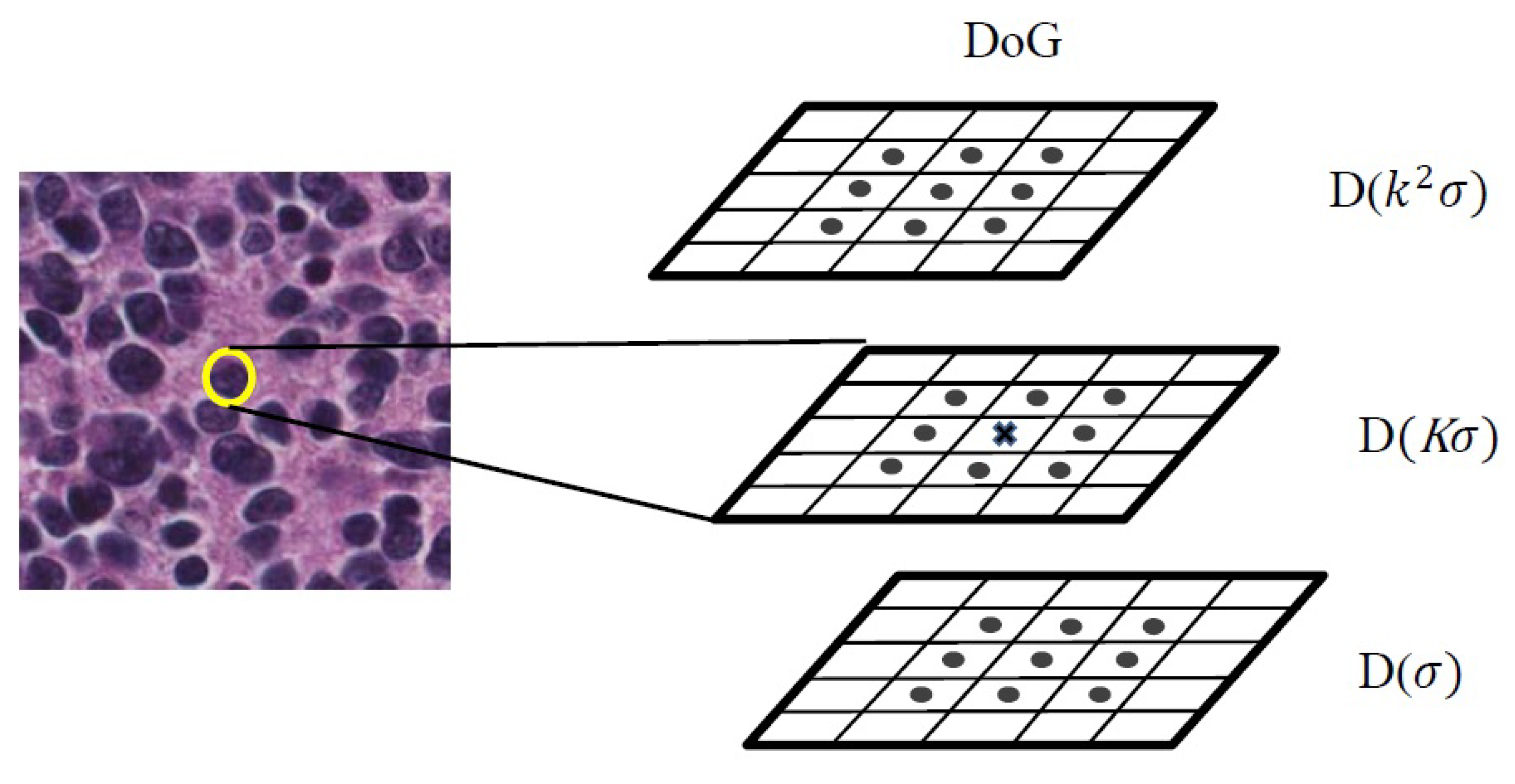
Figure 6.
The scheme of keypoint detecting. DoG, Difference of Gaussian.
Figure 6.
The scheme of keypoint detecting. DoG, Difference of Gaussian.
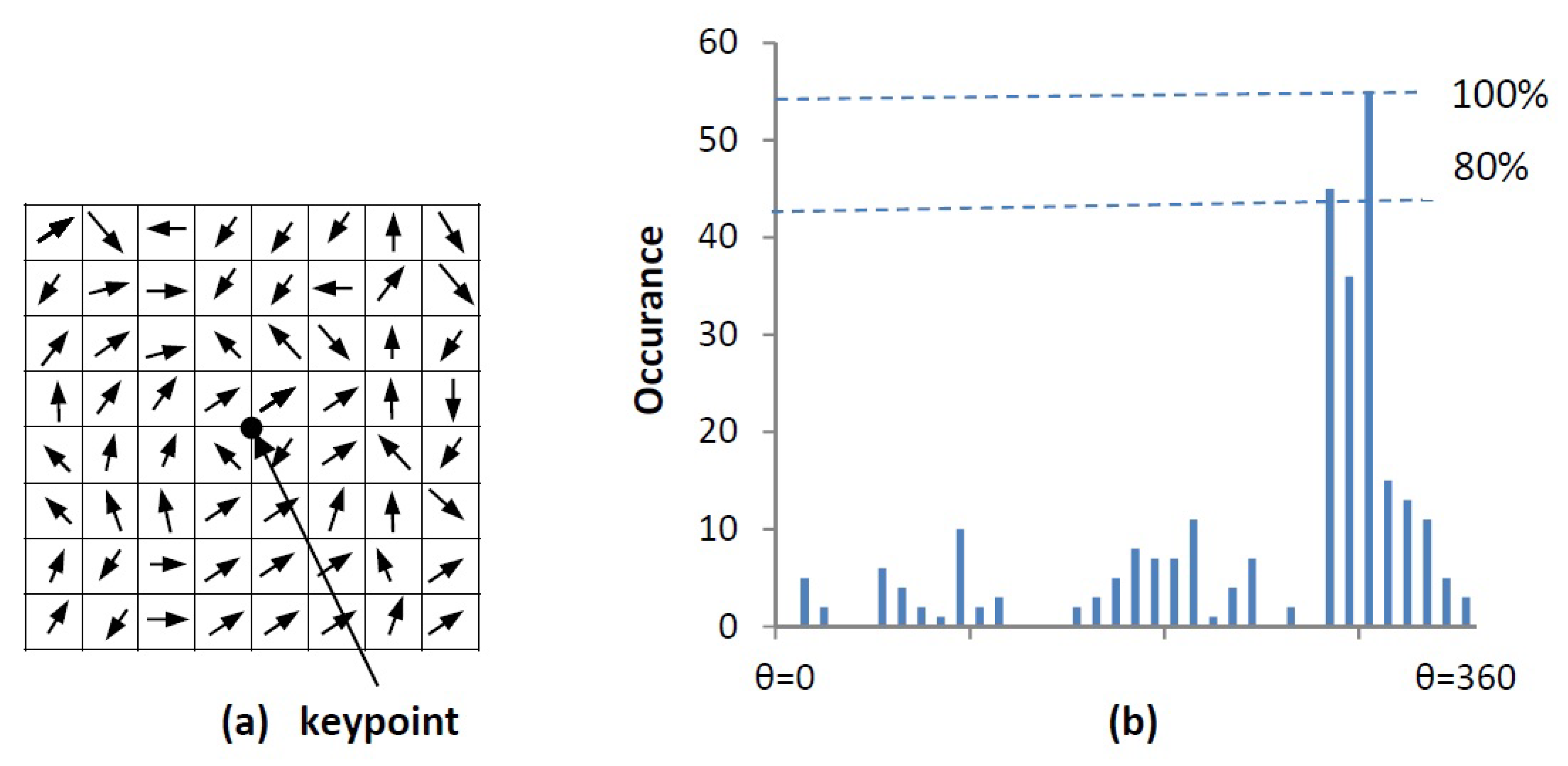
Figure 7.
Orientation calculation: (a) gradient orientations of sample points within a region around the keypoint (b) orientation histogram.
Figure 7.
Orientation calculation: (a) gradient orientations of sample points within a region around the keypoint (b) orientation histogram.
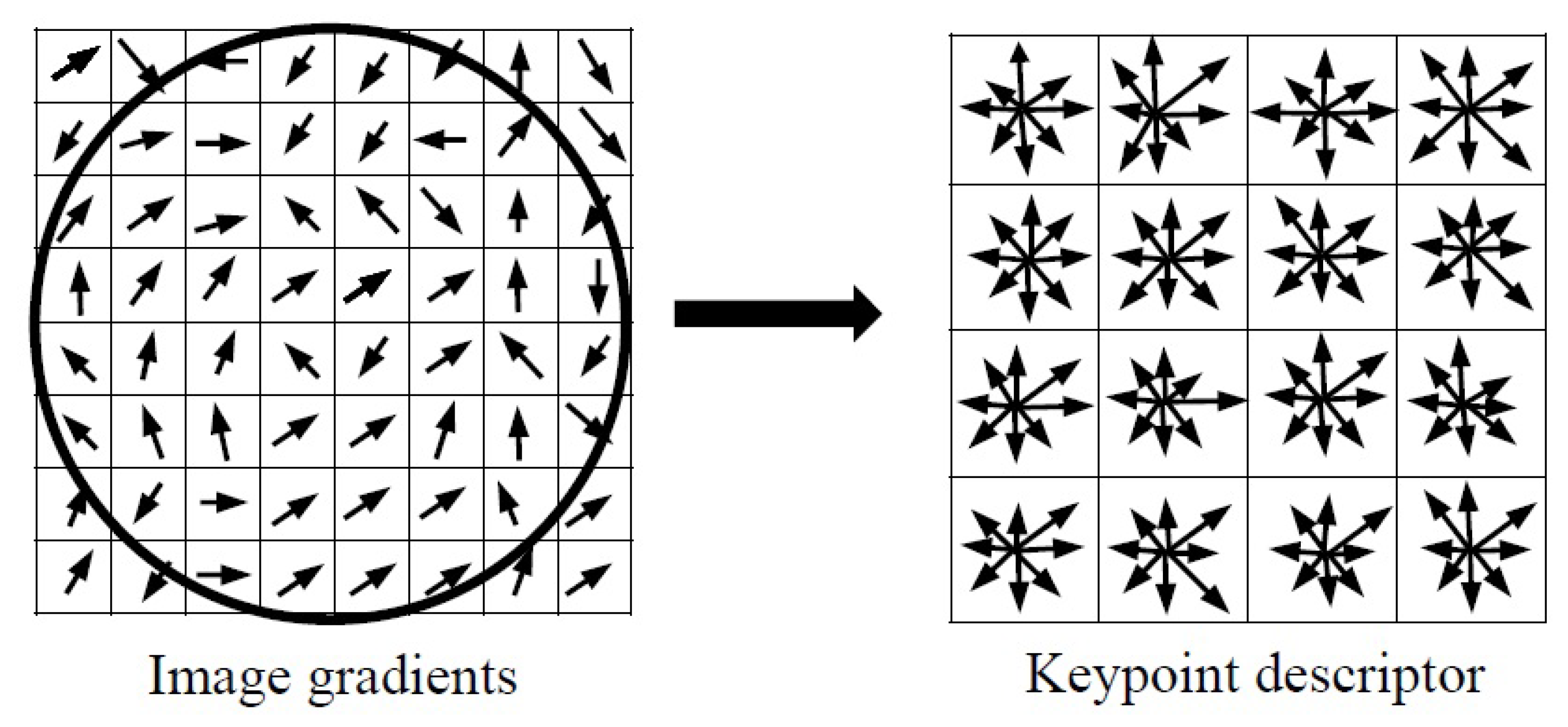
Figure 8.
Keypoint descriptor: (left) gradient magnitude and orientation are calculated in a region around the keypoint (right) a neighborhood around the keypoint is divided to subregions. In each subregion the gradient vectors are accumulated into 8-bins orientation histograms.
Figure 8.
Keypoint descriptor: (left) gradient magnitude and orientation are calculated in a region around the keypoint (right) a neighborhood around the keypoint is divided to subregions. In each subregion the gradient vectors are accumulated into 8-bins orientation histograms.
Figure 9.
Scheme of the feature encoding block. Different colours indicate different clusters and different codewords. BOF, Bag of Features.
Figure 9.
Scheme of the feature encoding block. Different colours indicate different clusters and different codewords. BOF, Bag of Features.
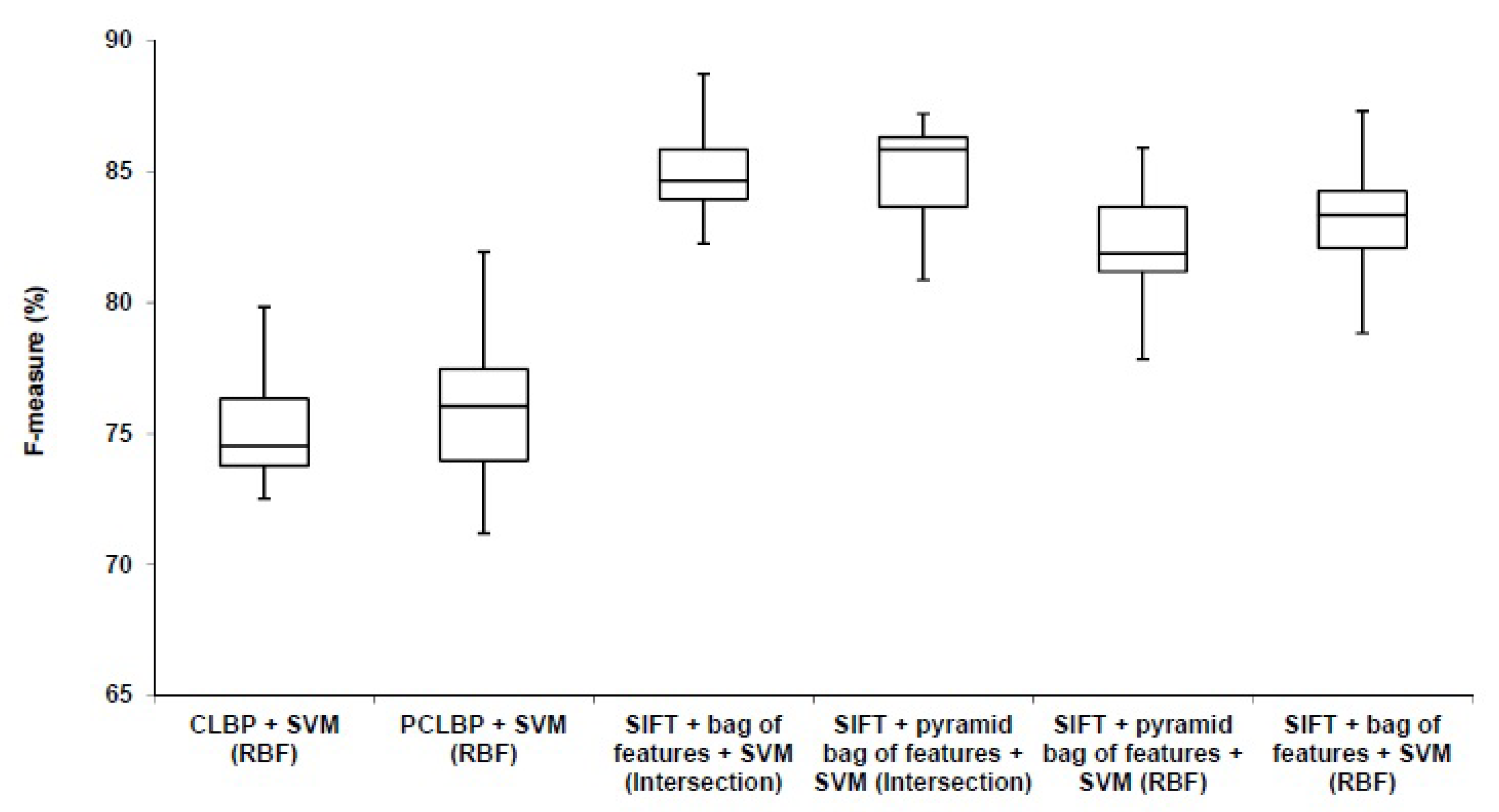
Figure 10.
Comparison between our algorithm (SIFT + bag of feature) with the benchmarks (CLBP) and (PCLBP).
Figure 10.
Comparison between our algorithm (SIFT + bag of feature) with the benchmarks (CLBP) and (PCLBP).
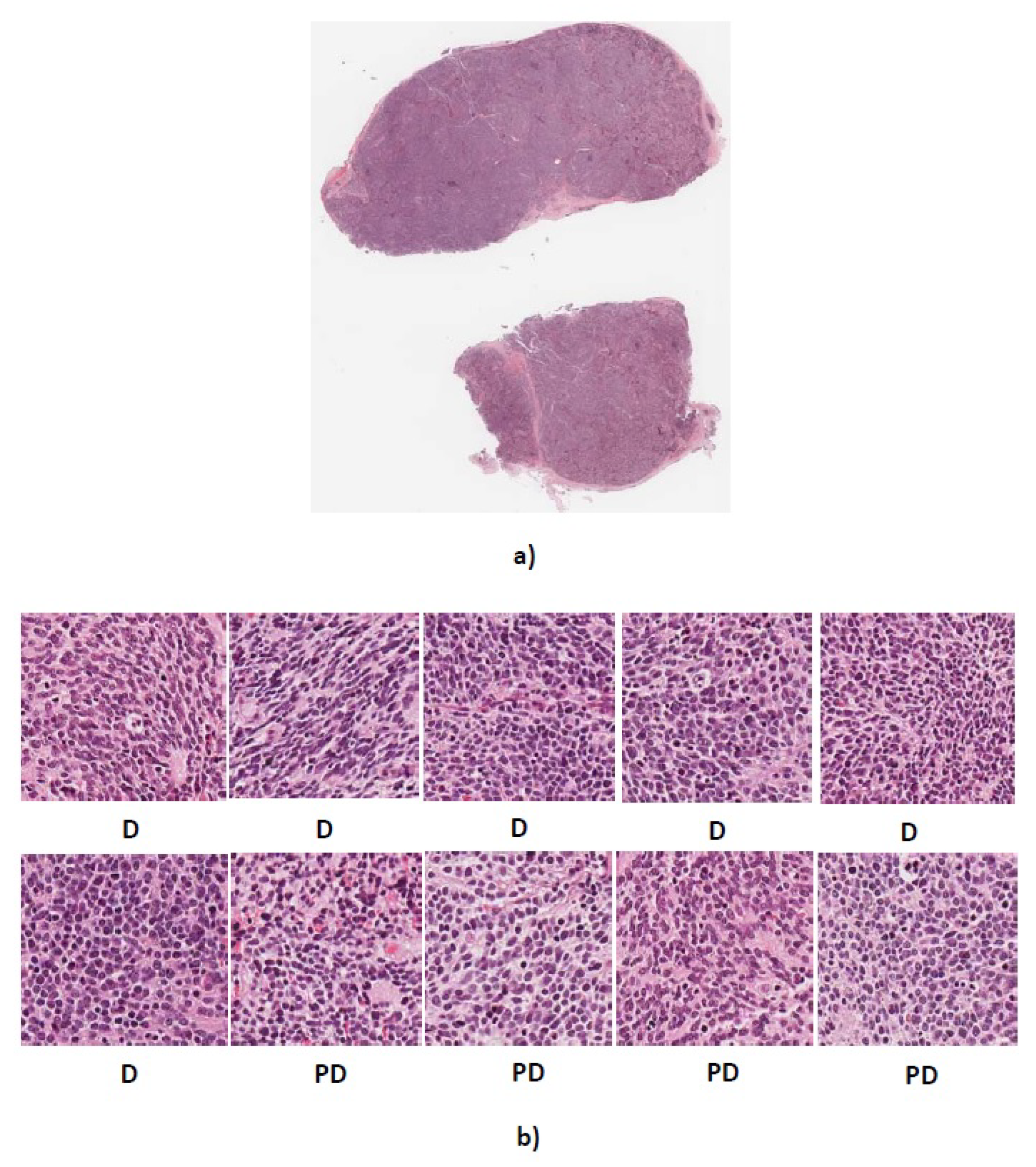
Figure 11.
(a) Whole tissue section 4906 with actual label PD (b) Predicted labels for ten randomly cropped images from whole tissue section. D, differentiating neuroblastoma; PD, poorly-differentiated neuroblastoma.
Figure 11.
(a) Whole tissue section 4906 with actual label PD (b) Predicted labels for ten randomly cropped images from whole tissue section. D, differentiating neuroblastoma; PD, poorly-differentiated neuroblastoma.
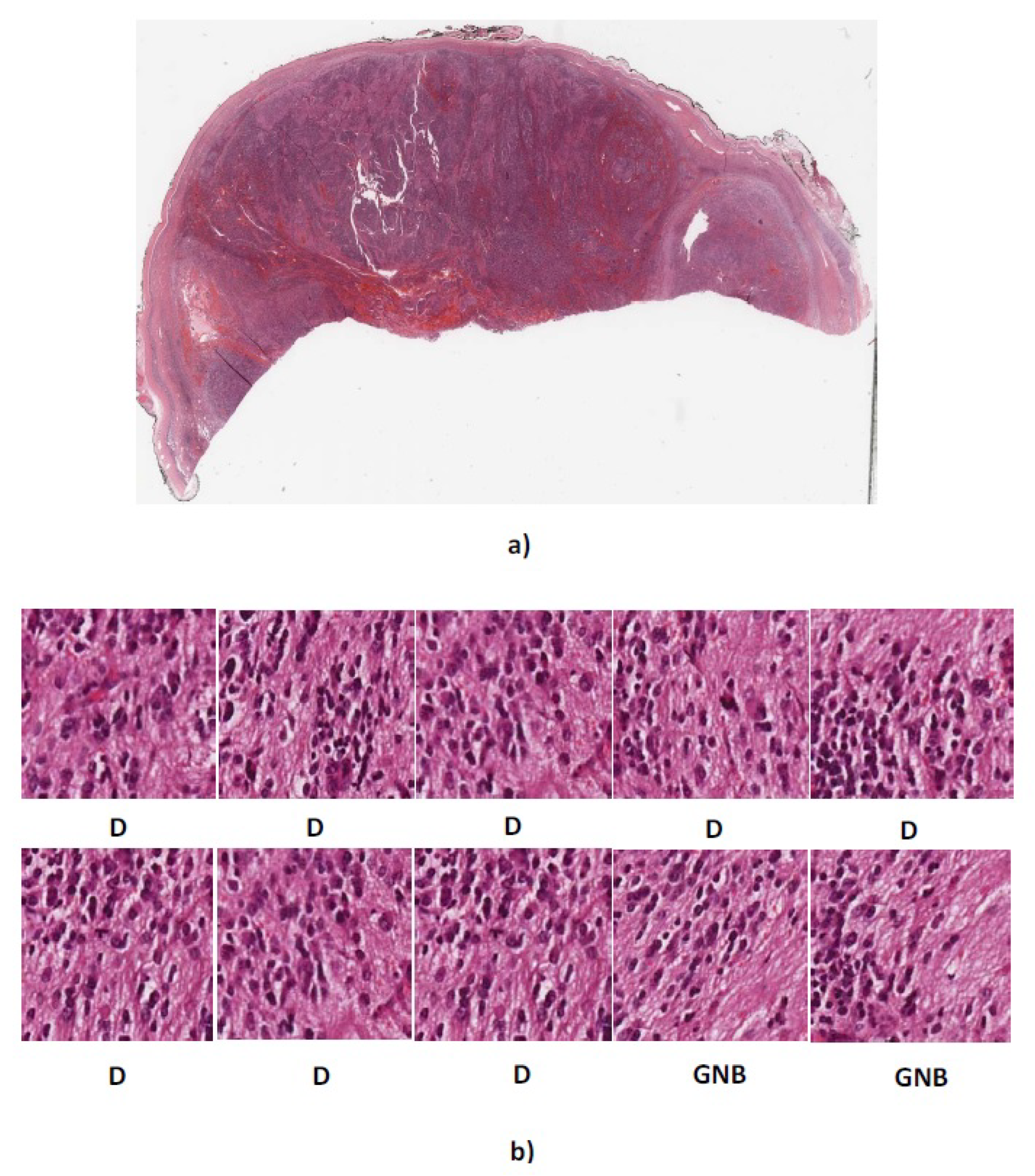
Figure 12.
(a) Whole tissue section 4909 with actual label GNB (b) Predicted labels for ten randomly cropped images from whole tissue section. D, differentiating neuroblastoma; GNB = ganglioneuroblastoma.
Figure 12.
(a) Whole tissue section 4909 with actual label GNB (b) Predicted labels for ten randomly cropped images from whole tissue section. D, differentiating neuroblastoma; GNB = ganglioneuroblastoma.
Table 1.
Number of different categories of neuroblastic tumour cropped images.
Table 1.
Number of different categories of neuroblastic tumour cropped images.
| Category of Neuroblastic Tumour | Number of Cropped Images | Number of Patients |
|---|
| poorly-differentiated | 571 | 77 |
| differentiating | 187 | 12 |
| undifferentiated | 155 | 10 |
| ganglioneuroma | 84 | 18 |
| ganglioneuroblastoma | 46 | 8 |
| Total | 1043 | 125 |
Table 2.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different values for . Bold value indicates the highest classification accuracy.
Table 2.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different values for . Bold value indicates the highest classification accuracy.
| Classification Accuracy (%) |
|---|
| 0.1 | 73.02 |
| 0.5 | 73.25 |
| 0.9 | 75.24 |
| 1.3 | 76.52 |
| 1.7 | 78.96 |
| 2.1 | 76.24 |
Table 3.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different values for contrast threshold (). Bold value indicates the highest classification accuracy.
Table 3.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different values for contrast threshold (). Bold value indicates the highest classification accuracy.
| Contrast Threshold | Classification Accuracy (%) |
|---|
| 0.02 | 73.19 |
| 0.03 | 76.21 |
| 0.04 | 76.58 |
| 0.05 | 75.68 |
| 0.06 | 74.25 |
Table 4.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different values for edge threshold (). Bold value indicates the highest classification accuracy.
Table 4.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different values for edge threshold (). Bold value indicates the highest classification accuracy.
| Edge Threshold | Classification Accuracy (%) |
|---|
| 5 | 78.25 |
| 11 | 81.76 |
| 17 | 77.24 |
| 23 | 76.15 |
| 29 | 74.18 |
Table 5.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different codebook sizes. Bold value indicates the highest classification accuracy.
Table 5.
Average classification accuracy of the SIFT over neuroblastic tumour dataset using different codebook sizes. Bold value indicates the highest classification accuracy.
| Size of the Codebook | Classification Accuracy (%) |
|---|
| 300 | 78.2 |
| 400 | 80.31 |
| 500 | 82.25 |
| 600 | 79.77 |
| 700 | 81.62 |
Table 6.
Weighted average precision, recall and F-measure of the proposed method and benchmarks. Bold value indicates the highest F-measure. CLBP, Completed Local Binary Pattern; SVM, Support Vector Machine; RBF, Radial Basis Function; PCLBP, Patched Completed Local Binary Pattern; SIFT, Scale Invariant Feature Transform.
Table 6.
Weighted average precision, recall and F-measure of the proposed method and benchmarks. Bold value indicates the highest F-measure. CLBP, Completed Local Binary Pattern; SVM, Support Vector Machine; RBF, Radial Basis Function; PCLBP, Patched Completed Local Binary Pattern; SIFT, Scale Invariant Feature Transform.
| Method | Precision (%) | Recall (%) | F-measure (%) |
|---|
| CLBP + SVM (RBF) | 74.1 ± 2.35 | 76.25 ± 2.23 | 75.15 ± 2.28 |
| PCLBP + SVM (RBF) | 75.59 ± 3.15 | 76.35 ± 3.41 | 75.96 ± 3.27 |
| SIFT + bag of features + SVM (RBF) | 81.62 ± 3.72 | 84.54 ± 1.66 | 83.03 ± 2.63 |
| SIFT + pyramid bag of features + SVM (RBF) | 80.63 ± 3.55 | 83.57 ± 1.81 | 82.08 ± 2.65 |
| SIFT + bag of features + SVM (histogram intersection) | 83.81 ± 3.33 | 86.61 ± 1.87 | 85.19 ± 2.42 |
| SIFT + pyramid bag of features + SVM (histogram intersection) | 83.5 ± 3.64 | 86.41 ± 1.22 | 84.93 ± 2.35 |
Table 7.
A representative confusion matrix for dataset from Children’s Hospital at Westmead.
Table 7.
A representative confusion matrix for dataset from Children’s Hospital at Westmead.
| | | | | Predicted | | |
|---|
| | | Differentiating | Ganglio- | Ganglio- | Poorly- | |
| | | | | | differentiated | Undifferentiated |
| | | neuroblastoma | neuroma | neuroblastoma | neuroblastoma | neuroblastoma |
| | Differentiating | | | | | |
| | neuroblastoma | 6 | 1 | 4 | 12 | 0 |
| | Ganglioneuroma | 0 | 14 | 5 | 0 | 0 |
| Actual | Ganglio- | | | | | |
| | neuroblastoma | 1 | 0 | 34 | 0 | 0 |
| | Poorly- | | | | | |
| | differentiated | | | | | |
| | neuroblastoma | 8 | 1 | 0 | 119 | 0 |
| | Undifferentiated | | | | | |
| | neuroblastoma | 0 | 0 | 0 | 2 | 1 |
Table 8.
The actual and predicted labels for dataset from University of Bristol.
Table 8.
The actual and predicted labels for dataset from University of Bristol.
| Tissue Section Number | Actual Label | Predicted Label | Majority Vote |
|---|
| 4905 | ganglioneuroma | ganglioneuroma | 10 out of 10 |
| 4906 | poorly-differentiated | differentiating | 4 out of 10 |
| 4907 | poorly-differentiated | poorly-differentiated | 8 out of 10 |
| 4908 | poorly-differentiated | poorly-differentiated | 9 out of 10 |
| 4909 | ganglioneuroblastoma | differentiating | 2 out of 10 |
Table 9.
Image distribution of BreaKHis dataset by magnification factor and class.
Table 9.
Image distribution of BreaKHis dataset by magnification factor and class.
| Magnification | Benign | Malignant | Total |
|---|
| 40× | 625 | 1370 | 1995 |
| 100× | 644 | 1437 | 2081 |
| 200× | 623 | 1390 | 2013 |
| 400× | 588 | 1232 | 1820 |
| Total | 2480 | 5429 | 7909 |
| No of Patients | 24 | 58 | 82 |
Table 10.
Best average recognition rates (%) of the classifiers trained with different descriptors tested by Spanhol et al. [
10] on BreaKHis dataset. Bold values indicate the highest recognition rate in each magnification. PFTAS, Parameter-Free Threshold Adjacency Statistics; 1-NN, 1-Nearest-Neighbor; QDA, Quadratic Discriminant Analysis; RF, Random Forest; SVM, Support Vector Machine.
Table 10.
Best average recognition rates (%) of the classifiers trained with different descriptors tested by Spanhol et al. [
10] on BreaKHis dataset. Bold values indicate the highest recognition rate in each magnification. PFTAS, Parameter-Free Threshold Adjacency Statistics; 1-NN, 1-Nearest-Neighbor; QDA, Quadratic Discriminant Analysis; RF, Random Forest; SVM, Support Vector Machine.
| Descriptor | Classifier | 40× | 100× | 200× | 400× |
|---|
| PFTAS | 1-NN | 80.9 ± 2.0 | 80.7 ± 2.4 | 81.5 ± 2.7 | 79.4 ± 3.9 |
| PFTAS | QDA | 83.8 ± 4.1 | 82.1 ± 4.9 | 84.2 ± 4.1 | 78.2 ± 5.9 |
| PFTAS | RF | 81.8 ± 2 | 81.3 ± 2.8 | 83.5 ± 2.3 | 81.0 ± 3.8 |
| PFTAS | SVM | 81.6 ± 3.0 | 79.9 ± 5.4 | 85.1 ± 3.1 | 82.3 ± 3.8 |
Table 11.
Average recognition rate (%) of our proposed method and Spanhol’s method in different magnifications. Bold values indicate the highest average recognition rate in different magnifications. SIFT, Scale Invariant Feature Transform; SVM, Support Vector Machine; RBF, Radial Basis Function.
Table 11.
Average recognition rate (%) of our proposed method and Spanhol’s method in different magnifications. Bold values indicate the highest average recognition rate in different magnifications. SIFT, Scale Invariant Feature Transform; SVM, Support Vector Machine; RBF, Radial Basis Function.
| Method | 40× | 100× | 200× | 400× |
|---|
| Spanhol et al. [10] | 83.8 ± 4.1 | 82.1 ± 4.9 | 85.1 ± 3.1 | 82.3 ± 3.8 |
| SIFT + bag of features + SVM (RBF) | 82.86 ± 1.51 | 85.11 ± 0.87 | 81.55 ± 0.78 | 84.15 ± 0.69 |
| SIFT + pyramid bag of features + SVM (RBF) | 80.07 ± 1.56 | 80.75 ± 3.91 | 76.31 ± 0.99 | 79.21 ± 2.85 |
| SIFT + bag of features + SVM (histogram intersection) | 85.4 ± 1.39 | 87.25 ± 2.51 | 85.6 ± 0.76 | 86.04 ± 1.56 |
| SIFT + pyramid bag of features + SVM (histogram intersection) | 83.06 ± 1.4 | 85.6 ± 0.43 | 81.29 ± 1.64 | 84.65 ± 0.25 |