1. Introduction
Cancer remains a significant global health challenge, necessitating advancements in diagnostic and treatment methodologies [
1]. The advent of microarray technology has revolutionized molecular oncology, enabling the simultaneous analysis of thousands of genes to identify potential biomarkers for various cancers. This technological leap has brought new opportunities for precision medicine [
2]. Still, these high-dimensional datasets—often incorporating thousands of genes but only a limited number of patient samples—can lead to complications, including an elevated risk of overfitting, unwieldy computational demands, and interpretive complexity.
A commonly used strategy to address these issues is feature (gene) selection. The idea is to single out a smaller set of genes that captures the essence of the data, thereby enhancing model accuracy, reducing noise, and keeping the analysis computationally manageable [
3]. Throughout this paper, the terms “feature” and “gene” refer to the same concept, as each feature in the dataset represents the expression level of a specific gene. Therefore, “feature selection” and “gene selection” are used interchangeably. A variety of methods have been developed for this task, including a growing list of bio-inspired optimization algorithms. Particle Swarm Optimization (PSO) [
4] and Harris Hawks Optimization (HHO) [
5] have demonstrated significant capabilities in high-dimensional spaces. These methods have been successfully applied to feature-selection tasks in cancer classification, achieving high performance in identifying optimal gene subsets.
This study is the first to explore the potential of the Nuclear Reaction Optimization (NRO) algorithm [
6] for optimizing gene selection in cancer microarray data. Introduced in 2019 as a general optimization algorithm, NRO has been previously applied in gene selection for cancer classification using RNA Sequencing (RNA-Seq) data [
7]. However, its effectiveness with microarray data remains unexamined. This research assessed the standalone capability of the NRO algorithm to select gene subsets for cancer classification across six benchmark microarray datasets.
Here, we focused solely on the inherent strengths of the NRO algorithm, foregoing additional dimensionality-reduction techniques. By dimensionality reduction, we refer to preprocessing methods—such as filtering, statistical ranking, or feature extraction—that reduce the number of genes before applying optimization algorithms. To provide a clear baseline for NRO’s performance, we intentionally excluded prior dimensionality reduction. This approach allowed us to evaluate NRO’s capability in handling raw, high-dimensional microarray data without external influence from filtering methods.
The selected gene subsets were subsequently evaluated using robust machine learning classifiers, such as Support Vector Machines (SVMs) and k-Nearest Neighbors (k-NNs), with a primary focus on classification accuracy. The outcomes of this study were intended to position the NRO algorithm as a formidable and reliable tool in bioinformatics feature selection, thus facilitating the development of more effective and interpretable diagnostic models.
The rest of this paper is organized as follows:
Section 2 provides a detailed background on classification techniques and optimization algorithms, with a focus on NRO.
Section 3 reviews related works in the domain of gene selection for cancer classification.
Section 4 describes the materials and methods used in this study, including the datasets, preprocessing techniques, and the implementation of the NRO algorithm.
Section 5 presents the results and analysis, comparing NRO’s performance with those of other optimization methods. Finally,
Section 6 concludes the paper with key findings, limitations, and directions for future research.
3. Related Works
Gene selection for cancer classification is critical for addressing the challenges of high-dimensional microarray datasets. Numerous bio-inspired optimization algorithms have been proposed to enhance dimensionality reduction and improve classification accuracy, some of which apply dimensionality reduction before optimization [
15] while others rely solely on the optimization algorithm without any prior filtering. This section reviews recent advancements in optimization-based gene-selection approaches, focusing on their methodologies and relevance to this study.
AlMazrua and AlShamlan [
16] proposed Harris Hawks Optimization (HHO) for gene selection combined with SVM and k-NN classifiers to tackle the dimensionality of microarray datasets. Their approach integrated redundancy analysis and relevance scoring for preprocessing, followed by HHO-based feature selection. Evaluated on six datasets, the method achieved superior classification accuracy and reduced gene subsets compared with traditional algorithms, showcasing the efficiency of HHO in bioinformatics applications.
Alweshah et al. [
17] introduced the Monarch Butterfly Optimization (MBO) algorithm as a wrapper-based feature-selection method, utilizing the k-nearest neighbor (k-NN) classifier to enhance classification accuracy and reduce computational complexity. Evaluated across 18 benchmark datasets, the MBO approach demonstrated superior performance compared with other metaheuristic algorithms, achieving an average classification accuracy of 93% while significantly reducing the number of selected features. This study highlights MBO’s effectiveness in balancing global and local search capabilities for feature-selection tasks.
Almugren and Alshamlan [
18] proposed FF-SVM, a wrapper-based gene-selection algorithm combining the Firefly Algorithm (FFA) with a Support Vector Machine (SVM) classifier. The method aims to optimize cancer classification by identifying the most informative genes from high-dimensional microarray datasets. Using FFA for feature selection, followed by SVM classification with Leave-One-Out Cross-Validation, the algorithm achieved high classification accuracy with a minimal subset of genes across five benchmark datasets. Comparative experiments demonstrated the FF-SVM’s superior performance over several state-of-the-art methods in terms of accuracy and dimensionality reduction, highlighting its effectiveness in bioinformatics applications.
Nssibi et al. [
19] introduced a hybrid optimization approach called iBABC-CGO, which combines an island-based Artificial Bee Colony (iABC) algorithm with Chaos Game Optimization (CGO) for gene selection. The method addresses the challenges of high-dimensional microarray datasets by using a binary representation to identify informative genes while maintaining classification accuracy. The hybrid algorithm leverages CGO principles to improve convergence and avoid local optima during the migration process, and its binary version, iBABC-CGO, ensures efficient exploration and exploitation. Experimental results on 15 biological datasets demonstrated the approach’s superior performance compared with state-of-the-art methods, highlighting its ability to achieve high accuracy with minimal feature subsets.
AlMazrua and AlShamlan [
20] proposed a novel feature-selection approach for cancer classification using the Gray Wolf Optimizer (GWO). This bio-inspired optimization algorithm mimics the leadership hierarchy and cooperative hunting behavior of gray wolves to effectively explore and exploit high-dimensional datasets. Their framework utilized the GWO to identify the most significant features, achieving a balance between classification accuracy and dimensionality reduction. Their experimental results demonstrated that the method successfully reduced the number of selected features while maintaining high classification performance, highlighting its potential for bioinformatics and medical diagnostic applications.
Overall, the reviewed studies demonstrate the effectiveness of bio-inspired optimization algorithms in gene selection for cancer classification. Methods such as HHO, MBO, FFA, iBABC-CGO, and GWO have achieved high classification accuracy while selecting minimal and informative gene subsets. This study evaluates the Nuclear Reaction Optimization (NRO) algorithm as a novel contribution to further enhance gene selection and classification performance.
4. Materials and Methods
This study explores the application of the Nuclear Reaction Optimization (NRO) algorithm for gene selection in cancer classification. The methodology consists of dataset preprocessing, optimization using NRO, evaluation through machine learning classifiers, and fitness assessment. The implementation was carried out using Python (version 3.x), with numpy and pandas for preprocessing gene-expression data, scipy.io.arff for handling microarray datasets, and sklearn for feature scaling and classification. The NRO algorithm was implemented by coding its mathematical foundations, including nuclear fission and fusion processes, Lévy flight-based step size adjustments, and mutation mechanisms for optimal gene selection.
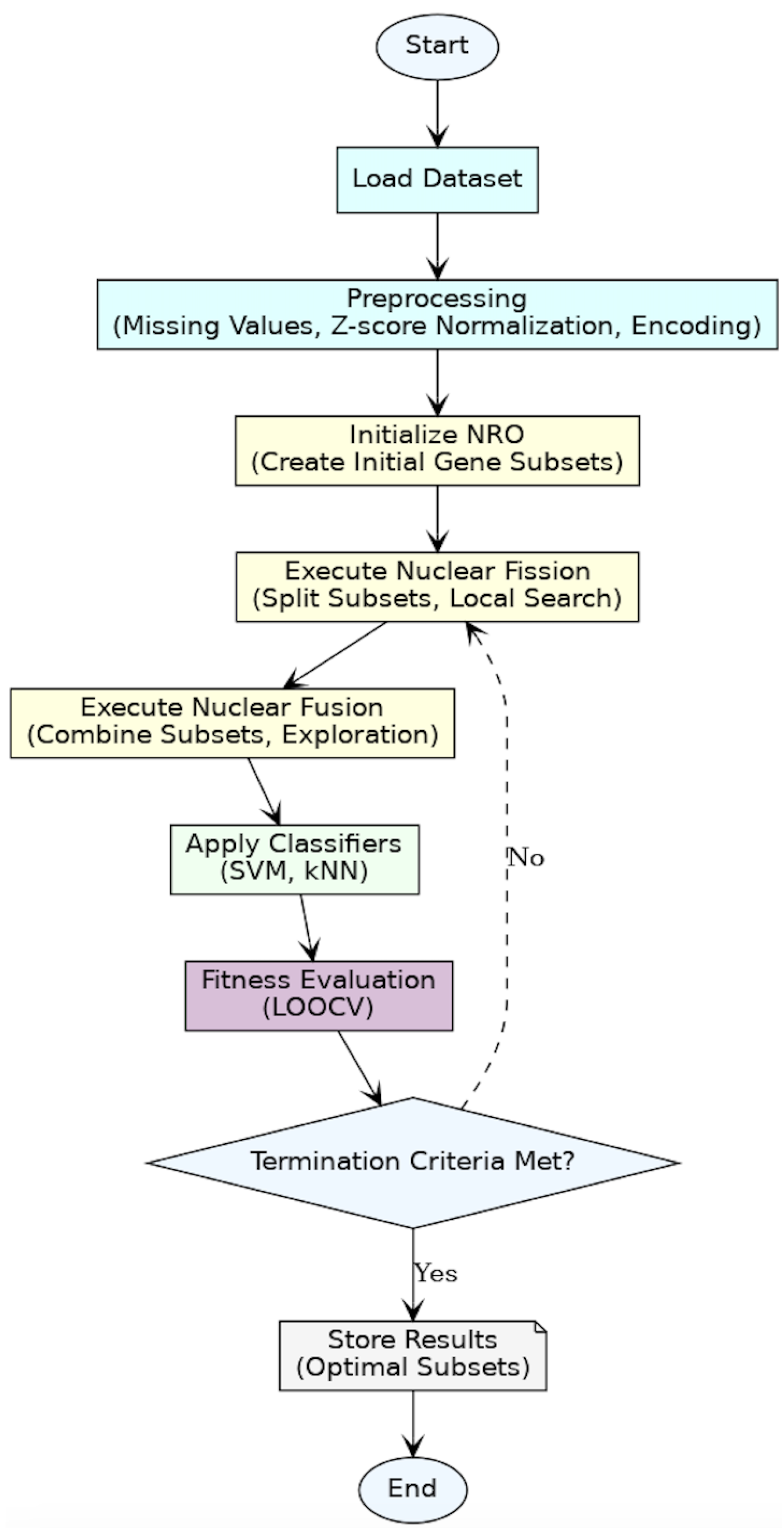
Figure 3 shows the flowchart summarizing the entire methodology, from data preprocessing and optimization to fitness evaluation and termination.
4.1. Dataset and Preprocessing
Using six well-known binary and multiclass microarray cancer datasets that we obtained from
http://www.gems-system.org/ (accessed on 15 February 2025), we assessed the overall effectiveness of the gene-selection techniques. In the discipline of bioinformatics, these datasets are frequently used to compare the effectiveness of gene-selection techniques. SRBCT [
21], Lymphoma [
22], and Leukemia2 [
23] are multiclass microarray datasets, whereas the binary-class microarray datasets are Lung [
24], Colon [
25], and Leukemia1 [
25,
26]. We provide a thorough description of these six benchmark microarray gene-expression datasets in
Table 1, including information on the number of classes, samples, and genes.
To prepare the datasets for gene selection and classification, we applied a series of preprocessing techniques commonly used in bioinformatics to ensure the datasets were clean, consistent, and suitable for machine learning algorithms. Firstly, any missing values in the datasets were handled by replacing them with the mean value of the respective gene’s expression levels using mean imputation. In our analysis, missing values were found only in the Lymphoma dataset, accounting for 4.91% of its total data, affecting 2796 genes. Given this relatively low percentage, mean imputation was applied to maintain data integrity without significantly impacting the classification performance. To standardize the features and eliminate the effects of varying scales across genes, we applied Z-score normalization, transforming the expression levels of each gene to have a mean of 0 and a standard deviation of 1. Additionally, for multiclass datasets, we employed label encoding to convert categorical class labels into a numerical format, making them compatible with classification algorithms. These preprocessing steps ensured that the datasets were optimally prepared for the subsequent feature-selection and classification phases.
4.2. Apply Nuclear Reaction Optimization (NRO) Algorithm
The Nuclear Reaction Optimization (NRO) algorithm was adapted in this study specifically for gene selection in cancer classification using microarray data. Microarray datasets are characterized by their high dimensionality, with thousands of genes but relatively few samples, posing challenges for classification and optimization algorithms. NRO addresses these challenges by iteratively refining subsets of genes, balancing the need for compact feature sets with high classification accuracy.
Each candidate solution in the NRO algorithm is a binary vector, where 1 indicates that a gene is selected, and 0 indicates exclusion. The algorithm initialized a population of 500 such solutions, each representing a potential subset of genes. We chose a population size of 500 to ensure a diverse set of candidate solutions, which helps in effectively exploring the high-dimensional gene space while maintaining computational efficiency. A smaller population might limit diversity and lead to premature convergence, whereas a significantly larger one would increase computational cost without substantial accuracy gains. Over a maximum of 30 generations, the population evolved through nuclear fission and fusion processes. This number of generations was selected as a balance between exploration and convergence, allowing the algorithm sufficient iterations to optimize gene selection while avoiding excessive computational overhead. In our empirical tests, increasing the generations beyond 30 provided no improvements in classification accuracy.
In the context of microarray data, the nuclear fission phase introduced diversity by splitting solutions into smaller fragments, which correspond to alternative gene subsets. Equation (1) governs this process, generating new solutions by mutating the existing ones. Step sizes, dynamically adjusted using Equations (2) and (3), control the degree of variability, enabling broad exploration in early generations to identify different sets of candidate genes. As the algorithm progresses, these step sizes decrease, focusing on the refinement of the most promising gene subsets. Mutation factors from Equations (4) and (5) further adjust the solutions, ensuring that the algorithm does not converge prematurely and continues to explore the potential of unselected genes.
The nuclear fusion phase refines gene subsets by combining promising solutions. During the ionization step, solutions are adjusted using differences between randomly selected subsets, following Equation (6). This step ensures the algorithm can evaluate combinations of genes that might not have been initially included in a single solution. For microarray data, in which many genes have weak but complementary contributions to classification, this step is crucial. When the differences between the selected solutions are small, Lévy flight from Equation (7) is applied to introduce large jumps, allowing the algorithm to escape local optima and explore new subsets of genes.
In the fusion step, refined subsets are combined using Equation (8), producing solutions that integrate information from the best-performing gene subsets of previous generations. Lévy flight, applied when necessary through Equation (9), ensures that the fusion phase continues to explore new regions of the search space rather than stagnating on similar subsets. This capability was critical for handling the complexity of microarray data, in which interactions among genes can lead to nonlinear relationships affecting the classification accuracy.
The algorithm evaluated each solution using the fitness function described in
Section 4.4, which combines LOOCV-based classification accuracy with a penalty for large subsets. The process continued until the maximum number of generations was reached. The final output was an optimized subset of genes that balanced high classification accuracy with minimal dimensionality, ensuring that the selected genes were both computationally efficient and biologically informative for cancer classification. The pseudo code of the NRO algorithm is shown in Algorithm 1.
| Algorithm 1: Nuclear Reaction Optimization (NRO) Algorithm for Gene Selection |
| > Require: Population size N = 500, Maximum generations T = 30 Ensure: Optimized subset of gene ▷ Initialization 1: Initialize a population of 500 binary solutions , where [j] = 1 if gene j is selected, otherwise [j] = 0 2: Set bounds [0, 1] for solutions 3: Initialize global best solution 4: Compute initial fitness of using LOOCV 5: for g = 1 to T do ▷ Fission Phase: Introduce Diversity 6: for each solution in the population do 7: Generate new solutions as per Equation (1) 8: Adjust step sizes dynamically as per Equations (2) and (3) 9: Apply mutation factors as per Equations (4) and (5) 10: end for ▷ Fusion Phase: Refine Solutions 11: for each solution in the population do 12: Adjust solutions through ionization as per Equation (6) 13: if Ionized solutions are nearly identical then 14: Apply Lévy flight adjustment as per Equation (7) 15: end if 16: Combine solutions through fusion as per Equation (8) 17: if Fused solutions are nearly identical then 18: Apply Lévy flight adjustment as per Equation (9) 19: end if 20: end for ▷ Fitness Evaluation using LOOCV 21: for each solution in the population do 22: Compute classification accuracy using LOOCV 23: Compute fitness: Fitness() = Accuracy − Penalty(size()) 24: if ) then 25: ← 26: end if 27: end for 28: end for 29: Return Optimized subset of genes |
4.3. Apply Classifiers
To evaluate the performance of the gene subsets selected by the NRO algorithm, two machine learning classifiers were employed: Support Vector Machine (SVM) and k-Nearest Neighbors (k-NNs). These classifiers were chosen for their established effectiveness in handling high-dimensional data, making them particularly suitable for microarray datasets with thousands of genes but relatively few samples.
The SVM was configured with a linear kernel and a penalty parameter (C = 1), which is effective for binary classification tasks in which the data are high-dimensional and sparse. Its ability to maximize the margin between classes ensures robustness in separating cancerous and non-cancerous samples, as well as in distinguishing between different cancer subtypes.
The k-NN classifier was configured with k = 5, using Euclidean distance to measure similarity between samples. Its non-parametric nature allows it to adapt well to the inherent clustering within microarray datasets, particularly when the dimensionality has been reduced through gene selection.
Both classifiers were integrated into the fitness evaluation process, in which they were used to calculate the classification accuracy through Leave-One-Out Cross-Validation (LOOCV). By applying SVM and k-NNs to the gene subsets generated by NRO, the methodology ensures that the selected subsets are rigorously evaluated for their ability to distinguish between cancer classes.
4.4. Fitness Evaluation
The fitness evaluation process measures the quality of each candidate gene subset by balancing classification performance with dimensionality reduction. The fitness of a solution is computed as follows:
where Equation (10) outlines the basic computation. The classification accuracy was calculated using LOOCV (Leave-One-Out Cross-Validation), a robust cross-validation technique suited to the small sample sizes typical of microarray datasets. In LOOCV, each sample serves as the test set exactly once, while the remaining samples form the training set. This ensures that the evaluation is both comprehensive and unbiased.
The penalty term was designed to discourage the selection of excessively large gene subsets, promoting dimensionality reduction. It was defined as follows:
where Equation (11) indicates how the penalty scales with both the size of the gene subset and the progress of the optimization process, ensuring that the algorithm focuses on selecting compact subsets in later generations.
During the evaluation of alternative cross-validation frameworks, both 5-fold and 10-fold methods were tested across all datasets. These approaches resulted in classification accuracies approximately 1–2% lower than those obtained using Leave-One-Out Cross-Validation (LOOCV). Although LOOCV required significantly more computational time—typically 2 to 10 times longer depending on the dataset—it consistently produced higher accuracy. Therefore, LOOCV was selected as the cross-validation method in this study. This reflects a deliberate decision to prioritize accuracy over computational efficiency, especially in the context of small sample sizes in which each data point is critical. Moreover, numerous studies in bioinformatics have demonstrated that LOOCV provides better model reliability and generalization for high-dimensional microarray data [
27,
28,
29,
30], further supporting its adoption.
5. Results and Analysis
This section presents the results of applying the Nuclear Reaction Optimization (NRO) algorithm for gene selection in cancer classification across six benchmark microarray datasets. The performance of NRO was evaluated in terms of the number of selected genes and classification accuracy, followed by an analysis of precision, recall, and F1-score to further assess classification robustness. Additionally, the results are compared with state-of-the-art gene-selection algorithms to assess the relative effectiveness of NRO.
The results presented in
Table 2 reveal that the NRO algorithm effectively selects informative gene subsets for cancer classification, yielding high classification accuracies across multiple datasets. However, due to the absence of dimensionality-reduction or filtering techniques, the number of selected genes remains relatively high. This was expected, as no feature-elimination techniques were applied before the optimization process.
Notably, the classification accuracy achieved with SVM consistently outperformed that of k-NNs across all the datasets. This aligned with the expectation that SVM, being more robust to high-dimensional data, would be better suited for the gene-expression datasets. The best accuracy for SVM was observed in the SRBCT dataset (99.26%), followed by Lymphoma (98.81%) and Lung (95.36%). Meanwhile, k-NNs yielded its highest accuracy in the Lung dataset (97.78%), but its overall performance was less stable, particularly for high-dimensional datasets like Leukemia1 and Leukemia2, where the classification accuracy dropped significantly for lower-performing runs.
Another key observation is that the number of selected genes varies across datasets, with some requiring a larger subset for optimal classification. For example, while only 74 genes were selected in the SRBCT dataset for SVM, the Colon dataset required 494 genes for its best-performing result. This indicates that NRO was highly adaptive in its selection process, though the lack of dimensionality reduction results in relatively large gene subsets, which could be further refined in future research.
NRO’s performance varied across datasets due to differences in gene count, sample size, and data complexity. It achieved the highest accuracy on SRBCT and Lymphoma, which had moderate gene counts and yielded smaller gene subsets. Lung also performed well despite high dimensionality, likely due to its larger sample size. Leukemia1 and Leukemia2 showed more variability, reflecting the challenge of optimizing in high-dimensional, small-sample datasets. Colon, despite having fewer genes, resulted in the lowest accuracy and the largest subsets, suggesting that feature selection was more difficult, possibly due to dataset-specific complexity.
To complement the evaluation of classification accuracy, a detailed analysis of the 95% confidence intervals (CIs) offers valuable insights into the stability and reliability of the results presented in
Table 2. Confidence intervals provide a statistical range within which the true average accuracy is expected to fall, offering a measure of how consistently the NRO algorithm performs across multiple runs. In this study, the CIs were remarkably narrow, with widths ranging from 0.0019 to 0.0061 and an average width of 0.0036, indicating minimal variability and high repeatability in classification outcomes. For instance, the narrowest CI was observed for the Colon dataset using k-NNs ([0.6197, 0.6216]), while the widest CI appeared in Leukemia1 with k-NNs ([0.3731, 0.3792]); even in this case, the interval remained tight and statistically sound. Additionally, all the CIs were logically bounded between 0 and 1, validating the accuracy of the calculations. These results underscore the consistency of NRO’s performance and affirm that the reported accuracies are not outliers but represent stable, repeatable outcomes. Including confidence intervals, therefore, enriches the analysis by quantifying uncertainty and reinforcing the robustness of the findings.
While accuracy provides an overall measure of classification performance, it does not fully capture the model’s ability to minimize false positives and false negatives. To further evaluate the effectiveness of NRO-selected genes,
Table 3 presents the precision, recall, and F1-score, which offer a deeper understanding of classification reliability.
Precision measures the proportion of correctly predicted positive cases out of all predicted positives. A higher precision means fewer false positives, which is crucial in medical applications to avoid unnecessary treatments. As shown in
Table 3, SVM achieved perfect precision (100%) in the Lung, Lymphoma, and SRBCT datasets, indicating that it classifies all positive cases correctly without false positives. In other datasets, SVM maintained high precision, such as in Leukemia1 (98.60%) and Leukemia2 (95.81%). Meanwhile, k-NNs generally had lower precision, with its best performance in Lymphoma and Lung but lower values in other datasets, such as Colon (75.70%).
Recall, or sensitivity, measures the ability of the classifier to correctly identify all actual positive cases. A high recall reduces the risk of missing cancer cases, which is critical in medical diagnostics. SVM achieved perfect recall (100%) in the Lung, Lymphoma, and SRBCT datasets, ensuring that no positive cases are overlooked. In other datasets, recall remained high, such as in Leukemia1 (98.57%) and Leukemia2 (95.72%). The k-NNs also achieved 100% recall in the Lymphoma dataset, matching SVM, but in other cases, it performed worse than SVM, such as in Leukemia2 (80.70%) and Colon (74.39%).
The F1-score is the harmonic mean of the precision and recall, providing a balanced measure of classification performance. A high F1-score indicates that the classifier effectively minimizes both false positives and false negatives. SVM achieved an F1-score of 100% in the Lung, Lymphoma, and SRBCT datasets, reflecting its strong performance in these cases. In Leukemia1 and Leukemia2, SVM also maintained high F1-scores (98.57% and 95.70%, respectively). k-NNs reached 100% in the Lymphoma dataset but struggled in others, particularly Colon (71.34%) and SRBCT (79.70%), where its lower recall affected the overall performance.
To further evaluate the performance of NRO,
Table 4 compared its SVM-based classification accuracy with other gene-selection algorithms, including Harris Hawks Optimization (HHO), Artificial Bee Colony (ABC), Particle Swarm Optimization (PSO), and Firefly Algorithm (FF). This comparison focuses solely on classification accuracy, as the majority of studies on gene-selection algorithms evaluate performance based only on accuracy. Other metrics such as precision, recall, and F1-score are not included, as they are rarely reported in gene-selection research. Accuracy remains the primary benchmark for assessing the effectiveness of selected gene subsets in classification tasks.
The results show that NRO was competitive but did not consistently outperform other methods. It achieved the highest accuracy only in the SRBCT dataset (99.26%), surpassing FF (98.8%) and other algorithms. However, in all other datasets, NRO was outperformed. For example, in the Colon dataset, NRO’s accuracy (82.16%) was the lowest, while FF achieved 98.2%. In Leukemia1, NRO reached 95.53%, which was lower than HHO (97.22%) and FF (100%). In Lung, both HHO and FF achieved 100% accuracy, surpassing NRO’s 95.36%. Similarly, in Leukemia2, NRO’s 92.47% was outperformed by ABC (97.22%) and FF (97.2%). In Lymphoma, NRO achieved 98.81%, slightly below HHO (100%).
Despite not achieving the highest accuracy in all the datasets, NRO consistently delivered a strong and reliable performance across diverse cancer datasets. Its ability to outperform methods like HHO and ABC in datasets such as Leukemia2 and SRBCT, and to achieve near-perfect accuracy in Lymphoma (98.81%) and SRBCT (99.26%), demonstrates its robustness in handling high-dimensional gene-expression data. These results highlight NRO’s effectiveness and adaptability, validating its optimization approach based on nuclear reaction mechanisms. Overall, NRO proved to be a promising and competitive algorithm for gene selection in cancer classification, with the potential for further enhancement through hybrid or refined optimization strategies.
6. Conclusions
This study explored the application of the Nuclear Reaction Optimization (NRO) algorithm for gene selection in cancer classification using six benchmark microarray datasets. The results demonstrated that NRO effectively identified relevant gene subsets, leading to high classification accuracy, particularly when paired with SVM. Compared with state-of-the-art optimization methods, including HHO, ABC, PSO, and FF, NRO showed competitive performance, outperforming some approaches in specific datasets such as SRBCT and Leukemia2. NRO demonstrated strong adaptability in high-dimensional feature spaces. Its ability to refine solutions through nuclear fission and fusion highlights its potential as a powerful bioinformatics tool for cancer classification. However, despite its promising results, certain limitations hinder its full efficiency in gene-selection tasks.
A key limitation of this study is the large number of selected genes. Since no dimensionality-reduction techniques were applied before running NRO, this led to reduced interpretability and higher computational costs. Additionally, the Leave-One-Out Cross-Validation (LOOCV) method, while chosen for its superior accuracy, further increased computational expense due to its iterative training process. Future work should integrate filtering techniques before applying NRO to remove irrelevant genes, improving both classification accuracy and efficiency. Furthermore, hybrid optimization approaches, in which a secondary metaheuristic is used before NRO to refine the initial population, could help accelerate convergence, enhance feature-selection quality, and reduce unnecessary computations. These improvements would make the method more scalable, interpretable, and effective for larger and more complex datasets.
Additionally, this study did not assess the biological relevance of the selected genes. Future research will include pathway enrichment analysis and comparison with known cancer biomarkers to enhance the interpretability of the results. While NRO has previously been applied to RNA-Seq data, this study demonstrates its effectiveness on microarray data. Building on these findings, future studies will evaluate NRO’s scalability and performance on larger and more complex genomic datasets.