Figure 1.
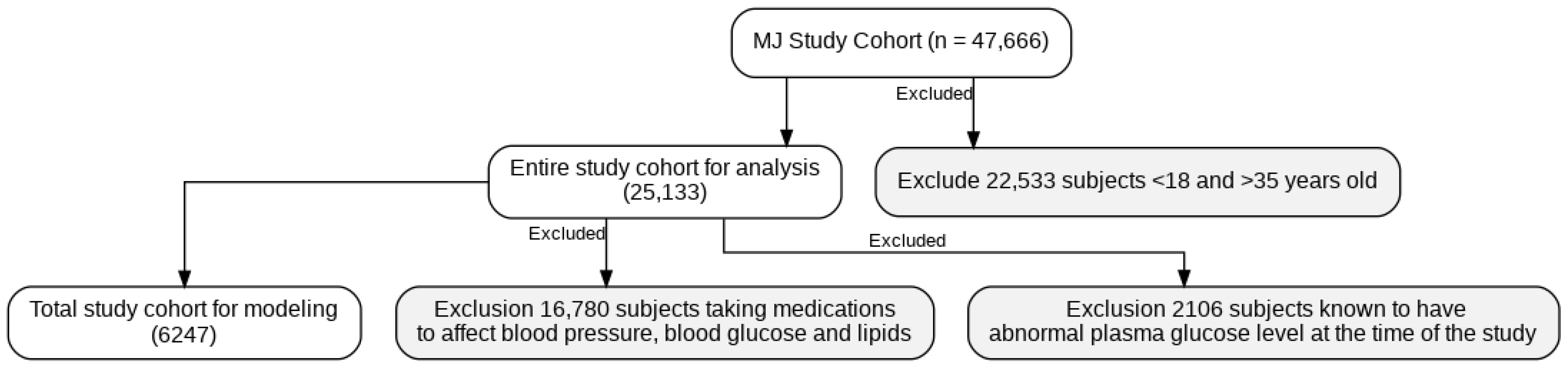
The scheme of participant selection.
Figure 1.
The scheme of participant selection.
Figure 2.
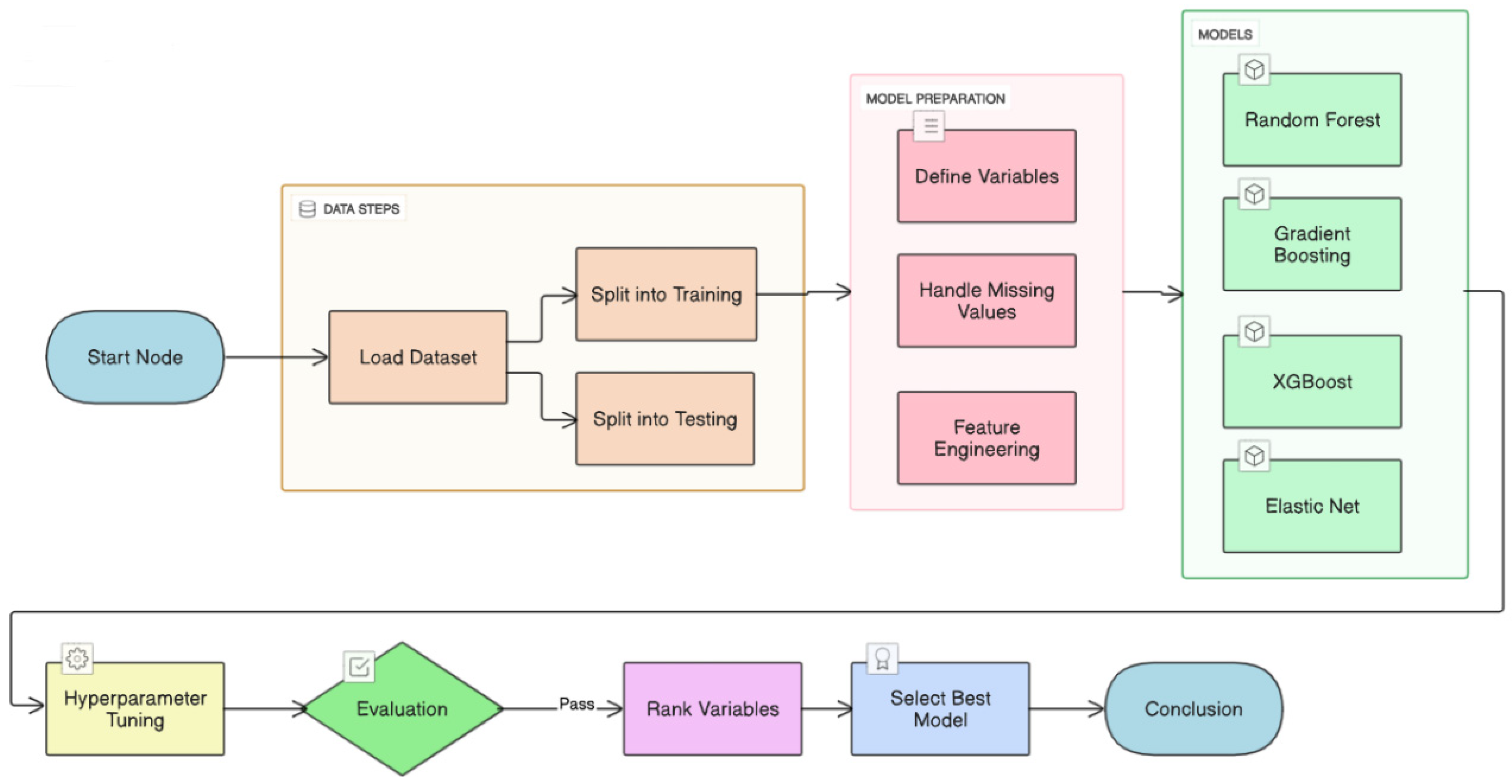
Proposed machine learning prediction scheme.
Figure 2.
Proposed machine learning prediction scheme.
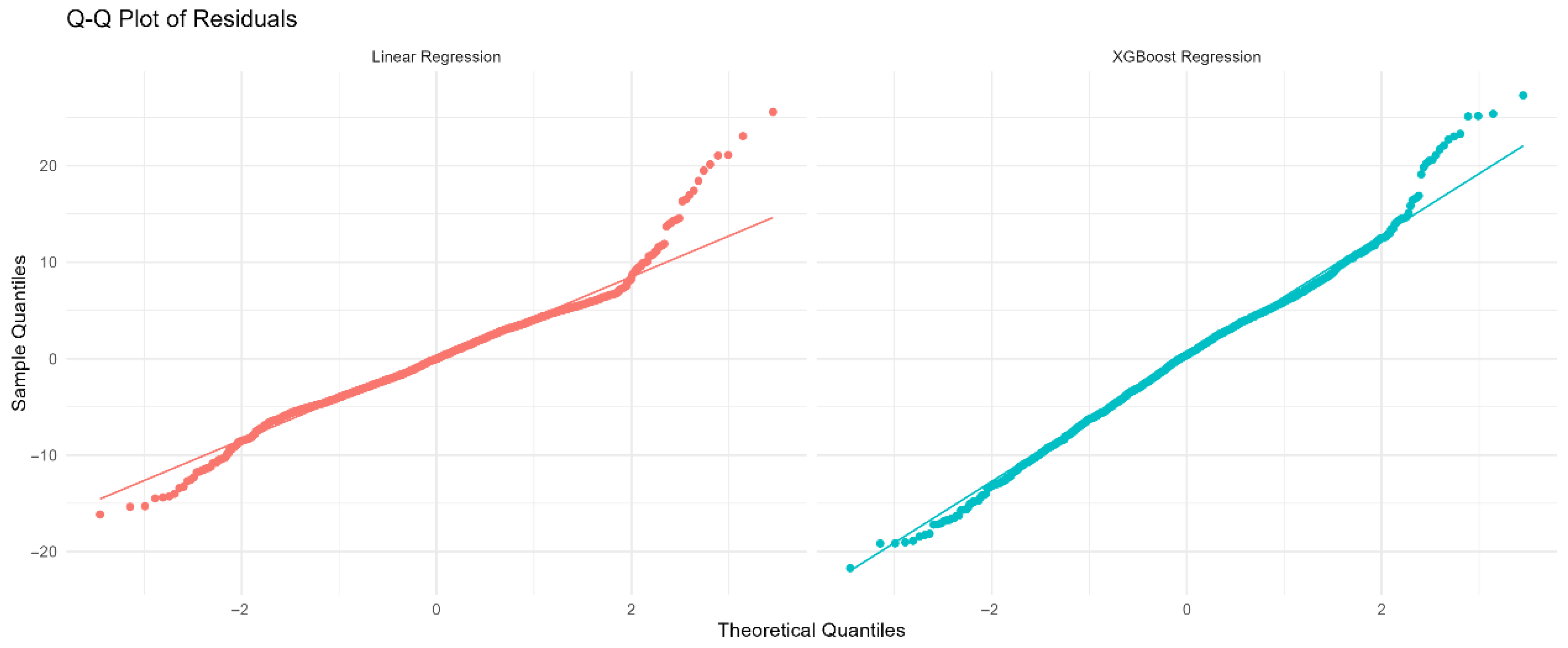
Figure 3.
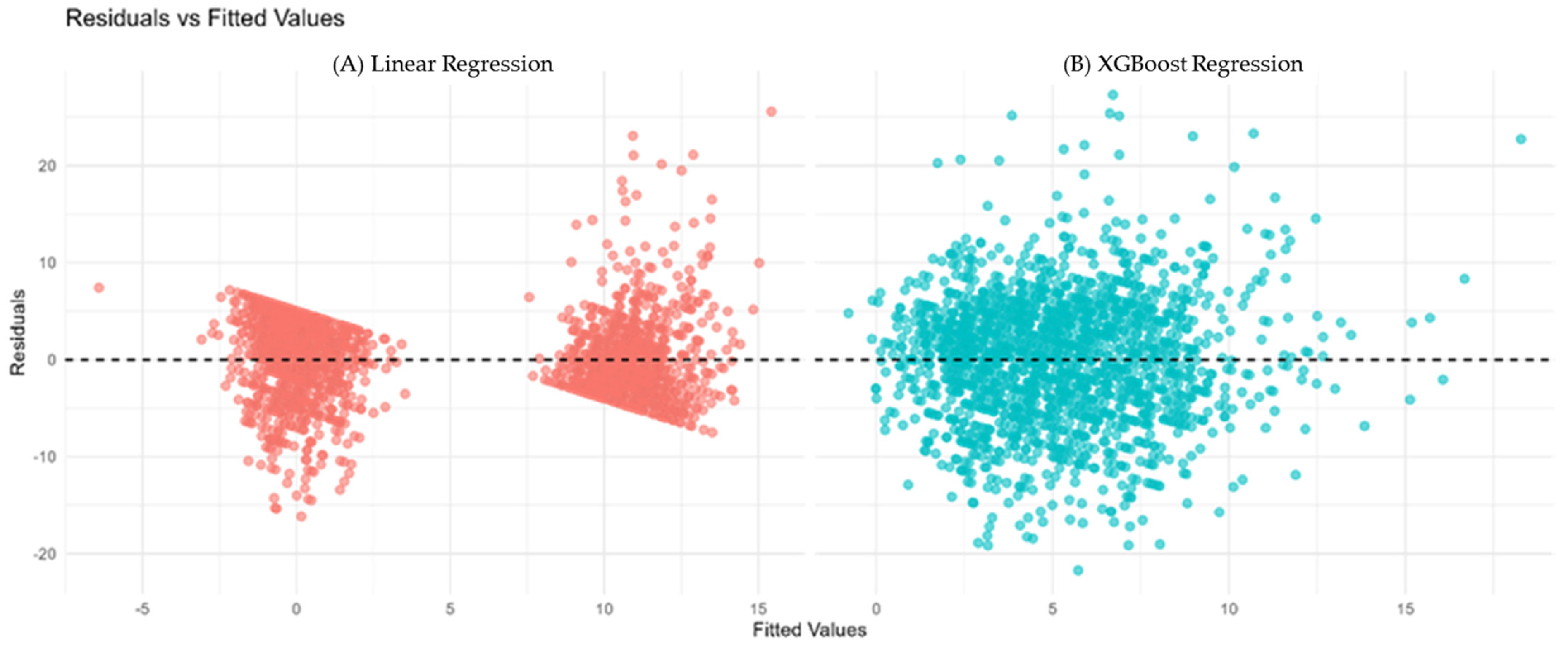
(A) Residuals vs. fitted values for Linear Regression (red). (B) Residuals vs. fitted values for XGBoost Regression (cyan). The horizontal dashed line at zero indicates no residual bias. Patterns or funnel shapes may suggest heteroscedasticity or model misspecification.
Figure 3.
(A) Residuals vs. fitted values for Linear Regression (red). (B) Residuals vs. fitted values for XGBoost Regression (cyan). The horizontal dashed line at zero indicates no residual bias. Patterns or funnel shapes may suggest heteroscedasticity or model misspecification.
Figure 4.
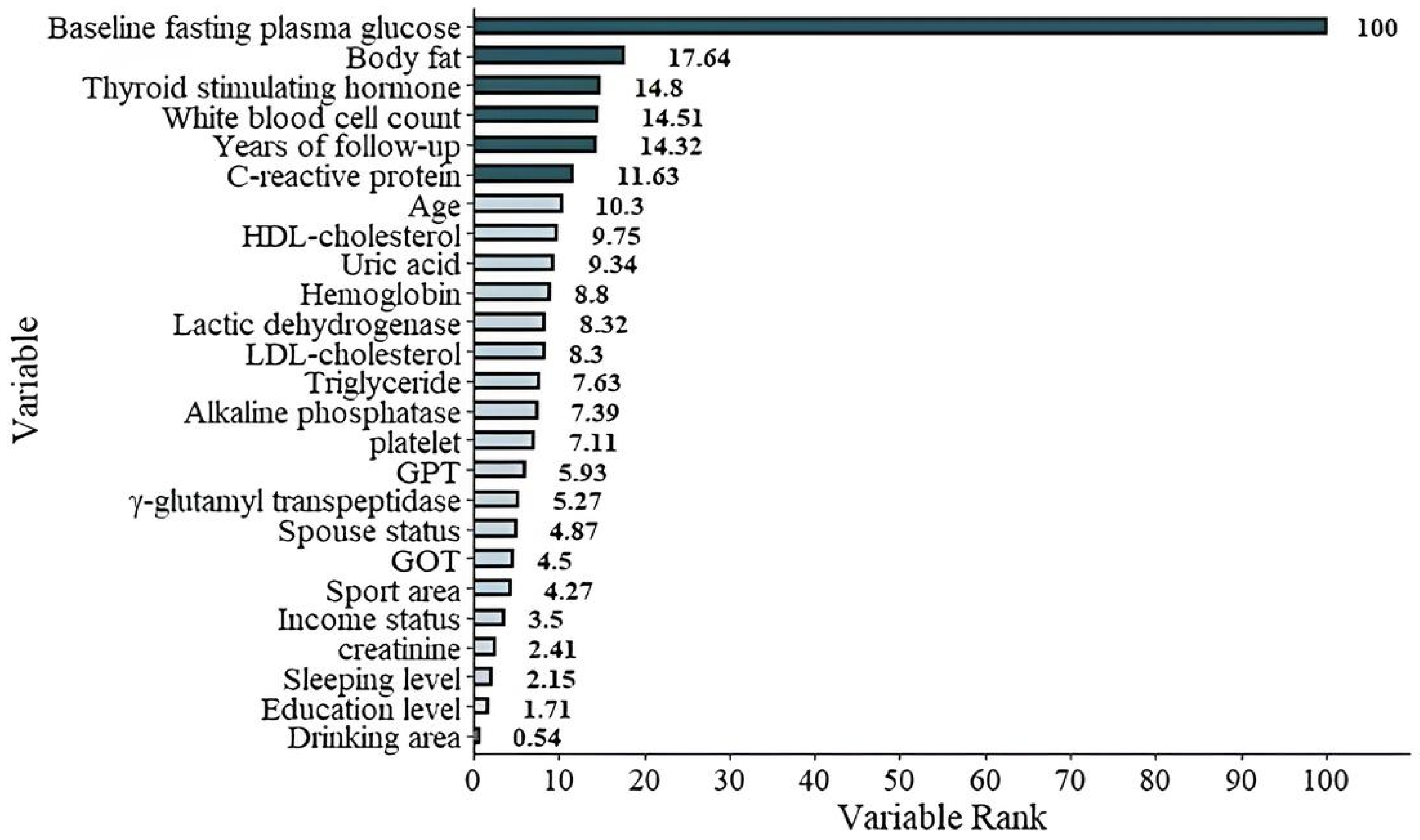
The graphic demonstration of the importance percentage in Model 1 (with FPGbase included). The darker green bars show the most important six features of the study.
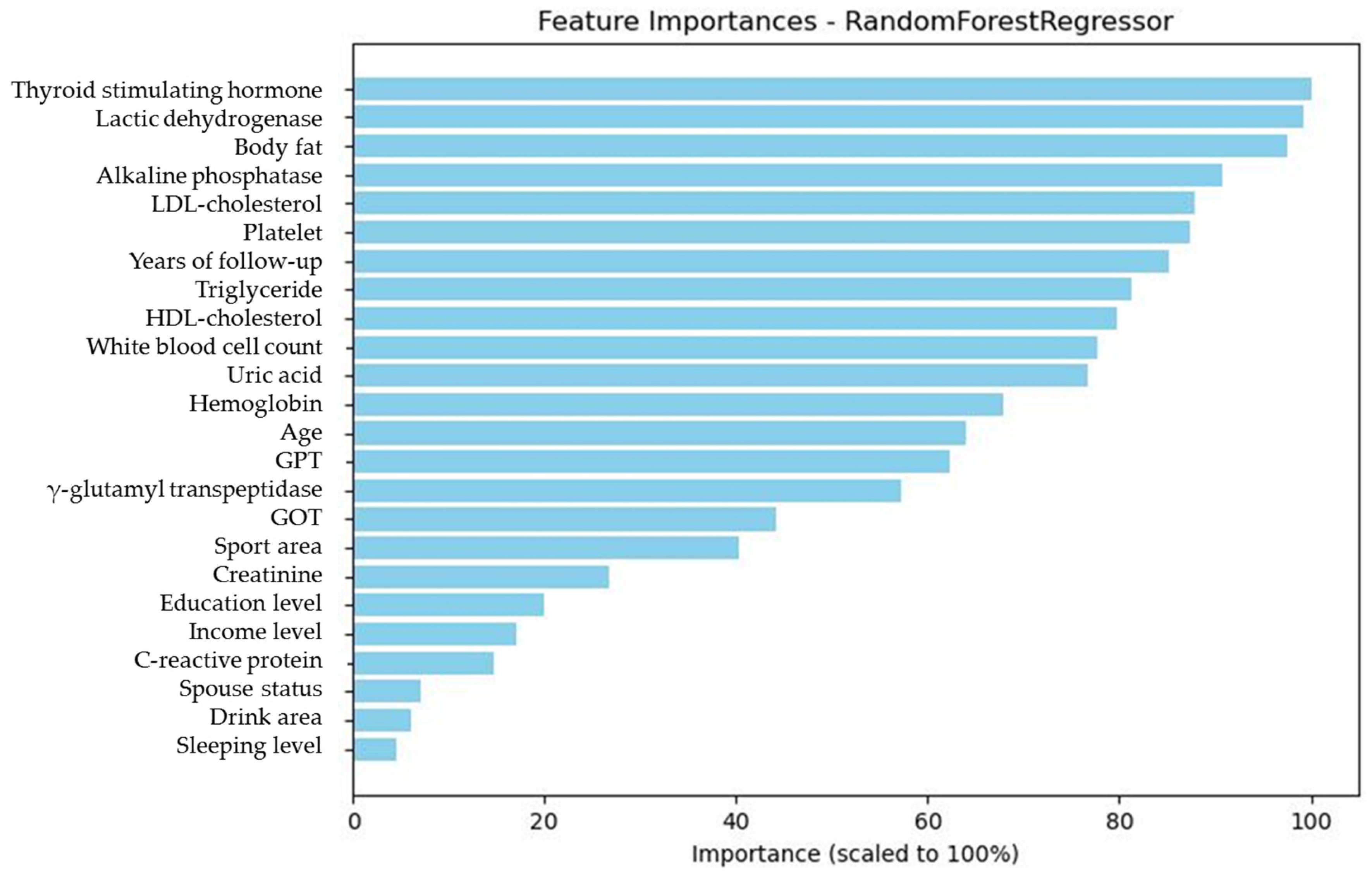
Figure 4.
The graphic demonstration of the importance percentage in Model 1 (with FPGbase included). The darker green bars show the most important six features of the study.
Figure 5.
The graphic demonstration of the importance percentage in Model 2 (excluding FPGbase). The darker green bars show the most important six features of the study.
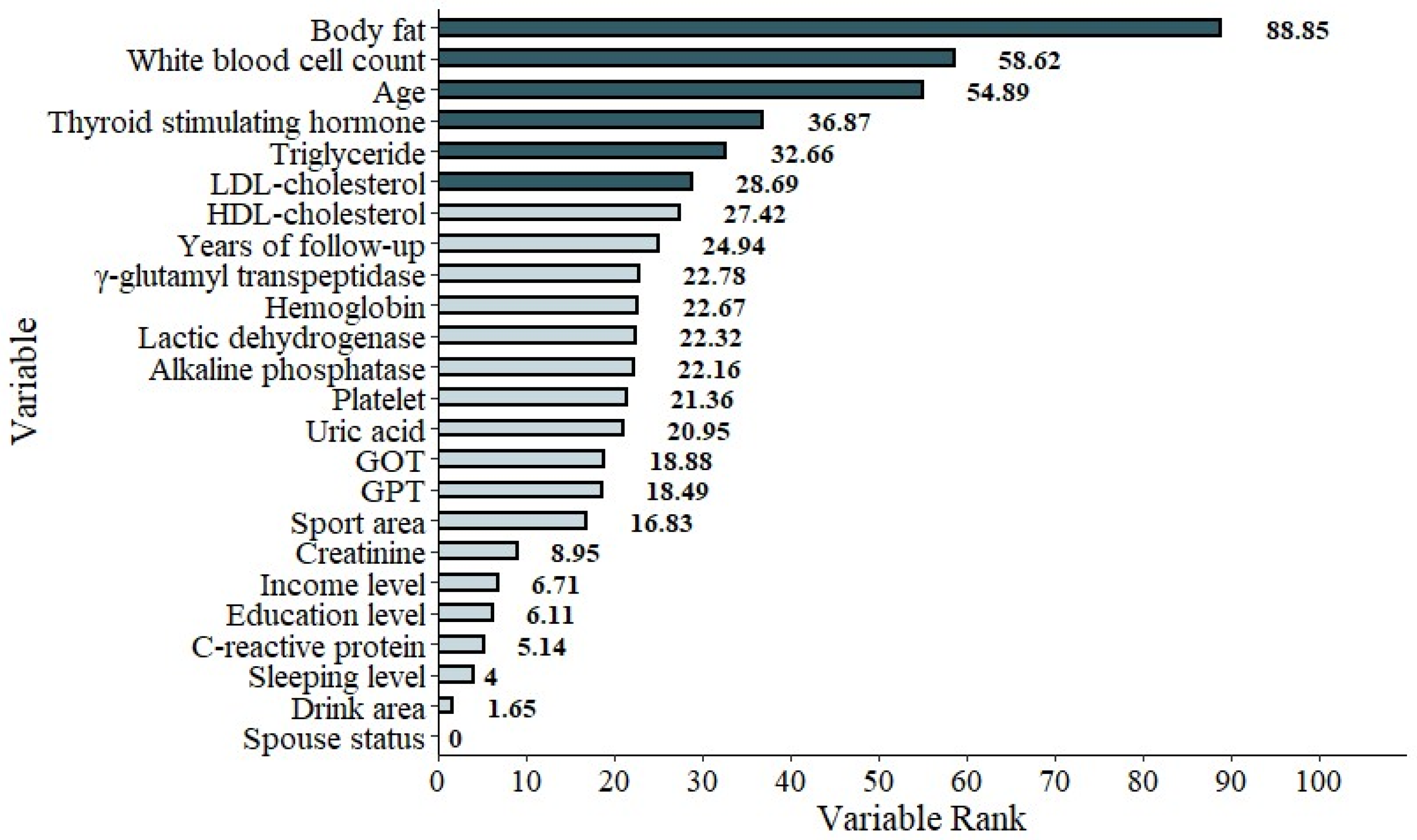
Figure 5.
The graphic demonstration of the importance percentage in Model 2 (excluding FPGbase). The darker green bars show the most important six features of the study.
Figure 6.
SHAP bee swarm plot of the random forest model, illustrating the distribution and magnitude of predictor effects (red = higher values, blue = lower values). Note: Red dots (higher feature value) push predictions upward (worsening glycemia); blue dots (lower feature value) push predictions downward (improving glycemia). For example, higher body fat consistently increases predicted glucose rise, while higher HDL-C is protective.
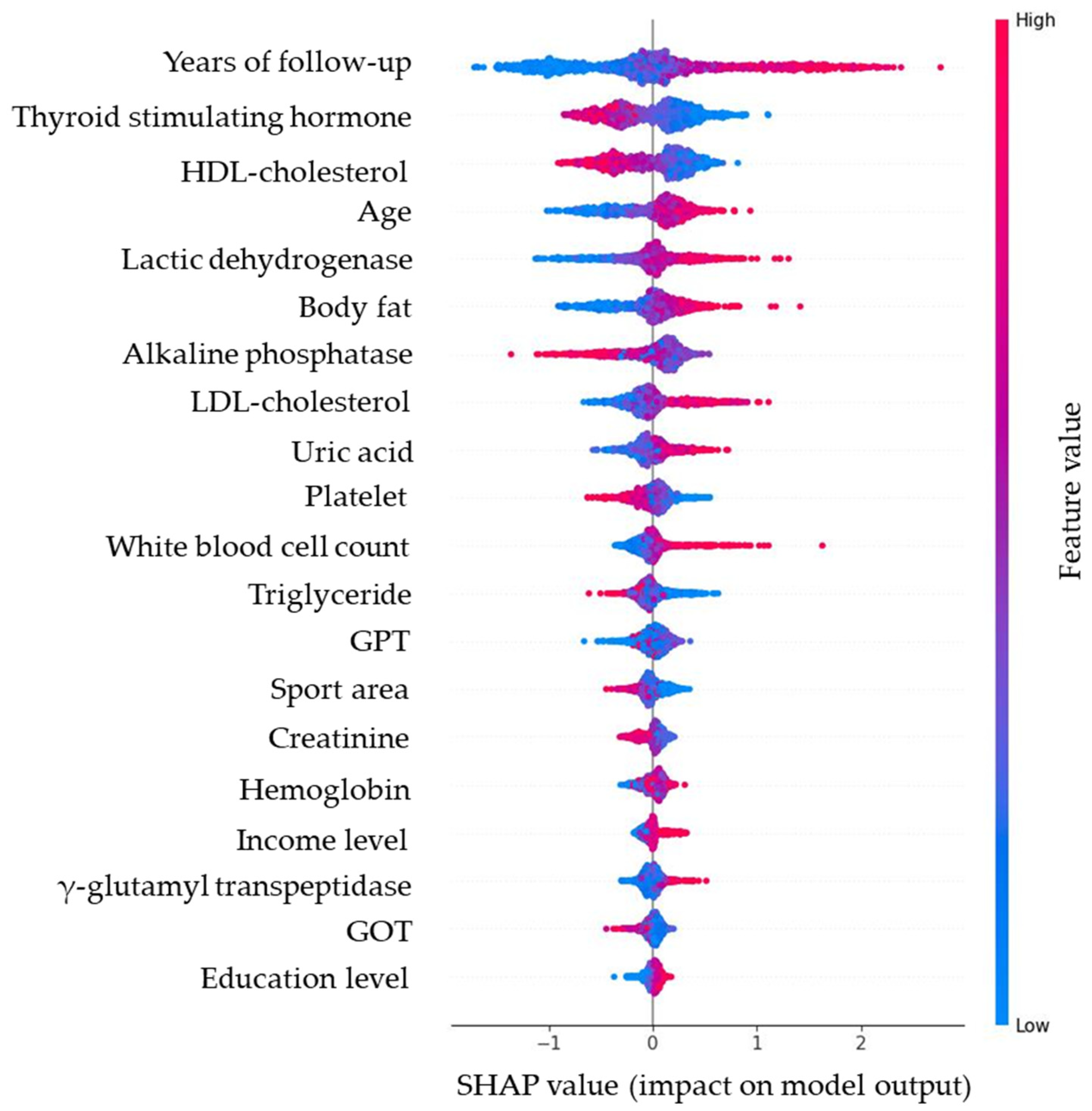
Figure 6.
SHAP bee swarm plot of the random forest model, illustrating the distribution and magnitude of predictor effects (red = higher values, blue = lower values). Note: Red dots (higher feature value) push predictions upward (worsening glycemia); blue dots (lower feature value) push predictions downward (improving glycemia). For example, higher body fat consistently increases predicted glucose rise, while higher HDL-C is protective.
Figure 7.
Absolute SHAP value ranking of predictors, showing the magnitude of each variable’s contribution to glycemic trajectory.
Figure 7.
Absolute SHAP value ranking of predictors, showing the magnitude of each variable’s contribution to glycemic trajectory.
Figure 8.
Net SHAP value plot of predictors, demonstrating the overall directional impact of features on glycemic outcomes.
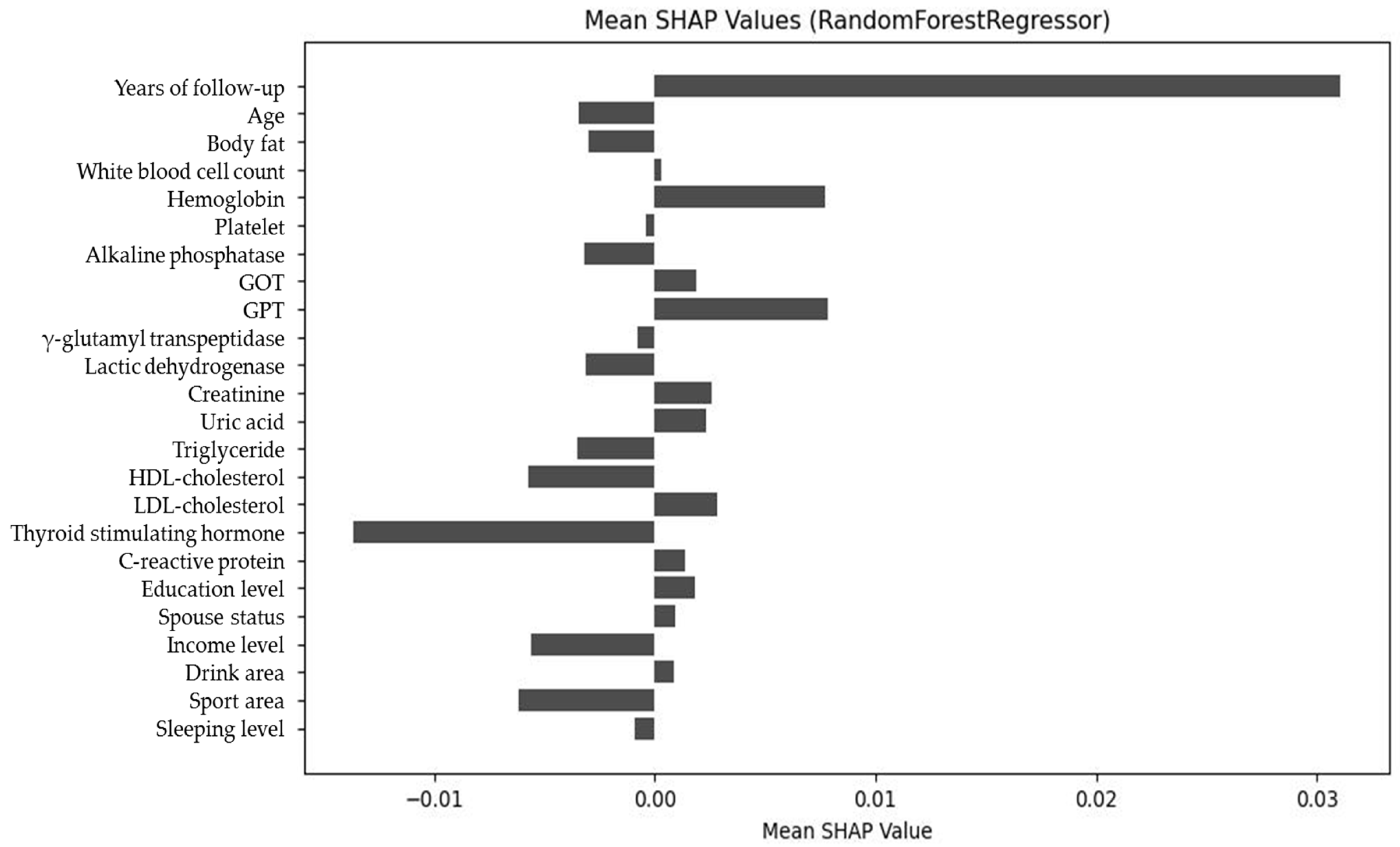
Figure 8.
Net SHAP value plot of predictors, demonstrating the overall directional impact of features on glycemic outcomes.
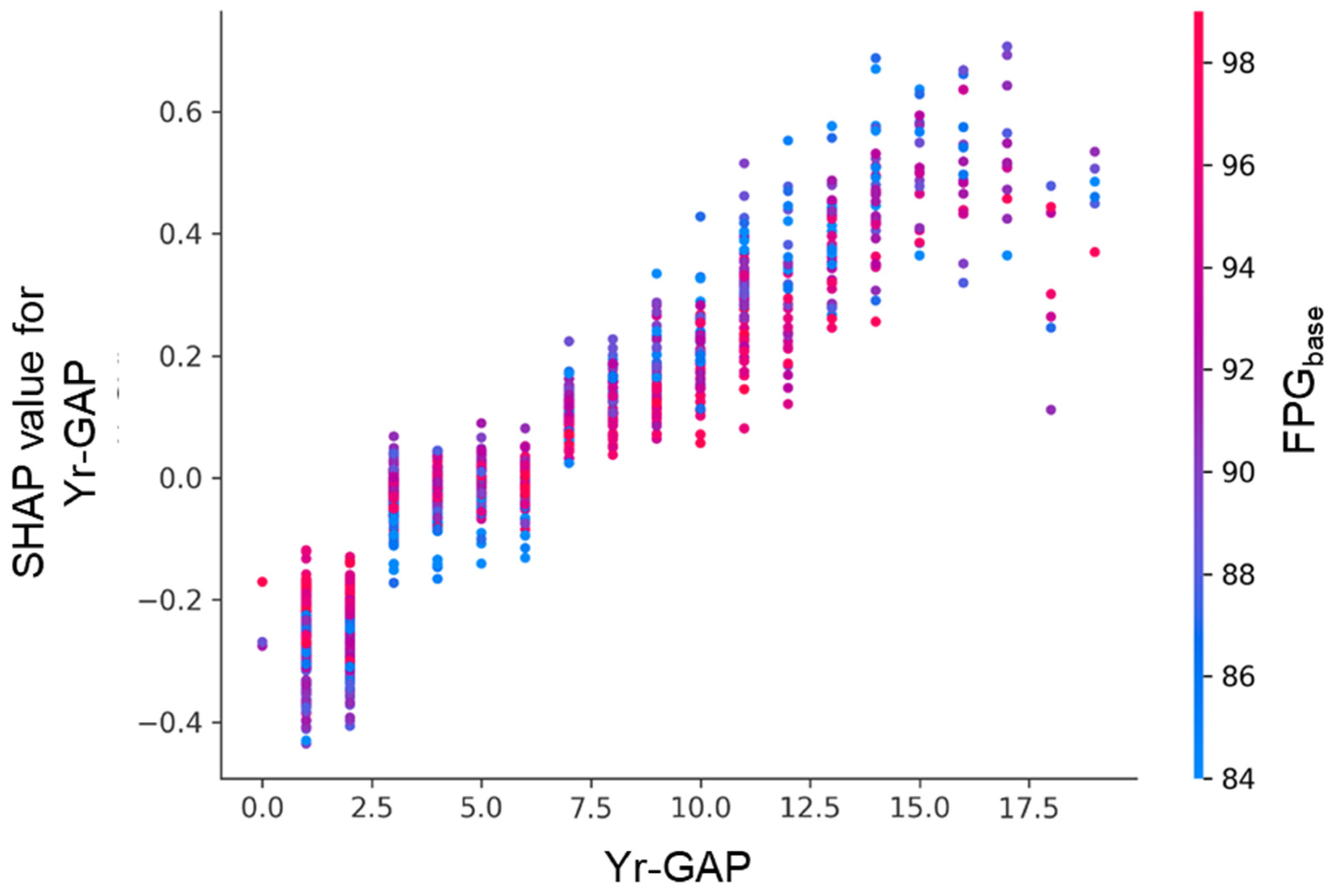
Figure 9.
SHAP dependence plot for follow-up interval (Yr-GAP), colored by FPGbase.
Figure 9.
SHAP dependence plot for follow-up interval (Yr-GAP), colored by FPGbase.
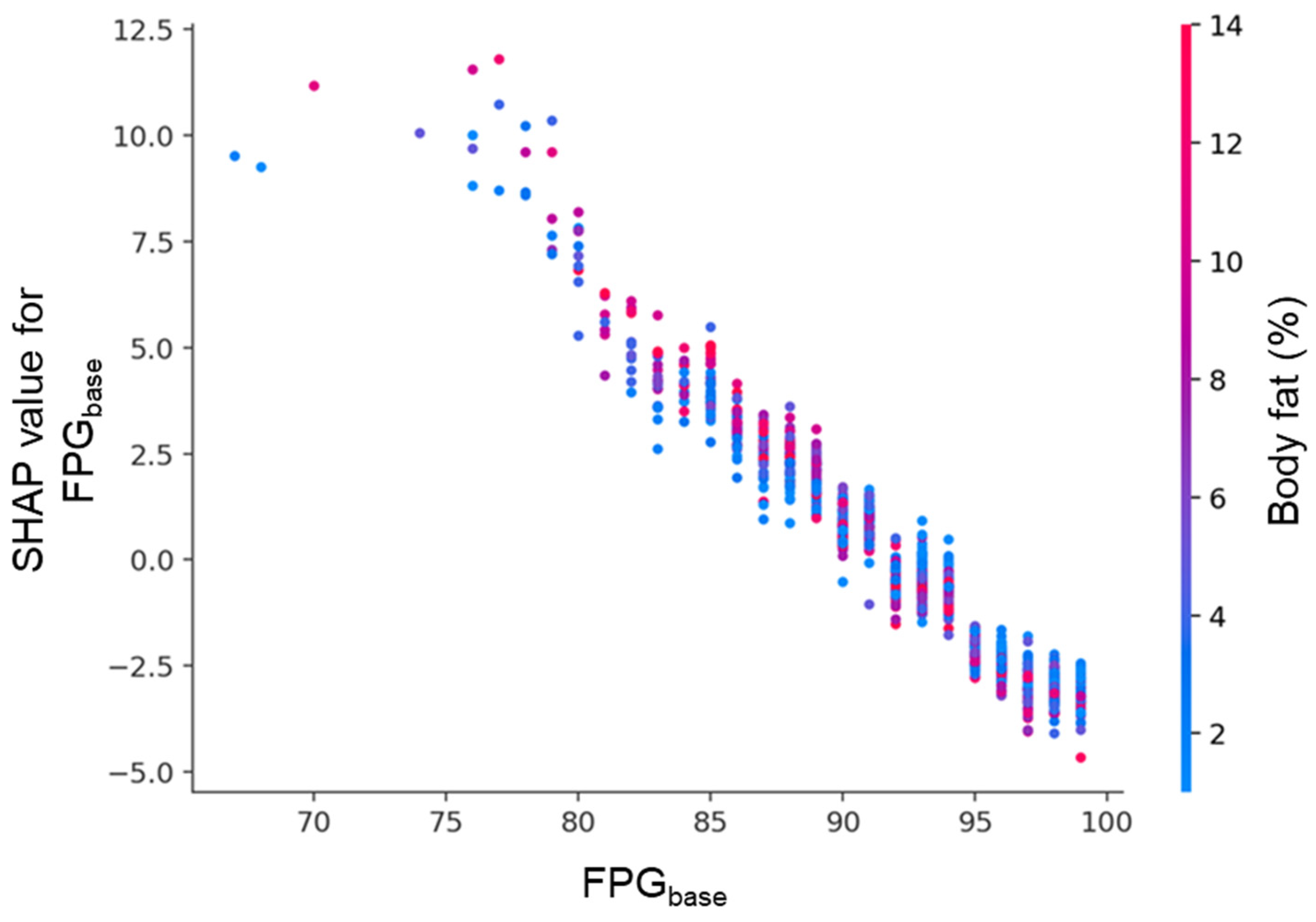
Figure 10.
SHAP dependence plot for FPGbase, colored by body fat percentage. Each point represents an individual participant. The x-axis shows FPGbase, and the y-axis indicates its SHAP value. Lower FPGbase levels were associated with strong positive SHAP values, while higher levels showed negative contributions. Body fat percentage, represented by the color gradient, further modulated this relationship.
Figure 10.
SHAP dependence plot for FPGbase, colored by body fat percentage. Each point represents an individual participant. The x-axis shows FPGbase, and the y-axis indicates its SHAP value. Lower FPGbase levels were associated with strong positive SHAP values, while higher levels showed negative contributions. Body fat percentage, represented by the color gradient, further modulated this relationship.
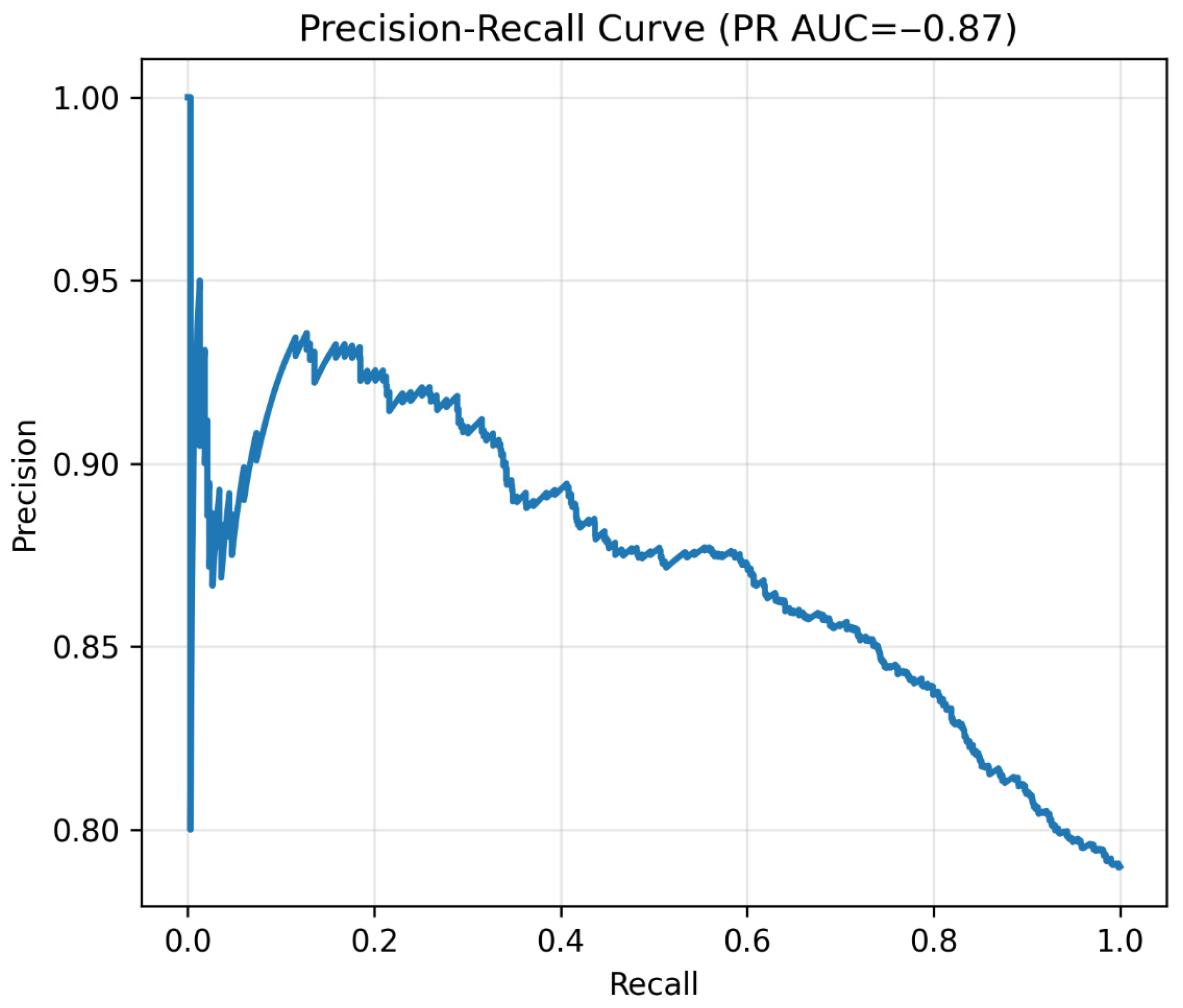
Figure 11.
Precision–recall curve. Note: Precision–recall curve of the binary classifier. High recall confirmed excellent sensitivity for prediabetes detection.
Figure 11.
Precision–recall curve. Note: Precision–recall curve of the binary classifier. High recall confirmed excellent sensitivity for prediabetes detection.
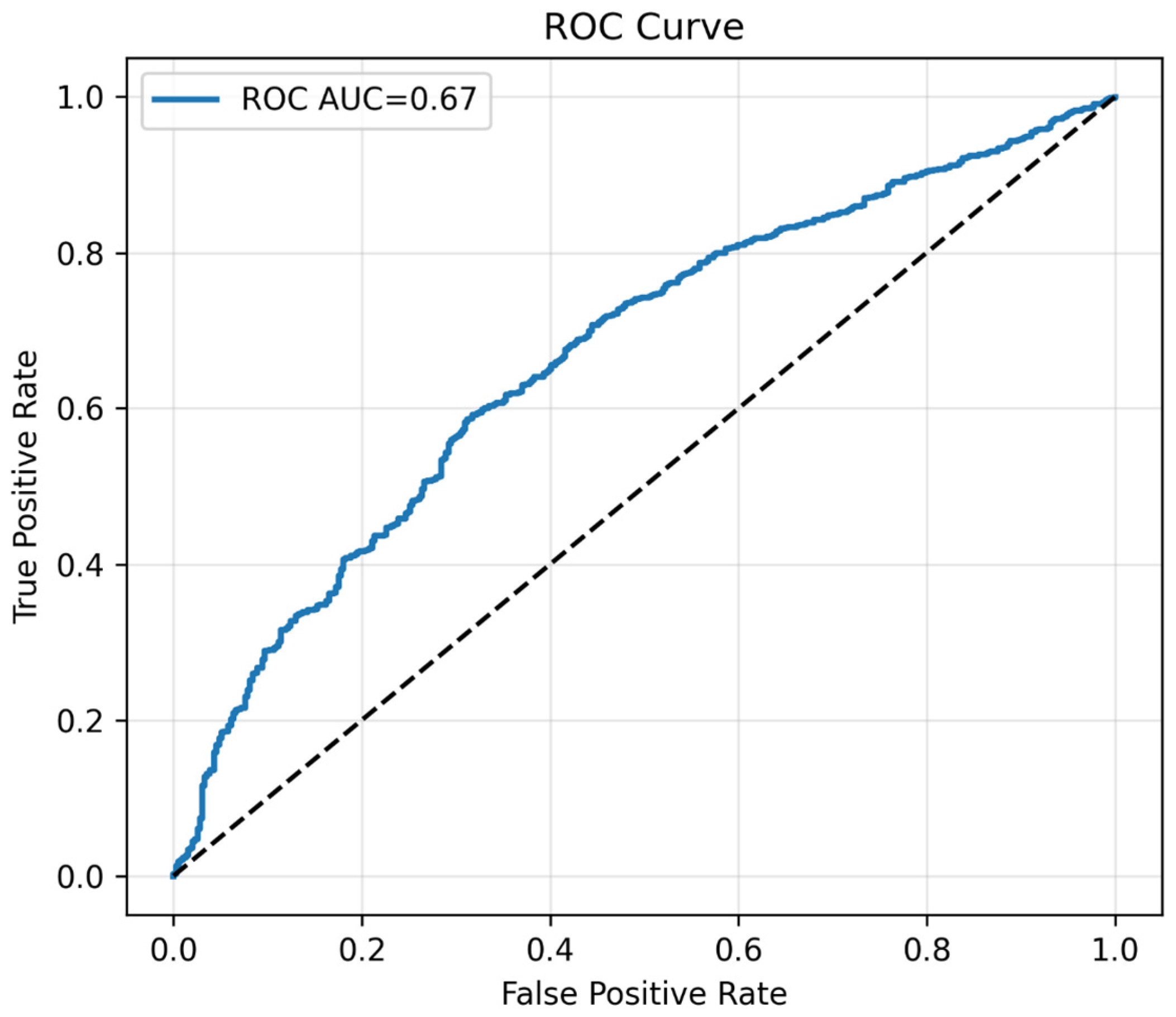
Figure 12.
The plot of ROC curve. Note: ROC curve of the binary classifier. Demonstrates moderate discrimination, consistent with prioritization of sensitivity. The black dotted line represents the performance of a random classifier (AUC = 0.5) which indicates no significance.
Figure 12.
The plot of ROC curve. Note: ROC curve of the binary classifier. Demonstrates moderate discrimination, consistent with prioritization of sensitivity. The black dotted line represents the performance of a random classifier (AUC = 0.5) which indicates no significance.
Figure 13.
Confusion matrix at chosen threshold. Confusion matrix at the prespecified threshold of 0.50. Cell values indicate the number of true positives, false positives, true negatives, and false negatives.
Figure 13.
Confusion matrix at chosen threshold. Confusion matrix at the prespecified threshold of 0.50. Cell values indicate the number of true positives, false positives, true negatives, and false negatives.
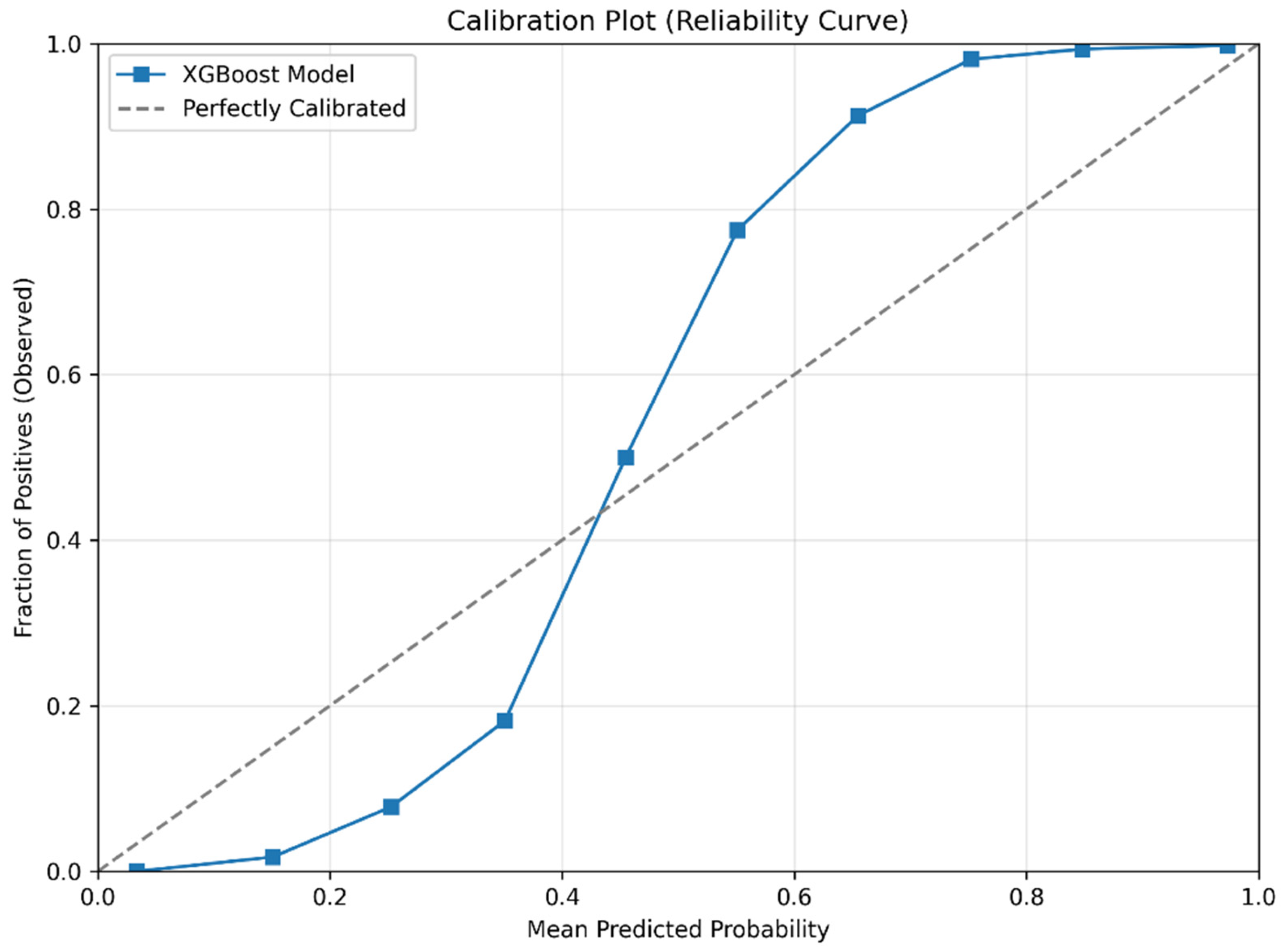
Figure 14.
Calibration plot (reliability curve) of the XGBoost model for predicting prediabetes.
Figure 14.
Calibration plot (reliability curve) of the XGBoost model for predicting prediabetes.
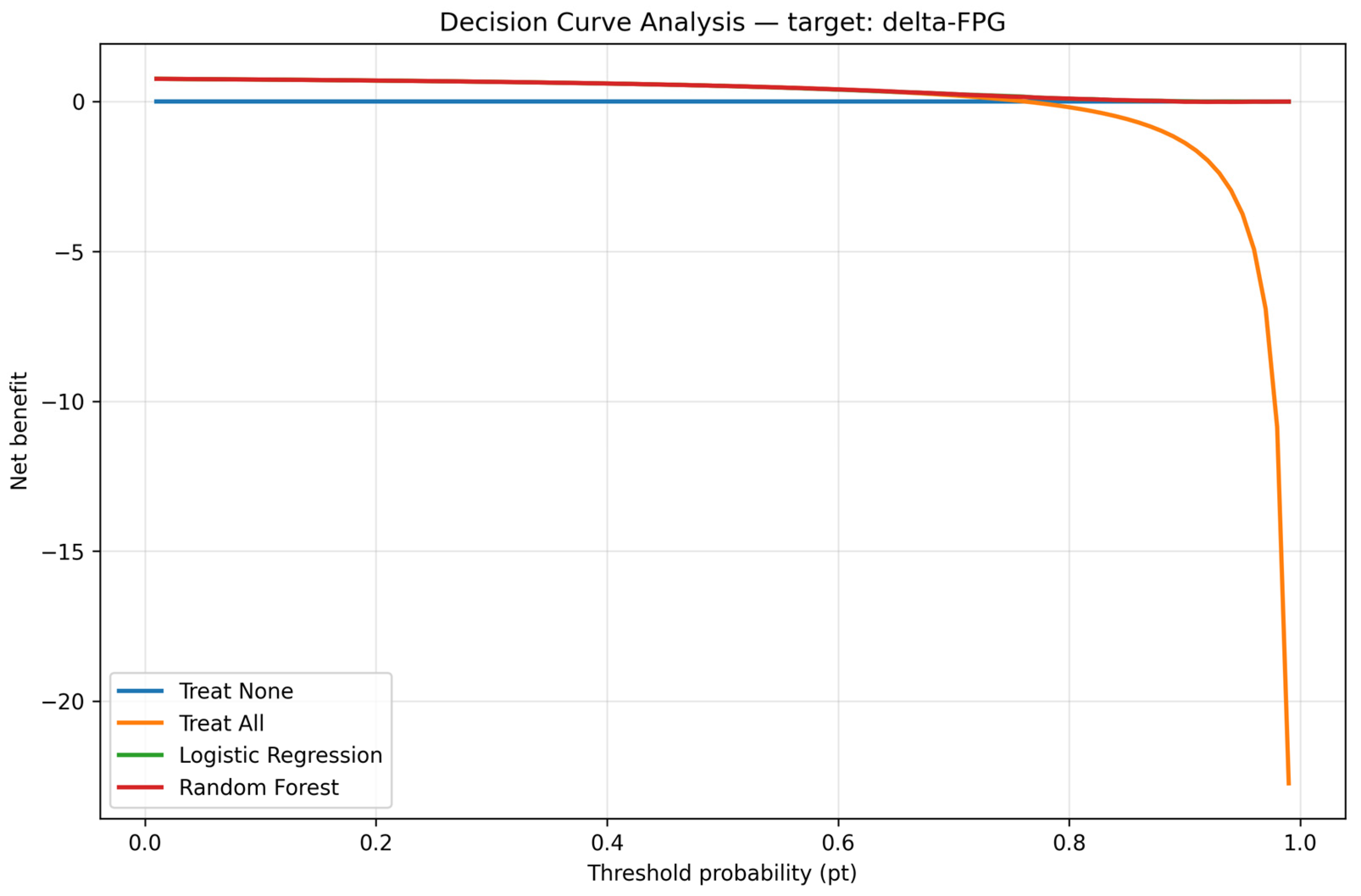
Figure 15.
Decision curve analysis. Note: The DCA model provided superior net clinical benefit compared to ‘treat all’ and ‘treat none’.
Figure 15.
Decision curve analysis. Note: The DCA model provided superior net clinical benefit compared to ‘treat all’ and ‘treat none’.
Table 1.
Comparison of previous studies predicting prediabetes/diabetes risk versus the present study. Includes study population, design, methods, outcomes, interpretability, and key findings, highlighting how the present dual-framework approach differs.
Table 1.
Comparison of previous studies predicting prediabetes/diabetes risk versus the present study. Includes study population, design, methods, outcomes, interpretability, and key findings, highlighting how the present dual-framework approach differs.
| Study | Population | Study Design | Method(s) | Outcome | Interpretability | Key Findings | Difference from Present Study |
|---|
| Huang et al., 2022 [8] | Korean adults | Cross-
sectional | Genetic risk score + oxidative stress score | Diabetes and prediabetes | None | Combined genetic and oxidative scores improved prediction | Not longitudinal, no ML, no SHAP |
| Wu et al., 2021 [9] | Middle-aged and elderly Chinese | Prospective cohort | Logistic regression | Prediabetes risk | None | Identified age, BMI, TG as key risk factors | Older population, single binary model |
| Yuk et al., 2022 [10] | Korean health checkup data | Cross-
sectional | ML (AI algorithms) | Diabetes and prediabetes | Limited | Applied AI for screening | Cross-sectional only, no continuous δ-FPG |
| Liu et al., 2024 [12] | Young Chinese men (~5.8 y follow-up) | Prospective cohort | ML (RF, XGBoost, etc.) | Prediabetes | None | Developed predictive models | Did not use dual framework or SHAP |
| Present study (2025) | Young Taiwanese men, 18–35 y, n = 6247, mean follow-up 5.9 y | Prospective cohort | Dual ML framework (RF, SGB, XGBoost, EN vs. MLR) | Continuous δ-FPG + binary prediabetes | SHAP applied | FPGbase strongest predictor; BF, WBC, age, TSH, TG, LDL-C important without FPGbase | First dual-framework ML + SHAP interpretability in young Taiwanese men; reproducibility tested with repeated runs and CI estimates |
Table 2.
Baseline demographic, biochemical, and lifestyle characteristics of the study cohort (n = 6247). Data are presented as mean ± SE for continuous variables and n (%) for categorical variables.
Table 2.
Baseline demographic, biochemical, and lifestyle characteristics of the study cohort (n = 6247). Data are presented as mean ± SE for continuous variables and n (%) for categorical variables.
| Variable | Mean ± SE |
|---|
| Age (year) | 27.75 ± 5.11 |
| Years of follow-up | 5.89 ± 4.21 |
| Body fat (%) | 21.38 ± 5.50 |
| White blood cell count (×103/μL) | 6.23 ± 1.44 |
| Hemoglobin (×106/μL) | 15.43 ± 0.99 |
| Platelets (×103/μL) | 236.72 ± 49.57 |
| Fasting plasma glucose-baseline (mg/dL) | 92.01 ± 4.74 |
| Glutamic pyruvic transaminase (IU/L) | 31.51 ± 47.78 |
| Glutamic oxaloacetic transaminase (IU/L) | 24.13 ± 20.85 |
| γ-Glutamyl transpeptidase (IU/L) | 19.88 ± 16.96 |
| Lactate dehydrogenase (IU/L) | 287.87 ± 66.74 |
| Uric acid (mg/dL) | 7.08 ± 1.40 |
| Creatinine (mg/dL) | 1.08 ± 0.13 |
| Triglyceride (mg/dL) | 100.36 ± 60.99 |
| High-density lipoprotein cholesterol (mg/dL) | 49.25 ± 11.87 |
| Low-density lipoprotein cholesterol (mg/dL) | 112.56 ± 31.15 |
| Alkaline phosphatase (IU/L) | 147.33 ± 47.38 |
| Thyroid stimulating hormone (IU/mL) | 1.61 ± 1.66 |
| C-reactive protein (mg/dL) | 0.21 ± 0.40 |
| Drinking area | 1.60 ± 7.29 |
| Sport area | 9.55 ± 9.03 |
| δ-Fasting plasma glucose (mg/dL) | 5.21 ± 7.02 |
| Spouse status | n (%) |
| Single | 3957 (63.9%) *** |
| With spouse | 2232 (36.1%) |
| Sleep hours | n (%) |
| 0–4 h/day | 24 (0.4%) |
| 4–6 h/day | 1054 (16.9%) |
| 6–8 h/day | 4745 (76.2%) |
| >8 h/day | 408 (6.5%) |
| Education level | n (%) |
| Primary school | 3 (0.1%) |
| Junior high school | 51 (0.8%) |
| Senior high school | 1012 (16.2%) |
| College | 1830 (29.3%) |
| University | 2293 (36.8%) |
| Higher than master’s degree | 1031 (16.8%) |
| Income level (thousand USD/year) | n (%) |
| 0 | 1232 (19.7%) * |
| 12.7/year | 1029 (16.5%) |
| 12.7–25.3/year | 2822 (45.2%) |
| 25.3–38.0/year | 883 (14.1%) |
| 38.0–50.6/year | 130 (2.1%) |
| 50.6–63.3/year | 73 (1.2%) |
| >63.3/year | 78 (1.2%) |
Table 3.
Equations and descriptions of performance metrics used to evaluate continuous outcome prediction models: SMAPE, RAE, RRSE, and RMSE.
Table 3.
Equations and descriptions of performance metrics used to evaluate continuous outcome prediction models: SMAPE, RAE, RRSE, and RMSE.
| Metrics | Description | Calculation |
|---|
| SMAPE | Symmetric mean absolute percentage error | |
| RAE | Relative absolute error | |
| RRSE | Root relative squared error | |
| RMSE | Root mean squared error | |
Table 4.
Demographic and biochemical characteristics of participants stratified by glycemic outcome (prediabetes and normal). Continuous variables are shown as mean ± SE and categorical variables as n (%).
Table 4.
Demographic and biochemical characteristics of participants stratified by glycemic outcome (prediabetes and normal). Continuous variables are shown as mean ± SE and categorical variables as n (%).
| Variable | Prediabetes | Normal |
|---|
| n | 2789 | 3458 |
| Age (year) | 28.4 ± 5.0 | 27.3 ± 5.1 *** |
| Years of follow-up | 5.6 ± 4.0 | 6.1 ± 4.4 *** |
| Body fat (%) | 22.1 ± 5.5 | 20.8 ± 5.5 *** |
| White blood cell count (×103/μL) | 6.3 ± 1.5 | 6.2 ± 1.4 *** |
| Hemoglobin (×106/μL) | 15.5 ± 1.0 | 15.4 ± 1 |
| Platelets (×103/μL) | 237.1 ± 49.8 | 236.4 ± 49.4 |
| Fasting plasma glucose—baseline (mg/dL) | 93.3 ± 4.3 | 91.0 ± 4.8 *** |
| Glutamic pyruvic transaminase (IU/L) | 32.7 ± 50.6 | 30.5 ± 45.4 |
| Glutamic oxaloacetic transaminase (IU/L) | 24.2 ± 20.2 | 24.1 ± 21.4 |
| γ-Glutamyl transpeptidase (IU/L) | 20.6 ± 17.1 | 19.3 ± 16.8 *** |
| Lactate dehydrogenase (IU/L) | 290.6 ± 63 | 285.6 ± 69.6 *** |
| Uric acid (mg/dL) | 7.2 ± 1.4 | 7.0 ± 1.4 *** |
| Creatinine (mg/dL) | 1.1 ± 0.1 | 1.1 ± 0.1 |
| Triglyceride (mg/dL) | 105.8 ± 66.1 | 96.0 ± 56.2 *** |
| High-density lipoprotein cholesterol (mg/dL) | 48.4 ± 11.6 | 50.0 ± 12.1 *** |
| Low-density lipoprotein cholesterol (mg/dL) | 115.0 ± 32.0 | 110.6 ± 30.3 *** |
| Alkaline phosphatase (IU/L) | 146.7 ± 45.0 | 147.8 ± 49.3 |
| Thyroid-stimulating hormone (IU/mL) | 1.6 ± 0.8 | 1.7 ± 2.1 * |
| C-reactive protein (mg/dL) | 0.2 ± 0.4 | 0.2 ± 0.4 |
| Drinking area | 1.8 ± 7.4 | 1.5 ± 7.2 |
| Sport area | 9.2 ± 8.9 | 9.8 ± 9.1 * |
| δ-Fasting plasma glucose (mg/dL) | 9.88 ± 5.45 | 1.44 ± 5.77 *** |
| Spouse status |
| Single | 1660 (60.1%) | 2297 (67.1%) *** |
| With spouse | 1104 (39.9%) | 1128 (32.9%) |
| Sleep hours |
| 0–4 h/day | 8 (0.3%) | 16 (0.5%) |
| 4–6 h/day | 474 (17.0%) | 580 (16.8%) |
| 6–8 h/day | 2129 (76.6%) | 2616 (75.8%) |
| >8 h/day | 170 (6.1%) | 238 (6.9%) |
| Education level |
| Primary school | 1 (0.04%) | 2 (0.1%) * |
| Junior high school | 18 (0.7%) | 33 (1.0%) |
| Senior high school | 425 (15.3%) | 587 (17.1%) |
| College | 835 (30.0%) | 995 (28.9%) |
| University | 1006 (36.2%) | 1287 (37.4%) |
| Higher than master’s degree | 496 (17.8%) | 535 (15.6%) |
| Income level (thousand USD/year) |
| 0 | 471 (16.9%) | 761 (22.0%) *** |
| 12.7/year | 430 (15.4%) | 599 (17.3%) |
| 12.7–25.3/year | 1292 (46.3%) | 1530 (44.3%) |
| 25.3–38.0/year | 448 (16.1%) | 435 (12.6%) |
| 38.0–50.6/year | 70 (2.5%) | 60 (1.7%) |
| 50.6–63.3/year | 42 (1.5%) | 31 (0.9%) |
| >63.3/year | 36 (1.3%) | 42 (1.2%) |
Table 5.
Average performance of linear regression and machine learning methods for predicting continuous glycemic change (δ-FPG), with and without FPGbase.
Table 5.
Average performance of linear regression and machine learning methods for predicting continuous glycemic change (δ-FPG), with and without FPGbase.
| With FPGbase |
|---|
| Methods | SMAPE | RAE | RRSE | RMSE |
| MLR | 0.968 | 0.9283 | 0.9077 | 6.4156 |
| RF | 0.9571 | 0.9273 | 0.9074 | 6.4133 |
| SGB | 0.9426 | 0.9306 | 0.9113 | 6.4407 |
| XGBoost | 0.9443 | 0.929 | 0.9102 | 6.4329 |
| EN | 0.9599 | 0.9266 | 0.9068 | 6.4092 |
| WithoutFPGbase |
| Methods | SMAPE | RAE | RRSE | RMSE |
| MLR | 0.951 | 0.9845 | 0.9832 | 6.9022 |
| RF | 0.9477 | 0.9887 | 0.9854 | 6.9175 |
| SGB | 0.9489 | 0.9839 | 0.9817 | 6.8916 |
| XGBoost | 0.9498 | 0.9878 | 0.985 | 6.9149 |
| EN | 0.9492 | 0.9845 | 0.9827 | 6.8985 |
Table 6.
Mean and 95% confidence intervals (CIs) of performance metrics (SMAPE, RMSE, RAE, RRSE) across 10 repeated runs for continuous outcome prediction models, demonstrating reproducibility and stability.
Table 6.
Mean and 95% confidence intervals (CIs) of performance metrics (SMAPE, RMSE, RAE, RRSE) across 10 repeated runs for continuous outcome prediction models, demonstrating reproducibility and stability.
| Model | Metric | Mean | SE | 95% CI Lower | 95% CI Upper |
|---|
| EN | SMAPE | 96.46007 | 0.016408 | 96.42295 | 96.49719 |
| EN | RMSE | 6.427868 | 0.00196 | 6.423434 | 6.432301 |
| EN | RAE | 0.922647 | 0.000325 | 0.921912 | 0.923382 |
| EN | RRSE | 0.905753 | 0.00021 | 0.905279 | 0.906227 |
| RF | SMAPE | 96.84203 | 0.021496 | 96.7934 | 96.89066 |
| RF | RMSE | 6.471158 | 0.00179 | 6.467109 | 6.475208 |
| RF | RAE | 0.920818 | 0.000309 | 0.920119 | 0.921517 |
| RF | RRSE | 0.912466 | 0.000341 | 0.911695 | 0.913237 |
| XGBoost | SMAPE | 104.8296 | 0.024476 | 104.7742 | 104.8849 |
| XGBoost | RMSE | 7.056346 | 0.002225 | 7.051313 | 7.06138 |
| XGBoost | RAE | 1.004276 | 0.000322 | 1.003548 | 1.005003 |
| XGBoost | RRSE | 0.994844 | 0.000363 | 0.994023 | 0.995666 |
Table 7.
Relative importance percentages of predictors in Model 1 (with FPGbase included) across four machine learning methods (RF, SGB, XGBoost, EN).
Table 7.
Relative importance percentages of predictors in Model 1 (with FPGbase included) across four machine learning methods (RF, SGB, XGBoost, EN).
| Variables | MOIP |
|---|
| Baseline fasting plasma glucose | 100 |
| Body fat | 17.64 |
| Thyroid-stimulating hormone | 14.8 |
| White blood cell count | 14.51 |
| Years of follow-up | 14.32 |
| C-reactive protein | 11.63 |
| Age | 10.30 |
| HDL-cholesterol (HDL-C) | 9.75 |
| Uric acid | 9.34 |
| Hemoglobin | 8.80 |
| Lactic dehydrogenase | 8.32 |
| LDL-cholesterol (LDL-C) | 8.30 |
| Triglyceride (TG) | 7.63 |
| Alkaline phosphatase | 7.39 |
| Platelet | 7.11 |
| Glutamic pyruvic transaminase (GPT) | 5.93 |
| γ-Glutamyl transpeptidase | 5.27 |
| Spouse status | 4.87 |
| Glutamic oxaloacetic transaminase (GOT) | 4.50 |
| Sport area | 4.27 |
| Income status | 3.50 |
| Creatinine | 2.41 |
| Sleeping level | 2.15 |
| Education level | 1.71 |
| Drinking area | 0.54 |
Table 8.
Relative importance percentages of predictors in Model 2 (excluding FPGbase) across four machine learning methods (RF, SGB, XGBoost, EN).
Table 8.
Relative importance percentages of predictors in Model 2 (excluding FPGbase) across four machine learning methods (RF, SGB, XGBoost, EN).
| Variables | MOIP |
|---|
| Body fat | 88.85 |
| White blood cell count | 58.62 |
| Age | 54.89 |
| Thyroid stimulating hormone | 36.87 |
| Triglyceride | 32.66 |
| LDL-cholesterol | 28.69 |
| HDL-cholesterol | 27.42 |
| Years of follow-up | 24.94 |
| γ-Glutamyl transpeptidase | 22.78 |
| Hemoglobin | 22.67 |
| Lactic dehydrogenase | 22.32 |
| Alkaline phosphatase | 22.16 |
| Platelet | 21.36 |
| Uric acid | 20.95 |
| Glutamic oxaloacetic transaminase (GOT) | 18.88 |
| Glutamic pyruvic transaminase (GPT) | 18.49 |
| Sport area | 16.83 |
| Creatinine | 8.95 |
| Income level | 6.71 |
| Education level | 6.11 |
| C-reactive protein | 5.14 |
| Sleeping level | 4.00 |
| Drink area | 1.65 |
| Spouse status | 0 |
Table 9.
Performance metrics of the categorical (binary) model for predicting prediabetes versus normal outcomes, including accuracy, precision, recall, specificity, false positive rate, F1 score, ROC-AUC, PR-AUC, and classification counts.
Table 9.
Performance metrics of the categorical (binary) model for predicting prediabetes versus normal outcomes, including accuracy, precision, recall, specificity, false positive rate, F1 score, ROC-AUC, PR-AUC, and classification counts.
| Accuracy | Precision | Sensitivity (Recall) | Specificity | False Positive Rate | F1 Score | ROC-AUC | PR-AUC | True Positives | False Positives | True Negatives | False Negatives |
|---|
| 0.788 | 0.791 | 0.995 | 0.010 | 0.990 | 0.881 | 0.667 | 0.873 | 1473 | 390 | 4 | 8 |
Table 10.
Performance of the binary model at a high-sensitivity threshold (0.2892), prioritizing minimization of false negatives for screening purposes.
Table 10.
Performance of the binary model at a high-sensitivity threshold (0.2892), prioritizing minimization of false negatives for screening purposes.
| Metric | Value |
|---|
| Threshold | 0.2892 |
| Sensitivity | 0.9953 |
| Specificity | 0.4746 |
Table 11.
Performance of the binary model at the optimal balanced threshold (0.5683), determined by Youden’s J statistic, representing a trade-off between sensitivity and specificity suitable for diagnostic settings.
Table 11.
Performance of the binary model at the optimal balanced threshold (0.5683), determined by Youden’s J statistic, representing a trade-off between sensitivity and specificity suitable for diagnostic settings.
| Metric | Value |
|---|
| Threshold | 0.5683 |
| Sensitivity | 0.8869 |
| Specificity | 0.9061 |
| Youden’s J | 0.7930 |
Table 12.
Sensitivity and ablation analysis.
Table 12.
Sensitivity and ablation analysis.
| Model | ROC-AUC |
|---|
| Original XGBoost | 0.6753 |
| XGBoost (top 3 features removed) | 0.5588 |