Using Machine Learning to Create Prognostic Systems for Primary Prostate Cancer
Abstract
1. Introduction
2. Methods
2.1. Clinical–Pathologic Datasets
2.2. EACCD
- Define the initial dissimilarity for any pair and .
- For each with , apply the two-phase Partitioning Around Medoids and the initial dissimilarities in Step 1 to partition combinations into clusters. is defined as 1 if and are not assigned into the same cluster, otherwise was defined as 0. Then the learned dissimilarity is defined as follows: .
- Perform hierarchical clustering to cluster the combinations by using .
2.3. Prognostic Systems
2.4. Software
3. Results
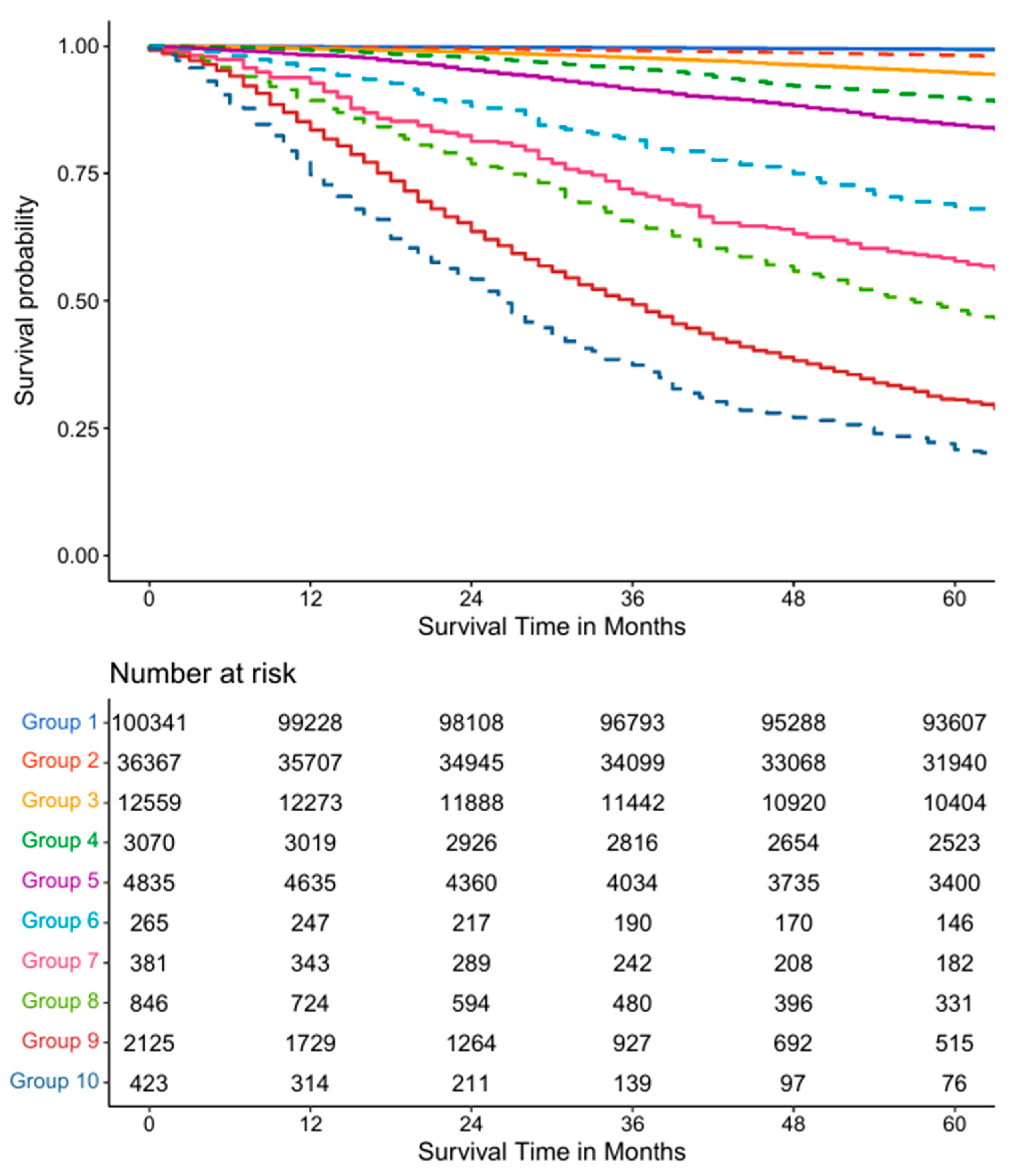
3.1. Five Variable AJCC System
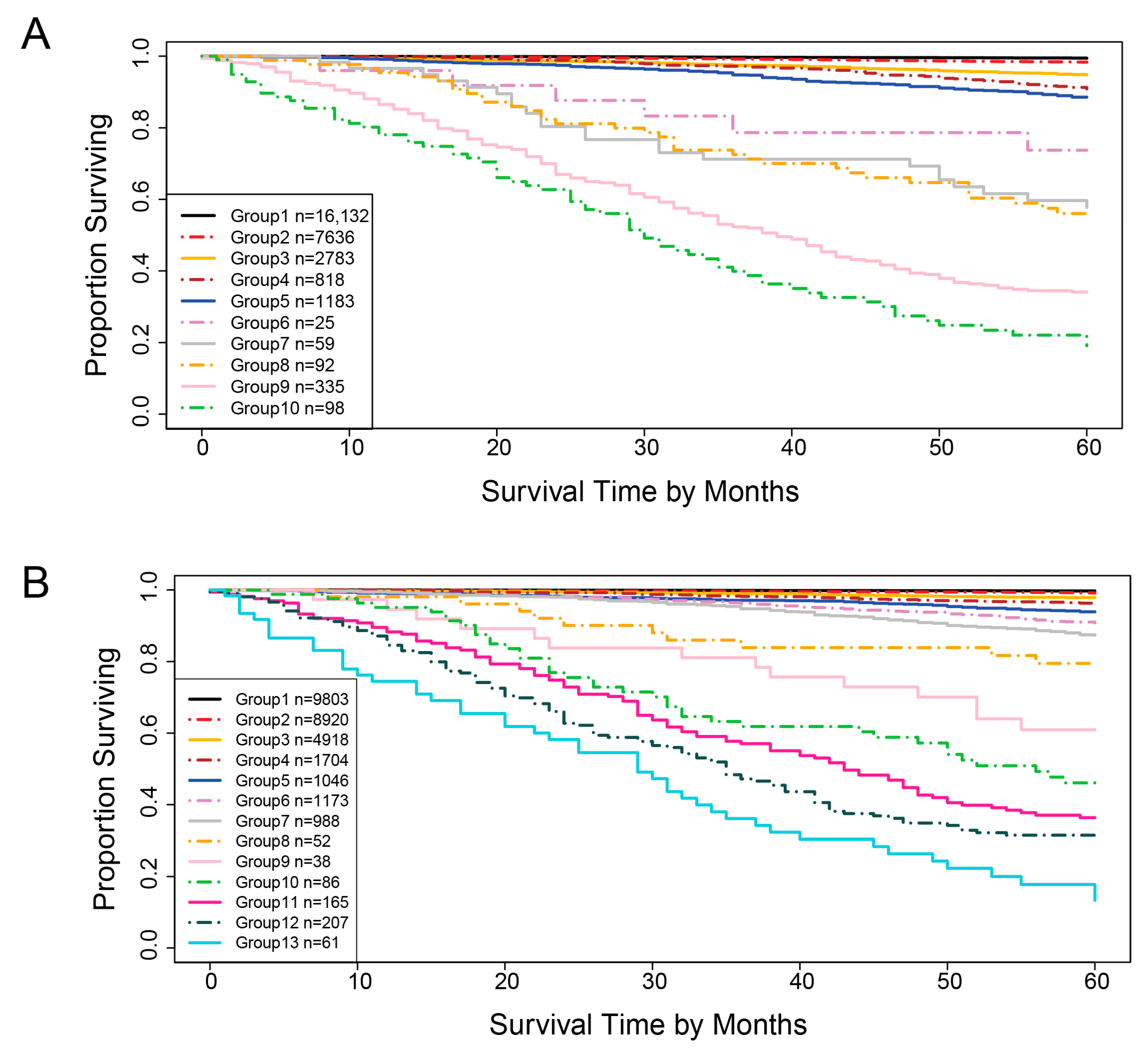
3.2. Five Variable EACCD System
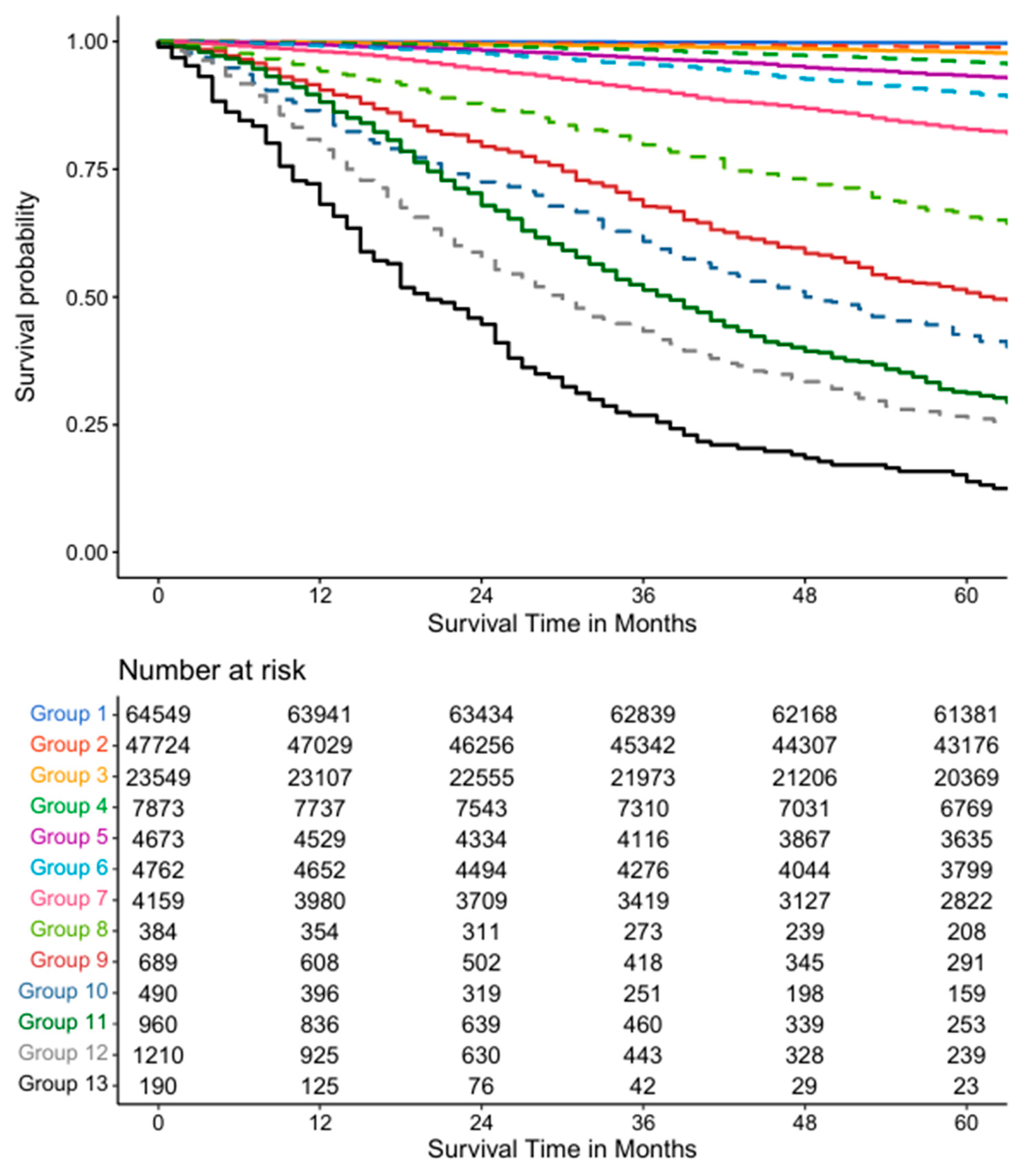
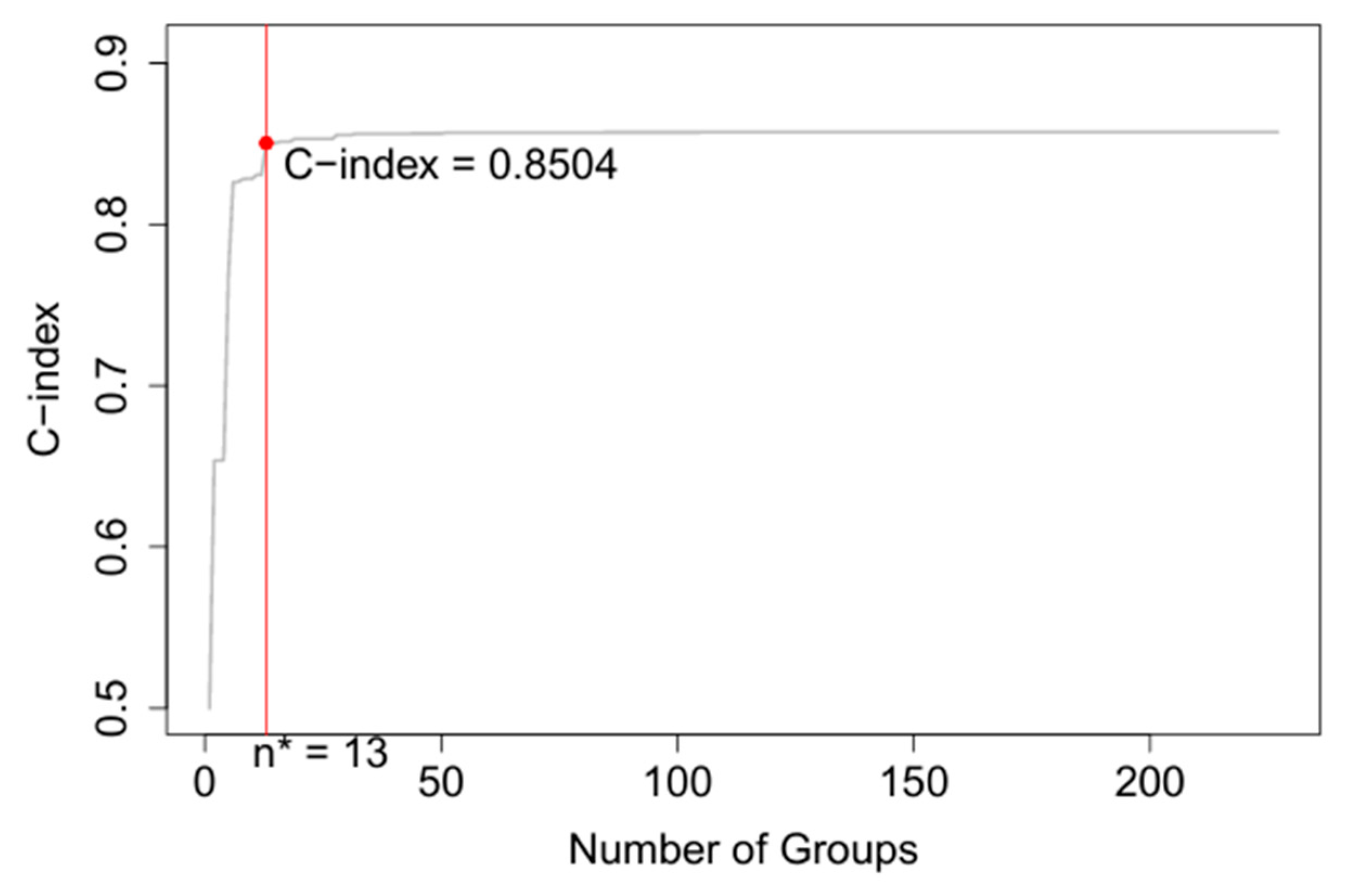
3.3. Seven Variable EACCD System
3.4. Validation
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Siegel, R.L.; Giaquinto, A.N.; Jemal, A. Cancer statistics, 2024. CA Cancer J. Clin. 2024, 74, 12–49. [Google Scholar] [CrossRef] [PubMed]
- Etzioni, R.; Tsodikov, A.; Mariotto, A.; Szabo, A.; Falcon, S.; Wegelin, J.; DiTommaso, D.; Karnofski, K.; Gulati, R.; Penson, D.F.; et al. Quantifying the role of PSA screening in the US prostate cancer mortality decline. Cancer Causes Control 2008, 19, 175–181. [Google Scholar] [CrossRef] [PubMed]
- Tsodikov, A.; Gulati, R.; Etzioni, R. Reconciling the Effects of Screening on Prostate Cancer Mortality in the ERSPC and PLCO Trials. Ann. Intern. Med. 2018, 168, 608–609. [Google Scholar] [CrossRef] [PubMed]
- Matsukawa, A.; Yanagisawa, T.; Bekku, K.; Kardoust Parizi, M.; Laukhtina, E.; Klemm, J.; Chiujdea, S.; Mori, K.; Kimura, S.; Fazekas, T.; et al. Comparing the Performance of Digital Rectal Examination and Prostate-specific Antigen as a Screening Test for Prostate Cancer: A Systematic Review and Meta-analysis. Eur. Urol. Oncol. 2024, 7, 697–704. [Google Scholar] [CrossRef]
- Borregales, L.D.; DeMeo, G.; Gu, X.; Cheng, E.; Dudley, V.; Schaeffer, E.M.; Nagar, H.; Carlsson, S.; Vickers, A.; Hu, J.C. Grade Migration of Prostate Cancer in the United States During the Last Decade. J. Natl. Cancer Inst. 2022, 114, 1012–1019. [Google Scholar] [CrossRef]
- Jemal, A.; Fedewa, S.A.; Ma, J.; Siegel, R.; Lin, C.C.; Brawley, O.; Ward, E.M. Prostate Cancer Incidence and PSA Testing Patterns in Relation to USPSTF Screening Recommendations. JAMA 2015, 314, 2054–2061. [Google Scholar] [CrossRef]
- Moyer, V.A.; U.S. Preventive Services Task Force. Screening for prostate cancer: U.S. Preventive Services Task Force recommendation statement. Ann. Intern. Med. 2012, 157, 120–134. [Google Scholar] [CrossRef]
- Siegel, D.A.; O’Neil, M.E.; Richards, T.B.; Dowling, N.F.; Weir, H.K. Prostate Cancer Incidence and Survival, by Stage and Race/Ethnicity—United States, 2001–2017. MMWR Morb. Mortal. Wkly. Rep. 2020, 69, 1473–1480. [Google Scholar] [CrossRef]
- Amin, M.B.; Greene, F.L.; Edge, S.B.; Compton, C.C.; Gershenwald, J.E.; Brookland, R.K.; Meyer, L.; Gress, D.M.; Byrd, D.R.; Winchester, D.P. The Eighth Edition AJCC Cancer Staging Manual: Continuing to build a bridge from a population-based to a more “personalized” approach to cancer staging. CA Cancer J. Clin. 2017, 67, 93–99. [Google Scholar] [CrossRef]
- Edge, S.B.; Compton, C.C. The American Joint Committee on Cancer: The 7th Edition of the AJCC Cancer Staging Manual and the Future of TNM. Ann. Surg. Oncol. 2010, 17, 1471–1474. [Google Scholar] [CrossRef]
- Epstein, J.I.; Zelefsky, M.J.; Sjoberg, D.D.; Nelson, J.B.; Egevad, L.; Magi-Galluzzi, C.; Vickers, A.J.; Parwani, A.V.; Reuter, V.E.; Fine, S.W.; et al. A Contemporary Prostate Cancer Grading System: A Validated Alternative to the Gleason Score. Eur. Urol. 2016, 69, 428–435. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Yang, D.; Zhu, J.; Zhou, Y.; Xiang, C.; Wu, S. Modified the 8th AJCC staging system for patients with advanced prostate cancer: A study based on SEER database. BMC Urol. 2022, 22, 185. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Xing, K.; Henson, D.; Sheng, L.; Schwartz, A.M.; Cheng, X. Developing prognostic systems of cancer patients by ensemble clustering. J. Biomed. Biotechnol. 2009, 2009, 632786. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chen, D.; Pan, Q.; Hueman, M.T. Using Weighted Differences in Hazards as Effect Sizes for Survival Data. J. Stat. Theory Pract. 2022, 16, 12. [Google Scholar] [CrossRef]
- Hueman, M.T.; Wang, H.; Yang, C.Q.; Sheng, L.; Henson, D.E.; Schwartz, A.M.; Chen, D. Creating prognostic systems for cancer patients: A demonstration using breast cancer. Cancer Med. 2018, 7, 3611–3621. [Google Scholar] [CrossRef]
- Qi, R.; Wu, D.; Sheng, L.; Henson, D.; Schwartz, A.; Xu, E.; Xing, K.; Chen, D. On an ensemble algorithm for clustering cancer patient data. BMC Syst. Biol. 2013, 7 (Suppl. 4), S9. [Google Scholar] [CrossRef]
- Henson, D.E.; Hueman, M.T.; Chen, D.; Patel, J.A.; Wang, H.; Schwartz, A.M. The anatomy of the TNM for colon cancer. J. Gastrointest. Oncol. 2017, 8, 12–19. [Google Scholar] [CrossRef]
- Hueman, M.; Wang, H.; Liu, Z.; Henson, D.; Nguyen, C.; Park, D.; Sheng, L.; Chen, D. Expanding TNM for lung cancer through machine learning. Thorac. Cancer 2021, 12, 1423–1430. [Google Scholar] [CrossRef]
- Grimley, P.M.; Liu, Z.; Darcy, K.M.; Hueman, M.T.; Wang, H.; Sheng, L.; Henson, D.E.; Chen, D. A prognostic system for epithelial ovarian carcinomas using machine learning. Acta Obstet. Gynecol. Scand. 2021, 100, 1511–1519. [Google Scholar] [CrossRef]
- Praiss, A.M.; Huang, Y.; St Clair, C.M.; Tergas, A.I.; Melamed, A.; Khoury-Collado, F.; Hou, J.Y.; Hu, J.; Hur, C.; Hershman, D.L.; et al. Using machine learning to create prognostic systems for endometrial cancer. Gynecol. Oncol. 2020, 159, 744–750. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Yang, J.; Sheng, L.; Chen, D. Using Machine Learning to Expand the Ann Arbor Staging System for Hodgkin and Non-Hodgkin Lymphoma. Bio. Med. Informatics 2023, 3, 514–525. [Google Scholar] [CrossRef]
- Yang, C.Q.; Wang, H.; Liu, Z.; Hueman, M.T.; Bhaskaran, A.; Henson, D.E.; Sheng, L.; Chen, D. Integrating additional factors into the TNM staging for cutaneous melanoma by machine learning. PLoS ONE 2021, 16, e0257949. [Google Scholar] [CrossRef] [PubMed]
- Surveillance, Epidemiology, and End Results (SEER) Program. SEER*Stat Database: Incidence—SEER Research Data, 17 Registries, November 2023 Submission (2000–2021). Available online: https://seer.cancer.gov/data-software/documentation/seerstat/nov2023/ (accessed on 6 February 2025).
- Dess, R.T.; Hartman, H.E.; Mahal, B.A.; Soni, P.D.; Jackson, W.C.; Cooperberg, M.R.; Amling, C.L.; Aronson, W.J.; Kane, C.J.; Terris, M.K.; et al. Association of Black Race with Prostate Cancer-Specific and Other-Cause Mortality. JAMA Oncol. 2019, 5, 975–983. [Google Scholar] [CrossRef] [PubMed]
- Banez, L.L.; Terris, M.K.; Aronson, W.J.; Presti, J.C., Jr.; Kane, C.J.; Amling, C.L.; Freedland, S.J. Race and time from diagnosis to radical prostatectomy: Does equal access mean equal timely access to the operating room?—Results from the SEARCH database. Cancer Epidemiol. Biomark. Prev. 2009, 18, 1208–1212. [Google Scholar] [CrossRef] [PubMed]
- Wenzel, M.; Deuker, M.; Stolzenbach, F.; Nocera, L.; Colla Ruvolo, C.; Tian, Z.; Shariat, S.F.; Saad, F.; Briganti, A.; Kluth, L.A.; et al. The effect of race/ethnicity on histological subtype distribution, stage at presentation and cancer specific survival in urethral cancer. Urol. Oncol. 2021, 39, 369.e9–369.e17. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Song, J.; Jung, G.; Song, S.H.; Hong, S.K. Prognosis after radical prostatectomy in men older than 75 years: Long-term results from a single tertiary center. Prostate Int. 2024, 12, 15–19. [Google Scholar] [CrossRef]
- Huan, W.; Li, S.; Dechang, C. Perspective Chapter: Using Effect Sizes to Study the Survival Difference between Two Groups. In Recent Advances in Biostatistics; Kumar, B.S., Ed.; IntechOpen: Rijeka, Croatia, 2023; p. 6. [Google Scholar]
- Bien, J.; Tibshirani, R. Hierarchical Clustering with Prototypes via Minimax Linkage. J. Am. Stat. Assoc. 2011, 106, 1075–1084. [Google Scholar] [CrossRef]
- Harrell, F.E., Jr.; Lee, K.L.; Mark, D.B. Multivariable prognostic models: Issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat. Med. 1996, 15, 361–387. [Google Scholar] [CrossRef]
- Tan, Y.G.; Fang, A.H.S.; Lim, J.K.S.; Khalid, F.; Chen, K.; Ho, H.S.S.; Yuen, J.S.P.; Huang, H.H.; Tay, K.J. Incorporating artificial intelligence in urology: Supervised machine learning algorithms demonstrate comparative advantage over nomograms in predicting biochemical recurrence after prostatectomy. Prostate 2022, 82, 298–305. [Google Scholar] [CrossRef]
- Ekşi, M.; Evren, İ.; Akkaş, F.; Arıkan, Y.; Özdemir, O.; Özlü, D.N.; Ayten, A.; Sahin, S.; Tuğcu, V.; Taşçı, A.I. Machine learning algorithms can more efficiently predict biochemical recurrence after robot-assisted radical prostatectomy. Prostate 2021, 81, 913–920. [Google Scholar] [CrossRef]
- Semwal, H.; Ladbury, C.; Sabbagh, A.; Mohamad, O.; Tilki, D.; Amini, A.; Wong, J.; Li, Y.R.; Glaser, S.; Yuh, B.; et al. Machine learning and explainable artificial intelligence to predict pathologic stage in men with localized prostate cancer. Prostate 2025, 85, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Martelin, N.; De Witt, B.; Chen, B.; Eschwège, P. Development and validation of an imageless machine-learning algorithm for the initial screening of prostate cancer. Prostate 2024, 84, 842–849. [Google Scholar] [CrossRef] [PubMed]
- Nayan, M.; Salari, K.; Bozzo, A.; Ganglberger, W.; Carvalho, F.; Feldman, A.S.; Trinh, Q.D. Predicting survival after radical prostatectomy: Variation of machine learning performance by race. Prostate 2021, 81, 1355–1364. [Google Scholar] [CrossRef]
- Fonseca, N.M.; Maurice-Dror, C.; Herberts, C.; Tu, W.; Fan, W.; Murtha, A.J.; Kollmannsberger, C.; Kwan, E.M.; Parekh, K.; Schönlau, E.; et al. Prediction of plasma ctDNA fraction and prognostic implications of liquid biopsy in advanced prostate cancer. Nat. Commun. 2024, 15, 1828. [Google Scholar] [CrossRef]
- Markert, E.K.; Mizuno, H.; Vazquez, A.; Levine, A.J. Molecular classification of prostate cancer using curated expression signatures. Proc. Natl. Acad. Sci. USA 2011, 108, 21276–21281. [Google Scholar] [CrossRef]
- Sun, R.; Jun, A.; Yu, H.; Wang, Y.; He, M.; Tan, L.; Cheng, H.; Zhang, J.; Wang, Y.; Sun, X.; et al. Proteomic landscape profiling of primary prostate cancer reveals a 16-protein panel for prognosis prediction. Cell Rep. Med. 2024, 5, 101679. [Google Scholar] [CrossRef]
- Hu, J.; Miao, Q.; Ren, J.; Su, H.; Zhang, X.; Bi, J.; Zhang, G. An online clustering algorithm predicting model for prostate cancer based on PHI-related variables and PI-RADS in different PSA populations. Cancer Cell Int. 2025, 25, 44. [Google Scholar] [CrossRef] [PubMed]
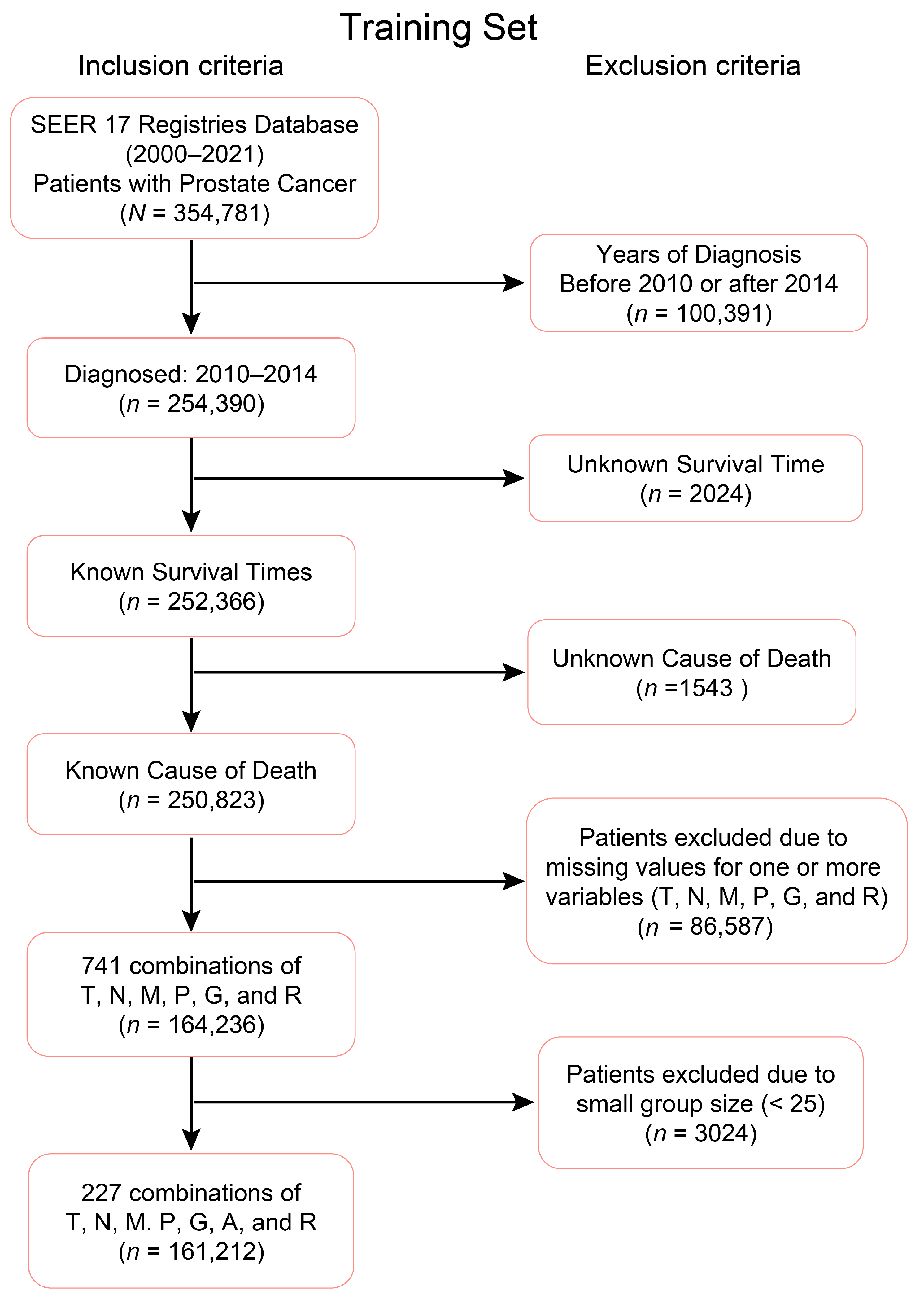
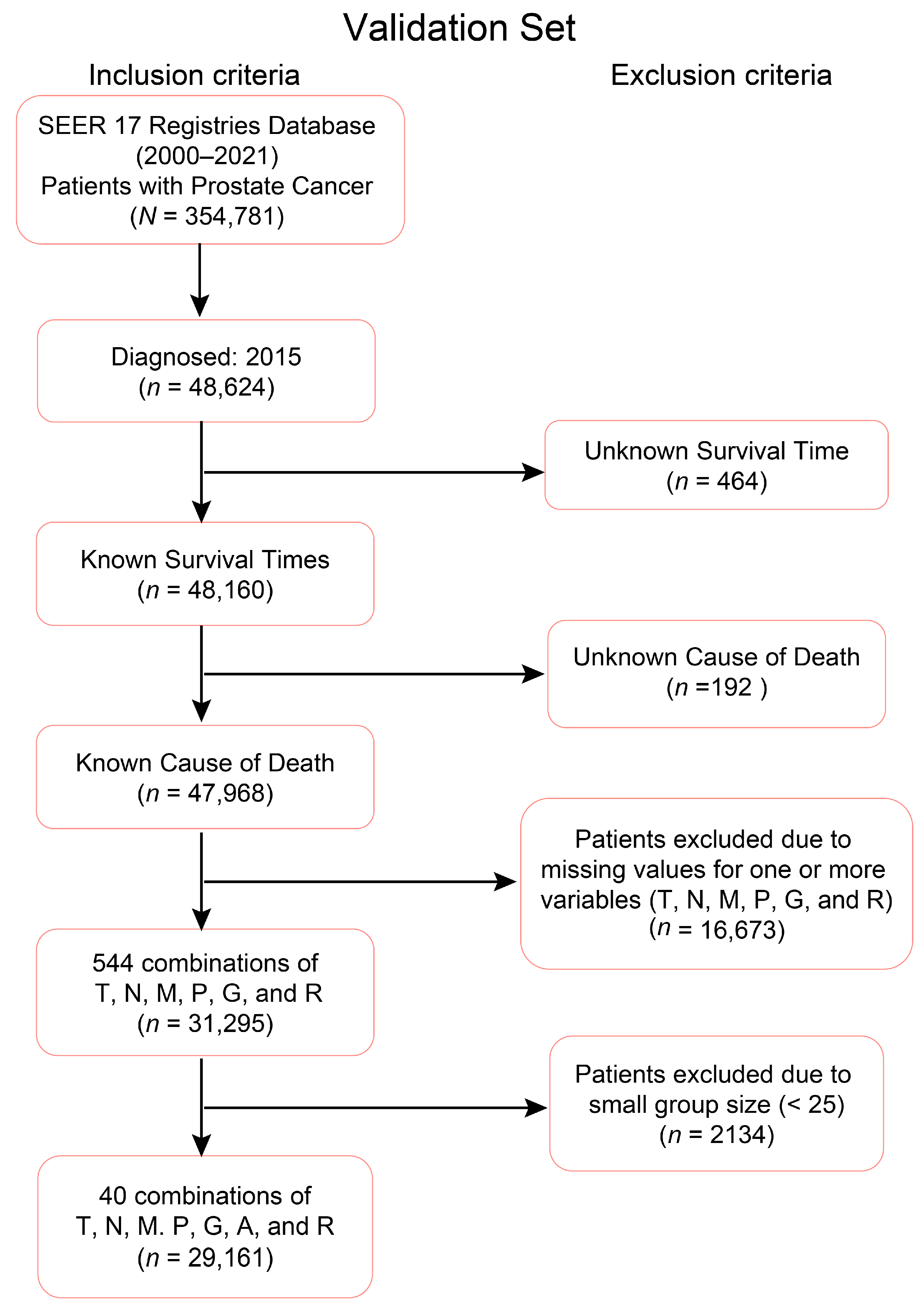
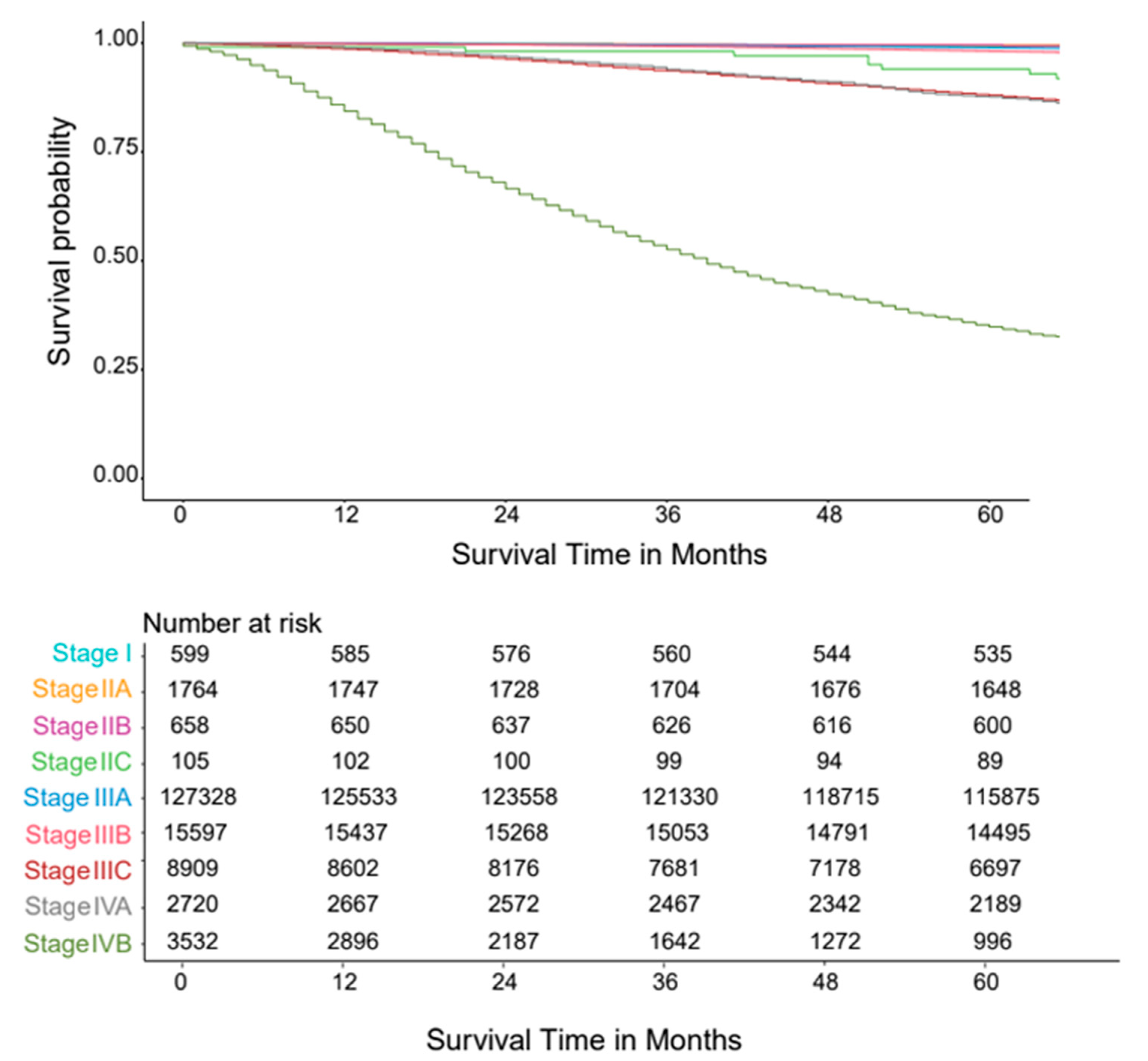
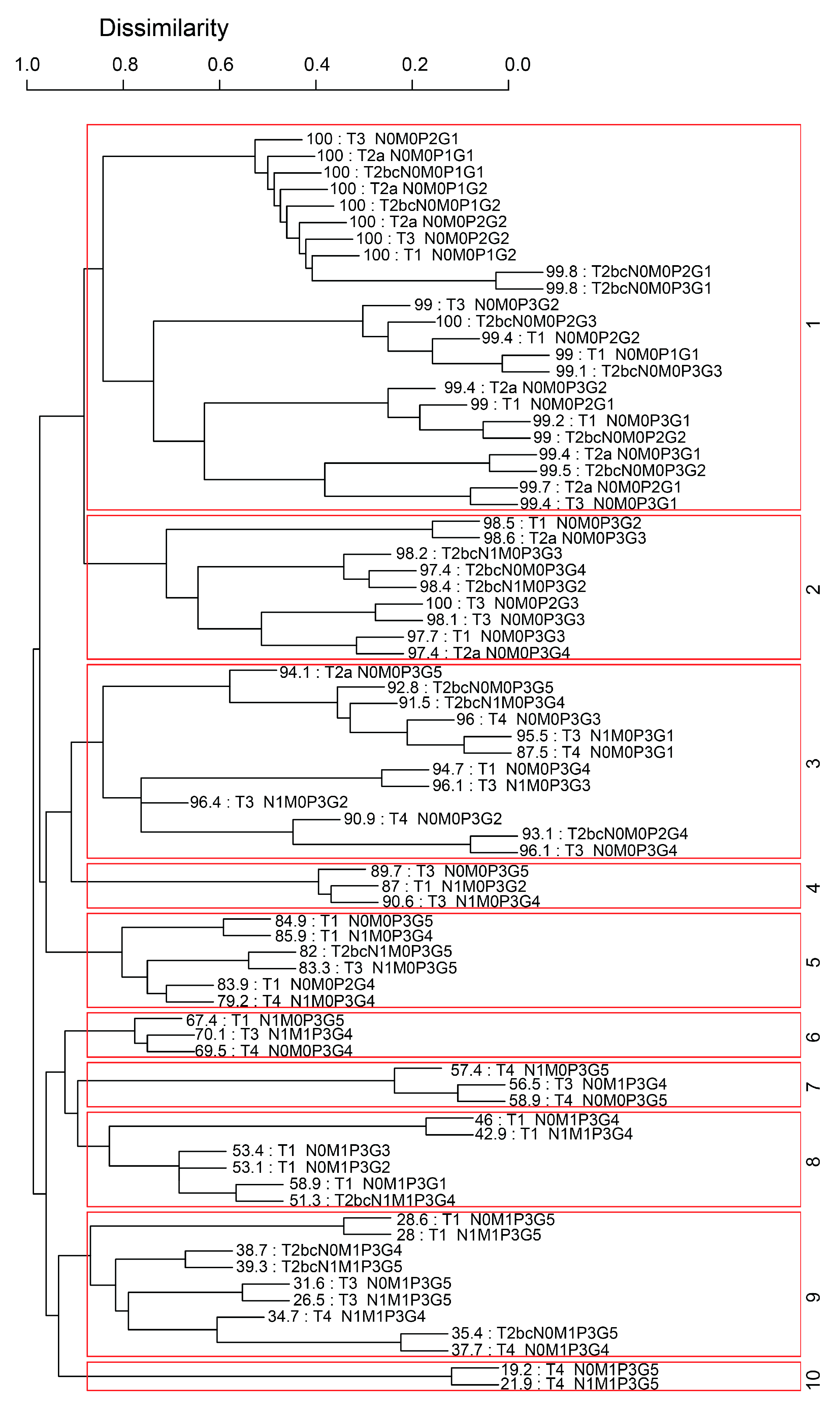


| Variables | Levels | Definition/Description |
|---|---|---|
| Tumor stage (T) | Tx | Tumor was not evaluated |
| T0 | No evidence of the primary tumor | |
| T1 | Tumor was not detected during Digital Rectal Exam (DRE) and not seen in imaging | |
| T2 | Tumor is detected in DRE but locally confined in the prostate T2a: Tumor is half or less than one side of the prostate lobe T2b: Tumor is in more than ½ of the prostate lobe but not in the other lobe T2c: Tumor is present in both lobes | |
| T3 | Tumor extends outside of the prostate T3a: Tumor extends outside of the prostate on one or both sides T3b: Tumor has spread to the seminal vesicles | |
| T4 | Tumor has spread to nearby tissues outside of the prostate and seminal vesicles. | |
| Metastasis to nearby or regional lymph nodes (N) | Nx | Nearby lymph nodes are not evaluated |
| N0 | No cancer cells are found in the lymph nodes | |
| N1 | Cancer cells are found in the lymph nodes | |
| Distant metastasis (M) | M0 | Cancer has not spread past the prostate |
| M1 | Cancer has spread past the prostate M1a: Cancer has spread to the distant lymph nodes M1b: Cancer has spread to bones M1c: Cancer has spread to other organs and sites with or without bone disease | |
| PSA (ng/mL) | P1 | P < 10 |
| P2 | 10 ≤ P < 20 | |
| P3 | P ≥ 20 | |
| Grade Group (G) /Gleason Score (GS) | G1: GS ≤ 6 | Only individual discrete well-formed glands |
| G2: GS 7 (3 + 4) | Predominantly well-formed glands with lesser components of poorly formed, fused cribriform glands | |
| G3: GS 7 (4 + 3) | Predominantly poorly formed, fused, cribriform glands with lesser components of well-formed glands | |
| G4: GS 8 | Only poorly formed, fused, cribriform glands or predominantly well-formed glands with a lesser component lacking or predominately lacking glands with a lesser component of well-formed glands | |
| G5: GS 9–10 | Lacks gland formation (or with necrosis) with or without poorly formed/fused/cribriform gland | |
| Age (years) | A0 | <70 |
| A1 | ≥70 | |
| Race | R1 | White, Caucasian, or European Ancestry |
| R2 | Black or African Ancestry | |
| R3 | Other |
| AJCC TNM Prostate Cancer Stages | Stage Subgroups | Grade Group | Tumor | Lymph Node | Metastasis | PSA |
|---|---|---|---|---|---|---|
| Stage I (Localized) Cancer is small and only in the prostate | I | 1 | cT1a–c cT2a pT2 | N0 | M0 | <10 |
| Stage II (Localized) Cancer is larger and may be in both prostate lobes but still confined in the prostate | IIA | 1 | cT1–ac cT2a pT2 | N0 | M0 | 10–20 |
| IIA | 1 | cT2b–c | N0 | M0 | 10–20 | |
| IIB | 2 | T1–2 | N0 | M0 | <20 | |
| IIC | 3 4 | T1–2 | N0 | M0 | <20 | |
| Stage III (Locally Advanced) Cancer has spread from the prostate to nearby lymph nodes or seminal vesicles | IIIA | 1–4 | T1–2 | N0 | M0 | ≥20 |
| IIIB | 1–4 | T3–4 | N0 | M0 | Any | |
| IIIC | 5 | Any T | N0 | M0 | Any | |
| Stage IV (Metastatic/Advanced) Cancer has spread to other parts of the body such as bones, liver, or lungs. | IVA | Any | Any T | N1 | M0 | Any |
| IVB | Any | Any T | Any N | M1 | Any |
| Variables in the Training Dataset (N = 161, 212) | n |
|---|---|
| Tumor stage (T) | |
| T1 | 80,384 (50%) |
| T2a | 12,897 (8.0%) |
| T2bc | 46,316 (29%) |
| T3 | 20,599 (13%) |
| T4 | 1016 (0.6%) |
| Lymph node metastasis (N) | |
| N0 | 157,398 (98%) |
| N1 | 3814 (2.4%) |
| Metastasis (M) | |
| M0 | 157,680 (98%) |
| M1 | 3532 (2.2%) |
| Prostate-Specific Antigen (P) | |
| P1 | 926 (0.6%) |
| P2 | 2311 (1.4%) |
| P3 | 157,975 (98%) |
| Grade Group (G) | |
| G1 | 70,901 (44%) |
| G2 | 42,718 (26%) |
| G3 | 19,395 (12%) |
| G4 | 15,823 (9.8%) |
| G5 | 12,375 (7.7%) |
| Age (A) | |
| A0 | 115,078 (71%) |
| A1 | 46,134 (29%) |
| Race (R) | |
| R1 | 127,971 (79%) |
| R2 | 24,701 (15%) |
| R3 | 8540 (5.3%) |
| Variables in the Validation Dataset (N = 29, 161) | n |
|---|---|
| Tumor stage (T) | |
| T1 | 15,360 (53%) |
| T2a | 1801 (6.2%) |
| T2bc | 7229 (25%) |
| T3 | 4614 (16%) |
| T4 | 157 (0.5%) |
| Lymph node metastasis (N) | |
| N0 | 28,293 (97%) |
| N1 | 868 (3.0%) |
| Metastasis (M) | |
| M0 | 28,636 (98%) |
| M1 | 525 (1.8%) |
| Prostate-Specific Antigen (P) | |
| P1 | 106 (0.4%) |
| P2 | 262 (0.9%) |
| P3 | 28,793 (99%) |
| Grade Group (G) | |
| G1 | 10,443 (36%) |
| G2 | 8357 (29%) |
| G3 | 4253 (15%) |
| G4 | 3252 (11%) |
| G5 | 2856 (9.8%) |
| Age (A) | |
| A0 | 20,725 (71%) |
| A1 | 8436 (29%) |
| Race (R) | |
| R1 | 23,308 (80%) |
| R2 | 4470 (15%) |
| R3 | 1383 (4.7%) |
| Number of Variables | Data Type | Method | C-Index | 95%CI |
|---|---|---|---|---|
| 5 | Training | AJCC | 0.7676 | 0.7622–0.7731 |
| 5 | Training | EACCD | 0.8293 | 0.8245–0.8341 |
| 5 | Validation | EACCD | 0.8437 | 0.8308–0.8566 |
| 7 | Training | EACCD | 0.8504 | 0.8461–0.8547 |
| 7 | Validation | EACCD | 0.8585 | 0.8468–0.8703 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, K.; Guan, A.; Ahmed, A.E.; Waters, A.J.; Tan, S.-H.; Chen, D. Using Machine Learning to Create Prognostic Systems for Primary Prostate Cancer. Diagnostics 2025, 15, 2462. https://doi.org/10.3390/diagnostics15192462
Guan K, Guan A, Ahmed AE, Waters AJ, Tan S-H, Chen D. Using Machine Learning to Create Prognostic Systems for Primary Prostate Cancer. Diagnostics. 2025; 15(19):2462. https://doi.org/10.3390/diagnostics15192462
Chicago/Turabian StyleGuan, Kevin, Andy Guan, Anwar E. Ahmed, Andrew J. Waters, Shyh-Han Tan, and Dechang Chen. 2025. "Using Machine Learning to Create Prognostic Systems for Primary Prostate Cancer" Diagnostics 15, no. 19: 2462. https://doi.org/10.3390/diagnostics15192462
APA StyleGuan, K., Guan, A., Ahmed, A. E., Waters, A. J., Tan, S.-H., & Chen, D. (2025). Using Machine Learning to Create Prognostic Systems for Primary Prostate Cancer. Diagnostics, 15(19), 2462. https://doi.org/10.3390/diagnostics15192462









