Improving Automatic Coronary Stenosis Classification Using a Hybrid Metaheuristic with Diversity Control
Abstract
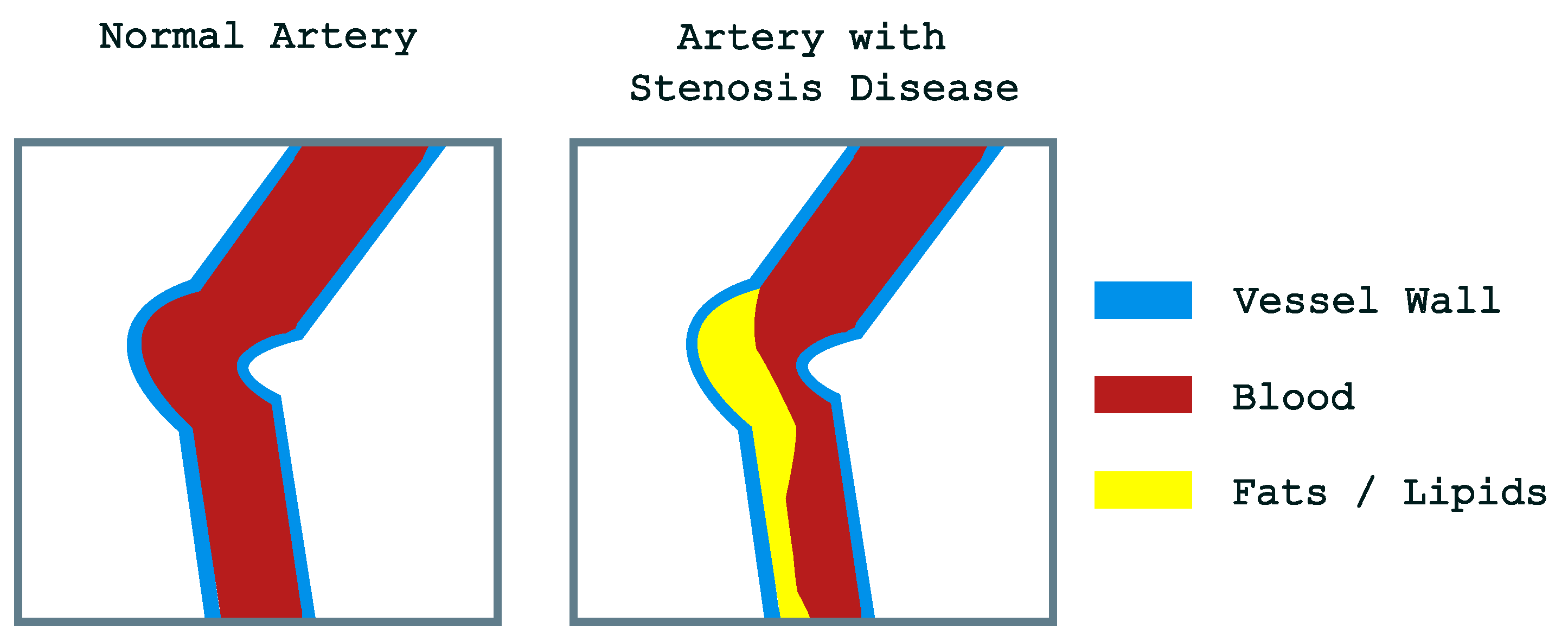
1. Introduction
- Identification of 16 features that are relevant for the classification of positive and negative coronary stenosis cases.
- Development of a feature vector consisting of 473 distinct features extracted from the original images and responses from vessel enhancement filters.
- Implementation of a diversity control strategy to decrease the probability of premature convergence during the automatic feature selection process.
2. Methods
2.1. Feature Extraction
2.2. Feature Selection
2.3. Metaheuristics
2.3.1. Boltzmann-Univariate Marginal Distribution Algorithm
2.3.2. Simulated Annealing
2.4. Support Vector Machine
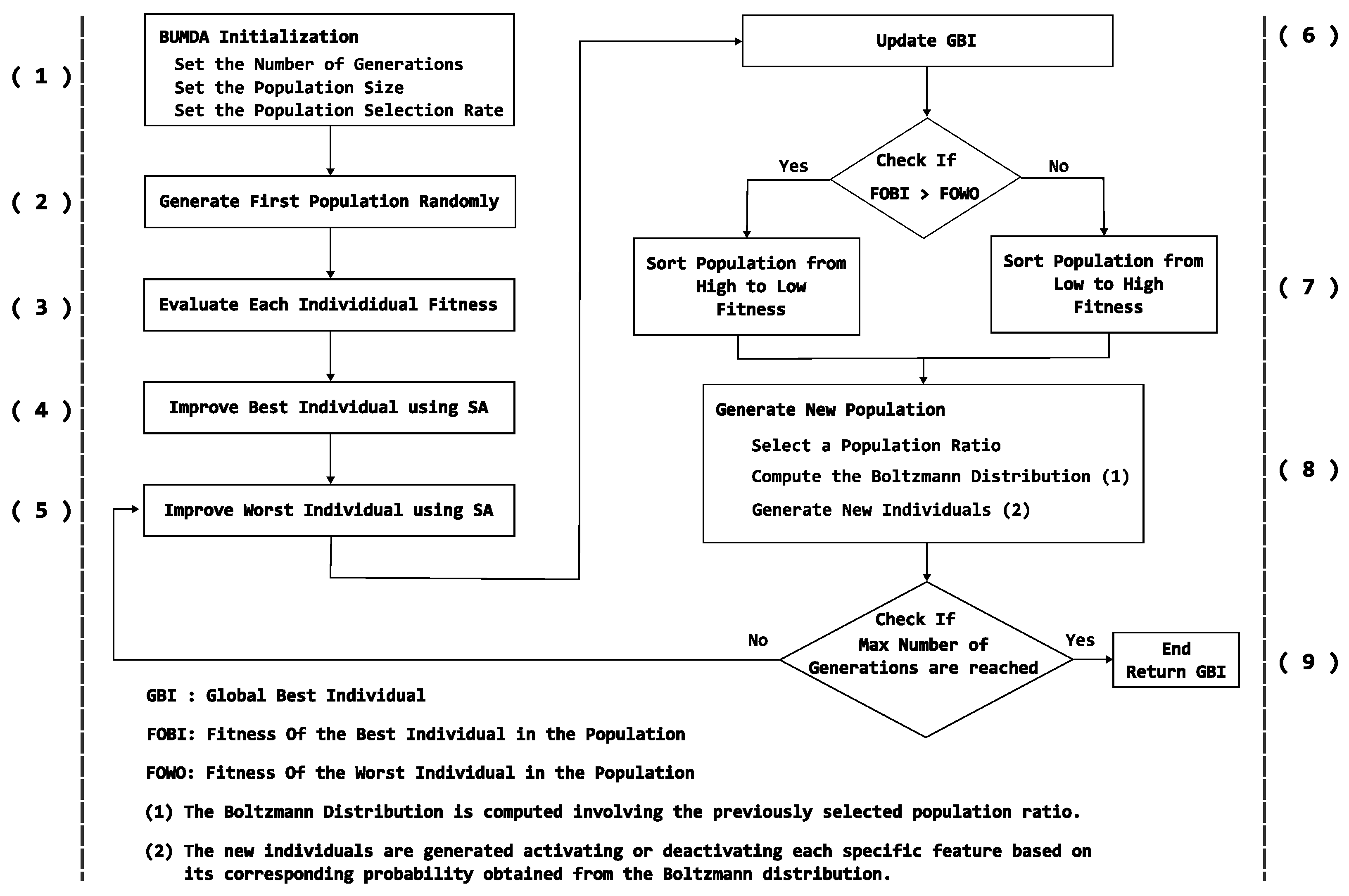
3. Proposed Method Using a Diversity Strategy
4. Results
4.1. Image Database
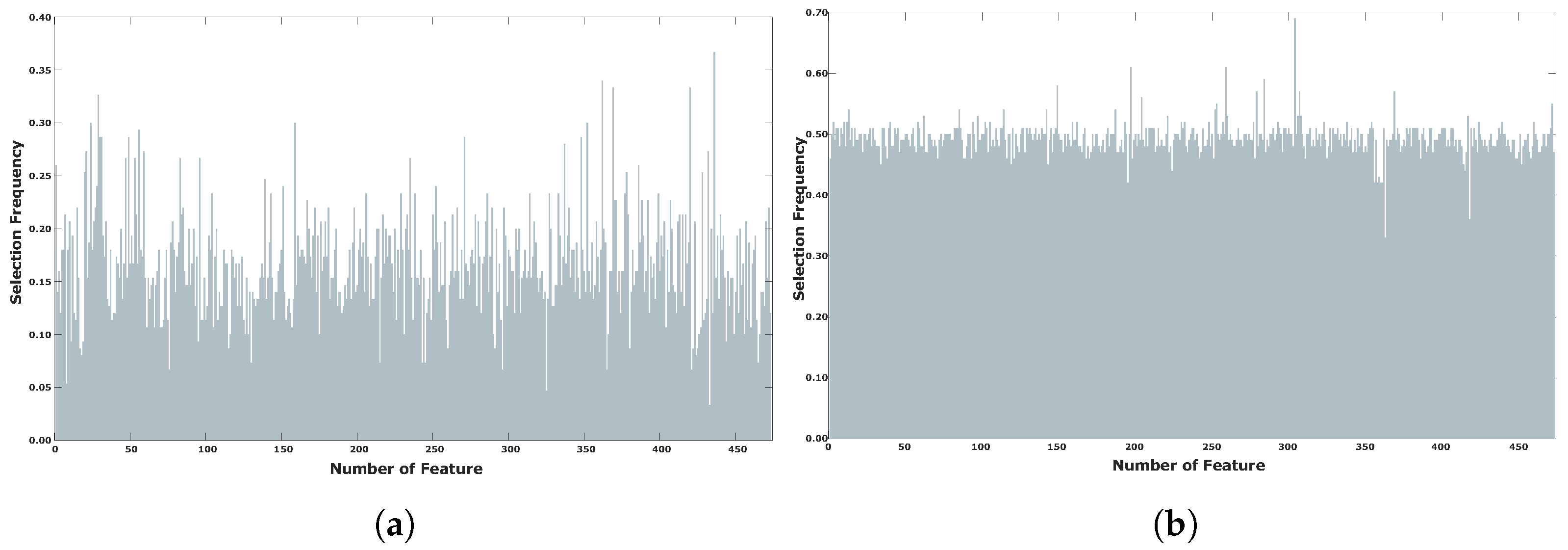
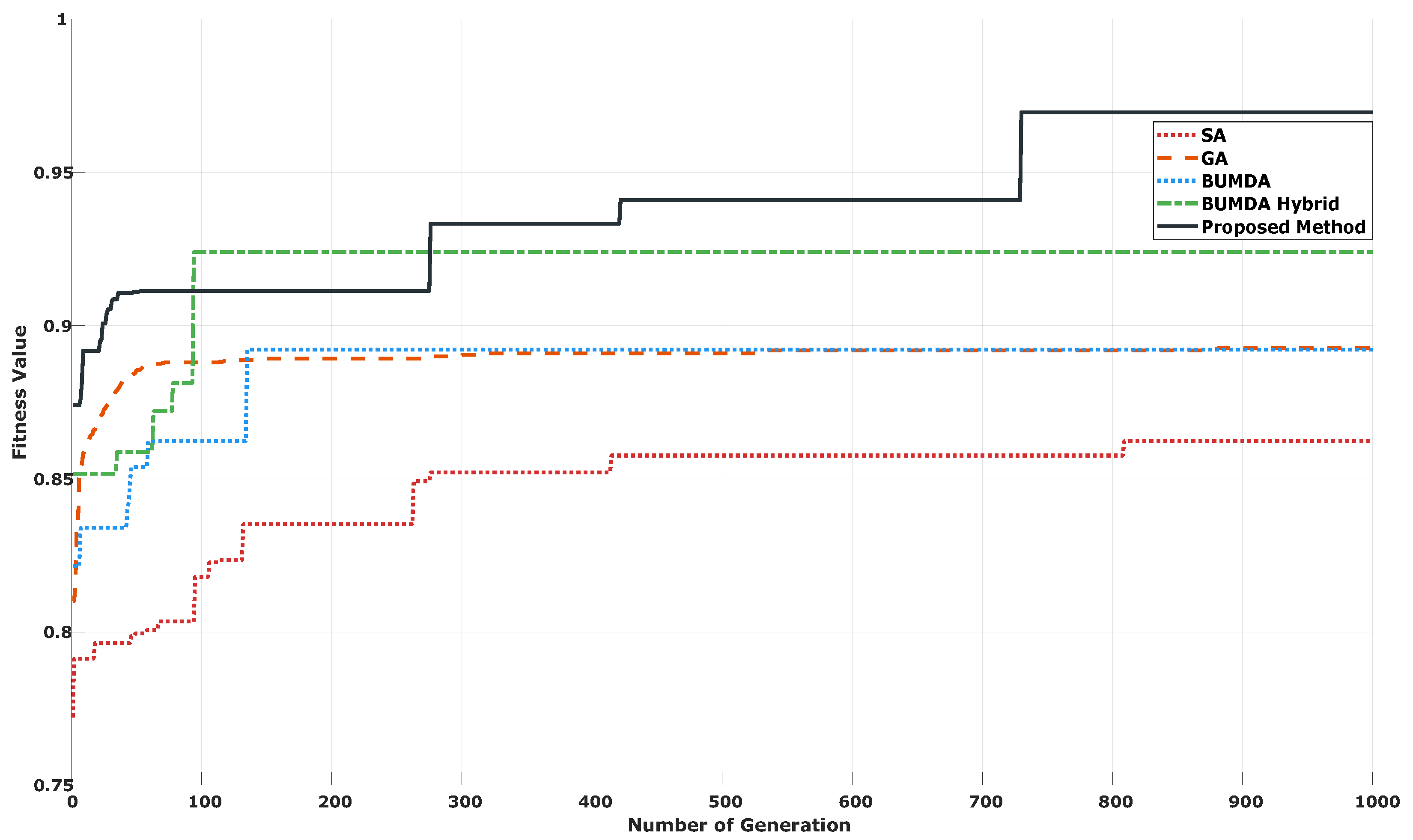
4.2. Experiment Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BUMDA | Boltzmann Univariate Marginal Distribution Algorithm |
| FDR | Feature Decreasing Rate |
| GA | Genetic Algorithm |
| JC | Jaccard Coefficient |
| MSGF | Multi-Scale Gabor Filter |
| MSGMF | Multi-Scale Gaussian-Matched Filter |
| NSF | Number of Selected Features |
| SA | Simulated Annealing |
| SSGF | Single-Scale Gabor Filter |
| SSGMF | Single-Scale Gaussian-Matched Filter |
| SVM | Support Vector Machine |
| UMDA | Univariate Marginal Distribution Algorithm |
References
- Qi, X.T.; Wag, H.; Zhu, D.G.; Zheng, L.; Cheng, X.; Zhang, R.J.; Dong, H.L. Global trends in coronary artery disease and artificial intelligence relevant studies: A bibliometric analysis. Eur. Rev. Med. Pharmacol. Sci. 2024, 28, 1. [Google Scholar] [PubMed]
- Thakur, U.; Nogic, J.; Comella, A.; Nerlekar, N.; Chan, J.; Abrahams, T.; Michail, M.; Nelson, A.; Dey, D.; Ko, B.; et al. Computed tomography coronary angiography assessment of left main coronary artery stenosis severity. J. Cardiovasc. Comput. Tomogr. 2024, in press. [Google Scholar] [CrossRef] [PubMed]
- Cervantes-Sanchez, F.; Cruz-Aceves, I.; Hernandez-Aguirre, A. Automatic detection of coronary artery stenosis in X-ray angiograms using Gaussian filters and genetic algorithms. AIP Conf. Proc. 2016, 1747, 020005. [Google Scholar] [CrossRef]
- Cervantes-Sanchez, F.; Cruz-Aceves, I.; Hernandez-Aguirre, A.; Hernandez-Gonzalez, M.A.; Solorio-Meza, S.E. Automatic Segmentation of Coronary Arteries in X-ray Angiograms using Multiscale Analysis and Artificial Neural Networks. Appl. Sci. 2019, 9, 5507. [Google Scholar] [CrossRef]
- Wan, T.; Feng, H.; Tong, C.; Li, D.; Qin, Z. Automated identification and grading of coronary artery stenoses with X-ray angiography. Comput. Methods Programs Biomed. 2018, 167, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Sameh, S.; Azim, M.A.; AbdelRaouf, A. Narrowed Coronary Artery Detection and Classification using Angiographic Scans. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES), IEEE, Cairo, Egypt, 19–20 December 2017; pp. 73–79. [Google Scholar] [CrossRef]
- Antczak, K.; Liberadzki, Ł. Stenosis Detection with Deep Convolutional Neural Networks. In Proceedings of the MATEC Web of Conferences; EDP Sciences: Ulis, France, 2018; Volume 210, p. 04001. [Google Scholar] [CrossRef]
- Ovalle-Magallanes, E.; Avina-Cervantes, J.G.; Cruz-Aceves, I.; Ruiz-Pinales, J. Transfer Learning for Stenosis Detection in X-ray Coronary Angiography. Mathematics 2020, 8, 1510. [Google Scholar] [CrossRef]
- Chlap, P.; Min, H.; Vandenberg, N.; Dowling, J.; Holloway, L.; Haworth, A. A review of medical image data augmentation techniques for deep learning applications. Med.-Imaging-Radiat. Oncol. 2021, 65, 545–563. [Google Scholar] [CrossRef]
- Garcea, F.; Serra, A.; Lamberti, F.; Morra, L. Data augmentation for medical imaging: A systematic literature review. Comput. Biol. Med. 2023, 152, 106391. [Google Scholar] [CrossRef]
- Haralick, R.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Chowdhary, C.L.; Acharjya, D. Segmentation and Feature Extraction in Medical Imaging: A Systematic Review. Procedia Comput. Sci. 2020, 167, 26–36. [Google Scholar] [CrossRef]
- Gil-Rios, M.A.; Guryev, I.V.; Cruz-Aceves, I.; Avina-Cervantes, J.G.; Hernandez-Gonzalez, M.A.; Solorio-Meza, S.E.; Lopez-Hernandez, J.M. Automatic Feature Selection for Stenosis Detection in X-ray Coronary Angiograms. Mathematics 2021, 9, 2471. [Google Scholar] [CrossRef]
- Welikala, R.; Fraz, M.; Dehmeshki, J.; Hoppe, A.; Tah, V.; Mann, S.; Williamson, T.; Barman, S. Genetic algorithm based feature selection combined with dual classification for the automated detection of proliferative diabetic retinopathy. Comput. Med. Imaging Graph. 2015, 43, 64–77. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.A.; Lu, K. Class-specific feature selection using neighborhood mutual information with relevance-redundancy weight. Knowl.-Based Syst. 2024, 300, 112212. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z.; Li, H.; Lei, Z.; Cheng, J.; Gao, S. Information gain-based multi-objective evolutionary algorithm for feature selection. Inf. Sci. 2024, 677, 120901. [Google Scholar] [CrossRef]
- Gil-Rios, M.A.; Chalopin, C.; Cruz-Aceves, I.; Lopez-Hernandez, J.M.; Hernandez-Gonzalez, M.A.; Solorio-Meza, S.E. Automatic Classification of Coronary Stenosis Using Feature Selection and a Hybrid Evolutionary Algorithm. Axioms 2023, 12, 462. [Google Scholar] [CrossRef]
- Suhaidi, M.; Kadir, R.A.; Tiun, S. A Review of Feature Extraction Methods on Machine Learning. J. Inf. Technol. Manag. (JISTM) 2021, 6, 51–59. [Google Scholar] [CrossRef]
- Saliha, A.; Idir, A.h.; Izem, H. A new approach for texture segmentation based on the Gray Level Co-occurrence Matrix. Multimed. Tools Appl. 2021, 80, 24027–24052. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Choudhry, A.; Wadhwani, R. Analysis of digital image filters in frequency domain. Int. J. Comput. Appl. 2016, 140, 12–19. [Google Scholar]
- Gil-Rios, M.A.; Cruz-Aceves, I.; Cervantes-Sanchez, F.; Guryev, I.; Lopez-Hernandez, J.M. Automatic enhancement of coronary arteries using convolutional gray-level templates and path-based metaheuristics. In Recent Trends in Computational Intelligence Enabled Research; Academic Press: Cambridge, MA, USA, 2021; pp. 129–153. [Google Scholar] [CrossRef]
- Giacinti, D.J.; Cervantes-Sanchez, F.; Cruz-Aceves, I.; Hernandez-Gonzalez, M.A.; Lopez-Montero, L.M. Determination of the parabola of the retinal vasculature using a segmentation computational algorithm. Nova Sci. 2019, 11, 87–107. [Google Scholar] [CrossRef]
- Cruz-Aceves, I.; Oloumi, F.; Rangayyan, R.M.; Aviña-Cervantes, J.G.; Hernandez-Aguirre, A. Automatic segmentation of coronary arteries using Gabor filters and thresholding based on multiobjective optimization. Biomed. Signal Process. Control 2016, 25, 76–85. [Google Scholar] [CrossRef]
- Cruz-Aceves, I.; Cervantes-Sanchez, F.; Avila-Garcia, M.S. A Novel Multiscale Gaussian-Matched Filter Using Neural Networks for the Segmentation of X-Ray Coronary Angiograms. J. Healthc. Eng. 2018, 2018, 5812059. [Google Scholar] [CrossRef] [PubMed]
- Eiho, S.; Qian, Y. Detection of coronary artery tree using morphological operator. In Proceedings of the Computers in Cardiology 1997, Lund, Sweden, 7–10 September 1997; pp. 525–528. [Google Scholar] [CrossRef]
- Zebari, R.R.; Abdulazeez, A.M.; Zeebaree, D.Q.; Zebari, D.A.; Saeed, J.N. A Comprehensive Review of Dimensionality Reduction Techniques for Feature Selection and Feature Extraction 2020. J. Appl. Sci. Technol. Trends 2020, 1, 56–70. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Visalakshi, S.; Radha, V. A literature review of feature selection techniques and applications: Review of feature selection in data mining. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 18–20 December 2014; pp. 1–6. [Google Scholar] [CrossRef]
- John Henry, H. Genetic Algorithms and Adaptation. In Adaptive Control of Ill-Defined Systems. NATO Conference Series (II Systems Science); Springer: Boston, MA, USA, 1984; pp. 317–333. [Google Scholar] [CrossRef]
- John Henry, H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Hashemi, M.; Reza-Meybodi, M. Univariate Marginal Distribution Algorithm in Combination with Extremal Optimization (EO, GEO). In International Conference on Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 220–227. [Google Scholar] [CrossRef]
- Valdez-Peña, S.I.; Hernández, A.; Botello, S. A Boltzmann based estimation of distribution algorithm. Inf. Sci. 2013, 236, 126–137. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef]
- Hari, B.N.; Salankar, S.S.; Bora, V.R. MRI brain cancer classification using Support Vector Machine. In Proceedings of the 2014 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, 1–2 March 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Segura, C.; Miranda, G.; Segredo, E.; Chacón, J. A Novel Memetic Algorithm with Explicit Control of Diversity for the Menu Planning Problem. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2191–2198. [Google Scholar] [CrossRef]
- Gil-Rios, M.A.; Cruz-Aceves, I.; Hernandez-Aguirre, A.; Moya-Albor, E.; Brieva, J.; Hernandez-Gonzalez, M.A.; Solorio-Meza, S.E. High-Dimensional Feature Selection for Automatic Classification of Coronary Stenosis Using an Evolutionary Algorithm. Diagnostics 2024, 14, 268. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Deniz, A.; Kiziloz, H.E. A comprehensive survey on recent metaheuristics for feature selection. Neurocomputing 2022, 494, 269–296. [Google Scholar] [CrossRef]
- Frangi, A.; Nielsen, W.; Vincken, K.; Viergever, M. Multiscale vessel enhancement filtering. In Medical Image Computing and Computer-Assisted Intervention (MICCAI’98); Springer: Berlin/Heidelberg, Germany, 1998; pp. 130–137. [Google Scholar] [CrossRef]
- Salem, N.M.; Salem, S.A.; Nandi, A.K. Segmentation of retinal blood vessels based on analysis of the hessian matrix and Clustering Algorithm. In Proceedings of the 2007 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 428–432. [Google Scholar]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng.-Part III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper With Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Karen, S.; Andrew, Z. Very Deep Convolutional Networks for Large-Scale Image Recognition. Comput. Vis. Pattern Recognit. 2015, 6, 1–14. [Google Scholar] [CrossRef]




| Method | Parameters | Value |
|---|---|---|
| Frangi, Salem | [1, 12] | |
| 0.5 | ||
| 0.5 | ||
| 15 | ||
| Single-Scale Gabor Filter | K | 45 |
| T | 5 | |
| L | 2.5 | |
| Multi-Scale Gabor Filter | I | 3 |
| T | [2, 20] | |
| K | 45 | |
| Multi-Scale Linear Matched-Filter | L | [1, 15] |
| K | 12 | |
| Single-Scale Gaussian Matched-Filter | L | 13 |
| T | 15 | |
| 2.82 | ||
| Multi-Scale Gaussian Matched-Filter | I | 13 |
| T | 15 | |
| K | 12 | |
| [1.5, 2.5] | ||
| 0.5 | ||
| Eiho Top-Hat Operator | shape | disk |
| size | 19 |
| Method | Min | Max | Median | Avg. | Variance | Std. Dev. |
|---|---|---|---|---|---|---|
| GA | 0.0000 | 1.0000 | 0.4010 | 0.4103 | 0.0704 | 0.2653 |
| BUMDA | 0.0000 | 0.6000 | 0.0333 | 0.0858 | 0.0173 | 0.1316 |
| SA | 0.0000 | 0.4200 | 0.0800 | 0.0794 | 0.0021 | 0.0455 |
| Hybrid Metaheuristic | 0.0333 | 0.3667 | 0.1600 | 0.1664 | 0.0024 | 0.0490 |
| Proposed Method | 0.1895 | 0.4830 | 0.3125 | 0.3128 | 0.0006 | 0.0242 |
| Method | Min | Max | Median | Avg. | Variance | Std. Dev. |
|---|---|---|---|---|---|---|
| SA | 43 | 809 | 121 | 202 | 46,074 | 215 |
| GA | 79 | 882 | 126 | 229 | 52,245 | 229 |
| BUMDA | 97 | 321 | 188 | 183 | 4180 | 65 |
| Hybrid Metaheuristic | 79 | 203 | 108 | 117 | 1210 | 35 |
| Proposed Method | 151 | 998 | 473 | 566 | 83,245 | 288 |
| Method | NSF | FDR | Accuracy | JC | F1 | Sens. | Spec. |
|---|---|---|---|---|---|---|---|
| ResNet50 [43] | – | – | 0.81 | 0.68 | 0.80 | 0.78 | 0.84 |
| Inception-v3 [44] | – | – | 0.72 | 0.56 | 0.70 | 0.66 | 0.78 |
| VGG16 [45] | – | – | 0.84 | 0.72 | 0.82 | 0.74 | 0.94 |
| CNN-16C [7] | – | – | 0.86 | 0.74 | 0.84 | 0.76 | 0.94 |
| – | 473 | 0.00 | 0.78 | 0.64 | 0.77 | 0.72 | 0.84 |
| SA | 16 | 0.97 | 0.78 | 0.64 | 0.78 | 0.76 | 0.80 |
| GA | 29 | 0.94 | 0.80 | 0.67 | 0.80 | 0.80 | 0.80 |
| BUMDA | 205 | 0.57 | 0.80 | 0.67 | 0.77 | 0.66 | 0.94 |
| Hybrid Metaheuristic | 4 | 0.99 | 0.86 | 0.75 | 0.84 | 0.74 | 0.98 |
| Proposed Method | 16 | 0.97 | 0.92 | 0.85 | 0.92 | 0.88 | 0.96 |
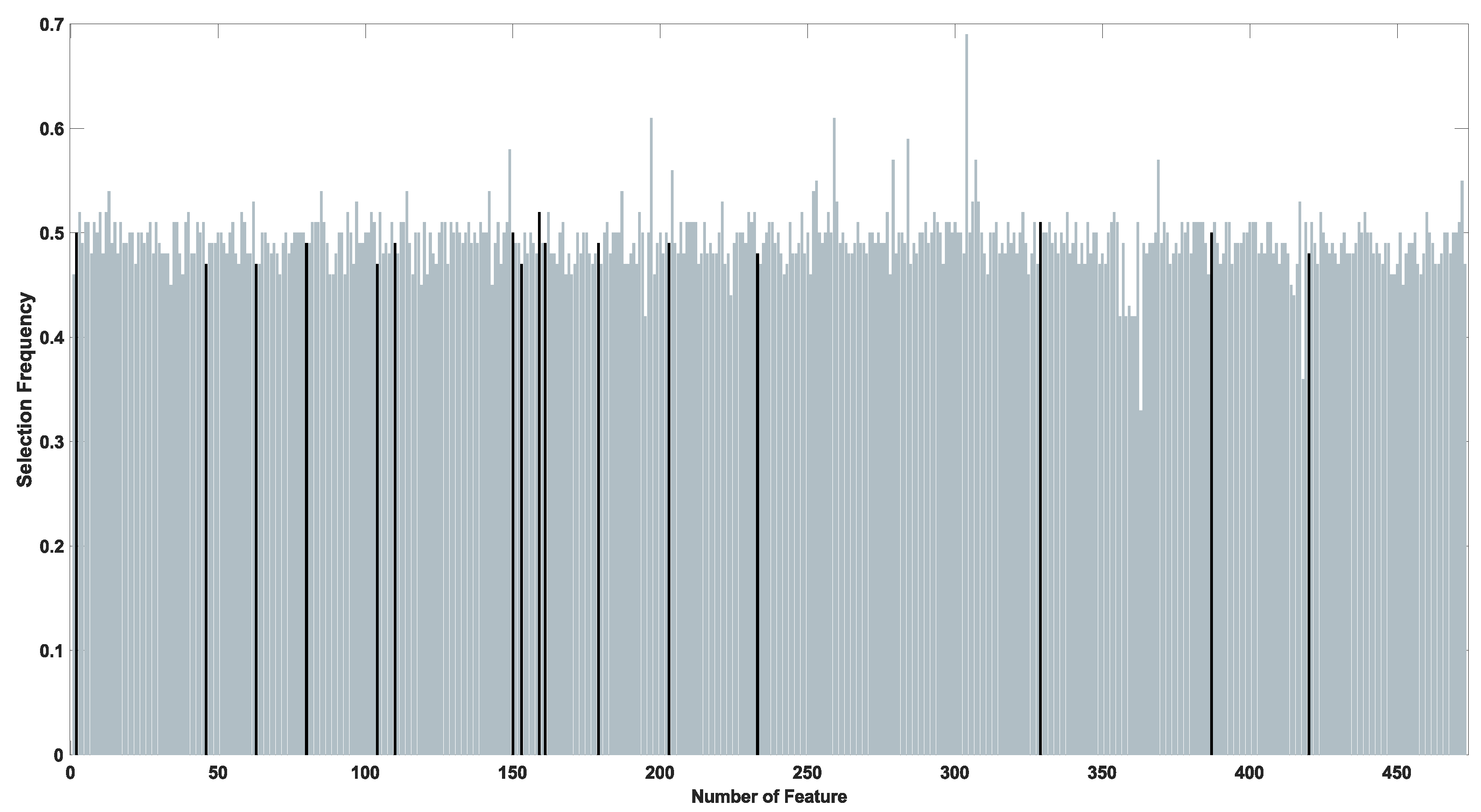
| Identifier | Name | Type | VEM |
|---|---|---|---|
| F002 | Maximum Intensity | Intensity | - |
| F046 | Mean Vessel Length | Morphological | Frangi |
| F063 | Minimum Compactness | Morphological | Frangi |
| F080 | Median Elongatedness | Morphological | Frangi |
| F104 | Gray Level Coefficient of Variation | Morphological | Salem |
| F110 | Median Standard Deviation of Segments Length in all Arterial Sections | Morphological | Salem |
| F150 | Number Of Vessel Segments | Morphological | SSGF |
| F153 | Minimum Vessel Length | Morphological | SSGF |
| F159 | Gray Level Coefficient of Variation | Morphological | SSGF |
| F161 | Gradient Coefficient of Variation | Morphological | SSGF |
| F179 | Maximum Circularity Ratio | Morphological | SSGF |
| F203 | Standard Deviation of the Intensities | Intensity | MSGF |
| F233 | Minimum Circularity Ratio | Morphological | MSGF |
| F329 | Maximum Standard Deviation of the Standard Deviations of Segments Length in all Arterial Sections | Morphological | MSGMF |
| F387 | Standard Deviation of the Standard Deviations of Segments Length in all Arterial Sections | Morphological | SSGMF |
| F420 | Max Intensity | Morphological | Top-Hat Operator |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-Rios, M.-A.; Cruz-Aceves, I.; Hernandez-Aguirre, A.; Hernandez-Gonzalez, M.-A.; Solorio-Meza, S.-E. Improving Automatic Coronary Stenosis Classification Using a Hybrid Metaheuristic with Diversity Control. Diagnostics 2024, 14, 2372. https://doi.org/10.3390/diagnostics14212372
Gil-Rios M-A, Cruz-Aceves I, Hernandez-Aguirre A, Hernandez-Gonzalez M-A, Solorio-Meza S-E. Improving Automatic Coronary Stenosis Classification Using a Hybrid Metaheuristic with Diversity Control. Diagnostics. 2024; 14(21):2372. https://doi.org/10.3390/diagnostics14212372
Chicago/Turabian StyleGil-Rios, Miguel-Angel, Ivan Cruz-Aceves, Arturo Hernandez-Aguirre, Martha-Alicia Hernandez-Gonzalez, and Sergio-Eduardo Solorio-Meza. 2024. "Improving Automatic Coronary Stenosis Classification Using a Hybrid Metaheuristic with Diversity Control" Diagnostics 14, no. 21: 2372. https://doi.org/10.3390/diagnostics14212372
APA StyleGil-Rios, M.-A., Cruz-Aceves, I., Hernandez-Aguirre, A., Hernandez-Gonzalez, M.-A., & Solorio-Meza, S.-E. (2024). Improving Automatic Coronary Stenosis Classification Using a Hybrid Metaheuristic with Diversity Control. Diagnostics, 14(21), 2372. https://doi.org/10.3390/diagnostics14212372






