A Model for Diagnosing Autism Patients Using Spatial and Statistical Measures Using rs-fMRI and sMRI by Adopting Graphical Neural Networks
Abstract
1. Introduction
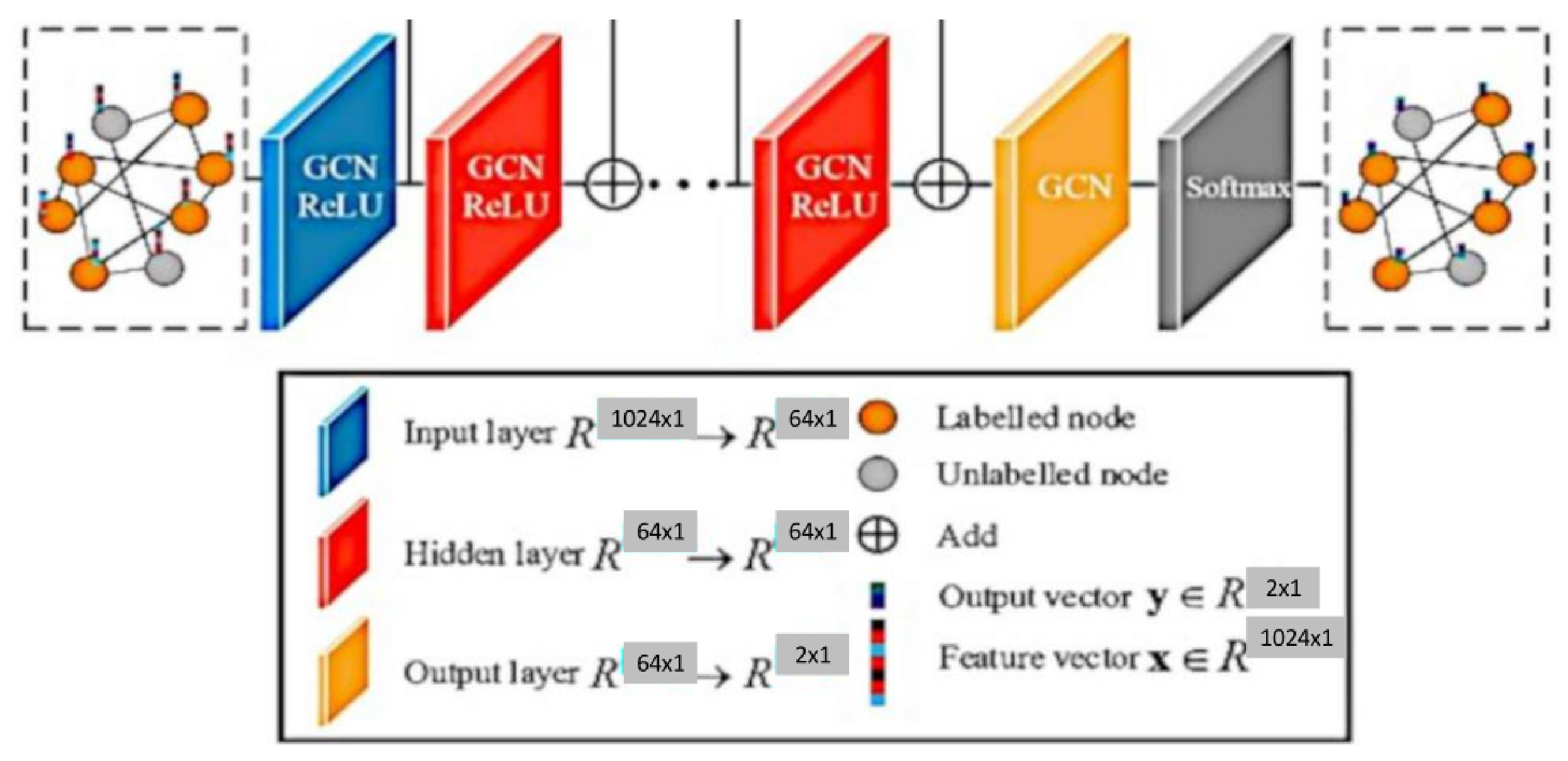
- Feature propagation involves averaging the feature of each node at the beginning of layer with its local neighbourhood, as shown in Equation (1).The normalised matrix representation is specified in Equation (2)where and is the Degree matrix of A.
- Feature and nonlinear transformations associate each layer with a learned weight matrix , and hidden layer transformations are transformed linearly. A feature representation of layer is generated after applying ReLU. This step is followed by feature propagation for the next layer. Equation (3) provides the criteria for updating the layer [10].
- The classification of a node in a layer GCN is obtained using Equation (4).
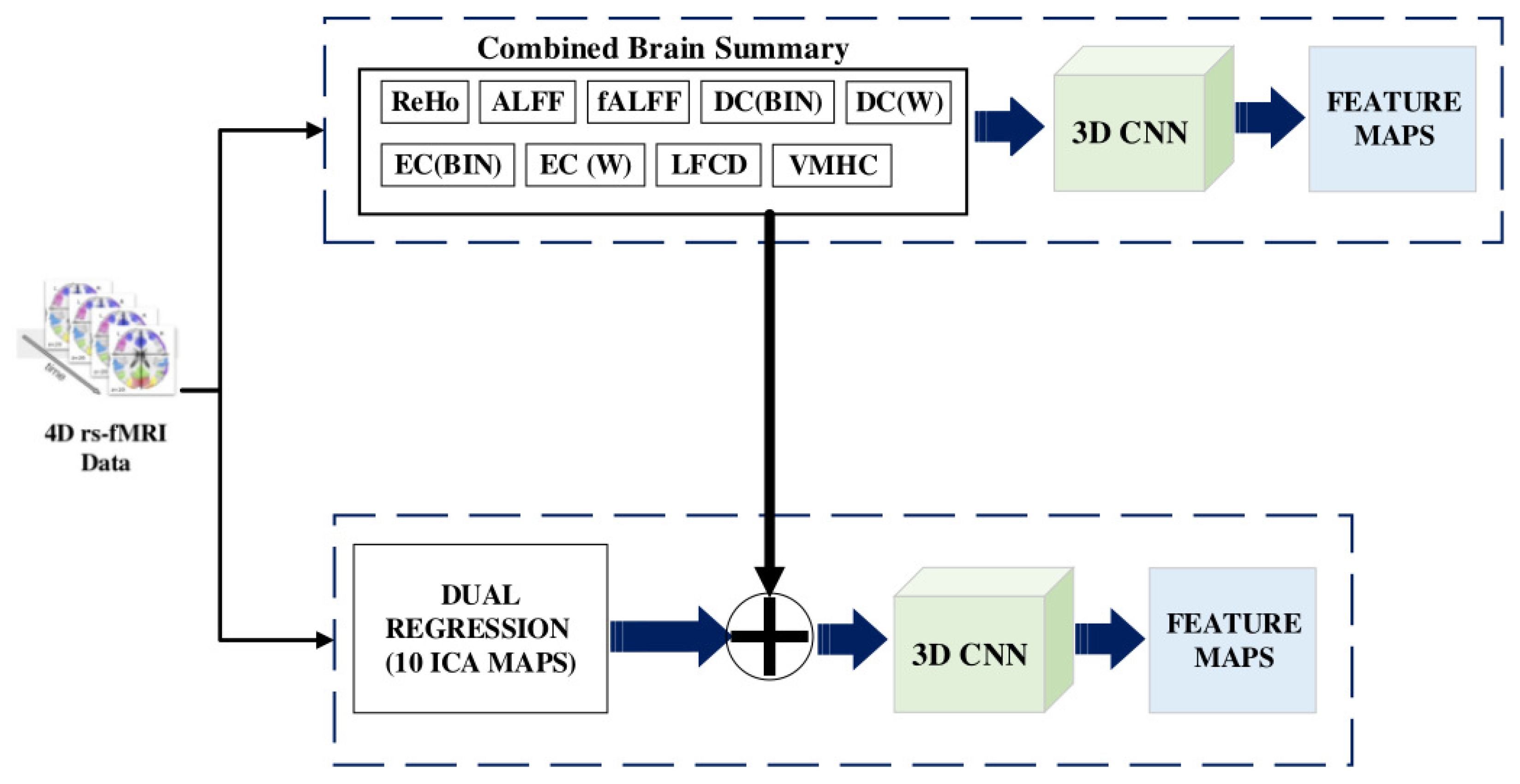
- First, the Regional Homogeneity (ReHo) uses Kendall’s coefficient of concordance to calculate the similarity between the time series of a voxel and its neighbour.
- Second, the Amplitude of Low-Frequency Fluctuations (ALFF) uses the amplitude of each region of interest (ROI) in the frequency band of 0.1 to 0.08 Hz. It shows the spontaneous neuro behaviour in rs-fMRI data. The power spectrum is obtained from the time series signal by a fast Fourier transform. The averaged square root value of each voxel in the power spectrum across the frequency range is considered the ALFF value.
- Third, the Fractional Amplitude of Low-Frequency Fluctuations (fALFF) finds the power ratio in the frequency band relative to the full frequency band of 0 to 0.25 Hz.
- Fourth, the Degree Centrality () measures the edge count of a region. It specifies the number of regions to which the current node is related. This measure proves higher associations in cortical regions.
- Fifth, the Eigenvector Centrality () provides the centrality of a node based on the number of edges connecting central nodes; i.e., a node is important if it is connected to more important nodes.
- Sixth, the Local Functional Connectivity Density (LFCD) calculates the local functional connection of a voxel within a ROI and the functional connections of voxels between hemispheres.
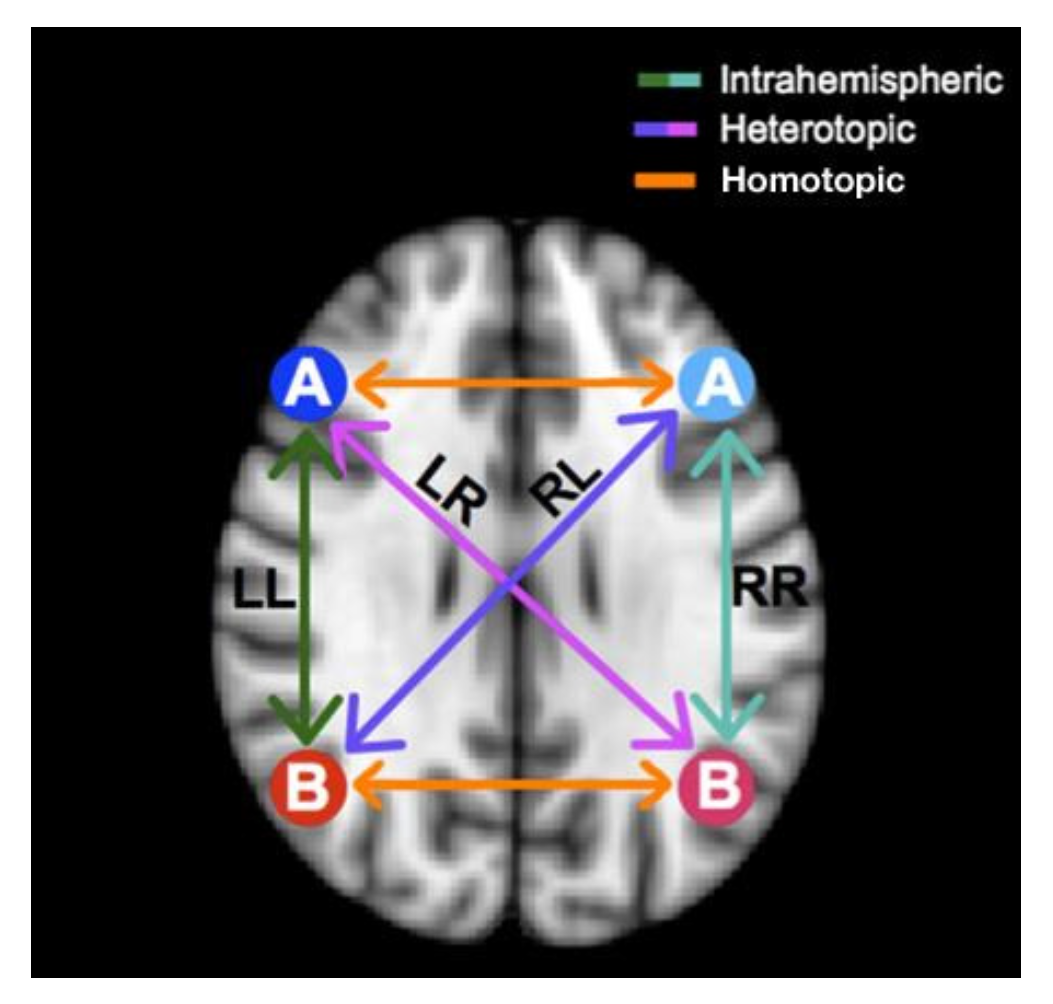
- Seventh, the Voxel-Mirrored Homotopic Connectivity (VMHC) calculates the voxel-wise connectivity between symmetrical brain hemispheres. ROIs that show high connectivity between the left hemisphere, and its right mirrored counterpart have high VHMC values, as shown in Figure 2.
- Eighth, dual regression uses the independent component group maps obtained from the independent component analysis (ICA) as network templates. A spatial regressor uses the spatial map to identify the time series associated with voxels on the corresponding map, followed by a temporal regressor, which uses the time series to fetch the complete set of voxels activated in that time series. The result of these steps is a subject-specific spatial map based on the original spatial map.
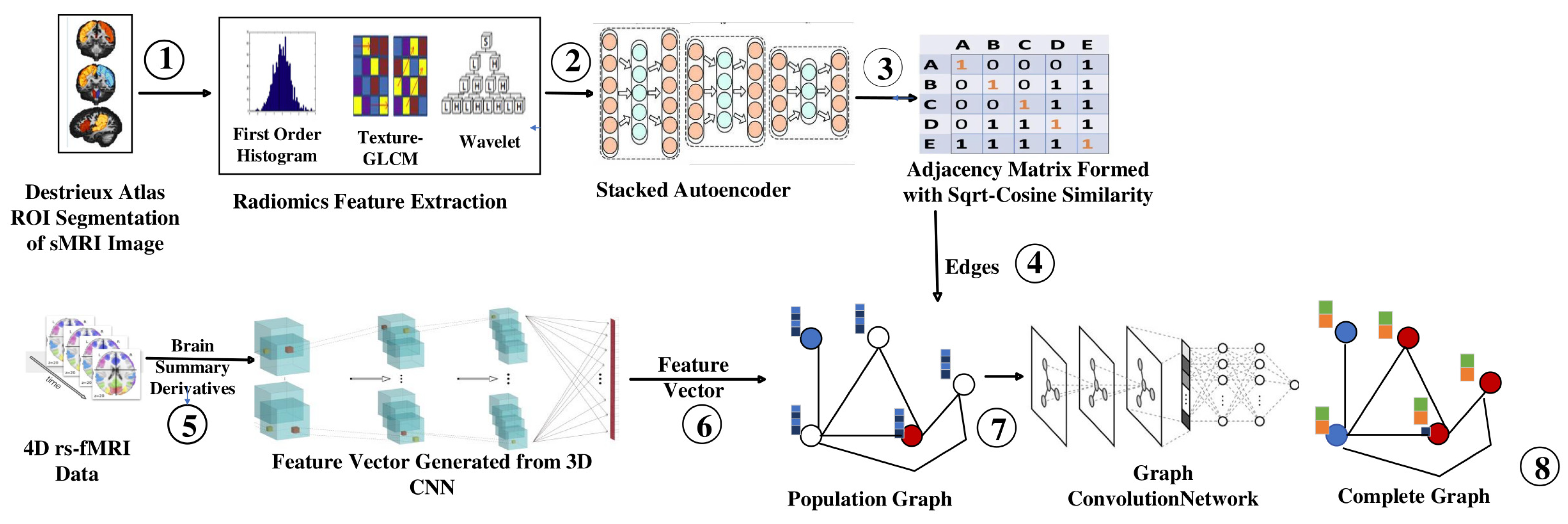
- Radiomic features obtained from sMRI using the Destrieux atlas were used to identify similarities between individuals (nodes) to construct an edge for the graph. These features can capture information about various aspects of the image, such as the texture, shape, size, intensity, and spatial relationship.
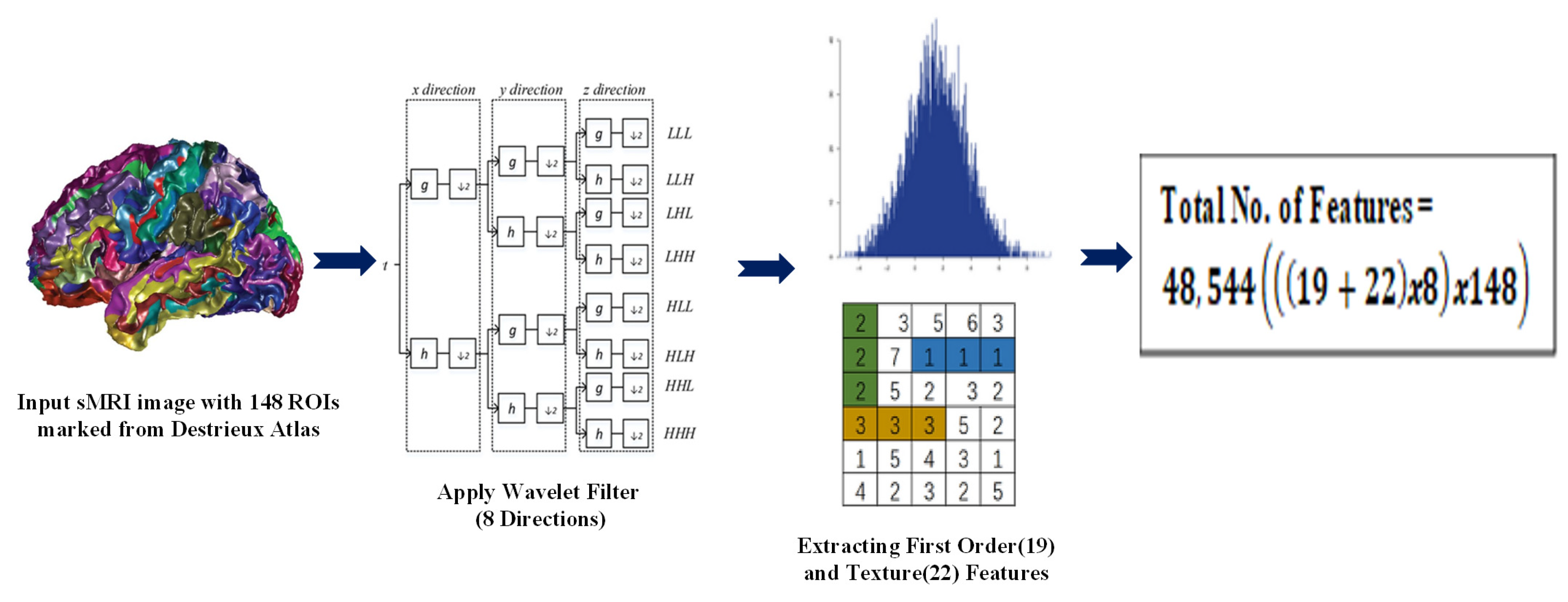
- We extracted 48,544 radiomic features passed to stacked autoencoders for a dimensionality reduction. We obtained a similarity index between the 150 features of each node using an improved sqrt cosine similarity function to draw an edge between the nodes.
- Brain summaries provide spatial features passed to the Multichannel CNN to obtain the feature vector for each node. We obtained 3D volume images for each brain summary derivative and combined them on the fourth (channel) axis. The multichannel 3D CNN produces a feature vector with a size of 1024.
- Population Graphs were constructed with each subject as a node and edges based on the similarities identified in the brain’s structure. The consideration of structural similarities reduced the heterogeneity of the ABIDE dataset, as MRI data were collected from 16 locations.
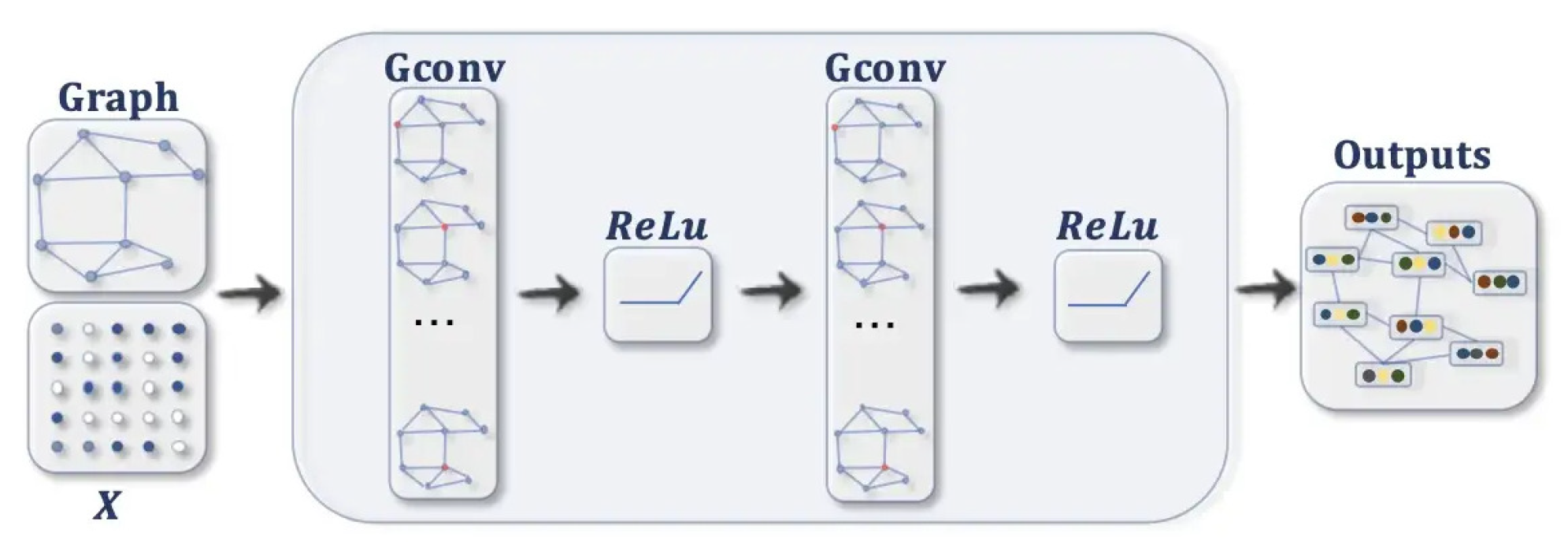
- Graph convolution networks were used to produce complete graphs, which helped to classify nodes as ASD or Typical Controls (TC).
2. Related Work
2.1. Nongraph Deep Learning Methods
2.2. Graph-Based Deep Learning Methods
2.3. Radiomics
3. Materials and Methods
3.1. Proposed Method
3.2. Building the Adjacency Matrix
| Algorithm 1: Feature Ranking using Fischer’s Score |
 |
| Algorithm 2: Stacked Autoencoder |
 |
3.3. Feature Selection
3.4. Graph Convolution
4. Experimental Results
4.1. Dataset
- Motion correction: To reduce the impact of head movement on the fMRI data, the images were corrected for motion using tools such as MCFLIRT and MotionCorr.
- Spatial normalisation: To ensure a consistent representation of brain structures across participants, the data were transformed into a shared space using a standard brain template ( Montreal Neurological Institute template).
- Noise reduction: Various noise sources, such as physiological noise from the heart and respiratory system, were removed from the data using physiological regression or CompCor.
- Data cleaning: The data were checked for quality and outliers, and any poorly performing time points or participants were removed from the dataset.
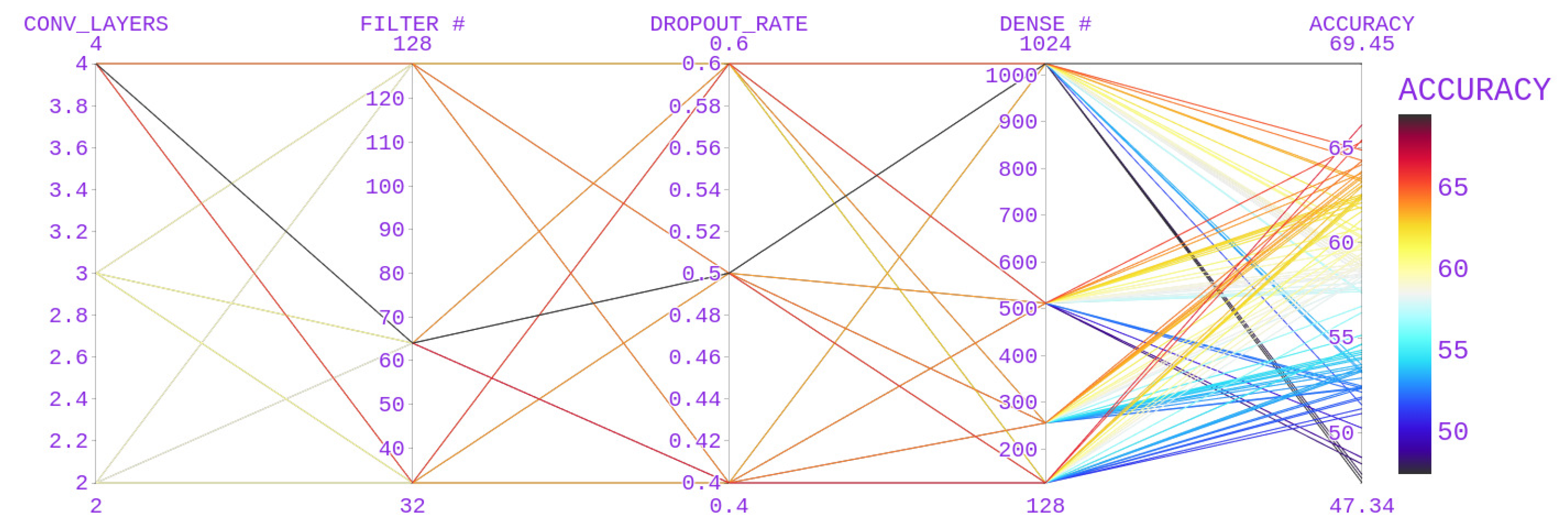
4.2. Parameter Search
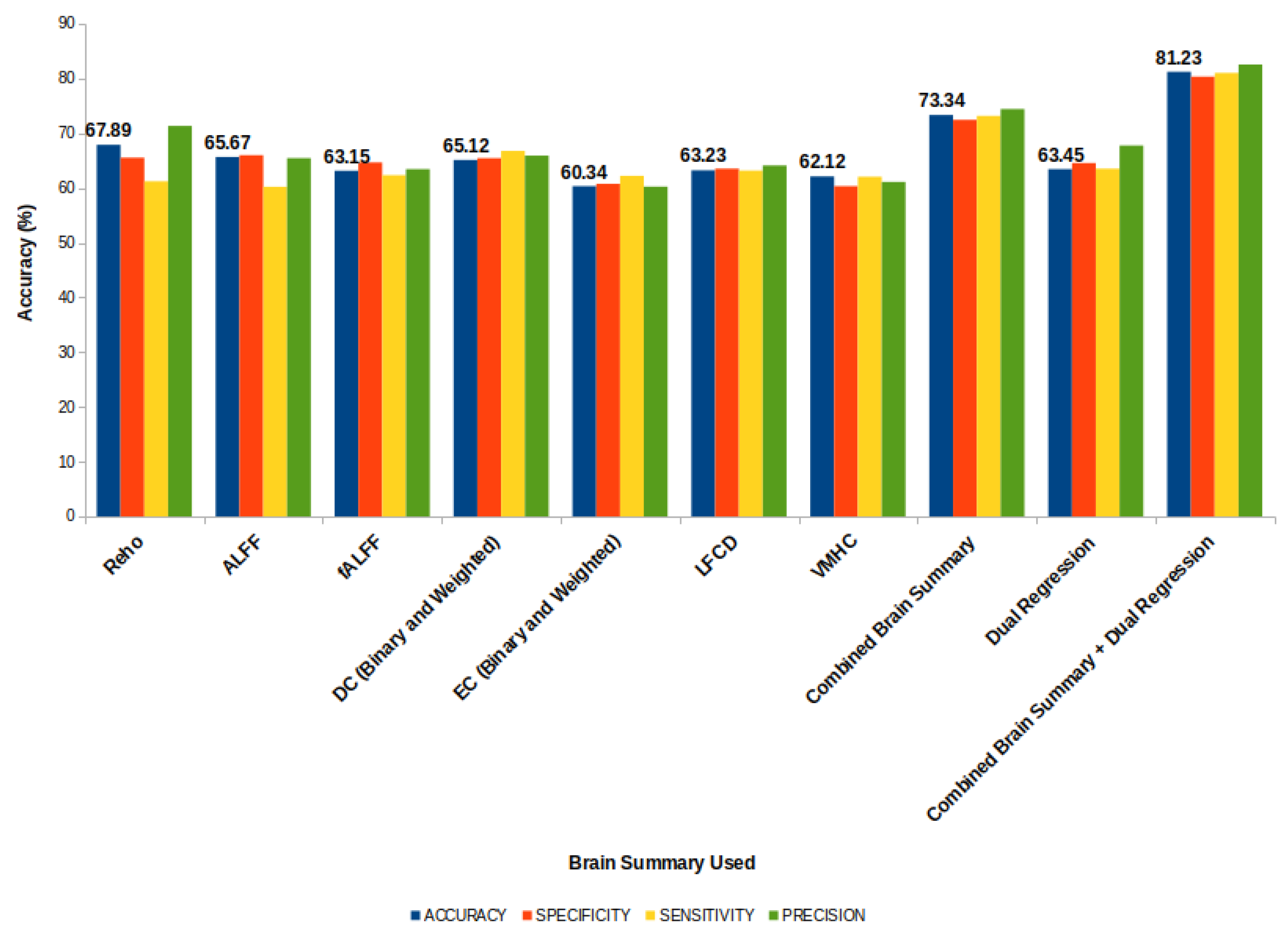
4.3. Experiments
4.4. Evaluation
- The accuracy measures the proportion of correct predictions made by the model. It is a useful metric to evaluate the model’s overall performance, but it may not be the best metric for imbalanced datasets.
- The sensitivity (also called the recall or true positive rate) measures the proportion of actual positive cases correctly identified by the model. It helps to detect false negatives and is essential in applications where the identification of positive cases is critical.
- The specificity (also called the true negative rate) measures the proportion of actual negative cases correctly identified by the model. It helps to detect false positives and is essential in applications where avoiding false alarms is critical.
- The precision measures the accuracy of positive predictions made by the model. It tells us how many of the positive predictions made by the model were actually correct.
5. Discussion
Comparison with the State-of-the-Art Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASD | Autism Spectrum Disorder |
| TC | Typical Controls |
| ABIDE | Autism Brain Imaging Data Exchange |
| MRI | Magnetic Resonance Imaging |
| sMRI | Structural MRI |
| fMRI | Functional MRI |
| rs-fMRI | Resting State Functional MRI |
| CNN | Convolutional Neural Network |
| GCN | Graph Convolutional Network |
| ROI | Region of Interest |
| ReHo | Regional Homogeneity |
| ALFF | Amplitude of Low Frequency Fluctuations |
| fALFF | Functional Amplitude of Low Frequency Fluctuations |
| DC | Degree Centrality |
| EC | Eigen vector Centrality |
| LFCD | Local Functional Connectivity Density |
| VMHC | Voxel-Mirrored Homotopic Connectivity |
| DR | Dual Regression |
| ICA | Independent Component Analysis |
| BOLD | Blood Oxygenation Level Dependent |
| GLCM | Gray Level Co-occurrence Matrix |
Appendix A
| S.No | First Order Feature | GLCM |
|---|---|---|
| 1 | Energy | Autocorrelation |
| 2 | Total Energy | Joint Average |
| 3 | Entropy | Cluster Prominence |
| 4 | Minimum | Cluster Shade |
| 5 | Maximum | Cluster Tendency |
| 6 | 10th percentile | Contrast |
| 7 | 90th percentile | Correlation |
| 8 | Mean | Difference Average |
| 9 | Median | Difference Entropy |
| 10 | Range | Difference Variance |
| 11 | Mean Absolute Deviation | Joint Energy |
| 12 | Robust Mean Absolute Deviation | Joint Entropy |
| 13 | Root Mean Squared | Inverse Variance |
| 14 | Standard Deviation | Inverse Difference Moment |
| 15 | Skewness | Maximal Correlation Coefficient |
| 16 | Variance | Inverse Difference Moment Normalized |
| 17 | Uniformity | Inverse Difference |
| 18 | Kurtosis | Inverse Difference Normalized |
| 19 | Interquartile Range | Sum of Squares |
| 20 | - | Maximum Probability |
| 21 | - | Sum Average |
| 22 | - | Sum Entropy |
| Terms | Definition |
|---|---|
| nv | Voxels in ROI |
| ng | discrete intensity levels |
| nb | the number of non-zero bins |
| X | set of nv voxels included in the ROI |
| normalized first order histogram | |
| ∈ | |
| co-occurrence matrix for an arbitrary distance d and angle | |
| N | number of discrete intensity levels in the image |
| Sub set of number of discrete intensity levels in the image between 10th and 90th Percentile | |
| mean gray level intensity of | |
| mean gray level intensity of | |
| standard deviation of | |
| standard deviation of |
| Terms | Definition |
|---|---|
| Mean of ith feature in jth class | |
| Variance of ith feature in jth class | |
| Number of instances in jth class | |
| Mean of ith Feature |
References
- Cheng, W.; Rolls, E.T.; Zhang, J.; Sheng, W.; Ma, L.; Wan, L.; Luo, Q.; Feng, J. Functional connectivity decreases in autism in emotion, self, and face circuits identified by Knowledge-based Enrichment Analysis. Neuroimage 2017, 148, 169–178. [Google Scholar] [CrossRef]
- Hazlett, H.C.; Gu, H.; Munsell, B.C.; Kim, S.H.; Styner, M.; Wolff, J.J.; Elison, J.T.; Swanson, M.R.; Zhu, H.; Botteron, K.N.; et al. Early brain development in infants at high risk for autism spectrum disorder. Nature 2017, 542, 348–351. [Google Scholar] [CrossRef]
- Giangiacomo, E.; Visaggi, M.C.; Aceti, F.; Giacchetti, N.; Martucci, M.; Giovannone, F.; Valente, D.; Galeoto, G.; Tofani, M.; Sogos, C. Early Neuro-Psychomotor Therapy Intervention for Theory of Mind and Emotion Recognition in Neurodevelop-mental Disorders: A Pilot Study. Children 2022, 9, 1142. [Google Scholar] [CrossRef] [PubMed]
- Kong, Y.; Gao, J.; Xu, Y.; Pan, Y.; Wang, J.; Liu, J. Classification of autism spectrum disorder by combining brain connectivity and deep neural network classifier. Neurocomputing 2018, 324, 63–68. [Google Scholar] [CrossRef]
- Cao, X.; Wang, X.; Xue, C.; Zhang, S.; Huang, Q.; Liu, W. A Radiomics Approach to Predicting Parkinson’s Disease by Incor-porating Whole-Brain Functional Activity and Gray Matter Structure. Front. Neurosci. 2020, 14, 751. [Google Scholar] [CrossRef] [PubMed]
- Donisi, L.; Cesarelli, G.; Castaldo, A.; De Lucia, D.R.; Nessuno, F.; Spadarella, G.; Ricciardi, C. A Combined Radiomics and Machine Learning Approach to Distinguish Clinically Significant Prostate Lesions on a Publicly Available MRI Dataset. J. Imaging 2021, 7, 215. [Google Scholar] [CrossRef] [PubMed]
- Dekhil, O.; Hajjdiab, H.; Shalaby, A.; Ali, M.T.; Ayinde, B.; Switala, A.; Elshamekh, A.; Ghazal, M.; Keynton, R.; Barnes, G.; et al. Using resting state functional MRI to build a personalized autism diagnosis system. PLoS ONE 2018, 13, e0206351. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Tripathi, A.R.; Satapathy, S.C.; Zhang, Y.-D. SARS-Net: COVID-19 detection from chest x-rays by combining graph convolutional network and convolutional neural network. Pattern Recognit. 2021, 122, 108255. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, M.; Kazi, A.; Baghshah, M.S.; Rabiee, H.R.; Navab, N. RA-GCN: Graph convolutional network for disease predic-tion problems with imbalanced data. Med. Image Anal. 2021, 75, 102272. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, F.; Zhao, X.; Xiao, W.; Zhang, W. Predicting drug–disease associations through layer attention graph convolu-tional network. Brief. Bioinform. 2020, 22, bbaa243. [Google Scholar] [CrossRef]
- Ahammed, S.; Niu, S.; Ahmed, R.; Dong, J.; Gao, X.; Chen, Y. DarkASDNet: Classification of ASD on Functional MRI Using Deep Neural Network. Front. Neuroinform. 2021, 15, 635657. [Google Scholar] [CrossRef]
- Haweel, R.; Seada, N.; Ghoniemy, S.; Alghamdi, N.S.; El-Baz, A. A CNN Deep Local and Global ASD Classification Ap-proach with Continuous Wavelet Transform Using Task-Based FMRI. Sensors 2021, 21, 5822. [Google Scholar] [CrossRef]
- Li, X.; Dvornek, N.C.; Papademetris, X.; Zhuang, J.; Staib, L.H.; Ventola, P.; Duncan, J.S. 2-Channel convolutional 3D deep neural network (2CC3D) for fMRI Analysis: ASD classification and feature learning. In Proceedings of the IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 1252–1255. [Google Scholar] [CrossRef]
- Leming, M.J.; Baron-Cohen, S.; Suckling, J. Single-participant structural similarity matrices lead to greater accuracy in classi-fication of participants than function in autism in MRI. Mol. Autism. 2021, 12, 1–15. [Google Scholar] [CrossRef]
- Eslami, T.; Mirjalili, V.; Fong, A.; Laird, A.R.; Saeed, F. ASD-DiagNet: A Hybrid Learning Approach for Detection of Autism Spectrum Disorder Using fMRI Data. Front. Neuroinformatics 2019, 13, 70. [Google Scholar] [CrossRef]
- Sewani, H.; Kashef, R. An Autoencoder-Based Deep Learning Classifier for Efficient Diagnosis of Autism. Children 2020, 7, 182. [Google Scholar] [CrossRef] [PubMed]
- Ali, L.; He, Z.; Cao, W.; Rauf, H.T.; Imrana, Y.; Bin Heyat, B. MMDD-Ensemble: A Multimodal Data–Driven Ensemble Ap-proach for Parkinson’s Disease Detection. Front. Neurosci. 2021, 15, 754058. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, S.; Aggarwal, C.C.; Tang, J. Graph Convolutional Networks with Eigen Pooling. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery Data Mining (KDD 19), Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 723–731. [Google Scholar] [CrossRef]
- Wen, G.; Cao, P.; Bao, H.; Yang, W.; Zheng, T.; Zaiane, O. MVS-GCN: A prior brain structure learning-guided multi-view graph convolution network for autism spectrum disorder diagnosis. Comput. Biol. Med. 2022, 142, 105239. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Zhou, F.; Frangi, A.F.; Cao, J.; Xiao, X.; Lei, Y.; Wang, T.; Lei, B. Graph convolution network with similarity awareness and adaptive calibration for disease-induced deterioration prediction. Med. Image Anal. 2020, 69, 101947. [Google Scholar] [CrossRef] [PubMed]
- Lei, B.; Zhu, Y.; Yu, S.; Hu, H.; Xu, Y.; Yue, G.; Wang, T.; Zhao, C.; Chen, S.; Yang, P.; et al. Multi-scale enhanced graph convolutional network for mild cognitive impairment detection. Pattern Recognit. 2023, 134, 109106. [Google Scholar] [CrossRef]
- Parisot, S.; Ktena, S.I.; Ferrante, E.; Lee, M.; Guerrero, R.; Glocker, B.; Rueckert, D. Disease prediction using graph convolutional networks: Application to Autism Spectrum Disorder and Alzheimer’s disease. Med. Image Anal. 2018, 48, 117–130. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Zhang, H.; Wang, G.; Wang, S.; Yao, X.; Li, Y.; Guo, Q.; Zheng, S.; Ren, K. Machine Learning for Detecting Parkinson’s Disease by Resting-State Functional Magnetic Resonance Imaging: A Multicenter Radiomics Analysis. Front. Aging Neurosci. 2022, 14, 806828. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Feng, Q.; Ge, X.; Chen, F.; Yu, B.; Chen, B.; Liao, Z.; Lin, B.; Lv, Y.; Ding, Z. Textural features reflecting local activi-ty of the hippocampus improve the diagnosis of Alzheimer’s disease and amnestic mild cognitive impairment: A radiomics study based on functional magnetic resonance imaging. Front. Neurosci. 2022, 16, 970245. [Google Scholar] [CrossRef] [PubMed]
- Sohangir, S.; Wang, D. Improved sqrt-cosine similarity measurement. J. Big Data 2017, 4, 25. [Google Scholar] [CrossRef]
- Dekhil, O.; Ali, M.; El-Nakieb, Y.; Shalaby, A.; Soliman, A.; Switala, A.; Mahmoud, A.; Ghazal, M.; Hajjdiab, H.; Casanova, M.F.; et al. A Personalized Autism Diagnosis CAD System Using a Fusion of Structural MRI and Resting-State Functional MRI Data. Front. Psychiatry 2019, 10, 392. [Google Scholar] [CrossRef] [PubMed]
- Py-Radiomic Features. Radiomic Features. Available online: https://pyradiomics.readthedocs.io/en/latest/features.html (accessed on 20 October 2022).
- Howsmon, D.P.; Kruger, U.; Melnyk, S.; James, S.J.; Hahn, J. Classification and adaptive behavior prediction of children with autism spectrum disorder based upon multivariate data analysis of markers of oxidative stress and DNA methylation. PLoS Comput. Biol. 2017, 13, e1005385. [Google Scholar] [CrossRef]
- Williams, B.; Kabbage, M.; Kim, H.J.; Britt, R.; Dickman, M.B. Tipping the balance: Sclerotinia sclerotiorum secreted oxalic acid suppresses host defenses by manipulating the host redox environment. PLoS Pathog. 2011, 7, e1002107. [Google Scholar] [CrossRef]
- Nie, W.; Chang, R.; Ren, M.; Su, Y.; Liu, A. I-GCN: Incremental Graph Convolution Network for Conversation Emotion Detection. IEEE Trans. Multimedia 2021, 24, 4471–4481. [Google Scholar] [CrossRef]
- Chu, Y.; Wang, G.; Cao, L.; Qiao, L.; Liu, M. Multi-Scale Graph Representation Learning for Autism Identification with Func-tional MRI. Front. Neuroinform. 2022, 15, 802305. [Google Scholar] [CrossRef]
| Authors, Paper Title (Year) | Contribution | Drawback | Deep Learning Method | Dataset |
|---|---|---|---|---|
| MS Ahammed et al., Classification of ASD on Functional MRI Using Deep Neural Network (2021) [11] | Learned features of 3D fMRI images by increasing the number of convolution layers. | Topographical heterogeneity of dataset not considered | 2D CNN | ABIDE1 (NYU) |
| MJ Leming et al., Single-participant structural similarity matrices lead to greater accuracy in classification of participants than function in autism in MRI (2021) [14] | Derived a structural similarity metric with grey matter volume data from structural MRI images | Generalisation of data not proven | 2D CNN | Open fMRI, UK Biobank, ABIDE I, ABIDE II, NDAR |
| R Haweel et al., A CNN Deep Local and Global ASD Classification Approach with Continuous Wavelet Transform Using Task-Based FMRI (2021) [12] | Used K-means clustering to cluster BOLD signals in fMRI data and continuous wavelet transform to obtain a detailed representation of BOLD signals. | The choice of wavelet parameters is challenging and may affect the model’s performance | Clustered BOLD signals passed to CNN | NDAR |
| X Li et al., Two-Channel Convolutional 3D Deep Neural Network (2CC3D) for fMRI Analysis: ASD Classification and Feature Learning (2018) [13] | Two channels, the mean and standard deviation of temporal fMRI data are passed to the CNN. | The sliding window involves computing the convolution operation multiple times for overlapping regions of the input image. This can result in redundant computation, as the same features may be detected multiple times. | 2 -Channel 3D CNN | Self |
| Eslami et al., A Hybrid Learning Approach for Detection of Autism Spectrum Disorder Using fMRI Data (2019) [15] | Used autoencoders to capture the complex patterns in fMRI data and single layer perceptron to provide a solution. | Used only the functional connectivity matrix features for the classification | Autoencoder and a Single–Layer Perceptron | ABIDE-I |
| H Sewani et al., An Autoencoder-Based Deep Learning Classifier for Efficient Diagnosis of Autism (2020) [16] | Autoencoder-based deep learning model followed by a sequence of two 1D CNNs for better feature learning. | Used only Pearson’s correlation matrix for extracting features from fMRI. No specific atlases or statistical measures were used to obtain regions of interest. | Autoencoder + 1D CNN | ABIDE |
| L Ali et.al, MMDD-Ensemble: A Multimodal Data–Driven Ensemble Approach for Parkinson’s Disease Detection (2021) [17] | Ensembling method for combining the features obtained from different modalities. | Voting after classification results does not ensure the feature selection accuracy of a modality used. | Machine Learning | Self |
| Y Ma et.al, Graph Convolutional Networks with Eigen Pooling (2019) [18] | Used Eigen Pooling to reduce the graph. | Eigen decomposition may lead to loss of important characteristics from a node | GCN | ENZYMES, PROTEINS, Mutagenicity |
| G Wen et.al, MVS-GCN: A prior brain structure learning-guided multi-view graph convolution network for autism spectrum disorder diagnosis (2022) [19] | Used graph structure learning to learn features from multiple views of a graph. | Used only fMRI and did not include the structural components of the brain | Graph Convolutional Network | ABIDE |
| X Song et.al, Graph convolution network with similarity awareness and adaptive calibration for disease-induced deterioration prediction (2021) [20] | Used the similarity between nodes for predictions and adaptive calibration for parameter tuning. | Used only fMRI and did not include the structural components of the brain | GCN | ADNI |
| Baiying Lei et.al, Multiscale enhanced graph convolutional network for mild cognitive impairment detection (2023) [21] | Used the functional connectivity matrix to construct a brain graph. | Structural features were not considered | Attention Graph Convolution Network | Self |
| S Parisot et.al, Disease prediction using graph convolutional networks: Application to Autism Spectrum Disorder and Alzheimer’s disease (2018) [22] | Used an autoencoder to obtain the features of a node from a graph and phenotypic data to build edges. | Using phenotypic data in a topographically heterogenous dataset to find similarities between nodes might reduce the model’s performance. | GCN | ABIDE |
| D Shi et al., Machine Learning for Detecting Parkinson’s Disease by Resting-State Functional Magnetic Resonance Imaging: A Multicentre Radiomics Analysis (2022) [23] | Used radiomics features to identify spontaneously abnormal brain activities as biomarkers. | Did not include cerebellum or multimodal data | Radiomics + SVM | figshare |
| L Wang et al., Textural features reflecting local activity of the hippocampus improve the diagnosis of Alzheimer’s disease and amnestic mild cognitive impairment: A radiomics study based on functional magnetic resonance imaging (2022) [24] | Investigated the use of textural features derived from functional magnetic resonance imaging (fMRI) of the hippocampus to improve the diagnosis. | Aimed to use imaging data to extract textural features that reflect local activity only in this region | Radiomics + Statistics | Self |
| S.No | Model | Methodology | Findings |
|---|---|---|---|
| 1 | ASD-DiagNet | Feature Map obtained from VAE [rs-fMRI] | Correlation coefficients can be influenced by head motion, the signal-to-noise ratio and individual differences in brain anatomy |
| 2 | DBN | Feature Map obtained from the Restricted Boltzmann Machine [rs-fMRI] | Correlation coefficients can be influenced by head motion, the signal-to-noise ratio and individual differences in brain anatomy |
| 3 | MMDC | Classification results of different modalities (phonation: voicing of vowels, voiced and unvoiced) are ensembled by blending or voting | Ensembling multiple modalities before classification can improve the accuracy compared to the ensembling of classification results |
| 4 | s-GCN | Nodes-> Atlas [rs-fMRI] Edges-> Phenotype data | The use of phenotype data for constructing edges might lead to a lack of heterogeneity since phenotype data do not consider variation in topographical locations |
| 5 | EigenGCN | Nodes-> Functional Connectivity Matrix (FCM) [rs-fMRI] Edges-> Graph Kernel Function [FCM] | Loss of crucial information about features due to multiple pooling layers |
| 6 | MVS-GCN | Brain graph constructed with multiple views from the subnetwork | The heterogeneity of the brain is not considered when forming subnetworks, which may result in a lack of functional connectivity between regions across subnetworks. |
| 7 | Proposed Model | Nodes-> Feature Maps obtained from Combined BS + Dual RegressionEdges->Similarity Measure calculated using Radiomics from sMRI | - |
| Hyper Parameters | Values |
|---|---|
| No. of Convolutional blocks after the First layer | 2,3,4 |
| Number of Filters | 32,64,128 |
| Dropout Rate | 0.4, 0.5, 0.6 |
| No. of nodes in the dense layer | 128,256,512,1024 |
| S.No | Model | Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|
| 1 | ASD-DiagNet | 70.3 | 68.3 | 72.2 |
| 2 | DBN | 65.56 | 84 | 32.96 |
| 3 | s-GCN | 65.74 | 64.73 | 60.12 |
| 4 | EigenGCN | 57.5 | 58.81 | 59.94 |
| 5 | MVS-GCN | 69.38 | 69.93 | 71.22 |
| 6 | Proposed Model | 81.23 | 81.36 | 81.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manikantan, K.; Jaganathan, S. A Model for Diagnosing Autism Patients Using Spatial and Statistical Measures Using rs-fMRI and sMRI by Adopting Graphical Neural Networks. Diagnostics 2023, 13, 1143. https://doi.org/10.3390/diagnostics13061143
Manikantan K, Jaganathan S. A Model for Diagnosing Autism Patients Using Spatial and Statistical Measures Using rs-fMRI and sMRI by Adopting Graphical Neural Networks. Diagnostics. 2023; 13(6):1143. https://doi.org/10.3390/diagnostics13061143
Chicago/Turabian StyleManikantan, Kiruthigha, and Suresh Jaganathan. 2023. "A Model for Diagnosing Autism Patients Using Spatial and Statistical Measures Using rs-fMRI and sMRI by Adopting Graphical Neural Networks" Diagnostics 13, no. 6: 1143. https://doi.org/10.3390/diagnostics13061143
APA StyleManikantan, K., & Jaganathan, S. (2023). A Model for Diagnosing Autism Patients Using Spatial and Statistical Measures Using rs-fMRI and sMRI by Adopting Graphical Neural Networks. Diagnostics, 13(6), 1143. https://doi.org/10.3390/diagnostics13061143






