Radar-Based Microwave Breast Imaging Using Neurocomputational Models
Abstract
1. Introduction
- In this study, conventional imaging was carried out utilizing CSAR-based numerical data and an MP-based algorithm.
- For imaging, both the matching-pursuit-based method and the neurocomputational models utilized raw, unprocessed real-valued, and complex-valued numerical data. Computed or measured scattered electric field data can therefore be applied directly to models without preprocessing.
- RV-DNN and RV-CNN models are proposed, followed by two combined neurocomputational models (RV-MWINet and CV-MWINet) employing the proposed CNN model structure, which combines the U-Net structure. The images generated by the proposed models are compared to those generated by the matching-pursuit algorithm. The study demonstrates that the processing and generation speeds of the proposed models are faster than those of conventional imaging techniques, and that the resulting images are of higher quality.
- By placing a screw in the sand and an unhealthy tumor phantom in a healthy phantom, a total of 12 measurements were taken in the range of 1 GHz to 10 GHz, using the measurement setup. In order to train the CV-MWINet model, measurement data were added to the dataset obtained from simulated data. Also, the performance of the proposed model on both simulated and measured data is discussed.
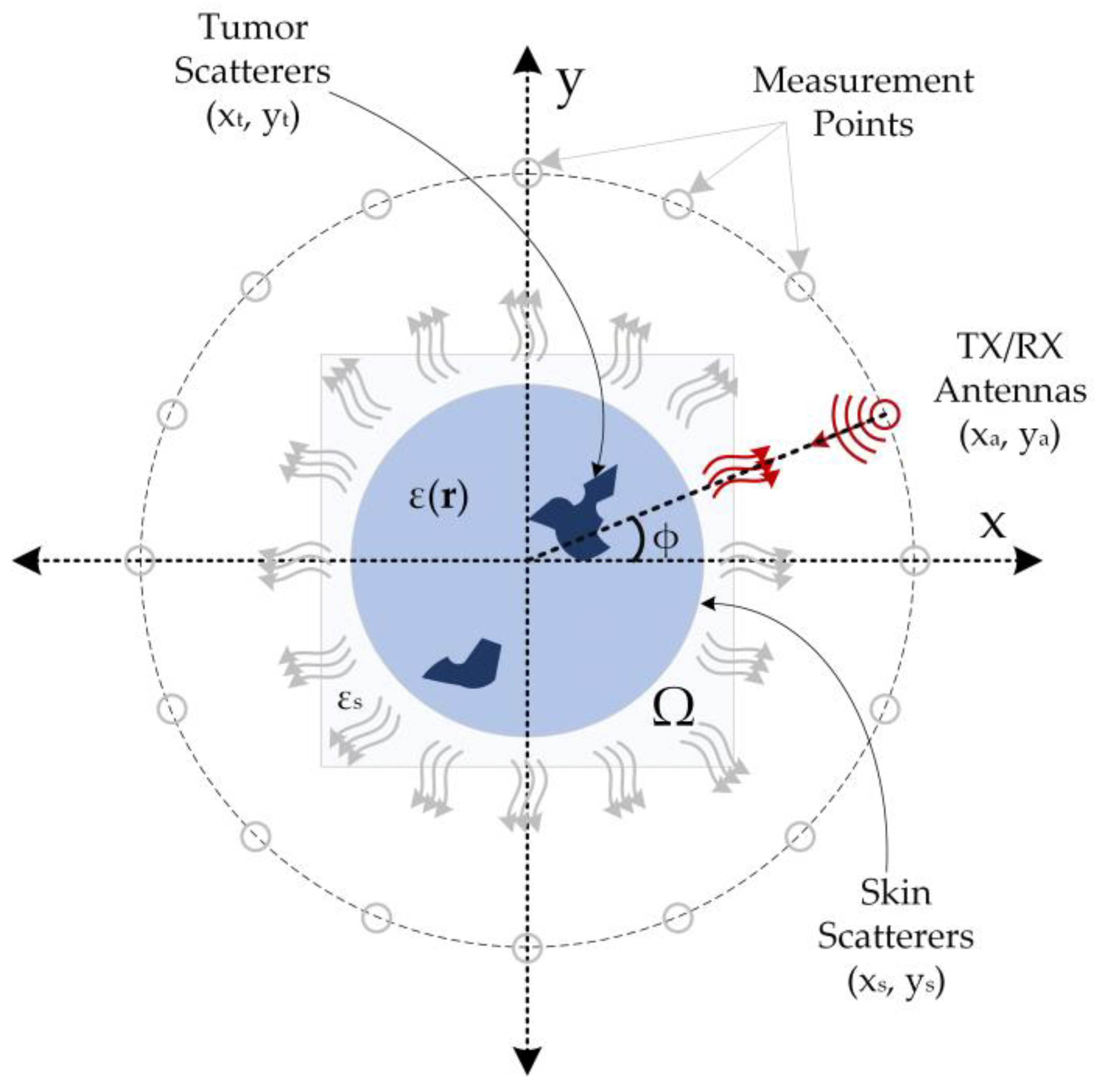
2. The Forward Problem Based on the Circular Synthetic Aperture Radar (CSAR) Principle
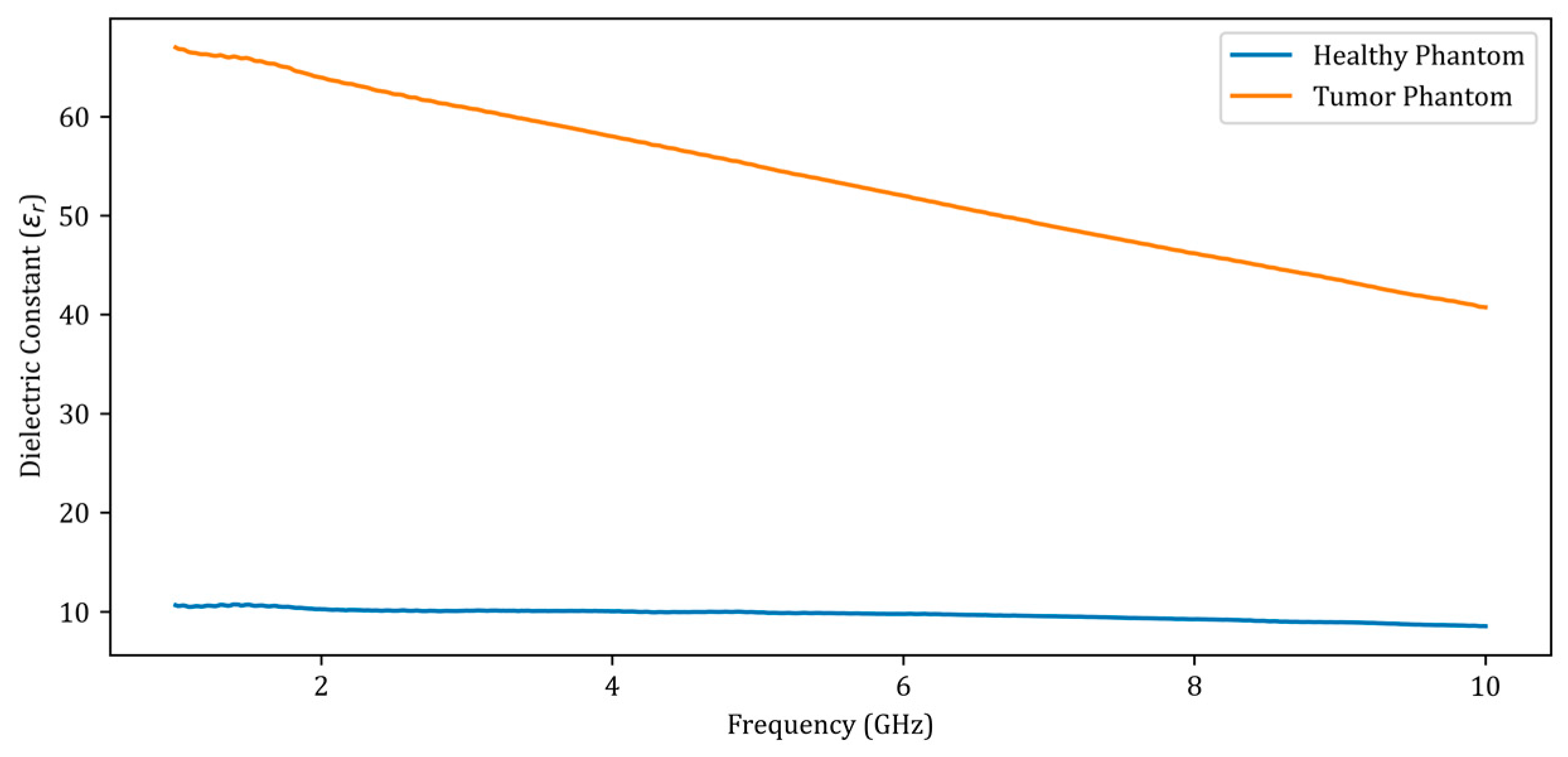
3. Phantom Fabrication and Measurement
4. Microwave Imaging (MWI) Using Deep Learning (DL) Models
4.1. Similarities between DL and Non-Linear Electromagnetic Scattering
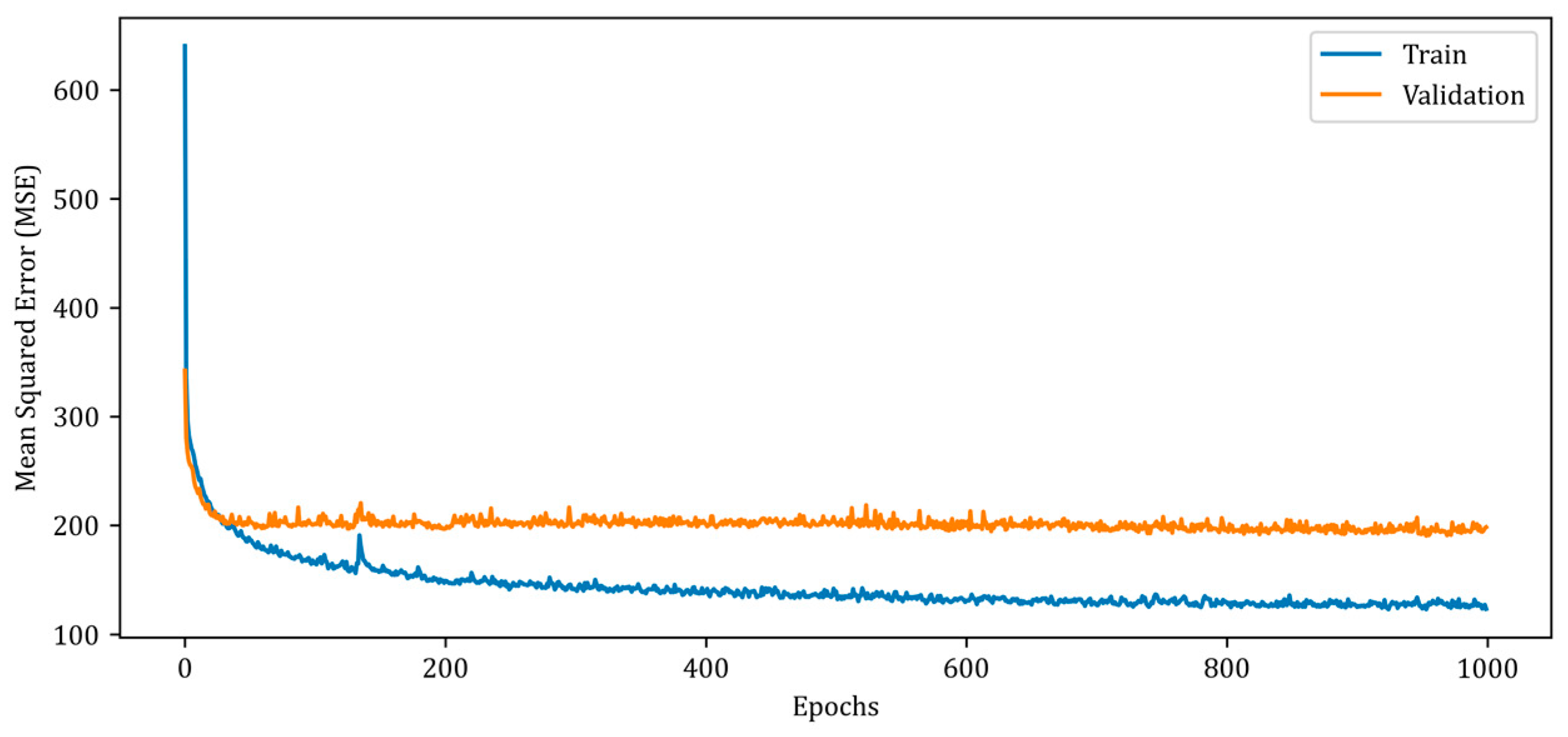
4.2. Deep Neural Network-Based (DNN-Based) Imaging
4.3. Convolutional Neural Networks-Based (CNN-Based) Imaging
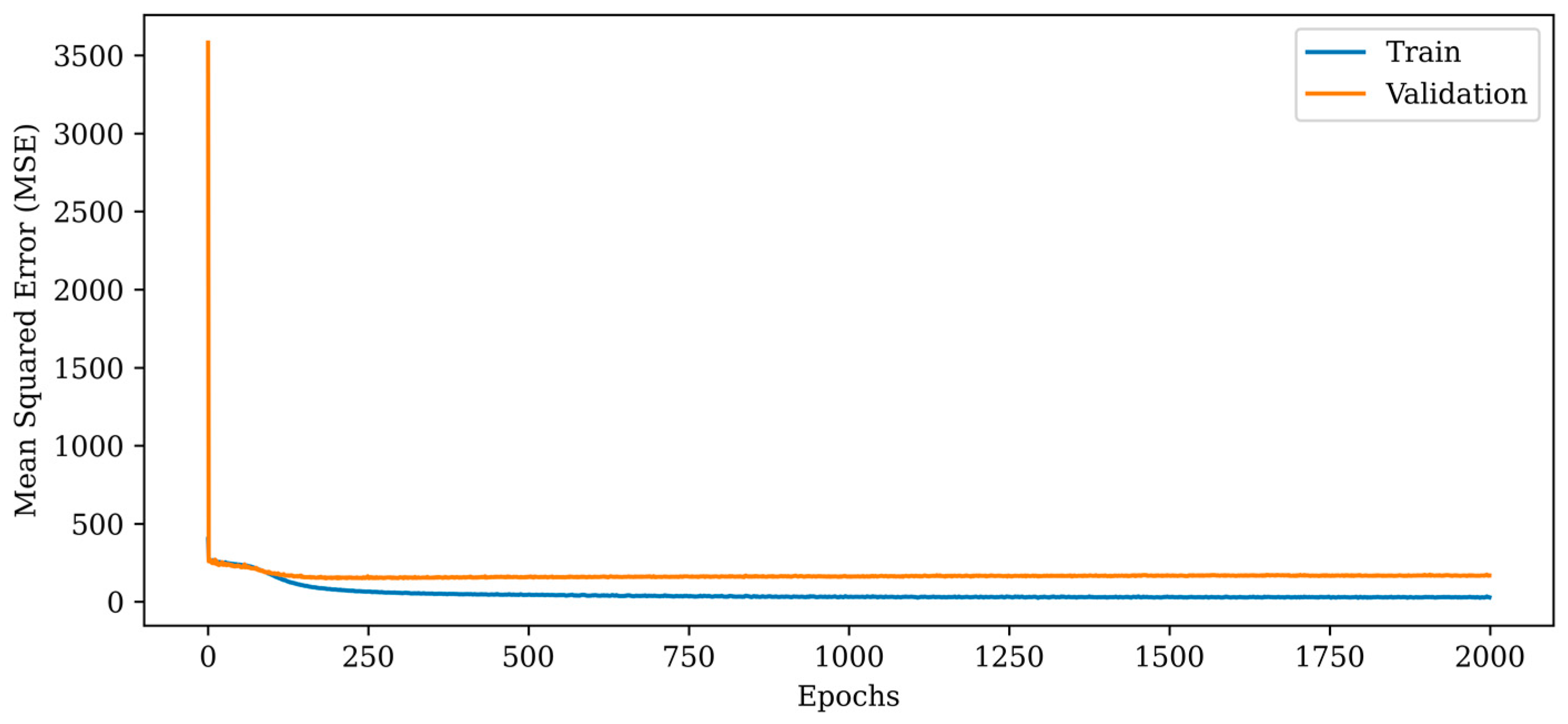
4.4. U-Net-Based Combined Neurocomputational Imaging Model
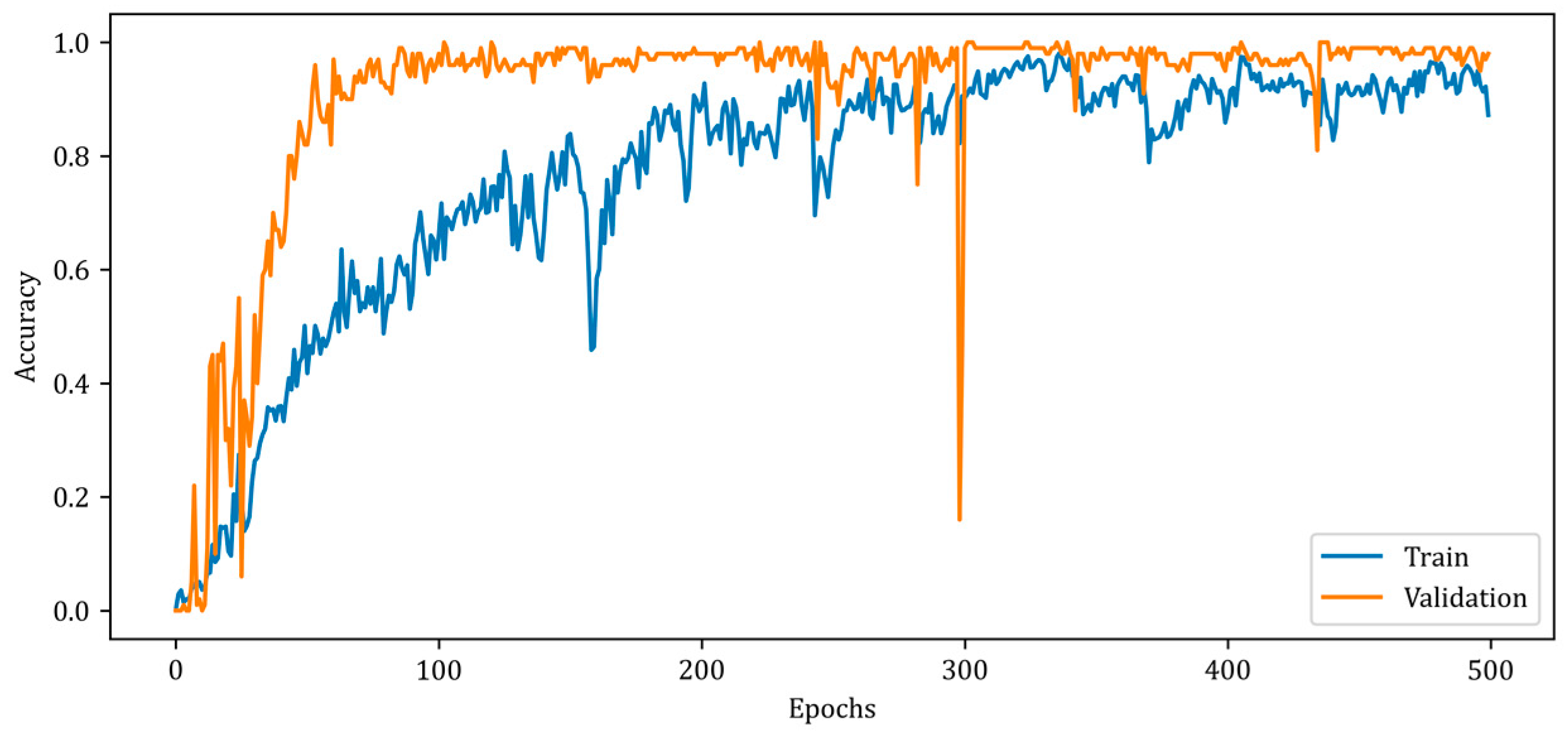
4.5. Evaluation Metrics
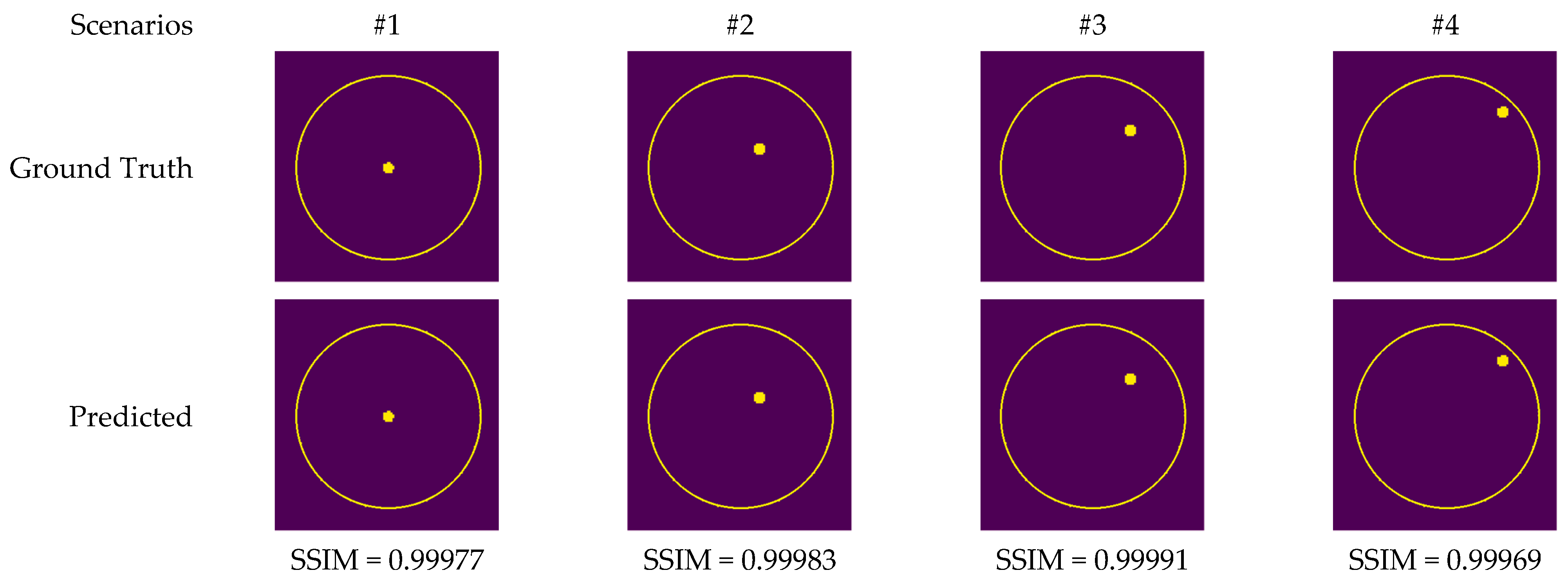
5. Numerical Results and Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- What Do People Die from?—Our World in Data. Available online: https://ourworldindata.org/what-does-the-world-die-from (accessed on 9 January 2023).
- FastStats—Leading Causes of Death. Available online: https://www.cdc.gov/nchs/fastats/leading-causes-of-death.htm (accessed on 9 January 2023).
- Hassan, A.M.; El-Shenawee, M. Review of Electromagnetic Techniques for Breast Cancer Detection. IEEE Rev. Biomed. Eng. 2011, 4, 103–118. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Liu, Q.H. Three-Dimensional Nonlinear Image Reconstruction for Microwave Biomedical Imaging. IEEE Trans. Biomed. Eng. 2004, 51, 544–548. [Google Scholar] [CrossRef] [PubMed]
- Mirza, A.F.; See, C.H.; Danjuma, I.M.; Asif, R.; Abd-Alhameed, R.A.; Noras, J.M.; Clarke, R.W.; Excell, P.S. An Active Microwave Sensor for Near Field Imaging. IEEE Sens. J. 2017, 17, 2749–2757. [Google Scholar] [CrossRef]
- Kranold, L.; Hazarika, P.; Popovic, M. Investigation of antenna array configurations for dispersive breast models. In Proceedings of the 2017 11th European Conference on Antennas and Propagation, EUCAP 2017, Paris, France, 19–24 March 2017; pp. 2737–2741. [Google Scholar] [CrossRef]
- Hossain, D.; Mohan, A.S. Cancer Detection in Highly Dense Breasts Using Coherently Focused Time-Reversal Microwave Imaging. IEEE Trans. Comput. Imaging 2017, 3, 928–939. [Google Scholar] [CrossRef]
- Elahi, M.; Curtis, C.; Lavoie, B.; Glavin, M.; Jones, E.; Fear, E.; O’Halloran, M. Performance of leading artifact removal algorithms assessed across microwave breast imaging prototype scan configurations. Comput. Med. Imaging Graph. 2017, 58, 33–44. [Google Scholar] [CrossRef] [PubMed]
- Ji, J.; Tong, K.-F.; Al-Armaghany, A.; Leung, T.S. A feasibility study of elastography based confocal microwave imaging technique for breast cancer detection. Optik 2017, 144, 108–114. [Google Scholar] [CrossRef]
- Aydın, E.A.; Keleş, M.K. Breast cancer detection using K-nearest neighbors data mining method obtained from the bow-tie antenna dataset. Int. J. RF Microw. Comput.-Aided Eng. 2017, 27, e21098. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, X.; Wang, L.; Song, H.; Kono, H.; Liu, P.; Lu, H.; Kikkawa, T. Direct Extraction of Tumor Response Based on Ensemble Empirical Mode Decomposition for Image Reconstruction of Early Breast Cancer Detection by UWB. IEEE Trans. Biomed. Circuits Syst. 2015, 9, 710–724. [Google Scholar] [CrossRef]
- Bah, M.H.; Hong, J.-S.; Jamro, D.A. UWB patch antenna and breast mimicking phantom design and implementation for microwave breast cancer detection using TIME REVERSAL MUSIC. Microw. Opt. Technol. Lett. 2016, 58, 549–554. [Google Scholar] [CrossRef]
- Yin, T.; Ali, F.H.; Reyes-Aldasoro, C.C. A Robust and Artifact Resistant Algorithm of Ultrawideband Imaging System for Breast Cancer Detection. IEEE Trans. Biomed. Eng. 2015, 62, 1514–1525. [Google Scholar] [CrossRef]
- Wang, F.; Arslan, T.; Wang, G. Breast cancer detection with microwave imaging system using wearable conformal antenna arrays. In Proceedings of the IST 2017—IEEE International Conference on Imaging Systems and Techniques, Beijing, China, 18–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ünal, I.; Türetken, B.; Canbay, C. Spherical Conformal Bow-Tie Antenna for Ultra-Wide Band Microwave Imaging of Breast Cancer Tumor. Appl. Comput. Electromagn. Soc. J. (ACES) 2021, 29, 124–133. Available online: https://journals.riverpublishers.com/index.php/ACES/article/view/11071 (accessed on 9 January 2023).
- Fear, E.C.; Bourqui, J.; Curtis, C.; Mew, D.; Docktor, B.; Romano, C. Microwave Breast Imaging with a Monostatic Radar-Based System: A Study of Application to Patients. IEEE Trans. Microw. Theory Tech. 2013, 61, 2119–2128. [Google Scholar] [CrossRef]
- Bicer, M.B.; Akdagli, A. An Experimental Study on Microwave Imaging of Breast Cancer with the Use of Tumor Phantom. Appl Comput. Electromagn. Soc. J. 2017, 32, 941–947. [Google Scholar] [CrossRef]
- Bicer, M.B.; Akdagli, A. Implementation of the inverse circular radon transform-based imaging approach for breast cancer screening. Int. J. RF Microw. Comput. Eng. 2018, 28, e21279. [Google Scholar] [CrossRef]
- Bicer, M.B.; Akdagli, A.; Ozdemir, C. A Matching-pursuit based approach for detecting and imaging breast cancer tumor. Prog. Electromagn. Res. M 2018, 64, 65–76. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.G.; Teixeira, F.L.; Liu, C.; Nehorai, A.; Cui, T.J. DeepNIS: Deep Neural Network for Nonlinear Electromagnetic Inverse Scattering. IEEE Trans. Antennas Propag. 2018, 67, 1819–1825. [Google Scholar] [CrossRef]
- Dey, M.; Rana, S.P.; Loretoni, R.; Duranti, M.; Sani, L.; Vispa, A.; Raspa, G.; Ghavami, M.; Dudley, S.; Tiberi, G. Automated breast lesion localisation in microwave imaging employing simplified pulse coupled neural network. PLoS ONE 2022, 17, e0271377. [Google Scholar] [CrossRef]
- Khoshdel, V.; Asefi, M.; Ashraf, A.; LoVetri, J. Full 3D Microwave Breast Imaging Using a Deep-Learning Technique. J. Imaging 2020, 6, 80. [Google Scholar] [CrossRef]
- Qin, Y.; Ran, P.; Rodet, T.; Lesselier, D. Breast Imaging by Convolutional Neural Networks From Joint Microwave and Ultrasonic Data. IEEE Trans. Antennas Propag. 2022, 70, 6265–6276. [Google Scholar] [CrossRef]
- Bicer, M.B. Radar-Based Microwave Imaging Using Deep Complex Neural Networks: A Simulation Study on Breast Cancer. In Proceedings of the V. International Halich Congress on Multidisciplinary Scientific Research, Istanbul, Türkiye, 15 January 2023; p. 175. [Google Scholar]
- Barrachina, J.A.; Ren, C.; Morisseau, C.; Vieiliard, G.; Ovarlez, J.-P. Impact of PolSAR pre-processing and balancing methods on complex-valued neural networks segmentation tasks. arXiv 2022, arXiv:2210.17419. [Google Scholar] [CrossRef]
- Jing, H.; Li, S.; Miao, K.; Wang, S.; Cui, X.; Zhao, G.; Sun, H. Enhanced Millimeter-Wave 3-D Imaging via Complex-Valued Fully Convolutional Neural Network. Electronics 2022, 11, 147. [Google Scholar] [CrossRef]
- Yadav, R.; Omrani, A.; Link, G.; Vauhkonen, M.; Lähivaara, T. Microwave Tomography Using Neural Networks for Its Application in an Industrial Microwave Drying System. Sensors 2021, 21, 6919. [Google Scholar] [CrossRef] [PubMed]
- Ambrosanio, M.; Franceschini, S.; Pascazio, V.; Baselice, F. An End-to-End Deep Learning Approach for Quantitative Microwave Breast Imaging in Real-Time Applications. Bioengineering 2022, 9, 651. [Google Scholar] [CrossRef]
- Sun, S.; Kooij, B.J.; Jin, T.; Yarovoy, A.G. Cross-Correlated Contrast Source Inversion. IEEE Trans. Antennas Propag. 2017, 65, 2592–2603. [Google Scholar] [CrossRef]
- Ambrosanio, M.; Kosmas, P.; Pascazio, V. A Multithreshold Iterative DBIM-Based Algorithm for the Imaging of Heterogeneous Breast Tissues. IEEE Trans. Biomed. Eng. 2018, 66, 509–520. [Google Scholar] [CrossRef] [PubMed]
- Shao, W.; Du, Y. Microwave Imaging by Deep Learning Network: Feasibility and Training Method. IEEE Trans. Antennas Propag. 2020, 68, 5626–5635. [Google Scholar] [CrossRef]
- Chiu, C.C.; Kang, T.H.; Chen, P.H.; Jiang, H.; Chen, Y.K. Comparison of U-Net and OASRN neural network for microwave imaging. J. Electromagn. Waves Appl. 2022, 37, 93–109. [Google Scholar] [CrossRef]
- Dispirito, A.; Li, D.; Vu, T.; Chen, M.; Zhang, D.; Luo, J.; Horstmeyer, R.; Yao, J. Reconstructing Undersampled Photoacoustic Microscopy Images Using Deep Learning. IEEE Trans. Med. Imaging 2020, 40, 562–570. [Google Scholar] [CrossRef]
- Kim, J.S. Improved image resolution during zooming in ultrasound image using deep learning technique. In Proceedings of the IEEE International Ultrasonics Symposium, IUS 2020, Las Vegas, NV, USA, 7–11 September 2020. [Google Scholar] [CrossRef]
- Chanumolu, R.; Alla, L.; Chirala, P.; Chennampalli, N.C.; Kolla, B.P. Multimodal Medical Imaging Using Modern Deep Learning Approaches. In Proceedings of the IEEE VLSI DCS 2022: 3rd IEEE Conference on VLSI Device, Circuit and System 2022, Kolkata, India, 26–27 February 2022; pp. 184–187. [Google Scholar] [CrossRef]
- Ruiz, Y.; Cavagnaro, M.; Crocco, L. An Effective Framework for Deep-Learning-Enhanced Quantitative Microwave Imaging and Its Potential for Medical Applications. Sensors 2023, 23, 643. [Google Scholar] [CrossRef]
- Su, T.; Ozdemir, C.; Ling, H. On extracting the radiation center representation of antenna radiation patterns on a complex platform. Microw. Opt. Technol. Lett. 2000, 26, 4–7. [Google Scholar] [CrossRef]
- Ozdemir, C. Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 2012; ISBN 9780470284841. [Google Scholar]
- Ortega-Palacios, R.; Leija, L.; Vera, A.; Cepeda, M.F.J. Measurement of Breast—Tumor Phantom Dielectric Properties for Mi-crowave Breast Cancer Treatment Evaluation. In Proceedings of the Program and Abstract Book—2010 7th International Conference on Electrical Engineering, Computing Science and Automatic Control, CCE 2010, Tuxtla Gutierrez, Mexico, 8–10 September 2010; pp. 216–219. [Google Scholar]
- Wu, J. Introduction to Convolutional Neural Networks; National Key Lab Novel Software Technology, Nanjing University: Nanjing, China, 2017. [Google Scholar]









| Parameter | Value |
|---|---|
| Start Frequency (GHz) | 1 |
| Stop Frequency (GHz) | 10 |
| Frequency Count | 301 |
| Skin Radius (cm) | 7 |
| Gap Between Skin and Antenna (cm) | 2 |
| Number of Tumor Scatterers | 1–3 |
| Radius Range of Tumor Scatterers (cm) | 0.2–0.9 |
| Rotation Angle Increment (°) | 4 |
| Layer | Output Shape | Number of Parameters |
|---|---|---|
| Convolution 2D | (299, 89, 32) | 288 |
| Batch Normalization | (299, 89, 32) | 128 |
| Convolution 2D | (297, 86, 32) | 9216 |
| Batch Normalization | (297, 86, 32) | 128 |
| Maximum Pooling 2D | (99, 28, 32) | - |
| Convolution 2D | (97, 26, 64) | 18,432 |
| Batch Normalization | (97, 26, 64) | 256 |
| Convolution 2D | (95, 24, 64) | 36,864 |
| Batch Normalization | (95, 24, 64) | 256 |
| Maximum Pooling 2D | (31, 8, 64) | - |
| Convolution 2D | (29, 6, 128) | 73,728 |
| Batch Normalization | (29, 6, 128) | 512 |
| Convolution 2D | (27, 4, 128) | 147,456 |
| Batch Normalization | (27, 4, 128) | 512 |
| Convolution 2D | (25, 2, 128) | 147,456 |
| Batch Normalization | (25, 2, 128) | 512 |
| Flatten | 6400 | - |
| Fully Connected #1 | 2048 | 13,107,200 |
| Batch Normalization | 2048 | 8192 |
| Fully Connected #2 | 2048 | 4,196,352 |
| Fully Connected #3 | 16,384 | 33,570,816 |
| Parameters | RV-DNN | RV-CNN | RV-MWINet | CV-MWI-Net | |||||
|---|---|---|---|---|---|---|---|---|---|
| MSE | SSIM | MSE | SSIM | ACC | SIM | ACC | SSIM | ||
| 10-fold Cross-Validation | Fold #1 | 97.784 ± 45.153 | 0.918 ± 0.031 | 62.731 ± 33.540 | 0.897 ± 0.051 | 0.999 ± 0.001 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 |
| Fold #2 | 100.917 ± 47.951 | 0.925 ± 0.029 | 75.192 ± 42.959 | 0.893 ± 0.052 | 0.988 ± 0.005 | 0.998 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #3 | 102.443 ± 48.706 | 0.922 ± 0.030 | 65.007 ± 41.774 | 0.888 ± 0.054 | 0.998 ± 0.002 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #4 | 92.100 ± 43.208 | 0.925 ± 0.029 | 74.251 ± 48.942 | 0.886 ± 0.053 | 0.994 ± 0.004 | 0.999 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #5 | 101.076 ± 47.054 | 0.924 ± 0.031 | 61.865 ± 38.730 | 0.887 ± 0.054 | 0.998 ±0.001 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #6 | 92.854 ± 41.111 | 0.924 ± 0.031 | 79.385 ± 47.123 | 0.890 ± 0.058 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #7 | 98.932 ± 46.810 | 0.924 ± 0.030 | 65.930 ± 49.868 | 0.891 ± 0.056 | 0.999 ± 0.001 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #8 | 98.564 ± 45.503 | 0.925 ± 0.030 | 61.795 ± 39.846 | 0.890 ± 0.052 | 0.999 ± 0.001 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #9 | 102.653 ± 49.134 | 0.921 ± 0.031 | 61.114 ± 43.199 | 0.892 ± 0.053 | 0.994 ± 0.004 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Fold #10 | 93.116 ± 43.122 | 0.927 ± 0.030 | 71.750 ± 58.493 | 0.888 ± 0.057 | 0.996 ± 0.003 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Average | 98.044 ± 45.775 | 0.924 ± 0.030 | 67.902 ± 44.447 | 0.890 ± 0.054 | 0.997 ± 0.002 | 1.000 ± 0.000 | 1.000 ± 0.000 | 1.000 ± 0.000 | |
| Parameters | RV-DNN | RV-CNN | RV-MWINet | CV-MWINet | |||||
|---|---|---|---|---|---|---|---|---|---|
| MSE | SSIM | MSE | SSIM | ACC | SSIM | ACC | SSIM | ||
| 10-fold Cross-Validation | Fold #1 | 185.183 ± 124.598 | 0.914 ± 0.030 | 157.868 ± 108.600 | 0.915 ± 0.030 | 0.995 ± 0.004 | 1.000 ± 0.000 | 0.992 ± 0.005 | 0.999 ± 0.001 |
| Fold #2 | 207.658 ± 136.553 | 0.912 ± 0.033 | 162.565 ± 107.290 | 0.910 ± 0.033 | 0.987 ± 0.005 | 0.998 ± 0.000 | 0.993 ± 0.005 | 0.999 ± 0.001 | |
| Fold #3 | 195.671 ± 132.356 | 0.911 ± 0.032 | 156.713 ± 109.397 | 0.910 ± 0.027 | 0.993 ± 0.004 | 0.999 ± 0.001 | 0.993 ± 0.004 | 0.999 ± 0.001 | |
| Fold #4 | 200.928 ± 137.845 | 0.919 ± 0.027 | 163.380 ± 109.841 | 0.906 ± 0.032 | 0.992 ± 0.005 | 0.999 ± 0.001 | 0.993 ± 0.004 | 0.999 ± 0.001 | |
| Fold #5 | 181.389 ± 119.239 | 0.916 ± 0.031 | 152.357 ± 107.160 | 0.915 ± 0.028 | 0.993 ± 0.004 | 0.999 ± 0.000 | 0.993 ± 0.005 | 0.999 ± 0.001 | |
| Fold #6 | 216.705 ± 140.831 | 0.912 ± 0.030 | 178.969 ± 122.073 | 0.909 ± 0.033 | 0.993 ± 0.005 | 0.999 ± 0.001 | 0.993 ± 0.005 | 0.999 ± 0.001 | |
| Fold #7 | 202.940 ± 135.807 | 0.915 ± 0.029 | 168.076 ± 117.404 | 0.910 ± 0.032 | 0.993 ± 0.004 | 0.999 ± 0.001 | 0.994 ± 0.004 | 0.999 ± 0.000 | |
| Fold #8 | 187.140 ± 126.529 | 0.914 ± 0.024 | 150.096 ± 112.963 | 0.911 ± 0.030 | 0.995 ± 0.004 | 1.000 ± 0.000 | 0.994 ± 0.004 | 0.999 ± 0.000 | |
| Fold #9 | 198.709 ± 135.104 | 0.914 ± 0.028 | 164.587 ± 112.925 | 0.913 ± 0.028 | 0.991 ± 0.006 | 0.999 ± 0.001 | 0.992 ± 0.005 | 0.999 ± 0.001 | |
| Fold #10 | 197.682 ± 123.131 | 0.916 ± 0.029 | 166.285 ± 111.977 | 0.910 ± 0.029 | 0.993 ± 0.004 | 0.999 ± 0.001 | 0.993 ± 0.005 | 0.999 ± 0.001 | |
| Average | 197.401 ± 131.199 | 0.914 ± 0.030 | 162.089 ± 111.963 | 0.911 ± 0.030 | 0.993 ± 0.005 | 0.999 ± 0.001 | 0.993 ± 0.004 | 0.999 ± 0.001 | |
| Scenarios | Materials | Distance from the Center (cm) |
|---|---|---|
| #1 | Metal screw in fine sand | 0 |
| #2 | 2 | |
| #3 | 4 | |
| #4 | 6 | |
| #5 | Tumor phantom in healthy phantom | 0 |
| #6 | 2 | |
| #7 | 4 | |
| #8 | 5.5 |
| Metrics/Models | Train Data | Test Data | Avgs. ± Stds. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 Tumor | 2 Tumor | 3 Tumor | 1 Tumor | 2 Tumor | 3 Tumor | All Train Set | All Test Set | ||
| PSNR (dB) | MP-Based Algorithm | 25.87656 | 24.14579 | 22.83756 | 19.78088 | 23.12839 | 22.51522 | – | – |
| RV-DNN Model | 23.0948 | 22.02725 | 17.7845 | 23.76579 | 18.924 | 21.27754 | 20.37510 ± 2.89746 | 20.52958 ± 2.93180 | |
| RV-CNN Model | 23.62187 | 22.1329 | 19.95046 | 21.513 | 20.54329 | 19.71726 | 21.22355 ± 2.27647 | 21.38717 ± 2.62633 | |
| RV-MWINet Model | 42.35213 | 34.39235 | 34.32751 | 37.00931 | 35.94595 | 34.00697 | 34.68058 ± 3.24353 | 34.57853 ± 3.53797 | |
| CV-MWINet Model | 217.02188 | 207.71069 | 209.097967 | 210.92949 | 207.84857 | 206.52970 | 209.09540 ± 3.56411 | 209.46525 ± 3.59434 | |
| UQI | MP-based Algorithm | 0.914 | 0.92553 | 0.90138 | 0.82 | 0.91924 | 0.89136 | – | – |
| RV-DNN Model | 0.74023 | 0.73941 | 0.71659 | 0.74554 | 0.72334 | 0.73738 | 0.72929 ± 0.01239 | 0.72974 ± 0.1239 | |
| RV-CNN Model | 0.74212 | 0.73895 | 0.72828 | 0.73449 | 0.73098 | 0.72887 | 0.73380 ± 0.00854 | 0.73426 ± 0.00957 | |
| RV-MWINet Model | 0.9995 | 0.99792 | 0.99783 | 0.9986 | 0.99842 | 0.99758 | 0.99759 ± 0.00172 | 0.99750 ± 0.00211 | |
| CV-MWINet Model | 0.99118 | 0.967916 | 0.966361 | 0.98312 | 0.96825 | 0.95368 | 0.96754 ± 0.01632 | 0.96995 ± 0.01479 | |
| SSIM | MP- Based Algorithm | 0.82675 | 0.84876 | 0.80792 | 0.67093 | 0.83687 | 0.78471 | – | – |
| RV-DNN Model | 0.75538 | 0.74624 | 0.7142 | 0.75802 | 0.7257 | 0.73583 | 0.73705 ± 0.02006 | 0.73754 ± 0.01913 | |
| RV-CNN Model | 0.75643 | 0.72977 | 0.725 | 0.74177 | 0.7018 | 0.72572 | 0.73220 ± 0.01953 | 0.73457 ± 0.02198 | |
| RV-MWINet Model | 0.99878 | 0.99291 | 0.99312 | 0.99642 | 0.99473 | 0.99159 | 0.99295 ± 0.00396 | 0.99302 ± 0.00419 | |
| CV-MWINet Model | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 ± 0.00000 | 1.00000 ± 0.00000 | |
| Mesh Points | 9061 Points | 16,105 Points | |
|---|---|---|---|
| Train Data | 1 Tumor | 189.96657 s | 385.11506 s |
| 2 Tumor | 186.09587 s | 391.25924 s | |
| 3 Tumor | 184.26689 s | 337.86427 s | |
| Test Data | 1 Tumor | 180.65272 s | 386.98390 s |
| 2 Tumor | 185.19212 s | 370.29391 s | |
| 3 Tumor | 184.13824 s | 376.40420 s | |
| Avgs. ± Stds. | 185.05210 ± 3.03536 s | 374.6534 ± 19.55980 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bicer, M.B. Radar-Based Microwave Breast Imaging Using Neurocomputational Models. Diagnostics 2023, 13, 930. https://doi.org/10.3390/diagnostics13050930
Bicer MB. Radar-Based Microwave Breast Imaging Using Neurocomputational Models. Diagnostics. 2023; 13(5):930. https://doi.org/10.3390/diagnostics13050930
Chicago/Turabian StyleBicer, Mustafa Berkan. 2023. "Radar-Based Microwave Breast Imaging Using Neurocomputational Models" Diagnostics 13, no. 5: 930. https://doi.org/10.3390/diagnostics13050930
APA StyleBicer, M. B. (2023). Radar-Based Microwave Breast Imaging Using Neurocomputational Models. Diagnostics, 13(5), 930. https://doi.org/10.3390/diagnostics13050930





