1. Introduction
Blood is a crucial fluid in the human body that is essential for life. Human blood is made up of plasma and blood cells. Plasma is the yellowish liquid component of blood that is largely water and accounts for
of blood volume [
1]. The blood also includes proteins, carbohydrates, minerals, hormones, carbon dioxide, and blood cells. Red blood cells (RBCs), white blood cells (WBCs), and platelets (thrombocytes) are the three different types of cellular components found in the blood, each distinguished by their color, texture, and appearance. RBCs, also known as erythrocytes, carry hemoglobin, an iron-containing protein that aids in the delivery of oxygen from the lungs to the tissues. WBCs, also known as leukocytes, are an essential component of the human immune system, assisting the body in fighting infectious diseases and foreign substances [
2,
3].
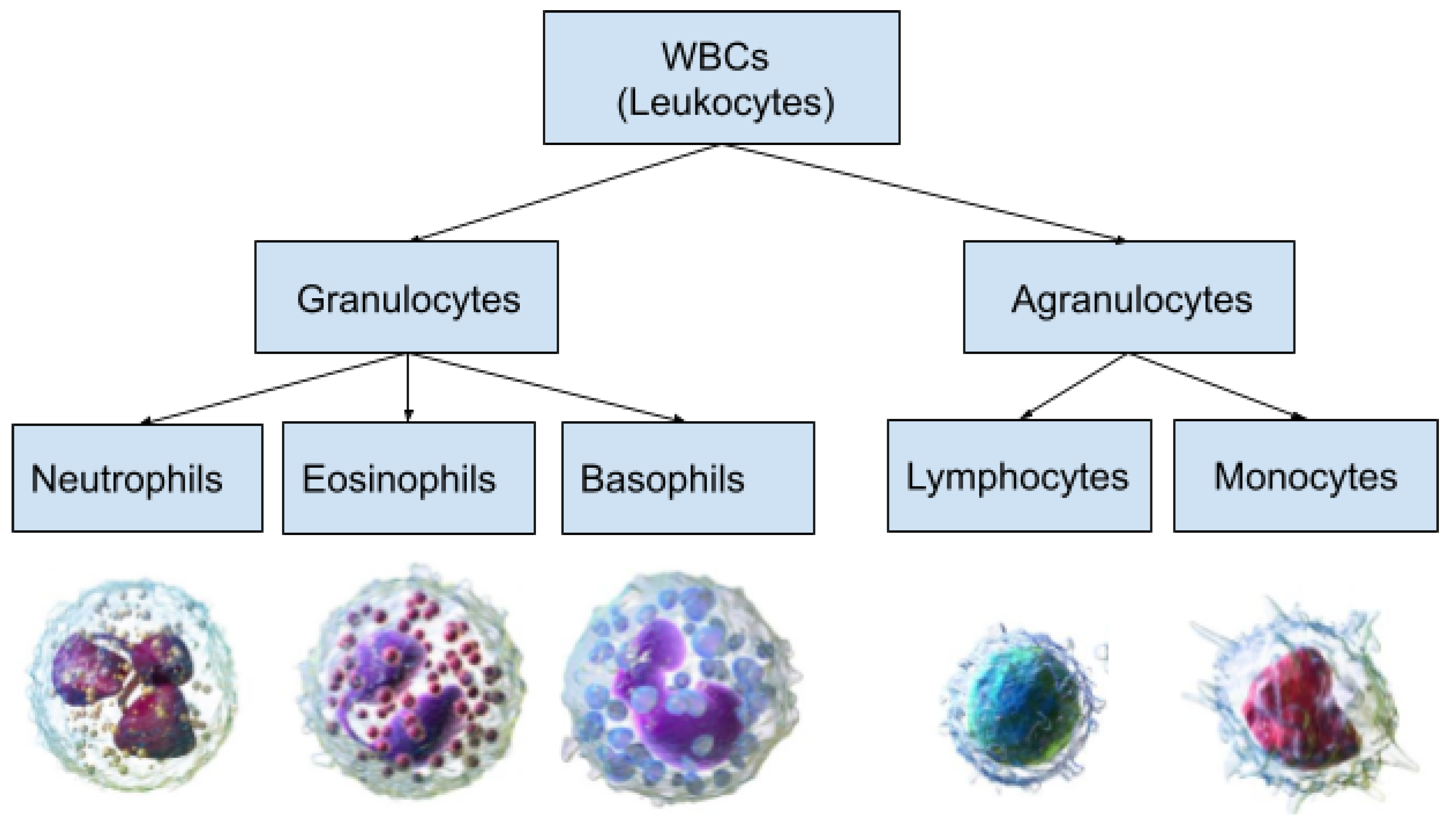
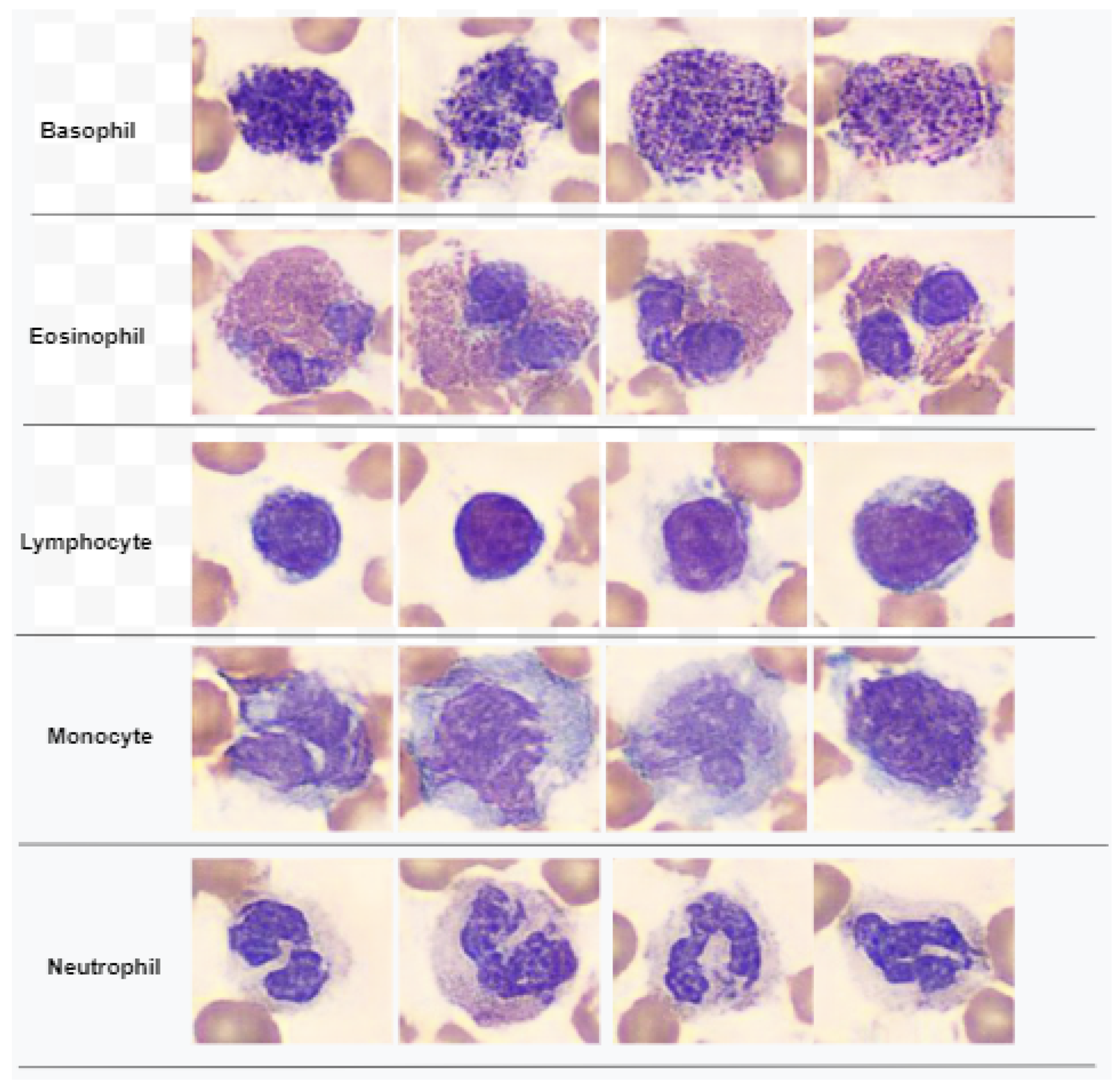
Figure 1 demonstrates a classification of WBCs on the basis of their structure. WBCs are primarily of two types, i.e., granulocytes and agranulocytes. The granulocytes have their origin in the bone marrow and are present within the cytoplasm in the form of granules of protein. There are three types of granulocyte cells, namely basophils, eosinophils, and neutrophils. Agranulocytes, which are defined as cells without granules in their cytoplasm, are further divided into two types, i.e., lymphocytes and monocytes [
4]. Each type of cell has a unique role in the immune system of the body. For example, neutrophils act as scavengers that surround and destroy bacteria and fungi present in the body. Eosinophils play a role in the general immune and inflammatory responses of the body. An increased level of basophils results in a blood disorder after an allergic reaction. Monocytes fight against infections, remove dead or damaged tissues, and kill cancerous cells; lymphocytes combat bacteria, viruses, and other cells that pose a threat to the body’s ability to function [
5]. A detailed analysis of WBCs is very important to assess the overall condition of the human immune system. In particular, WBC analysis is crucial in the diagnosis of leukemia, a type of blood cancer that occurs due to the excessive production of malignant WBCs in the bone marrow. Leukemia diagnosis is performed by one of three main clinical tests, i.e., physical test, complete blood count (CBC) test, and bone marrow test. The first step of CBC is to determine different types of WBCs from the blood samples. This task is mainly performed by hematologists through the visual examination of microscopic images of blood smears. This manual method is labor-intensive, time-consuming, and prone to inaccuracy due to judgment errors influenced by several external factors.
With the recent advancement in digital image processing technology, the automated classification of WBCs using computer vision techniques has attracted significant research interest. However, due to morphological overlap between different subclasses and their structural irregularities, the machine learning-based classification and localization of WBCs is challenging. Deep learning with convolutional neural networks (CNNs) is the most promising method for classification and detection tasks in the field of contemporary medical imaging [
6,
7]. Despite the fact that CNNs perform best on large datasets, training them takes a lot of data and computational power. The dataset is frequently small and may not be sufficient to train a CNN from scratch. In such a case, transfer learning is frequently used to maximize the effectiveness of CNNs while also decreasing the computational costs [
8]. In this approach, the CNN is initially pre-trained on a large dataset consisting of a diverse range of classes and then applied to a specific task [
9]. There are various pre-trained neural networks that have won international contests, including VGGNet [
10], Resnet [
11], Darknet [
12], Densenet [
13], Mobilenet [
14], Inception [
15], Xception, [
16] etc. Through their capacity for self-learning, these models are able to extract a rich set of features from images that contain substantial semantic information. This helps to achieve a significant level of accuracy for a variety of image classification scenarios. In modern deep learning applications, feature selection is a crucial step which reduces the difficulty of model learning by removing irrelevant or redundant features. The present research is focused on achieving a high level of accuracy with a smaller feature set to reduce the computation costs and memory requirements of expert systems.
The existing works on WBC classification are broadly classified into two categories, i.e., (a) classical methods and (b) deep learning methods. The classical methods consist of approaches which propose efficient preprocessing techniques to extract strong features from WBC images and classify them using baseline classifiers. Some remarkable works in this domain are discussed as follows. In [
17], the authors proposed a method which selects the eigenvectors from color images of blood cells based on the minimization of similarities. The Bayesian classifier is then used to classify the eigen cells on the basis of density and color information. In [
18], Fuzzy C-means clustering is applied to separate the nucleus and cytoplasm of leukocytes. Then, various geometric, color, and statistical properties are extracted and classified by support vector machines (SVMs). In [
19], an image segmentation method is proposed based on mean-shift clustering and boundary removal rules with a gradient vector flow. An ensemble of features is extracted from the segmented nucleus and cytoplasm, which is then classified using a random forest algorithm. In [
20], the authors tested the performance of six different machine learning algorithms on 35 different geometric and statistical features. The multinomial logistic regression algorithm outperformed other methods. A stepwise linear discriminant analysis method is proposed in [
21], which extracts specific features from blood structure images and classifies them using reversion values such as partial F values. In [
22], the authors presented a WBC cancer detection method which combines various morphological, clustering, and image pre-processing steps with random forest classifier. The suggested method uses a decision tree learning method, which uses predictors at each node to make better decisions, in order to categorize various types of cancer.
The second category of works is based on deep learning approaches for WBC classification. The works in this category primarily employ transfer learning of a pretrained deep neural network for feature extraction or classification. Some important works are discussed as follows. In [
23], the authors proposed a deep learning method that uses the DenseNet121 [
13] model to classify WBC subtypes. The model is optimized with the preprocessing techniques of normalization and data augmentation applied to a Kaggle dataset. The work in [
24] first applies a thresholding-based segmentation on the WBC images. Feature extraction from segmented images is performed using VGG16 CNN [
10] model learning. The extracted feature vectors are classified using the K-nearest neighbor (KNN) algorithm. In [
25], the authors investigated generative adversarial networks (GANs) for data augmentation and employed the DenseNet169 [
13] network for WBC classification. In [
26], the authors applied Gaussian and median filtering before training the images using multiple deep neural networks. The authors in [
27] applied a you-only-look-once (YOLO) algorithm for the detection of blood cells from a smear images. In [
28], two techniques are proposed for blood cell identification, namely single-shot multibox detector and an incrementally improved version of YOLO.
Although modern approaches based on transfer learning on deep CNN models achieve a decent level of accuracy for a variety of classification tasks, they all share the use of a large number of features extracted from deep neural networks. This suffers from high computational cost and memory requirements for practical deployment. In most biomedical scenarios, many of these deep features are redundant or contain zeros. Effective dimensionality reduction, or choosing only powerful, discriminant features, increases classifier accuracy while decreasing computational time and expense. WBC classification using deep feature selection is an emerging research area. Few works have reported population-based meta-heuristics for deep feature selection. The authors of [
29] have proposed a leukemia detection system in which various features, such as color, texture, shape, and hybrid features, are first extracted from WBC images and then an optimization algorithm inspired by social spiders is used to select the most useful features. In [
30], a leukemia detection approach is proposed which combines deep feature extraction using VGGNet and a statistically enhanced salp swarm algorithm for feature selection. Furthermore, the classification of reduced feature vectors was performed using a baseline classifier. The work in [
31] proposes a self-designed neural network named W-Net to classify five subtypes of WBCs. The authors also generated a synthetic WBC dataset using a generative adversarial network (GAN).
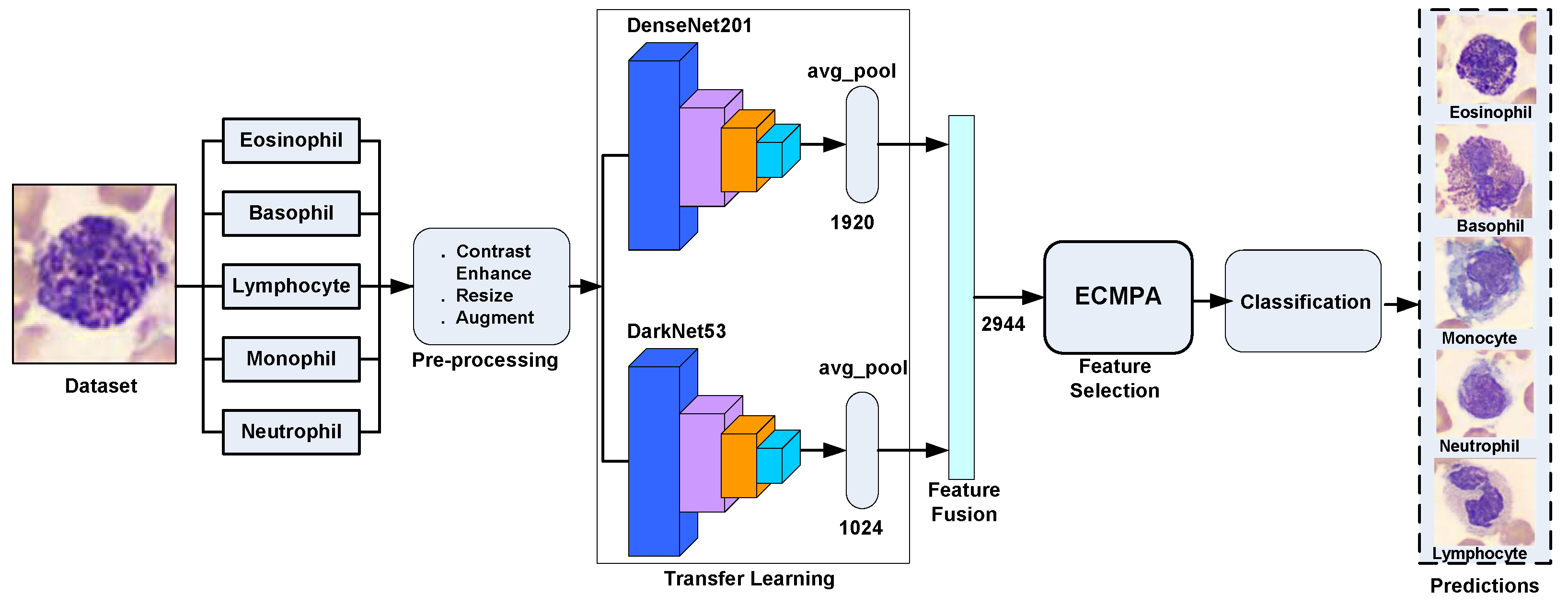
In this study, we have proposed a hybrid approach for WBCs classification. The proposed approach first creates an ensemble of deep features extracted by applying transfer learning of multiple deep CNNs on WBC images and then performs feature selection using an entropy-controlled nature-inspired algorithm. The main contributions of this work can be summarized in the following steps.
Using a synthetic, real-world, large-scale dataset of five WBC types, transfer learning is performed using two deep CNNs, namely Darknet53 and Densenet201, followed by their feature fusion;
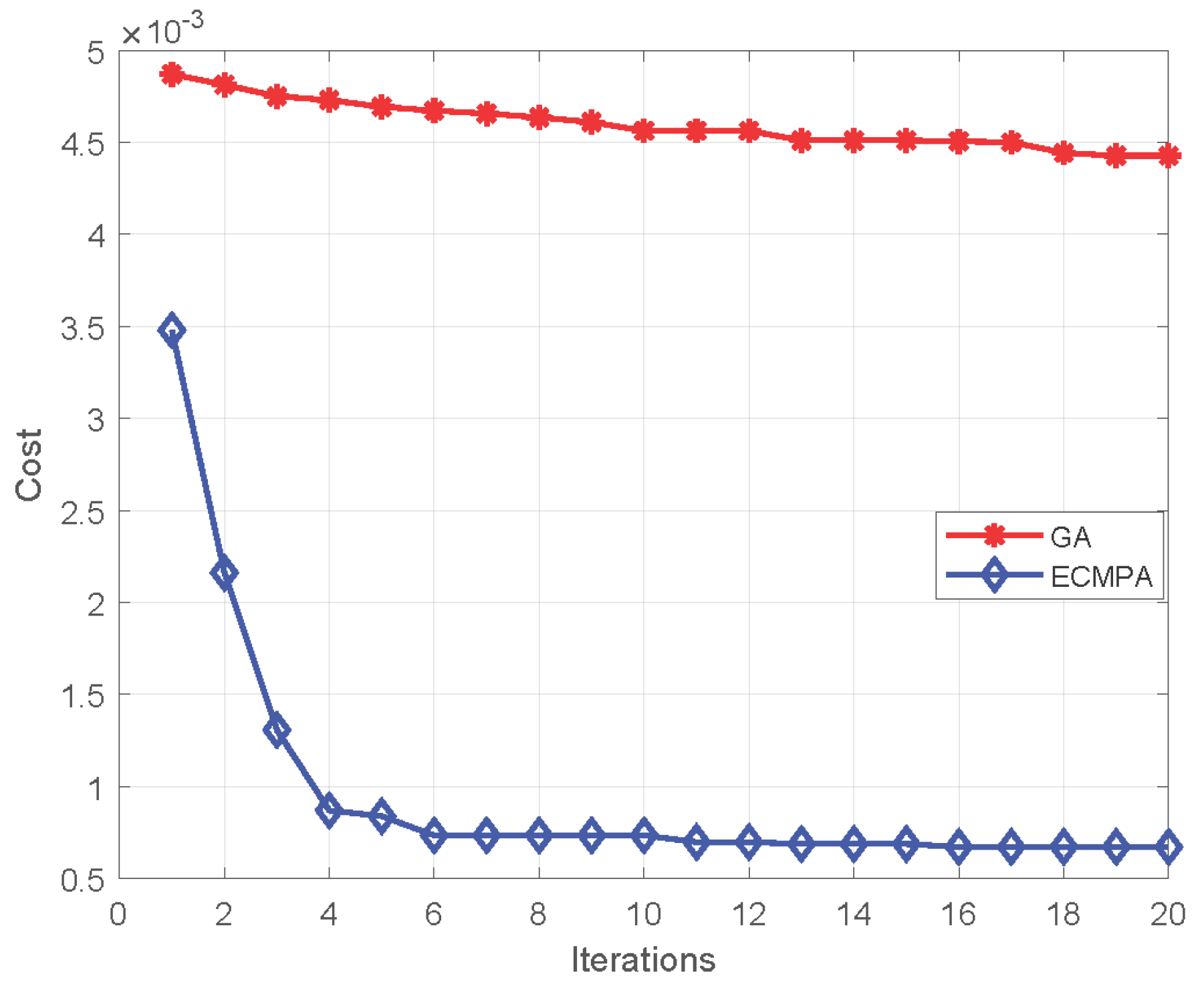
For feature selection, a nature-inspired meta-heuristic named entropy-controlled marine predators algorithm (ECMPA) is proposed. The proposed algorithm effectively selects only the most dominant features;
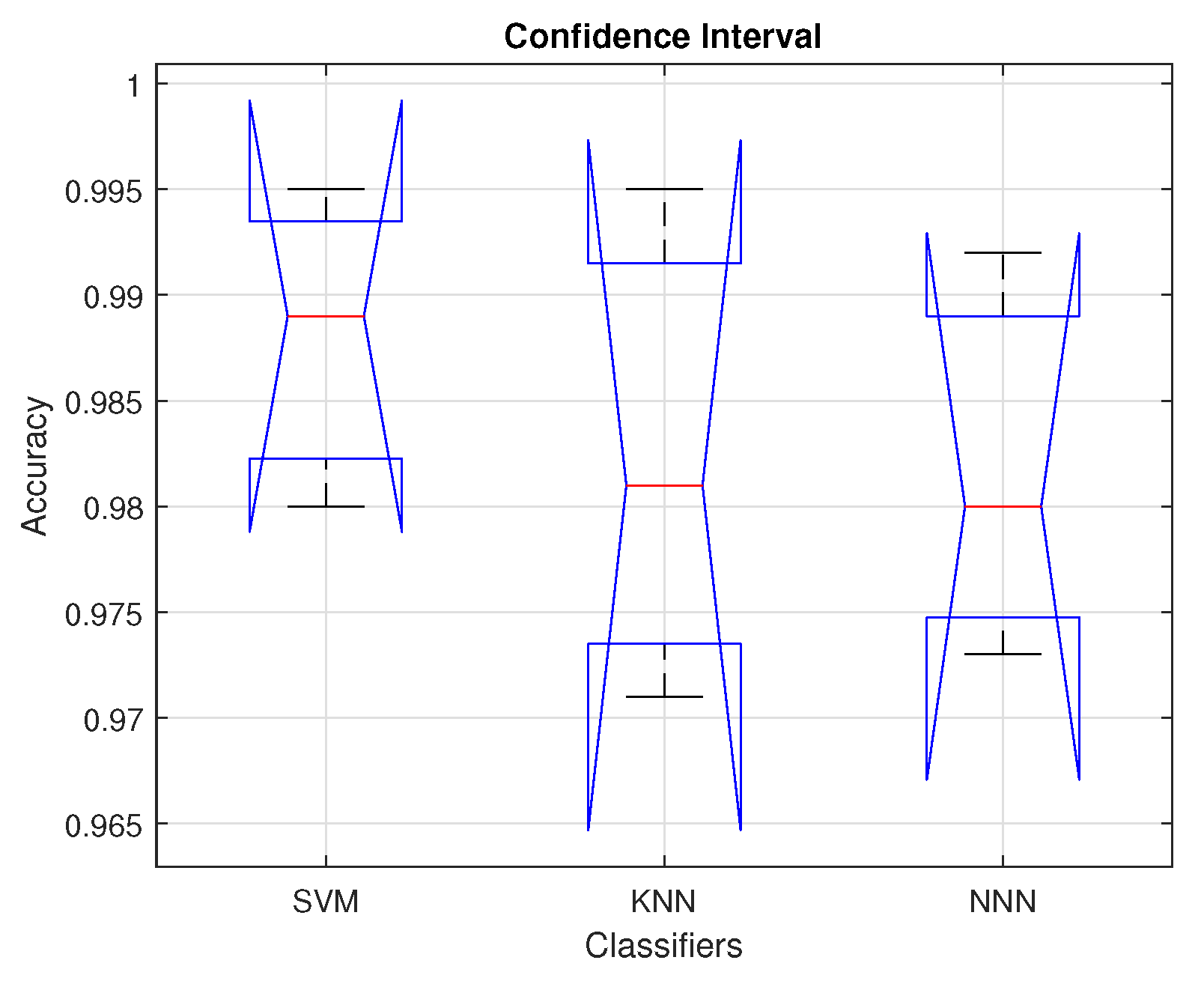
The reduced feature set is classified using various baseline classifiers with multiple kernel settings;
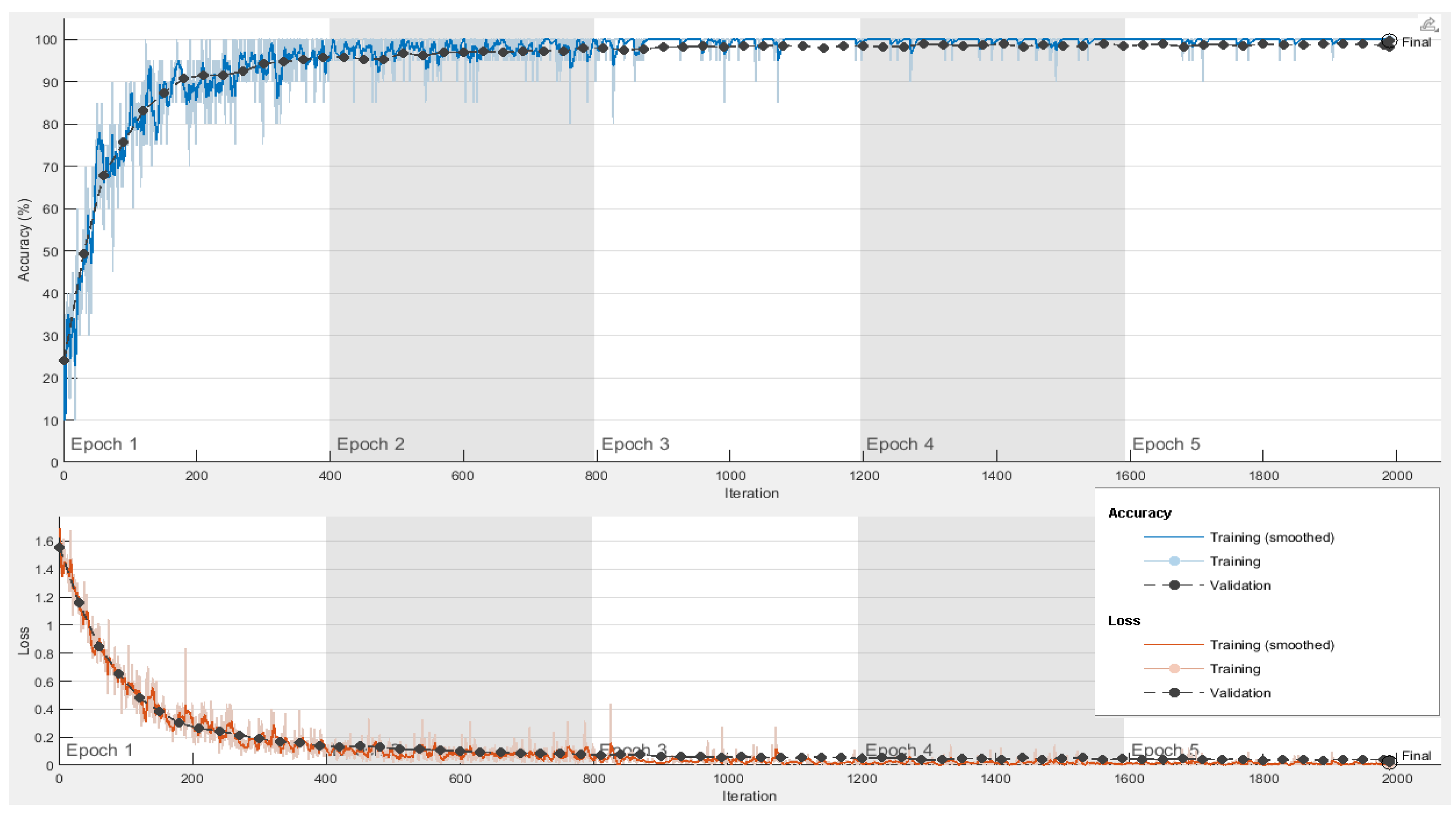
The proposed feature selection algorithm demonstrates a high accuracy with significant reduction in feature size. The algorithm also achieves a better convergence rate as compared to classical population-based selection methods.
The main focus of our manuscript is to present a novel method of deep-feature selection using an entropy-controlled population-based algorithm and show its effectiveness in the domain of WBCs classification for leukemia detection. Since the definition of appropriate image features is a very difficult task due to the morphological similarity of images and subject variability, WBC classification is a pertinent design case for such an approach. The rest of this paper is organized as follows.
Section 2 discusses all steps of the proposed WBC classification pipeline,
Section 3 presents the results and analysis, and
Section 4 concludes the paper.