Mammographic Breast Density Model Using Semi-Supervised Learning Reduces Inter-/Intra-Reader Variability
Abstract
:1. Introduction
2. Materials and Methods
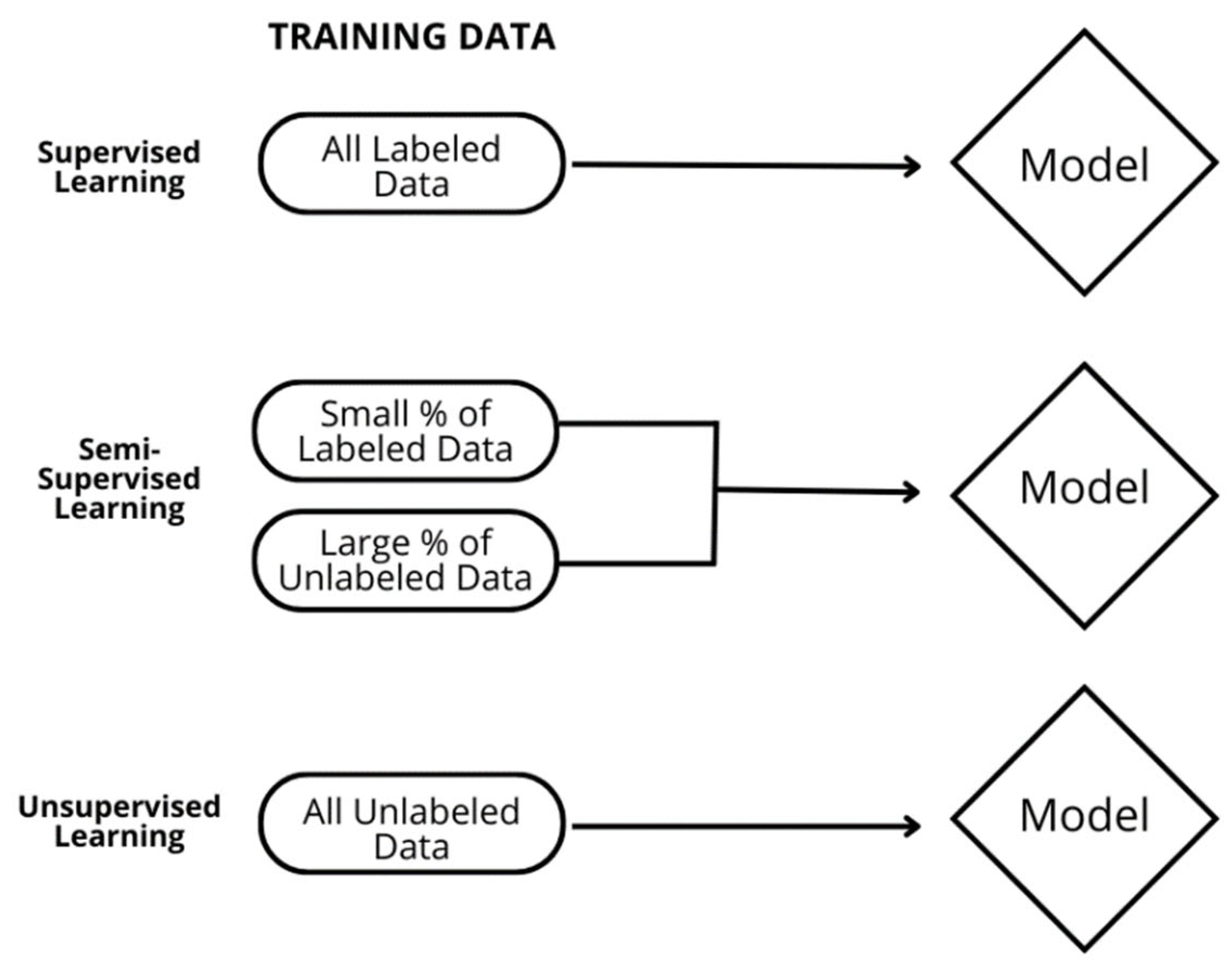
2.1. Model Description
2.2. Reader Study Data Selection
- Exams with less than 4 views;
- Images with non-standard images (where standard is defined as CC and MLO);
- Images with implants (implant-displaced images were not excluded);
- Mastectomy;
- Images without corresponding ipsilateral CC or MLO view.
2.3. Reader Study Design
2.4. Reader Qualification
2.5. Statistical Analysis
- Inter-reader agreement for the unaided session is the average reader pairwise κ when not aided by the DL model:
- Inter-reader agreement for the aided session is the average reader pairwise κ when aided by the DL model:
- Intra-reader agreement for the unaided session is the average reader to reader themselves κ when not aided by the DL model:
- Intra-reader agreement for the aided session is the average reader to reader themselves κ when aided by the DL model:
2.5.1. DL Model Standalone Performance Testing
2.5.2. Inter-Reader Variability Testing
2.5.3. Intra-Reader Variability Testing
2.5.4. Reading Time Testing
3. Results
3.1. DL Model Standalone Performance Testing
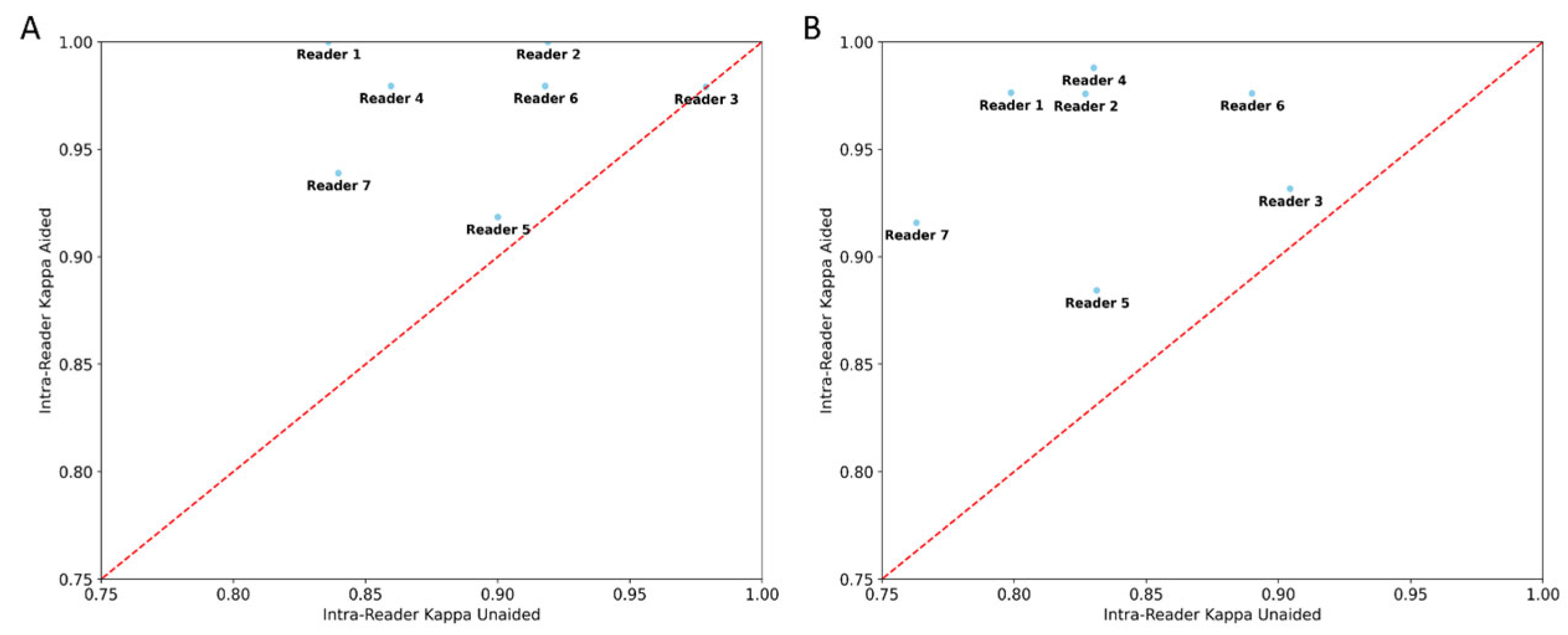
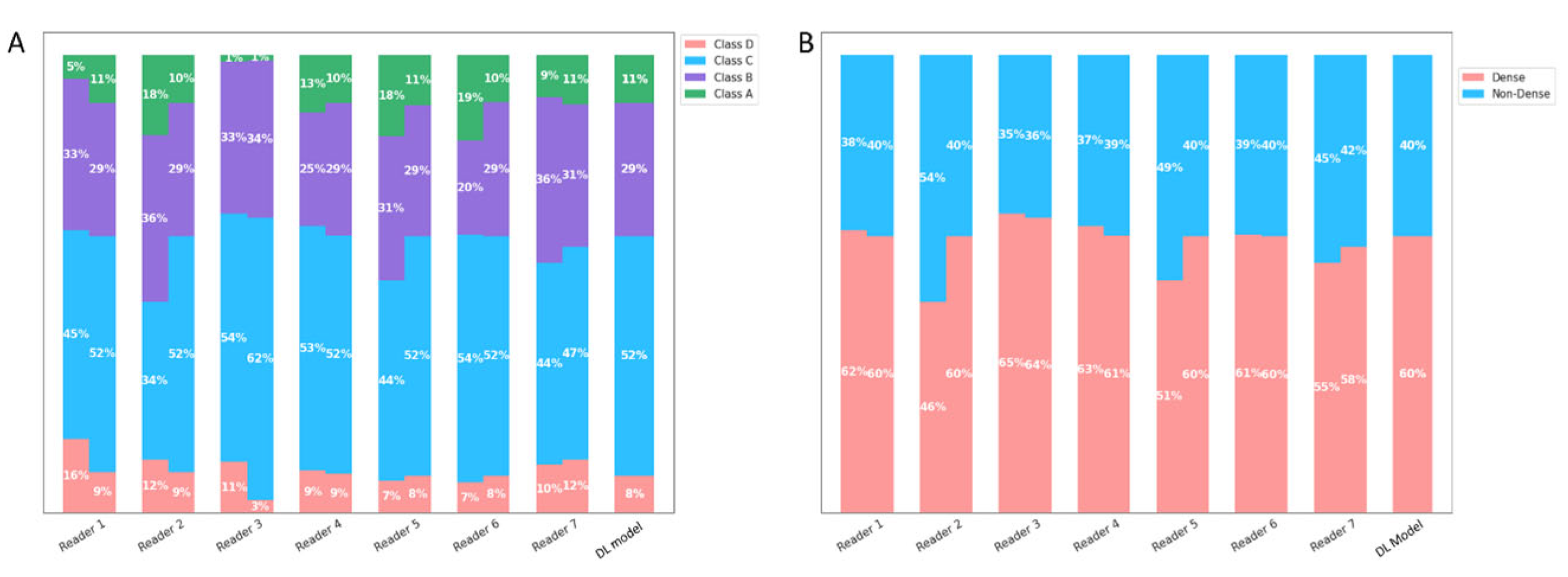
3.2. Inter-/Intra-Reader Variability Testing
3.3. Reading Time Testing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mammograms-NCI. Available online: https://www.cancer.gov/types/breast/mammograms-fact-sheet (accessed on 29 June 2023).
- Boyd, N.F.; Guo, H.; Martin, L.J.; Sun, L.; Stone, J.; Fishell, E.; Jong, R.A.; Hislop, G.; Chiarelli, A.; Minkin, S.; et al. Mammographic density and the risk and detection of breast cancer. New Engl. J. Med. 2007, 356, 227–236. [Google Scholar] [CrossRef]
- Warwick, J.; Birke, H.; Stone, J.; Warren, R.M.; Pinney, E.; Brentnall, A.R.; Duffy, S.W.; Howell, A.; Cuzick, J. Mammographic breast density refines Tyrer-Cuzick estimates of breast cancer risk in high-risk women: Findings from the placebo arm of the International Breast Cancer Intervention Study I. Breast Cancer Res. 2014, 16, 451. [Google Scholar] [CrossRef] [PubMed]
- Dense Breast Tissue | Breast Density and Mammogram Reports. Available online: https://www.cancer.org/cancer/types/breast-cancer/screening-tests-and-early-detection/mammograms/breast-density-and-your-mammogram-report.html (accessed on 29 June 2023).
- D’Orsi, C.J.; Sickles, E.A.; Mendelson, E.B.; Morris, E.A. ACR BI-RADS® Atlas; American College of Radiology: Washington, DC, USA, 2013. [Google Scholar]
- Sprague, B.L.; Gangnon, R.E.; Burt, V.; Trentham-Dietz, A.; Hampton, J.M.; Wellman, R.D.; Kerlikowske, K.; Miglioretti, D.L. Prevalence of Mammographically Dense Breasts in the United States. JNCI J. Natl. Cancer Inst. 2014, 106, dju255. [Google Scholar] [CrossRef] [PubMed]
- Portnow, L.H.; Georgian-Smith, D.; Haider, I.; Barrios, M.; Bay, C.P.; Nelson, K.P.; Raza, S. Persistent inter-observer variability of breast density assessment using BI-RADS® 5th edition guidelines. Clin. Imaging 2022, 83, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Eom, H.-J.; Cha, J.H.; Kang, J.-W.; Choi, W.J.; Kim, H.J.; Go, E. Comparison of variability in breast density assessment by BI-RADS category according to the level of experience. Acta Radiol. 2018, 59, 527–532. [Google Scholar] [CrossRef] [PubMed]
- Haas, B.M.; Kalra, V.; Geisel, J.; Raghu, M.; Durand, M.; Philpotts, L.E. Comparison of tomosynthesis plus digital mammography and digital mammography alone for breast cancer screening. Radiology 2013, 269, 694–700. [Google Scholar] [CrossRef] [PubMed]
- Lehman, C.D.; Yala, A.; Schuster, T.; Dontchos, B.; Bahl, M.; Swanson, K.; Barzilay, R. Mammographic Breast Density Assessment Using Deep Learning: Clinical Implementation. Radiology 2019, 290, 52–58. [Google Scholar] [CrossRef] [PubMed]
- Maclin, R.; Opitz, D. Popular Ensemble Methods: An Empirical Study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Wen, Y.; Vicol, P.; Ba, J.; Tran, D.; Grosse, R. Flipout: Efficient Pseudo-Independent Weight Perturbations on Mini-Batches. arXiv 2018. [Google Scholar] [CrossRef]
- Goan, E.; Fookes, C. Bayesian Neural Networks: An Introduction and Survey. arXiv 2020. [Google Scholar] [CrossRef]
- Laine, S.; Aila, T. Temporal Ensembling for Semi-Supervised Learning. arXiv 2017. [Google Scholar] [CrossRef]
- Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep Learning Results. arXiv 2018. [Google Scholar] [CrossRef]
- Zhai, X.; Oliver, A.; Kolesnikov, A.; Beyer, L. S4L: Self-Supervised Semi-Supervised Learning. arXiv 2019. [Google Scholar] [CrossRef]
- ImageNet: A Large-Scale Hierarchical Image Database|IEEE Conference Publication|IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/5206848 (accessed on 29 June 2023).
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. Zagreb 2012, 22, 276–282. [Google Scholar] [CrossRef] [PubMed]
- Mann, R.M.; Athanasiou, A.; Baltzer, P.A.T.; Camps-Herrero, J.; Clauser, P.; Fallenberg, E.M.; Forrai, G.; Fuchsjäger, M.H.; Helbich, T.H.; Killburn-Toppin, F.; et al. Breast cancer screening in women with extremely dense breasts recommendations of the European Society of Breast Imaging (EUSOBI). Eur. Radiol. 2022, 32, 4036–4045. [Google Scholar] [CrossRef] [PubMed]
- Destounis, S.V.; Santacroce, A.; Arieno, A. Update on Breast Density, Risk Estimation, and Supplemental Screening. Am. J. Roentgenol. 2020, 214, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Conant, E.F.; Sprague, B.L.; Kontos, D. Beyond BI-RADS Density: A Call for Quantification in the Breast Imaging Clinic. Radiology 2018, 286, 401–404. [Google Scholar] [CrossRef] [PubMed]
- Sprague, B.L.; Conant, E.F.; Onega, T.; Garcia, M.P.; Beaber, E.F.; Herschorn, S.D.; Lehman, C.D.; Tosteson, A.N.A.; Lacson, R.; Schnall, M.D.; et al. Variation in Mammographic Breast Density Assessments Among Radiologists in Clinical Practice. Ann. Intern. Med. 2016, 165, 457–464. [Google Scholar] [CrossRef]
- Youk, J.H.; Gweon, H.M.; Son, E.J.; Kim, J.-A. Automated Volumetric Breast Density Measurements in the Era of the BI-RADS Fifth Edition: A Comparison with Visual Assessment. AJR Am. J. Roentgenol. 2016, 206, 1056–1062. [Google Scholar] [CrossRef]
- Brandt, K.R.; Scott, C.G.; Ma, L.; Mahmoudzadeh, A.P.; Jensen, M.R.; Whaley, D.H.; Wu, F.F.; Malkov, S.; Hruska, C.B.; Norman, A.D.; et al. Comparison of Clinical and Automated Breast Density Measurements: Implications for Risk Prediction and Supplemental Screening. Radiology 2016, 279, 710–719. [Google Scholar] [CrossRef]
- Lehman, C.D. Artificial Intelligence to Support Independent Assessment of Screening Mammograms-The Time Has Come. JAMA Oncol. 2020, 6, 1588–1589. [Google Scholar] [CrossRef]
- Chang, K.; Beers, A.L.; Brink, L.; Patel, J.B.; Singh, P.; Arun, N.T.; Hoebel, K.V.; Gaw, N.; Shah, M.; Pisano, E.D.; et al. Multi-Institutional Assessment and Crowdsourcing Evaluation of Deep Learning for Automated Classification of Breast Density. J. Am. Coll. Radiol. 2020, 17, 1653–1662. [Google Scholar] [CrossRef]


| Reader | Experience (Years) in Mammography | MQSA and ABR Certified | >75% of Time in Mammography | Average Number of Mammograms/Year |
|---|---|---|---|---|
| 1 | >20 | Y | Y | 2500 |
| 2 | 31 | Y | Y | >10,000 |
| 3 | 9 | Y | Y | 5700 |
| 4 | 6 | Y | N | 560 |
| 5 | 11 | Y | N | 1700 |
| 6 | >20 | Y | Y | 8000 |
| 7 | >20 | Y | Y | 4500 |
| Reader Agreement | Unaided | ||||
|---|---|---|---|---|---|
| Reader 1 | Reader 2 | … | Reader 7 | ||
| Unaided | Reader 1 | … | |||
| Reader 2 | … | ||||
| … | … | … | … | … | |
| Reader 7 | … | ||||
| Reader Agreement | Aided | ||||
| Reader 1 | Reader2 | … | Reader 7 | ||
| Aided | Reader 1 | … | |||
| Reader 2 | … | ||||
| … | … | … | … | … | |
| Reader 7 | … | ||||
| Test | Unaided | Aided | 95% CI | p-Value |
|---|---|---|---|---|
| H1 4 class | 0.70 | 0.88 | (0.16, ∞) | 1.71 × 10−16 |
| H1 Binary | 0.77 | 0.96 | (0.16, ∞) | 6.98 × 10−18 |
| H2 4 class | 0.83 | 0.95 | (0.07, ∞) | 1.03 × 10−3 |
| H2 Binary | 0.89 | 0.97 | (0.04, ∞) | 5.57 × 10−3 |
| Reader | Unaided | Aided | % Change | 95% CI | p-Value |
|---|---|---|---|---|---|
| Reader 1 | 3.60 | 1.72 | −52% | (1.68, 2.07) | 9.37 × 10−69 |
| Reader 2 | 2.00 | 1.724 | −14% | (0.18, 0.37) | 5.94 × 10−8 |
| Reader 3 | 1.64 | 2.04 | 24% | (−0.52, −0.28) | 1.74 × 10−10 |
| Reader 4 | 3.04 | 1.11 | −63% | (1.59, 2.27) | 4.08 × 10−27 |
| Reader 5 | 1.92 | 1.48 | −24% | (0.30, 0.58) | 2.18 × 10−9 |
| Reader 6 | 4.38 | 2.80 | −36% | (1.32, 1.85) | 2.03 × 10−29 |
| Reader 7 | 3.51 | 3.20 | −9% | (−0.03, 0.65) | 7.23 × 10−2 |
| Average | 2.87 | 2.01 | −30% | (0.01, 1.71) | 4.9 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, A.T.; Retson, T.; Wang, J.; Mantey, R.; Chim, C.; Karimabadi, H. Mammographic Breast Density Model Using Semi-Supervised Learning Reduces Inter-/Intra-Reader Variability. Diagnostics 2023, 13, 2694. https://doi.org/10.3390/diagnostics13162694
Watanabe AT, Retson T, Wang J, Mantey R, Chim C, Karimabadi H. Mammographic Breast Density Model Using Semi-Supervised Learning Reduces Inter-/Intra-Reader Variability. Diagnostics. 2023; 13(16):2694. https://doi.org/10.3390/diagnostics13162694
Chicago/Turabian StyleWatanabe, Alyssa T., Tara Retson, Junhao Wang, Richard Mantey, Chiyung Chim, and Homa Karimabadi. 2023. "Mammographic Breast Density Model Using Semi-Supervised Learning Reduces Inter-/Intra-Reader Variability" Diagnostics 13, no. 16: 2694. https://doi.org/10.3390/diagnostics13162694
APA StyleWatanabe, A. T., Retson, T., Wang, J., Mantey, R., Chim, C., & Karimabadi, H. (2023). Mammographic Breast Density Model Using Semi-Supervised Learning Reduces Inter-/Intra-Reader Variability. Diagnostics, 13(16), 2694. https://doi.org/10.3390/diagnostics13162694






