A Radiation-Free Classification Pipeline for Craniosynostosis Using Statistical Shape Modeling
Abstract
:1. Introduction
1.1. Craniosynostosis
1.2. Assessment and Classification of Craniosynostosis Using Statistical Shape Modeling
1.3. Scope of This Work
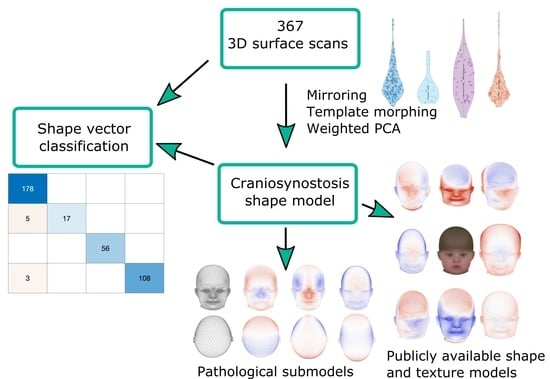
- We present an alternative classification approach for craniosynostosis to distinguish between controls and three different types of craniosynostosis directly on the parameter vector of our ssm built from 3D photogrammetric surface scans. We test five different machine-learning-based classifiers on our database consisting of 367 subjects and achieve state-of-the-art results. To the best of our knowledge, we conducted the largest classification study of craniosynostosis to date.
- We propose the first publicly available ssm of craniosynostosis patients using 3D surface scans, including pathology-specific submodels, texture, and 100 synthetic instances of each class. It is the first publicly available model of children younger than 1.5 years and ssm of craniosynostosis patients including both full head and texture. Our model is compatible with the Liverpool-York head model [24], as it makes use of the same point identifiers for correspondence establishment. This enables combining the texture and shape of both models.
- We demonstrate two applications of our ssm, which can easily be performed with the publicly available model: First, with regard to patient counseling, we apply attribute regression as proposed by [19] to remove the scaphocephaly head shape of a patient. Second, for pathology specific data augmentation, we use a generalized eigenvalue problem to define fixed points on the cranium and maximize changes on face and ears as proposed by [28]. To the best of our knowledge, neither of these applications have been applied to patients using a craniosynostosis shape model before.
2. Materials and Methods
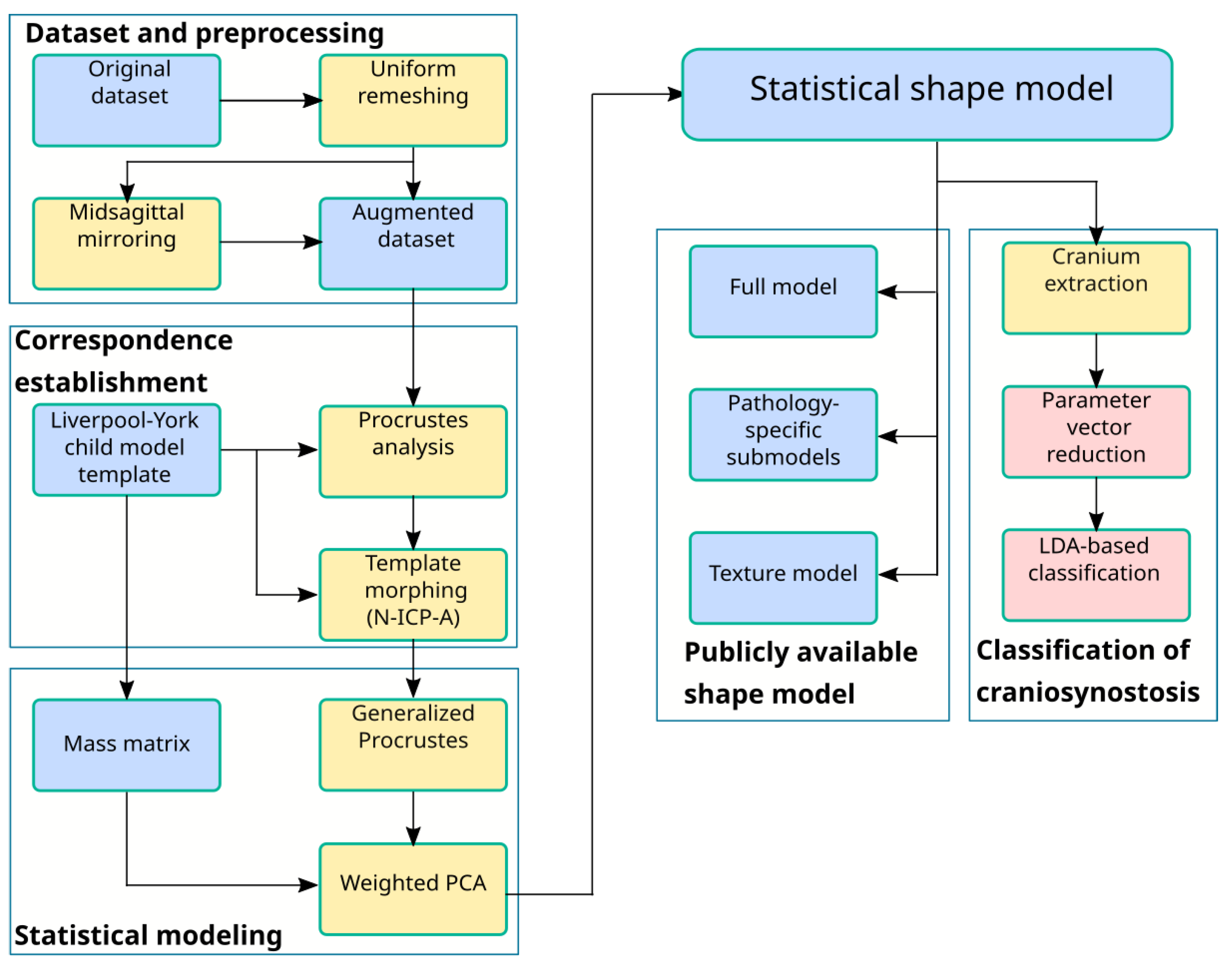
2.1. Dataset and Preprocessing
2.2. Correspondence Establishment
2.3. Statistical Modeling
2.4. Classification of Craniosynostosis
3. Results
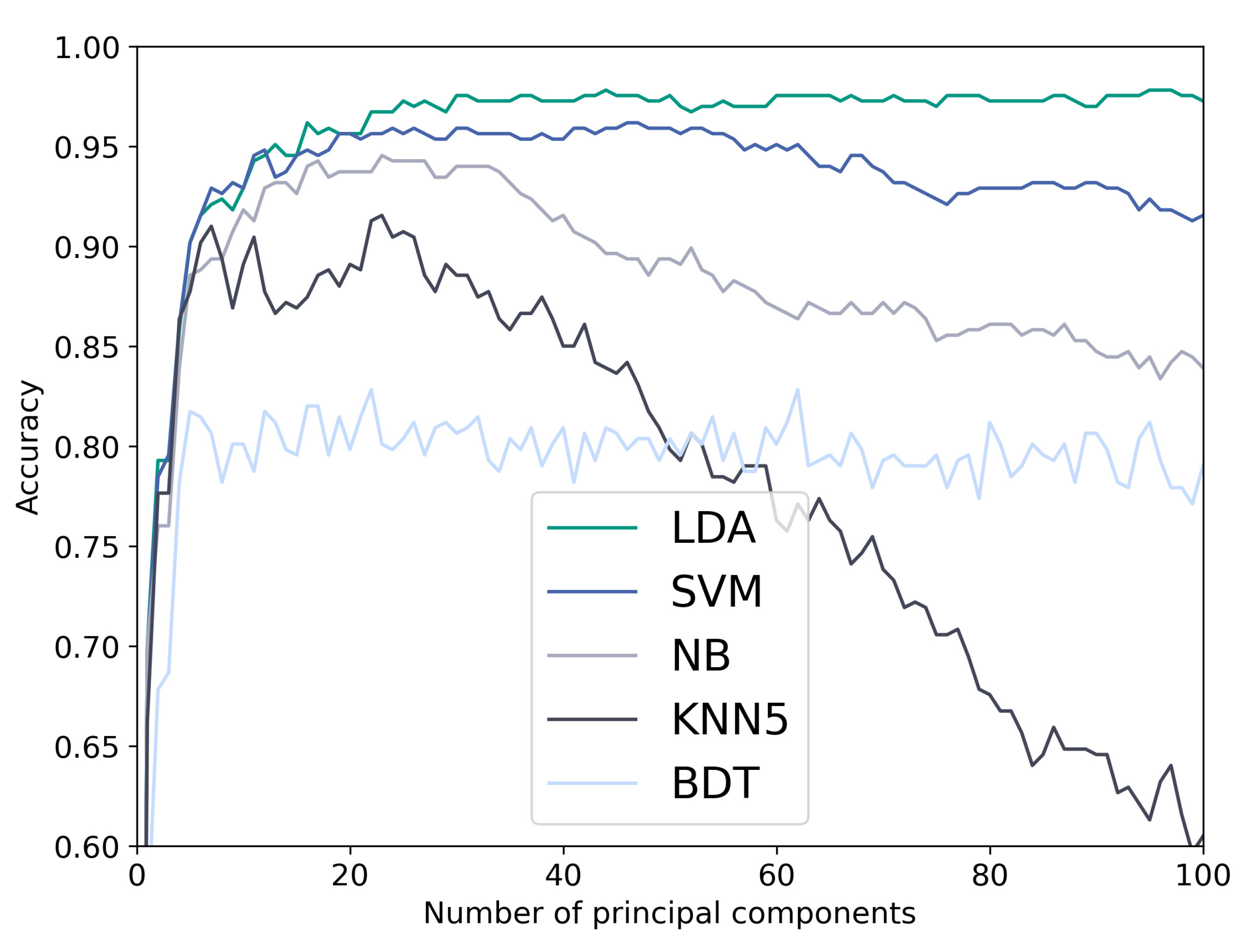
3.1. Classification Results
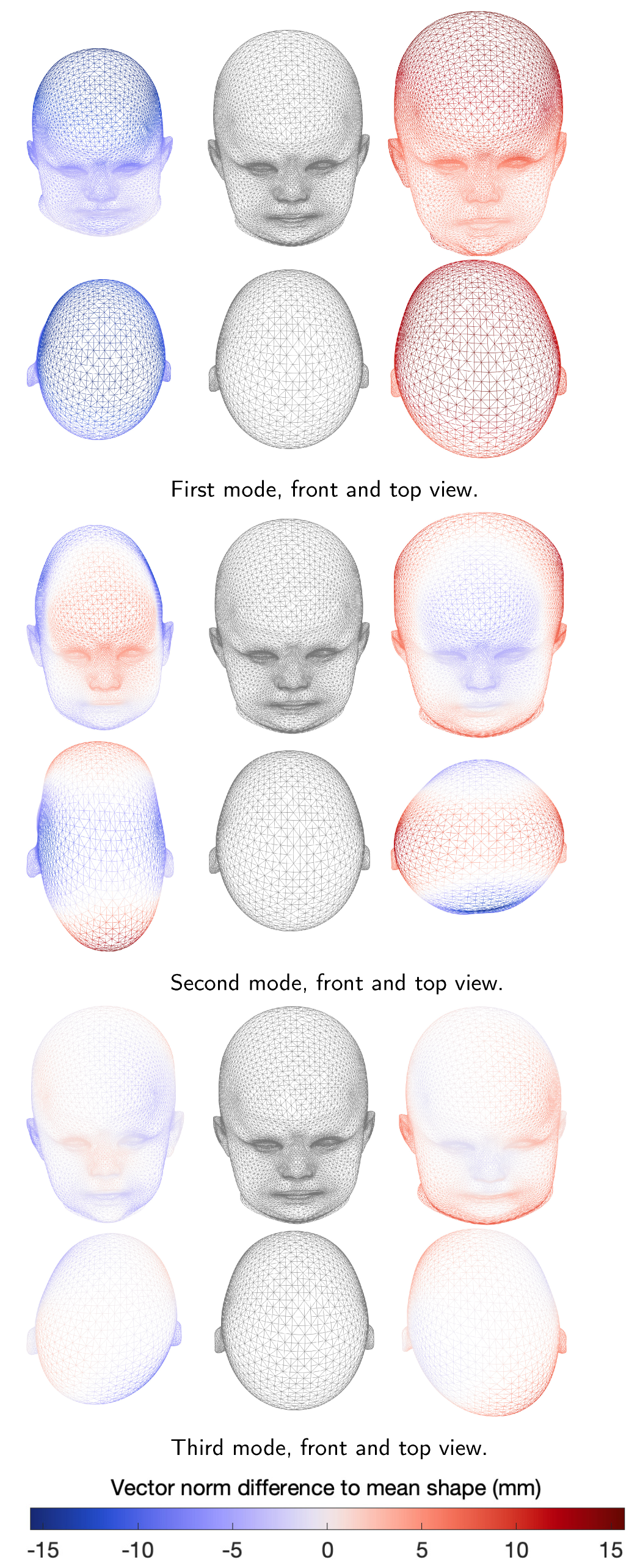
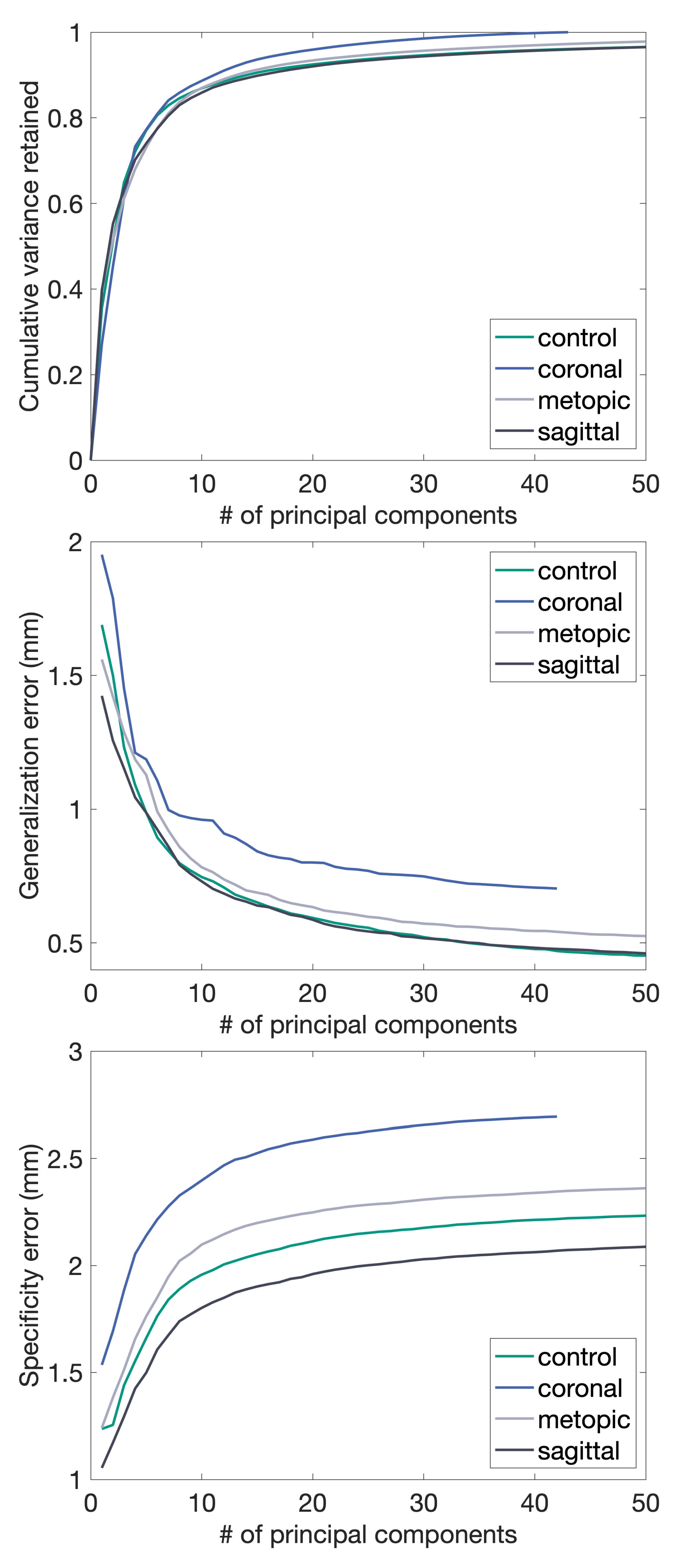
3.2. Morphing and Shape Model Evaluation
3.3. Publicly Available Shape Model
3.4. Shape Model Applications
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boulet, S.L.; Rasmussen, S.A.; Honein, M.A. A Population-Based Study of Craniosynostosis in Metropolitan Atlanta, 1989–2003. Am. J. Med. Genet. Part A 2008, 146A, 984–991. [Google Scholar] [CrossRef] [PubMed]
- French, L.; Jackson, I.T.; Melton, L. A Population-Based Study of Craniosynostosis. J. Clin. Epidemiol. 1990, 43, 69–73. [Google Scholar] [CrossRef]
- Shuper, A. The Incidence of Isolated Craniosynostosis in the Newborn Infant. Arch. Pediatr. Adolesc. Med. 1985, 139, 85. [Google Scholar] [CrossRef] [PubMed]
- Coussens, A.K.; Wilkinson, C.R.; Hughes, I.P.; Morris, C.P.; van Daal, A.; Anderson, P.J.; Powell, B.C. Unravelling the Molecular Control of Calvarial Suture Fusion in Children with Craniosynostosis. BMC Genom. 2007, 8, 458. [Google Scholar] [CrossRef] [Green Version]
- Renier, D.; Sainte-Rose, C.; Marchac, D.; Hirsch, J.F. Intracranial Pressure in Craniostenosis. J. Neurosurg. 1982, 57, 370–377. [Google Scholar] [CrossRef] [Green Version]
- Kapp-Simon, K.A.; Speltz, M.L.; Cunningham, M.L.; Patel, P.K.; Tomita, T. Neurodevelopment of Children with Single Suture Craniosynostosis: A Review. Child’s Nerv. Syst. 2007, 23, 269–281. [Google Scholar] [CrossRef]
- Judy, B.F.; Swanson, J.W.; Yang, W.; Storm, P.B.; Bartlett, S.P.; Taylor, J.A.; Heuer, G.G.; Lang, S.S. Intraoperative Intracranial Pressure Monitoring in the Pediatric Craniosynostosis Population. J. Neurosurg. Pediatr. 2018, 22, 475–480. [Google Scholar] [CrossRef]
- Engel, M.; Castrillon-Oberndorfer, G.; Hoffmann, J.; Freudlsperger, C. Value of Preoperative Imaging in the Diagnostics of Isolated Metopic Suture Synostosis: A Risk–Benefit Analysis. J. Plast. Reconstr. Aesthetic Surg. 2012, 65, 1246–1251. [Google Scholar] [CrossRef]
- Bannink, N.; Nout, E.; Wolvius, E.; Hoeve, H.; Joosten, K.; Mathijssen, I. Obstructive Sleep Apnea in Children with Syndromic Craniosynostosis: Long-Term Respiratory Outcome of Midface Advancement. Int. J. Oral Maxillofac. Surg. 2010, 39, 115–121. [Google Scholar] [CrossRef]
- Fearon, J.A.; Ruotolo, R.A.; Kolar, J.C. Single Sutural Craniosynostoses: Surgical Outcomes and Long-Term Growth. Plast. Reconstr. Surg. 2009, 123, 635–642. [Google Scholar] [CrossRef]
- Freudlsperger, C.; Steinmacher, S.; Saure, D.; Bodem, J.P.; Kühle, R.; Hoffmann, J.; Engel, M. Impact of Severity and Therapy Onset on Helmet Therapy in Positional Plagiocephaly. J. Cranio-Maxillofac. Surg. 2016, 44, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Nagaraja, S.; Anslow, P.; Winter, B. Craniosynostosis. Clin. Radiol. 2013, 68, 284–292. [Google Scholar] [CrossRef] [PubMed]
- Persing, J.A.; Jane, J.A.; Shaffrey, M. Virchow and the Pathogenesis of Craniosynostosis: A Translation of His Original Work. Plast. Reconstr. Surg. 1989, 83, 738–742. [Google Scholar] [CrossRef] [PubMed]
- Eley, K.A.; Watt-Smith, S.R.; Sheerin, F.; Golding, S.J. “Black Bone” MRI: A Potential Alternative to CT with Three-Dimensional Reconstruction of the Craniofacial Skeleton in the Diagnosis of Craniosynostosis. Eur. Radiol. 2014, 24, 2417–2426. [Google Scholar] [CrossRef]
- Saarikko, A.; Mellanen, E.; Kuusela, L.; Leikola, J.; Karppinen, A.; Autti, T.; Virtanen, P.; Brandstack, N. Comparison of Black Bone MRI and 3D-CT in the Preoperative Evaluation of Patients with Craniosynostosis. J. Plast. Reconstr. Aesthet. Surg. 2020, 73, 723–731. [Google Scholar] [CrossRef]
- Cacciaguerra, G.; Palermo, M.; Marino, L.; Rapisarda, F.A.S.; Pavone, P.; Falsaperla, R.; Ruggieri, M.; Marino, S. The Evolution of the Role of Imaging in the Diagnosis of Craniosynostosis: A Narrative Review. Children 2021, 8, 727. [Google Scholar] [CrossRef]
- Mertens, C.; Wessel, E.; Berger, M.; Ristow, O.; Hoffmann, J.; Kansy, K.; Freudlsperger, C.; Bächli, H.; Engel, M. The Value of Three-Dimensional Photogrammetry in Isolated Sagittal Synostosis: Impact of Age and Surgical Technique on Intracranial Volume and Cephalic Index-a Retrospective Cohort Study. J. Cranio-Maxillofac. Surg. 2017, 45, 2010–2016. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Training Models of Shape from Sets of Examples. In BMVC92; Hogg, D., Boyle, R., Eds.; Springer: London, UK, 1992; pp. 9–18. [Google Scholar] [CrossRef] [Green Version]
- Blanz, V.; Vetter, T. A Morphable Model for the Synthesis of 3D Faces. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH ’99, Los Angeles, CA, USA, 8–13 August 1999; ACM Press: New York, NY, USA, 1999; pp. 187–194. [Google Scholar] [CrossRef]
- Gerig, T.; Morel-Forster, A.; Blumer, C.; Egger, B.; Lüthi, M.; Schönborn, S.; Vetter, T. Morphable Face Models—An Open Framework. arXiv 2017, arXiv:1709.08398. [Google Scholar]
- Dai, H.; Pears, N.; Duncan, C. A 2D Morphable Model of Craniofacial Profile and Its Application to Craniosynostosis. In Medical Image Understanding and Analysis; Valdés Hernández, M., González-Castro, V., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 723, pp. 731–742. [Google Scholar] [CrossRef]
- Egger, B.; Smith, W.A.P.; Tewari, A.; Wuhrer, S.; Zollhoefer, M.; Beeler, T.; Bernard, F.; Bolkart, T.; Kortylewski, A.; Romdhani, S.; et al. 3D Morphable Face Models—Past, Present, and Future. ACM Trans. Graph. 2020, 39, 1–38. [Google Scholar] [CrossRef]
- Meulstee, J.; Verhamme, L.; Borstlap, W.; Van der Heijden, F.; De Jong, G.; Xi, T.; Bergé, S.; Delye, H.; Maal, T. A New Method for Three-Dimensional Evaluation of the Cranial Shape and the Automatic Identification of Craniosynostosis Using 3D Stereophotogrammetry. Int. J. Oral Maxillofac. Surg. 2017, 46, 819–826. [Google Scholar] [CrossRef]
- Dai, H.; Pears, N.; Smith, W.; Duncan, C. Statistical Modeling of Craniofacial Shape and Texture. Int. J. Comput. Vis. 2020, 128, 547–571. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Florez, N.; Bruse, J.L.; Borghi, A.; Vercruysse, H.; Ong, J.; James, G.; Pennec, X.; Dunaway, D.J.; Jeelani, N.U.O.; Schievano, S. Statistical Shape Modelling to Aid Surgical Planning: Associations between Surgical Parameters and Head Shapes Following Spring-Assisted Cranioplasty. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 1739–1749. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, C.S.; Safdar, N.; Okada, K.; Myers, E.; Rogers, G.F.; Linguraru, M.G. Personalized Assessment of Craniosynostosis via Statistical Shape Modeling. Med Image Anal. 2014, 18, 635–646. [Google Scholar] [CrossRef] [PubMed]
- de Jong, G.; Bijlsma, E.; Meulstee, J.; Wennen, M.; van Lindert, E.; Maal, T.; Aquarius, R.; Delye, H. Combining Deep Learning with 3D Stereophotogrammetry for Craniosynostosis Diagnosis. Sci. Rep. 2020, 10, 15346. [Google Scholar] [CrossRef]
- Albrecht, T.; Knothe, R.; Vetter, T. Modeling the remaining flexibility of partially fixed statistical shape models. In Proceedings of the in Workshop on the Mathematical Foundations of Computational Anatomy, New York, NY, USA, 6 September 2008. [Google Scholar]
- Hintze, J.L.; Nelson, R.D. Violin Plots: A Box Plot-Density Trace Synergism. Am. Stat. 1998, 52, 181. [Google Scholar] [CrossRef]
- Bechtold, B.; Fletcher, P.; Seamusholden; Gorur-Shandilya, S. Bastibe/Violinplot-Matlab: A Good Starting Point; Zenodo: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: An Open-Source Mesh Processing Tool. In Proceedings of the Eurographics Italian Chapter Conference, Salerno, Italy, 2 July 2008; p. 8. [Google Scholar] [CrossRef]
- Pietroni, N.; Tarini, M.; Cignoni, P. Almost Isometric Mesh Parameterization through Abstract Domains. IEEE Trans. Vis. Comput. Graph. 2010, 16, 621–635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Besl, P.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point Set Registration: Coherent Point Drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [Green Version]
- Allen, B.; Curless, B.; Popović, Z. The Space of Human Body Shapes: Reconstruction and Parameterization from Range Scans. ACM Trans. Graph. 2003, 22, 587–594. [Google Scholar] [CrossRef]
- Booth, J.; Roussos, A.; Zafeiriou, S.; Ponniah, A.; Dunaway, D. A 3D Morphable Model Learnt from 10,000 Faces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 5543–5552. [Google Scholar] [CrossRef] [Green Version]
- Amberg, B.; Romdhani, S.; Vetter, T. Optimal Step Nonrigid ICP Algorithms for Surface Registration. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Shen, K.K.; Fripp, J.; Mériaudeau, F.; Chételat, G.; Salvado, O.; Bourgeat, P. Detecting Global and Local Hippocampal Shape Changes in Alzheimer’s Disease Using Statistical Shape Models. NeuroImage 2012, 59, 2155–2166. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Zhang, H. The Optimality of Naive Bayes. Aa 2004, 1, 3. [Google Scholar]
- Gordon, A.D.; Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees. Biometrics 1984, 40, 874. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Styner, M.A.; Rajamani, K.T.; Nolte, L.P.; Zsemlye, G.; Székely, G.; Taylor, C.J.; Davies, R.H. Evaluation of 3D Correspondence Methods for Model Building. In Information Processing in Medical Imaging; Goos, G., Hartmanis, J., van Leeuwen, J., Taylor, C., Noble, J.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2732, pp. 63–75. [Google Scholar] [CrossRef]
- Davies, R.H. Learning Shape: Optimal Models for Analysing Natural Variability. Ph.D. Thesis, University of Manchester, Manchester, UK, 2002. [Google Scholar]
- Schaufelberger, M.; Kühle, R.P.; Wachter, A.; Weichel, F.; Hagen, N.; Ringwald, F.; Eisenmann, U.; Hoffmann, J.; Engel, M.; Freudlsperger, C.; et al. A Statistical Shape Model of Craniosynostosis Patients and 100 Model Instances of Each Pathology; Zenodo: Geneve, Switzerland, 2021. [Google Scholar] [CrossRef]
- Albrecht, T.; Lüthi, M.; Gerig, T.; Vetter, T. Posterior Shape Models. Med Image Anal. 2013, 17, 959–973. [Google Scholar] [CrossRef] [Green Version]
- Heutinck, P.; Knoops, P.; Florez, N.R.; Biffi, B.; Breakey, W.; James, G.; Koudstaal, M.; Schievano, S.; Dunaway, D.; Jeelani, O.; et al. Statistical Shape Modelling for the Analysis of Head Shape Variations. J. Cranio-Maxillofac. Surg. 2021, 49, 449–455. [Google Scholar] [CrossRef]
- Lamecker, H.; Zachow, S.; Hege, H.C.; Zöckler, M.; Haberl, E. Surgical Treatment of Craniosynostosis based on a Statistical 3D-Shape Model: First Clinical Application. Int. J. Comput. Assist. Radiol. Surg. 2006, 1, 253. [Google Scholar]
- Lüthi, M.; Albrecht, T.; Vetter, T. Building Shape Models from Lousy Data. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2009; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5762, pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Wei, M.; Szymczak, A.; Petrella, A.; Xie, H.; Qin, J.; Wang, J.; Wang, F.L. Nonrigid Iterative Closest Points for Registration of 3D Biomedical Surfaces. Opt. Lasers Eng. 2018, 100, 141–154. [Google Scholar] [CrossRef]
- Davies, R.H.; Twining, C.J.; Daniel Allen, P.; Cootes, T.F.; Taylor, C.J. Building Optimal 2D Statistical Shape Models. Image Vis. Comput. 2003, 21, 1171–1182. [Google Scholar] [CrossRef]
- Dai, H.; Pears, N.; Smith, W. Augmenting a 3D Morphable Model of the Human Head with High Resolution Ears. Pattern Recognit. Lett. 2019, 128, 378–384. [Google Scholar] [CrossRef]
- Ploumpis, S.; Wang, H.; Pears, N.; Smith, W.A.P.; Zafeiriou, S. Combining 3D Morphable Models: A Large Scale Face-And-Head Model. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 10926–10935. [Google Scholar] [CrossRef] [Green Version]
- Ploumpis, S.; Ververas, E.; Sullivan, E.O.; Moschoglou, S.; Wang, H.; Pears, N.; Smith, W.A.P.; Gecer, B.; Zafeiriou, S. Towards a Complete 3D Morphable Model of the Human Head. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4142–4160. [Google Scholar] [CrossRef] [PubMed]
- Luthi, M.; Gerig, T.; Jud, C.; Vetter, T. Gaussian Process Morphable Models. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1860–1873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swennen, G.R.; Schutyser, F.A.; Hausamen, J.E. Three-Dimensional Cephalometry; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Jeter, M.W. Mathematical Programming: An Introduction to Optimization; Number 102 in Monographs and Textbooks in Pure and Applied Mathematics; Routledge: New York, NY, USA, 1986. [Google Scholar]
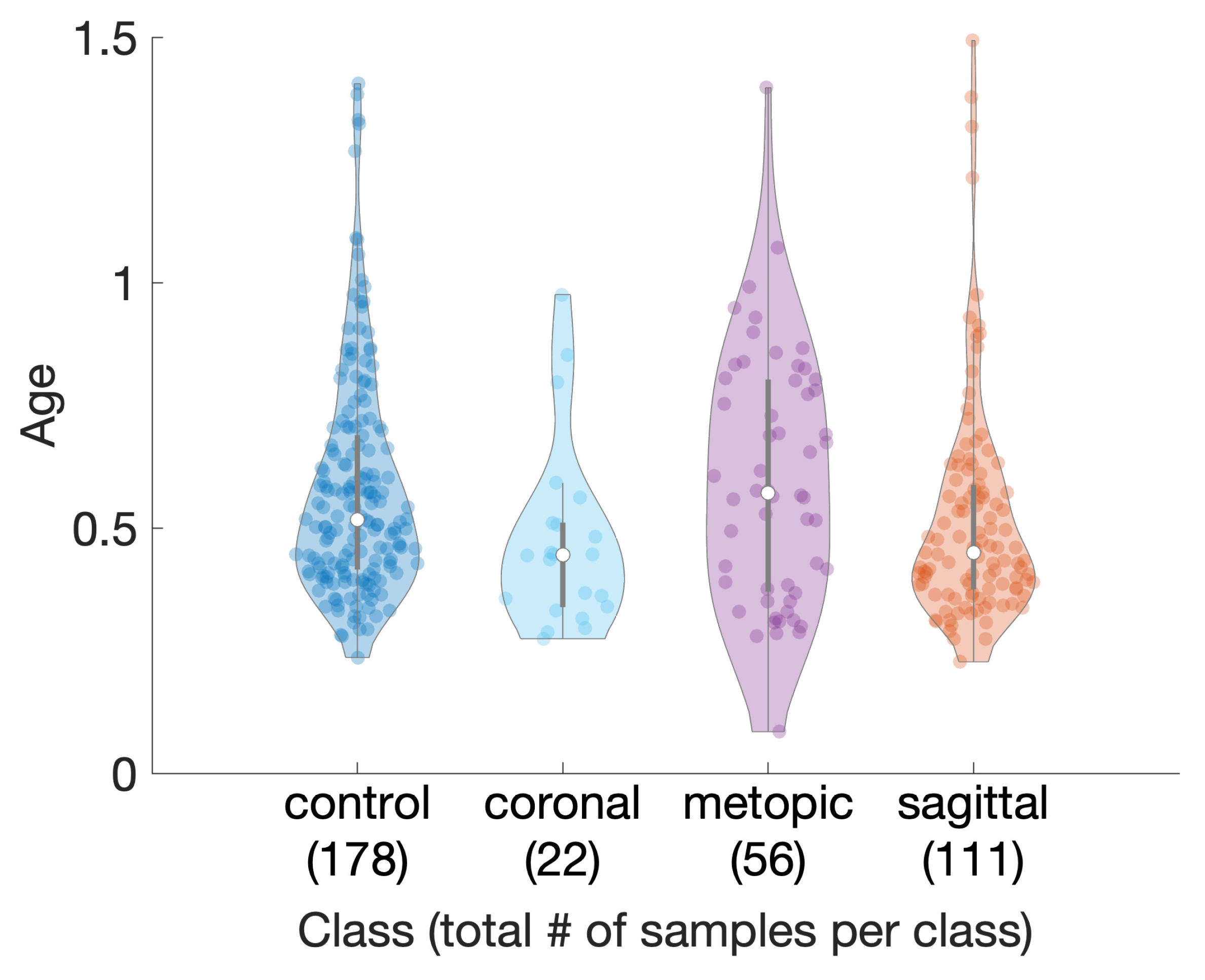



| True Class | Predicted Class | Sensitivity | Specificity | |||
|---|---|---|---|---|---|---|
| Con | Cor | Met | Sag | |||
| Con | 178 | 0 | 0 | 0 | 1.000 | 0.958 |
| Cor | 5 | 17 | 0 | 0 | 0.773 | 1.000 |
| Met | 0 | 0 | 56 | 0 | 1.000 | 1.000 |
| Sag | 3 | 0 | 0 | 108 | 0.973 | 1.000 |
| G-mean | 0.931 | |||||
| Total accuracy | 0.978 | |||||
| Mean Landmark Error (mm) | Mean Vertex-to-Nearest-Neighbor Distance (mm) | Mean Surface Normals Deviations (Degree) |
|---|---|---|
| Model | Included Principal Components |
|---|---|
| Full shape model | 100 |
| Texture model | 100 |
| Control model | 30 |
| Sagittal model | 30 |
| Metopic model | 25 |
| Coronal model | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schaufelberger, M.; Kühle, R.; Wachter, A.; Weichel, F.; Hagen, N.; Ringwald, F.; Eisenmann, U.; Hoffmann, J.; Engel, M.; Freudlsperger, C.; et al. A Radiation-Free Classification Pipeline for Craniosynostosis Using Statistical Shape Modeling. Diagnostics 2022, 12, 1516. https://doi.org/10.3390/diagnostics12071516
Schaufelberger M, Kühle R, Wachter A, Weichel F, Hagen N, Ringwald F, Eisenmann U, Hoffmann J, Engel M, Freudlsperger C, et al. A Radiation-Free Classification Pipeline for Craniosynostosis Using Statistical Shape Modeling. Diagnostics. 2022; 12(7):1516. https://doi.org/10.3390/diagnostics12071516
Chicago/Turabian StyleSchaufelberger, Matthias, Reinald Kühle, Andreas Wachter, Frederic Weichel, Niclas Hagen, Friedemann Ringwald, Urs Eisenmann, Jürgen Hoffmann, Michael Engel, Christian Freudlsperger, and et al. 2022. "A Radiation-Free Classification Pipeline for Craniosynostosis Using Statistical Shape Modeling" Diagnostics 12, no. 7: 1516. https://doi.org/10.3390/diagnostics12071516
APA StyleSchaufelberger, M., Kühle, R., Wachter, A., Weichel, F., Hagen, N., Ringwald, F., Eisenmann, U., Hoffmann, J., Engel, M., Freudlsperger, C., & Nahm, W. (2022). A Radiation-Free Classification Pipeline for Craniosynostosis Using Statistical Shape Modeling. Diagnostics, 12(7), 1516. https://doi.org/10.3390/diagnostics12071516