Deep Learning-Based Total Kidney Volume Segmentation in Autosomal Dominant Polycystic Kidney Disease Using Attention, Cosine Loss, and Sharpness Aware Minimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Image Data
2.2. Image Annotation
2.3. Pre-Processing
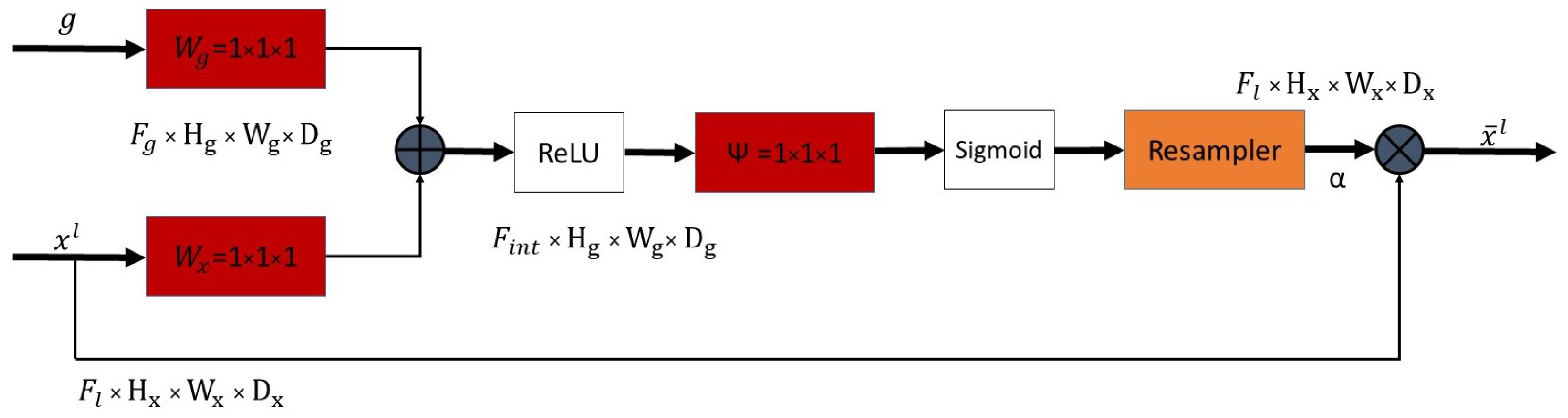
2.4. Attention Module
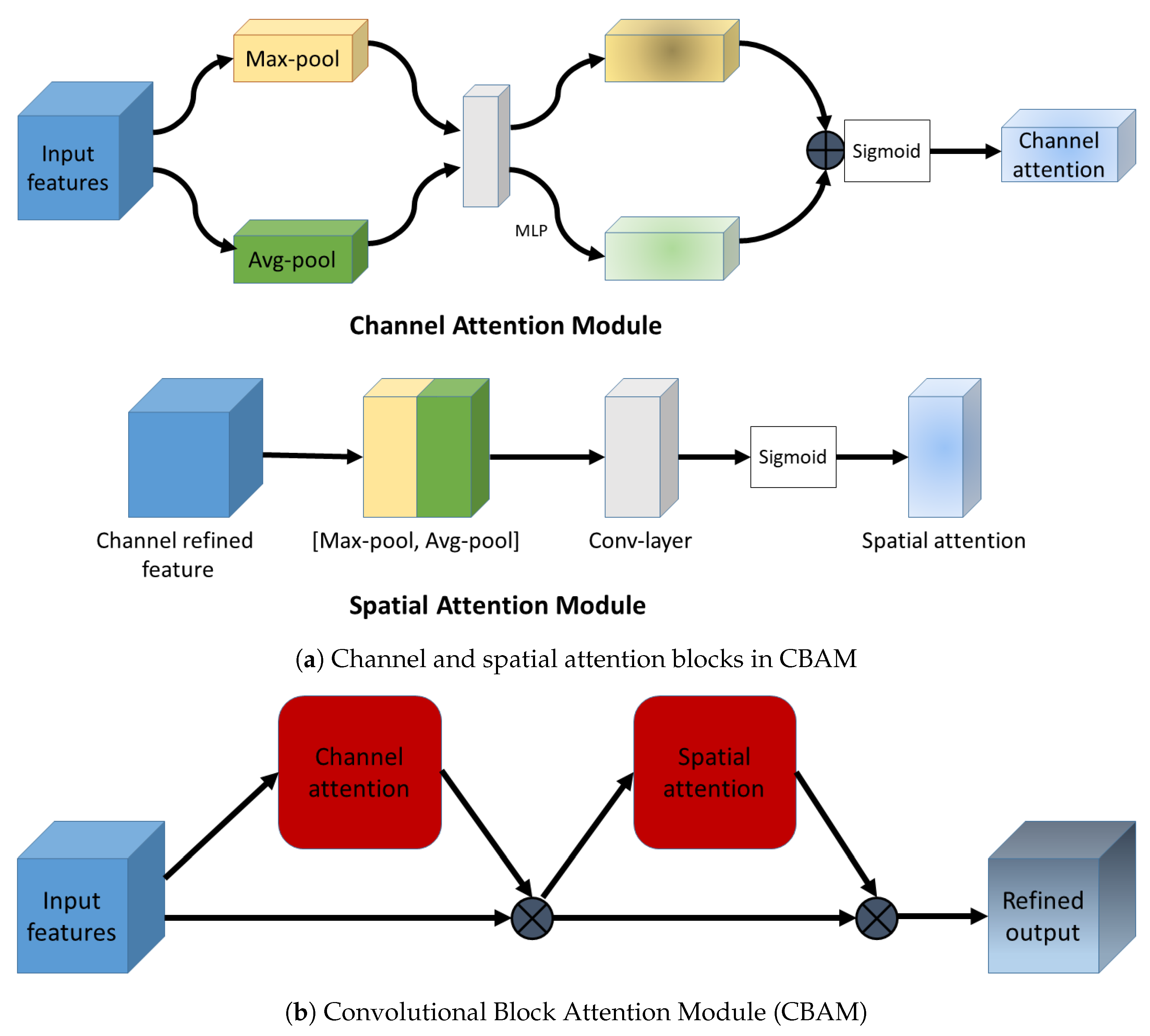
2.5. Convolutional Block Attention Module
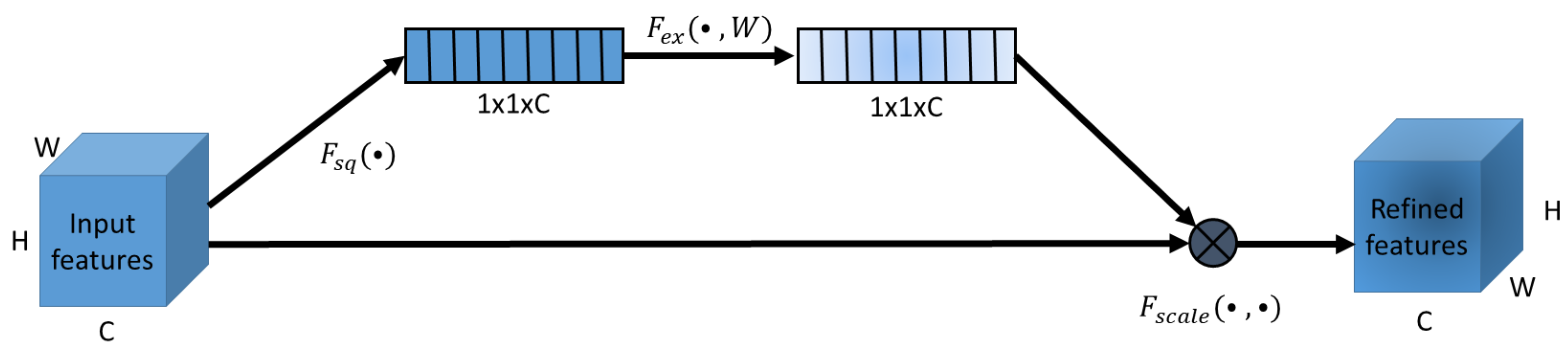
2.5.1. Squeeze and Excitation Attention
2.5.2. Channel Attention in CBAM
2.6. Cosine Loss
2.7. Sharpness Aware Minimization
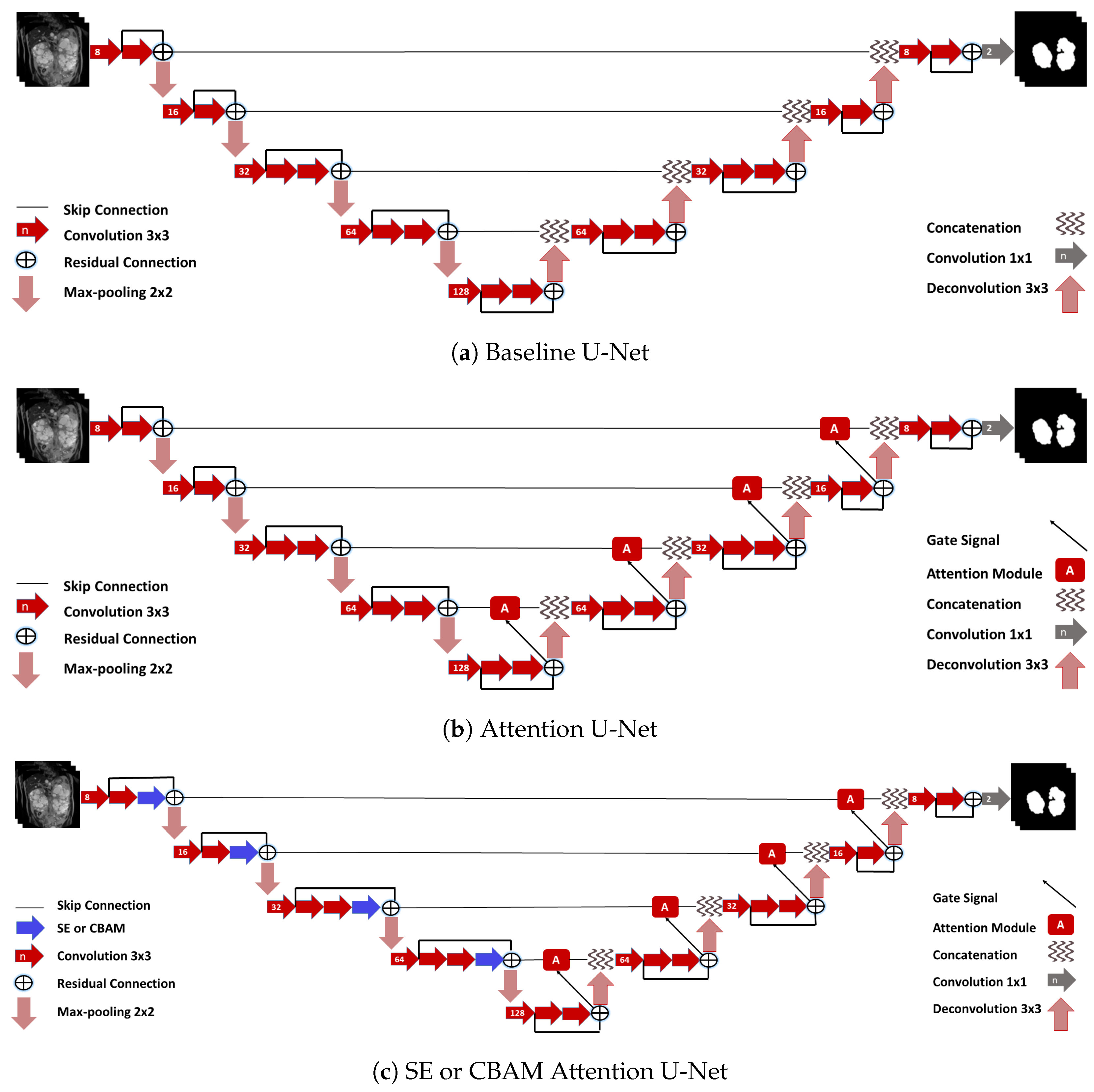
2.8. Networks
2.9. Training
2.10. Ensembles
2.11. Evaluation
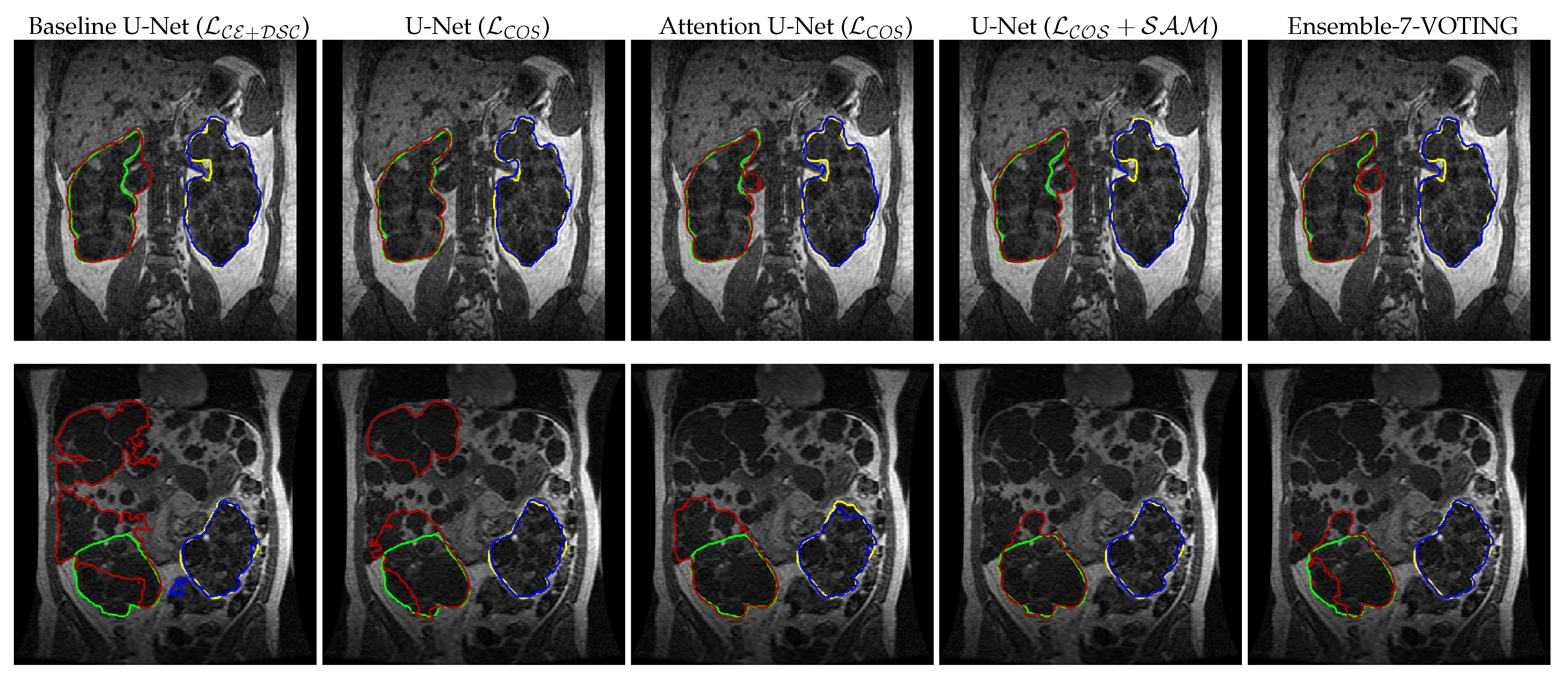
3. Results
3.1. Attention Mechanisms
3.2. Cosine Loss
3.3. SAM
3.4. Ensemble
3.5. Evaluation of Total Kidney Volume
4. Discussion
4.1. Individual Networks
4.2. Ensembles
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Architecture | Loss | DSC (Left) ↑ | DSC (Right) ↑ | MSSD (mm) (Left) ↓ | MSSD (mm) (Right) ↓ | DSC (Left) ↑ | DSC (Right) ↑ | MSSD (mm) (Left) ↓ | MSSD (mm) (Right) ↓ |
|---|---|---|---|---|---|---|---|---|---|
| 96 × 96 | 96 × 96 | 96 × 96 | 96 × 96 | 128 × 128 | 128 × 128 | 128 × 128 | 128 × 128 | ||
| Baseline U-Net | 0.886 ± 0.061 | 0.877 ± 0.099 | 1.992 ± 1.828 | 2.578 ± 4.388 | 0.901 ± 0.058 | 0.907 ± 0.083 | 1.381 ± 1.121 | 1.447 ± 3.727 | |
| SE U-net | 0.899 ± 0.064 | 0.894 ± 0.076 | 1.594 ± 2.330 | 1.614 ± 2.123 | 0.900 ± 0.060 | 0.897 ± 0.071 | 1.630 ± 2.286 | 1.494 ± 2.232 | |
| 0.887 ± 0.111 | 0.882 ± 0.111 | 2.140 ± 4.858 | 1.694 ± 2.248 | 0.899 ± 0.059 | 0.901 ± 0.068 | 1.592 ± 2.116 | 1.377 ± 2.000 | ||
| 0.888 ± 0.080 | 0.900 ± 0.087 | 1.512 ± 1.416 | 1.559 ± 3.308 | 0.912 ± 0.044 | 0.893 ± 0.095 | 1.129 ± 0.847 | 1.344 ± 1.941 | ||
| 0.912 ± 0.045 | 0.891 ± 0.099 | 1.222 ± 0.957 | 1.547 ± 2.447 | 0.895 ± 0.112 | 0.905 ± 0.077 | 1.813 ± 4.790 | 1.367 ± 2.210 | ||
| CBAM U-Net | 0.894 ± 0.070 | 0.890 ± 0.098 | 1.682 ± 2.310 | 1.845 ± 3.532 | 0.905 ± 0.064 | 0.907 ± 0.064 | 1.285 ± 1.164 | 1.363 ± 2.223 | |
| 0.905 ± 0.053 | 0.900 ± 0.082 | 1.316 ± 0.984 | 1.293 ± 1.678 | 0.905 ± 0.061 | 0.904 ± 0.077 | 1.404 ± 1.727 | 1.429 ± 2.537 | ||
| 0.891 ± 0.068 | 0.896 ± 0.080 | 1.893 ± 2.575 | 1.709 ± 2.596 | 0.917 ± 0.046 | 0.904 ± 0.081 | 1.072 ± 0.889 | 1.346 ± 2.486 | ||
| 0.897 ± 0.067 | 0.899 ± 0.085 | 1.832 ± 2.626 | 1.701 ± 3.604 | 0.910 ± 0.054 | 0.908 ± 0.072 | 1.265 ± 1.406 | 1.270 ± 2.429 | ||
| Attn. U-Net | 0.894 ± 0.074 | 0.890 ± 0.093 | 1.662 ± 1.637 | 1.771 ± 2.655 | 0.914 ± 0.043 | 0.907 ± 0.061 | 1.224 ± 0.914 | 1.403 ± 2.080 | |
| 0.901 ± 0.057 | 0.907 ± 0.072 | 1.741 ± 2.455 | 1.366 ± 2.212 | 0.910 ± 0.049 | 0.909 ± 0.073 | 1.286 ± 1.573 | 1.304 ± 2.253 | ||
| 0.894 ± 0.058 | 0.897 ± 0.093 | 1.910 ± 2.745 | 1.776 ± 3.212 | 0.913 ± 0.051 | 0.909 ± 0.069 | 1.353 ± 1.697 | 1.399 ± 2.374 | ||
| 0.905 ± 0.059 | 0.907 ± 0.075 | 1.442 ± 1.940 | 1.321 ± 2.018 | 0.914 ± 0.048 | 0.915 ± 0.072 | 1.184 ± 1.190 | 1.257 ± 2.536 | ||
| U-Net | 0.898 ± 0.074 | 0.897 ± 0.093 | 1.725 ± 2.479 | 1.794 ± 3.727 | 0.908 ± 0.059 | 0.909 ± 0.076 | 1.208 ± 1.104 | 1.342 ± 2.909 | |
| 0.909 ± 0.051 | 0.910 ± 0.075 | 1.454 ± 2.109 | 1.313 ± 2.326 | 0.921 ± 0.043 | 0.914 ± 0.062 | 1.009 ± 0.843 | 1.274 ± 2.331 | ||
| Ensemble-4-STAPLE | 0.911 ± 0.054 | 0.909 ± 0.077 | 1.556 ± 2.498 | 1.351 ± 2.413 | 0.920 ± 0.046 | 0.919 ± 0.068 | 1.112 ± 1.144 | 1.158 ± 2.240 | |
| Ensemble-7-STAPLE | 0.911 ± 0.053 | 0.909 ± 0.077 | 1.484 ± 2.145 | 1.399 ± 2.343 | 0.923 ± 0.045 | 0.919 ± 0.069 | 1.079 ± 1.162 | 1.134 ± 2.224 | |
| Ensemble-4-VOTING | 0.918 ± 0.048 | 0.910 ± 0.074 | 1.086 ± 1.037 | 1.219 ± 2.029 | 0.919 ± 0.050 | 0.916 ± 0.066 | 1.035 ± 0.979 | 1.102 ± 1.989 | |
| Ensemble-7-VOTING | 0.916 ± 0.049 | 0.914 ± 0.073 | 1.238 ± 1.779 | 1.213 ± 2.035 | 0.925 ± 0.044 | 0.919 ± 0.067 | 0.993 ± 0.998 | 1.085 ± 2.072 |
References
- Grantham, J.J. Polycystic kidney disease: From the bedside to the gene and back. Curr. Opin. Nephrol. Hy. 2001, 10, 533–542. [Google Scholar] [CrossRef] [PubMed]
- Chapman, A.B.; Guay-Woodford, L.M.; Grantham, J.J.; Torres, V.E.; Bae, K.T.; Baumgarten, D.A.; Kenney, P.J.; King, B.F., Jr.; Glockner, J.F.; Wetzel, L.H.; et al. Renal structure in early autosomal-dominant polycystic kidney disease (ADPKD): The Consortium for Radiologic Imaging Studies of Polycystic Kidney Disease (CRISP) cohort. Kidney Intl. 2003, 64, 1035–1045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dalgaard, O.Z. Bilateral polycystic disease of the kidneys: A follow-up of two hundred and eighty four paients and their families. Acta Med. Scand. 1957, 328, 1–251. [Google Scholar]
- Irazabal, M.V.; Rangel, L.J.; Bergstralh, E.J.; Osborn, S.L.; Harmon, A.J.; Sundsbak, J.L.; Bae, K.T.; Chapman, A.B.; Grantham, J.J.; Mrug, M.; et al. Imaging classification of autosomal dominant polycystic kidney disease: A simple model for selecting patients for clinical trials. J. Am. Soc. Nephrol. 2015, 26, 160–172. [Google Scholar] [CrossRef]
- Grantham, J.J.; Torres, V.E.; Chapman, A.B.; Guay-Woodford, L.M.; Bae, K.T.; King, B.F., Jr.; Wetzel, L.H.; Baumgarten, D.A.; Kenney, P.J.; Harris, P.C.; et al. Volume Progression in Polycystic Kidney Disease. N. Engl. J. Med. 2006, 354, 2122–2130. [Google Scholar] [CrossRef] [Green Version]
- US Food and Drug Administration. Qualification of Biomarker—Total Kidney Volume in Studies for Treatment of Autosomal Dominant Polycystic Kidney Disease. 2016. Available online: https://www.fda.gov/drugs/drug-development-tool-ddt-qualification-programs/reviews-qualification-biomarker-total-kidney-volume-studies-treatment-autosomal-dominant-polycystic (accessed on 17 May 2021).
- Zöllner, F.G.; Kociński, M.; Hansen, L.; Golla, A.K.; Trbalić, A.Š.; Lundervold, A.; Materka, A.; Rogelj, P. Kidney Segmentation in Renal Magnetic Resonance Imaging—Current Status and Prospects. IEEE Access 2021, 9, 71577–71605. [Google Scholar] [CrossRef]
- Zöllner, F.G.; Svarstad, E.; Munthe-Kaas, A.Z.; Schad, L.R.; Lundervold, A.; Rørvik, J. Assessment of kidney volumes from MRI: Acquisition and segmentation techniques. Am. J. Roentgenol. 2012, 199, 1060–1069. [Google Scholar] [CrossRef]
- Lundervold, A.S.; Lundervold, A. An overview of deep learning in medical imaging focusing on MRI. Z. Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef]
- Kline, T.L.; Korfiatis, P.; Edwards, M.E.; Blais, J.D.; Czerwiec, F.S.; Harris, P.C.; King, B.F.; Torres, V.E.; Erickson, B.J. Performance of an artificial multi-observer deep neural network for fully automated segmentation of polycystic kidneys. J. Digit. Imaging 2017, 30, 442–448. [Google Scholar] [CrossRef]
- van Gastel, M.D.; Edwards, M.E.; Torres, V.E.; Erickson, B.J.; Gansevoort, R.T.; Kline, T.L. Automatic Measurement of Kidney and Liver Volumes from MR Images of Patients Affected by Autosomal Dominant Polycystic Kidney Disease. J. Am. Soc. Nephrol. 2019, 30, 1514–1522. [Google Scholar] [CrossRef]
- Bevilacqua, V.; Brunetti, A.; Cascarano, G.D.; Palmieri, F.; Guerriero, A.; Moschetta, M. A deep learning approach for the automatic detection and segmentation in autosomal dominant polycystic kidney disease based on magnetic resonance images. In Proceedings of the International Conference on Intelligent Computing, Wuhan, China, 15–18 August 2018; pp. 643–649. [Google Scholar]
- Mu, G.; Ma, Y.; Han, M.; Zhan, Y.; Zhou, X.; Gao, Y. Automatic MR kidney segmentation for autosomal dominant polycystic kidney disease. In Proceedings of the Medical Imaging 2019: Computer-Aided Diagnosis, San Diego, CA, USA, 17–20 February 2019; Volume 10950, p. 109500X. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Daniel, A.J.; Buchanan, C.E.; Allcock, T.; Scerri, D.; Cox, E.F.; Prestwich, B.L.; Francis, S.T. Automated renal segmentation in healthy and chronic kidney disease subjects using a convolutional neural network. Magn. Reson. Med. 2021, 86, 1125–1136. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Bauer, D.F.; Russ, T.; Waldkirch, B.I.; Tönnes, C.; Segars, W.P.; Schad, L.R.; Zöllner, F.G.; Golla, A.K. Generation of annotated multimodal ground truth datasets for abdominal medical image registration. Int. J. Comput. Assist. Rad. Surg. 2021, 16, 1277–1285. [Google Scholar] [CrossRef] [PubMed]
- Russ, T.; Goerttler, S.; Schnurr, A.; Bauer, D.; Hatamikia, S.; Schad, L.R.; Zöllner, F.G.; Chung, K. Synthesis of CT images from digital body phantoms using CycleGAN. Int. J. CARS 2019, 14, 1741–1750. [Google Scholar] [CrossRef]
- Foret, P.; Kleiner, A.; Mobahi, H.; Neyshabur, B. Sharpness-aware Minimization for Efficiently Improving Generalization. arXiv 2021, arXiv:2010.01412. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. In Proceedings of the 1st Conference on Medical Imaging with Deep Learning (MIDL2018), Amsterdam, The Netherlands, 4–6 July 2018. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Zhou, T.; Li, L.; Li, X.; Feng, C.M.; Li, J.; Shao, L. Group-Wise Learning for Weakly Supervised Semantic Segmentation. IEEE Trans. Image Process. 2021, 31, 799–811. [Google Scholar] [CrossRef]
- Zhou, T.; Li, J.; Wang, S.; Tao, R.; Shen, J. Matnet: Motion-attentive transition network for zero-shot video object segmentation. IEEE Trans. Image Process. 2020, 29, 8326–8338. [Google Scholar] [CrossRef]
- Schnurr, A.K.; Drees, C.; Schad, L.R.; Zöllner, F.G. Comparing sample mining schemes for CNN kidney segmentation in T1w MRI. In Proceedings of the 3rd International Symposium on Functional Renal Imaging, Nottingham, UK, 15–17 October 2019. [Google Scholar]
- Yaniv, Z.; Lowekamp, B.C.; Johnson, H.J.; Beare, R. SimpleITK image-analysis notebooks: A collaborative environment for education and reproducible research. J. Digit. Imaging 2018, 31, 290–303. [Google Scholar] [CrossRef] [Green Version]
- Barz, B.; Denzler, J. Deep learning on small datasets without pre-training using cosine loss. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2020; pp. 1371–1380. [Google Scholar]
- Golla, A.K.; Bauer, D.F.; Schmidt, R.; Russ, T.; Nörenberg, D.; Chung, K.; Tönnes, C.; Schad, L.R.; Zöllner, F.G. Convolutional Neural Network Ensemble Segmentation With Ratio-Based Sampling for the Arteries and Veins in Abdominal CT Scans. IEEE Trans. Biomed. Eng. 2020, 68, 1518–1526. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Warfield, S.K.; Zou, K.H.; Wells, W.M. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. IEEE Trans. Med. Imaging 2004, 23, 903–921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Payer, C.; Štern, D.; Neff, T.; Bischof, H.; Urschler, M. Instance segmentation and tracking with cosine embeddings and recurrent hourglass networks. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; pp. 3–11. [Google Scholar]
- Zöllner, F.G.; Sance, R.; Rogelj, P.; Ledesma-Carbayo, M.J.; Rørvik, J.; Santos, A.; Lundervold, A. Assessment of 3D DCE-MRI of the kidneys using non-rigid image registration and segmentation of voxel time courses. Comp. Med. Imaging Graph. 2009, 33, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Wang, W.; Konukoglu, E.; Van Gool, L. Rethinking Semantic Segmentation: A Prototype View. arXiv 2022, arXiv:2203.15102. [Google Scholar]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Scene parsing through ade20k dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 633–641. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 1–26 July 2016; pp. 3213–3223. [Google Scholar]
- Caesar, H.; Uijlings, J.; Ferrari, V. Coco-stuff: Thing and stuff classes in context. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1209–1218. [Google Scholar]
- Kavur, A.E.; Kuncheva, L.I.; Selver, M.A. Basic ensembles of vanilla-style deep learning models improve liver segmentation from ct images. arXiv 2020, arXiv:2001.09647. [Google Scholar]
- Polikar, R. Ensemble Learning. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: New York, NY, USA, 2012; pp. 1–34. [Google Scholar]
- Heller, N.; Sathianathen, N.; Kalapara, A.; Walczak, E.; Moore, K.; Kaluzniak, H.; Rosenberg, J.; Blake, P.; Rengel, Z.; Oestreich, M.; et al. The kits19 challenge data: 300 kidney tumor cases with clinical context, ct semantic segmentations, and surgical outcomes. arXiv 2019, arXiv:1904.00445. [Google Scholar]
| Architecture | Loss | DSC ↑ | MSSD (mm) ↓ | DSC ↑ | MSSD (mm) ↓ |
|---|---|---|---|---|---|
| 96 × 96 | 96 × 96 | 128 × 128 | 128 × 128 | ||
| Baseline U-Net | 0.789 ± 0.109 | 8.803 ± 5.947 | 0.855 ± 0.079 | 5.435 ± 5.257 | |
| 0.865 ± 0.075 | 4.229 ± 4.094 | 0.888 ± 0.067 | 3.297 ± 3.951 | ||
| SE U-Net | 0.889 ± 0.060 | 3.199 ± 3.941 | 0.892 ± 0.060 | 2.805 ± 3.087 | |
| 0.879 ± 0.080 | 3.566 ± 4.164 | 0.892 ± 0.057 | 2.654 ± 2.843 | ||
| 0.895 ± 0.060 | 2.357 ± 2.790 | 0.903 ± 0.052 | 2.248 ± 2.719 | ||
| 0.902 ± 0.055 | 2.228 ± 3.045 | 0.899 ± 0.058 | 2.450 ± 3.272 | ||
| CBAM U-Net | 0.878 ± 0.080 | 3.517 ± 4.327 | 0.899 ± 0.056 | 2.490 ± 3.013 | |
| 0.894 ± 0.056 | 2.636 ± 2.648 | 0.898 ± 0.057 | 2.332 ± 2.568 | ||
| 0.880 ± 0.064 | 3.689 ± 4.120 | 0.903 ± 0.060 | 2.549 ± 4.997 | ||
| 0.885 ± 0.073 | 3.520 ± 5.274 | 0.902 ± 0.056 | 2.090 ± 2.683 | ||
| Attention U-Net | 0.882 ± 0.069 | 3.331 ± 3.681 | 0.898 ± 0.057 | 3.158 ± 4.191 | |
| 0.892 ± 0.060 | 3.382 ± 4.790 | 0.901 ± 0.061 | 2.427 ± 3.250 | ||
| 0.886 ± 0.068 | 3.144 ± 4.266 | 0.903 ± 0.054 | 2.461 ± 2.717 | ||
| 0.896 ± 0.060 | 2.621 ± 3.270 | 0.907 ± 0.057 | 2.338 ± 3.987 | ||
| U-Net | 0.885 ± 0.069 | 3.007 ± 3.317 | 0.902 ± 0.061 | 2.228 ± 2.856 | |
| 0.899 ± 0.056 | 2.754 ± 3.541 | 0.909 ± 0.049 | 2.417 ± 3.542 | ||
| Ensemble-4-STAPLE | 0.904 ± 0.058 | 2.479 ± 3.621 | 0.913 ± 0.052 | 1.967 ± 2.841 | |
| Ensemble-7-STAPLE | 0.903 ± 0.059 | 2.472 ± 3.575 | 0.916 ± 0.052 | 1.732 ± 2.467 | |
| Ensemble-4-VOTING | 0.910 ± 0.051 | 1.886 ± 2.615 | 0.914 ± 0.049 | 1.506 ± 2.018 | |
| Ensemble-7-VOTING | 0.910 ± 0.051 | 1.934 ± 2.690 | 0.918 ± 0.048 | 1.484 ± 2.083 |
| Architecture | Loss | DSC ↑ | MSSD (mm) ↓ | DSC ↑ | MSSD (mm) ↓ |
|---|---|---|---|---|---|
| 96 × 96 | 96 × 96 | 128 × 128 | 128 × 128 | ||
| Baseline U-Net | 0.880 ± 0.071 | 2.382 ± 2.950 | 0.902 ± 0.600 | 1.530 ± 2.542 | |
| SE U-Net | 0.897 ± 0.058 | 1.687 ± 1.970 | 0.899 ± 0.055 | 1.630 ± 2.054 | |
| 0.884 ± 0.088 | 2.002 ± 3.000 | 0.899 ± 0.051 | 1.579 ± 1.791 | ||
| 0.894 ± 0.070 | 1.580 ± 1.941 | 0.904 ± 0.057 | 1.290 ± 1.225 | ||
| 0.902 ± 0.060 | 1.438 ± 1.600 | 0.900 ± 0.079 | 1.593 ± 2.912 | ||
| CBAM U-Net | 0.890 ± 0.070 | 1.937 ± 2.620 | 0.906 ± 0.052 | 1.395 ± 1.480 | |
| 0.901 ± 0.057 | 1.367 ± 1.158 | 0.903 ± 0.058 | 1.504 ± 1.863 | ||
| 0.892 ± 0.059 | 1.947 ± 2.228 | 0.910 ± 0.054 | 1.294 ± 1.644 | ||
| 0.896 ± 0.065 | 1.926 ± 2.717 | 0.908 ± 0.054 | 1.346 ± 1.705 | ||
| Attention U-Net | 0.891 ± 0.076 | 1.794 ± 2.046 | 0.910 ± 0.042 | 1.371 ± 1.297 | |
| 0.904 ± 0.056 | 1.588 ± 1.912 | 0.910 ± 0.052 | 1.377 ± 1.671 | ||
| 0.895 ± 0.065 | 1.922 ± 2.757 | 0.911 ± 0.051 | 1.398 ± 1.852 | ||
| 0.905 ± 0.056 | 1.470 ± 1.713 | 0.913 ± 0.051 | 1.312 ± 1.708 | ||
| U-Net | 0.896 ± 0.074 | 1.812 ± 2.643 | 0.909 ± 0.057 | 1.358 ± 1.970 | |
| 0.908 ± 0.054 | 1.480 ± 1.885 | 0.918 ± 0.044 | 1.199 ± 1.525 | ||
| Ensemble-4-STAPLE | 0.909 ± 0.055 | 1.560 ± 2.087 | 0.919 ± 0.048 | 1.204 ± 1.508 | |
| Ensemble-7-STAPLE | 0.909 ± 0.054 | 1.534 ± 1.881 | 0.921 ± 0.048 | 1.174 ± 1.528 | |
| Ensemble-4-VOTING | 0.914 ± 0.053 | 1.204 ± 1.367 | 0.917 ± 0.048 | 1.125 ± 1.340 | |
| Ensemble-7-VOTING | 0.914 ± 0.052 | 1.299 ± 1.620 | 0.922 ± 0.047 | 1.094 ± 1.376 |
| Architecture | Loss | R ↑ | Mean TKV Difference (%) ↓ |
|---|---|---|---|
| Baseline U-Net | 0.915 | −4.43 ± 18.90 | |
| Attention U-Net | 0.962 | −2.04 ± 12.20 | |
| 0.946 | −1.94 ± 16.14 | ||
| 0.951 | −1.63 ± 15.73 | ||
| U-Net | 0.914 | 0.16 ± 16.79 | |
| 0.958 | −1.72 ± 12.50 | ||
| Ensemble-4-STAPLE | 0.953 | −3.11 ± 14.63 | |
| Ensemble-7-STAPLE | 0.957 | −4.00 ± 14.82 | |
| Ensemble-7-VOTING | 0.952 | −0.65 ± 13.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, A.; Tollens, F.; Hansen, L.; Golla, A.-K.; Schad, L.R.; Nörenberg, D.; Zöllner, F.G. Deep Learning-Based Total Kidney Volume Segmentation in Autosomal Dominant Polycystic Kidney Disease Using Attention, Cosine Loss, and Sharpness Aware Minimization. Diagnostics 2022, 12, 1159. https://doi.org/10.3390/diagnostics12051159
Raj A, Tollens F, Hansen L, Golla A-K, Schad LR, Nörenberg D, Zöllner FG. Deep Learning-Based Total Kidney Volume Segmentation in Autosomal Dominant Polycystic Kidney Disease Using Attention, Cosine Loss, and Sharpness Aware Minimization. Diagnostics. 2022; 12(5):1159. https://doi.org/10.3390/diagnostics12051159
Chicago/Turabian StyleRaj, Anish, Fabian Tollens, Laura Hansen, Alena-Kathrin Golla, Lothar R. Schad, Dominik Nörenberg, and Frank G. Zöllner. 2022. "Deep Learning-Based Total Kidney Volume Segmentation in Autosomal Dominant Polycystic Kidney Disease Using Attention, Cosine Loss, and Sharpness Aware Minimization" Diagnostics 12, no. 5: 1159. https://doi.org/10.3390/diagnostics12051159
APA StyleRaj, A., Tollens, F., Hansen, L., Golla, A.-K., Schad, L. R., Nörenberg, D., & Zöllner, F. G. (2022). Deep Learning-Based Total Kidney Volume Segmentation in Autosomal Dominant Polycystic Kidney Disease Using Attention, Cosine Loss, and Sharpness Aware Minimization. Diagnostics, 12(5), 1159. https://doi.org/10.3390/diagnostics12051159






