EEG-Based Mental Tasks Recognition via a Deep Learning-Driven Anomaly Detector
Abstract
1. Introduction
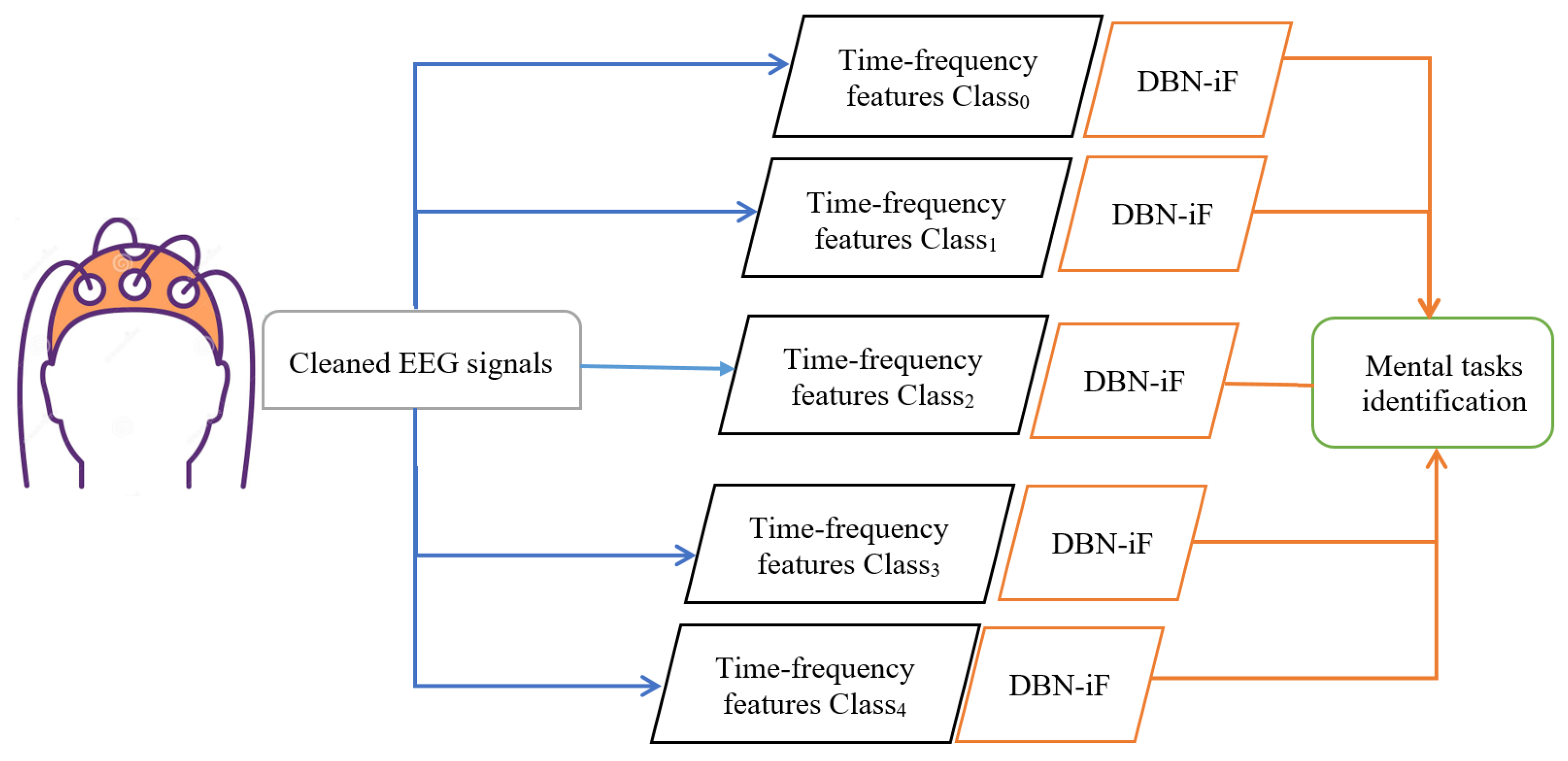
- This work presents a deep learning-based anomaly detection strategy to enhance mental tasks recognition by EEG data. This strategy comprises several stages, i.e., artifacts removal, extraction of time-frequency features of EEG signals, anomaly detection, and classes discrimination. Specifically, the EEG signals are first filtered using the Multichannel Wiener filter (MWF) to remove artifacts and achieve robust recognition. We adopted a quadratic time-frequency distribution (QTFD) for extracting high-resolution time-frequency signal representation of the EEG signals. The employment of a QTFD technique is expected to improve the recognition of mental tasks by capturing the EEG signals’ spectral variations over time. The extracted time-frequency features are inputs to the proposed unsupervised deep learning-based approach for classifying the EEG signals. Indeed, this study treated multiclass classification as a multiple-binary discrimination problem. Specifically, this approach combines the desirable characteristics of both a deep belief network (DBN) and an isolation forest (IF) technique for separating mental tasks based on the time-frequency features of EEG signals. Crucially, this technique profits from the greedy learning characteristics of the DBN for extracting pertinent information from the QTFD features and the capacity of the IF detector to sense outliers. The IF algorithm’s key characteristic is its ability to reveal anomalies without using distance or density metrics. This enables eliminating computational costs related to distance computation in all distance-driven and density-driven models. In addition, the iF detector can handle large-sized datasets with many irrelevant features [13]. Indeed, a single DBN-based IF detector is constructed based on training data in the targeted class, i.e., the samples in such class are considered inliers, and all remaining samples are considered anomalies (i.e., one-vs.-rest). We evaluated the efficacy of this technique through experimental data comprising five mental tasks: mental word association, mental subtraction, spatial navigation, right-hand motor imagery, and feet motor imagery, from a publicly available database from the Institute for Knowledge Discovery, Graz University of Technology, Austria. Thus, to separate the five mental tasks by EEG signals, by using one-vs.-rest method, we constructed five DBN-IF detectors.
- Furthermore, the discrimination capabilities of the DBN-IF scheme have been compared with those of DBN-based Local Outlier Factor (LOF) and Elliptical Envelope (EE) anomaly detection methods. As we know, DBN-based LOF and EE methods have not previously been used for EEG-based mental tasks identification. The essence of LOF is based on the idea of local anomalies [14], while the EE senses anomalies by fitting an ellipse around the data utilizing the Minimum Covariance Determinant [15]. We assessed the performance of the investigated technique using four commonly used statistical scores. Results revealed that the proposed DBN-IF approach dominates the other investigated approaches.
- In addition, the results of the DBN-IF approach are compared with the state-of-the-art techniques; the results demonstrated the proposed approach’s outperformance in improving the separation of metal tasks based on EEG signals.
2. Related Works
3. Materials and Methods
3.1. EEG Artifacts Removal Using Multi-Channel Wienner Filter
3.2. Time-Frequency Representation of EEG Data via a QTFD
3.3. Deep Belief Network (DBN)
3.4. Isolation Forest Approach
4. Deep-Learning-Driven Mental Tasks Detector
5. Results and Discussion
5.1. Data Description
5.2. Experiments and Settings
5.3. Discussion and Analysis
5.4. Comparison with the State-of-the-Art
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Guo, L.; Liu, Y.; Liu, J.; Meng, F. A Temporal-Spectral-Based Squeeze-and-Excitation Feature Fusion Network for Motor Imagery EEG Decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1534–1545. [Google Scholar] [CrossRef]
- Yang, L.; Song, Y.; Ma, K.; Xie, L. Motor imagery EEG decoding method based on a discriminative feature learning strategy. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 368–379. [Google Scholar] [CrossRef] [PubMed]
- Taran, S.; Bajaj, V. Motor imagery tasks-based EEG signals classification using tunable-Q wavelet transform. Neural Comput. Appl. 2019, 31, 6925–6932. [Google Scholar] [CrossRef]
- Dai, M.; Wang, S.; Zheng, D.; Na, R.; Zhang, S. Domain Transfer Multiple Kernel Boosting for Classification of EEG Motor Imagery Signals. IEEE Access 2019, 7, 49951–49960. [Google Scholar] [CrossRef]
- Duan, L.; Li, J.; Ji, H.; Pang, Z.; Zheng, X.; Lu, R.; Li, M.; Zhuang, J. Zero-Shot Learning for EEG Classification in Motor Imagery-Based BCI System. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2411–2419. [Google Scholar] [CrossRef]
- Taran, S.; Bajaj, V.; Sharma, D.; Siuly, S.; Sengur, A. Features based on analytic IMF for classifying motor imagery EEG signals in BCI applications. Measurement 2018, 116, 68–76. [Google Scholar] [CrossRef]
- Siuly, S.; Li, Y. Discriminating the brain activities for brain–computer interface applications through the optimal allocation-based approach. Neural Comput. Appl. 2015, 26, 799–811. [Google Scholar] [CrossRef]
- Kevric, J.; Subasi, A. Comparison of signal decomposition methods in classification of EEG signals for motor-imagery BCI system. Biomed. Signal Process. Control 2017, 31, 398–406. [Google Scholar] [CrossRef]
- Gaur, P.; Gupta, H.; Chowdhury, A.; McCreadie, K.; Pachori, R.B.; Wang, H. A Sliding Window Common Spatial Pattern for Enhancing Motor Imagery Classification in EEG-BCI. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Z.; Zhang, B.; Feng, B.; Yu, T.; Li, Z. Fused Group Lasso: A New EEG Classification Model With Spatial Smooth Constraint for Motor Imagery-Based Brain–Computer Interface. IEEE Sens. J. 2021, 21, 1764–1778. [Google Scholar] [CrossRef]
- Verma, N.K.; Rao, L.V.S.; Sharma, S.K. Motor imagery EEG signal classification on DWT and crosscorrelated signal features. In Proceedings of the 2014 IEEE 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; pp. 1–6. [Google Scholar]
- Chatterjee, R.; Maitra, T.; Islam, S.H.; Hassan, M.M.; Alamri, A.; Fortino, G. A novel machine learning based feature selection for motor imagery EEG signal classification in Internet of medical things environment. Future Gener. Comput. Syst. 2019, 98, 419–434. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 IEEE Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. ACM Sigmod Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Hubert, M.; Debruyne, M.; Rousseeuw, P.J. Minimum covariance determinant and extensions. Wiley Interdiscip. Rev. Comput. Stat. 2018, 10, e1421. [Google Scholar] [CrossRef]
- Harrou, F.; Sun, Y.; Hering, A.S.; Madakyaru, M. Statistical Process Monitoring Using Advanced Data-driven and Deep Learning Approaches: Theory and Practical Applications; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Dairi, A.; Harrou, F.; Sun, Y. Deep Generative Learning-based 1-SVM Detectors for Unsupervised COVID-19 Infection Detection Using Blood Tests. IEEE Trans. Instrum. Meas. 2021, 71, 2500211. [Google Scholar] [CrossRef]
- Wang, W.; Lee, J.; Harrou, F.; Sun, Y. Early detection of Parkinson’s disease using deep learning and machine learning. IEEE Access 2020, 8, 147635–147646. [Google Scholar] [CrossRef]
- Bashivan, P.; Rish, I.; Yeasin, M.; Codella, N. Learning representations from EEG with deep recurrent-convolutional neural networks. arXiv 2015, arXiv:1511.06448. [Google Scholar]
- Liang, N.Y.; Saratchandran, P.; Huang, G.B.; Sundararajan, N. Classification of mental tasks from EEG signals using extreme learning machine. Int. J. Neural Syst. 2006, 16, 29–38. [Google Scholar] [CrossRef]
- Zeng, H.; Yang, C.; Dai, G.; Qin, F.; Zhang, J.; Kong, W. EEG classification of driver mental states by deep learning. Cogn. Neurodyn. 2018, 12, 597–606. [Google Scholar] [CrossRef]
- Opałka, S.; Stasiak, B.; Szajerman, D.; Wojciechowski, A. Multi-channel convolutional neural networks architecture feeding for effective EEG mental tasks classification. Sensors 2018, 18, 3451. [Google Scholar] [CrossRef]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2016, 14, 016003. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, A.; Liu, X.; Shang, J.; Zhang, L. LSTM-Based EEG Classification in Motor Imagery Tasks. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2086–2095. [Google Scholar] [CrossRef]
- Lu, N.; Li, T.; Ren, X.; Miao, H. A Deep Learning Scheme for Motor Imagery Classification based on Restricted Boltzmann Machines. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 566–576. [Google Scholar] [CrossRef]
- Jeong, J.H.; Lee, B.H.; Lee, D.H.; Yun, Y.D.; Lee, S.W. EEG classification of forearm movement imagery using a hierarchical flow convolutional neural network. IEEE Access 2020, 8, 66941–66950. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, K.; Jian, D.; Yao, L. Motor Imagery Classification via Temporal Attention Cues of Graph Embedded EEG Signals. IEEE J. Biomed. Health Inform. 2020, 24, 2570–2579. [Google Scholar] [CrossRef]
- Chaudhary, S.; Taran, S.; Bajaj, V.; Sengur, A. Convolutional Neural Network Based Approach Towards Motor Imagery Tasks EEG Signals Classification. IEEE Sens. J. 2019, 19, 4494–4500. [Google Scholar] [CrossRef]
- Zhang, G.; Davoodnia, V.; Sepas-Moghaddam, A.; Zhang, Y.; Etemad, A. Classification of Hand Movements from EEG Using a Deep Attention-Based LSTM Network. IEEE Sens. J. 2020, 20, 3113–3122. [Google Scholar] [CrossRef]
- Jiang, X.; Bian, G.B.; Tian, Z. Removal of artifacts from EEG signals: A review. Sensors 2019, 19, 987. [Google Scholar] [CrossRef]
- Alazrai, R.; Alwanni, H.; Baslan, Y.; Alnuman, N.; Daoud, M.I. Eeg-based brain-computer interface for decoding motor imagery tasks within the same hand using choi-williams time-frequency distribution. Sensors 2017, 17, 1937. [Google Scholar] [CrossRef]
- Hahn, S.L. Hilbert Transforms in Signal Processing; Artech House Signal Processing: Norwood, MA, USA, 1996. [Google Scholar]
- Smolensky, P. Information Processing in Dynamical Systems: Foundations of Harmony Theory. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1987; pp. 194–281. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends® Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Li, T.; Wang, B.; Jiang, Y.; Zhang, Y.; Yan, Y. Restricted Boltzmann machine-based approaches for link prediction in dynamic networks. IEEE Access 2018, 6, 29940–29951. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mensi, A.; Bicego, M. Enhanced Anomaly Scores for Isolation Forests. Pattern Recognit. 2021, 120, 108115. [Google Scholar] [CrossRef]
- Dairi, A.; Harrou, F.; Sun, Y. Efficient Driver Drunk Detection by Sensors: A Manifold Learning-Based Anomaly Detector. IEEE Access 2022, 10, 119001–119012. [Google Scholar] [CrossRef]
- Scherer, R.; Faller, J.; Friedrich, E.V.; Opisso, E.; Costa, U.; Kübler, A.; Müller-Putz, G.R. Individually adapted imagery improves brain-computer interface performance in end-users with disability. PLoS ONE 2015, 10, e0123727. [Google Scholar] [CrossRef]
- Homan, R.W.; Herman, J.; Purdy, P. Cerebral location of international 10–20 system electrode placement. Electroencephalogr. Clin. Neurophysiol. 1987, 66, 376–382. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Driessen, K.V. A fast algorithm for the minimum covariance determinant estimator. Technometrics 1999, 41, 212–223. [Google Scholar] [CrossRef]
- Zhang, C.; Kim, Y.K.; Eskandarian, A. EEG-inception: An accurate and robust end-to-end neural network for EEG-based motor imagery classification. J. Neural Eng. 2021, 18, 046014. [Google Scholar] [CrossRef]
- Roy, A.M. A CNN Model with Feature Integration for MI EEG Subject Classification in BMI. Available online: https://www.biorxiv.org/content/10.1101/2022.01.05.475058v3.full (accessed on 28 February 2022).
- Dairi, A.; Harrou, F.; Khadraoui, S.; Sun, Y. Integrated multiple directed attention-based deep learning for improved air pollution forecasting. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, T.; Sun, S.; Liu, Z. Research and improvement of isolation forest in detection of local anomaly points. J. Phys. Conf. Ser. 2019, 1237, 052023. [Google Scholar] [CrossRef]
- Kadri, F.; Dairi, A.; Harrou, F.; Sun, Y. Towards accurate prediction of patient length of stay at emergency department: A GAN-driven deep learning framework. J. Ambient. Intell. Humaniz. Comput. 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Harrou, F.; Dairi, A.; Zeroual, A.; Sun, Y. Forecasting of Bicycle and Pedestrian Traffic Using Flexible and Efficient Hybrid Deep Learning Approach. Appl. Sci. 2022, 12, 4482. [Google Scholar] [CrossRef]
- Harrou, F.; Fillatre, L.; Bobbia, M.; Nikiforov, I. Statistical detection of abnormal ozone measurements based on constrained generalized likelihood ratio test. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 4997–5002. [Google Scholar]








| CLASS | OTHERS | Accuracy | Precision | F1-Score | AUC |
|---|---|---|---|---|---|
| 1 | 2 | 0.9779 | 0.9666 | 0.9781 | 0.9779 |
| 1 | 3 | 0.9870 | 0.9841 | 0.9870 | 0.9870 |
| 1 | 4 | 0.9902 | 0.9905 | 0.9902 | 0.9902 |
| 1 | 5 | 0.9840 | 0.9782 | 0.9840 | 0.9840 |
| 2 | 1 | 0.9918 | 0.9936 | 0.9918 | 0.9918 |
| 2 | 3 | 0.9912 | 0.9925 | 0.9912 | 0.9912 |
| 2 | 4 | 0.9924 | 0.9948 | 0.9924 | 0.9924 |
| 2 | 5 | 0.9920 | 0.9941 | 0.9920 | 0.9920 |
| 3 | 1 | 0.9917 | 0.9934 | 0.9917 | 0.9917 |
| 3 | 2 | 0.9867 | 0.9836 | 0.9867 | 0.9867 |
| 3 | 4 | 0.9909 | 0.9918 | 0.9908 | 0.9909 |
| 3 | 5 | 0.9892 | 0.9883 | 0.9892 | 0.9892 |
| 4 | 1 | 0.9806 | 0.9716 | 0.9808 | 0.9806 |
| 4 | 2 | 0.9593 | 0.9327 | 0.9605 | 0.9593 |
| 4 | 3 | 0.9762 | 0.9636 | 0.9766 | 0.9762 |
| 4 | 5 | 0.9580 | 0.9304 | 0.9593 | 0.9580 |
| 5 | 1 | 0.9910 | 0.9921 | 0.9910 | 0.9910 |
| 5 | 2 | 0.9881 | 0.9862 | 0.9881 | 0.9881 |
| 5 | 3 | 0.9899 | 0.9898 | 0.9899 | 0.9899 |
| 5 | 4 | 0.9917 | 0.9934 | 0.9917 | 0.9917 |
| CLASS | OTHERS | Accuracy | Precision | F1-Score | AUC |
|---|---|---|---|---|---|
| 1 | 2 | 0.9083 | 0.8498 | 0.9154 | 0.9083 |
| 1 | 3 | 0.9172 | 0.8628 | 0.9229 | 0.9172 |
| 1 | 4 | 0.9779 | 0.9647 | 0.9782 | 0.9779 |
| 1 | 5 | 0.8799 | 0.8103 | 0.8920 | 0.8799 |
| 2 | 1 | 0.8983 | 0.8345 | 0.9072 | 0.8983 |
| 2 | 3 | 0.9321 | 0.8847 | 0.9360 | 0.9321 |
| 2 | 4 | 0.9621 | 0.9346 | 0.9632 | 0.9621 |
| 2 | 5 | 0.9604 | 0.9317 | 0.9617 | 0.9604 |
| 3 | 1 | 0.9607 | 0.9313 | 0.9620 | 0.9607 |
| 3 | 2 | 0.9588 | 0.9279 | 0.9602 | 0.9588 |
| 3 | 4 | 0.9951 | 0.9955 | 0.9951 | 0.9951 |
| 3 | 5 | 0.9611 | 0.9320 | 0.9623 | 0.9611 |
| 4 | 1 | 0.9050 | 0.8463 | 0.9124 | 0.9050 |
| 4 | 2 | 0.8979 | 0.8363 | 0.9065 | 0.8979 |
| 4 | 3 | 0.9383 | 0.8975 | 0.9413 | 0.9383 |
| 4 | 5 | 0.9070 | 0.8492 | 0.9141 | 0.9070 |
| 5 | 1 | 0.9478 | 0.9107 | 0.9501 | 0.9478 |
| 5 | 2 | 0.9866 | 0.9805 | 0.9867 | 0.9866 |
| 5 | 3 | 0.9850 | 0.9774 | 0.9851 | 0.9850 |
| 5 | 4 | 0.9876 | 0.9823 | 0.9876 | 0.9876 |
| CLASS | OTHERS | Accuracy | Precision | F1-Score | AUC |
|---|---|---|---|---|---|
| 1 | 2 | 0.9187 | 0.8664 | 0.9241 | 0.9187 |
| 1 | 3 | 0.8995 | 0.8383 | 0.9078 | 0.8995 |
| 1 | 4 | 0.9015 | 0.8411 | 0.9095 | 0.9015 |
| 1 | 5 | 0.8436 | 0.7659 | 0.8636 | 0.8436 |
| 2 | 1 | 0.7846 | 0.7017 | 0.8213 | 0.7846 |
| 2 | 3 | 0.9122 | 0.8567 | 0.9185 | 0.9122 |
| 2 | 4 | 0.9421 | 0.9035 | 0.9447 | 0.9421 |
| 2 | 5 | 0.9168 | 0.8637 | 0.9225 | 0.9168 |
| 3 | 1 | 0.9606 | 0.9350 | 0.9617 | 0.9606 |
| 3 | 2 | 0.9716 | 0.9550 | 0.9722 | 0.9716 |
| 3 | 4 | 0.9905 | 0.9912 | 0.9905 | 0.9905 |
| 3 | 5 | 0.9718 | 0.9553 | 0.9723 | 0.9718 |
| 4 | 1 | 0.9172 | 0.8643 | 0.9228 | 0.9172 |
| 4 | 2 | 0.7579 | 0.6762 | 0.8035 | 0.7579 |
| 4 | 3 | 0.9134 | 0.8585 | 0.9195 | 0.9134 |
| 4 | 5 | 0.7833 | 0.7004 | 0.8204 | 0.7832 |
| 5 | 1 | 0.9126 | 0.8574 | 0.9189 | 0.9126 |
| 5 | 2 | 0.9769 | 0.9648 | 0.9772 | 0.9769 |
| 5 | 3 | 0.9790 | 0.9687 | 0.9792 | 0.9790 |
| 5 | 4 | 0.9705 | 0.9528 | 0.9710 | 0.9705 |
| CLASS | iF | LOF | EE |
|---|---|---|---|
| 1 | 0.9848 | 0.9208 | 0.8908 |
| 2 | 0.9919 | 0.9382 | 0.8889 |
| 3 | 0.9896 | 0.9689 | 0.9736 |
| 4 | 0.9685 | 0.9120 | 0.8429 |
| 5 | 0.9902 | 0.9768 | 0.9597 |
| Paper | The Used Features | Approach | Accuracy (%) |
|---|---|---|---|
| [6] | EMD | LS-SVM | 97.56 |
| [3] | TQWT | LS-SVM | 96.89 |
| [23] | STFT and electrode location information | CNN-SAE | 90 |
| [8] | MSPCA, DWT and WPD | KNN | 92.8 |
| [11] | cross-correlation and DWT coefficients | LR | 92.3 |
| KLR | 94.3 | ||
| MLP | 94.9 | ||
| PNN | 92.9 | ||
| LS-SVM | 96.1 | ||
| [7] | Optimal allocation features | LS-SVM | 96.62 |
| Naive Bayes | 96.36 | ||
| [44] | EEG-inception (time-series signals) with data augmentation | CNN | 88.58 |
| [45] | Semantic, intrinsic, and user-specific features (with data augmentation) | multi-scale CNN | 93.74 |
| This study | QTFD | DBN-iF | 98.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dairi, A.; Zerrouki, N.; Harrou, F.; Sun, Y. EEG-Based Mental Tasks Recognition via a Deep Learning-Driven Anomaly Detector. Diagnostics 2022, 12, 2984. https://doi.org/10.3390/diagnostics12122984
Dairi A, Zerrouki N, Harrou F, Sun Y. EEG-Based Mental Tasks Recognition via a Deep Learning-Driven Anomaly Detector. Diagnostics. 2022; 12(12):2984. https://doi.org/10.3390/diagnostics12122984
Chicago/Turabian StyleDairi, Abdelkader, Nabil Zerrouki, Fouzi Harrou, and Ying Sun. 2022. "EEG-Based Mental Tasks Recognition via a Deep Learning-Driven Anomaly Detector" Diagnostics 12, no. 12: 2984. https://doi.org/10.3390/diagnostics12122984
APA StyleDairi, A., Zerrouki, N., Harrou, F., & Sun, Y. (2022). EEG-Based Mental Tasks Recognition via a Deep Learning-Driven Anomaly Detector. Diagnostics, 12(12), 2984. https://doi.org/10.3390/diagnostics12122984






