A 3-D Full Convolution Electromagnetic Reconstruction Neural Network (3-D FCERNN) for Fast Super-Resolution Electromagnetic Inversion of Human Brain
Abstract
1. Introduction
2. Materials and Methods
2.1. Mixed FEM for Forward Simulation
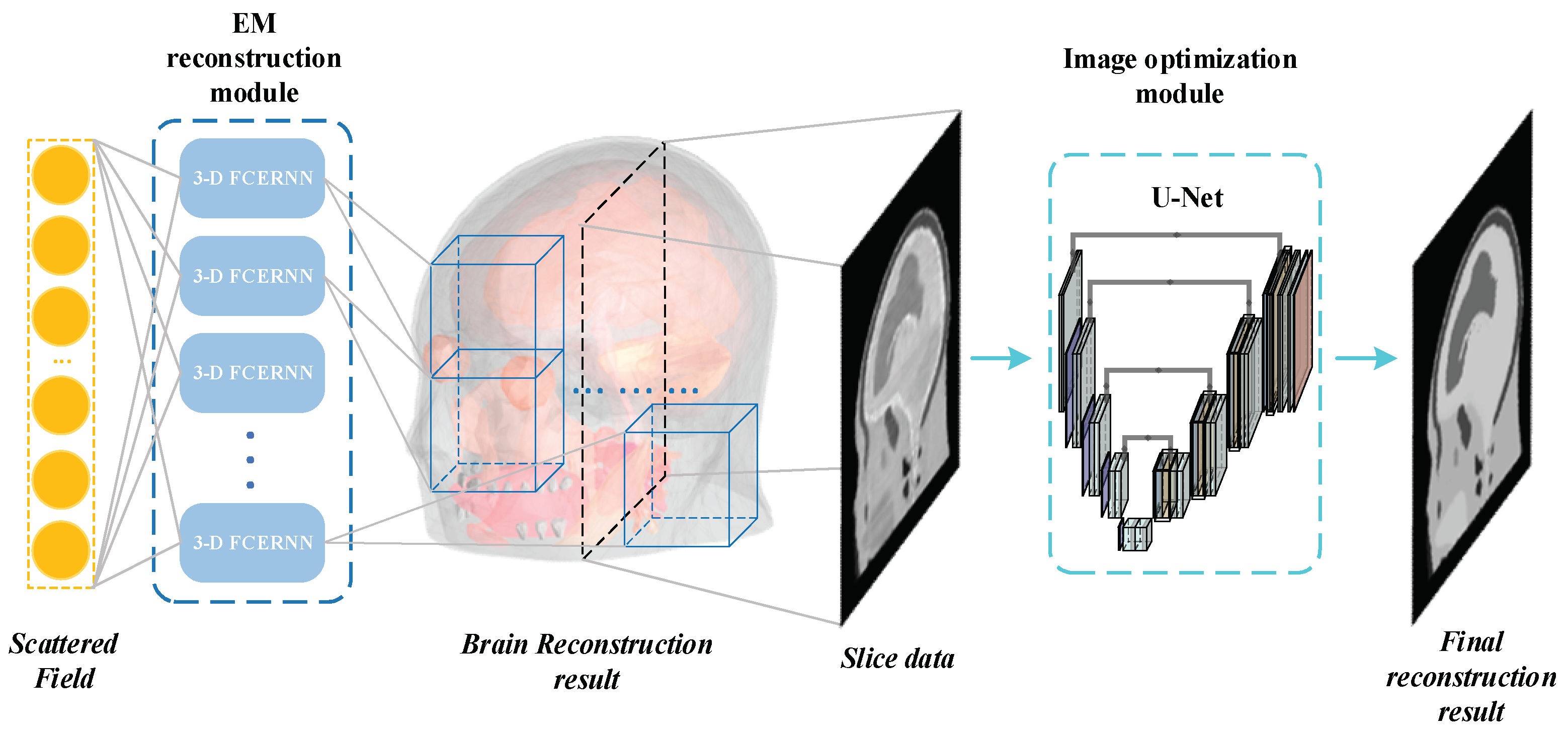
2.2. Proposed Deep Learning Inversion Scheme
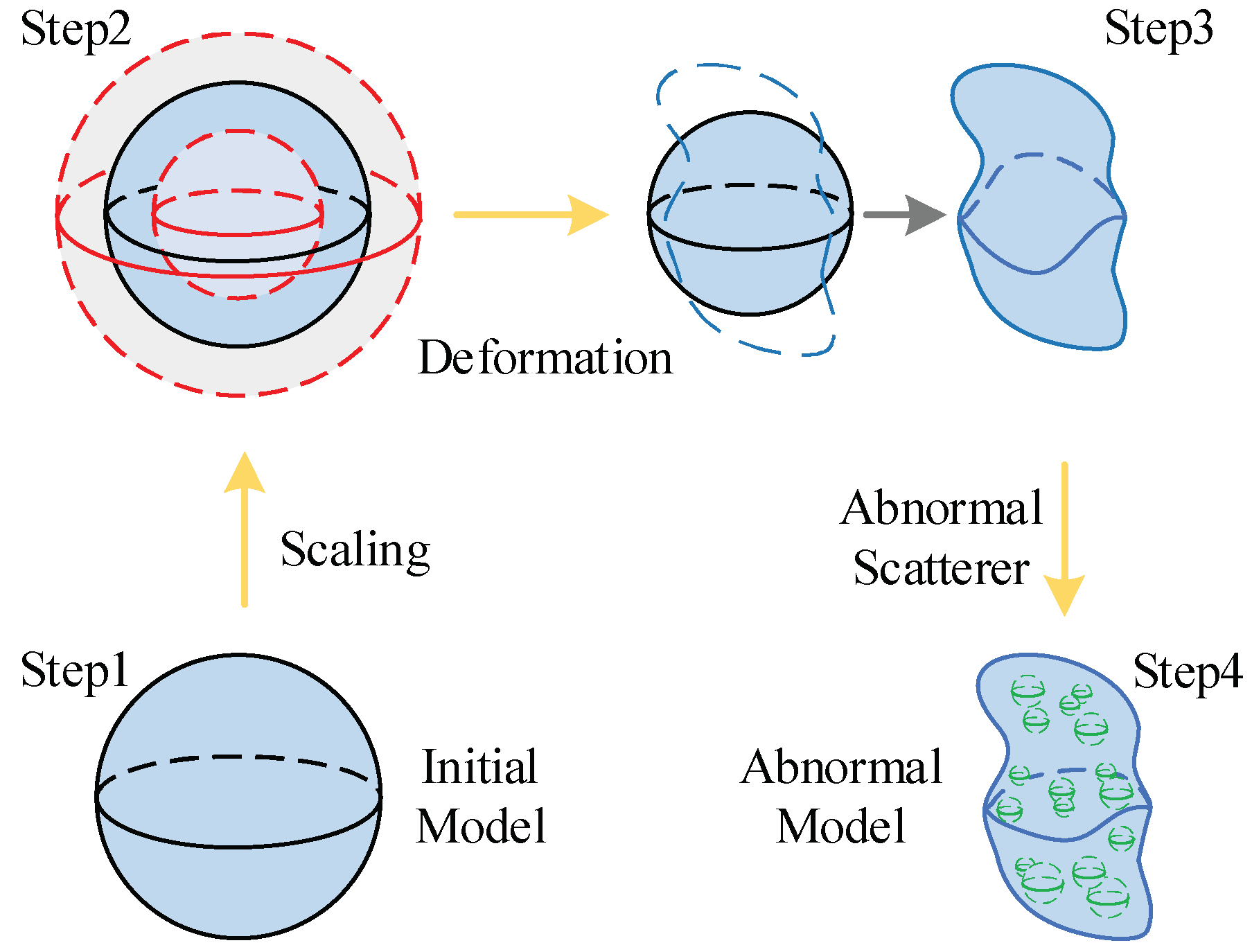
2.2.1. Training Dataset Building Strategy
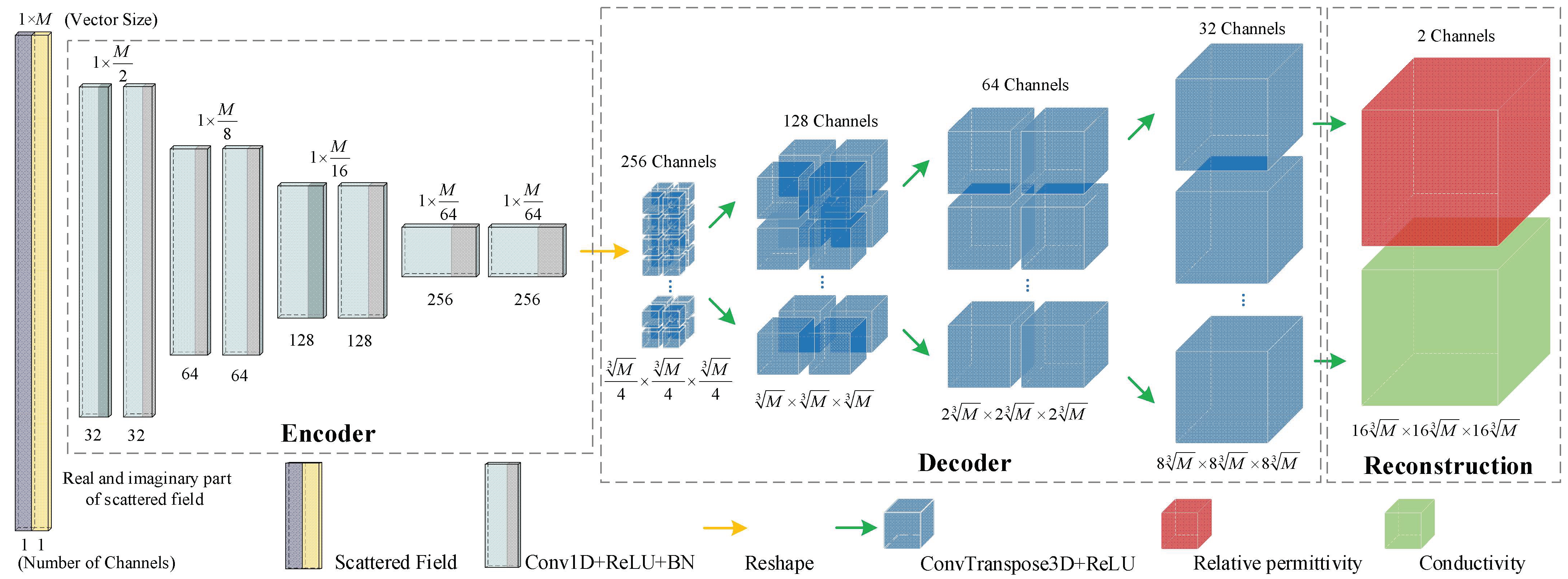
2.2.2. 3-D FCERNN
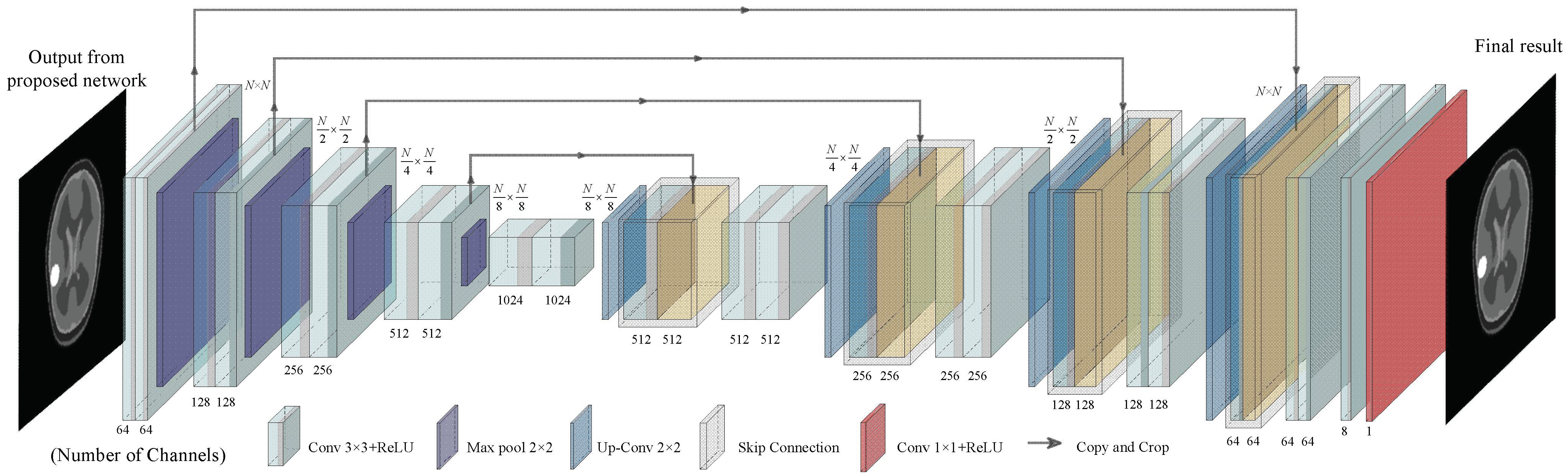
2.2.3. U-Net
3. Results
3.1. Electromagnetic Inversion Simulation Experiment Settings
3.2. Setups of Training Sample and Network
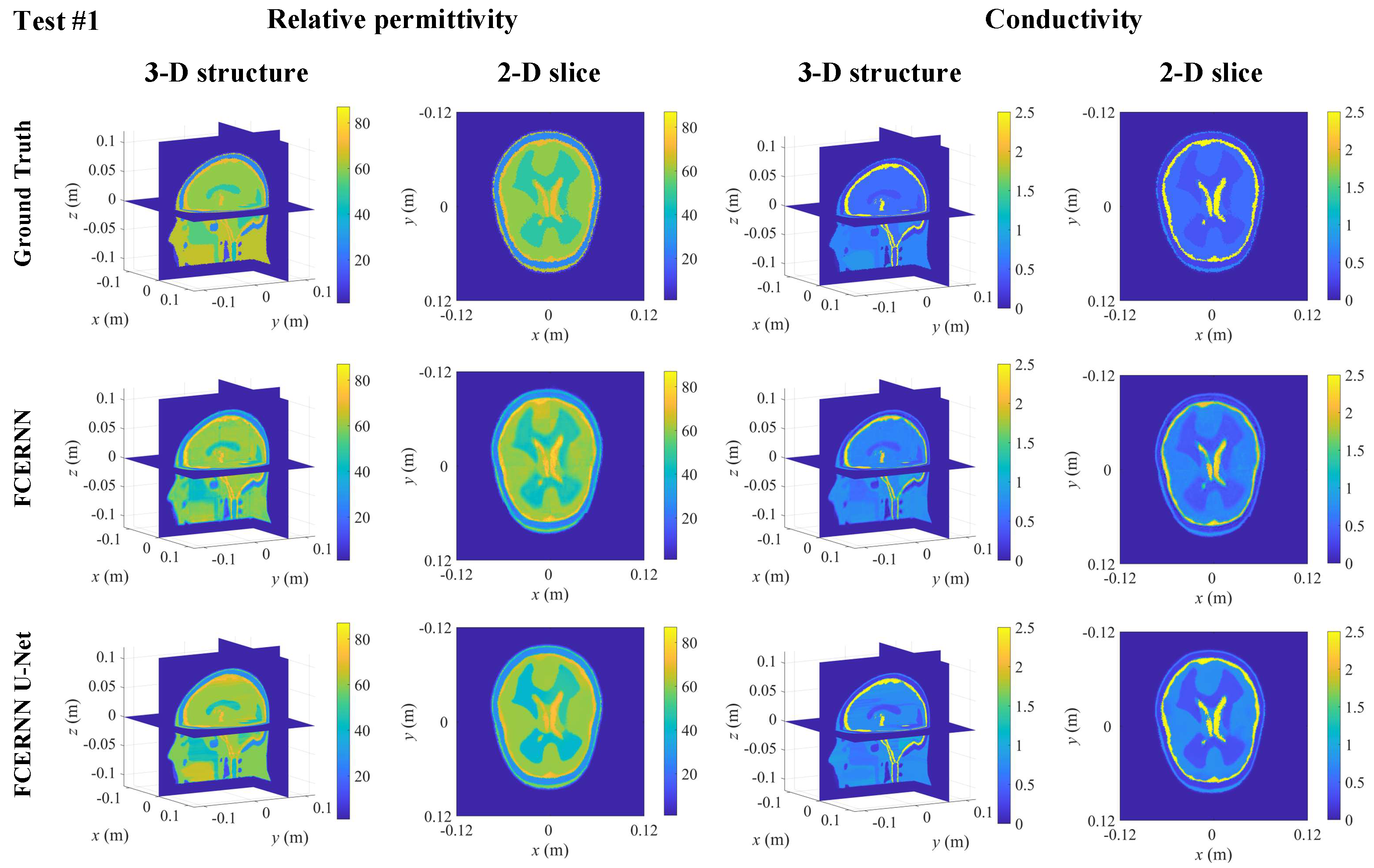
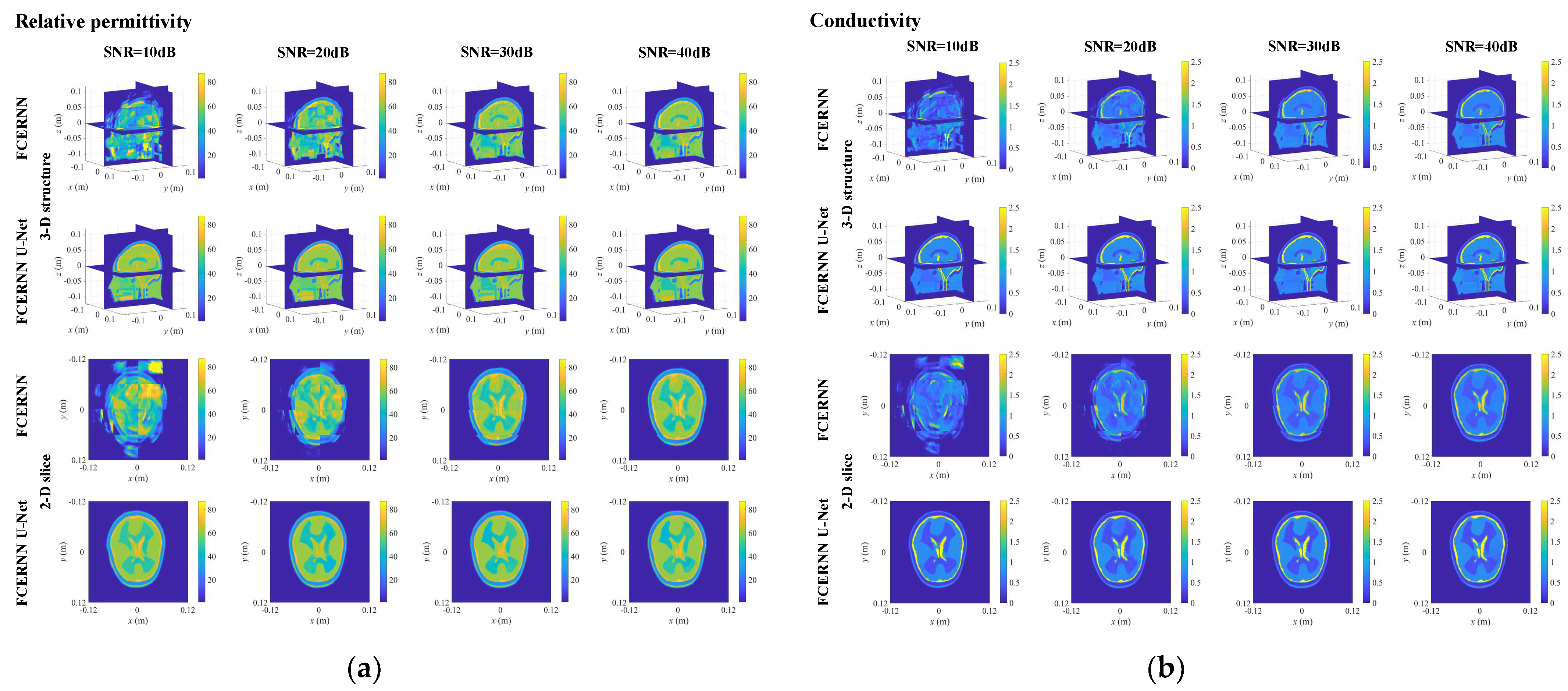
3.3. Case I: Normal Human Brain
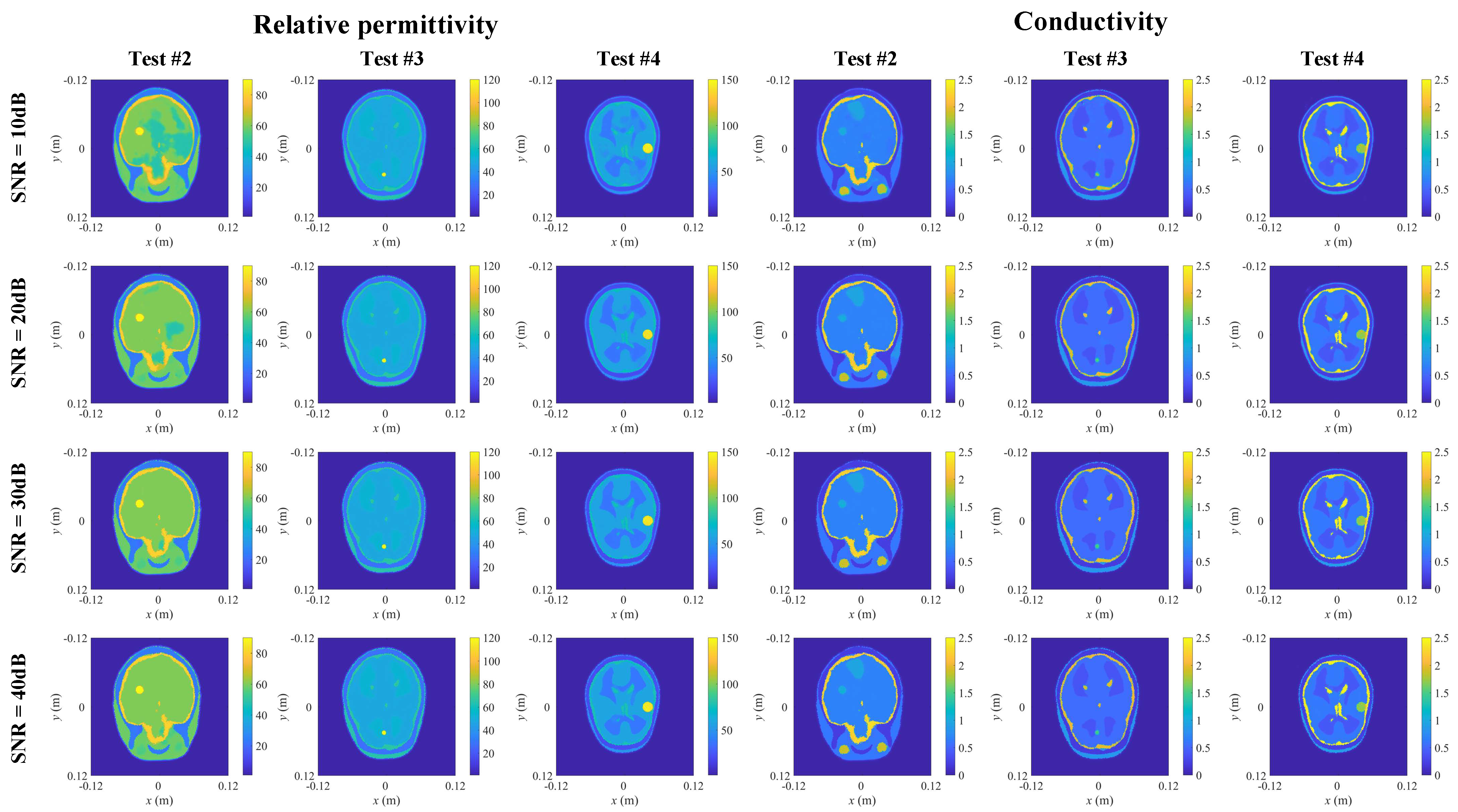
3.4. Case II: Detection of Anomalies
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tournier, P.-H.; Bonazzoli, M.; Dolean, V.; Rapetti, F.; Hecht, F.; Nataf, F.; Aliferis, I.; El Kanfoud, I.; Migliaccio, C.; de Buhan, M.; et al. Numerical modeling and high-speed parallel computing: New perspectives on tomographic microwave imaging for brain stroke detection and monitoring. IEEE Antennas Propag. Mag. 2017, 59, 98–110. [Google Scholar] [CrossRef]
- Meaney, P.M.; Fanning, M.W.; Li SP, P.D.; Paulsen, K.D. A clinical prototype for active microwave imaging of the breast. IEEE Trans. Microw. Theory Tech. 2000, 48, 1841–1853. [Google Scholar]
- Abubakar, A.; Van den Berg, P.M.; Mallorqui, J.J. Imaging of biomedical data using a multiplicative regularized contrast source inversion method. IEEE Trans. Microw. Theory Tech. 2002, 50, 1761–1771. [Google Scholar] [CrossRef]
- Cui, T.J.; Chew, W.C.; Aydiner, A.A.; Chen, S. Inverse scattering of two-dimensional dielectric objects buried in a lossy earth using the distorted Born iterative method. IEEE Trans. Geosci. Rremote Sens. 2001, 39, 339–346. [Google Scholar]
- Catapano, I.; Randazzo, A.; Slob, E.; Solimene, R. GPR imaging via qualitative and quantitative approaches. In Civil Engineering Applications of Ground Penetrating Radar; Benedetto, A., Pajewski, L., Eds.; Springer: Cham, Switzerland, 2015; pp. 239–280. [Google Scholar]
- Zhong, Y.; Chen, X. An FFT twofold subspace-based optimization method for solving electromagnetic inverse scattering problems. IEEE Trans. Antennas Propag. 2011, 59, 914–927. [Google Scholar] [CrossRef]
- Caorsi, S.; Massa, A.; Pastorino, M.; Donelli, M. Improved microwave imaging procedure for nondestructive evaluations of twodimensional structures. IEEE Trans. Antennas Propag. 2004, 52, 2793–2798. [Google Scholar] [CrossRef]
- Pastorino, M. Stochastic optimization methods applied to microwave imaging: A review. IEEE Trans. Antennas Propag. 2007, 55, 538–548. [Google Scholar] [CrossRef]
- Solimene, R.; Soldovieri, F.; Prisco, G. A multiarray tomographic approach for through-wall imaging. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1192–1199. [Google Scholar] [CrossRef]
- Song, L.-P.; Liu, Q.H. A new approximation to three-dimensional electromagnetic scattering. IEEE Geosci. Remote Sens. Lett. 2005, 2, 238–242. [Google Scholar] [CrossRef]
- Monte, L.L.; Erricolo, D.; Soldovieri, F.; Wicks, M.C. Radio frequency tomography for tunnel detection. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1128–1137. [Google Scholar] [CrossRef]
- Xu, K.; Zhong, Y.; Wang, G. A hybrid regularization technique for solving highly nonlinear inverse scattering problems. IEEE Trans. Microw. Theory Techn. 2018, 66, 11–21. [Google Scholar] [CrossRef]
- Habashy, T.M.; Oristaglio, M.L.; de Hoop, A.T. Simultaneous nonlinear reconstruction of two-dimensional permittivity and conductivity. Radio Sci. 1994, 29, 1101–1118. [Google Scholar] [CrossRef]
- Berg, P.M.V.D.; Kleinman, R.E. A contrast source inversion method. Inverse Probl. 1997, 13, 1607–1620. [Google Scholar] [CrossRef]
- Berg, P.M.V.D.; Broekhoven, A.L.V.; Abubakar, A. Extended contrast source inversion. Inverse Probl. 1999, 15, 1325–1344. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chew, W.C. An iterative solution of the twodimensional electromagnetic inverse scattering problem. Int. J. Imageing Syst. Technol. 1989, 1, 100–108. [Google Scholar] [CrossRef]
- Chen, X. Subspace-based optimization method for solving inverse-scattering problems. IEEE Trans. Geosci. Remote Sens. 2010, 48, 42–49. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, X. Physics-inspired convolutional neural network for solving full-wave inverse scattering problems. IEEE Trans. Antennas Propag. 2019, 67, 6138–6148. [Google Scholar] [CrossRef]
- Chen, X.; Wei, Z.; Li, M.; Rocca, P. A review of deep learning approaches for inverse scattering problems (invited review). Prog. Electromagn. Res. 2020, 167, 67–81. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.G.; Teixeira, F.L.; Liu, C.; Nehorai, A.; Cui, T.J. DeepNIS: Deep neural network for nonlinear electromagnetic inverse scattering. IEEE Trans. Antennas Propag. 2019, 67, 1819–1825. [Google Scholar] [CrossRef]
- Yao, H.M.; Jiang, L.; Sha, W. Enhanced Deep Learning Approach Based on the Deep Convolutional Encoder–Decoder Architecture for Electromagnetic Inverse Scattering Problems. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1211–1215. [Google Scholar] [CrossRef]
- Xiao, L.-Y.; Li, J.; Han, F.; Hu, H.-J.; Zhuang, M.; Liu, Q.H. Super-Resolution 3-D Microwave Imaging of Objects With High Contrasts by a Semijoin Extreme Learning Machine. IEEE Trans. Microw. Theory Tech. 2021, 69, 4840–4855. [Google Scholar] [CrossRef]
- Jorgenson, L.A.; Newsome, W.T.; Anderson, D.J.; Bargmann, C.I.; Brown, E.N.; Deisseroth, K.; Donoghue, J.P. The BRAIN initiative: Developing technology to catalyse neuroscience discovery. Philos. Trans. R. Soc. B 2015, 370, 20140164. [Google Scholar] [CrossRef] [PubMed]
- Saeed, S.; Abdullah, A.B. Investigation of a Brain Cancer with Interfacing of 3-Dimensional Image Processing. In Proceedings of the 2019 International Conference on Information Science and Communication Technology (ICISCT), Karachi, Pakistan, 9–10 March 2019; pp. 1–6. [Google Scholar]
- Mariano, V.; Vasquez, J.A.T.; Scapaticci, R.; Crocco, L.; Kosmas, P.; Vipiana, F. Comparison of Reconstruction Algorithms for Brain Stroke Microwave Imaging. In Proceedings of the 2020 IEEE MTT-S International Microwave Biomedical Conference (IMBioC), Toulouse, France, 14–17 December 2020; pp. 1–3. [Google Scholar]
- Fedeli, A.; Schenone, V.; Randazzo, A.; Pastorino, M.; Henriksson, T.; Semenov, S. Nonlinear S-parameters inversion for stroke imaging. IEEE Trans. Microw. Theory Technol. 2021, 69, 1760–1771. [Google Scholar] [CrossRef]
- Coli, V.L.; Tournier, P.-H.; Dolean, V.; El Kanfoud, I.; Pichot, C.; Migliaccio, C.; Blanc-Féraud, L. Detection of Simulated Brain Strokes Using Microwave Tomography. IEEE J. Electromagn. RF Microw. Med. Biol. 2019, 3, 254–260. [Google Scholar] [CrossRef]
- Bisio, I.; Estatico, C.; Fedeli, A.; Lavagetto, F.; Pastorino, M.; Randazzo, A.; Sciarrone, A. Variable-exponent lebesgue-space inversion for brain stroke microwave imaging. IEEE Trans. Microw. Theory Technol. 2020, 68, 1882–1895. [Google Scholar] [CrossRef]
- Ramamoorthy, M.; Qamar, S.; Manikandan, R.; Jhanjhi, N.Z.; Masud, M.; AlZain, M.A. Earlier Detection of Brain Tumor by PreProcessing Based on Histogram Equalization with Neural Network. Healthcare 2022, 10, 1218. [Google Scholar] [CrossRef]
- Xiao, L.-Y.; Hong, R.; Zhao, L.-Y.; Hu, H.-J.; Liu, Q.H. A Hybrid Neural Network Electromagnetic Inversion Scheme (HNNEMIS) for Super-Resolution 3-Dimensional Microwave Human Brain Imaging. IEEE Trans. Antennas Propag. 2022, 70, 6277–6286. [Google Scholar] [CrossRef]
- Hong, R.; Chen, K.; Hou, X.; Sun, Q.; Liu, N.; Liu, Q.H. Mixed finite element method for full-wave simulation of bioelectromagnetism from DC to microwave frequencies. IEEE Trans. Biomed. Eng. 2020, 67, 2765–2772. [Google Scholar] [CrossRef]
- Makarov, S.N.; Noetscher, G.M.; Yanamadala, J.; Piazza, M.W.; Louie, S.; Prokop, A.; Nazarian, A.; Nummenmaa, A. Virtual human models for electromagnetic studies and their applications. IEEE Rev. Biomed. Eng. 2017, 10, 95–121. [Google Scholar] [CrossRef]
- Gabriel, C. Compilation of the Dielectric Properties of Body Tissues at RF and Microwave Frequencies; Brooks Air Force Base: San Antonio, TX, USA, 1996. [Google Scholar]
- Bulò, S.R.; Porzi, L.; Kontschieder, P. In-place Activated BatchNorm for Memory-Optimized Training of DNNs. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 5639–5647. [Google Scholar]
- Ronneberge, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Lecture Notes in Computer Science, Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
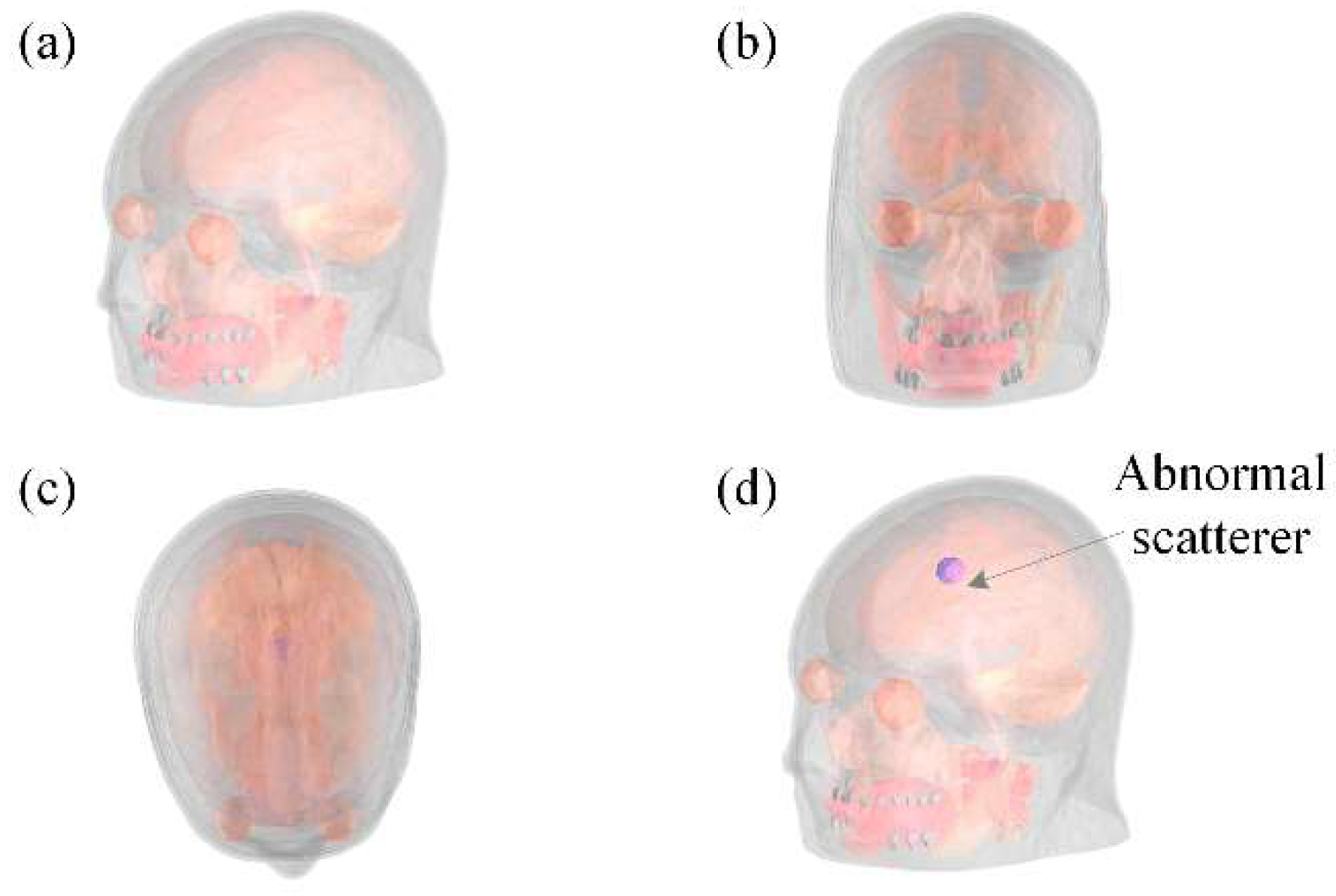

| Testing Model | Normal Model | Abnormal Model | ||
|---|---|---|---|---|
| Test #1 | Test #2 | Test #3 | Test #4 | |
| Model misfit | ||||
| Max model misfit (%) | 84.27 | 104.61 | 95.60 | 73.57 |
| Min model misfit (%) | 13.98 | 12.02 | 9.42 | 11.04 |
| Average model misfit (%) | 56.34 | 66.42 | 57.24 | 58.04 |
| Noise Level | 3-D FCERNN | 3-D FCERNN-U-Net | ||
|---|---|---|---|---|
| Model Misfit (%) | Data Misfit (%) | Model Misfit (%) | Data Misfit (%) | |
| Noise Free | 20.16 | 16.96 | 19.54 | 15.53 |
| −10 dB | 71.72 | 67.47 | 26.78 | 25.84 |
| −20 dB | 48.92 | 37.14 | 21.34 | 18.64 |
| −30 dB | 31.25 | 26.28 | 19.76 | 15.48 |
| −40 dB | 22.38 | 18.80 | 19.36 | 15.37 |
| Noise Level | Test | 3-D FCERNN | 3-D FCERNN-U-Net | ||
|---|---|---|---|---|---|
| Model Misfit (%) | Data Misfit (%) | Model Misfit (%) | Data Misfit (%) | ||
| Noise Free | Test #2 | 16.03 | 26.53 | 9.03 | 7.78 |
| Test #3 | 14.98 | 11.57 | 9.09 | 4.38 | |
| Test #4 | 16.60 | 12.39 | 10.64 | 6.97 | |
| −10 dB | Test #2 | 47.70 | 71.13 | 16.92 | 33.68 |
| Test #3 | 53.40 | 83.56 | 17.24 | 14.91 | |
| Test #4 | 60.59 | 136.91 | 19.45 | 16.29 | |
| −20 dB | Test #2 | 28.33 | 42.94 | 13.16 | 16.22 |
| Test #3 | 36.14 | 39.49 | 15.05 | 9.63 | |
| Test #4 | 45.41 | 84.91 | 17.90 | 25.28 | |
| −30 dB | Test #2 | 17.94 | 27.65 | 10.36 | 10.10 |
| Test #3 | 21.32 | 23.24 | 11.39 | 7.89 | |
| Test #4 | 29.87 | 34.07 | 14.64 | 10.19 | |
| −40 dB | Test #2 | 16.15 | 26.56 | 9.91 | 10.07 |
| Test #3 | 15.61 | 15.72 | 9.95 | 8.17 | |
| Test #4 | 18.94 | 17.18 | 11.81 | 8.91 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Xiao, L.-Y.; Zhao, L.-Y.; Hong, R.; Liu, Q.H. A 3-D Full Convolution Electromagnetic Reconstruction Neural Network (3-D FCERNN) for Fast Super-Resolution Electromagnetic Inversion of Human Brain. Diagnostics 2022, 12, 2786. https://doi.org/10.3390/diagnostics12112786
Cheng Y, Xiao L-Y, Zhao L-Y, Hong R, Liu QH. A 3-D Full Convolution Electromagnetic Reconstruction Neural Network (3-D FCERNN) for Fast Super-Resolution Electromagnetic Inversion of Human Brain. Diagnostics. 2022; 12(11):2786. https://doi.org/10.3390/diagnostics12112786
Chicago/Turabian StyleCheng, Yu, Li-Ye Xiao, Le-Yi Zhao, Ronghan Hong, and Qing Huo Liu. 2022. "A 3-D Full Convolution Electromagnetic Reconstruction Neural Network (3-D FCERNN) for Fast Super-Resolution Electromagnetic Inversion of Human Brain" Diagnostics 12, no. 11: 2786. https://doi.org/10.3390/diagnostics12112786
APA StyleCheng, Y., Xiao, L.-Y., Zhao, L.-Y., Hong, R., & Liu, Q. H. (2022). A 3-D Full Convolution Electromagnetic Reconstruction Neural Network (3-D FCERNN) for Fast Super-Resolution Electromagnetic Inversion of Human Brain. Diagnostics, 12(11), 2786. https://doi.org/10.3390/diagnostics12112786






