1. Introduction
We study mathematical models of absolute asymmetric synthesis [
1,
2] that are used to explain the emergence of biological homochirality, which is, according to Frank [
3], a natural property of life. Frank proposed, as early as 1953, a chemical mechanism to support his thesis. An important feature of this minimal model is that homochirality is produced by dynamic instability [
4]. After Frank many other more sophisticated networks have been proposed (see for instance [
5,
6,
7]), but all of them are based on the same idea: homochirality is the product of chemical instabilities. It is important to remark that the mathematical (stability) analysis [
8] of those complex models is a hard piece of work. Fortunately, we found a particular symmetry in the Jacobian matrices of those models [
9] that yields semialgebraic definitions of the instability regions where the symmetry-breaking can be observed. Most of those semialgebraic expressions are highly nonlinear and hard to sample. We used Clarke’s Stoichiometric Network Analysis (SNA) [
10] to reduce the complexity of those expressions.
All those ingredients were put together into an algorithmic tool, and software Listanalchem [
11], that can be used to test models proposed to explain the origin of homochirality, and which can also help us to build new and better models. Further thermodynamics constraints must be taken into account, but that point will not be discussed here.
We begin with a mathematical presentation of the method. After that, we use the developed algorithm to analyze three representative models of biological homochirality taken from the available literature.
2. Network Models of Absolute Asymmetric Synthesis
We use the term absolute asymmetric synthesis to designate all the possible chemical mechanisms that, operating in achiral environments, can transform a racemic mixture into an enantiopure one. We suppose that all those chemical processes reduce to finite sets of chemical reactions acting on finite sets of chemical species. Thus, we suppose that all those processes can be suitably described by chemical reaction networks.
Definition 1. A chemical reaction over the chemical species is an expression likewhere and are small integers (some of which could be equal to zero). The latter expression indicates that the mixture of units of and units of gives place to units of and units of A chemical reaction network over the species is a set of chemical reactions, say the set over this set of species.
Notation 1. Given a chemical network , we use the expressionto denote the reaction and we use the symbol to denote its reaction rate constant. We use variables to denote the concentrations of the n chemical species. Let us consider an example of a chemical reaction network. Frank network is the network , where:
| reaction : | L + A 2L, |
| reaction : | D + A 2D, and |
| reaction : | L + D P. |
Remark 1. It is important to remark that the network was the first, and it is the most elementary model of absolute asymmetric synthesis proposed in the literature [3]. The dynamics of a network
reduces to the temporal evolution of the
concentration variables We suppose that those temporal evolutions are completely determined by the
law of mass action[
12], that is: we suppose that the temporal evolution of the variables
is given by the system of Ordinary Differential Equations (ODE)
where given
the symbol
denotes the reaction rate constant of
. We get consequently that all those dynamics are deterministic: their evolution in time is entirely determined by their initial states.
Remark 2. Let be a (initial) state of network Ω, state is a vector that encodes the values of all the parameters that participate in the dynamics of Thus, we have that can be fully described by a -tupleof nonnegative reals. We must notice that the entries could remain constant along the dynamics, but in despite this, we choose to include the reaction rate constants in our notion of state. Definition 2. A state is said to be a steady state, if and only if, it satisfies the following system of polynomial equations: Notice that the steady states are the mathematical equilibria of the system. However, if one thinks in chemical equilibrium, it could be possible to consider the states for which only the set of forward reaction rates vanish. Also, it could be possible to consider the existence of complex networks containing loops, where not all forward rates vanish identically at the steady state.
Let us consider the case of network
when the reagent
is assumed constant, according to the pool chemical approximation, see [
13] chapters 2 and 3. The dynamics of this network is governed by the ODE system
The states of
are septuples
of nonnegative reals, and we have that such septuples encode racemic steady states, if and only if, the equality
hold. Observe that
must be equal to
; otherwise, the network encodes a chiral environment. This means
. It is important to remark, at this point, that any physical realization of Frank’s model implies a system open to matter flow to maintain
constant. Open systems used to have larger and more complex sets of steady states.
Analyzing the dynamics of corresponds to analyzing the set constituted by all its steady states, as well as the dynamics that can be triggered by arbitrary small perturbations of those states.
The Goal
We want to contribute to the investigation on the emergence of biological homochirality by providing the interested researchers with mathematical and algorithmic tools that can be used in the analysis of any network model of absolute asymmetric synthesis.
Definition 3. We say that a chemical reaction network Ω exhibits chiral amplification, if and only if, it has the ability of transforming negligible gaps between the concentrations of the chiral species into larger gaps.
We would like to characterize the set of chemical reaction networks that exhibit chiral amplification.
Let be a chemical reaction network, and suppose that is the -form of a chiral biomolecule, and that is the -form of the same molecule. Suppose that the system got stuck at a steady state satisfying the equality . There are physical mechanisms that may create small enantiomeric gaps (that could perturb this racemic steady state). Those perturbations trigger dynamics, and those latter dynamics could:
Evolve towards the original steady states, if, for instance, those states are stable.
Evolve towards different racemic states, if, for instance, those sets of racemic states are attractors of the dynamics.
Evolve towards states with large enantiomeric gaps (also called scalemic states).
We are interested in the latter case, and we say that in that case, the system undergoes homochiral dynamics. We want to characterize the steady states of that can undergo homochiral dynamics. We introduce, below, a precise formulation of the algorithmic problem that we study (and solve) in this paper.
3. Pseudochiral Networks
Let be a chemical reaction network, and suppose that it is a network model of absolute asymmetric synthesis. Then, the set must be constituted by three disjoint sets of chemical species, the sets ; and .
The set constitutes the l-side of , the set constitutes the d-side and the set is constituted by all the achiral species occurring in . Moreover, given we have that is an enantiomeric pair, that is: is the -form of a chiral molecule, while is the -form of the same molecule.
Definition 4. Let be a state of Ω
, and suppose that The enantiomeric gap of is equal to
A state of
is said to be
racemic, if and only if, its enantiomeric gap is equal to 0. Thus, the
racemic condition for
corresponds to the following set of polynomial equalities
Recall that we are interested in the racemic states of that can produce homochiral dynamics. It is important to take into account the indiscernibility of enantiomeric pairs: it is known that the two species of an enantiomeric pair react with the same achiral species at the same reaction rates. The indiscernibility of enantiomeric pairs implies that any feasible network model of absolute asymmetric synthesis must be a pseudochiral network, as defined below.
Definition 5. Let be a network model of absolute asymmetric synthesis, and suppose thatwhere is thel-side of Ω
, and is its d-side. We say that Ω
is a pseudochiral network, if and only if, it is indistinguishable from the network that is obtained when one switches the l-species and the d-species. Consider the following example of a pseudochiral network. Melvin Calvin, whose work laid the foundations of
chemical evolution, proposed an abstract model of biological homochirality [
14]. Calvin’s mechanism can be suitably described by a chemical reaction network that we denote with the symbol
, and which is defined as follows:
The constituent species of are the species and The chemical reactions in are:
A pair of
autocatalytic reactions
as well as the reverse reactions
The
racemization reactions
The
enantiomeric conversion reactions
as well as their reverse reactions
Notice that the reactions in are organized in pairs: for each reaction involving the species of the l-side there is a dual reaction involving the species of the d-side. We have, for instance, that if the reaction occurs, then the dual reaction must also occur; otherwise, the network would distinguish between the species of the l-side and the species of the d-side. The existence of dual reactions is a consequence and is somewhat equivalent to the pseudochirality of network . Moreover, given a reaction and its dual the reaction rate constants of those two reactions are the same. In the particular case of Calvin’s mechanism, we have , , , , and .
Notation 2. In the Calvin model, we use the symbol to denote the reaction rate constant of the dual pair of autocatalytic reactions, the symbol to denote the reaction rate constant of their reverse reactions, the symbol to denote the reaction rate constant of the dual pair of racemization reactions, the symbols to denote the reaction rate constants of the enantiomeric conversions and to denote the reaction rate constants of their reverse reactions.
We have that is a pseudochiral network of order Does network exhibit homochiral dynamics? Calvin claimed that it is the case, but we think that the evidence provided by him is weak, and we would like to consider this question more carefully.
Remark 3. Let Ω be a network, and suppose that Ω is not pseudochiral. Then, there is an asymmetry in Ω that distinguishes the L-side and the D-side. Thus, if Ω is not pseudochiral, it models a chemical mechanism that works on a chiral environment, and because of this it cannot be regarded as a network model of absolute asymmetric synthesis. We claim that: feasible network models of absolute asymmetric synthesis are pseudochiral networks.
4. The Algorithmic Problem
Suppose that one wants to introduce a new network model of absolute asymmetric synthesis. One must show that this new model exhibits homochiral dynamics, and one must also show that the model is sound from a thermodynamical point of view. We focus on the first task, which is solved if one exhibits racemic steady states which, after being perturbed, trigger homochiral dynamics. Therefore, we consider the following algorithmic problem:
Problem 1. CPVEH: Computing the Parameter Values for the Emergence of Homochirality.
Input: Ω, where Ω is a pseudochiral network.
Problem: check if Ω has racemic steady states that give place to homochiral dynamics. In that case compute a sample of those states.
It has been argued that the asymmetric synthesis of chiral biomolecules was a prerequisite for the origin of life [
3]. It is supposed that there are chemical processes, which took place in prebiotic earth, and which transformed the initial racemic mixtures, present in prebiotic earth, into the homochiral mixtures that preceded the origin of life. Frank introduced in his seminal work [
3] an abstract chemical mechanism, which contains an enantiomeric pair, and which evolves towards enantiopure states independently of the initial state. The chemical mechanism introduced by Frank is well described by the chemical reaction network
. This network was the first network/mathematical model of absolute asymmetric synthesis introduced in the literature. After that, many other network models have been proposed, and we know that some of those proposed models are defective models that cannot support homochiral dynamics (we prove that the Calvin model [
14] does not exhibit homochiral dynamics, see below). Therefore, we ask: can we recognize and discard all those defective models? To answer the question, we need an algorithm able to:
Recognize the defective network models of absolute asymmetric synthesis that cannot exhibit homochiral dynamics.
Recognize the network models that are mathematically sound, and compute samples of their sets of racemic steady states that undergo homochiral dynamics.
Thus, we need an algorithm that solves problem CPVEH.
5. The MM-Condition
Let be a pseudochiral network, and suppose that we want to show that has racemic steady states that produce homochiral dynamics. How can those states be found? Most authors cope with the latter question using the tools of classical stability analysis: the states that produce homochiral dynamics are unstable (see below).
Remark 4. From now on we use the symbol Ω to denote a pseudochiral network of order k. Moreover, we suppose thatand we say that Ω
is a network of size n. Notation 3. We use the symbol to denote the Jacobian of Ω
. The Jacobian is a symbolic matrix whose entries are the partial derivatives [8] of the reaction rates [15]. The entries of are polynomials over the variables Thus, given a state , one can evaluate at and obtain a numerical matrix . We say that is the Jacobian of Ω at (state) .
Let us consider the pseudochiral network
. The steady state equations for the
l-species are equal to:
In addition, if we assume the racemic condition, those equalities get equal to
while the Jacobian matrix gets equal to
Remark 5. The reader must observe the symmetrical structure of the above matrix, which we call the racemic Jacobian of It happens that the racemic Jacobian of any pseudochiral network Ω
reveals the same type of symmetries [9]. The Jacobian matrix encodes important information related to the dynamics of :
Definition 6. We say that a steady state is unstable, if and only if, the spectrum of satisfies the following:
There exists λ that belongs to the spectrum of and such that the inequality holds.
We say that a polynomial is unstable, if and only if, the roots of satisfy the same condition imposed on the spectrum of the unstable states. Notice that is unstable, if and only if, the characteristic polynomial of is unstable.
Recall that the spectrum of a square matrix is the set constituted by all its eigenvalues.
The unstable states are the states that can get dramatically transformed by the effect of negligible perturbations. We use the term
symmetry-breaking states to designate the racemic steady states that can produce homochiral dynamics. Notice that those homochiral dynamics dramatically transform those racemic states. Thus, we get that any symmetry-breaking state is unstable. However, we must observe that there exist unstable states that do not produce homochiral dynamics. We must ask: which are the symmetry-breaking states of network
? Which is the mathematical condition that determines the symmetry-breaking status? We observed before that the symmetry-breaking status depends on the eigenvectors of
and not only on its eigenvalues, see [
9,
16,
17].
Definition 7. We say that a steady state is symmetry-breaking, if and only if, matrix satisfies:
- 1.
There exists λ that belongs to the spectrum of , and such that .
- 2.
There exists an eigenvector of λ, say , and there exists such that .
We get that the symmetry-breaking states of are the unstable states that satisfy a further constraint. The additional constraint refers to the eigenvectors of . In principle, this additional constraint should make harder the search of those states. However, and surprisingly, it is not the case: if one exploits the symmetries of , the latter problem becomes easier than the former.
Notation 4. Let Ω
be a pseudochiral network of order k (recall that the order k is equal to the number of enantiomeric pairs, for the Calvin model), we use the symbol to denote the submatrix of that is constituted by its first k rows and its first k columns. We use the symbol to denote the submatrix that is constituted by the first k rows of and the columns . For instance, if we consider Calvin network , we get that Theorem 1. (MM-condition) Let be a racemic steady state of the pseudochiral network Ω
, we have that is symmetry-breaking, if and only if, the characteristic polynomial of is unstable [9]. The above theorem allows us to analyze any pseudochiral network. Let us illustrate the latter claim with the analysis of the network .
The symmetry-breaking states of
are the 9-tuples
that satisfy the following constraints:
The steady state condition
The
non-negativity conditionThe (
symmetry-breaking)
MM-condition asserting that the characteristic polynomial of matrix
is unstable.
Notice that the first four constraints are polynomial inequalities (equalities) over the variables
. The last constraint can also be expressed in terms of polynomial inequalities. To this end one can use a suitable set of
Hurwitz-Routh inequalities [
18]. We have, for instance, that the
matrix
is unstable, if and only if, at least one of the following two inequalities is satisfied:
It is easy to prove that there are no steady states satisfying at least one of the above inequalities.
Theorem 2. The Calvin model does not have symmetry-breaking states.
Proof of Theorem 19. First we consider the inequality
Let us suppose that
. From the steady state condition, Equation (
28), we get that
and hence the Inequality (
32) cannot be satisfied.
On the other hand, if we suppose
we get that the symmetry-breaking states of
must be solutions of the system
which does not have solutions satisfying the constraints
and
.
Now, we consider the inequality
We get from the steady state condition (
28) that
and we get consequently that
Then, the Inequality (
32) cannot be satisfied, and the theorem is proved. □
The analysis of the Calvin network, as developed in the previous paragraphs, shows that it is possible to use the MM-condition to analyze small networks thoroughly. What can be done with larger networks? The MM-condition yields an algorithmic solution for the CPVEH problem. However, if the input network (mechanism) is too large, its analysis could be intractable. Consider the problem:
Problem 2. SA: Stability Analysis
Input: M, where M is a symbolic matrix such that all its entries are polynomials.
Problem: Determine whether the set of parameter values, which make the characteristic polynomial of M unstable, is nonempty. If this is the case, sample this set.
The MM-condition allows us to reduce the problem CPVEH to this latter problem. However, this reduction can be useless, given that problem SA is a hard, intractable problem. Thus, we must ask: can we efficiently solve problem CPVEH?
We claimed before that computing the symmetry-breaking states of
can be easier than computing its unstable states. The MM-condition strongly reduces the dimensionality of the problem. This mathematical criterion tells us that we must analyze a
symbolic matrix instead of the
symbolic matrix that we would have to analyze if we were to use classical stability analysis to compute, as in previous approaches, the unstable states of
(notice that
). It seems that it is not possible to further reduce the dimensionality of the problem, and it forces us to consider other completely different reductions. We must observe, at this point, that there are two main sources of complexity related to the instances of problem SA: the dimension of the input matrices, and the degree of their polynomial entries. Thus, we ask: can we also reduce the inherent nonlinearity of the instances of CPVEH? In the following section we introduce some tools of Clarke’s
Stoichiometric Network Analysis (SNA, see reference [
10]), which allow us to achieve the degree reduction we are looking for. We use SNA, and the degree reduction provided by it, to develop an algorithm that can be used in the analysis of pseudochiral networks.
6. Degree Reduction Using Stoichiometric Network Analysis
Clarke’s SNA provides us with tools that can be used in the linear stability analysis of chiral networks, see [
19] and the references therein. Here, we use SNA to develop a heuristic algorithm for the CPVEH problem.
A Crash Introduction to SNA
Let be a chemical reaction network and let be its set of steady states. SNA is based on a change of variables that linearize the definition of : this change of variables maps the latter set onto a polyhedral cone that we denote with the symbol
Notation 5. Along this section we use the symbol Θ
to denote a chemical reaction network. Moreover, we suppose thatand we suppose that is equal to Definition 8. The stoichiometric matrix of Θ
that we denote with the symbol , is a matrixwhose entries are called the stoichiometric coefficients of Θ
. The stoichiometric coefficients of the network Θ
are defined by: A second matrix related to is the matrix of orders of reaction denoted with the symbol , and which is the matrix Definition 9. The velocity function of Θ
is the function that is defined by Clarke observed that the dynamic equation of
can be written as
and it implies that the function
maps the set
onto the
polyhedral cone that is defined by the linear constraints
Thus, the function
allows us to identify the steady states of
with the points of
, and it happens that the points of
can be suitably described by the system of
convex coordinates provided by its
extreme currents[
10].
Remark 6. A set of extreme currents for is just a minimal set of extreme rays that spans the polyhedral cone , see [20]. Notation 6. We use the symbol to denote the set of s-dimensional nonnegative vectors, which is the set Definition 10. Let be a set of extreme currents for , and let ; the convex coordinates of are given by the unique tuple that satisfies the equality From now on, we use the symbols to denote the convex coordinates of the cone that are determined by
We have:
Given one can effectively compute the convex coordinates of
Given one can effectively sample the set , which is a nonempty subset of .
If one switches to the system of convex coordinates, then the Jacobian
can be factorized as
where
is a
scaling matrix, and
is the
diagonal matrix defined by
Remark 7. The term is a linear polynomial over the (convex) variables
Clarke noticed that the scaling matrix has little influence on the stability properties of , and that one can focus the analysis on the matrix . Thus, according to Clarke’s theory, the stability analysis of reduces to the stability analysis of the latter matrix. We must ask: what do we gain with this reduction? The entries of are linear polynomials over the variables , and it means that we get an important degree reduction.
We use the symbol to denote the matrix The SNA-based algorithmic analysis of chemical networks reduces to:
Compute a set of extreme currents for
Compute the symbolic matrix
Sample the set of parameter values that make the characteristic polynomial of matrix become unstable.
Given , a s-dimensional vector that belongs to the sample computed in step 3, compute a sample of the set Here, we use the symbols to denote the set of extreme currents for as computed in step 1.
Remark 8. The latter algorithmic routine can be effectively implemented, see [11]. An Illustrative and Trivial Example
Let be the network , where:
| reaction : | 3I →[k1] 3A |
| reaction : | 2I + A →[k2] 3I, and |
| reaction : | I + A →[k3] 2A. |
Clarke’s velocity function denoted by
is equal to the vector field
. The set
is the subset of
that is defined by the equation
Remark 9. Notice that is a 5-dimensional set with a quite complex structure.
The stoichiometric matrix of
is the matrix
and a set of extreme currents for
is given by
This means that the 5-dimensional set
is mapped by
onto the infinite triangle spanned by the vectors
and
Thus, we get that
has a pleasant conic structure. We can use the extreme currents of
(which are integer vectors located on the borders of
for instance the vectors
and
) to define a system of convex coordinates for
Notice that the points of this triangle are in bijective correspondence with the nonnegative linear combinations of the extreme currents
and
. Thus, if we choose nonnegative values for
, we can be sure that
is an element of
that represents a nonempty set of steady states. We can use this fact to sample the set
. We proceed in the following way:
Pick a tuple of positive convex coordinates; for instance, and.
Compute the corresponding convex combination of extreme rays; in our case, we computeequal to.
Compute the solution set of the nonlinear system Pick an element, say, of the set computed in the previous step.
This means that given a chemical network , we can use Clarke’s velocity function to define a system of convex coordinates for the set . Moreover, we can use this system of coordinates to sample the set . We can also use the factorization of to analyze the stability of network .
Additionally, it is important to illustrate how this procedure reduces the degree of the polynomials entries of the symbolic Jacobian
. In our illustrative and trivial example, the symbolic Jacobian is equal to
We have that
is equal to
and we have that
is equal to
According to Clarke’s factorization the matrix
is equal to
and this factorization allows us to focus the stability analysis on the matrix
which is equal to
Notice that the entries of the matrix are linear polynomials over the variables while the entries of are 3-degree polynomials over the parameters and . Thus, it is true that we gain an important degree reduction if we switch to the system of convex coordinates.
7. Using SNA in the Analysis of Pseudochiral Networks
We use the tools introduced in the previous paragraphs to develop an algorithm for the stability (symmetry-breaking) analysis of pseudochiral networks.
Let us consider the case of pseudochiral networks of order 1, which we call chiral networks. Thus, let
be a chiral network of order 1, and suppose that
The MM-condition reduces to the inequality
which is a linear inequality over the entries of
However, the linearity of this algebraic condition is just apparent, given that the terms
and
are nonlinear polynomials over the concentration variables
Notation 7. We use the symbol to denote the set of symmetry-breaking states of
We have that the set is a highly nonlinear set defined by the conditions:
The nonlinear steady state equations.
The non-negativity conditions
The positivity conditions
The racemic condition stating that the rate constants of the reactions that belong to the same dual pair are equal, and that the initial concentrations of the two enantiomeric species are also equal.
However, if we switch to Clarke’s system of convex coordinates, we get that this set is defined by the linear conditions:
where constitute the system of convex coordinates of network .
Remark 10. In the implementation of the algorithm, we forced condition five (the racemic condition) into the computation of the extreme currents, which are computed from the stoichiometric matrix; for this, we extended the stoichiometric matrix with rows that encode the equalities of the rate constants of the dual pairs; for example, given the stoichiometric matrix of the Calvin modelthe extended matrix, considering its dual pairs (Reactions (13), (14), (16), (17)), is equal to Forcing this condition into the computations of the extreme currents proved to reduce the number of extreme currents significantly.
The stoichiometric and extended stoichiometric matrices of the models analyzed with Listanalchem can be seen in the output of the computer program. The Supplementary Materials presents those matrices for the models studied in this work. Sets defined by linear inequalities are easy to sample, see [
21]. Then, if we switch to the system of convex coordinates, we will be able to efficiently sample the set of symmetry-breaking states of
. Thus, we can use the MM-condition and SNA to efficiently solve the CPVEH problem when it is restricted to pseudochiral networks of order 1.
What about higher orders? Suppose that
is a pseudochiral network of order
k, suppose that the variables
constitute a system of convex coordinates for
and let
be the appropriate submatrices of
. The set
is defined by the algebraic conditions:
Notice that we get a strong reduction on the degree of the polynomial expressions defining the set of symmetry-breaking states. The latter is the case given that:
However, if k is large, and despite all the reductions achieved so far, the stability analysis of matrix can be unfeasible. A full stability analysis of matrix presupposes the computation of its determinant, as well as the computation of other large subdeterminants. Take into account that computing symbolic determinants requires exponential time. If we want to avoid the computation of those large (symbolic) determinants, we will have to conform ourselves with a heuristic algorithm.
A Heuristic Algorithm for CPVEH Based on SNA and the MM-Condition
Let
be a pseudochiral network of order
k, let
be the symbolic matrix that we want to analyze and let
be the characteristic polynomial of this matrix.
The coefficient
is equal to the sum of all the diagonal subdeterminants of
of order
i, see [
22]. Notice that all those coefficients are polynomials over the set of parameters that we are analyzing, and notice that we are interested in determining the values of those parameters that make the latter (parameterized) polynomial become unstable. We must take into account the following fact: the roots of a polynomial are determined by its coefficients. Let us consider two instances of the latter phenomenon:
If the inequality holds, the polynomial has a positive real root.
can have positive real roots only if it has negative coefficients.
We could focus on the first item and conform ourselves with a sufficient condition for instability, or we could focus on the second item and conform ourselves with a necessary condition for the existence of positive real roots. Notice that
is equal to
and recall that we wanted to avoid the computation of large subdeterminants of the matrix
. This latter observation leads us to focus on the second item and consider the set
, which is the subset of
constituted by the steady states that satisfy the condition: there exists
such that
. We must ask: what do we gain if we focus on the second criterion? It was observed that in most cases, the chemical instabilities of
are determined by small subnetworks, see [
23]. Moreover, given
, the influence of all the subnetworks of size
i is encoded in the coefficient
. We can conclude that in most cases, the chemical instabilities of
are encoded in the first coefficients of
. We can use the latter as a further heuristic principle which tells us that: for most pseudochiral networks exhibiting homochiral dynamics, there exist small values of
i such that the inequality
gets satisfied for nonnegative values of the parameters. Therefore, we focus on the problem:
Problem 3. approx-CPVEH
Input: Ω, where Ω is a pseudochiral network.
Problem: compute the minimum i for which the inequality gets satisfied for nonnegative values of the parameters, and sample this set of nonnegative solutions.
Our heuristic approach for solving CPVEH consists of solving the problem approx-CPVEH. Consider the following algorithm that we denote with the symbol SNA-sampling.
Algorithm SNA-sampling works, on input, as follows:
Compute the matricesand.
Givendetermine the set of nonnegative solutions of the inequality. If all those sets are empty reject; otherwise, sample the union of those five sets.
Givenan element of the computed sample, compute a racemic steady state ofsay, such thatis the tuple of convex coordinates of. Do the same with all the members of the computed sample.
We notice that:
If is a pseudochiral network of order 1, the algorithm correctly and efficiently samples the set .
If is a pseudochiral network of order then the algorithm samples the set
If is a pseudochiral network of order , then the algorithm approximates the set by a semialgebraic set that is defined by polynomial expressions whose degree is upperbounded by 5.
SNA-sampling is a heuristic algorithm that is as efficient as possible, solves the problem CPVEH for pseudochiral networks of small order, and allows us to compute important information in the case of higher orders. We exemplify, in the next section, the power of this tool with the analysis of three pseudochiral networks that were taken from the literature dedicated to the study of biological homochirality.
8. Computer Experiments
The algorithm SNA-sampling, as described above, was implemented as a computer program called Listanalchem [
11], option six. The algorithm determines if a chemical network
, given as input, can produce spontaneous mirror-symmetric breaking (SMSB), and if so, samples the set of parameter values that can produce those dynamics. The computed samples are used to make numerical simulations of the dynamics. For this task, we use Chemkinlator [
24], a software tool that can also build bifurcation diagrams. Actually, we used bifurcation diagrams to find the SMSB region for a model which presented problems for the heuristic used in sampling. The construction of the bifurcation diagrams could be a necessary additional step, given that, depending on the model, the instability region can be so small that numerical error could place us out of, but close, to this region. Also, the heuristic used in the algorithm can cause the results to be out of the instability region. In those cases, a fast exploration around the computed values, using bifurcation diagrams, could be enough to find SMSB. Additionally, this procedure can be used to build phase diagrams such as the ones shown in references [
25,
26].
It is worth remembering that as mentioned in Remark 10, the implementation of the algorithm uses the extended stoichiometric matrix with rows that encode the duality of the pairs of reactions that involve enantiomers. We observed that after adding those constraints the number of extreme currents got reduced. The details of this process, including the extended stoichiometric matrix, and its manipulation, can be seen in the output of Listanalchem option six. These outputs are available in the
supplementary material.
Finally, we would like to remark that the units used for simulations are arbitrary. We do not set units to avoid huge or tiny numbers. Instead of that, we use numbers in the interval [0, 2]. This particular way to perform the analysis, for each model, does not change the qualitative behavior of the models, and it helps to show clearer images of the relevant facts. Particular units can be obtained using the corresponding factors in concentrations and rate constants, but that fact will be not explored here because we are interested, first of all, in the stability of the models that generate SMSB.
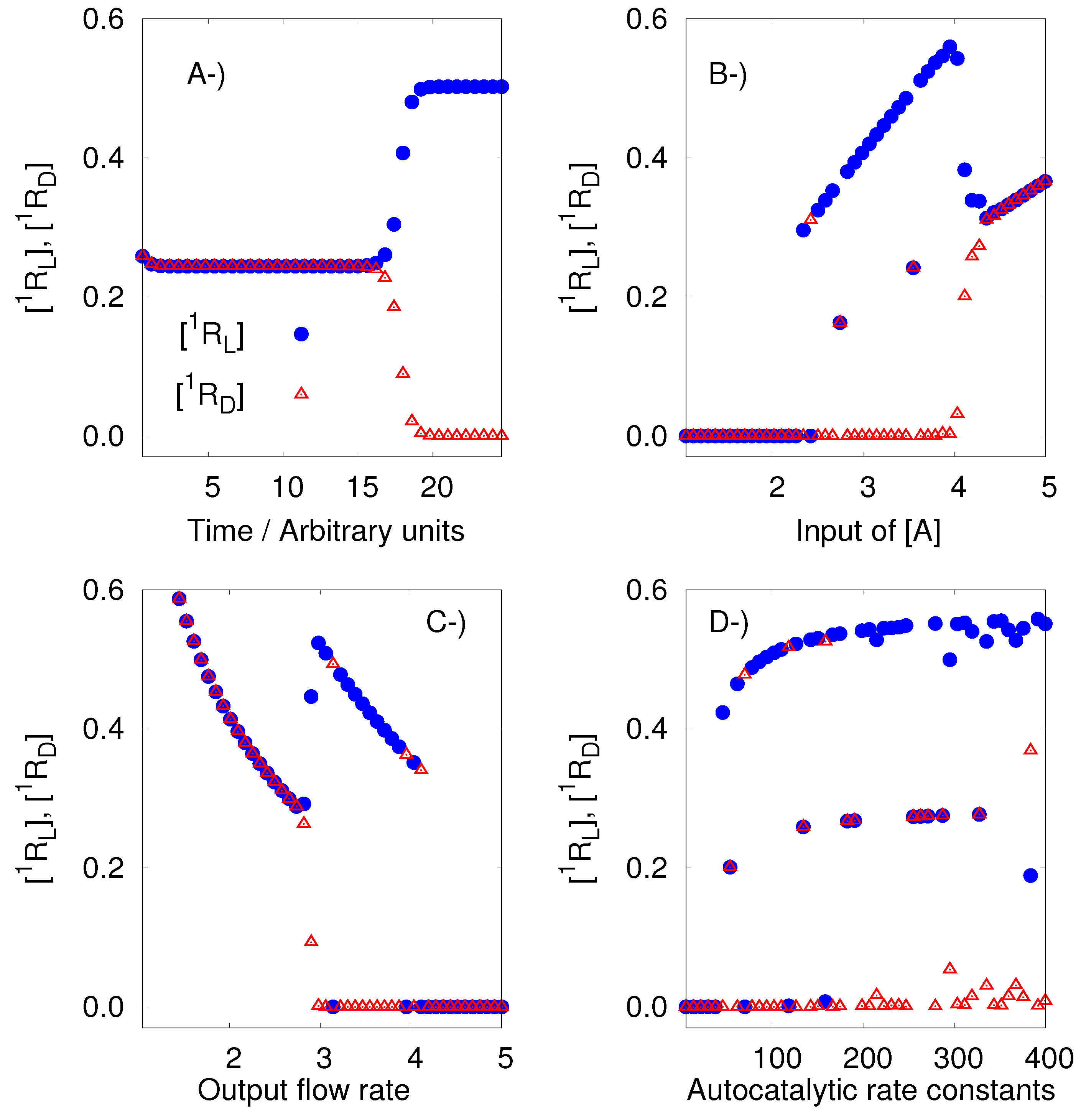
8.1. The Replicator Model of Hochberg and Ribo
Hochberg and Ribo [
27] have investigated the network described below.
| A + 1RD + 2RD 21RD + 2RD | A + 1RL + 2RL 21RL + 2RL |
| A + 2RD + 1RD 22RD + 1RD | A + 2RL + 1RL 22RL + 1RL |
| 1RD ⌀ | 1RL ⌀ |
| 2RD ⌀ | 2RL ⌀ |
| A |
| A ⌀. |
This model has two enantiomeric pairs, (
1R
D,
1R
L) and (
2R
D,
2R
L). This means, according to the previous definitions, that it is a pseudochiral network of order 2. The analysis of the model, using the developed algorithm, confirms its ability to generate SMSB. However, it is important to remark that the outputs obtained with Listanalchem did not always produce SMSB immediately. In those cases, bifurcation diagrams, around the computed values, allowed us to compute the range of values that produce the symmetric breaking. Those bifurcation diagrams were done using Chemkinlator [
24].
Figure 1 presents a typical example of the described situation, including three bifurcation diagrams. The right values are easy to find from the values given by the algorithm; for example, a fast way to find SMSB is by exploring the velocity of the entrance of A (
A), see
Figure 1B. In this way, it is easy to tune the region of SMSB.
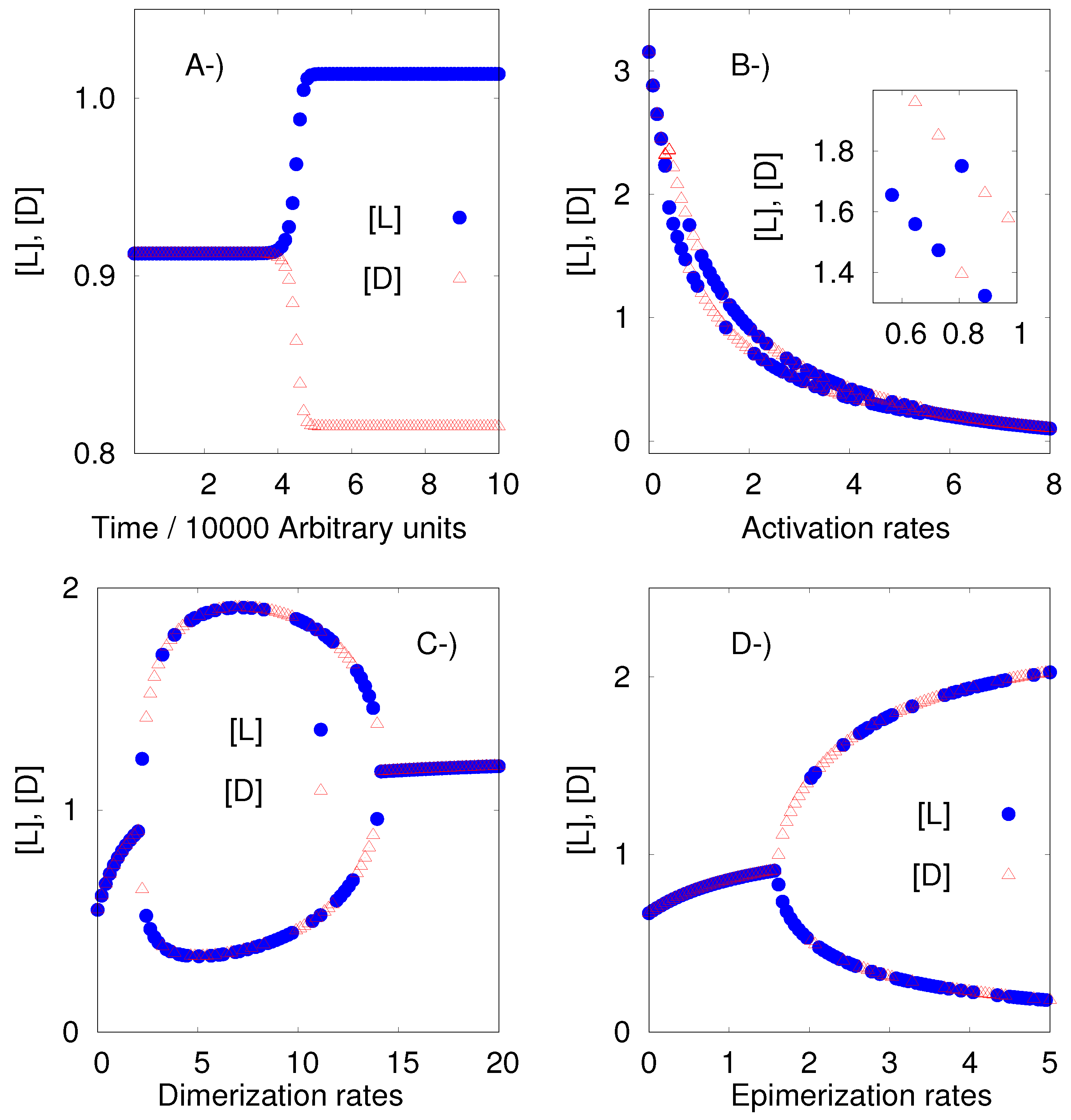
8.2. The APED Model
Plasson et al. [
25] have proposed the noncatalytic model presented below.
| L L* | LL L + L |
| D D* | DL L + D |
| L* L | LD L + D |
| D* D | DD D + D |
| L* + L LL | LD DD |
| D* + L DL | DD LD |
| L* + D LD | LL DL |
| D* + D DD | DL LL |
Our algorithm and software can find values of the rate constants for which the APED model exhibits the breaking of mirror symmetry. We could compute those values without the need for any additional work, as was necessary with the previous model.
Additionally, we would like to remark that the approach developed here to obtain the instability regions has a solid mathematical background which makes it more efficient and general than the brute-force approach used in the original paper of Plasson et al. [
25]: a systematic scan of the rate constants.
Figure 2 shows an example of the results given by the algorithm.
It is interesting to remark that Plasson et al. [
25] claimed that each one of the three sets of reactions:
Polymerization: L* + L LL, D* + L DL, L* + D LD, and D* + D DD,
Depolymerization: LL L + L, DL L + D, LD L + D,and DD D + D, and
Epimerization: LD DD, DD LD, LL DL, and DL LL,
must have different rate constants, and because of this, they introduce the parameters
,
and
, which are bigger than zero and different from 1. We found that those constraints are necessary because given
, the algorithm finds that the SMSB is not possible. Observe that under the equivalent condition, see the legend of
Figure 1, the previous model (Replicator Hochberg-Ribo) exhibited SMSB.
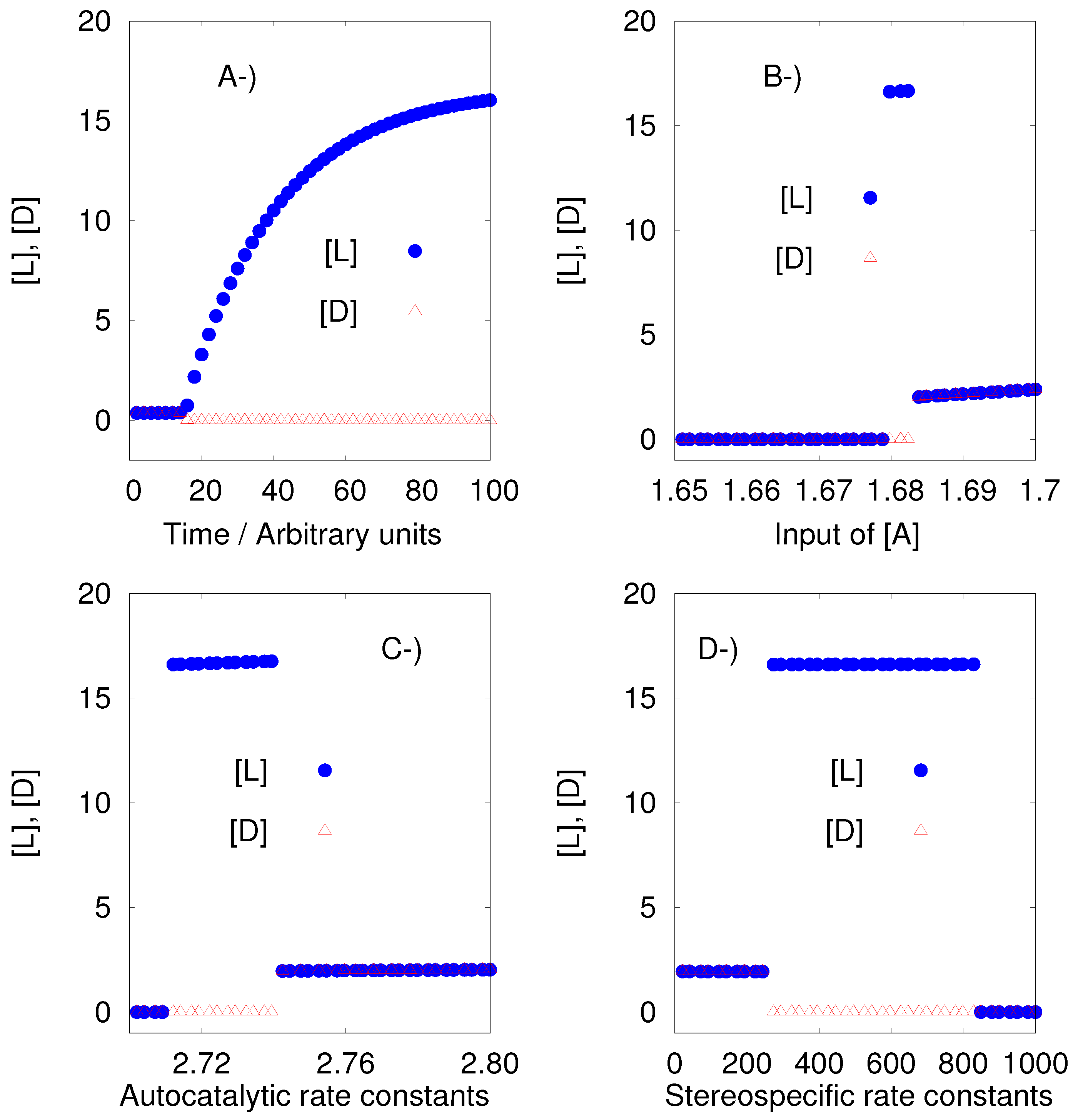
8.3. The Iwamoto Model
Iwamoto proposed a reaction model including Michaelis-Menten type catalytic reactions [
26]. The Iwamoto model is presented below, with perfect and imperfect conditions that depend on the stereoselectivity (R1, R1a, R2, and R2a), and stereospecificity (R3, R3a, R4, and R4a).
| Perfect | Imperfect | R |
| P A | P A | R0 |
| A + L 2L | A + L 2L | R1 |
| | A + L L + D | R1a |
| A + D 2D | A + D 2D | R2 |
| | A + D D + L | R2a |
| L + EL ZL | L + EL ZL | R3 |
| | L + ED YD | R3a |
| D + ED ZD | D + ED ZD | R4 |
| | D + EL YL | R4a |
| ZL EL + Q | ZL EL + Q | R5 |
| | YL EL + Q | R5a |
| ZD ED + Q | ZD ED + Q | R6 |
| | YD ED + Q | R6a |
Iwamoto considered to be variables only the species A, L, D, E
L and E
D. The Iwamoto model under perfect conditions shows SMSB. The instability region is a tiny one as shown by
Figure 3. However, the algorithm could sample this region without problem.
On the other hand, the Iwamoto model under imperfect conditions is stable if the stereoselective (R1, R1a, R2, and R2a) rate constants satisfy the equalities
and
, and at the same time the stereospecific (R3, R3a, R4, and R4a) rate constants satisfy
and
. However, if those rate constants are different, as the author assumes, the model presents SMSB, which means:
,
,
and
. This latter condition (different rate constants for particular sets of reactions), seems to be necessary to obtain the desired results in those particular models, but it is not clear that it is a condition that can be presupposed of the prebiotic environment. The results for the Iwamoto model under imperfect conditions can be seen in the
supplementary material and in the output of Listanalchem.
9. Discussion
The developed algorithm and the implemented software are powerful tools, capable of predicting the stability (instability) of models proposed to explain the emergence of homochirality in biological systems. The solid mathematics, behind the algorithm, makes it a robust tool to find the instability regions of chemical reaction mechanisms (networks models) of biological homochirality. This tool can be used to establish the particular rate constant values (intervals), for which a model breaks the initial racemic mixtures. The algorithm and the software can be used to generate phase diagrams of the models proposed to explain the origin of homochirality. Using the previous information, one could study the structure of those models proposed to explain the origin of homochirality in prebiotic earth.
It is important to remark, at this point, that we have focused on the homochiral dynamics that can be triggered by tiny perturbations of the racemic states. Enantiopure states can also be reached by alternate routes, like, for instance, the dynamics that are triggered by large perturbations of those states. We did not study the effect of large perturbations, given that we do not count with the required mathematical tools.