Three examples from our work on peptide-based assembly and catalysis are briefly described. A particular focus is placed on how numerical and statistical methods promote an effective linkage between modeling and experiment. In these case studies, the numerical and statistical methods are used to test hypotheses, uncover design principles, and design experiments.
3.1. Two-Step Nucleation
The folding of proteins is understood to proceed through a molten globule phase, in which the protein is condensed yet disordered. From this condensed state, the protein is then able to fold into its active structure. A similar intermediate state may also be critical for understanding peptide assembly in Alzheimer’s disease. This “two-step” nucleation process has been observed in crystallization via in situ TEM [
10]. Nucleation within particles was also observed in peptide assembly of A
(16-22), a truncated version of the Alzheimer peptide KLVFFAE [
11].
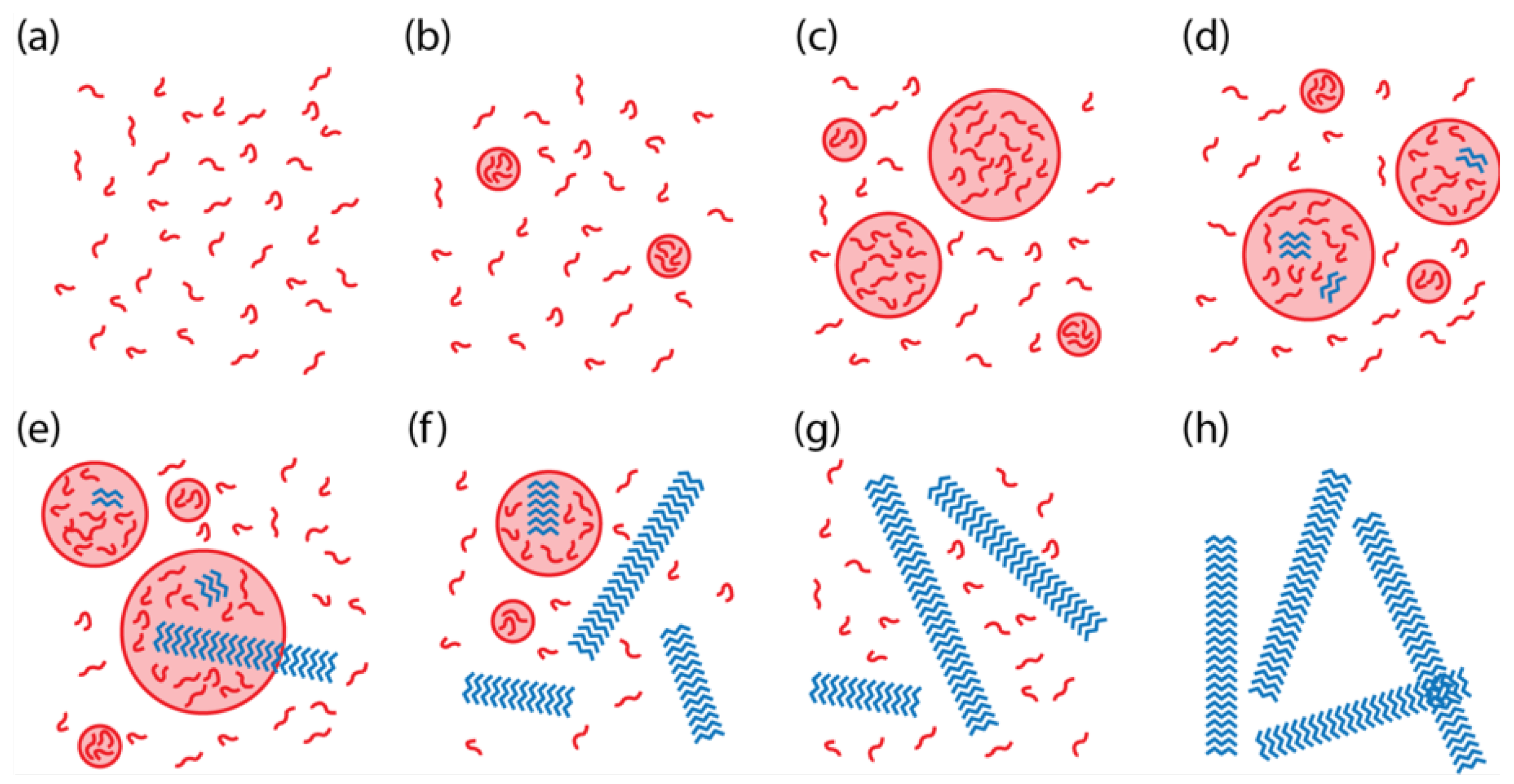
We constructed a model of two-step nucleation for KLVFFAE to better understand the key parameters and environmental conditions controlling the transitions between the solution phase, the disordered particle phase, and the ordered assembly phase (
Figure 1) [
12]. Here “assembly” refers to a structure with paracrystalline order, which may have either fiber [
12,
13] or nanotube [
14] morphology. A unique aspect of our system, relative to other two-step nucleation systems and models, is that the peptide assemblies nucleate in the particle phase and grow into the solution phase, thus competing with the particle phase for the free peptides in the solution phase.
The model constructed in Ref. [
12] is complicated; however, the study elucidated the critical role of solubility in determining the transitions between phases of the system, including the coexistence of phases. The key equations for the solubilities are
where
is the solubility of peptides from the particle phase, while
is the solubility of peptides from the assembly phase. Equation (
5) is based on Flory–Huggins theory, using the thermodynamics of mixing and a lattice assumption. In contrast, Equation (
6) equates kinetic expression for assembly growth and dissolution to predict the equilibrium solubility. The phase that has the greater solubility will thus dissolve into the solution, while the phase with the lesser solubility will incorporate the peptide from solution and grow over time. Key model parameters determining solubility are the Flory–Huggins parameter for the peptide–solvent interaction in solution
, the binding energy of the peptide assembly
, and the kinetic constant for assembly growth
.
Most parameters in the model were set to nominal representative values for KLVFFAE, such as
, the density of the peptide particle, and
, the peptide molecular weight. However, to explore the range of possible system-level behaviors, as illustrated in
Figure 1, 200 parameters sets were selected for
,
, and
using Latin hypercube sampling. Each parameter set was simulated using the stochastic simulation algorithm [
8] to sample a distribution of particle sizes and assembly lengths, and the long-term behavior of each simulation was classified according to
Figure 1. The simulation time was selected to match the length of time for a typical experiment.
Simulations with
C less than
and
(“undersaturated”) demonstrated behavior according to
Figure 1a. In the supersaturated regime (
C greater than
and/or
), simulations with
usually demonstrated behavior as in
Figure 1g. However, when
, then the system usually exhibited behavior such as in
Figure 1b. Overall, the simulations showed that the phase behavior could be predicted in most cases based purely on
C, the initial concentration of peptides in the system, and its relationship to the two solubilities. The phase with the smaller solubility is the observed phase at long times. However, if both phases are undersaturated (
C is less than
and
), then all peptide remains free in solution. In some cases, the kinetics were too slow to reach steady state during the simulation time, which may also be the case in the experiments.
As shown in Equation (
5), the Flory–Huggins parameter
impacts
, but not
. Simulations showed that particle size increases and particle number decreases with increasing
[
12]. Since
describes the peptide–solvent interaction, it can thus be tuned experimentally by changing the solvent composition. This interpretation was supported by experiments with KLVFFAE, as shown in the TEM images in
Figure 2. As the acetonitrile concentration is increased (i.e.,
is decreased), the number of particles increases and the size of particles decreases. Further experiments with circular dichroism demonstrated that increasing the acetonitrile concentration speeds up peptide assembly, reducing the formation of particles and driving the peptides more rapidly into the assembly phase. Together, the TEM and CD measurements supported the inverse relationship between acetonitrile concentration and Flory–Huggins constant, and the key role of
in determining the system-level phase behavior.
The use of numerical and statistical tools for simulation (stochastic simulation algorithm) and experimental design (Latin hypercube) enabled the prediction of system-level behavior as a function of three key parameter values. The study provided physical insight into the key role of solubility in determining phase behavior, and suggested a new set of experiments focused on solubility to further support this interpretation.
3.2. Selection of Monodisperse Assemblies
The first case study focused on noncovalent interactions, through the assembly of the pre-synthesized KLVFFAE peptide. This second case study includes both covalent and noncovalent interactions [
13]. As shown in
Figure 3, the tripeptide NFF is modified, such that the carboxylic acid group on F is reduced to an aldehyde, facilitating oligomerization. The imine bond is first formed, followed by cyclization to form N,N-acetal polymers.
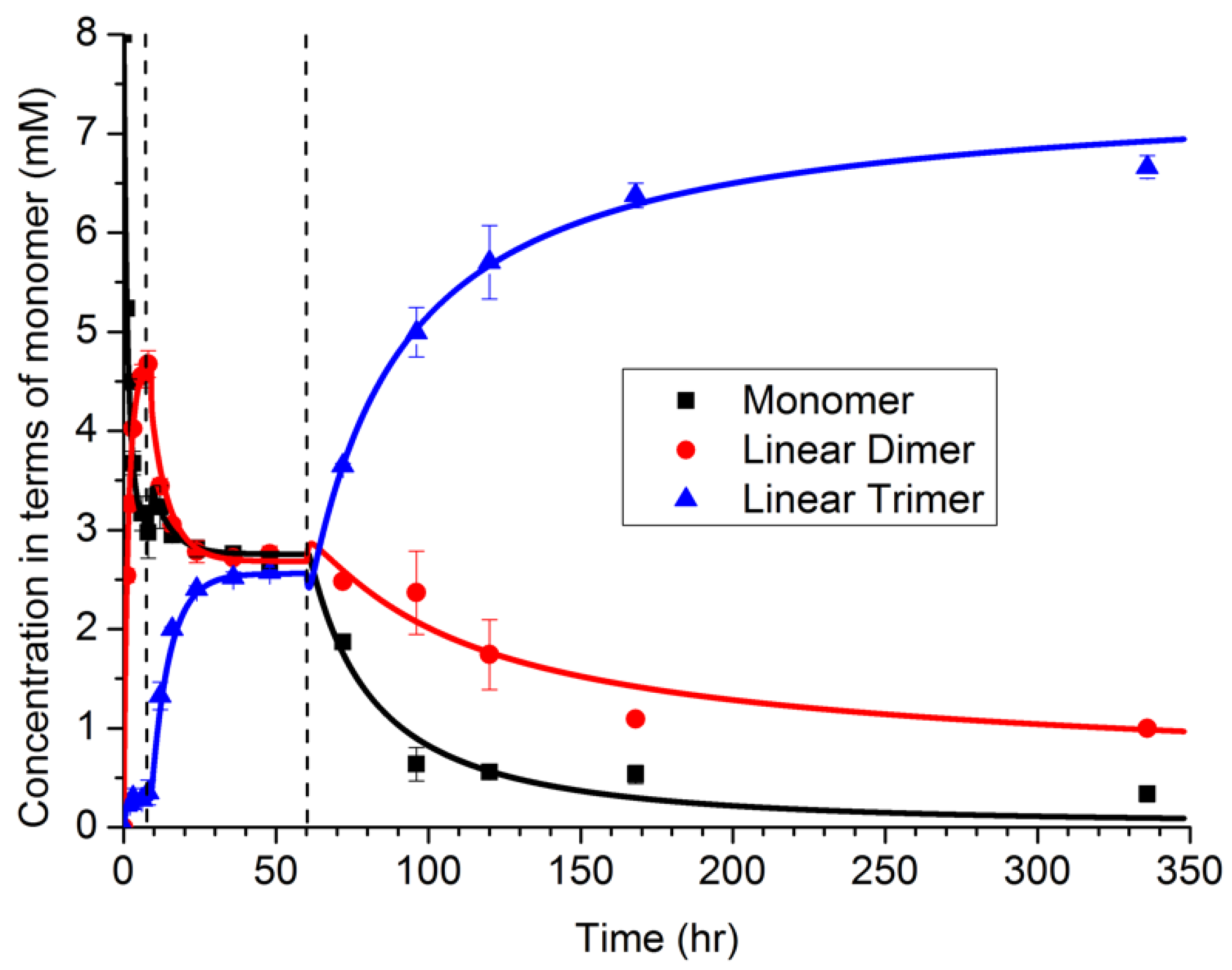
The NFF-CHO monomers were first dissolved in solution, at concentrations below their solubility limit. As shown in
Figure 4 via HPLC measurements, the monomers first form dimers in solution, with only a small amount of trimer present. At about 6 h, a sudden transition occurred, which was attributed to a phase transition producing particles (and supported by TEM observations). During the next period, 10–60 h, the distribution of polymers shifted toward a mixture of dimers and trimers. The dimer may be partitioned between both the solution and particle phases, while the trimer was assumed to be less soluble, and located primarily within the particle phase. From 10 to 60 h, the size of the particles was also observed to grow in TEM images, even while the oligomer distribution remained constant. At 60 h, a second transition was observed in the oligomer sequence, corresponding to the emergence of peptide assemblies. Notably, as the assembled fibers grew, the oligomer distribution shifted strongly toward the trimer. The degree to which structure in the particle can drive selection is a topic of ongoing investigation, but the assembly of the trimer by the network drives selection.
Each of the three periods in the data was modeled separately with the simple set of reactions:
where
M is the NFF-CHO monomer,
D is the dimer,
T is the trimer, and
is assembled trimer. The final reaction was added based on the hypothesis that assembly is a templating process, and therefore autocatalytic.
The model was simulated with a deterministic algorithm, with parameters estimated according to the values that minimize the sum-squared error. Additionally, various models were estimated using the data in
Figure 4, including the full set of four reactions with
rate constants, as well as subsets of the reaction set having fewer reactions with
. The Akaike Information Criterion (
) was then calculated for each model, and the model including only the first three reactions had the highest AIC score. Thus, the analysis suggested that autocatalysis was not needed to describe the data.
Based on our domain knowledge, we sought to further investigate the autocatalysis hypothesis, and designed a new experiment in which the assemblies were added as seeds into the network. The assemblies grew much faster under the seeded case, providing definitive support for the autocatalysis hypothesis, which could not be supported based only the evidence in
Figure 4.
Overall, this combined experimental and modeling study enabled the investigation of a hypothesis in a systematic and quantitative manner. It also demonstrated an interplay between chemical and physical phenomena, with one triggering the other in an alternating fashion, possibly reminiscent of biological emergence.
3.3. Catalytic Selection of A Chiral Product
Catalysis is a primary role of proteins in biology. Proteins fold to form enzymes that catalyze chemical reactions with high specificity. While shorter peptides may not fold by themselves, assemblies of multiple peptides can catalyze reactions on their surfaces, similar to enzymes [
15]. On the early Earth, such peptide assemblies may have been important catalysts in the origins of life [
16].
In Ref. [
14], we investigated the ability of KLVFFAL and (Orn)LVFFAL to assemble into nanotubes and to catalyze the cleavage of racemic methodol (
-hydroxyketone) through a retro-aldol reaction. (R)-methodol and (S)-methodol were cleaved with different rates, indicating a specificity reminiscent of enzymes. Several questions arose from these experimental studies, including “What is the nature of the binding site?” and “Is binding or reaction the rate limiting step for the reaction?”
A model was constructed to include both binding and reaction:
where
E is the enzyme,
S and
R are (S)-methodol and (R)-methodol, and
and
are the products of the reaction.
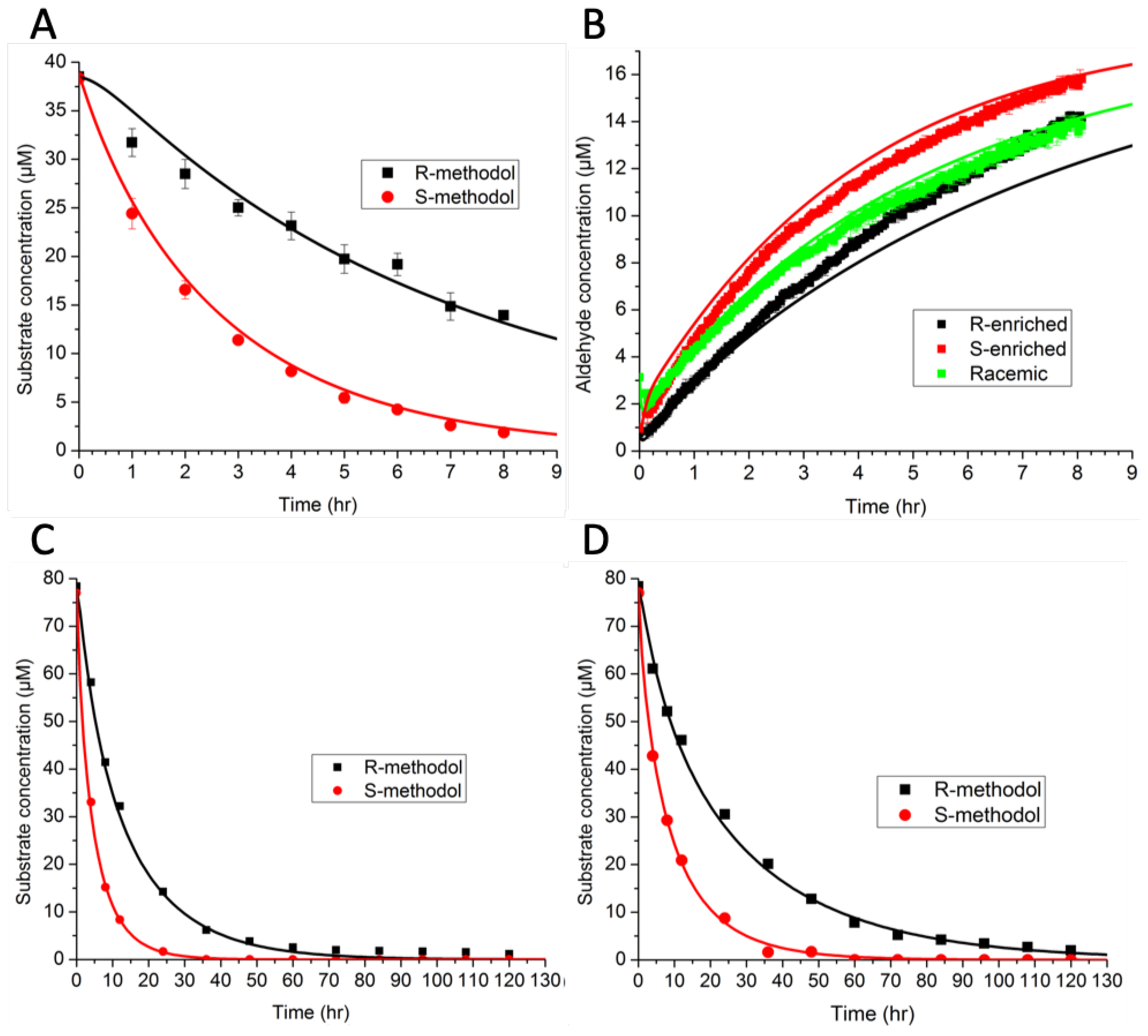
The model consisted of ordinary differential equations for each species, and was simulated using a deterministic method. Rate constants were estimated by minimizing the sum-squared error. The preliminary results in
Figure 5A,B indicate that binding favored (R)-methodol, while reaction favored (S)-methodol. Further experiments were conducted (
Figure 5C,D) to demonstrate this intriguing idea—that the selectivity was invertible based on catalyst loading. However, the additional experimental data did not demonstrate this inversion, invalidating the original hypothesis. Because there were not enough data initially, the parameter estimates were not unique (as indicated by large confidence intervals). The larger set of experimental data that was collected, as shown in
Figure 5, ultimately led to an improved model with tighter confidence intervals on parameters and a wider range of applicability.
Using the augmented dataset, an AIC analysis supported use of the full model with all four reactions, rather than simplified models based on arguments about rate-limiting steps. Thus, the modeling suggests that both binding and reaction are significant steps for this system, with neither being clearly rate limiting.
In addition to fitting continuous-valued parameters for rate constants, we also needed to specify the number of sites required for each binding event along the surface of the nanotube assembly. In this case, we fit parameters to models having an integer number of peptides constituting the binding sites, in the range of 1–15. The SSE was lowest for a value of 6, increasing significantly for higher and lower values. While we expected the minimal size of the binding site to be 4 based on molecular models, the value of 6 may indicate disorder on the surface, such that all substrate molecules do not tile perfectly in a regular lattice, but rather skip sites along the surface.
In summary, the use of modeling in this catalytic system enabled the investigation of hypotheses, some which were validated and others which were invalidated. The iterative feedback loop between experiments and modeling provides insights into reaction networks that were difficult to measure directly, such as the size of the binding site and the relative importance of binding and reaction.