Molecular Diversity and Network Complexity in Growing Protocells
Abstract
1. Introduction
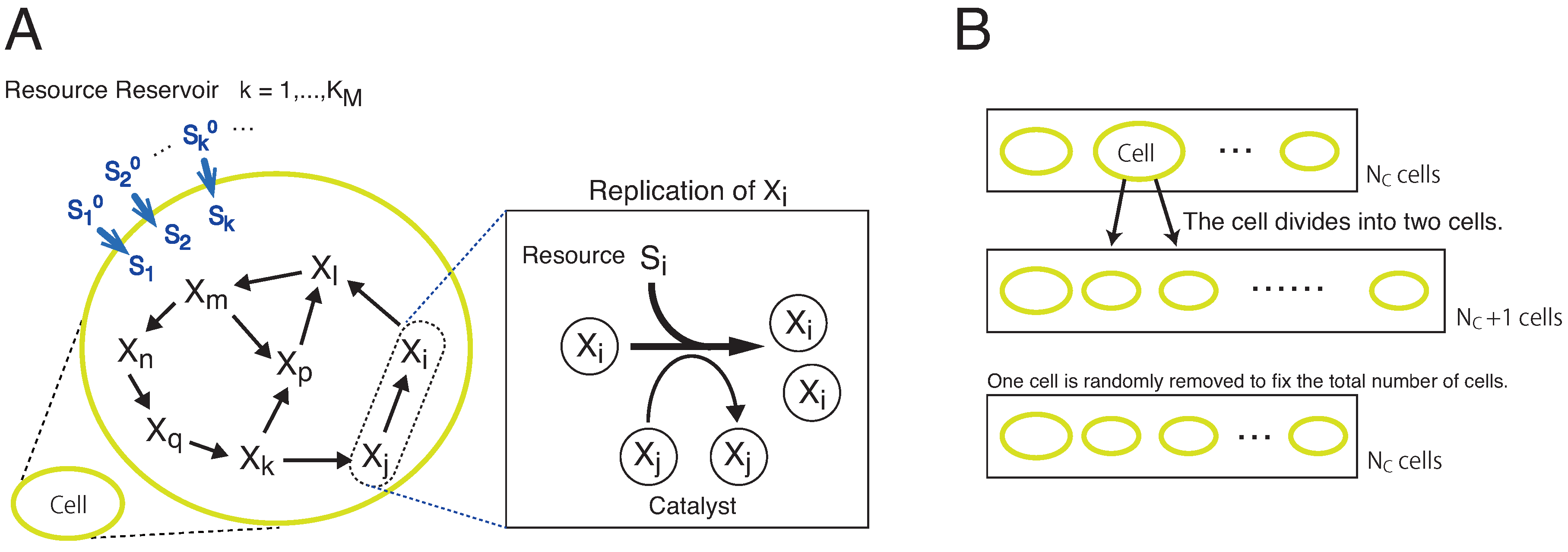
2. Model
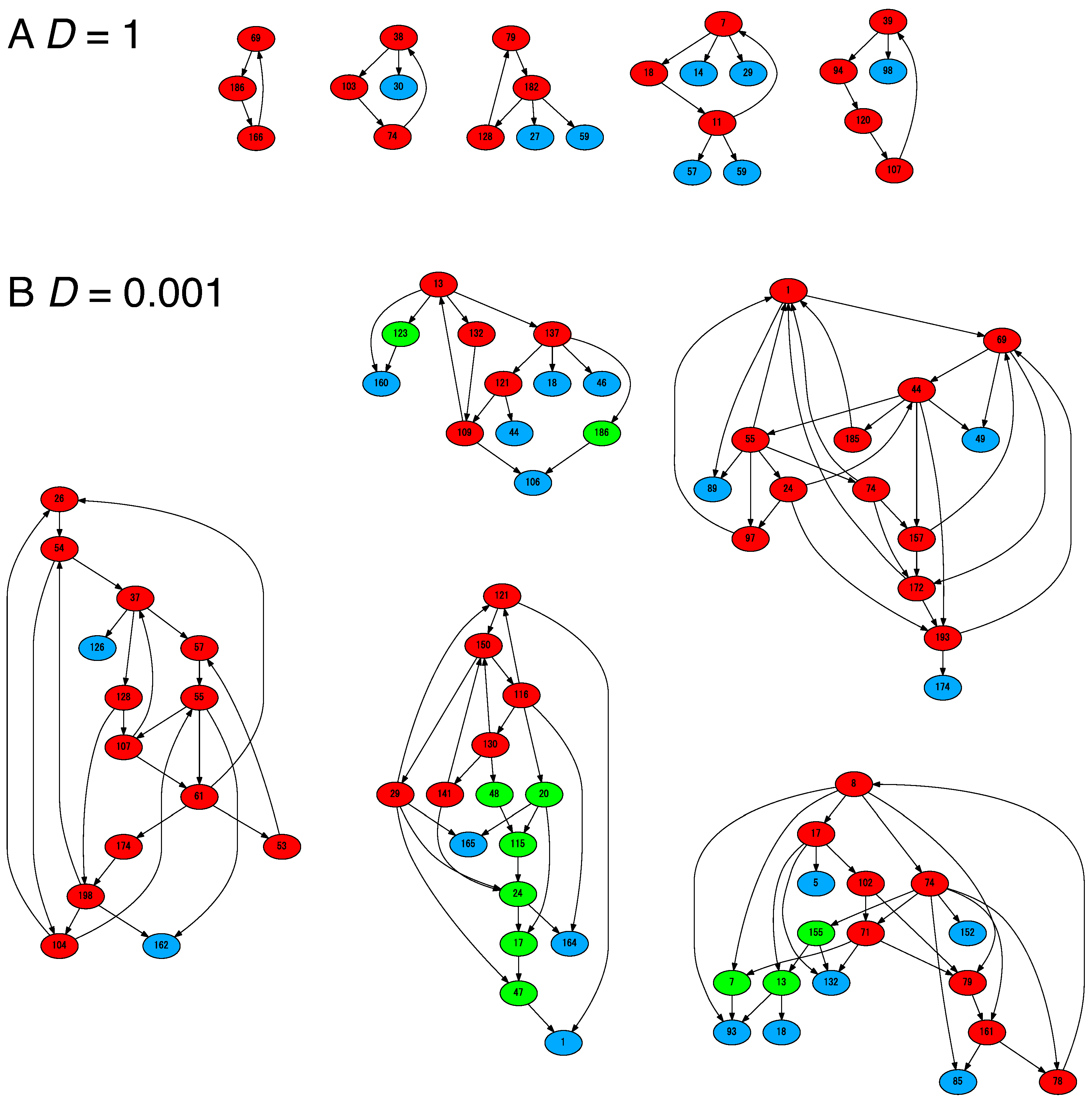
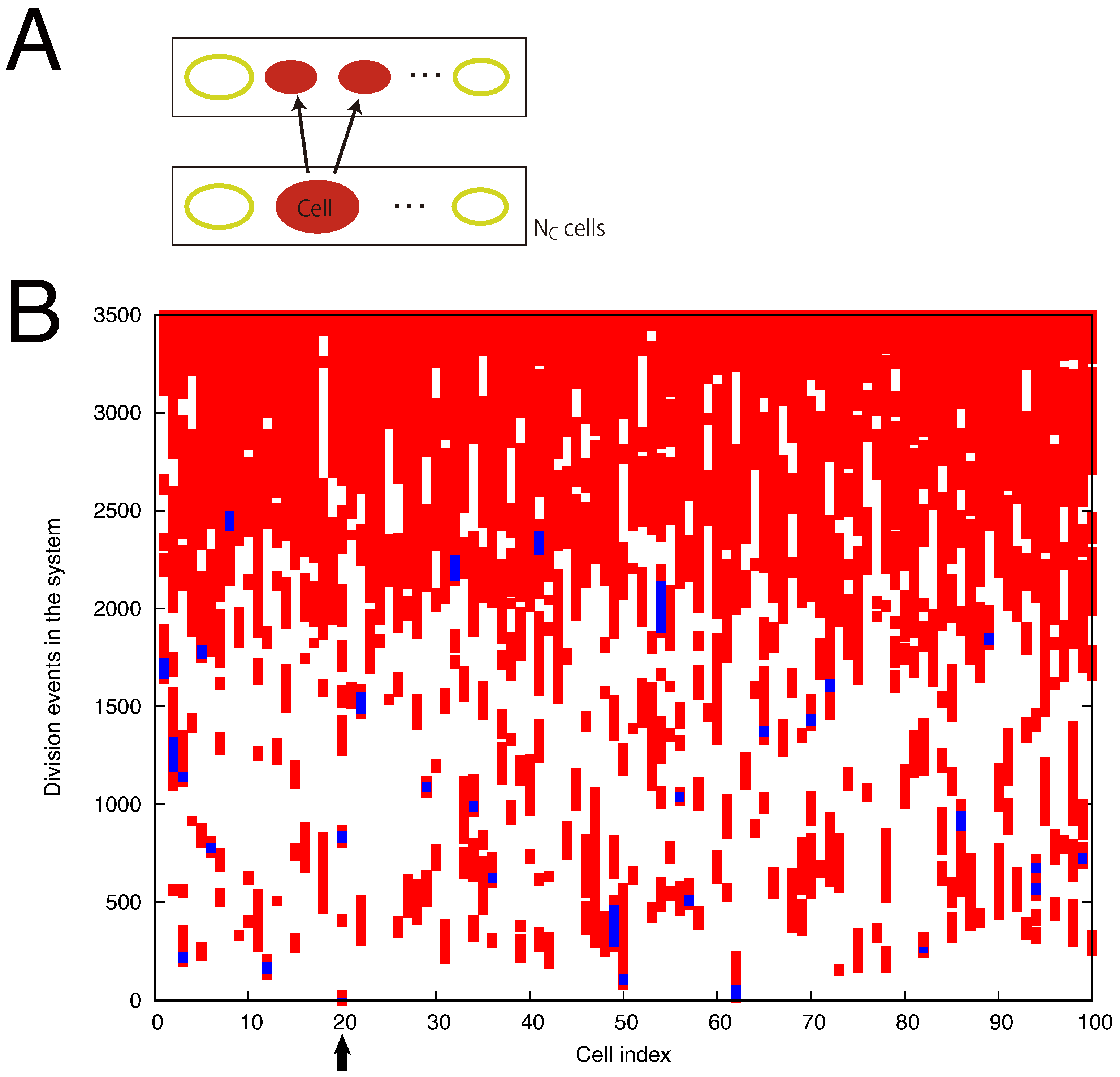
3. Diversification under Resource Limitation
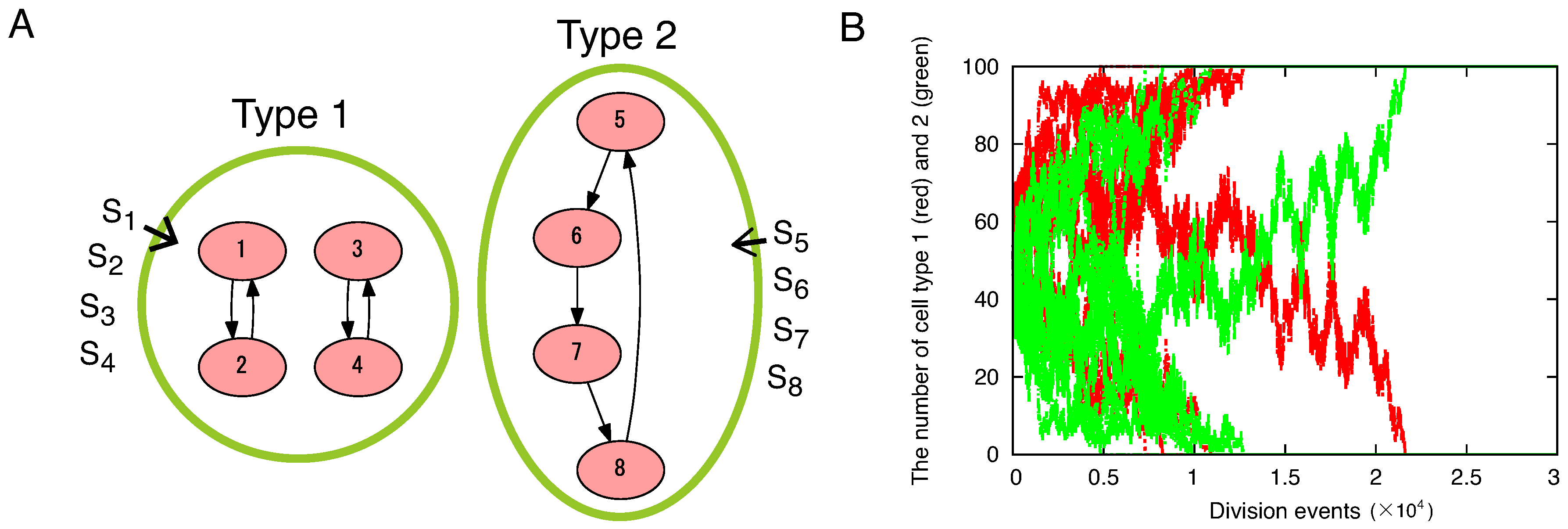
4. Evolutionary Constraints of the Catalytic Reaction Network
4.1. The Number of Species Is Essential for High Growth Rate
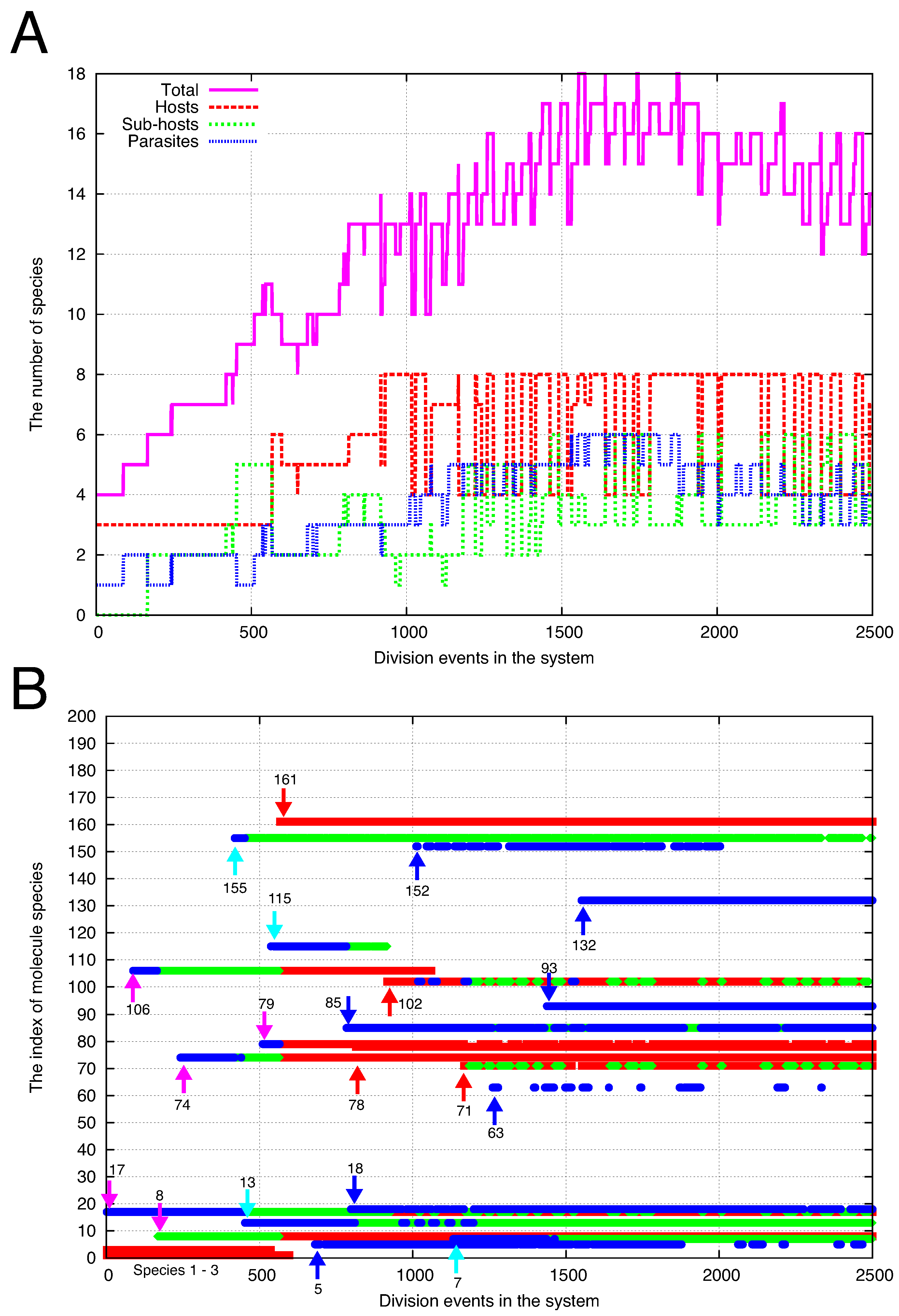
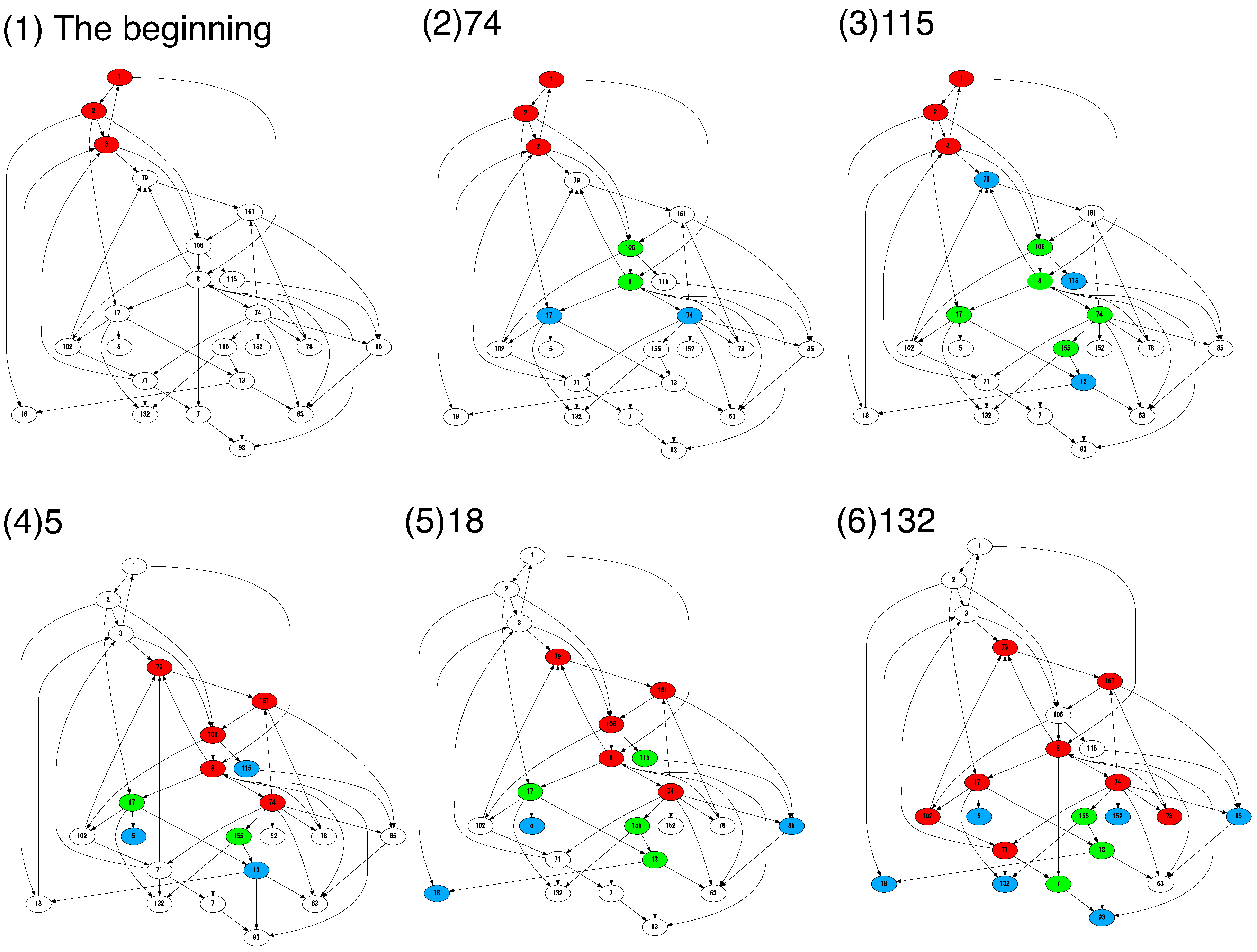
4.2. Cells Diversify Their Molecular Species by Adding Species One by One to the Existing Network
5. Discussion
6. Materials and Methods
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
References
- Mills, D.R.; Peterson, R.L.; Spiegelman, S. An extracellular Darwinian experiment with a self-duplicating nucleic acid molecule. Proc. Natl. Acad. Sci. USA 1967, 58, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Kacian, D.L.; Mills, D.R.; Kramer, F.R.; Spiegelman, S. A Replicating RNA Molecule Suitable for a Detailed Analysis of Extracellular Evolution and Replication. Proc. Natl. Acad. Sci. USA 1972, 69, 3038–3042. [Google Scholar] [CrossRef] [PubMed]
- Ichihashi, N.; Usui, K.; Kazuta, Y.; Sunami, T.; Matsuura, T.; Yomo, T. Darwinian evolution in a translation-coupled RNA replication system within a cell-like compartment. Nat. Commun. 2013, 4, 2494. [Google Scholar] [CrossRef] [PubMed]
- Fontana, W.; Buss, L.W. The arrival of the fittest: Toward a theory of biological organization. Bull. Math. Biol. 1994, 56, 1–64. [Google Scholar]
- Ray, T.S. An approach to the synthesis of life. In Artificial Life II; Langton, C., Taylor, C., Farmer, J.D., Rasmussen, S., Eds.; Addison-Wesley: Redwood City, CA, USA, 1991; Volume XI, pp. 371–408. [Google Scholar]
- Eigen, M.; Schuster, P. The Hypercycle: A Principle of Natural Self-Organization; Springer: Berlin, Germany, 1979. [Google Scholar]
- Dyson, F. Origins of Life; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Jain, S.; Krishna, S. Autocatalytic sets and the growth of complexity in an evolutionary model. Phys. Rev. Lett. 1998, 81, 5684. [Google Scholar] [CrossRef]
- Segré, D.; Ben-Eli, D.; Lancet, D. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2000, 97, 4112–4117. [Google Scholar] [CrossRef] [PubMed]
- Furusawa, C.; Kaneko, K. Zipf’s law in gene expression. Phys. Rev. Lett. 2003, 90, 088102. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, K. Recursiveness, switching, and fluctuations in a replicating catalytic network. Phys. Rev. E 2003, 68, 031909. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, A.; Kaneko, K. Reproduction of a protocell by replication of a minority molecule in a catalytic reaction network. Phys. Rev. Lett. 2010, 105, 268103. [Google Scholar] [CrossRef] [PubMed]
- Bedau, M.A.; Packard, N.H.; Rasmussen, S. Protocells: Bridging Nonliving and Living Matter; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Szostak, J.W.; Bartel, D.P.; Luisi, P.L. Synthesizing life. Nature 2001, 409, 387. [Google Scholar] [CrossRef] [PubMed]
- Gánti, T. The Principles of Life; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Luisi, P.L. The Emergence of Life: From Chemical Origins to Synthetic Biology; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Ruiz-Mirazo, K.; Briones, C.; de la Escosura, A. Prebiotic systems chemistry: New perspectives for the origins of life. Chem. Rev. 2013, 114, 285–366. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, A.; Kaneko, K. Transition to diversification by competition for multiple resources in catalytic reaction networks. J. Syst. Chem. 2015, 6, 5. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, A.; Kaneko, K. Negative scaling relationship between molecular diversity and resource abundances. Phys. Rev. E 2016, 93, 062419. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, Y.J.; Kaneko, K. Kinetic Selection of Template Polymer with Complex Sequences. Phys. Rev. Lett. 2018, 121, 118101. [Google Scholar] [CrossRef] [PubMed]
- Chesson, P. Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 2000, 31, 343–366. [Google Scholar] [CrossRef]
- Tilman, D. Resource Competition and Community Structure; Princeton University Press: Princeton, NJ, USA, 1982. [Google Scholar]
- Hogeweg, P. Multilevel evolution: Replicators and the evolution of diversity. Phys. D Nonlinear Phenom. 1994, 75, 275–291. [Google Scholar] [CrossRef]
- Kaneko, K. Life: An Introduction to Complex Systems Biology; Springer: Berlin, Germany, 2006. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamimura, A.; Kaneko, K. Molecular Diversity and Network Complexity in Growing Protocells. Life 2019, 9, 53. https://doi.org/10.3390/life9020053
Kamimura A, Kaneko K. Molecular Diversity and Network Complexity in Growing Protocells. Life. 2019; 9(2):53. https://doi.org/10.3390/life9020053
Chicago/Turabian StyleKamimura, Atsushi, and Kunihiko Kaneko. 2019. "Molecular Diversity and Network Complexity in Growing Protocells" Life 9, no. 2: 53. https://doi.org/10.3390/life9020053
APA StyleKamimura, A., & Kaneko, K. (2019). Molecular Diversity and Network Complexity in Growing Protocells. Life, 9(2), 53. https://doi.org/10.3390/life9020053




