Mathematical Analysis of a Prototypical Autocatalytic Reaction Network
Abstract
1. Introduction
2. Results and Discussion
2.1. Analysis of Kinetics for a Network with an Infinite Supply of Substrates
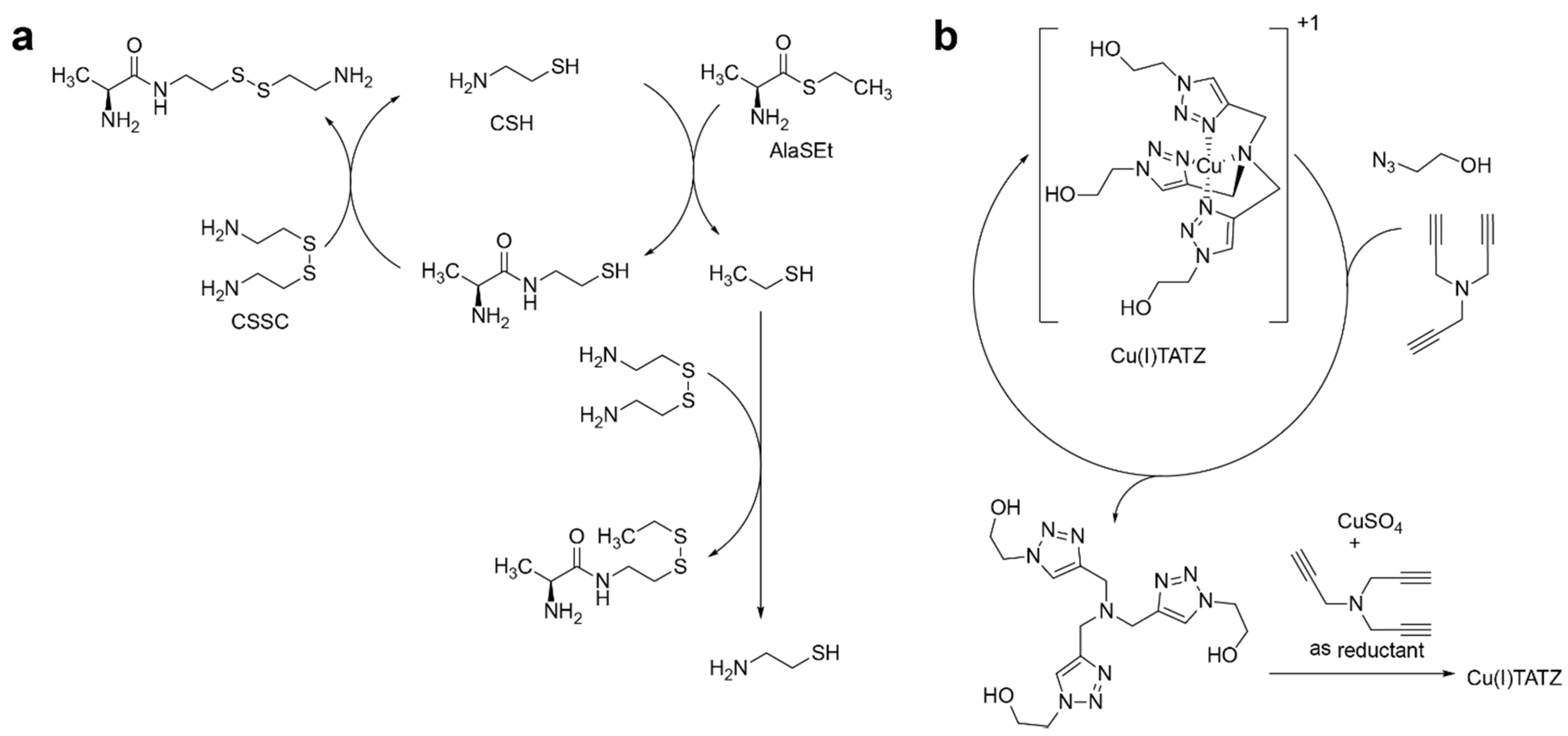
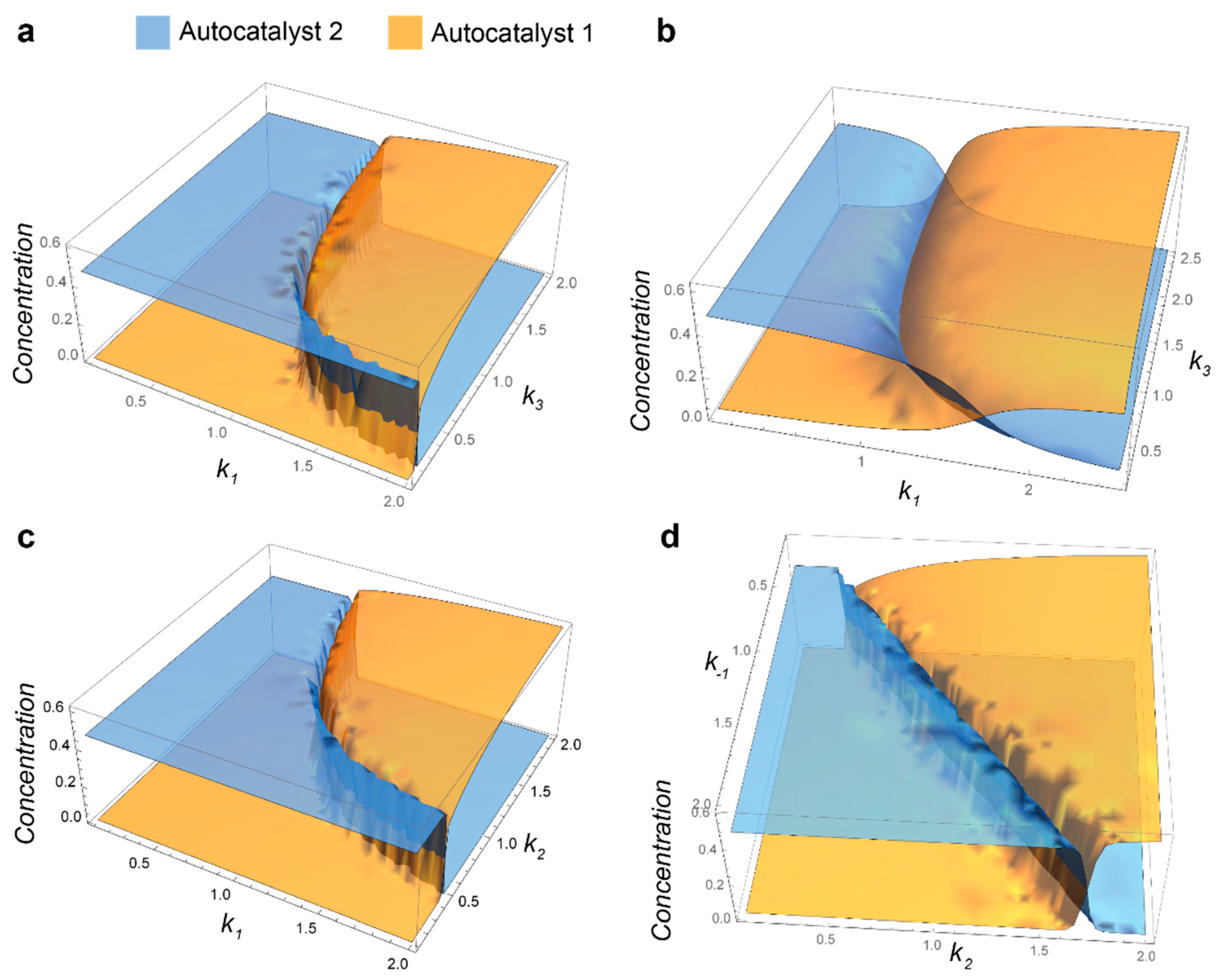
2.2. Competition of the Autocatalysts of Two Different Autocatalytic Networks for Common Substrates
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Equations (2)–(3) at and give:Substitution of (A3) and (A4) into (1) gives Equation (4)Equations (1) and (3) at and ) give:Substitution of (A7) into (2) gives Equation (5)
- Equation (6) at P(0) = 0 and A(0) = A0 => has a solution:Considering that:A(t) is described by Equation (7).
- In Equation (10) coefficients C1 and C2 are expressed by:
- Equations (1)–(3) are linear and a solution for this linear system of ODE has the following form:where λ1, λ2, and λ3 are eigenvalues, and ν1-3 are the corresponding eigenvectors of the matrix:λ1, λ2, and λ3 are roots of the equation:From Vieta’s formula:Because k1, k2, k3, S1, S2 are positive, one of the λ1-3 values must be positive.
- Steady-state conditions for 12-19 are as follows:If we consider S2 to be constant and the reaction rates are different for two networks, this system of equations does not have solutions where both A1 and A2 are nonzero.
- Mathematic script that generates the plot 3A. Plots 3B-C were generated by modifying this script.k0 = 0.1; k1 = 1; k1r = 1; k2 = 1; k3 = 1; k1z = 1; k1rz = 1; k2z = 1; k3z = 1; S01 = 1; S02 = 1;s = ParametricNDSolve[{a’[t] == -a[t]*(i*k1*s1[t] + k0) + b[t]*(k2 + k1r) + h*k3*s2[t]*p[t], b’[t] == i*k1*a[t]*s1[t] - b[t]*(k2 + k1r + k0), p’[t] == k2*b[t] - (h*k3*s2[t] + k0)*p[t], a1’[t] == -a1[t]*(k1z*s1[t] + k0) + b1[t]*(k2z + k1rz) + k3z*s2[t]*p1[t], b1’[t] == k1z*a1[t]*s1[t] - b1[t]*(k2z + k1rz + k0), p1’[t] == k2z*b1[t] - (k3z*s2[t] + k0)*p1[t], s1’[t] == -i*k1*a[t]*s1[t] - k1z*a1[t]*s1[t] + k1r*b[t] + k1rz*b1[t] - k0*s1[t] + k0*S01, s2’[t] == -h*k3*p[t]*s2[t] - k3z*p1[t]*s2[t] - k0*s2[t] + k0*S02, a[0] == 0.001, a1[0] == 0.001, b[0] == p[0] == b1[0] == p1[0] == 0, s1[0] == s2[0] == 1 }, {a, b, p, a1, b1, p1, s1, s2}, {t, 0, 2000}, {i, h}];Plot3D[{a[i, h][2000] /. s, a1[i, h][2000] /. s}, {i, 0.1, 2}, {h, 0.1, 2}, PlotStyle -> Opacity[0.7], Mesh -> None, AxesStyle -> 16]
References
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. Hypercycle—Principle of Natural Self-Organization. B. Abstract Hypercycle. Naturwissenschaften 1978, 65, 7–41. [Google Scholar] [CrossRef]
- Sievers, D.; Von Kiedrowski, G. Self Replication of Complementary Nucleotide-Based Oligomers. Nature 1994, 369, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Nicolaou, K.C. Chemical self-replication of palindromic duplex DNA. Nature 1994, 369, 218–221. [Google Scholar] [CrossRef]
- Lee, D.H.; Granja, J.R.; Martinez, J.A.; Severin, K.; Ghadiri, M.R. A self-replicating peptide. Nature 1996, 382, 525–528. [Google Scholar] [CrossRef]
- Ashkenasy, G.; Jagasia, R.; Yadav, M.; Ghadiri, M.R. Design of a directed molecular network. Proc. Natl. Acad. Sci. USA 2004, 101, 10872–10877. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations; Wiley: New York, NY, USA, 1977; pp. 40–233. [Google Scholar]
- Field, R.J.; Noyes, R.M. Oscillations in chemical systems. IV. Limit cycle behavior in a model of a real chemical reaction. J. Chem. Phys. 1974, 60, 1877–1884. [Google Scholar] [CrossRef]
- Kholodenko, B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Bio. 2006, 7, 165–176. [Google Scholar] [CrossRef]
- Dyson, F.J. A Model for the Origin of Life. J. Mol. Evol. 1982, 18, 344–350. [Google Scholar] [CrossRef]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Szathmary, E. Evolution before genes. Biol. Direct 2012, 7. [Google Scholar] [CrossRef]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.M.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. Biosyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Epstein, I.R.; Pojman, J.A. An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos; Oxford University Press: New York, NY, USA, 1998; pp. 17–324. [Google Scholar]
- Dekepper, P.; Epstein, I.R.; Kustin, K. A Systematically Designed Homogeneous Oscillating Reaction - the Arsenite-Iodate-Chlorite System. J. Am. Chem. Soc. 1981, 103, 2133–2134. [Google Scholar] [CrossRef]
- Lengyel, I.; Epstein, I.R. Modeling of Turing Structures in the Chlorite Iodide Malonic-Acid Starch Reaction System. Science 1991, 251, 650–652. [Google Scholar] [CrossRef] [PubMed]
- Turing, A.M. The Chemical Basis of Morphogenesis. Philos. T. Roy. Soc. B 1952, 237, 37–72. [Google Scholar]
- Lifson, S. On the crucial stages in the origin of animate matter. J. Mol. Evol. 1997, 44, 1–8. [Google Scholar] [CrossRef]
- Hordijk, W.; Hein, J.; Steel, M. Autocatalytic Sets and the Origin of Life. Entropy 2010, 12, 1733–1742. [Google Scholar] [CrossRef]
- Eschenmoser, A. Etiology of potentially primordial biomolecular structures: From vitamin B12 to the nucleic acids and an inquiry into the chemistry of life’s origin: A retrospective. Angew. Chem. Int. Ed. Engl. 2011, 50, 12412–12472. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M. Chasing the tail: The emergence of autocatalytic networks. Biosystems 2017, 152, 1–10. [Google Scholar] [CrossRef]
- Markovitch, O.; Lancet, D. Excess Mutual Catalysis Is Required for Effective Evolvability. Artif. Life 2012, 18, 243–266. [Google Scholar] [CrossRef] [PubMed]
- Lincoln, T.A.; Joyce, G.F. Self-Sustained Replication of an RNA Enzyme. Science 2009, 323, 1229–1232. [Google Scholar] [CrossRef] [PubMed]
- Plasson, R.; Brandenburg, A.; Jullien, L.; Bersini, H. Autocatalyses. J. Phys. Chem. A 2011, 115, 8073–8085. [Google Scholar] [CrossRef]
- Hinshelwood, C.N. On the Chemical Kinetics of Autosynthetic Systems. J. Chem. Soc. 1952, 745–755. [Google Scholar] [CrossRef]
- Blackmond, D.G. An examination of the role of autocatalytic cycles in the chemistry of proposed primordial reactions. Angew. Chem. Int. Ed. Engl. 2009, 48, 386–390. [Google Scholar] [CrossRef]
- Bissette, A.J.; Fletcher, S.P. Mechanisms of Autocatalysis. Angew. Chem. Int. Ed. 2013, 52, 12800–12826. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M.; Dittrich, P. Autocatalytic sets and chemical organizations: Modeling self-sustaining reaction networks at the origin of life. New J. Phys. 2018, 20, 015011. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M.; Kauffman, S. The structure of autocatalytic sets: Evolvability, enablement, and emergence. Acta Biotheor. 2012, 60, 379–392. [Google Scholar] [CrossRef]
- Szathmary, E. The origin of replicators and reproducers. Philos. Trans. R. Soc. Lond B Biol. Sci. 2006, 361, 1761–1776. [Google Scholar] [CrossRef]
- Szathmáry, E. Simple growth laws and selection consequences. Trends in Ecology & Evolution 1991, 6, 366–370. [Google Scholar]
- Wagner, N.; Ashkenasy, G. How Catalytic Order Drives the Complexification of Molecular Replication Networks. Isr. J. Chem. 2015, 55, 880–890. [Google Scholar] [CrossRef]
- Ashkenasy, G.; Hermans, T.M.; Otto, S.; Taylor, A.F. Systems chemistry. Chem. Soc. Rev. 2017, 46, 2543–2554. [Google Scholar] [CrossRef] [PubMed]
- Ludlow, R.F.; Otto, S. Systems chemistry. Chem. Soc. Rev. 2008, 37, 101–108. [Google Scholar] [CrossRef]
- Dadon, Z.; Wagner, N.; Alasibi, S.; Samiappan, M.; Mukherjee, R.; Ashkenasy, G. Competition and cooperation in dynamic replication networks. Chemistry 2015, 21, 648–654. [Google Scholar] [CrossRef]
- Semenov, S.N.; Kraft, L.J.; Ainla, A.; Zhao, M.; Baghbanzadeh, M.; Campbell, C.E.; Kang, K.; Fox, J.M.; Whitesides, G.M. Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions. Nature 2016, 537, 656–660. [Google Scholar] [CrossRef] [PubMed]
- Semenov, S.N.; Belding, L.; Cafferty, B.J.; Mousavi, M.P.S.; Finogenova, A.M.; Cruz, R.S.; Skorb, E.V.; Whitesides, G.M. Autocatalytic Cycles in a Copper-Catalyzed Azide-Alkyne Cycloaddition Reaction. J. Am. Chem. Soc. 2018, 140, 10221–10232. [Google Scholar] [CrossRef]
- Carnall, J.M.A.; Waudby, C.A.; Belenguer, A.M.; Stuart, M.C.A.; Peyralans, J.J.P.; Otto, S. Mechanosensitive Self-Replication Driven by Self-Organization. Science 2010, 327, 1502–1506. [Google Scholar] [CrossRef]
- Sadownik, J.W.; Mattia, E.; Nowak, P.; Otto, S. Diversification of self-replicating molecules. Nat. Chem. 2016, 8, 264–269. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skorb, E.V.; Semenov, S.N. Mathematical Analysis of a Prototypical Autocatalytic Reaction Network. Life 2019, 9, 42. https://doi.org/10.3390/life9020042
Skorb EV, Semenov SN. Mathematical Analysis of a Prototypical Autocatalytic Reaction Network. Life. 2019; 9(2):42. https://doi.org/10.3390/life9020042
Chicago/Turabian StyleSkorb, Ekaterina V., and Sergey N. Semenov. 2019. "Mathematical Analysis of a Prototypical Autocatalytic Reaction Network" Life 9, no. 2: 42. https://doi.org/10.3390/life9020042
APA StyleSkorb, E. V., & Semenov, S. N. (2019). Mathematical Analysis of a Prototypical Autocatalytic Reaction Network. Life, 9(2), 42. https://doi.org/10.3390/life9020042





