Molecular Diversity Required for the Formation of Autocatalytic Sets
Abstract
1. Introduction
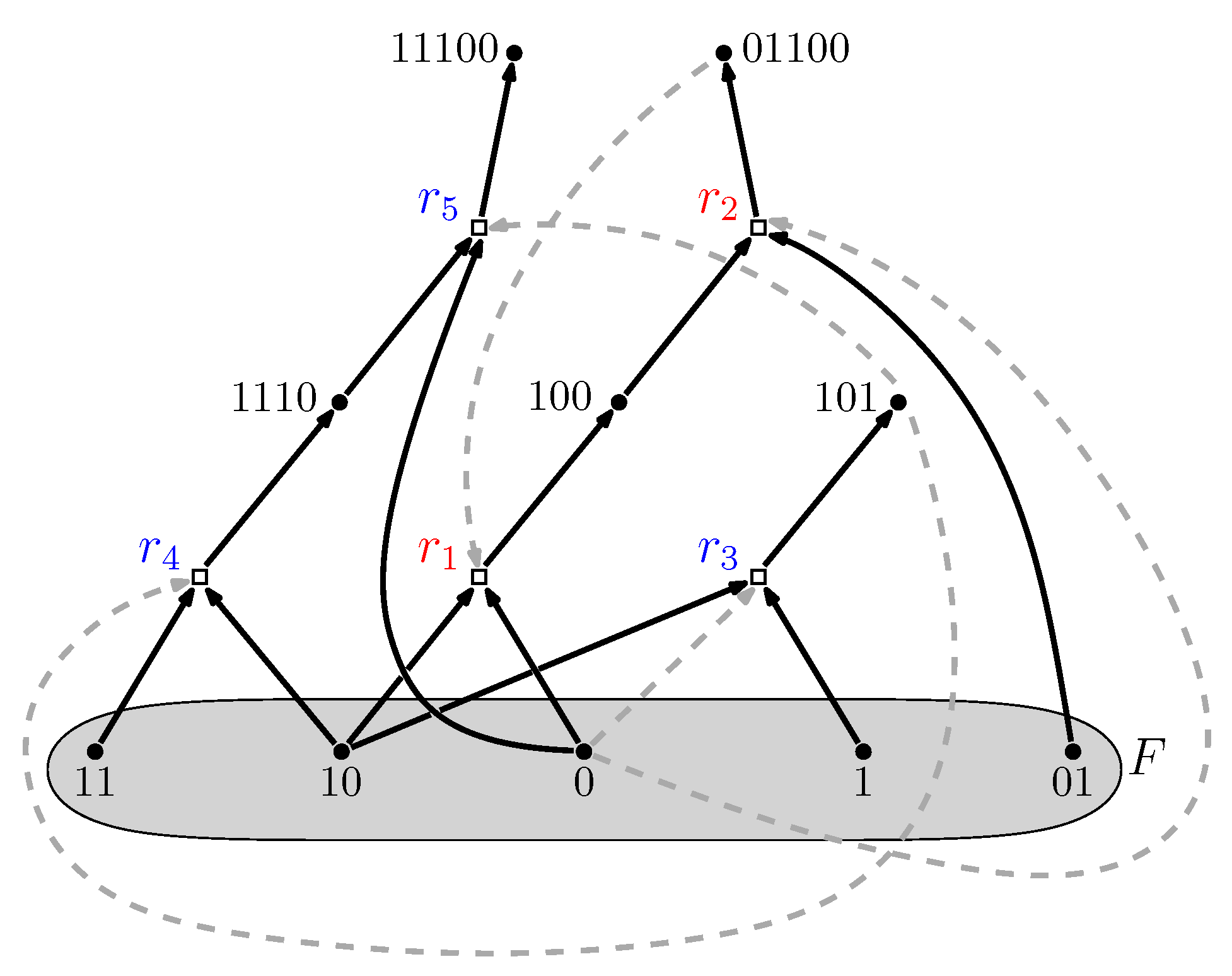
2. Background: Autocatalytic Sets
- Reflexively autocatalytic (RA): each reaction is catalyzed by at least one molecule type that is either a product of or is present in the food set F; and
- F-generated (F): all reactants involved in reactions in can be created from the food set F by using a series of reactions only from itself.
3. Results: Required Molecular Diversity for RAF Sets
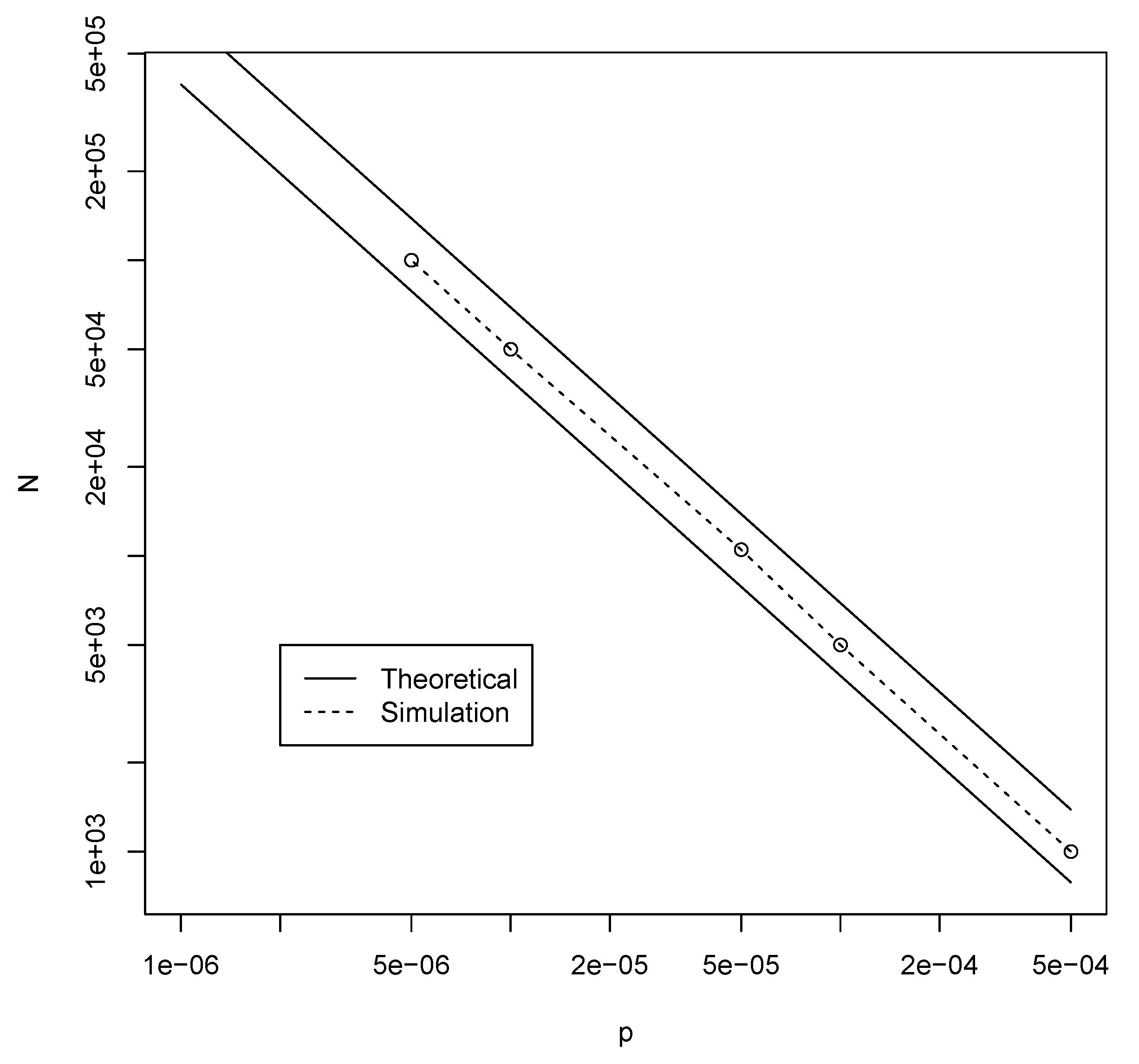
3.1. Binary Polymer Model
- (1)
- The E-R result is specifically for undirected graphs, while the catalysis graph is a directed graph. Getting a connected component in an undirected graph is much easier than getting a (strongly) connected component in a directed graph.
- (2)
- In the E-R setting the undirected graphs are simple (i.e., there is just a single edge between any two vertices) while in the setting described above there may be more than one edge.
- (3)
- In the E-R setting there is an equal probability p that each pair of nodes has an (undirected) edge. In other words, E-R random graphs are isotropic, but the catalysis graph is non-isotropic.
- (4)
- RAFs are required to be F-generated, and a giant connected component need not be (e.g., if the food set is a subset of the molecules not in the giant component).
- (5)
- RAFs might form well before a giant connected component does (i.e., a RAF is not required, a priori, to be large).
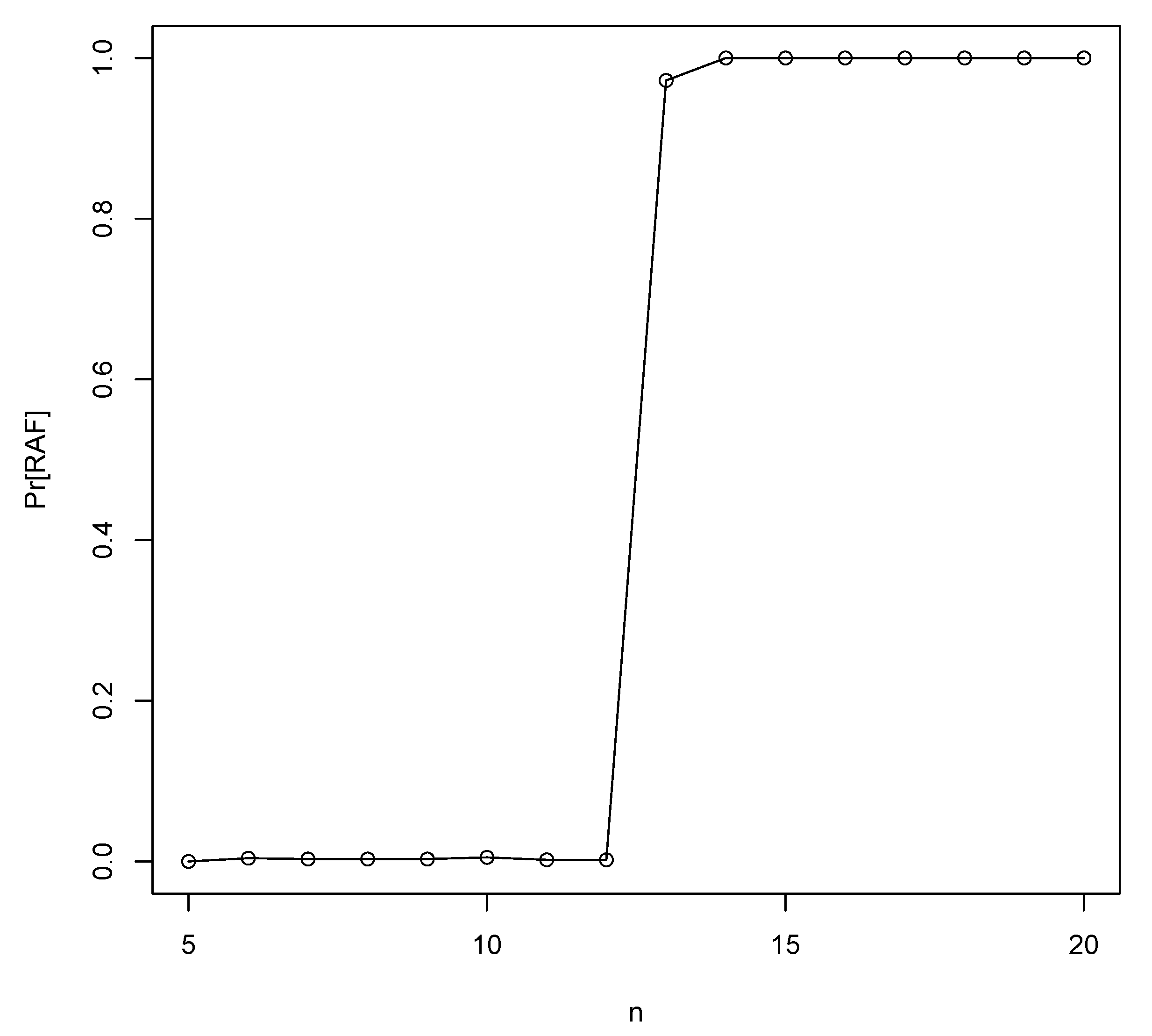
3.2. Jain–Krishna Model
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kauffman, S.A. Question 1: Origin of life and the living state. Orig. Life Evolut. Biosph. 2007, 37, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Hein, J.; Steel, M. Autocatalytic sets and the origin of life. Entropy 2010, 12, 1733–1742. [Google Scholar] [CrossRef]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.M.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. BioSyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef] [PubMed]
- Sousa, F.L.; Hordijk, W.; Steel, M.; Martin, W.F. Autocatalytic sets in E. coli metabolism. J. Syst. Chem. 2015, 6, 4. [Google Scholar] [CrossRef] [PubMed]
- Cazzolla Gatti, R.; Hordijk, W.; Kauffman, S. Biodiversity is autocatalytic. Ecol. Model. 2017, 346, 70–76. [Google Scholar] [CrossRef]
- Cazzolla Gatti, R.; Fath, B.; Hordijk, W.; Kauffman, S.; Ulanowicz, R. Niche emergence as an autocatalytic process in the evolution of ecosystems. J. Theor. Biol. 2018, 454, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Sievers, D.; von Kiedrowski, G. Self-replication of complementary nucleotide-based oligomers. Nature 1994, 369, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.E.; Joyce, G.F. Cross-catalytic replication of an RNA ligase ribozyme. Chem. Biol. 2004, 11, 1505–1512. [Google Scholar] [CrossRef] [PubMed]
- Ashkenasy, G.; Jegasia, R.; Yadav, M.; Ghadiri, M.R. Design of a directed molecular network. PNAS 2004, 101, 10872–10877. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, N.; Manapat, M.L.; Chen, I.A.; Xulvi-Brunet, R.; Hayden, E.J.; Lehman, N. Spontaneous network formation among cooperative RNA replicators. Nature 2012, 491, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Arsène, S.; Ameta, S.; Lehman, N.; Griffiths, A.D.; Nghe, P. Coupled catabolism and anabolism in autocatalytic RNA sets. Nucleic Acids Res. 2018, 46, 9660–9666. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Chasing the tail: The emergence of autocatalytic networks. BioSystems 2017, 152, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. A formal model of autocatalytic sets emerging in an RNA replicator system. J. Syst. Chem. 2013, 4, 3. [Google Scholar] [CrossRef]
- Hordijk, W.; Vaidya, N.; Lehman, N. Serial transfer can aid the evolution of autocatalytic sets. J. Syst. Chem. 2014, 5, 4. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Shichor, S.; Ashkenasy, G. The influence of modularity, seeding, and product inhibition on peptide autocatalytic network dynamics. ChemPhysChem 2018, 19, 2437–2444. [Google Scholar] [CrossRef] [PubMed]
- Damer, B.; Deamer, D. Coupled phases and combinatorial selection in fluctuating hydrothermal pools: A scenario to guide experimental approaches to the origin of cellular life. Life 2015, 5, 872–887. [Google Scholar] [CrossRef] [PubMed]
- Deamer, D.W. Assembling Life: How Can Life Begin on Earth and Other Habitable Planets? Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Watanabe, M.; Arai, S. The plastein reaction: Fundamentals and applications. In Biochemistry of Food Proteins; Springer: Boston, MA, USA, 1992; pp. 271–305. [Google Scholar]
- Kauffman, S.A. Cellular homeostasis, epigenesis and replication in randomly aggregated macromolecular systems. J. Cybern. 1971, 1, 71–96. [Google Scholar] [CrossRef]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Kauffman, S.A.; Steel, M. Required levels of catalysis for emergence of autocatalytic sets in models of chemical reaction systems. Int. J. Mol. Sci. 2011, 12, 3085–3101. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M.; Kauffman, S. The structure of autocatalytic sets: Evolvability, enablement, and emergence. Acta Biotheor. 2012, 60, 379–392. [Google Scholar] [CrossRef] [PubMed]
- Steel, M. The emergence of a self-catalysing structure in abstract origin-of-life models. Appl. Math. Lett. 2000, 3, 91–95. [Google Scholar] [CrossRef]
- Mossel, E.; Steel, M. Random biochemical networks: The probability of self-sustaining autocatalysis. J. Theor. Biol. 2005, 233, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Predicting template-based catalysis rates in a simple catalytic reaction model. J. Theor. Biol. 2012, 295. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Hasenclever, L.; Gao, J.; Mincheva, D.; Hein, J. An investigation into irreducible autocatalytic sets and power law distributed catalysis. Nat. Comput. 2014, 13, 287–296. [Google Scholar] [CrossRef]
- Hordijk, W.; Wills, P.R.; Steel, M. Autocatalytic sets and biological specificity. Bull. Math. Biol. 2014, 76, 201–224. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.; Steel, M.; Hordijk, W. Autocatalytic sets in a partitioned biochemical network. J. Syst. Chem. 2014, 5, 2. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Autocatalytic sets in polymer networks with variable catalysis distributions. J. Math. Chem. 2016, 54, 1997–2021. [Google Scholar] [CrossRef]
- Hordijk, W.; Smith, J.I.; Steel, M. Algorithms for detecting and analysing autocatalytic sets. Algorithms Mol. Biol. 2015, 10, 15. [Google Scholar] [CrossRef] [PubMed]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Sathmáry, E. Evolution before genes. Biol. Direct 2012, 7, 1. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Conditions for evolvability of autocatalytic sets: A formal example and analysis. Orig. Life Evolut. Biosph. 2014, 44, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W. Evolution of autocatalytic sets in computational models of chemical reaction networks. Orig. Life Evolut. Biosph. 2016, 46, 233–245. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Naylor, J.; Krasnogor, N.; Fellermann, H. Population dynamics of autocatalytic sets in a compartmentalized spatial world. Life 2018, 8, 33. [Google Scholar] [CrossRef] [PubMed]
- Erdős, P.; Rényi, A. On random graphs. Publ. Math. 1959, 6, 290–297. [Google Scholar]
- Erdős, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–61. [Google Scholar]
- Steel, M.; Hordijk, W.; Smith, J. Minimal autocatalytic networks. J. Theor. Biol. 2013, 332, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Steel, M.; Hordijk, W.; Xavier, J.C. Autocatalytic networks in biology: Structural theory and algorithms. J. R. Soc. Interface 2019, 16, 20180808. [Google Scholar] [CrossRef]
- Jain, S.; Krishna, S. Autocatalytic sets and the growth of complexity in an evolutionary model. Phys. Rev. Lett. 1998, 81, 5684–5687. [Google Scholar] [CrossRef]
- Jain, S.; Krishna, S. A model for the emergence of cooperation, interdependence, and structure in evolving networks. PNAS 2001, 98, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Krishna, S. Large extinctions in an evolutionary model: The role of innovation and keystone species. PNAS 2002, 99, 2055–2060. [Google Scholar] [CrossRef] [PubMed]
- Bollobás, B.; Rasmussen, S. First cycles in random directed graph processes. Discrete Math. 1989, 75, 55–68. [Google Scholar] [CrossRef]
- Scott, J.K.; Smith, G.P. Searching for peptide ligands with an epitope library. Science 1990, 249, 286–390. [Google Scholar] [CrossRef]
- Quintarelli, A. Systems Optimization for the Selection of Phage Display Random Peptide Libraries. Ph.D. Thesis, University of Rome III, Roma, Italy, 2011. [Google Scholar]
- Tramontano, A.; Janda, K.D.; Lerner, R.A. Catalytic antibodies. Science 1986, 234, 1566–1570. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, A.W.; de Graaf, R.M. The prebiotic synthesis of carbohydrates: A reassessment. J. Mol. Evol. 1993, 36, 101–106. [Google Scholar] [CrossRef]
- Zhang, X.V.; Martin, S.T. Driving parts of Krebs cycle in reverse through mineral photochemistry. J. Am. Chem. Soc. 2006, 128, 16032–16033. [Google Scholar] [CrossRef] [PubMed]
- Muchowska, K.B.; Varma, S.J.; Chevallot-Beroux, E.; Lethuillier-Karl, L.; Li, G.; Moran, J. Metals promote sequences of the reverse Krebs cycle. Nat. Ecol. Evolut. 2017, 1, 1716–1721. [Google Scholar] [CrossRef] [PubMed]
- Varma, S.J.; Muchowska, K.B.; Chatelain, P.; Moran, J. Native iron reduces CO2 to intermediates and end-products of the acetyl-CoA pathway. Nat. Ecol. Evolut. 2018, 2, 1019–1024. [Google Scholar] [CrossRef] [PubMed]
- Christen, P.; Mehta, P.K. From cofactor to enzymes: The molecular evolution of pyridoxal-5’-phosphate-dependent enzymes. Chem. Rec. 2001, 1, 436–447. [Google Scholar] [CrossRef] [PubMed]
- Rees, D.C.; Howard, J.B. The interface between the biological and inorganic worlds: Iron-sulfur metalloclusters. Science 2003, 300, 929–931. [Google Scholar] [CrossRef] [PubMed]
- Wieczorek, R.; Adamala, K.; Gasperi, T.; Polticelli, F.; Stano, P. Small and random peptides: An unexplored reservoir of potentially functional primitive organocatalysts. The case of Seryl-Histidine. Life 2017, 7, 19. [Google Scholar] [CrossRef] [PubMed]
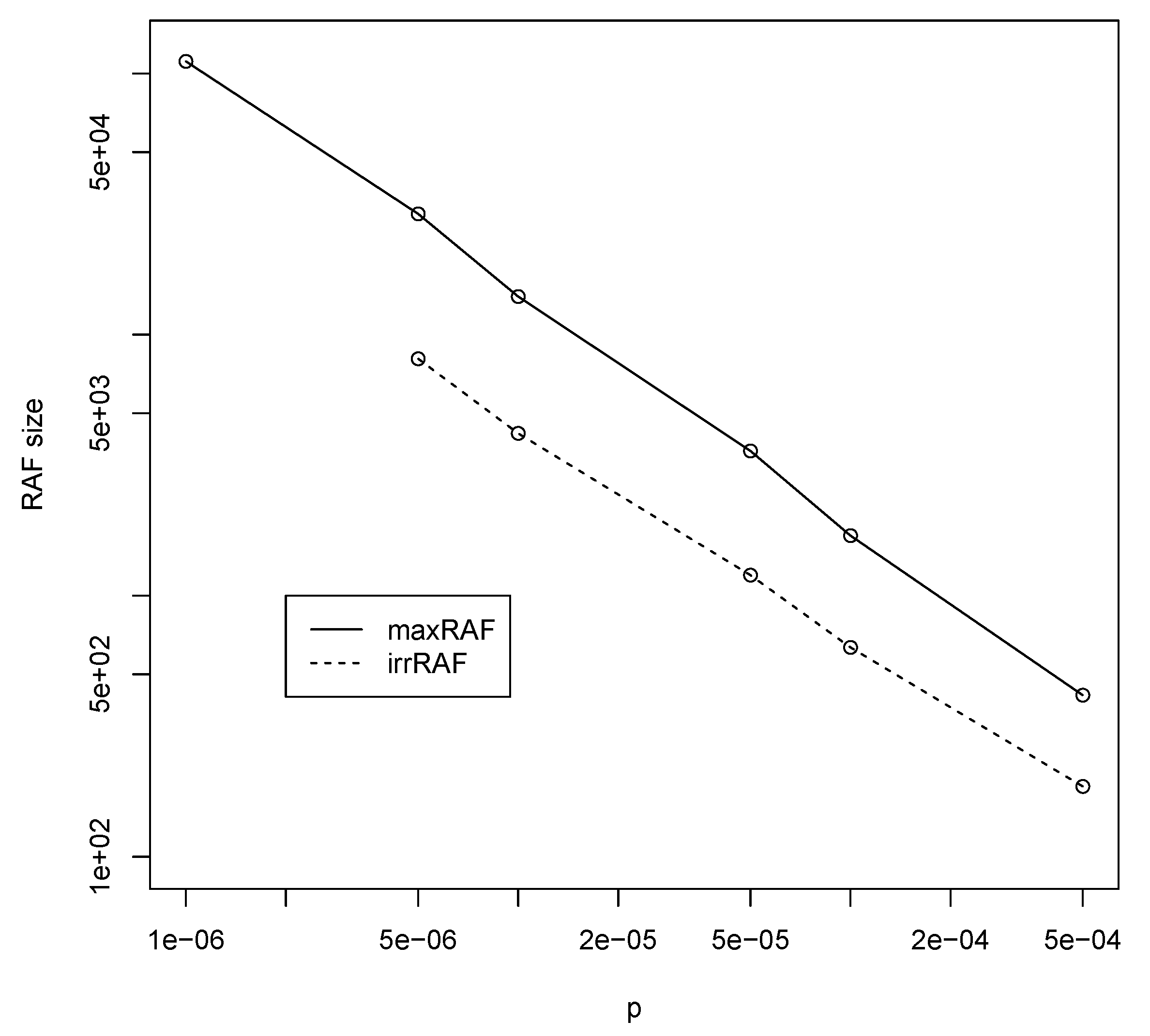

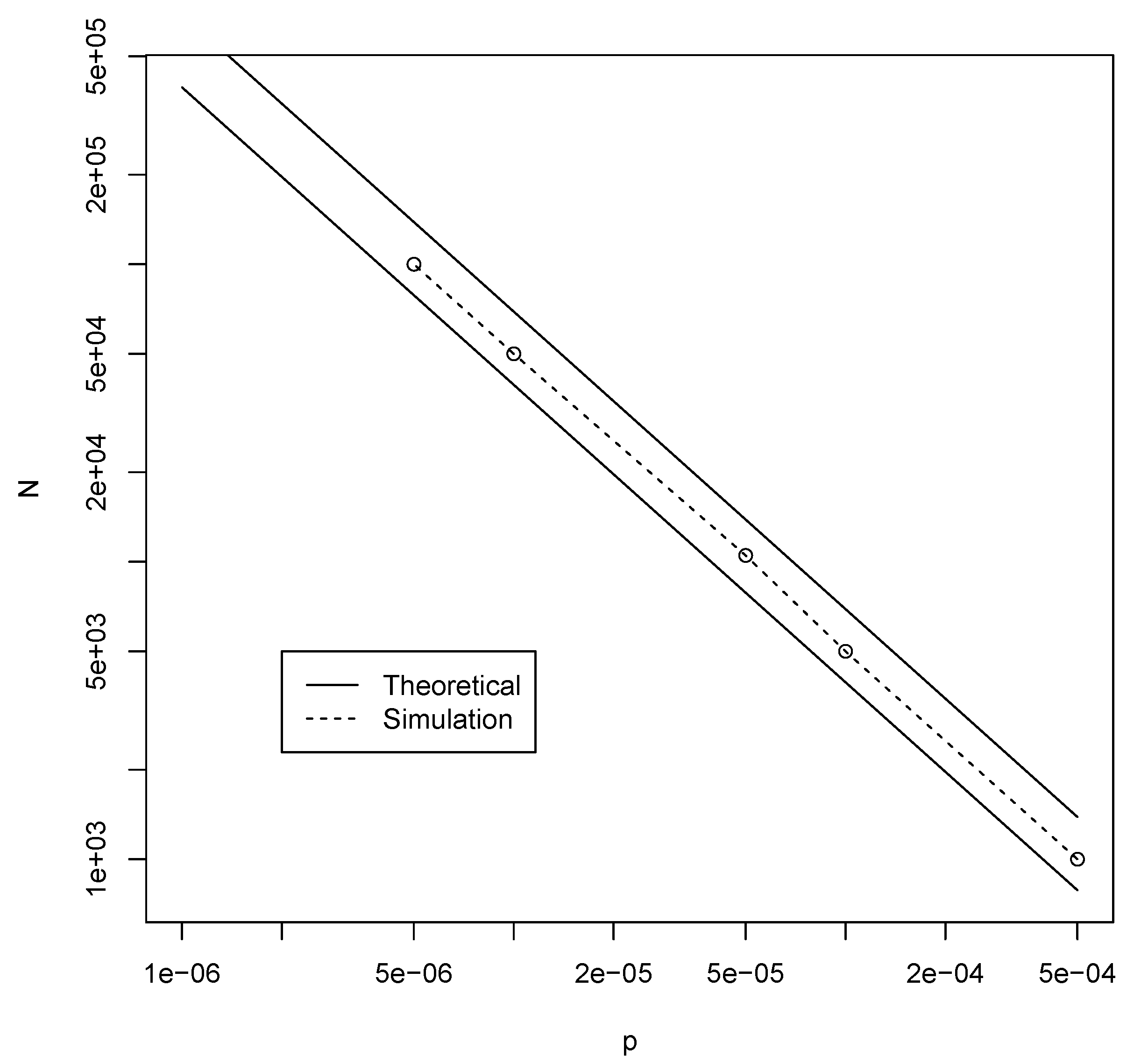
| p | ||||||
|---|---|---|---|---|---|---|
| BPM | 131,070 | 32,766 | 16,382 | 4094 | 2046 | 510 |
| JKM | 500,000 | 100,000 | 50,000 | 10,000 | 5000 | 1000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hordijk, W.; Steel, M.; Kauffman, S.A. Molecular Diversity Required for the Formation of Autocatalytic Sets. Life 2019, 9, 23. https://doi.org/10.3390/life9010023
Hordijk W, Steel M, Kauffman SA. Molecular Diversity Required for the Formation of Autocatalytic Sets. Life. 2019; 9(1):23. https://doi.org/10.3390/life9010023
Chicago/Turabian StyleHordijk, Wim, Mike Steel, and Stuart A. Kauffman. 2019. "Molecular Diversity Required for the Formation of Autocatalytic Sets" Life 9, no. 1: 23. https://doi.org/10.3390/life9010023
APA StyleHordijk, W., Steel, M., & Kauffman, S. A. (2019). Molecular Diversity Required for the Formation of Autocatalytic Sets. Life, 9(1), 23. https://doi.org/10.3390/life9010023






