Evolutionary Conflict Leads to Innovation: Symmetry Breaking in a Spatial Model of RNA-Like Replicators
Abstract
1. Introduction
2. Results
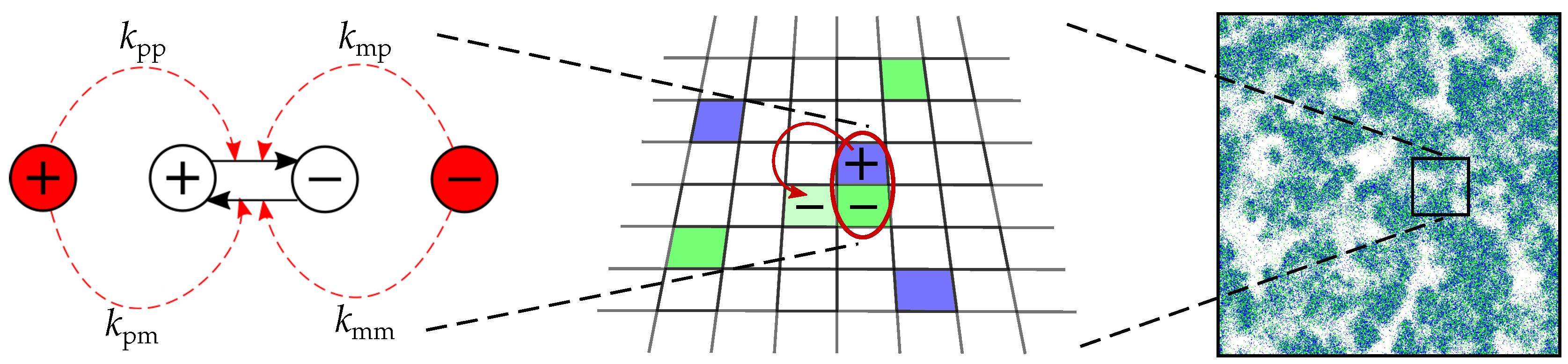
2.1. The Model
2.2. Evolutionary Dynamics of the Model
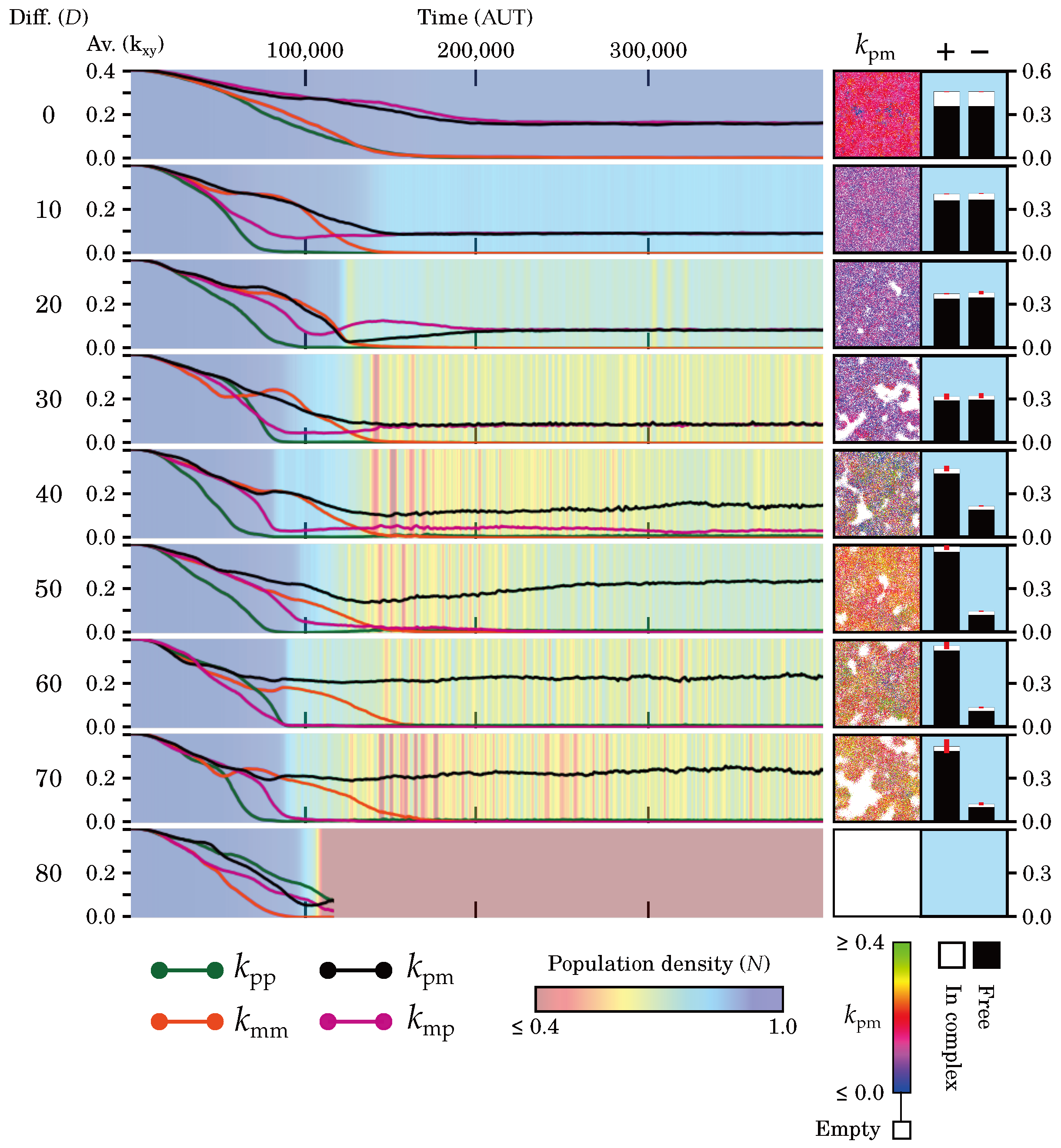
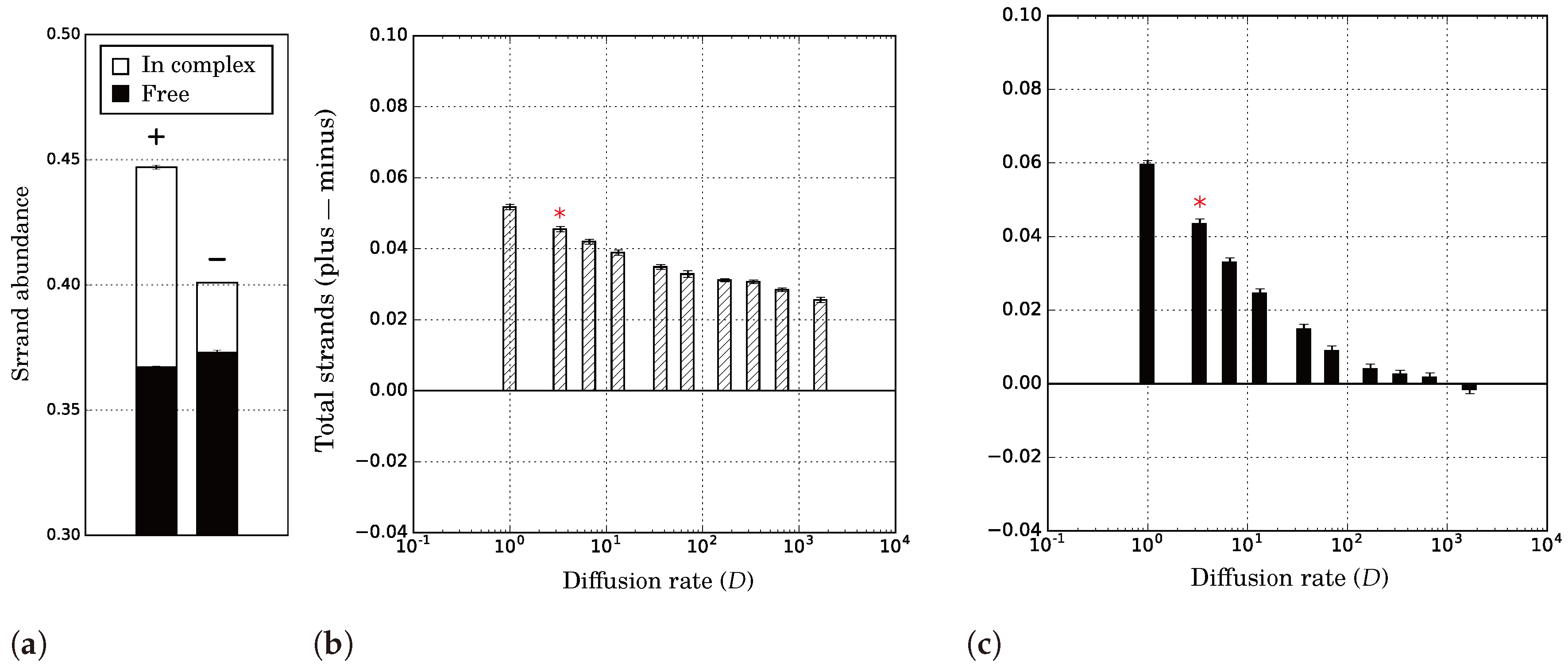
2.2.1. Evolutionary and Population Stability Depend on Diffusion
2.2.2. Diffusion Determines Interplay between Levels of Selection
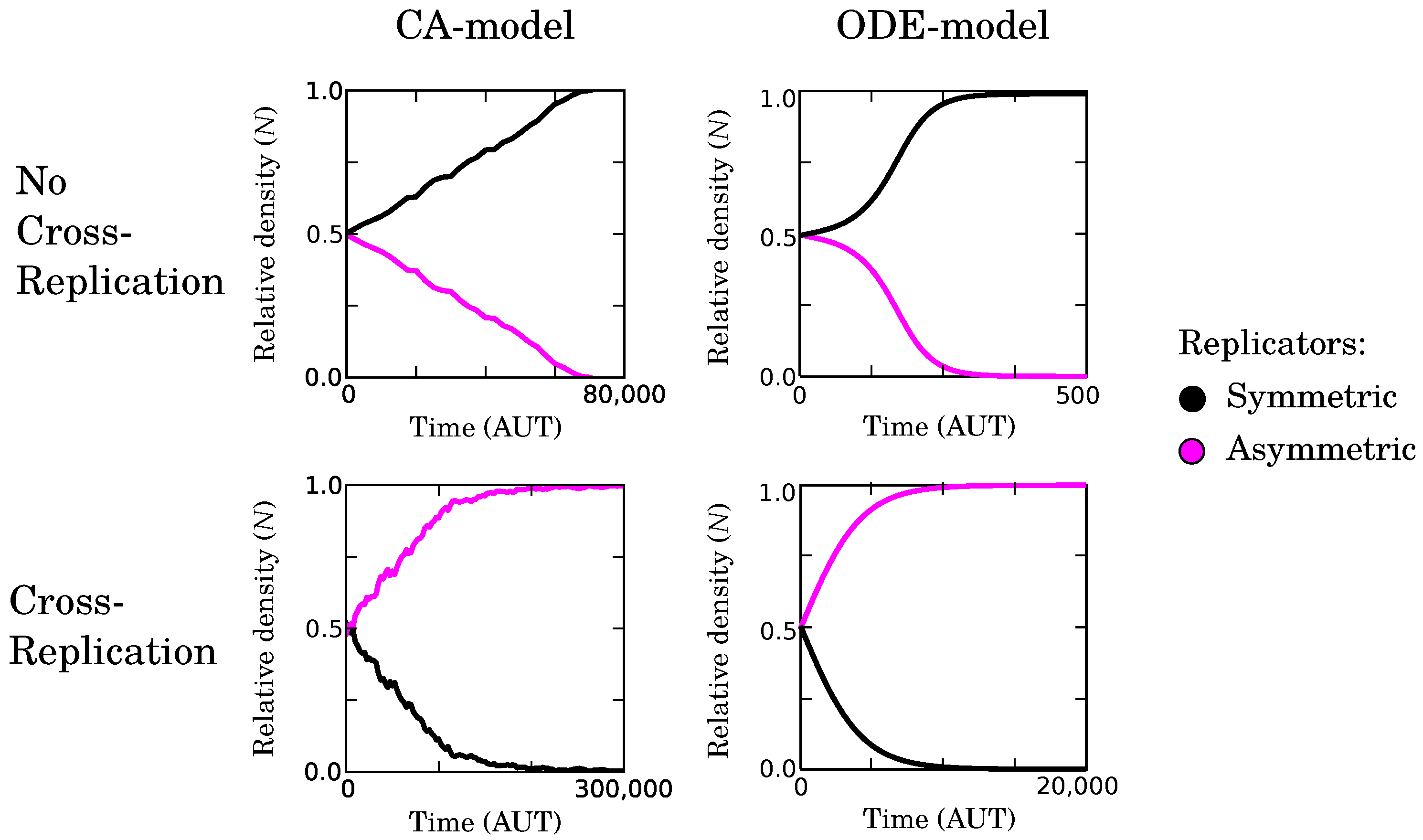
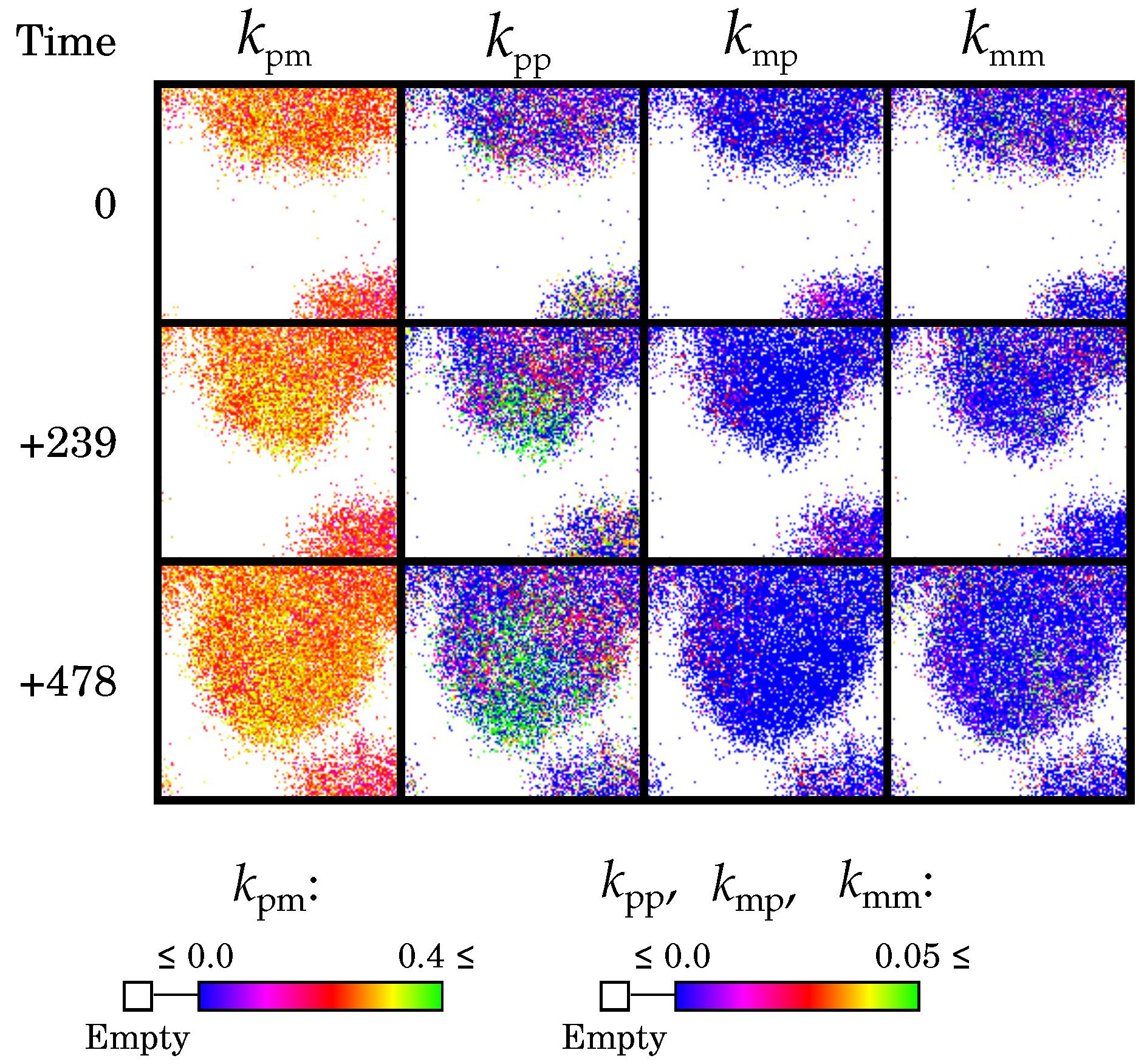
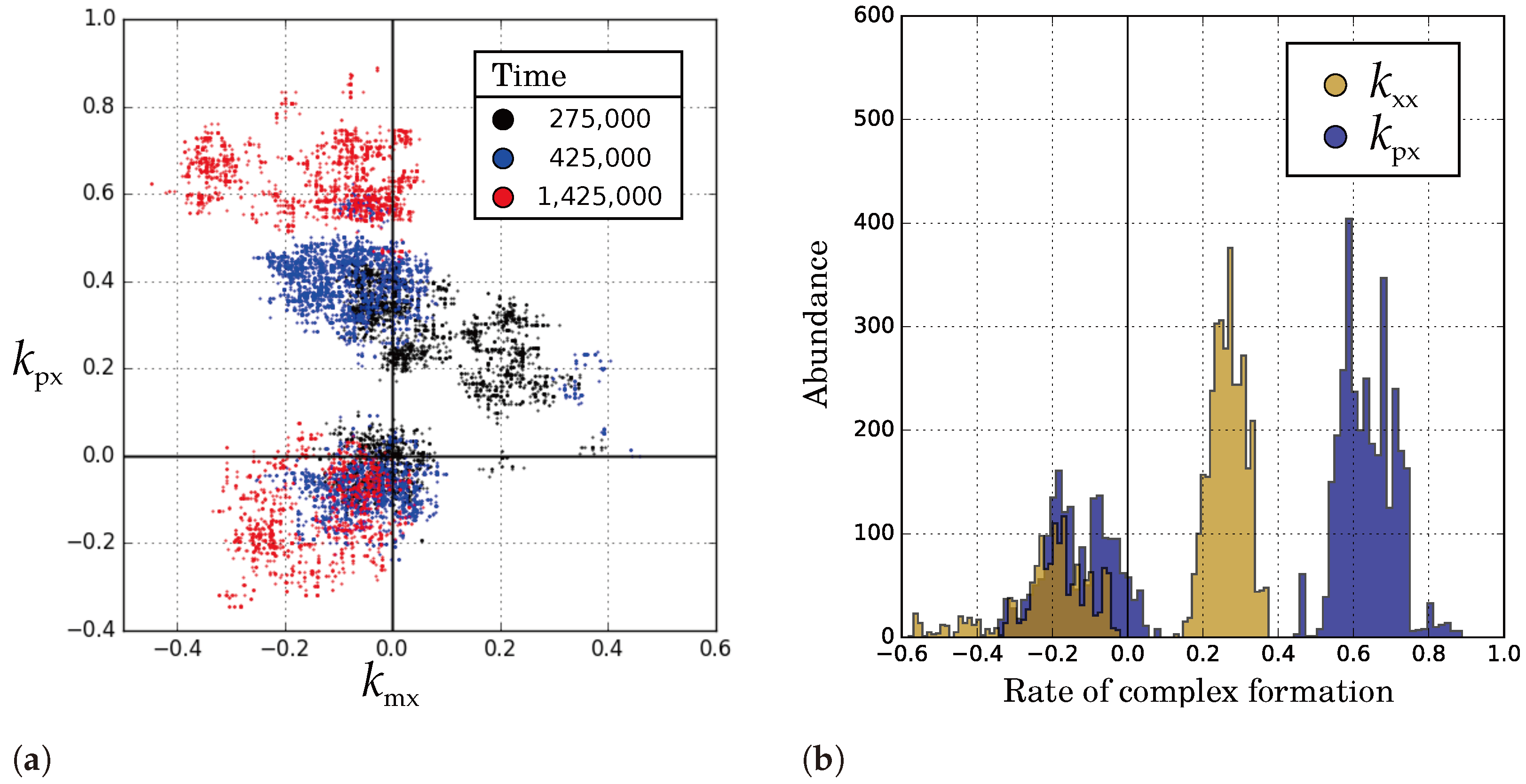
2.2.3. Diffusion Dictates Which Symmetry Breaks
2.2.4. Complementary Replication Allows for Beneficial Evolutionary Dynamics
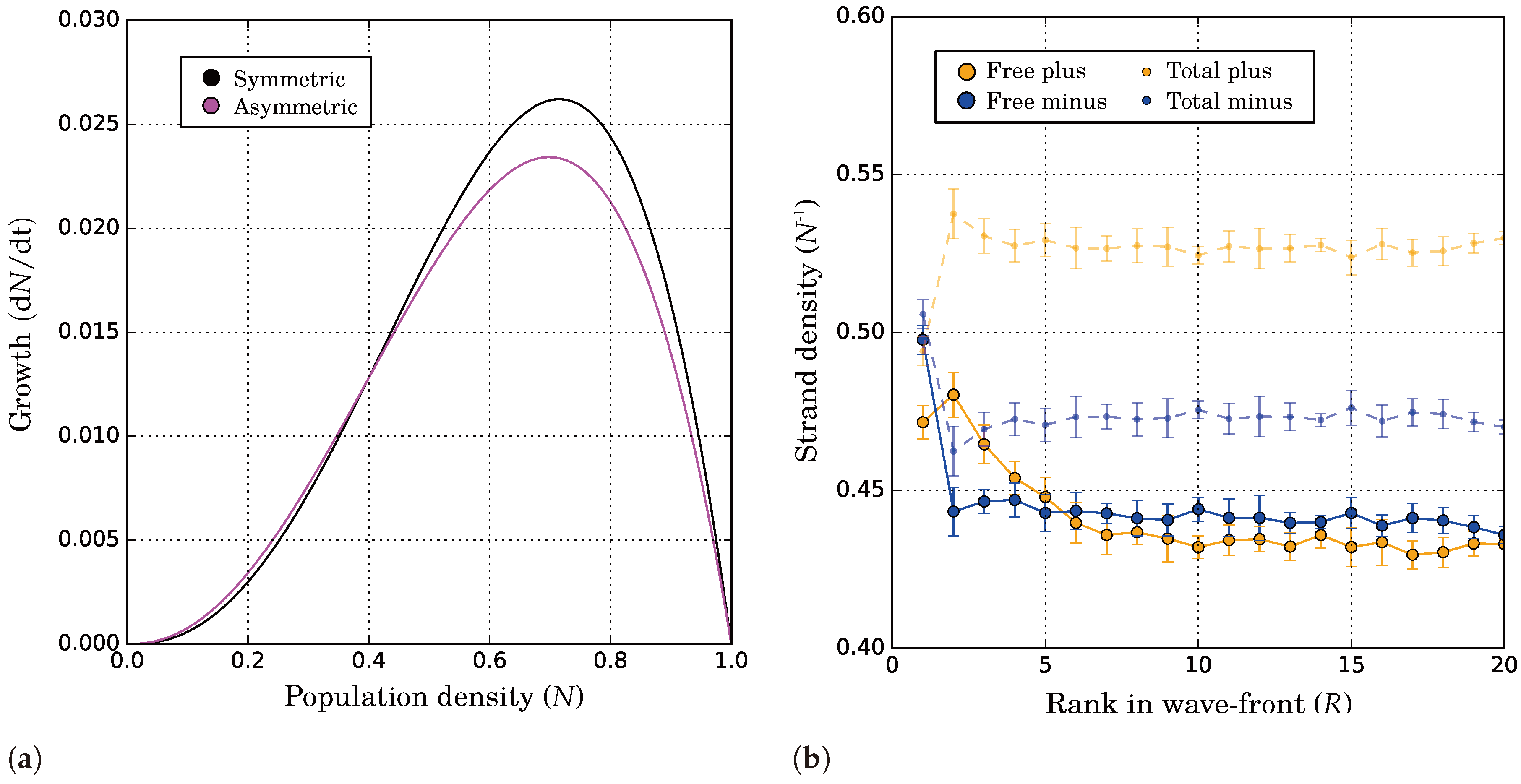
2.2.5. Causes and Consequences of Template Asymmetry
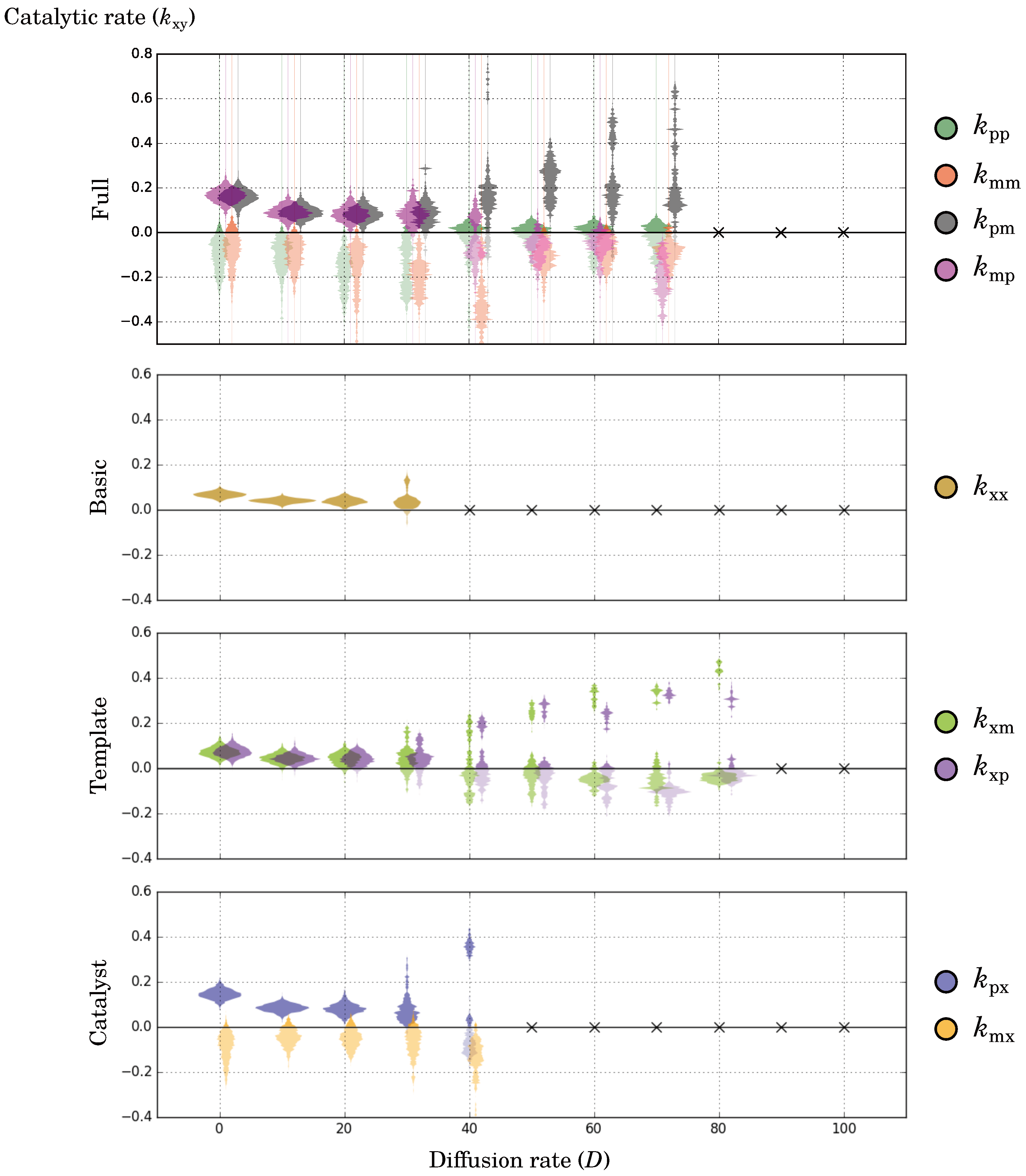
2.2.6. Catalytic and Directional Symmetry Breaking Enhance Replicators
2.2.7. Differential Growth as a Result of Complex Population Dynamics
2.2.8. Multiple Solutions to the Evolutionary Conflict
2.2.9. Lineage Differentiation and Symmetry Breaking Together Prevent Extinction
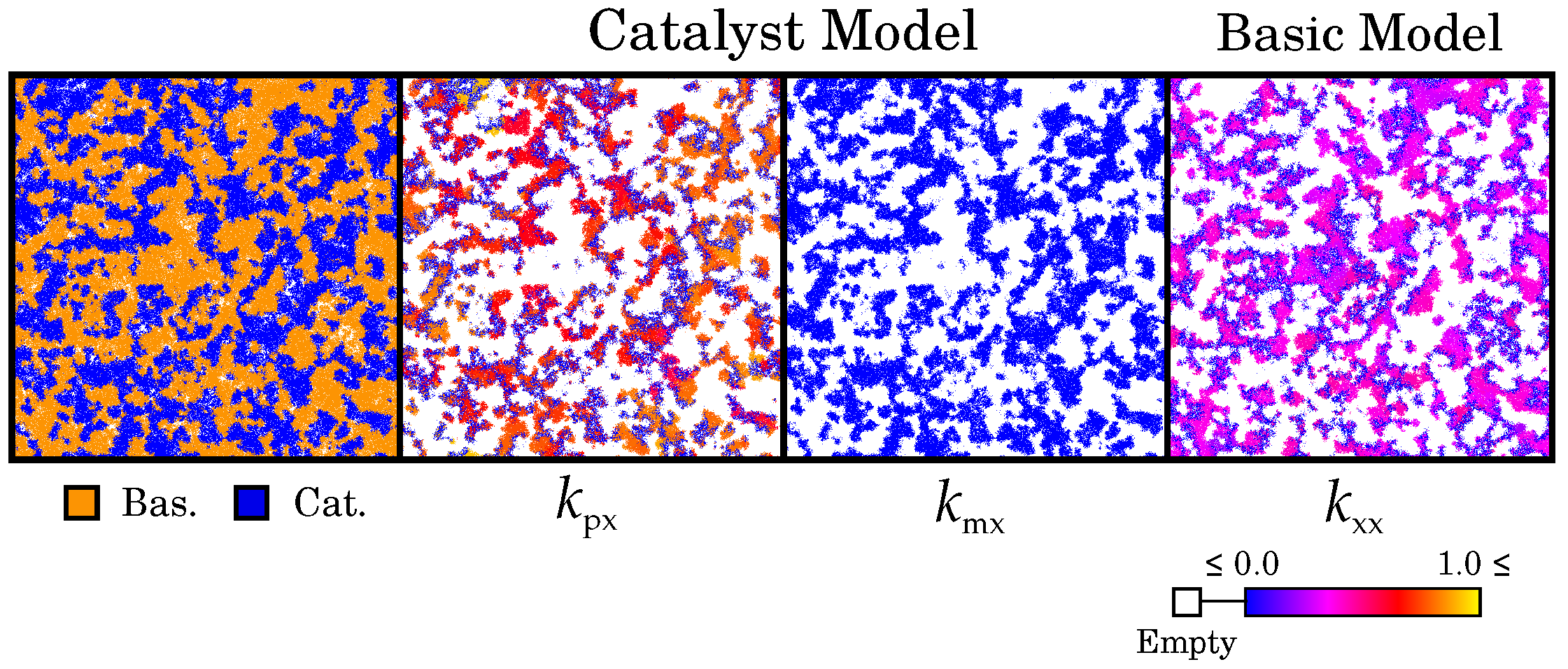
2.3. Two Competing Species: The Ecosystem-Based Solution for Maintaining Catalysis
3. Discussion and Conclusions
3.1. Catalysis Is Maintained by a Diverse Ecosystem
3.2. Population Dynamics as Substrate for Evolution
3.3. The Origins of Prebiotic Complexity
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Details of the Model
Appendix B. Differential Growth with Limited Diffusion
References
- Crick, F.H. The Biological Replication of Macromolecules; Academic Press, Inc.: New York, NY, USA, 1958; Volume 12, pp. 138–163. [Google Scholar]
- Crick, F.H. The origin of the genetic code. J. Mol. Biol. 1968, 38, 367–379. [Google Scholar] [CrossRef]
- Orgel, L.E. Evolution of the genetic apparatus. J. Mol. Biol. 1968, 38, 381–393. [Google Scholar] [CrossRef]
- Orgel, L.E. RNA catalysis and the origins of life. J. Theor. Biol. 1986, 123, 127–149. [Google Scholar] [CrossRef]
- Winston, M.L. The Biology of the Honey Bee; Harvard University Press: Cambridge, MA, USA, 1991. [Google Scholar]
- King, G.A. Symbiosis and the origin of life. Orig. Life Evol. Biosph. 1977, 8, 39–53. [Google Scholar] [CrossRef]
- Gilbert, W. Origin of life: The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Gesteland, R.; Cech, T.; Atkins, J. The RNA World, 3rd ed.; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2006. [Google Scholar]
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Sci. Nat. 1971, 58, 465–523. [Google Scholar] [CrossRef]
- Pace, N.R.; Marsh, T.L. RNA catalysis and the origin of life. Orig. Life Evol. Biosph. 1985, 16, 97–116. [Google Scholar] [CrossRef] [PubMed]
- Cech, T.R. A model for the RNA-catalyzed replication of RNA. Proc. Natl. Acad. Sci. USA 1986, 83, 4360–4363. [Google Scholar] [CrossRef]
- Szostak, J.W.; Bartel, D.P.; Luisi, P.L. Synthesizing life. Nature 2001, 409, 387–390. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J. Hypercycles and the origin of life. Nature 1979, 280, 445–446. [Google Scholar] [CrossRef]
- Bresch, C.; Niesert, U.; Harnasch, D. Hypercycles, parasites and packages. J. Theor. Biol. 1980, 85, 399–405. [Google Scholar] [CrossRef]
- Orgel, L.E.; Crick, F.H. Selfish DNA: The ultimate parasite. Nature 1980, 284, 604–607. [Google Scholar] [CrossRef] [PubMed]
- Doolittle, W.F.; Sapienza, C. Selfish genes, the phenotype paradigm and genome evolution. Nature 1980, 284, 601–603. [Google Scholar] [CrossRef] [PubMed]
- Niesert, U.; Harnasch, D.; Bresch, C. Origin of life between Scylla and Charybdis. J. Mol. Evol. 1981, 17, 348–353. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E.; Demeter, L. Group selection of early replicators and the origin of life. J. Theor. Biol. 1987, 128, 463–486. [Google Scholar] [CrossRef]
- Takeuchi, N.; Hogeweg, P. Multilevel selection in models of prebiotic evolution II: A direct comparison of compartmentalization and spatial self-organization. PLoS Comput. Biol. 2009, 5, e1000542. [Google Scholar] [CrossRef] [PubMed]
- Boza, G.; Szilágyi, A.; Kun, Á.; Santos, M.; Szathmáry, E. Evolution of the Division of Labor between Genes and Enzymes in the RNA World. PLoS Comput. Biol. 2014, 10, e1003936. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Takeuchi, N.; Kaneko, K.; Hogeweg, P. Evolutionarily stable disequilibrium: Endless dynamics of evolution in a stationary population. Proc. Biol. Sci. 2016, 283, 20153109. [Google Scholar] [CrossRef] [PubMed]
- Boerlijst, M.C.; Hogeweg, P. Spiral wave structure in pre-biotic evolution: Hypercycles stable against parasites. Phys. D Nonlinear Phenom. 1991, 48, 17–28. [Google Scholar] [CrossRef]
- Szabó, P.; Scheuring, I.; Czárán, T.; Szathmary, E. In silico simulations reveal that replicators with limited dispersal evolve towards higher efficiency and fidelity. Nature 2002, 420, 340–343. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.E.; Higgs, P.G. Co-operation between Polymerases and Nucleotide Synthetases in the RNA World. PLoS Comput. Biol. 2016, 12, e1005161. [Google Scholar] [CrossRef] [PubMed]
- Colizzi, E.; Hogeweg, P. Parasites Sustain and Enhance RNA-Like Replicators through Spatial Self- Organisation. PLoS Comput. Biol. 2016, 12, e1004902. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Takeuchi, N.; Hogeweg, P.; Kaneko, K. The origin of a primordial genome through spontaneous symmetry breaking. Nat. Commun. 2017, 8, 250. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E.; Maynard Smith, J. The evolution of chromosomes II. Molecular mechanisms. J. Theor. Biol. 1993, 164, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E.; Maynard Smith, J. The major evolutionary transitions. Nature 1995, 374, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Crick, F.H. Codon—Anticodon pairing: The wobble hypothesis. J. Mol. Biol. 1966, 19, 548–555. [Google Scholar] [CrossRef]
- Varani, G.; McClain, W.H. The G· U wobble base pair. EMBO Rep. 2000, 1, 18–23. [Google Scholar] [CrossRef] [PubMed]
- Ivica, N.A.; Obermayer, B.; Campbell, G.W.; Rajamani, S.; Gerland, U.; Chen, I.A. The paradox of dual roles in the RNA world: Resolving the conflict between stable folding and templating ability. J. Mol. Evol. 2013, 77, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, N.; Hogeweg, P. Evolution of complexity in RNA-like replicator systems. Biol. Direct 2008, 3, 11. [Google Scholar] [CrossRef] [PubMed]
- Colizzi, E.; Hogeweg, P. Evolution of functional diversification within quasispecies. Genome Biol. Evol. 2014, 6, 1990–2007. [Google Scholar] [CrossRef] [PubMed]
- Könnyü, B.; Czaran, T. Phenotype/genotype sequence complementarity and prebiotic replicator coexistence in the metabolically coupled replicator system. BMC Evol. Biol. 2014, 14, 234. [Google Scholar] [CrossRef] [PubMed]
- De Boer, R.J.; Staritsky, A.D. CASH. Available online: http://bioinformatics.bio.uu.nl/rdb/software.html (accessed on 2 November 2000).
- Hogeweg, P.; Takeuchi, N. Multilevel Selection in Models of Prebiotic Evolution: Compartments and Spatial Self-organization. Orig. Life Evol. Biosph. 2003, 33, 375–403. [Google Scholar] [CrossRef] [PubMed]
- Czárán, T.; Könnyü, B.; Szathmáry, E. Metabolically coupled replicator systems: Overview of an RNA-world model concept of prebiotic evolution on mineral surfaces. J. Theor. Biol. 2015, 381, 39–54. [Google Scholar] [CrossRef] [PubMed]
| Asymmetry | Description | Parameters | Observed |
|---|---|---|---|
| Directional | Both strands preferentially catalyse their complement. | equilibrium () | |
| Template | One of the strands (minus) is a better template. | transient (), | |
| equilibrium () | |||
| Catalytic | One of the strands (plus) is a better catalyst. | equilibrium () |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Von der Dunk, S.H.A.; Colizzi, E.S.; Hogeweg, P. Evolutionary Conflict Leads to Innovation: Symmetry Breaking in a Spatial Model of RNA-Like Replicators. Life 2017, 7, 43. https://doi.org/10.3390/life7040043
Von der Dunk SHA, Colizzi ES, Hogeweg P. Evolutionary Conflict Leads to Innovation: Symmetry Breaking in a Spatial Model of RNA-Like Replicators. Life. 2017; 7(4):43. https://doi.org/10.3390/life7040043
Chicago/Turabian StyleVon der Dunk, Samuel H. A., Enrico Sandro Colizzi, and Paulien Hogeweg. 2017. "Evolutionary Conflict Leads to Innovation: Symmetry Breaking in a Spatial Model of RNA-Like Replicators" Life 7, no. 4: 43. https://doi.org/10.3390/life7040043
APA StyleVon der Dunk, S. H. A., Colizzi, E. S., & Hogeweg, P. (2017). Evolutionary Conflict Leads to Innovation: Symmetry Breaking in a Spatial Model of RNA-Like Replicators. Life, 7(4), 43. https://doi.org/10.3390/life7040043





