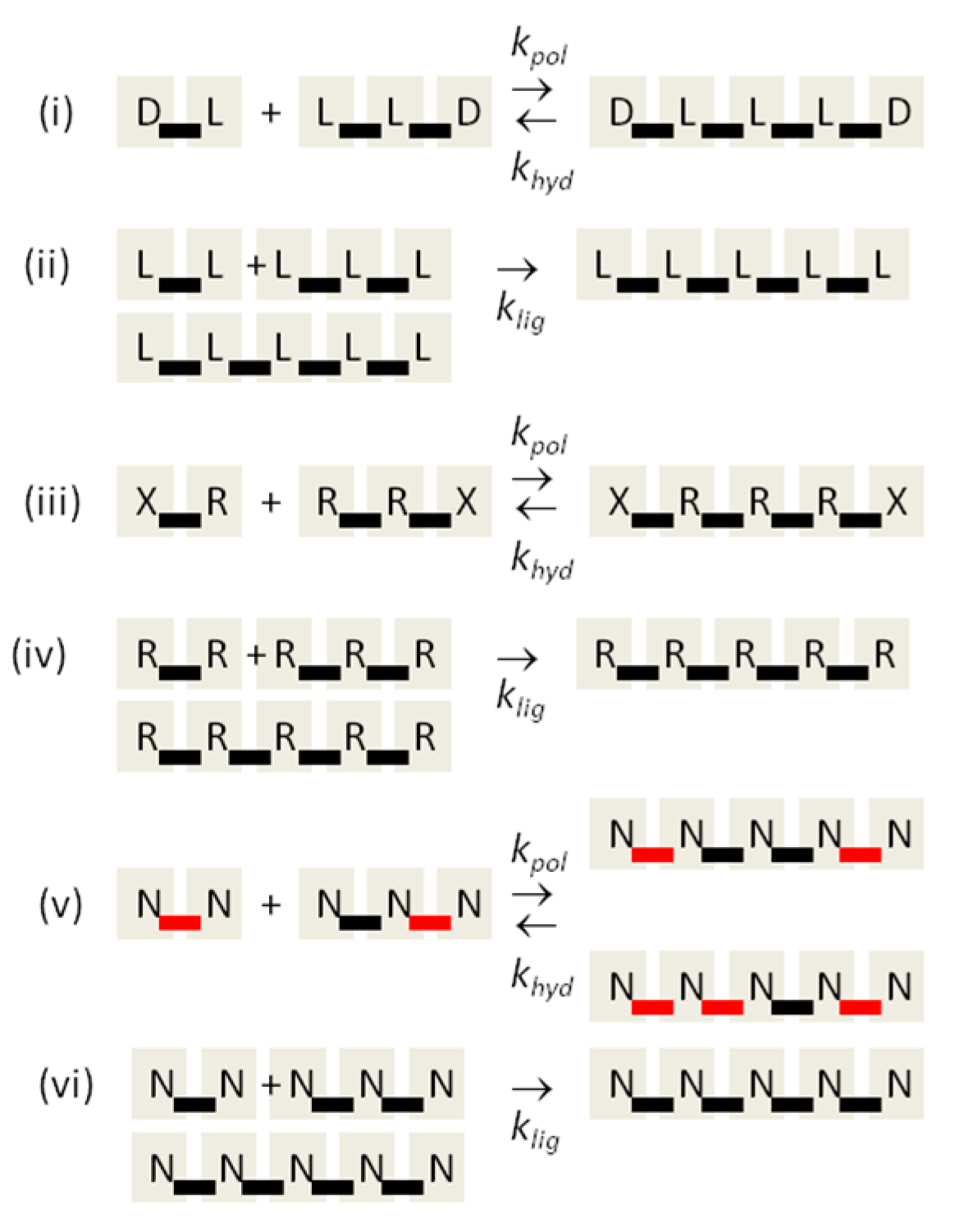
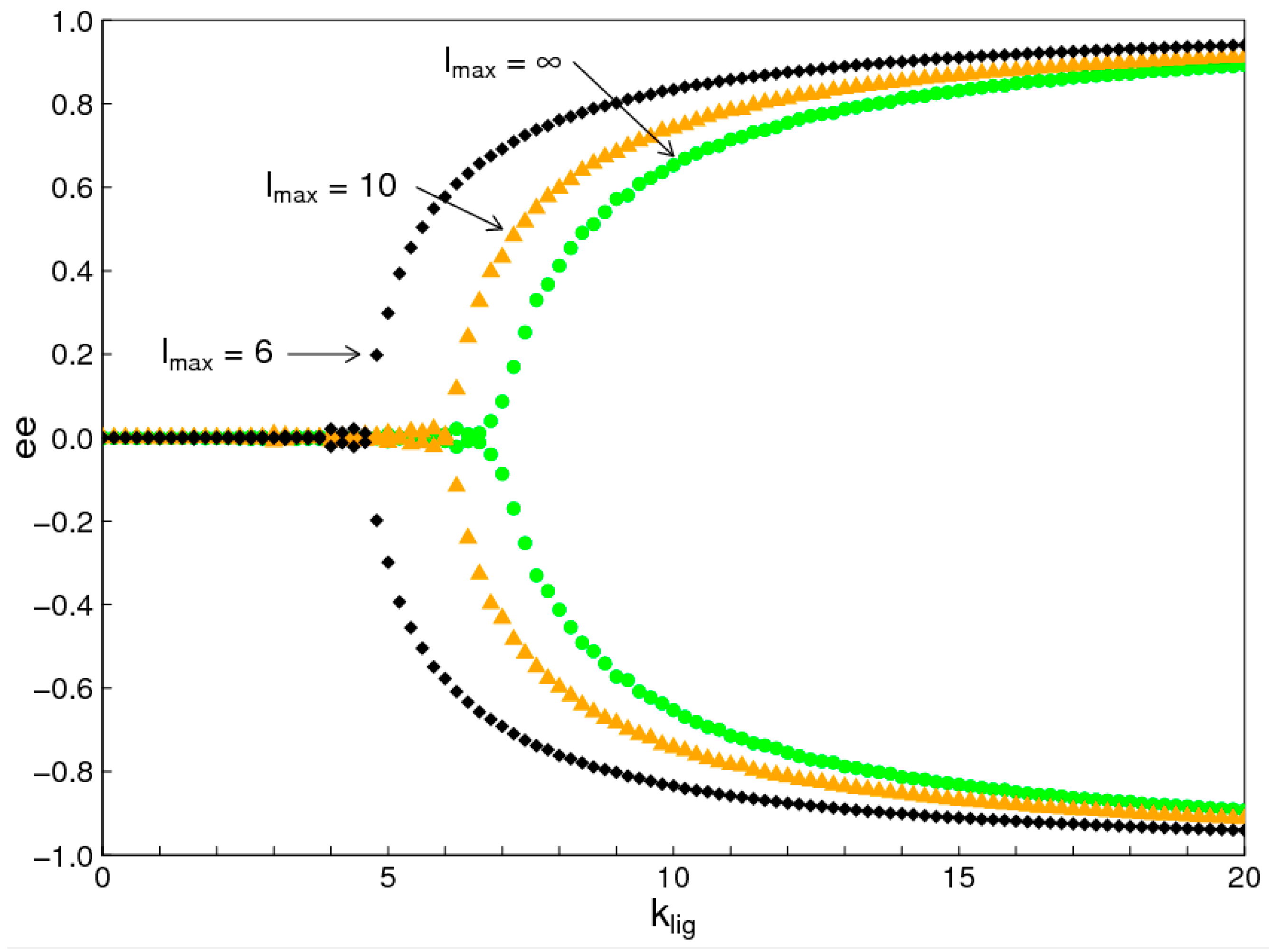
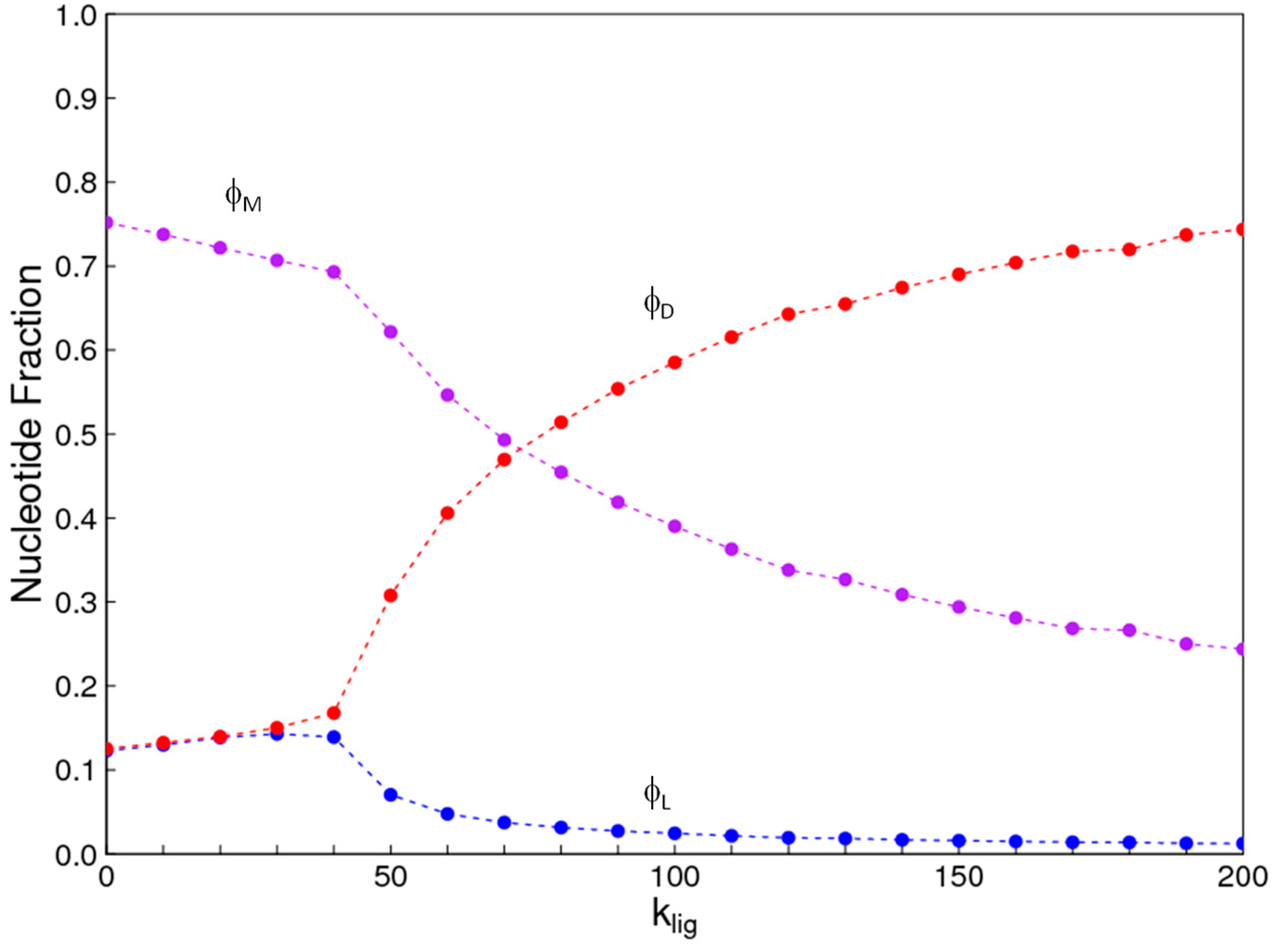
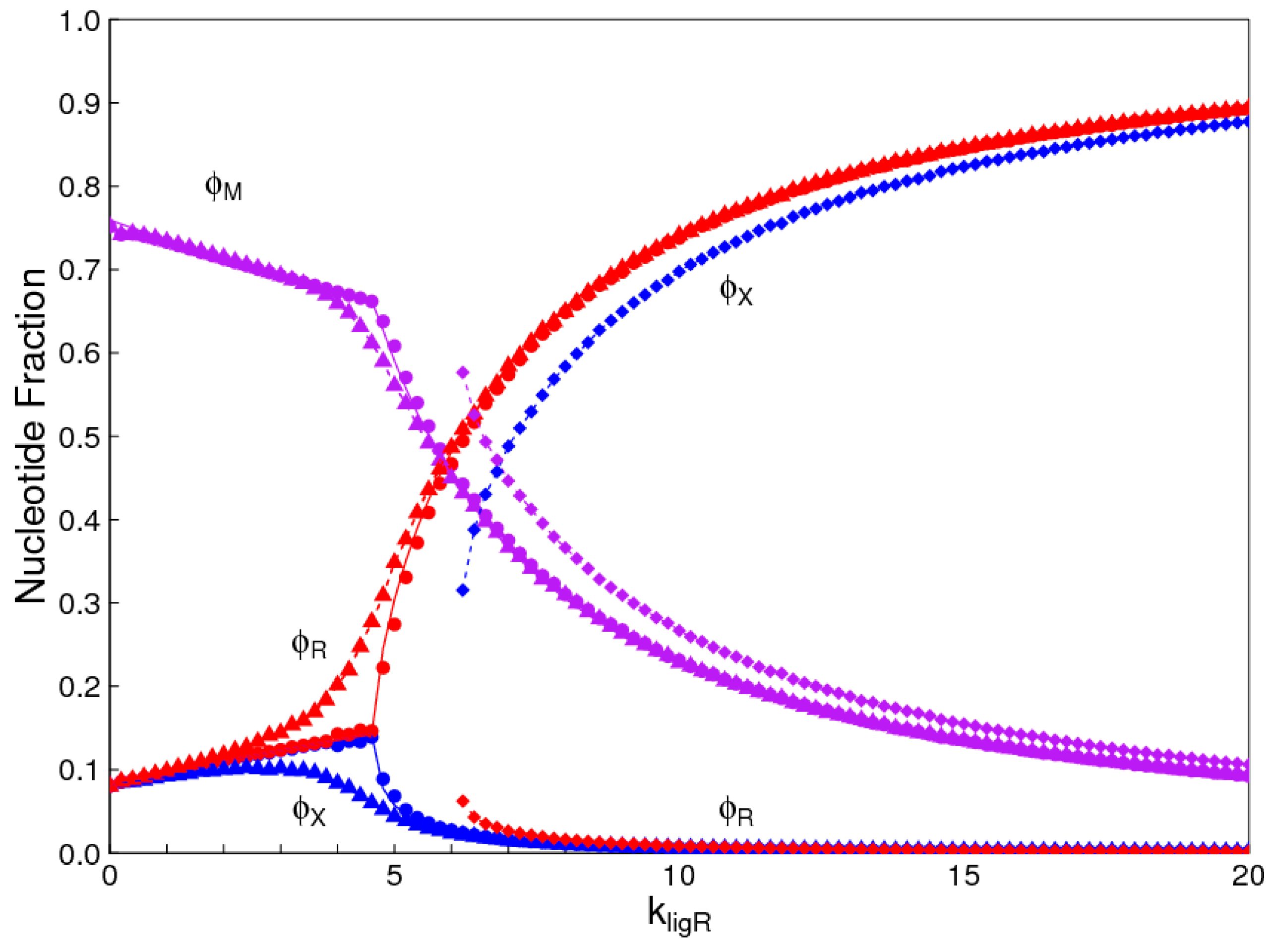
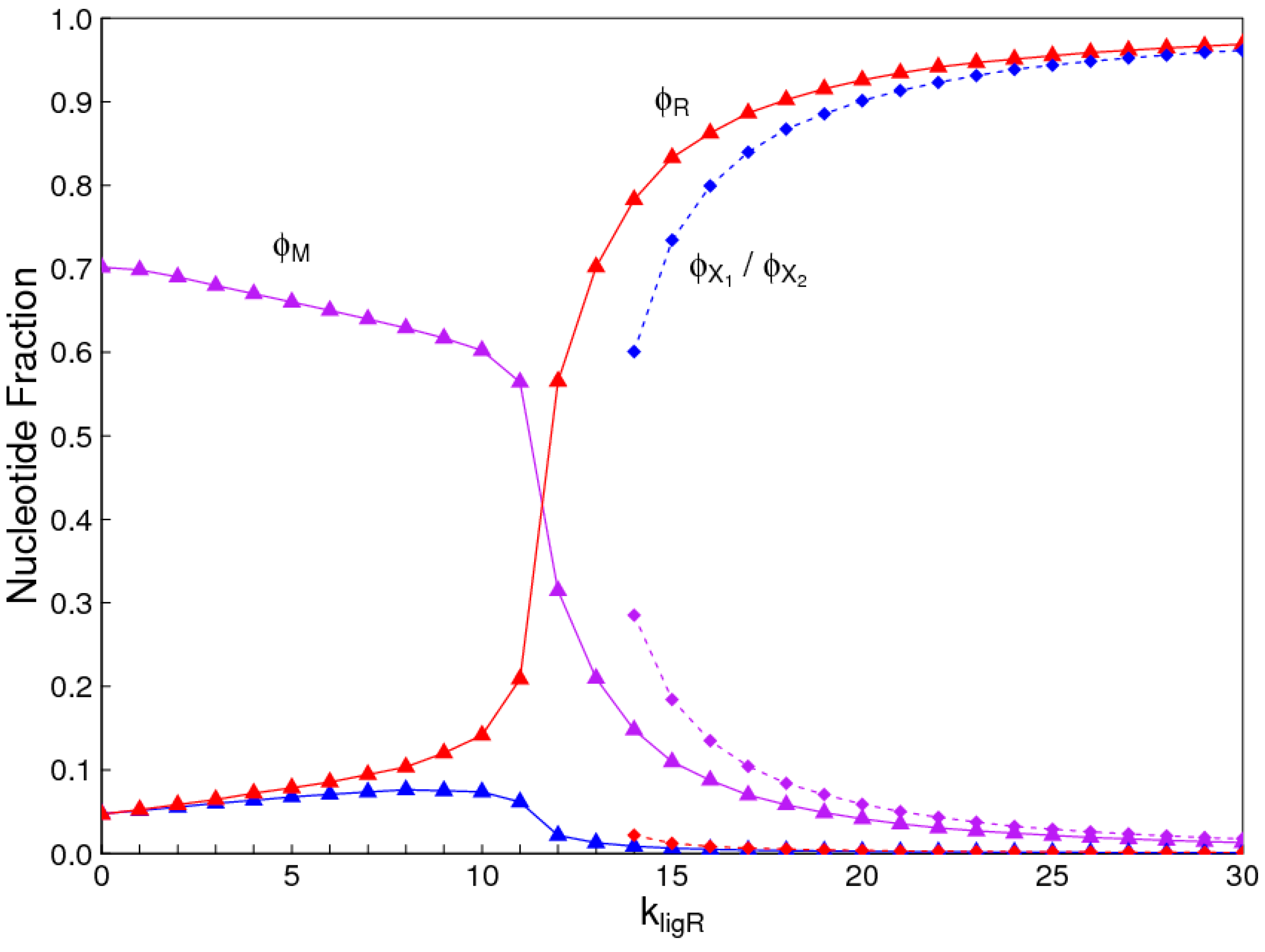
1. Introduction
An important feature of life is that it makes frequent use of a well-defined set of molecules, but it does not use many other kinds of molecules that have rather similar chemical properties. This has been called the ‘lego principle’ [
1], and it has been proposed that this feature could be used as a signature of life on other planets. This principle applies to amino acids, where the set of possible amino acids is much larger than the 20 used in biological proteins [
2], and to nucleotides, where there is a huge diversity of sugars [
3] and nucleobases [
4,
5] that could potentially form polymers similar to RNA and DNA. Non-living chemistry is governed by thermodynamics and reaction kinetics. Similar molecules will have similar free energies of formation and will undergo similar reactions; hence, they will be produced in similar quantities. Living biochemistry is autocatalytic. A subset of molecules is able to catalyze formation of more of the same set of molecules that it requires for growth and reproduction. Because there is continued flow of energy and matter into a living system, the relative frequencies of different molecules can be maintained far from what would be found in thermodynamic equilibrium.
One example of the way autocatalysis maintains biased sets of molecules is the homochirality observed in nucleic acids and proteins [
6]. Theoretical models assume that the formation of molecules of a given enantiomer (
D or
L) is catalyzed by molecules of the same handedness. In the simplest model of Frank [
7], monomers are autocatalytic; however, more complex models have been studied in which the catalysts are dimers [
8] or polymers [
9,
10]. All these models share the feature that it is the monomer synthesis reaction that is catalyzed (i.e., the synthesis of ribose or ribonucleotides, if we apply this to RNA). Here we consider the alternative that the asymmetric autocatalysis comes from template-directed synthesis of complementary oligomers, rather than from the catalysis of nucleotide synthesis. We assume that oligomers of uniform chirality (either
D or
L) are efficient templates for the ligation of shorter oligomers of the same chirality, whereas oligomers of mixed chirality are unable to act as templates. We show that if the template-directed reaction rate is fast, a symmetry-breaking phase transition occurs in which one or other enantiomer dominates the system.
Biological nucleic acids show two other kinds of uniform properties in addition to chirality. Firstly, biology uses a uniform set of monomers, rather than a mixture of many other similar molecules with different sugars, different bases, or both. Only four nucleotides are used in genetic information storage and transcription in DNA and RNA (although many modified nucleotides are used in specific positions in structural RNAs, such as tRNAs). We refer to the question of why these particular nucleotides are used as the monomer selection problem. Secondly, biology uses regular 3′-5′ bonds between ribose sugars rather than a mixture of 3′-5′ and 2′-5′ bonds. We refer to this as the backbone regioselectivity problem. The central point of this paper is that the monomer selection and backbone regioselectivity problems are similar problems to the chirality problem, and we may use a similar theory to explain all three. Our theory depends on two propositions: (1) that uniform oligomers of one kind are templates that catalyze synthesis of further oligomers of the same kind (i.e., the same chirality, the same monomers, or the same bond type); and (2) that uniform oligomers are good templates, but mixed oligomers (i.e., mixed chirality, mixed monomers, or mixed bond types) are not. These two propositions are supported by experiment in several ways, as we will now discuss.
In the case of chirality, Bolli et al., [
11] studied template-directed ligation of tetramers of pyranosyl-RNA, and showed that the ligation of the homochiral tetramers is faster by at least two orders of magnitude than the ligation of tetramers in which one of the nucleotides has the opposite chirality. In this example, both propositions are clearly satisfied. With standard RNA, Joyce et al. [
12] studied the polymerization of G monomers using a poly(C) template of the
D enantiomer, and showed that template-directed synthesis of G oligomers is efficient when the G monomers are also of the
D enantiomer, and not when they are of the
L enantiomer. When a racemic mixture of
D/
L monomers was used, the
L monomers inhibited the growth of the G oligomers to some extent, but the template-directed reaction was still an improvement over the case with no template at all. The chiral inhibition effect was presented as a problem for theories of the origin of life in [
12], however we see this effect as part of the solution, in the sense that some kind of chiral inhibition is necessary to drive the symmetry breaking between
D and
L. Without this, we would expect the two systems to mix and coexist.
The two propositions also apply with regard to the monomer selection problem. Oligomer duplexes of RNA and DNA have been studied in many combinations [
13]. It is found that duplexes of pure RNA or pure DNA have higher melting temperatures than hybrid duplexes (in which one strand is pure RNA and one is pure DNA) and mixed duplexes (in which strands are mixtures of ribonucleotides and deoxyribonucleotides). RNA and DNA are rather similar in structure, and hybridization between the two is clearly possible. Hybridization between the two allows for transcription in today’s organisms, and is also essential for the transfer of information from RNA to DNA that is proposed to occur at the end of the RNA World. Scenarios have also been proposed in which DNA arose concurrently with RNA, rather than as a late successor [
13]. However, the essential point here is that, even with two very similar kinds of monomers, each has a preference for its own kind, and this will tend to drive separation between the two, as we will see in the theoretical models below.
Several other alternative nucleic acid-like polymers have been studied that differ more substantially in structure from RNA. Melting temperatures of duplexes of these polymers differ significantly, and may be either higher or lower than for RNA duplexes [
14]. This suggests that RNA may be optimized for the conditions in which replication was originally occurring [
15,
16]. Some alternative nucleic acids can form hybrid duplexes with RNA, and some cannot. For example, Schöning et al. [
17] studied four pairs of complementary oligomers, each made with TNA (α-threofuranosyl nucleic acid), RNA, and DNA backbones, and measured the melting temperatures of the 24 possible hybrid duplexes. They found a general tendency to favour uniform duplexes, although the results are complex, and we will return to them in the discussion section.
Monomer selection also involves a choice between nucleotides that differ in bases but have the same backbone. It is clear that strands made from the standard ACGU ribonucleotide alphabet are effective as templates for strands of the same alphabet. Non-enzymatic, template-directed synthesis of RNA and DNA has been studied [
18], particularly with regard to the fidelity of sequence replication. A good monomer alphabet for genetics should allow little mismatch pairing. The possibility of GU pairing in the ACGU alphabet of RNA, and the absence of this possibility in the ACGT alphabet of DNA, is a potential reason for the transfer of information from RNA to DNA during evolutionary history [
18]. Furthermore, a number of other base pairs have been studied that can be used as an extension of the coding repertoire of RNA and DNA [
19,
20]. These bases are ‘orthogonal’ to the standard bases, i.e., there should be little or no pairing between them and the standard bases. This means that sequences made of either the standard alphabet or the alternative alphabet would be templates for complementary sequences in the same alphabet, which is our proposition 1. However alternative pairs that are compatible with the RNA or DNA helix may not satisfy proposition 2, because the mixed sequences may still be good templates in this case. Studies of template-directed synthesis [
21] have shown that the rate of nucleotide addition after a mismatch is much lower than after a match. This illustrates a close parallel between the monomer selection problem and the chirality problem, where the addition of a monomer of the wrong chirality can slow down the growth of an oligomer [
12]. Although these effects cause slower average growth of oligomers, they actually increase the degree of uniformity of the longer oligomers. Mismatch inhibition increases the overall fidelity of RNA replication [
21], and we expect that chiral inhibition would increase the enantiomeric excess of longer oligomers for the same reason.
Early studies on oligomerization of activated guanosine nucleotides using poly(C) templates [
22,
23] found that G-G bond formation is regioselective with a majority of 3′-5′ bonds, i.e., the template favours formation of the same bond type in the complementary strand (proposition 1 above). It was additionally shown [
24] that the A structure of the nucleic acid helix is important in bringing the nucleotides together in the correct conformation for 3′-5′ bond formation. Furthermore, there have been several experimental studies that look at the effects of mixing 2′-5′ and 3′-5′ bonds. When regular 3′-5′ strands are used as templates, the template-directed synthesis of the complementary strand is regioselective for 3′-5′ bonds [
25]. The duplex melting temperature is found to decrease systematically by around 15 °C as 2′-5′ bonds are added to the regular 3′-5′ structure [
26,
27]. This also suggests that strands of uniform bond type should be better templates than mixed strands (proposition 2). If 2′-5′ bonds and 3′-5′ bonds are similar with respect to rates of formation and hydrolysis, then the possibility arises that that strands of uniform bond type can be selected by symmetry breaking, as we discuss in this paper. However, it is already known that 2′-5′ bonds may be much less stable to hydrolysis than 3′-5′ bonds [
28], hence, there is no true symmetry in this problem, and it is possible for one bond type to be more frequent than the other without there being a symmetry-breaking transition. A recent experimental study has shown that iterative degradation and repair of bonds gradually converts 2′-5′ bonds to 3′-5′ bonds [
29] because bond formation in the context of the existing helix is regioselective. This effect is included in the model of backbone regioselectivity given here.
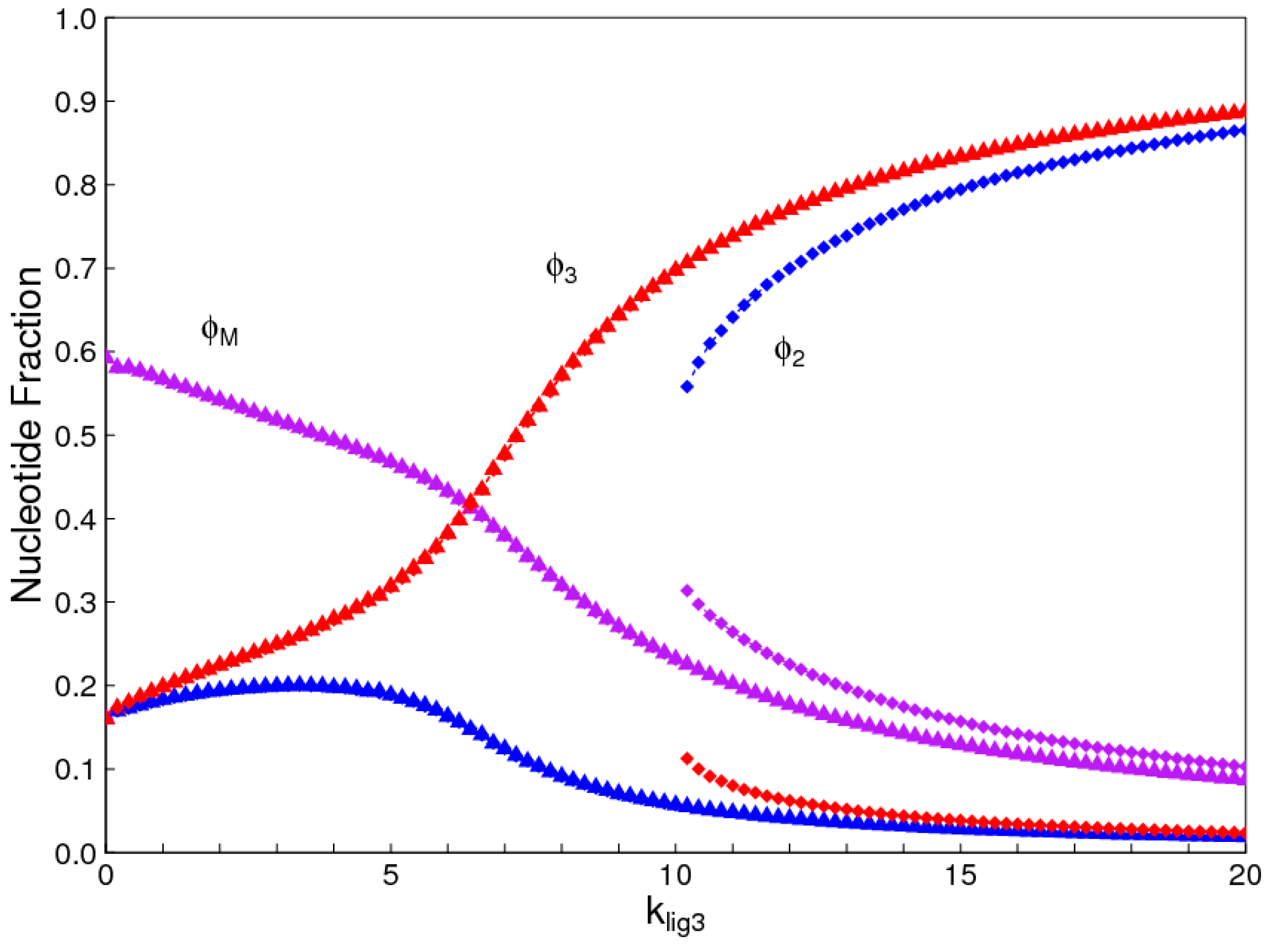
The aim of this paper is to present a simple computational model that is able to treat the problems of chirality, monomer selection, and backbone regioselectivity in the same way. We propose that all three types of order emerge when the rate of non-enzymatic template-directed synthesis is high, due to the fact that uniform strands are templates for their own kind, and that uniform strands are better templates than mixed strands. This mechanism is likely to occur at the level of oligomers, and does not require the synthesis of strands that are long enough to function as specific ribozymes.
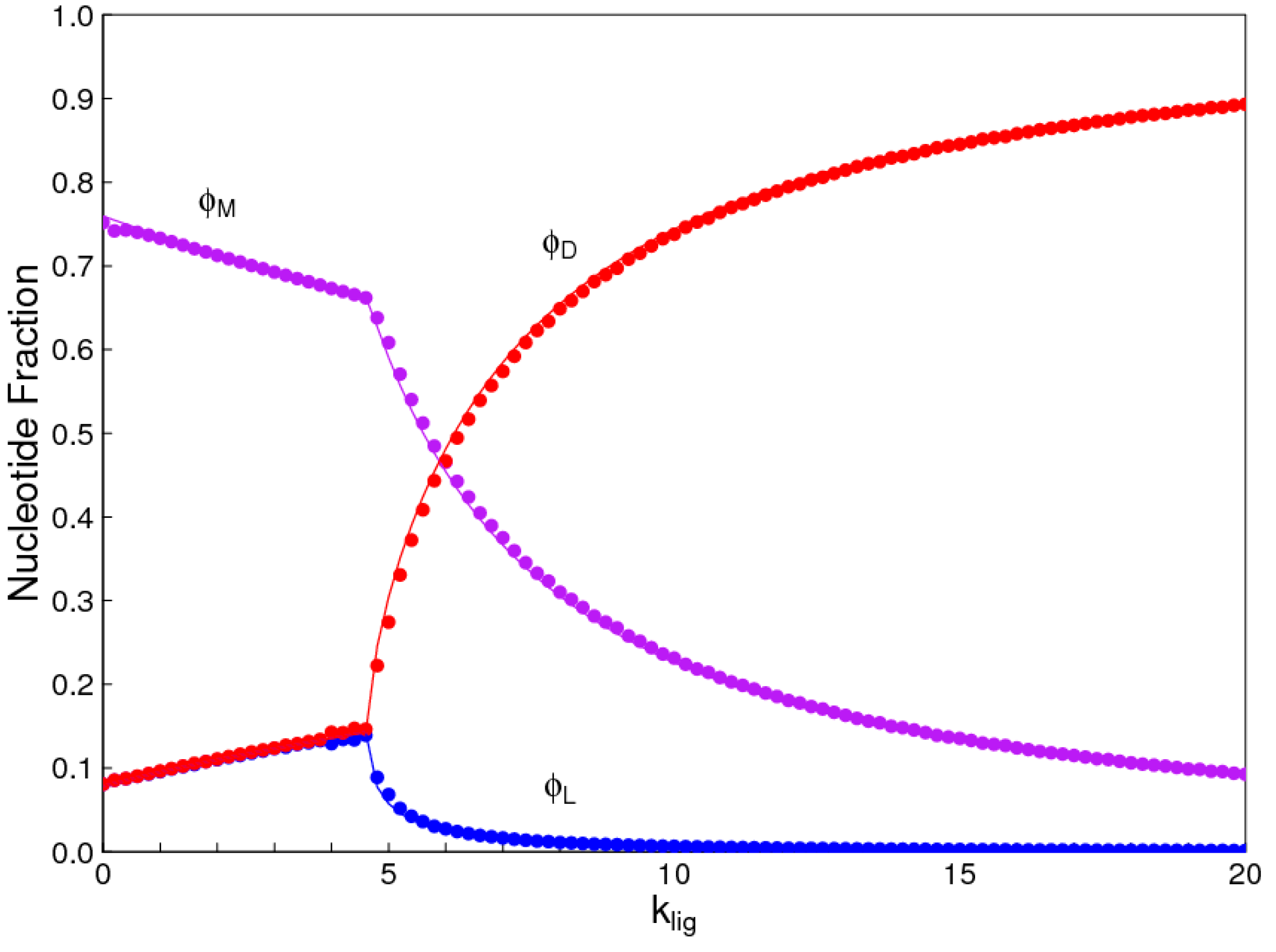
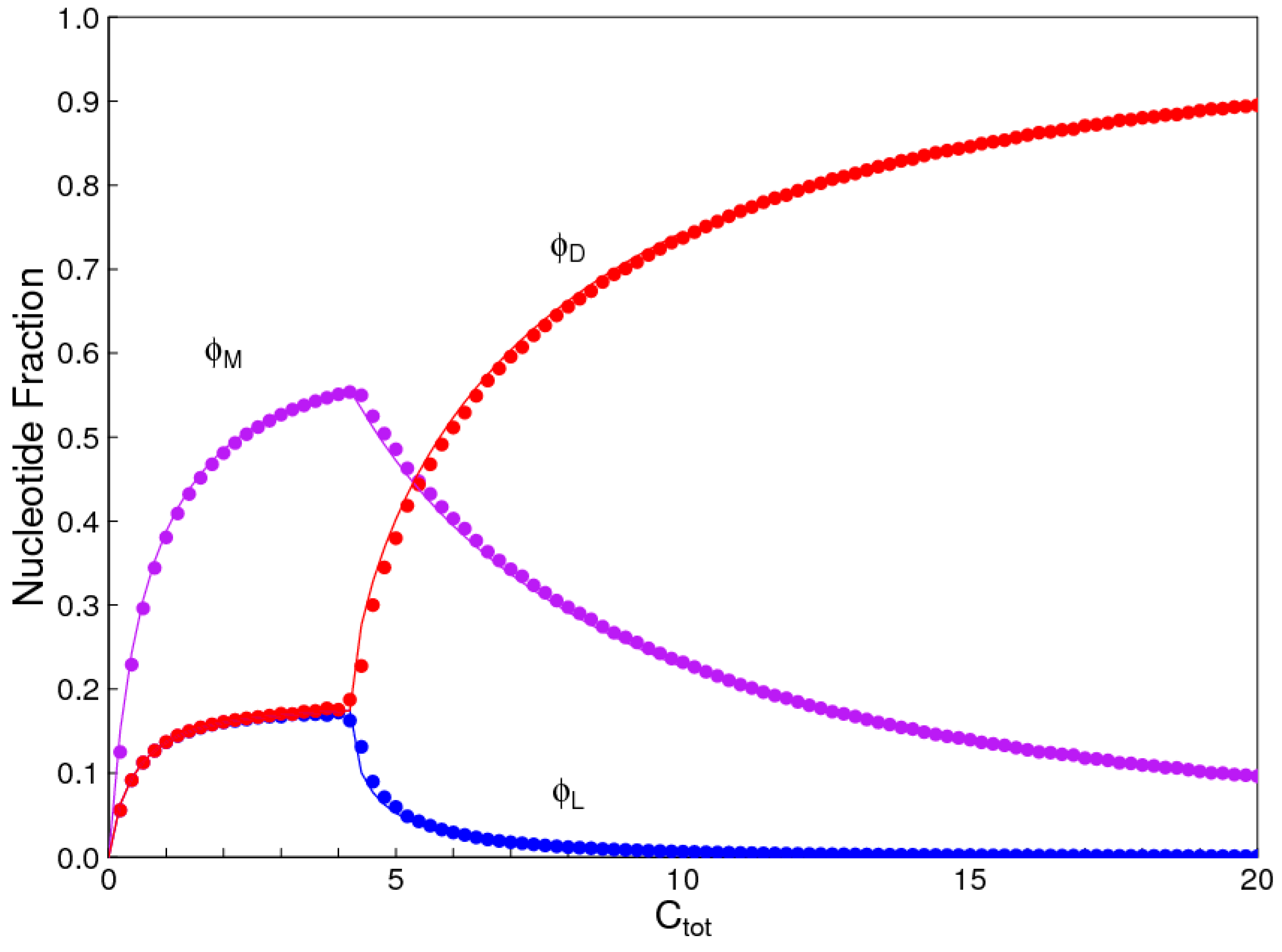
4. Discussion
In the introduction, we reviewed the experimental evidence that oligomers with uniform chirality, monomer composition, or bond type are effective templates for the growth of complementary strands with the same chirality, monomer composition, or bond type, and that oligomers that are mixed in any of these properties are less effective templates than uniform oligomers. The computational models studied in this paper incorporate these features, and show that, when template-directed ligation is fast compared to random polymerization without a template, we expect that uniform biopolymers will emerge, and that they are homochiral, use a restricted monomer set, and have a highly regioselective backbone. We thus argue that these essential properties of biological nucleic acids have emerged as a result of the importance of template-directed reactions in the early stages of evolution. Although models for the emergence of homochirality have been widely studied previously, the link between chirality, monomer selection, and regioselectivity has not been emphasized in the past. The present theory therefore contributes by showing in a simple way why these three problems are very similar. These results lead us to expect that RNA with the three uniform properties seen in biology could emerge from a prebiotic chemical mixture before the origin of life, in the sense that the proposed mechanism requires only the existence of short oligomers that can undergo template-directed replication, but it does not require the existence of specific sequences that would act as catalysts (ribozymes).
The mechanism we discuss here depends on the ability of nucleic acids to be templates; hence, it applies to RNA and polymers with similar structures, but not to other kinds of biomolecules that are also chiral in today’s organisms but cannot be templates. The ability of nucleic acids to be templates is, of course, a prime argument in favour of some kind of RNA World scenario for the origin of life. In an origins scenario where RNA replication arises early, and where ribozymes are the initial biological catalysts, it is possible to explain the transfer of chirality from RNA to other biomolecules by the fact that chiral RNAs catalyze the synthesis of the other molecules. In particular, if protein synthesis depended on chiral tRNAs and rRNAs, then amino acids of the appropriate chirality could be charged onto tRNAs, and protein sequences of uniform chirality could be synthesized. This would be true, even if the mixture of single amino acids were completely racemic, because amino acids of the wrong enantiomer would not be recognized by the ribozymes. On the other hand, if the amino acids were already chiral for some other reason at the time of the invention of protein synthesis, the early ribosome would simply make use of the existing supply of chiral amino acids.
Related to this is the possibility that the transfer of chirality was in the other direction: from amino acids to sugars and nucleotides. Several studies have shown [
31,
32] that chiral amino acids can catalyze the synthesis of chiral glyceraldehye and other sugars. There is also evidence for a moderate enantiomeric excess in amino acids found in meteorites [
30], which is presumed to originate by an abiotic mechanism outside the Earth, such as chirally biased degradation under the influence of circularly polarized light. We have previously considered the way that a small extraterrestial chiral bias can contribute to scenarios involving the emergence of homochirality [
10]. Understanding the direction of chiral transfer will require a more detailed picture of the full network of reactions involving biomolecules of all kinds at the time of the origin of life. The template-based mechanism presented here is not in conflict with other studies showing transfer of chirality from one molecule to another, whichever the direction of transfer, and it is quite possible that more than one mechanism jointly contributed to the creation of a biology in which several kinds of chiral biopolymer are inter-dependent. Nevertheless, we maintain that templating must have been an essential part of this process. Life requires the copying of sequence information that occurs via the template-directed synthesis of complementary strands of nucleic acids. A mixture of small molecules (whether chirally biased or not) that did not possess a mechanism of sequence replication would not yet constitute life, in our view. Templating is a straightforward mechanism that ‘purifies’ biopolymers at the level of chirality, chemical composition, and regioselectivity, as we have shown. The point of this paper is to show that templating alone can provide a mechanism for the emergence of all these properties, even in absence of other sources of asymmetry. If other sources, or other mechanisms, exist, then templating magnifies these effects to a much greater extent.
The mechanism for the emergence of RNA discussed in the present paper is an example of what we have termed
chemical evolution [
33]. The main distinctions between chemical evolution and biological evolution, as defined in [
33], are (1) that, for chemical evolution, the major part of the sequence diversity on which natural selection acts is provided by random polymer synthesis, rather than by mutations occurring during replication of previously existing sequences; and (2) that selection is acting on physicochemical properties possessed by all short oligomers (like ligation and hydrolysis rates) rather than on encoded function of long sequences (such as ribozymes) that are only possessed by a small number of sequences in a large sequence space. If RNA can emerge directly from a prebiotic mixture by chemical evolution, as envisaged here and previously [
15,
16], then it is not necessary to consider more complex pathways requiring the evolution of biological function in some pre-RNA polymer and the subsequent transfer of sequences and function to RNA, as has sometimes been proposed [
34].
The monomer selection problem is probably the most complex and least understood of the three problems considered in this paper. It is clear that the real world is much more complicated than the simple model we have studied. For example, hybrid duplexes of RNA, DNA, and TNA were studied experimentally [
17], and it was shown that the details of the nucleotide sequences and backbone structures significantly affect the melting temperatures (T
m) of helices, and presumably also affect the rates of polymerization, hydrolysis, and ligation. Table 2 of [
17] illustrates how complex this problem is. There are 14 cases where the hybrid duplex has a lower T
m than the uniform duplexes of both polymers, 8 cases where the hybrid has a T
m in between the two uniform duplexes, and 2 cases where the hybrid has a T
m higher than both the uniform duplexes. The latter two cases are surprising, but the effect only works one way round: if the sequences are switched, the hybrid has a lower T
m than both uniform duplexes. Although the thermodynamic details are rather complex, there is a general tendency to favour uniform duplexes, which is the essential point that we assume in our model. The case where both uniform duplexes are good templates and the hybrids are weak corresponds to the case studied here. There is an approximate symmetry between the two uniform polymers that is broken when the template-directed reaction is fast. If the hybrid is intermediate between the two uniform duplexes, then there will be a straightforward selection for the better of the two uniform systems. The monomer selection problem does not require symmetry breaking in that case.
We hope to continue this work to consider important details not included in the present paper, including differences in thermodynamic properties and rate constants between different base sequences with the same backbone, and adding separate steps for helix formation and melting, rather than combining them into a single effective ligation step. The simple model presented here is sufficient to demonstrate the similarity between the problems of chirality, monomer selection, and regioselectivy, and to establish the relevance of symmetry breaking transitions in all three cases.