Droplets: Unconventional Protocell Model with Life-Like Dynamics and Room to Grow
Abstract
:1. Droplets
2. Individuality
3. Self-Division and Replication Cycle
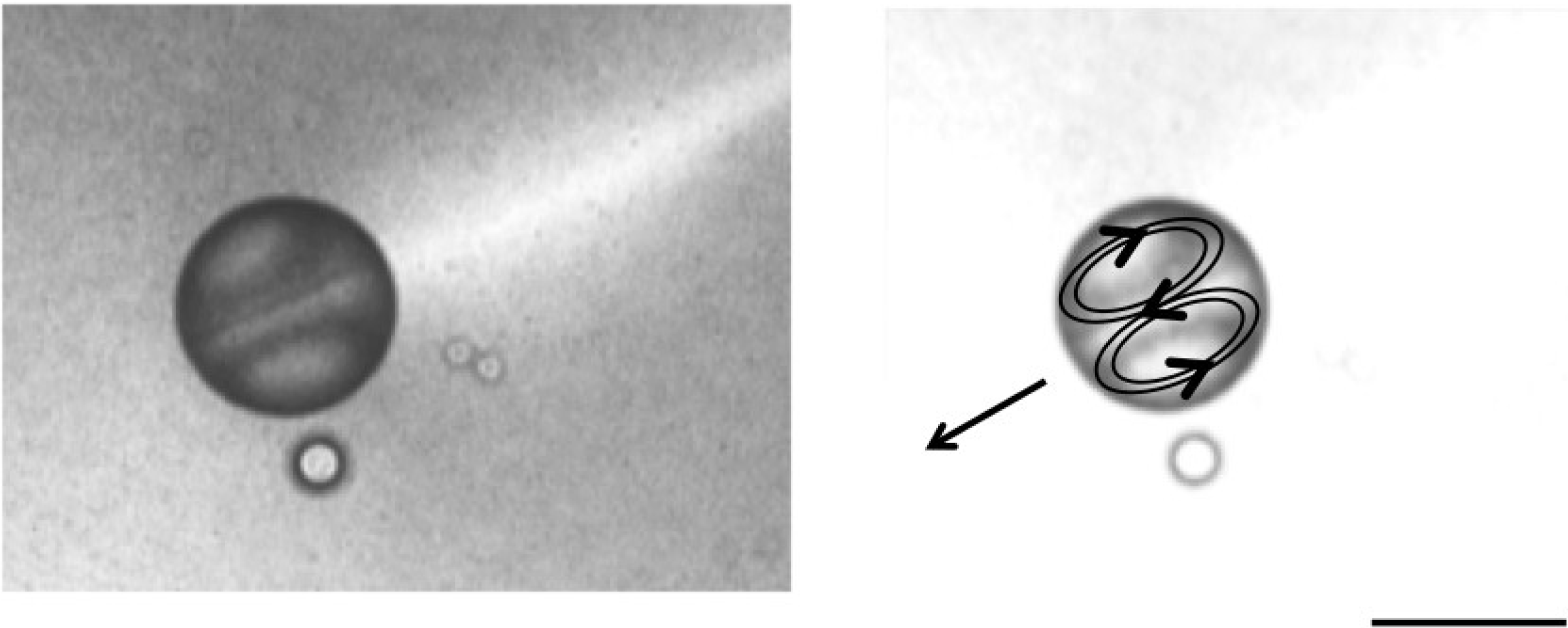
4. Self-Propelled Oil Droplet
- (1)
- no reactive chemistry
- (2)
- onboard fuel
- (3)
- onboard catalyst
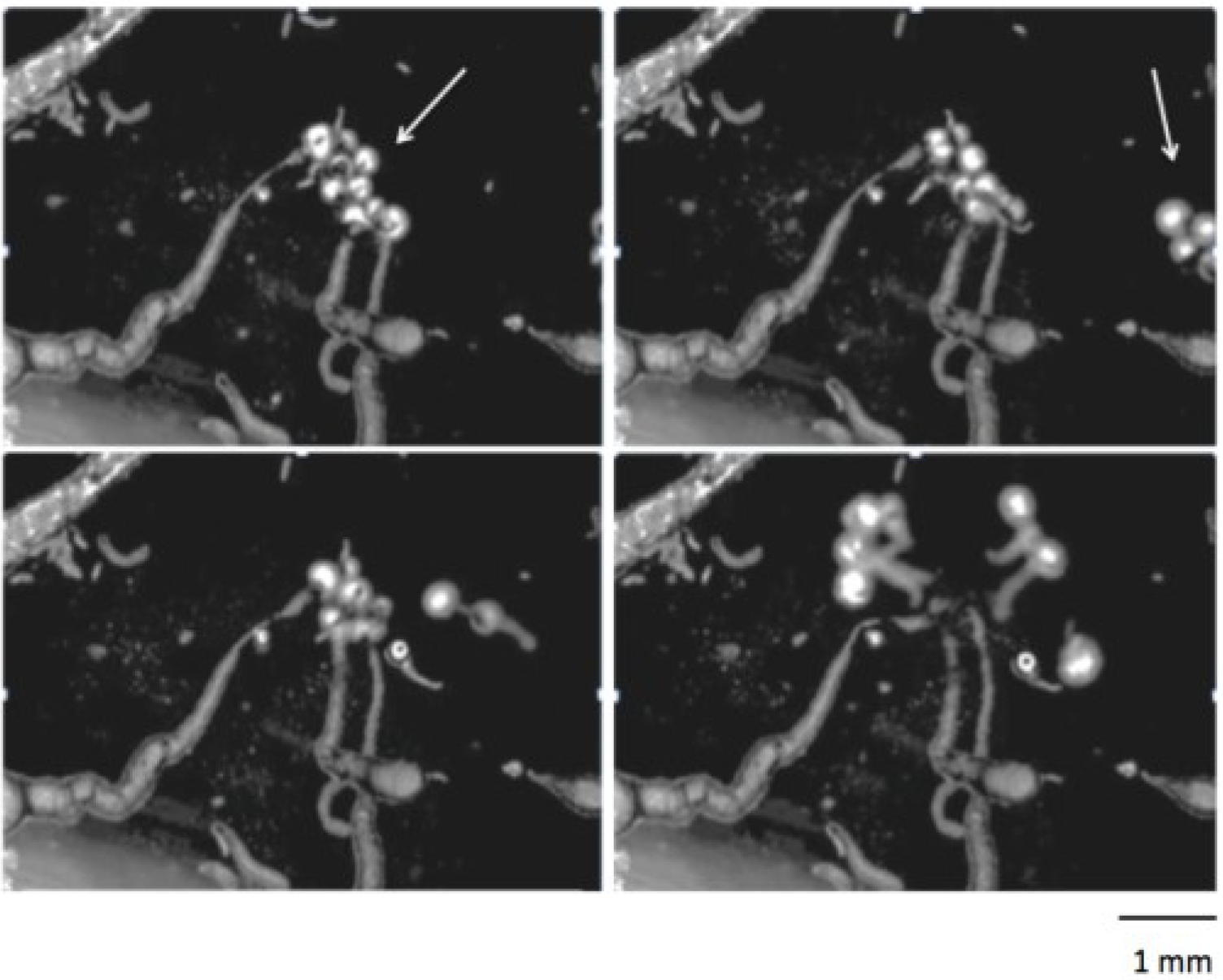
5. Group Dynamics and Higher Order
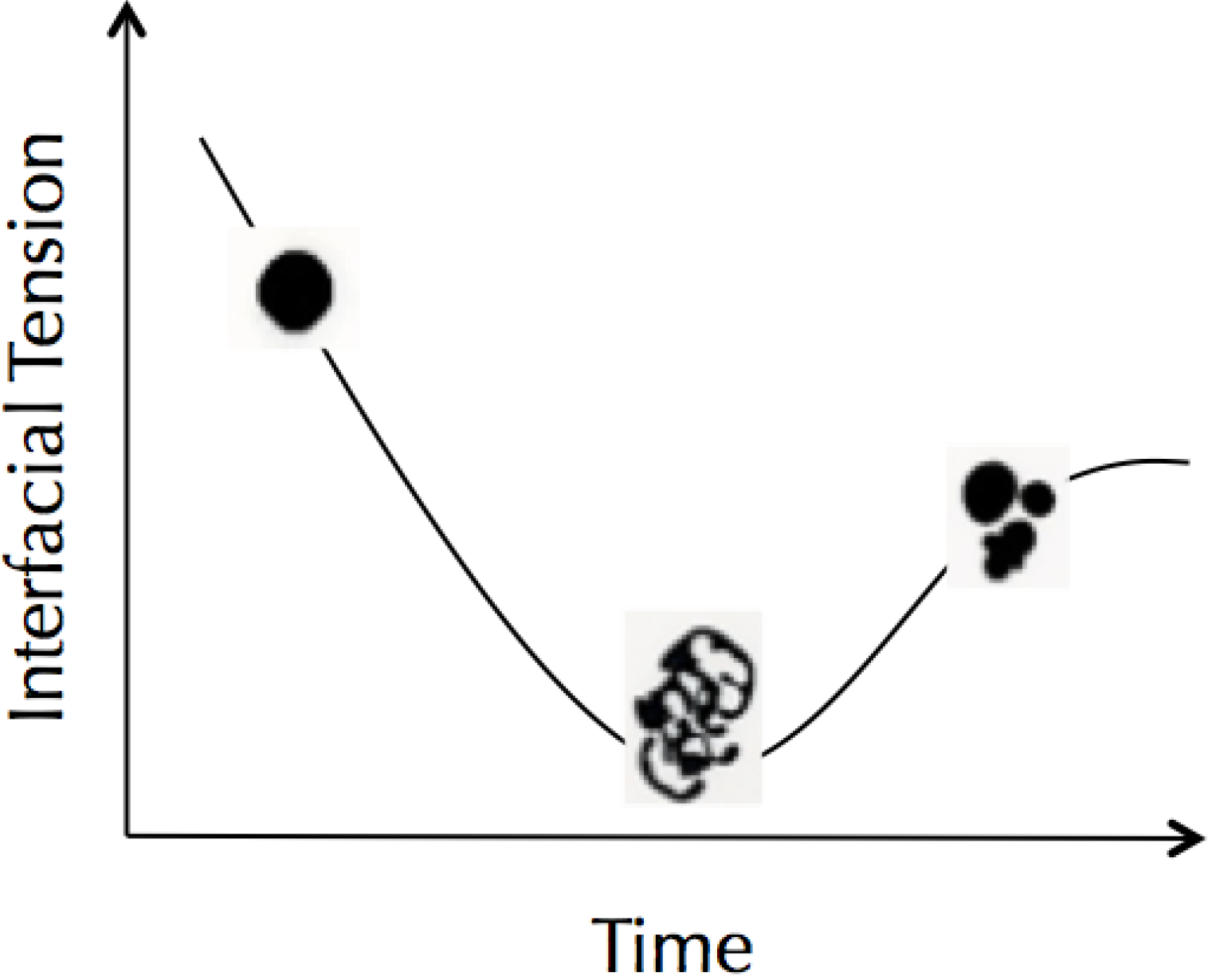
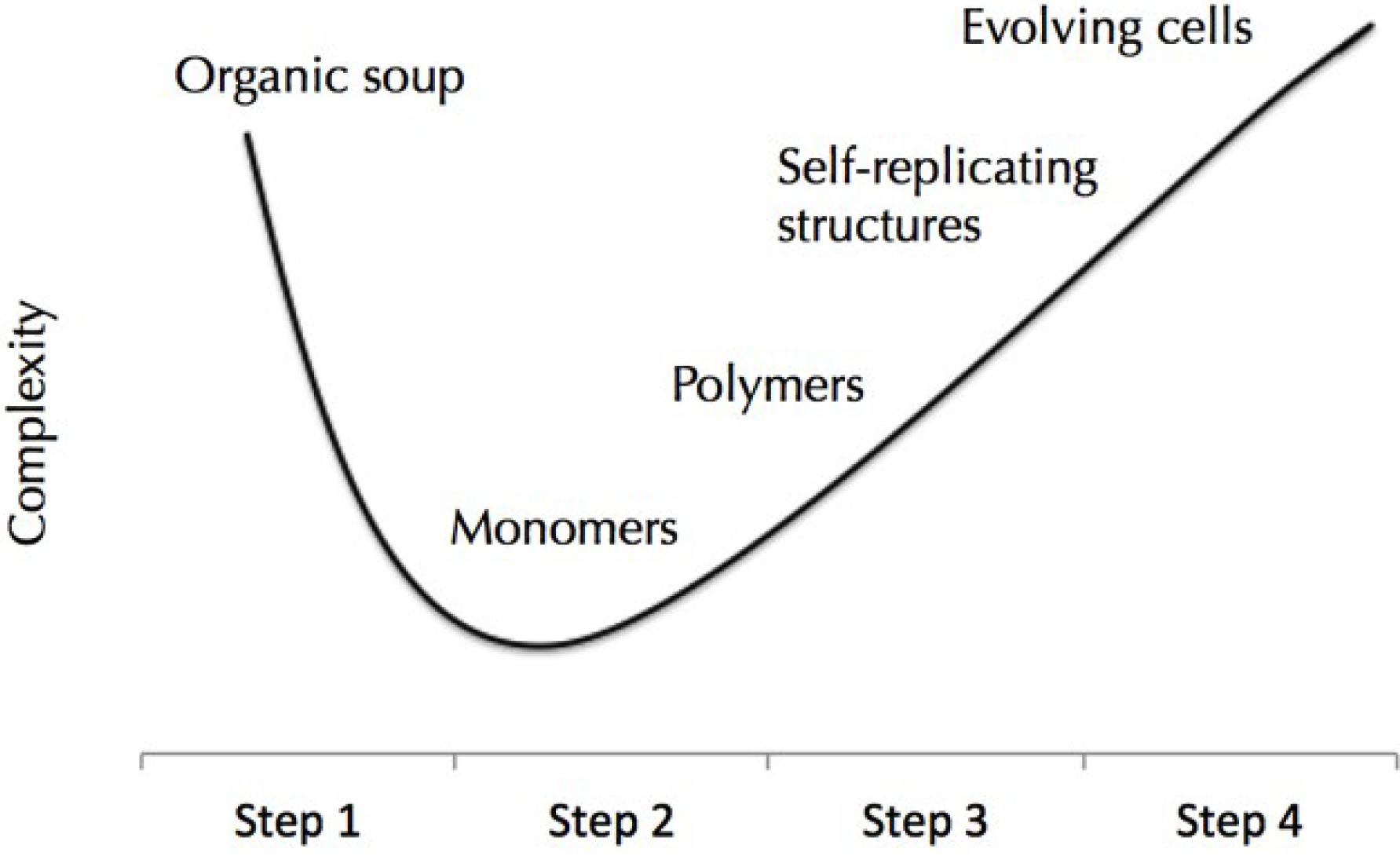
6. Prebiotic Droplets
7. DIY Protocells
8. Conclusions
Acknowledgments
Conflicts of Interest
References
- Duncan, P.B.; David, N. Microdroplet dissolution into a second-phase solvent using a micropipet technique: Test of the Epstein-Plesset model for an aniline-water system. Langmuir 2006, 22, 4190–4197. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, H.; Tatsuyuki, K. Convective instability and electric potential oscillation in a water-oil-water system. Biophys. Chem. 1992, 45, 153–159. [Google Scholar] [CrossRef]
- Ikezoe, Y.; Ishizaki, S.; Yui, H.; Fujinami, M.; Sawada, T. Direct observation of chemical oscillation at a water/nitrobenzene interface with a sodium-alkyl-sulfate system. Anal. Sci. 2004, 20, 435–440. [Google Scholar] [CrossRef] [PubMed]
- Ikezoe, Y.; Ishizaki, S.; Yui, H.; Fujinami, M.; Sawada, T. Chemical oscillation with periodic adsorption and desorption of surfactant ions at a water/nitrobenzene interface. Anal. Sci. 2004, 20, 1509–1514. [Google Scholar] [CrossRef] [PubMed]
- Thomson, J. On certain curious motions observable at the surfaces of wine and other alcoholic liquors. Philos. Mag. Ser. 1855, 10, 330–333. [Google Scholar]
- Agble, D.; Mendes-Tatsis, M.A. The effect of surfactants on interfacial mass transfer in binary liquid-liquid systems. Int. J. Heat Mass Transfer 2000, 43, 1025–1034. [Google Scholar] [CrossRef]
- Dos Santos, D.J.; Gomes, J.A. Molecular Dynamics Study of the Calcium Ion Transfer across the Water/Nitrobenzene Interface. ChemPhysChem 2002, 3, 946–951. [Google Scholar] [CrossRef] [PubMed]
- Leduc, S. The Mechanism of Life; William Heinemann: London, UK, 1914. [Google Scholar]
- Rasmussen, S.; Mark, B.; Liaohai, H.; David, D.; David, C.K.; Norman, H.P.; Peter, F.S. Protocells: Bridging Nonliving and Living Matter; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Pereira de Souza, T.; Steiniger, F.; Stano, P.; Fahr, A.; Luisi, P.L. Spontaneous crowding of ribosomes and proteins inside vesicles: A possible mechanism for the origin of cell metabolism. ChemBioChem 2011, 12, 2325–2330. [Google Scholar] [PubMed]
- Nishimura, K.; Tsuru, S.; Suzuki, H.; Yomo, T. Stochasticity in gene expression in a cell-sized compartment. ACS Synth. Biol. 2014. [Google Scholar] [CrossRef]
- Weitz, M.; Kim, J.; Kapsner, K.; Winfree, E.; Franco, E.; Simmel, F.C. Diversity in the dynamical behaviour of a compartmentalized programmable biochemical oscillator. Nat. Chem. 2014, 6, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Hrdlička, A. Normal Variation; American Philosophical Society: Philadelphia, PA, USA, 1934; Volume 74, pp. 226–253. [Google Scholar]
- Hanczyc, M.M.; Toyota, T.; Ikegami, T.; Packard, N.; Sugawara, T. Fatty acid chemistry at the oil-water interface: Self-propelled oil droplets. J. Am. Chem. Soc. 2007, 129, 9386–9391. [Google Scholar] [CrossRef] [PubMed]
- Caschera, F.; Steen, R.; Martin, M.H. An Oil Droplet Division-Fusion Cycle. ChemPlusChem 2013, 78, 52–54. [Google Scholar] [CrossRef]
- Banno, T.; Shingo, M.; Rie, K.; Toyota, T. Mode Changes Associated with Oil Droplet Movement in Solutions of Gemini Cationic Surfactants. Langmuir 2013, 29, 7689–7696. [Google Scholar] [CrossRef] [PubMed]
- Browne, K.P.; Walker, D.A.; Bishop, K.J.M.; Grzybowski, B.A. Self-Division of Macroscopic Droplets: Partitioning of Nanosized Cargo into Nanoscale Micelles. Angew. Chem. 2010, 122, 6908–6911. [Google Scholar] [CrossRef]
- Derényi, I.; Lagzi, I. Fatty acid droplet self-division driven by a chemical reaction. Phys. Chem. Chem. Phys. 2014, 16, 4639–4641. [Google Scholar] [CrossRef] [PubMed]
- Droplet self-division. Available online: https://www.youtube.com/watch?v=Jlabrw6nI3o (accessed on 12 December 2014).
- Yoshinaga, N.; Ken, H.N.; Yutaka, S.; Hiroyuki, K. Drift instability in the motion of a fluid droplet with a chemically reactive surface driven by Marangoni flow. Phys. Rev. E 2012, 86, 016108. [Google Scholar] [CrossRef]
- Izri, Z.; van der Linden, M.N.; Olivier, D. Self-propulsion of pure water droplets by spontaneous Marangoni stress driven motion. 2014; arXiv:1406.5950. [Google Scholar]
- Sumino, Y.; Yoshikawa, K. Amoeba-like motion of an oil droplet. Eur. Phys. J. Spec. Top. 2014, 223, 1345–1352. [Google Scholar] [CrossRef]
- Shioi, A.; Takahiko, B.; Youichi, M. Autonomously moving colloidal objects that resemble living matter. Entropy 2010, 12, 2308–2332. [Google Scholar] [CrossRef]
- Lagzi, I.; Siowling, S.; Paul, J.W.; Kevin, P.B.; Bartosz, A.G. Maze solving by chemotactic droplets. J. Am. Chem. Soc. 2010, 132, 1198–1199. [Google Scholar] [CrossRef] [PubMed]
- Cejkova, J.; Novák, M.; Štěpánek, F.; Hanczyc, M.M. Dynamics of chemotactic droplets in salt concentration gradients. Langmuir 2014, 30, 11937–11944. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, M.K.; George, M.W. How to make water run uphill. Science 1992, 256, 1539–1541. [Google Scholar] [CrossRef] [PubMed]
- Quéré, D.; Armand, A. Liquid drops: Surfing the hot spot. Nat. Mater. 2006, 5, 429–430. [Google Scholar] [CrossRef] [PubMed]
- Daniel, S.; Sanjoy, S.; Jill, G.; Manoj, K.C. Ratcheting motion of liquid drops on gradient surfaces. Langmuir 2004, 20, 4085–4092. [Google Scholar] [CrossRef] [PubMed]
- Bain, C.D.; Graham, D.B.-H.; Richard, R. Montgomerie. Rapid motion of liquid drops. Nature 1994, 372, 414–415. [Google Scholar] [CrossRef]
- Dos, S.; Fabrice, D.; Thierry, O. Free-running droplets. Phys. Rev. Lett. 1995, 75. [Google Scholar] [CrossRef] [PubMed]
- Toyota, T.; Naoto, M.; Martin, M.H.; Takashi, I.; Tadashi, S. Self-propelled oil droplets consuming “fuel” surfactant. J. Am. Chem. Soc. 2009, 131, 5012–5013. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Maeda, S.; Hara, Y.; Hashimoto, S. Capsule gel robot driven by self-propelled oil droplet. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012.
- Nakagaki, T.; Hiroyasu, Y.; Ágota, T. Intelligence: Maze-solving by an amoeboid organism. Nature 2000, 407. [Google Scholar] [CrossRef] [PubMed]
- Seah, T.H.; Guanjia, Z.; Martin, P. Surfactant Capsules Propel Interfacial Oil Droplets: An Environmental Cleanup Strategy. ChemPlusChem 2013, 78, 395–397. [Google Scholar] [CrossRef]
- Horibe, N.; Martin, M.H.; Takashi, I. Mode switching and collective behavior in chemical oil droplets. Entropy 2011, 13, 709–719. [Google Scholar] [CrossRef]
- Horibe, N.; Hanczyc, M.M.; Ikegami, T. Shape and motion dynamics in self-moving oil droplets. In Proceedings of the 3rd International Conference on Mobiligence, Awaji, Japan, 19–21 November 2009.
- Segré, D.; Dafna, B.-E.; Doron, L. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2000, 97, 4112–4117. [Google Scholar] [CrossRef] [PubMed]
- Hanczyc, M.M.; Takashi, I. Chemical basis for minimal cognition. Artif. Life 2010, 16, 233–243. [Google Scholar] [CrossRef] [PubMed]
- Bogdan, R.J. Information and semantic cognition: An ontological account. Mind Lang. 1988, 3, 81–122. [Google Scholar] [CrossRef]
- Hadorn, M.; Eva, B.; Kristian, T.S.; Harold, F.; Peter, E.H.; Martin, M.H. Specific and reversible DNA-directed self-assembly of oil-in-water emulsion droplets. Proc. Natl. Acad. Sci. USA 2012, 109, 20320–20325. [Google Scholar] [CrossRef] [PubMed]
- Hanczyc, M.M. Metabolism and motility in prebiotic structures. Philos. Trans. R. Soc. B 2011, 366, 2885–2893. [Google Scholar]
- Bütschli, O. Untersuchungen über Mikroskopische Schäume und das Protoplasma; Engelmann: Leipzig, Germany, 1892; Volume 1. [Google Scholar]
- Armstrong, R.; Martin, H. Bütschli dynamic droplet system. Artif. Life 2013, 19, 331–346. [Google Scholar] [CrossRef] [PubMed]
- Davy, H. The Bakerian Lecture: On Some New Phenomena of Chemical Changes Produced by Electricity, Particularly the Decomposition of the Fixed Alkalies, and the Exhibition of the New Substances Which Constitute Their Bases; and on the General Nature of Alkaline Bodies. In Philosophical Transactions of the Royal Society of London; The Royal Society: London, UK, 1808; pp. 1–44. [Google Scholar]
- Protocell Phase Transition Colony. Available online: https://www.youtube.com/watch?v=gB6MKMqbLIM (accessed on 12 December 2014).
- Hanczyc, M.M.; Parrilla, J.M.; Nicholson, A.; Yanev, K.; Stoy, K. Creating and maintaining chemical artificial life by robotic symbiosis. Artif. Life 2014, 21, 1–8. [Google Scholar] [CrossRef]
- Kohira, M.I.; Hayashima, Y.; Nagayama, M.; Nakata, S. Synchronized self-motion of two camphor boats. Langmuir 2001, 17, 7124–7129. [Google Scholar] [CrossRef]
- Soh, S.; Kyle, J.M.B.; Bartosz, A.G. Dynamic self-assembly in ensembles of camphor boats. J. Phys. Chem. B 2008, 112, 10848–10853. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.-G.; Raymond, K. Design of chemically propelled nanodimer motors. J. Chem. Phys. 2008, 128, 164518. [Google Scholar] [CrossRef] [PubMed]
- Eelkema, R.; Pollard, M.M.; Vicario, J.; Katsonis, N.; Ramon, B.S.; Bastiaansen, C.W.M.; Broer, D.J.; Feringa, B.L. Molecular machines: Nanomotor rotates microscale objects. Nature 2006, 440. [Google Scholar] [CrossRef]
- Paxton, W.F.; Kistler, K.C.; Olmeda, C.C.; Sen, A.; St. Angelo, S.K.; Cao, Y.; Mallouk, T.E.; Lammert, P.E.; Crespi, V.H. Catalytic nanomotors: Autonomous movement of striped nanorods. J. Am. Chem. Soc. 2004, 126, 13424–13431. [Google Scholar] [CrossRef] [PubMed]
- Walther, A.; Axel, H.E.M. Janus particles: Synthesis, self-assembly, physical properties, and applications. Chem. Rev. 2013, 113, 5194–5261. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, S.; Solovev, A.A.; Harazim, S.M.; Deneke, C.; Mei, Y.F.; Schmidt, O.G. The smallest man-made jet engine. Chem. Rec. 2011, 11, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Florea, L.; Wagner, K.; Wagner, P.; Wallace, G.G.; Benito-Lopez, F.; Officer, D.L.; Diamond, D. Photo-Chemopropulsion-Light-Stimulated Movement of Microdroplets. Adv. Mater. 2014, 26, 7339–7345. [Google Scholar] [CrossRef] [PubMed]
- Brochard, F. Motions of droplets on solid surfaces induced by chemical or thermal gradients. Langmuir 1989, 5, 432–438. [Google Scholar] [CrossRef]
- Kotz, K.T.; Noble, K.A.; Faris, G.W. Optical microfluidics. Appl. Phys. Lett. 2004, 85, 2658–2660. [Google Scholar] [CrossRef]
- Rybalko, S.; Nobuyuki, M.; Kenichi, Y. Forward and backward laser-guided motion of an oil droplet. Phys. Rev. E 2004, 70, 046301. [Google Scholar] [CrossRef]
- Miura, S.; Taisuke, B.; Taishi, T.; Toshihisa, O.; Shoji, T.; Taro, T. pH-Induced Motion Control of Self-Propelled Oil Droplets Using a Hydrolyzable Gemini Cationic Surfactant. Langmuir 2014, 30, 7977–7985. [Google Scholar] [CrossRef] [PubMed]
- Gallardo, B.S.; Vinay, K.G.; Franklin, D.E.; Lana, I.J.; Vincent, S.C.; Rahul, R.S.; Nicholas, L.A. Electrochemical principles for active control of liquids on submillimeter scales. Science 1999, 283, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Dorvee, J.R.; Austin, M.D.; Sangeeta, N.B.; Michael, J.S. Manipulation of liquid droplets using amphiphilic, magnetic one-dimensional photonic crystal chaperones. Nat. Mater. 2004, 3, 896–899. [Google Scholar] [CrossRef] [PubMed]
- Hanczyc, M.M. Structure and the synthesis of life. Archit. Des. 2011, 81, 26–33. [Google Scholar]
- Committee on the Limits of Organic Life in Planetary Systems; Committee on the Origins and Evolution of Life; National Research Council. The Limits of Organic Life in Planetary Systems; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanczyc, M.M. Droplets: Unconventional Protocell Model with Life-Like Dynamics and Room to Grow. Life 2014, 4, 1038-1049. https://doi.org/10.3390/life4041038
Hanczyc MM. Droplets: Unconventional Protocell Model with Life-Like Dynamics and Room to Grow. Life. 2014; 4(4):1038-1049. https://doi.org/10.3390/life4041038
Chicago/Turabian StyleHanczyc, Martin M. 2014. "Droplets: Unconventional Protocell Model with Life-Like Dynamics and Room to Grow" Life 4, no. 4: 1038-1049. https://doi.org/10.3390/life4041038
APA StyleHanczyc, M. M. (2014). Droplets: Unconventional Protocell Model with Life-Like Dynamics and Room to Grow. Life, 4(4), 1038-1049. https://doi.org/10.3390/life4041038




