Helix Folding in One Dimension: Effects of Proline Co-Solvent on Free Energy Landscape of Hydrogen Bond Dynamics in Alanine Peptides
Abstract
1. Introduction
2. Methods
3. Results and Discussion
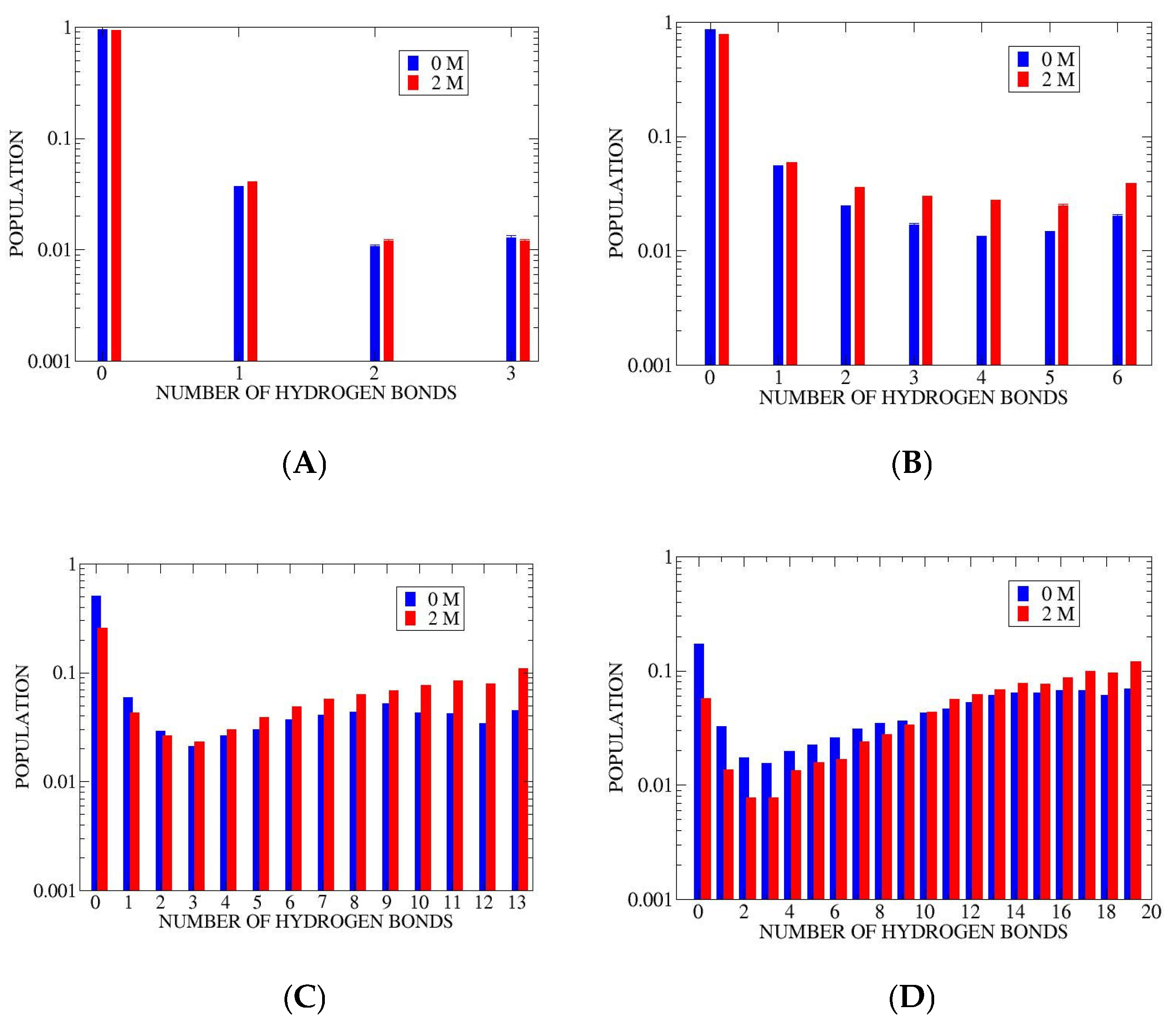
3.1. Microstate Populations
3.2. Folding Kinetics in Hydrogen Bond Space
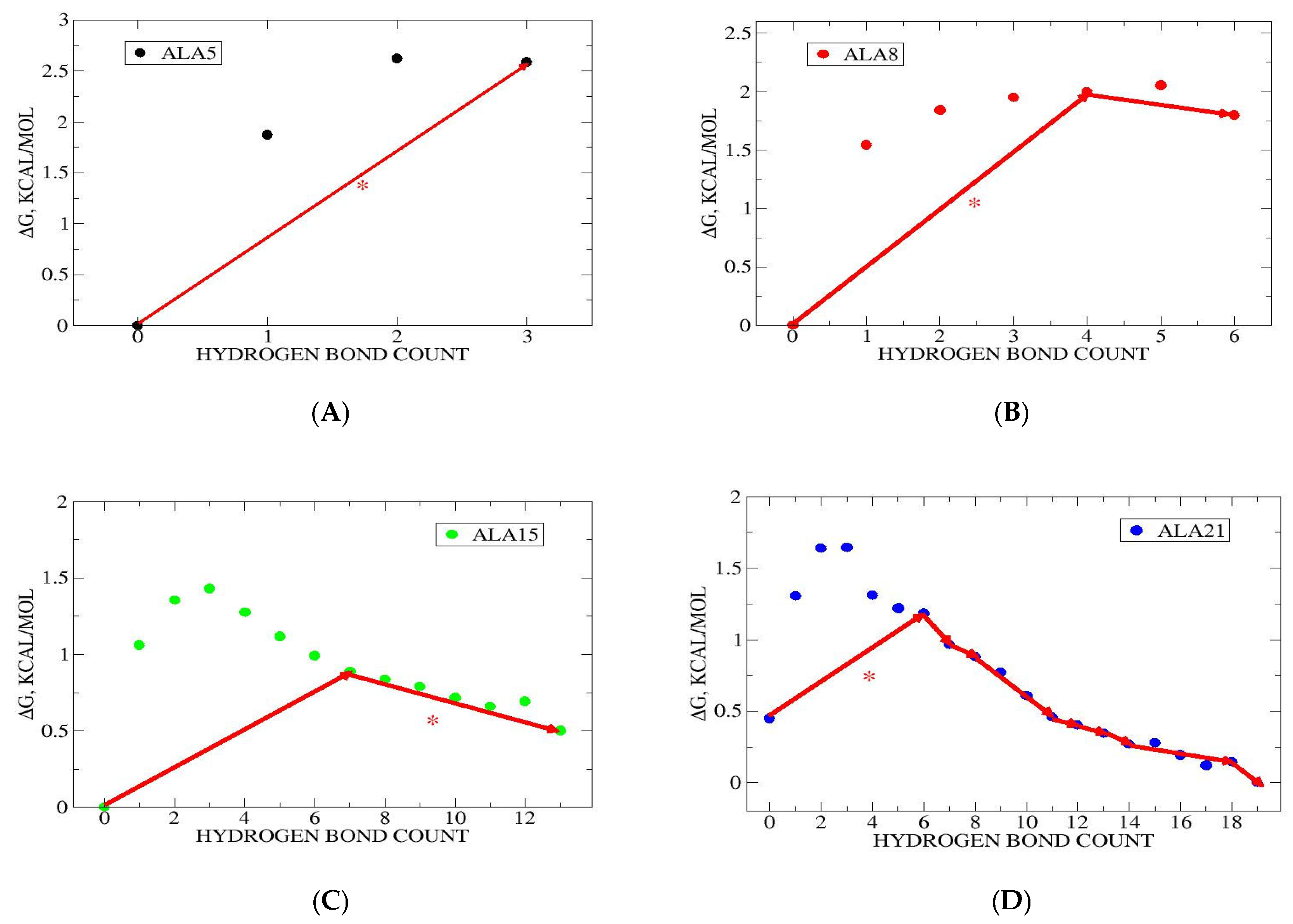
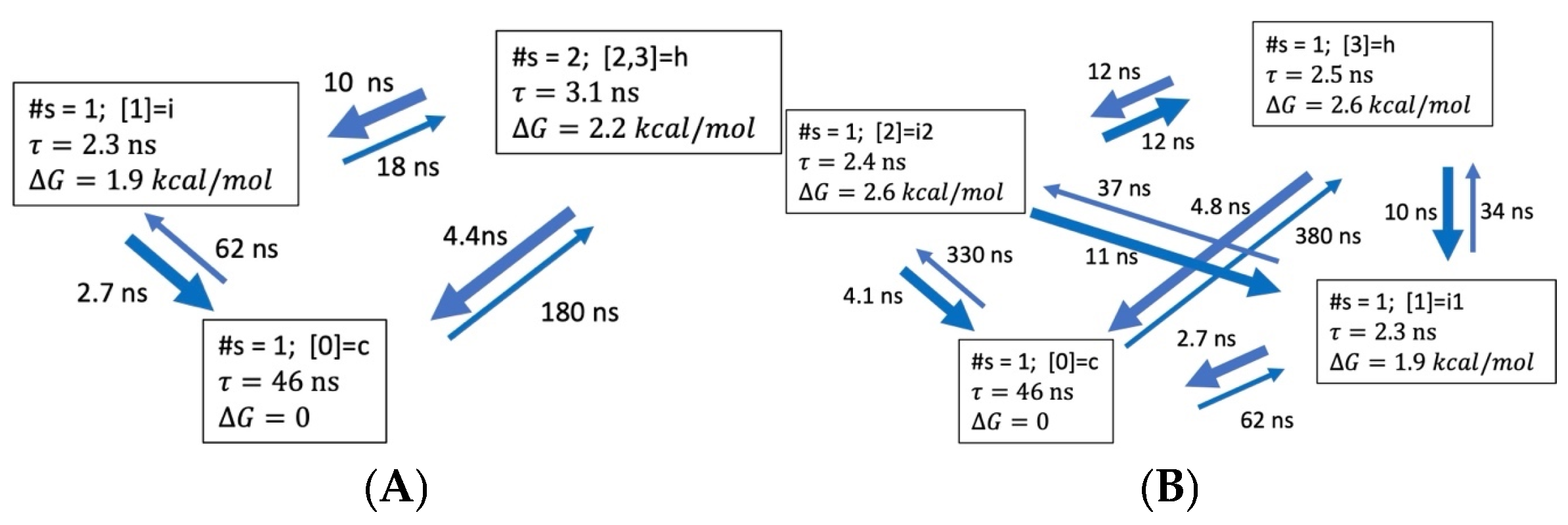
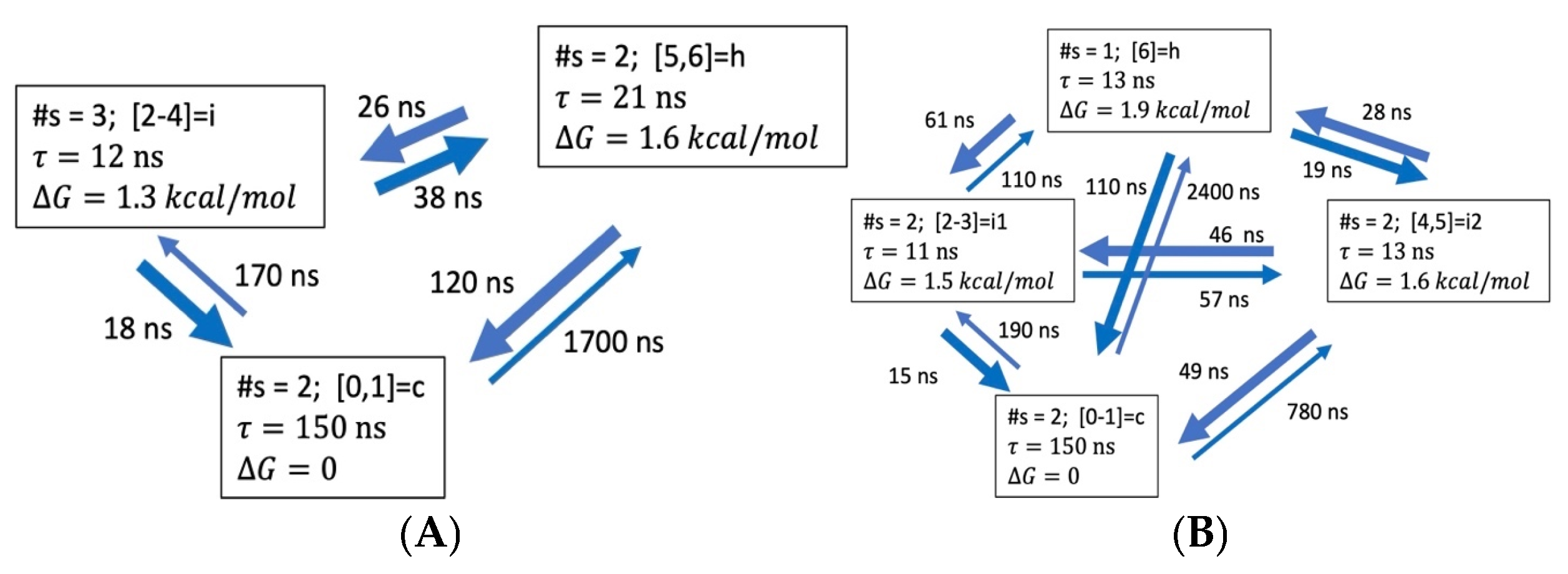
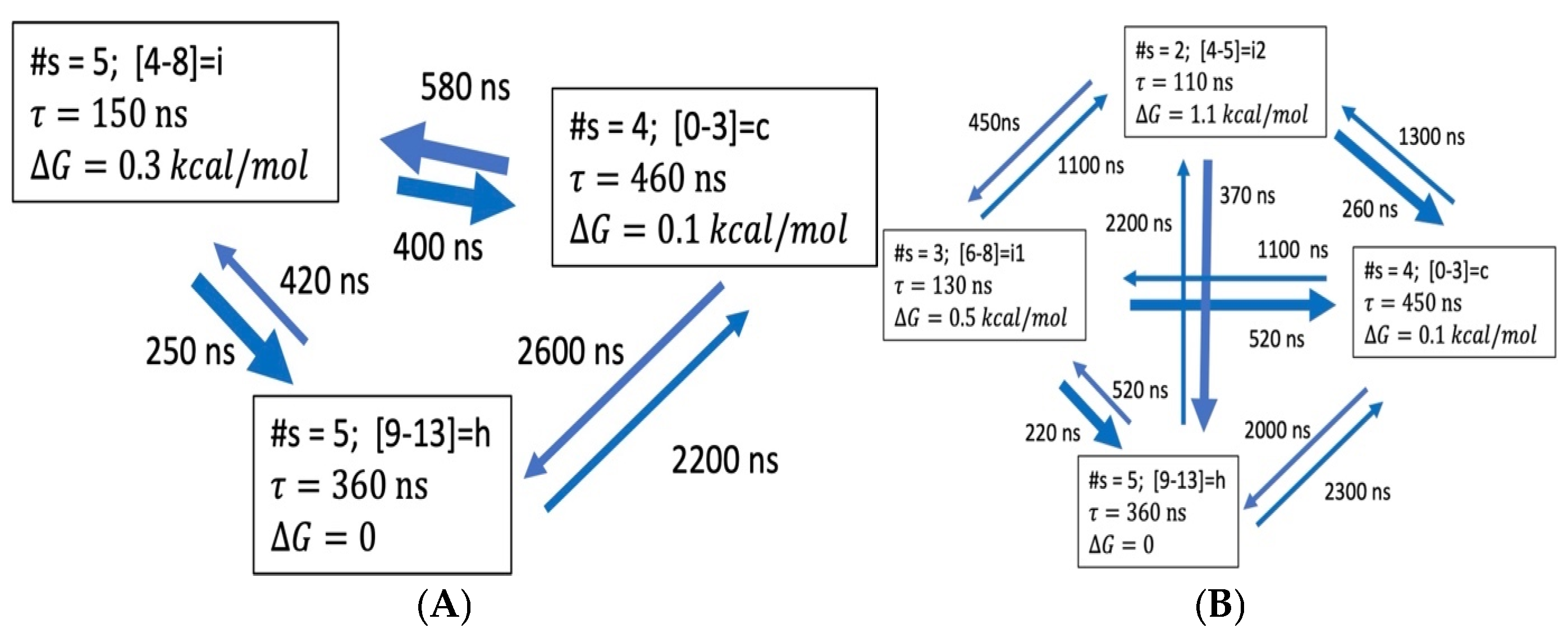
3.3. Global Maximum Weight Paths (GMWP)
3.3.1. Coarse-Grained Kinetic Models
3.3.2. Transition Path Theory
3.3.3. Comparing Helix Folding Paths from GMWP, ODR and TPT
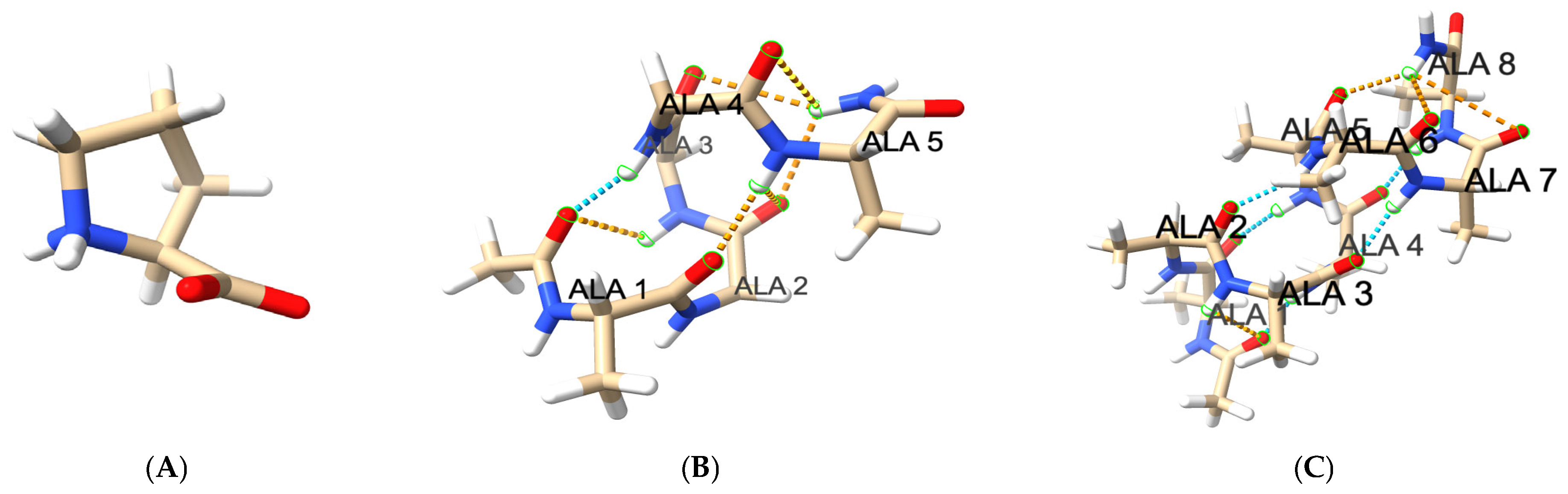
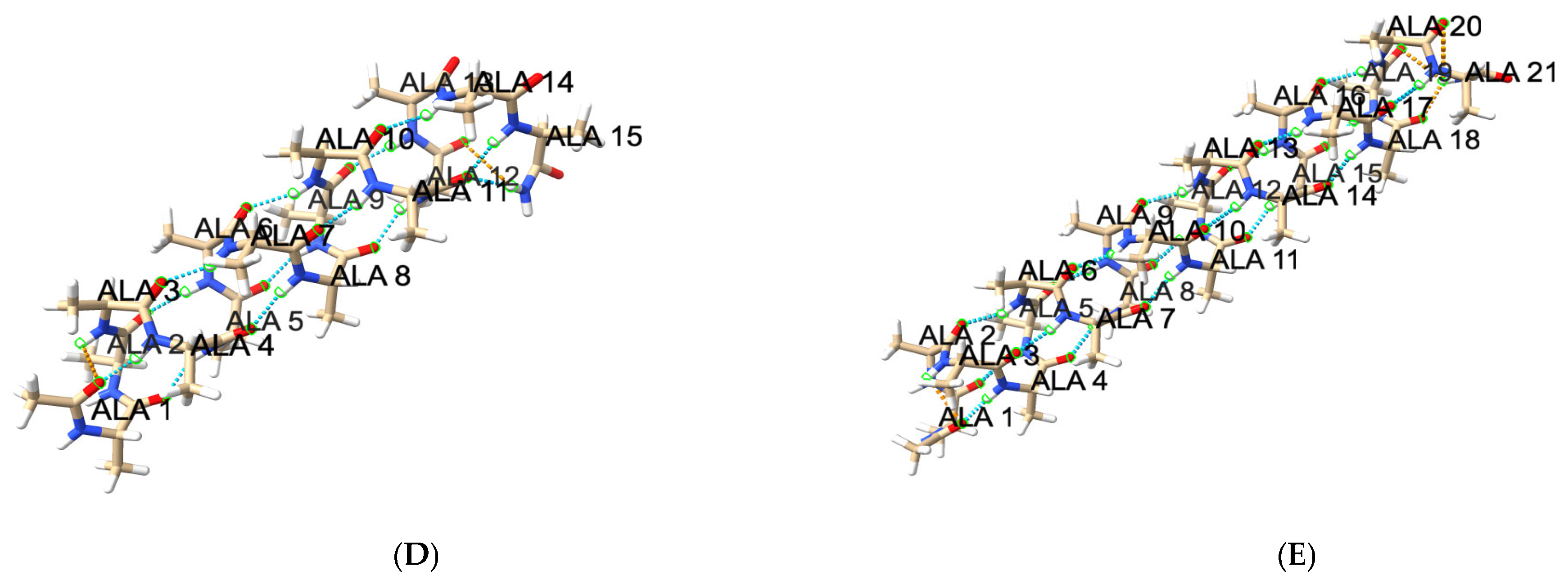
3.3.4. Hydrogen Bond Patterns and Folding Intermediates
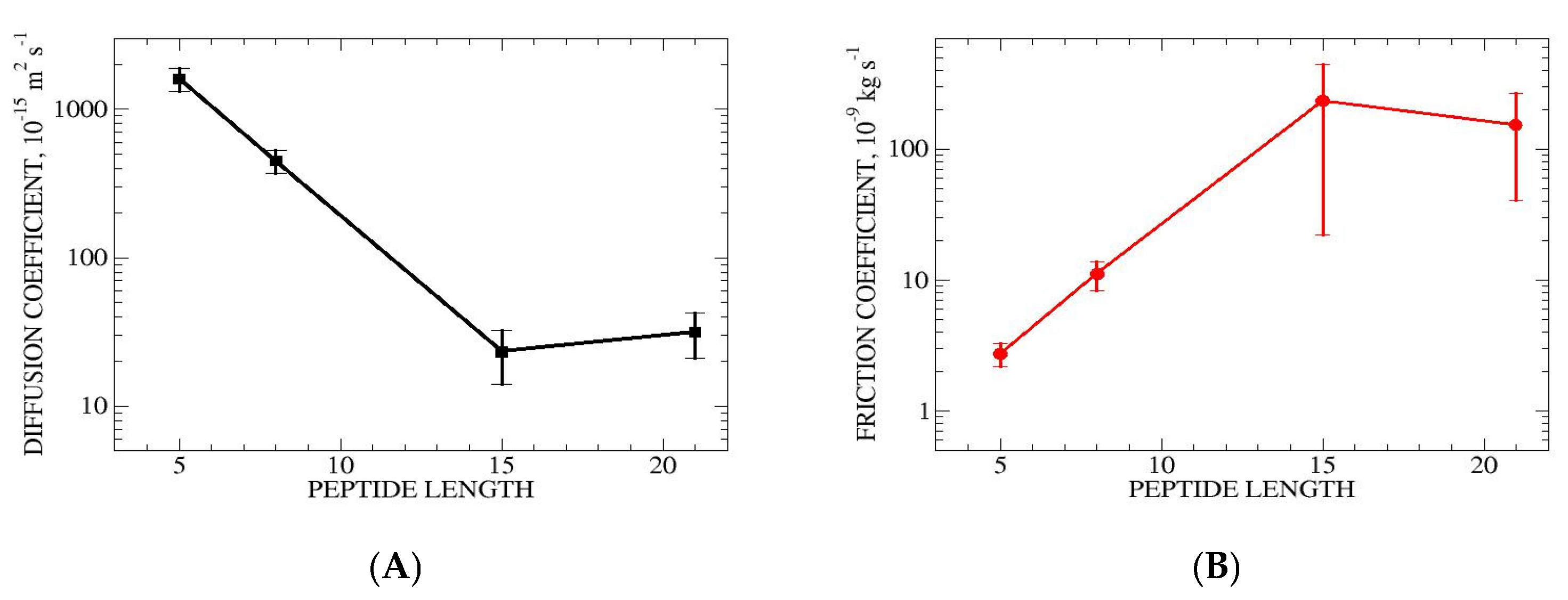
3.3.5. Diffusion and Friction
3.3.6. Effects of Proline on Helix Folding Free Energy Landscape
3.3.7. Comparison with Experimental Data
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuriyan, J.; Konforti, B.; Wemmer, D. The Molecules of Life; Garland Science: New York, NY, USA, 2013. [Google Scholar]
- Best, R.B.; Hummer, G.; Eaton, W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef]
- Ahalawat, N.; Mondal, J. Assessment and optimization of collective variables for protein conformational landscape: GB1 beta-hairpin as a case study. J. Chem. Phys. 2018, 149, 094101. [Google Scholar] [CrossRef] [PubMed]
- Kirmizialtin, S.; Elber, R. Revisiting and Computing Reaction Coordinates with Directional Milestoning. J. Phys. Chem. A 2011, 115, 6137–6148. [Google Scholar] [CrossRef] [PubMed]
- Kasprzak, Y.; Ruckert, J.; Ludolph, N.; Hubner, C.G.; Paulsen, H. Hydrogen bonds vs RMSD: Geometric reaction coordinates for protein folding. J. Chem. Phys. 2025, 162, 074107. [Google Scholar] [CrossRef] [PubMed]
- Mojtabavi, S.; Samadi, N.; Faramarzi, M.A. Osmolyte-Induced Folding and Stability of Proteins: Concepts and Characterization. IJ Pharm. Res. 2019, 18, 13–30. [Google Scholar] [CrossRef]
- Singh, L.R.; Poddar, N.K.; Dar, T.A.; Rahman, S.; Kumar, R.; Ahmad, F. Forty Years of Research on Osmolyte-Induced Protein Folding and Stability. J. Iran. Chem. Soc. 2011, 8, 1–23. [Google Scholar] [CrossRef]
- Canchi, D.R.; Garcia, A.E. Cosolvent effects on protein stability. Annu. Rev. Phys. Chem. 2013, 64, 273–293. [Google Scholar] [CrossRef]
- Arsiccio, A.; Ganguly, P.; Shea, J.E. A Transfer Free Energy Based Implicit Solvent Model for Protein Simulations in Solvent Mixtures: Urea-Induced Denaturation as a Case Study. J. Phys. Chem. B 2022, 126, 4472–4482. [Google Scholar] [CrossRef]
- Samuel, D.; Kumar, T.K.; Ganesh, G.; Jayaraman, G.; Yang, P.W.; Chang, M.M.; Trivedi, V.D.; Wang, S.L.; Hwang, K.C.; Chang, D.K.; et al. Proline inhibits aggregation during protein refolding. Protein Sci. 2000, 9, 344–352. [Google Scholar] [CrossRef]
- Kumar, R.; Serrette, J.M.; Khan, S.H.; Miller, A.L.; Thompson, E.B. Effects of different osmolytes on the induced folding of the N-terminal activation domain (AF1) of the glucocorticoid receptor. Arch. Biochem. Biophys. 2007, 465, 452–460. [Google Scholar] [CrossRef]
- Gazi, R.; Kumar, S.; Jana, M. Proline concentration driven thermostability of ubiquitin. J. Mol. Liq. 2025, 424, 127108. [Google Scholar] [CrossRef]
- Auton, M.; Rosgen, J.; Sinev, M.; Holthauzen, L.M.; Bolen, D.W. Osmolyte effects on protein stability and solubility: A balancing act between backbone and side-chains. Biophys. Chem. 2011, 159, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, S. Solvent accessible surface area-assessed molecular basis of osmolyte-induced protein stability. RSC Adv. 2024, 14, 25031–25041. [Google Scholar] [CrossRef] [PubMed]
- Miotto, M.; Warner, N.; Ruocco, G.; Tartaglia, G.G.; Scherman, O.A.; Milanetti, E. Osmolyte-Induced Protein Stability Changes Explained by Graph Theory. arXiv 2023, arXiv:2305.05038. [Google Scholar] [CrossRef]
- Kuczera, K.; Szoszkiewicz, R.; He, J.Y.; Jas, G.S. Length Dependent Folding Kinetics of Alanine-Based Helical Peptides from Optimal Dimensionality Reduction. Life 2021, 11, 385. [Google Scholar] [CrossRef]
- Kuczera, K.; Jas, G.S.; Szoszkiewicz, R. Helix Formation from Hydrogen Bond Kinetics in Alanine Homopeptides. Crystals 2024, 14, 532. [Google Scholar] [CrossRef]
- Kuczera, K.; Szoszkiewicz, R.; Jas, G.S. Microscopic effects of proline co-solvent on alanine homopeptide structure, solvation and helix folding dynamics. J. Biomol. Struct. Dyn. 2025. [Google Scholar] [CrossRef] [PubMed]
- Swiatek, A.; Kuczera, K.; Szoszkiewicz, R. Effects of Proline on Internal Friction in Simulated Folding Dynamics of Several Alanine-Based α-Helical Peptides. J. Phys. Chem. B 2024, 128, 3856–3869. [Google Scholar] [CrossRef]
- Jas, G.S.; Kuczera, K. Helix-Coil Transition Courses Through Multiple Pathways and Intermediates: Fast Kinetic Measurements and Dimensionality Reduction. J. Phys. Chem. B 2018, 122, 10806–10816. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–29. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmuller, H.; MacKerell, A.D. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Darden, T.; Perera, L.; Li, L.P.; Pedersen, L. New tricks for modelers from the crystallography toolkit: The particle mesh Ewald algorithm and its use in nucleic acid simulations. Structure 1999, 7, R55–R60. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.R.; Noé, F.; Pande, V.S. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Advances in Experimental Medicine and Biology; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Kube, S.; Weber, M. A coarse graining method for the identification of transition rates between molecular conformations. J. Chem. Phys. 2007, 126, 024103. [Google Scholar] [CrossRef]
- Hummer, G.; Szabo, A. Optimal Dimensionality Reduction of Multistate Kinetic and Markov-State Models. J. Phys. Chem. B 2015, 119, 9029–9037. [Google Scholar] [CrossRef] [PubMed]
- Senne, M.; Trendelkamp-Schroer, B.; Mey, A.S.J.S.; Schutte, C.; Noe, F. EMMA: A Software Package for Markov Model Building and Analysis. J. Chem. Theory Comput. 2012, 8, 2223–2238. [Google Scholar] [CrossRef]
- Viswanath, S.; Kreuzer, S.M.; Cardenas, A.E.; Elber, R. Analyzing milestoning networks for molecular kinetics: Definitions, algorithms, and examples. J. Chem. Phys. 2013, 139, 174105. [Google Scholar] [CrossRef]
- Bicout, D.J.; Szabo, A. Electron transfer reaction dynamics in non-Debye solvents. J. Chem. Phys. 1998, 109, 2325–2338. [Google Scholar] [CrossRef]
- Meng, E.C.; Goddard, T.D.; Pettersen, E.F.; Couch, G.S.; Pearson, Z.J.; Morris, J.H.; Ferrin, T.E. UCSF Chimera-X: Tools for structure building and analysis. Protein Sci. 2023, 11, e4792. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef]
- Dellago, C.; Bolhuis, P.G.; Geissler, P.L. Transition path sampling. In Advances in Chemical Physics; John Wiley and Sons: Hoboken, NJ, USA, 2002; Volume 123, pp. 1–78. [Google Scholar]
- Vanden-Eijnden, E. Transition Path Theory. Adv. Exp. Med. Biol. 2014, 797, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Jas, G.S.; Childs, E.W.; Middaugh, C.R.; Kuczera, K. Probing the Internal Dynamics and Shape of Simple Peptides in Urea, Guanidinium Hydrochloride, and Proline Solutions with Time-Resolved Fluorescence Anisotropy and Atomistic Cosolvent Simulations. J. Phys. Chem. B 2021, 125, 10972–10984. [Google Scholar] [CrossRef] [PubMed]
- Buchete, N.V.; Hummer, G. Coarse master equations for peptide folding dynamics. J. Phys. Chem. B 2008, 112, 6057–6069. [Google Scholar] [CrossRef] [PubMed]


| System | MD C(t) [18] | RMSD [18] | NHB | |||
|---|---|---|---|---|---|---|
| ALA5 | ~0.2 | 3 | 1.6 | 3.6 | 2.0 | 3.3 |
| ALA8 | ~2 | 34 | 2.0 | 33 | 8.0 | 33 |
| ALA15 | ~20 | 540 | 118 | 520 | 100 | 370 |
| ALA21 | ~20 | 460 | 139 | 470 | 80 | 470 |
| i/j | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | −21.8 | 374.9 | 245.7 | 206.9 |
| 1 | 16.2 | −431.0 | 93.1 | 101.3 |
| 2 | 3.0 | 26.7 | −424.2 | 84.3 |
| 3 | 2.6 | 29.4 | 85.4 | −392.5 |
| i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | −13.1 | 92.8 | 65.5 | 43.0 | 21.6 | 8.8 | 7.1 |
| 1 | 7.2 | −114.6 | 13.5 | 11.7 | 8.0 | 4.9 | 4.2 |
| 2 | 2.9 | 7.7 | −109.4 | 13.8 | 9.8 | 6.3 | 5.7 |
| 3 | 1.7 | 5.8 | 12.0 | −103.9 | 15.1 | 10.8 | 10.5 |
| 4 | 0.8 | 3.6 | 7.7 | 13.7 | −101.5 | 21.0 | 20.8 |
| 5 | 0.3 | 2.1 | 4.6 | 9.1 | 19.4 | −95.5 | 30.5 |
| 6 | 0.3 | 2.6 | 6.0 | 12.7 | 27.6 | 43.7 | −78.9 |
| System | ODR | MD | ||||
|---|---|---|---|---|---|---|
| , ns | , ns | , kcal/mol | , ns | , ns | , kcal/mol | |
| ALA5 | 3.2 | 130 | 2.2 | |||
| ALA8 | 33 | 330 | 0.9 | |||
| ALA15 | 900 | 550 | −0.3 | |||
| ALA21 | 3600 | 470 | −1.2 | |||
| Pattern | Population | NHB |
|---|---|---|
| 000 | 0.934696 | 0 |
| 001 | 0.018711 | 1 |
| 100 | 0.016182 | 1 |
| 010 | 0.006217 | 1 |
| 011 | 0.005538 | 2 |
| 110 | 0.005094 | 2 |
| 101 | 0.000923 | 2 |
| 111 | 0.012640 | 3 |
| Pattern | Population | NHB |
|---|---|---|
| 0000000000000 | 0.252415 | 0 |
| 0000001000000 | 0.004938 | 1 |
| 0000000000001 | 0.004704 | 1 |
| 1000000000000 | 0.004685 | 1 |
| 0000000001000 | 0.003824 | 1 |
| 0001000000000 | 0.003456 | 1 |
| 0000100000000 | 0.003210 | 1 |
| 0000010000000 | 0.003139 | 1 |
| 0000000010000 | 0.002747 | 1 |
| 0010000000000 | 0.002557 | 1 |
| 0000000000010 | 0.002550 | 1 |
| … | ||
| 0000001111111 | 0.012893 | 7 |
| 1111111000000 | 0.011977 | 7 |
| 0001111111000 | 0.006355 | 7 |
| 0000111111100 | 0.004585 | 7 |
| … | ||
| 1111111111110 | 0.035874 | 12 |
| 0111111111111 | 0.028596 | 12 |
| 1111111111101 | 0.003089 | 12 |
| 1011111111111 | 0.002312 | 12 |
| 1111111111011 | 0.001822 | 12 |
| 1101111111111 | 0.001099 | 12 |
| 1111111111111 | 0.116499 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuczera, K. Helix Folding in One Dimension: Effects of Proline Co-Solvent on Free Energy Landscape of Hydrogen Bond Dynamics in Alanine Peptides. Life 2025, 15, 809. https://doi.org/10.3390/life15050809
Kuczera K. Helix Folding in One Dimension: Effects of Proline Co-Solvent on Free Energy Landscape of Hydrogen Bond Dynamics in Alanine Peptides. Life. 2025; 15(5):809. https://doi.org/10.3390/life15050809
Chicago/Turabian StyleKuczera, Krzysztof. 2025. "Helix Folding in One Dimension: Effects of Proline Co-Solvent on Free Energy Landscape of Hydrogen Bond Dynamics in Alanine Peptides" Life 15, no. 5: 809. https://doi.org/10.3390/life15050809
APA StyleKuczera, K. (2025). Helix Folding in One Dimension: Effects of Proline Co-Solvent on Free Energy Landscape of Hydrogen Bond Dynamics in Alanine Peptides. Life, 15(5), 809. https://doi.org/10.3390/life15050809






