Multistable Protocells Can Aid the Evolution of Prebiotic Autocatalytic Sets
Abstract
:1. Introduction
2. The Model
3. Results
3.1. Deterministic Dynamics: Bistability with Two Distinct Growth Rates
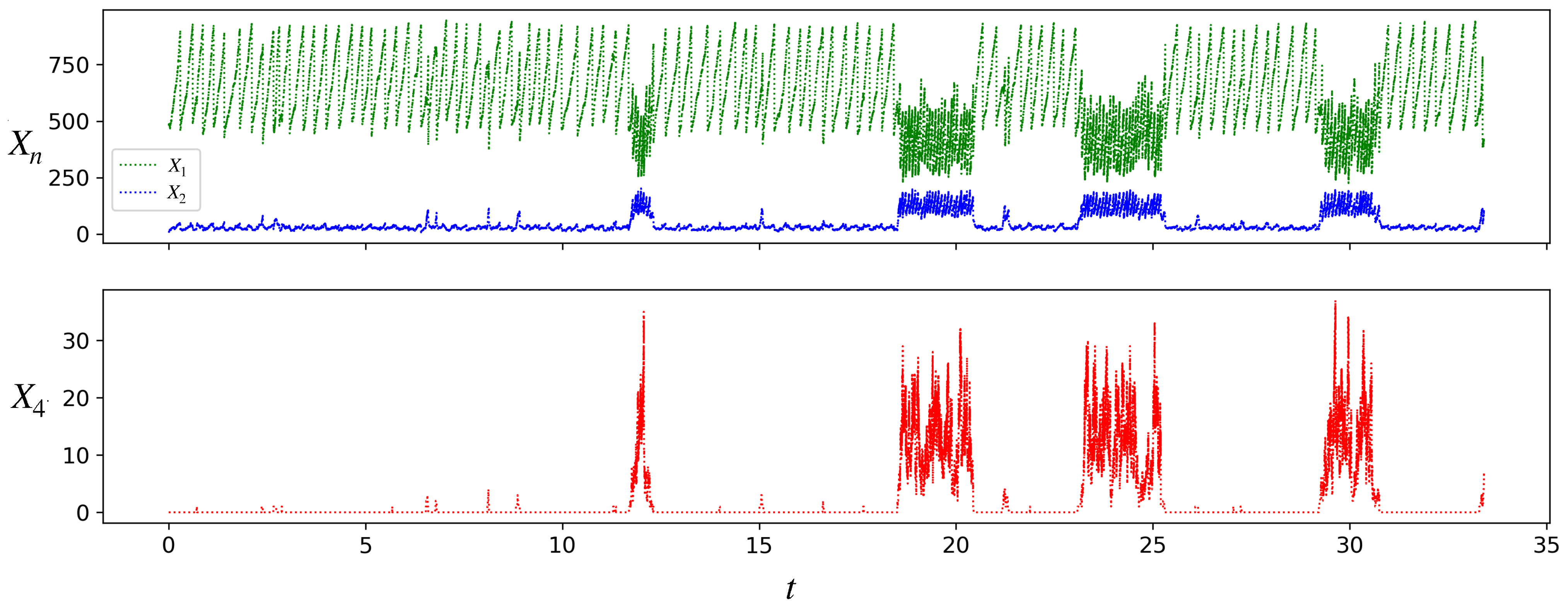
3.2. Stochastic Dynamics of a Single Protocell: Transitions between States of Different Growth Rates
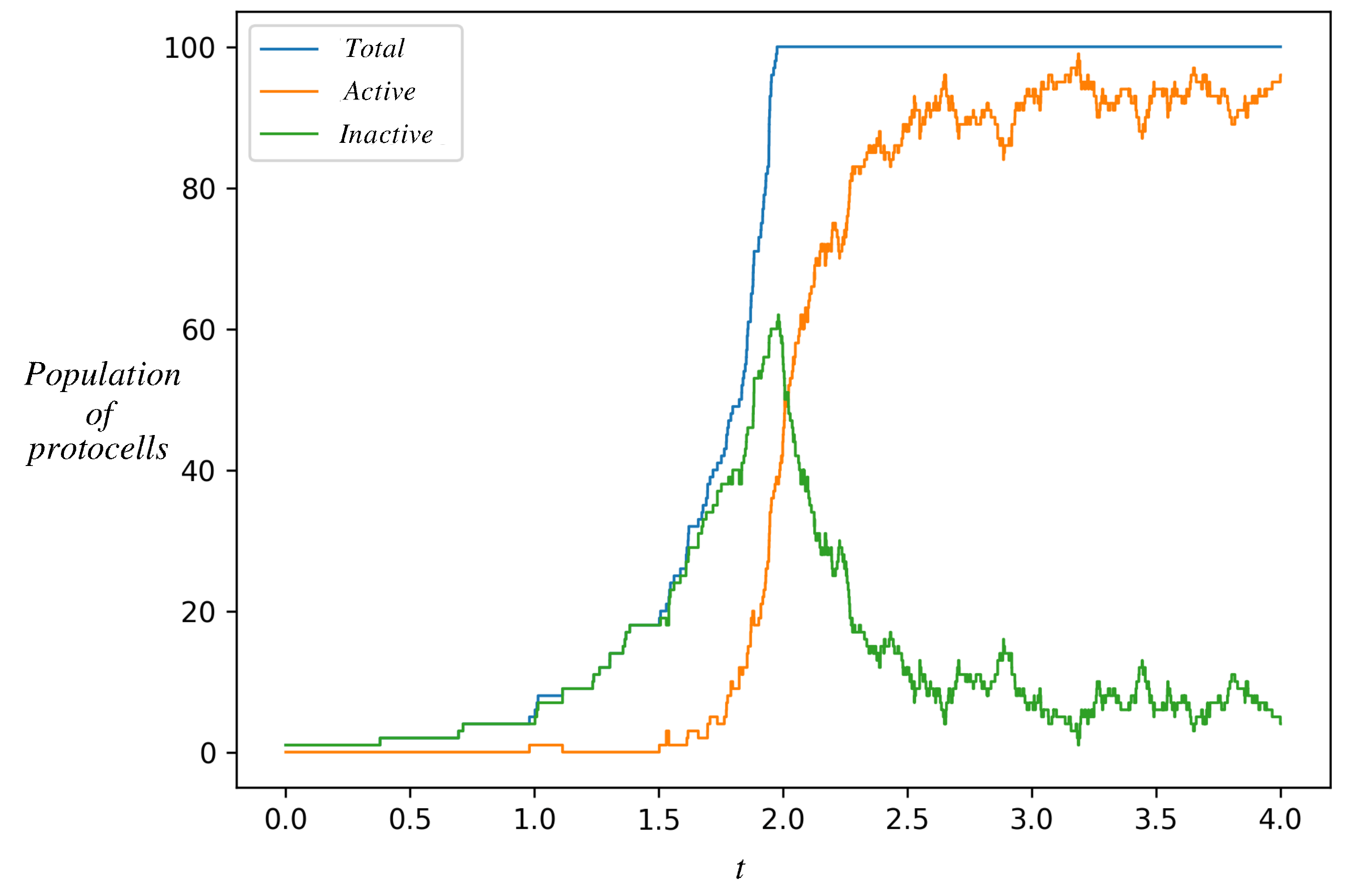
3.3. Protocell Population Dynamics: Dominance of the Autocatalytic State
4. Discussion And Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACS | Autocatalytic set |
Appendix A. Reaction Probabilities Used in Gillespie Algorithm
| Reaction | Reaction Type | Reaction Probability per Unit Time | Deterministic Rate of Reaction |
|---|---|---|---|
| transport | |||
| spontaneous | |||
| catalyzed | |||
| spontaneous | |||
| catalyzed | |||
| spontaneous | |||
| catalyzed | |||
| spontaneous | |||
| catalyzed | |||
| degradation | |||
| degradation |
Appendix B. Single-Cell Residence Time and Interdivision Time Distributions for Active/Inactive States of the Protocell
Appendix B.1. Definition of an Active/Inactive State of a Protocell
Appendix B.2. Definition of Residence Time and Interdivision Time
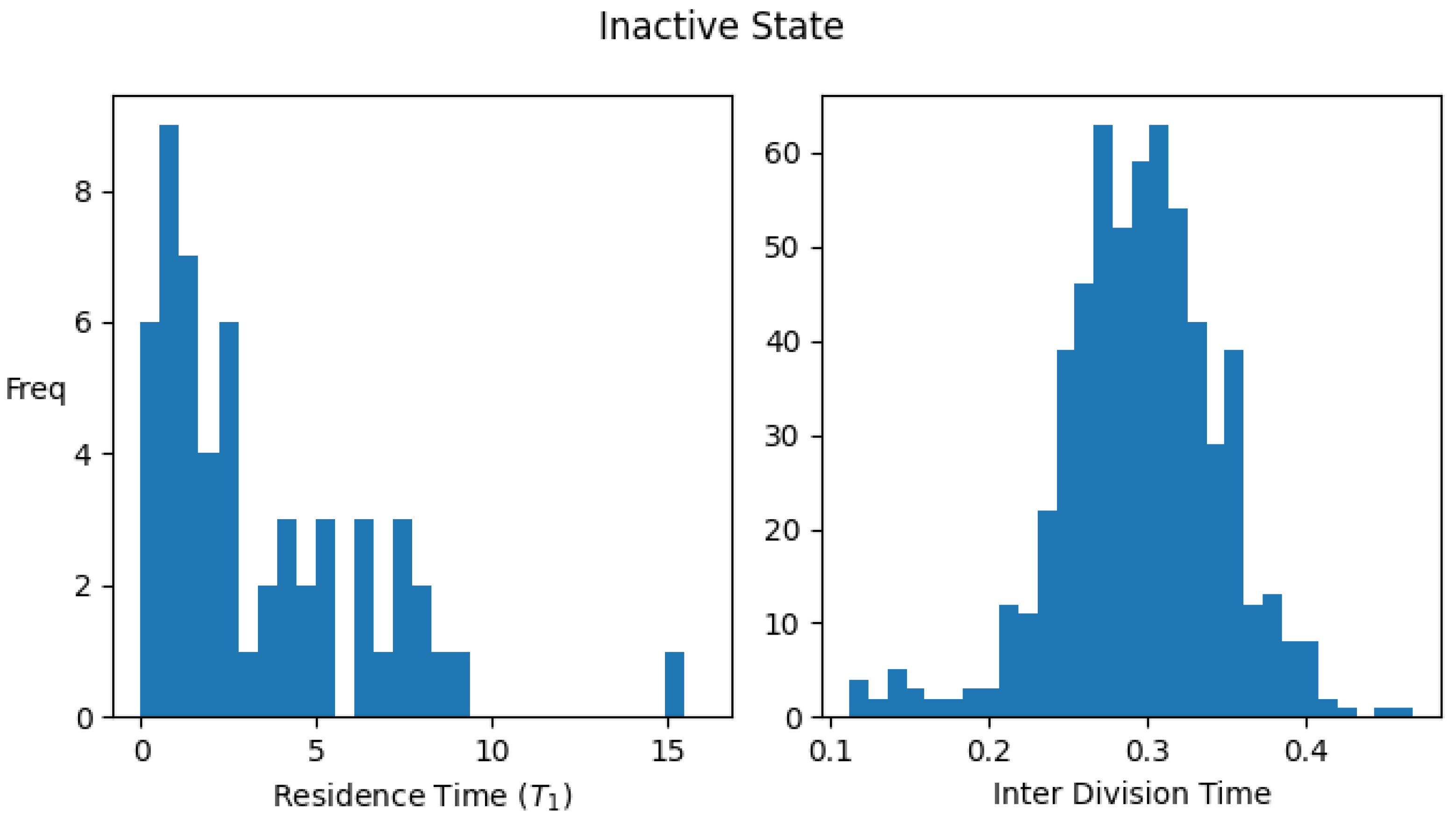
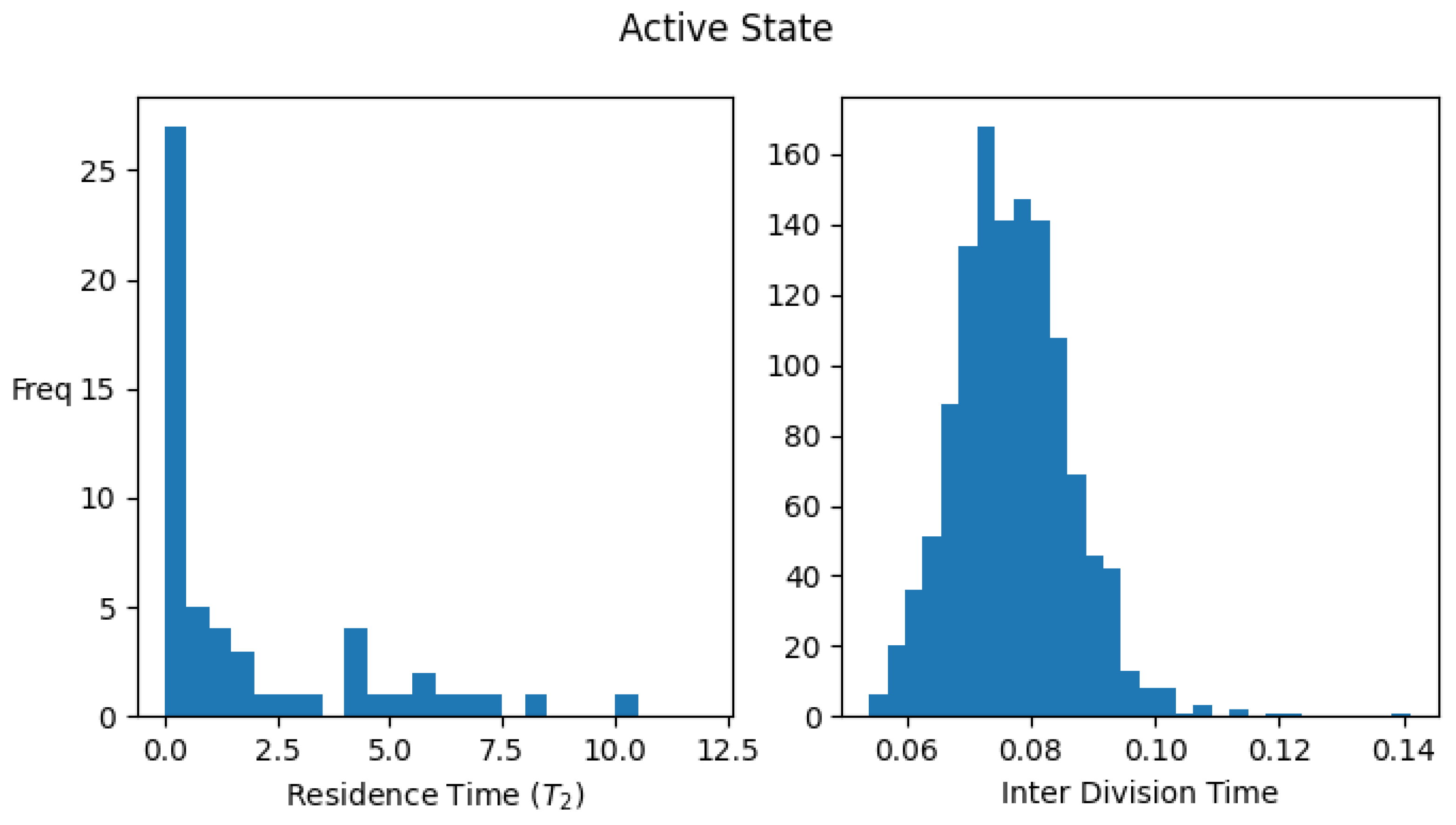
Appendix C. The Steady State Fraction of ACS-Active Protocells (f) in the Protocell Population
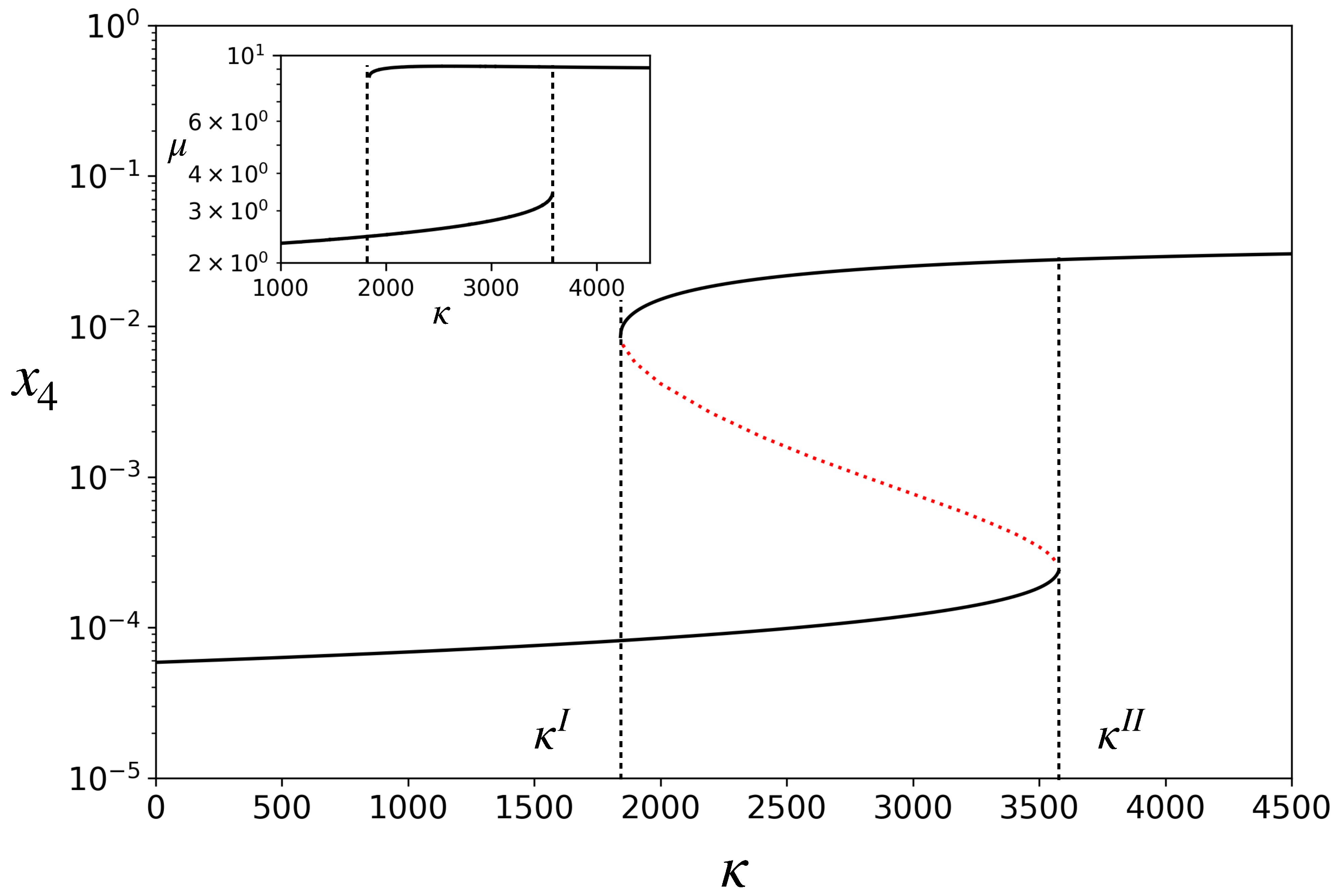
Appendix C.1. Calculation of f for a System with Finite-Ceiling K on the Total Population
Appendix C.2. Condition for Active Protocells to Dominate the Population
References
- Oparin 1924, A.I. Proiskhozhdenie Zhizni (The Origin of Life, Translation by Ann Synge). In The Origin of Life; Bernal, J.D., Ed.; Weidenfeld and Nicolson: London, UK, 1967. [Google Scholar]
- Haldane, J.B.S. Origin of life. Ration. Annu. 1929, 148, 3–10. [Google Scholar]
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef]
- Kauffman, S. Cellular Homeostasis, Epigenesis and Replication in Randomly Aggregated Macromolecular Systems. J. Cybern. 1971, 1, 71–96. [Google Scholar] [CrossRef]
- Rössler, O.E. Ein systemtheoretisches Modell zur Biogenese/A System Theoretic Model of Biogenesis. Z. Für Naturforschung B 1971, 26, 741–746. [Google Scholar] [CrossRef]
- Kauffman, S. The Origins of Order; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Hordijk, W. A History of Autocatalytic Sets. Biol. Theory 2019, 14, 224–246. [Google Scholar] [CrossRef]
- Farmer, J.D.; Kauffman, S.A.; Packard, N.H. Autocatalytic replication of polymers. Phys. D Nonlinear Phenom. 1986, 22, 50–67. [Google Scholar] [CrossRef]
- Bagley, R.; Farmer, J.D.; Fontana, W. Evolution of a metabolism. In Artificial Life II; Langton, C.G., Ed.; Addison-Wesley Publishing Company: Redwood City, CA, USA, 1991; pp. 141–158. [Google Scholar]
- Jain, S.; Krishna, S. Autocatalytic Sets and the Growth of Complexity in an Evolutionary Model. Phys. Rev. Lett. 1998, 81, 5684–5687. [Google Scholar] [CrossRef]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Szathmáry, E. Evolution before genes. Biol. Direct 2012, 7, 1. [Google Scholar] [CrossRef]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.M.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. BioSyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef]
- Ameta, S.; Matsubara, Y.J.; Chakraborty, N.; Krishna, S.; Thutupalli, S. Self-Reproduction and Darwinian Evolution in Autocatalytic Chemical Reaction Systems. Life 2021, 11, 308. [Google Scholar] [CrossRef]
- Gánti, T. Organization of chemical reactions into dividing and metabolizing units: The chemotons. Biosystems 1975, 7, 15–21. [Google Scholar] [CrossRef]
- Segré, D.; Lancet, D.; Kedem, O.; Pilpel, Y. Graded Autocatalysis Replication Domain (GARD): Kinetic Analysis of Self-Replication in Mutually Catalytic Sets. Orig. Life Evol. Biosph. 1998, 28, 501–514. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, S.; Chen, L.; Nilsson, M.; Abe, S. Bridging Nonliving and Living Matter. Artif. Life 2003, 9, 269–316. [Google Scholar] [CrossRef]
- Solé, R.V.; Munteanu, A.; Rodriguez-Caso, C.; Macía, J. Synthetic protocell biology: From reproduction to computation. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1727–1739. [Google Scholar] [CrossRef]
- Mavelli, F.; Ruiz-Mirazo, K. Stochastic simulations of minimal self-reproducing cellular systems. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1789–1802. [Google Scholar] [CrossRef] [PubMed]
- Carletti, T.; Serra, R.; Poli, I.; Villani, M.; Filisetti, A. Sufficient conditions for emergent synchronization in protocell models. J. Theor. Biol. 2008, 254, 741–751. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, A.; Kaneko, K. Reproduction of a Protocell by Replication of a Minority Molecule in a Catalytic Reaction Network. Phys. Rev. Lett. 2010, 105, 268103. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Naylor, J.; Krasnogor, N.; Fellermann, H. Population Dynamics of Autocatalytic Sets in a Compartmentalized Spatial World. Life 2018, 8, 33. [Google Scholar] [CrossRef]
- Luisi, P. The Emergence of Life: From Chemical Origins to Synthetic Biology; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Serra, R.; Villani, M. Modelling Protocells: The Emergent Synchronization of Reproduction and Molecular Replication; Understanding Complex Systems; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Lewontin, R.C. The Units of Selection. Annu. Rev. Ecol. Syst. 1970, 1, 1–18. [Google Scholar] [CrossRef]
- Godfrey-Smith, P. Conditions for Evolution by Natural Selection. J. Philos. 2007, 104, 489–516. [Google Scholar] [CrossRef]
- Segré, D.; Ben-Eli, D.; Lancet, D. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2000, 97, 4112–4117. [Google Scholar] [CrossRef]
- Villani, M.; Filisetti, A.; Graudenzi, A.; Damiani, C.; Carletti, T.; Serra, R. Growth and Division in a Dynamic Protocell Model. Life 2014, 4, 837–864. [Google Scholar] [CrossRef] [PubMed]
- Serra, R.; Villani, M. Sustainable Growth and Synchronization in Protocell Models. Life 2019, 9, 68. [Google Scholar] [CrossRef]
- Togashi, Y.; Kaneko, K. Transitions Induced by the Discreteness of Molecules in a Small Autocatalytic System. Phys. Rev. Lett. 2001, 86, 2459–2462. [Google Scholar] [CrossRef] [PubMed]
- Serra, R.; Filisetti, A.; Villani, M.; Graudenzi, A.; Damiani, C.; Panini, T. A stochastic model of catalytic reaction networks in protocells. Nat. Comput. 2014, 13, 367–377. [Google Scholar] [CrossRef]
- Kahana, A.; Segev, L.; Lancet, D. Attractor dynamics drives self-reproduction in protobiological catalytic networks. Cell Rep. Phys. Sci. 2023, 4, 101384. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef]
- Blokhuis, A.; Lacoste, D.; Nghe, P. Universal motifs and the diversity of autocatalytic systems. Proc. Natl. Acad. Sci. USA 2020, 117, 25230–25236. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Nowak, M.A. Prelife catalysts and replicators. Proc. R. Soc. B Biol. Sci. 2009, 276, 3783–3790. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Higgs, P.G. Origin of Self-Replicating Biopolymers: Autocatalytic Feedback Can Jump-Start the RNA World. J. Mol. Evol. 2009, 69, 541–554. [Google Scholar] [CrossRef]
- Piedrafita, G.; Montero, F.; Morán, F.; Cárdenas, M.L.; Cornish-Bowden, A. A Simple Self-Maintaining Metabolic System: Robustness, Autocatalysis, Bistability. PLoS Comput. Biol. 2010, 6, 1–9. [Google Scholar] [CrossRef]
- Giri, V.; Jain, S. The Origin of Large Molecules in Primordial Autocatalytic Reaction Networks. PLoS ONE 2012, 7, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, Y.J.; Kaneko, K. Optimal size for emergence of self-replicating polymer system. Phys. Rev. E 2016, 93, 032503. [Google Scholar] [CrossRef]
- Martínez-Salas, E.; Martín, J.A.; Vicente, M. Relationship of Escherichia coli density to growth rate and cell age. J. Bacteriol. 1981, 147, 97–100. [Google Scholar] [CrossRef] [PubMed]
- Campbell, A. Synchronization of cell division. Bacteriol. Rev. 1957, 21, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Pandey, P.P.; Singh, H.; Jain, S. Exponential trajectories, cell size fluctuations, and the adder property in bacteria follow from simple chemical dynamics and division control. Phys. Rev. E 2020, 101, 062406. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Lu, T.; Volfson, L.; Tsimring, L.; Hasty, J. Cellular growth and division in the Gillespie algorithm. Syst. Biol. 2004, 1, 121–128. [Google Scholar] [CrossRef]
- Carletti, T.; Filisetti, A. The Stochastic Evolution of a Protocell: The Gillespie Algorithm in a Dynamically Varying Volume. Comput. Math. Methods Med. 2012, 2012, 423627. [Google Scholar] [CrossRef]
- Balaban, N.Q.; Merrin, J.; Chait, R.; Kowalik, L.; Leibler, S. Bacterial Persistence as a Phenotypic Switch. Science 2004, 305, 1622–1625. [Google Scholar] [CrossRef] [PubMed]
- Maity, I.; Wagner, N.; Mukherjee, R.; Dev, D.; Peacock-Lopez, E.; Cohen-Luria, R.; Ashkenasy, G. A chemically fueled non-enzymatic bistable network. Nat. Commun. 2019, 10, 4636. [Google Scholar] [CrossRef] [PubMed]
- Gorlero, M.; Wieczorek, R.; Adamala, K.; Giorgi, A.; Schininà, M.E.; Stano, P.; Luisi, P.L. Ser-His catalyses the formation of peptides and PNAs. FEBS Lett. 2009, 583, 153–156. [Google Scholar] [CrossRef] [PubMed]
- Adamala, K.; Szostak, J.W. Competition between model protocells driven by an encapsulated catalyst. Nat. Chem. 2013, 5, 495–501. [Google Scholar] [CrossRef]
- Lu, H.; Blokhuis, A.; Turk-MacLeod, R.; Karuppusamy, J.; Franconi, A.; Woronoff, G.; Jeancolas, C.; Abrishamkar, A.; Loire, E.; Ferrage, F.; et al. Small-molecule autocatalysis drives compartment growth, competition and reproduction. Nat. Chem. 2023. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.Y.; Jain, S. Multistable Protocells Can Aid the Evolution of Prebiotic Autocatalytic Sets. Life 2023, 13, 2327. https://doi.org/10.3390/life13122327
Singh AY, Jain S. Multistable Protocells Can Aid the Evolution of Prebiotic Autocatalytic Sets. Life. 2023; 13(12):2327. https://doi.org/10.3390/life13122327
Chicago/Turabian StyleSingh, Angad Yuvraj, and Sanjay Jain. 2023. "Multistable Protocells Can Aid the Evolution of Prebiotic Autocatalytic Sets" Life 13, no. 12: 2327. https://doi.org/10.3390/life13122327
APA StyleSingh, A. Y., & Jain, S. (2023). Multistable Protocells Can Aid the Evolution of Prebiotic Autocatalytic Sets. Life, 13(12), 2327. https://doi.org/10.3390/life13122327






