Groups of Symmetries of the Two Classes of Synthetases in the Four-Dimensional Hypercubes of the Extended Code Type II

Marco V. José; Eberto R. Morgado; Juan R. Bobadilla

doi:10.3390/life13102002

,

and

¹

Theoretical Biology Group, Instituto de Investigaciones Biomédicas, Universidad Nacional Autónoma de México, Ciudad de México 04510, Mexico

²

Facultad de Matemática, Física y Computación, Universidad Central “Marta Abreu” de Las Villas, Santa Clara 50100, Cuba

^*

Author to whom correspondence should be addressed.

Life2023, 13(10), 2002;https://doi.org/10.3390/life13102002

This article belongs to the Special Issue The Origins and Evolution of the Genetic Code

Version Notes

Order Reprints

Abstract

Aminoacyl-tRNA synthetases (aaRSs) originated from an ancestral bidirectional gene (mirror symmetry), and through the evolution of the genetic code, the twenty aaRSs exhibit a symmetrical distribution in a 6-dimensional hypercube of the Standard Genetic Code. In this work, we assume a primeval RNY code and the Extended Genetic RNA code type II, which includes codons of the types YNY, YNR, and RNR. Each of the four subsets of codons can be represented in a 4-dimensional hypercube. Altogether, these 4 subcodes constitute the 6-dimensional representation of the SGC. We identify the aaRSs symmetry groups in each of these hypercubes. We show that each of the four hypercubes contains the following sets of symmetries for the two known Classes of synthetases: RNY: dihedral group of order 4; YNY: binary group; YNR: amplified octahedral group; and RNR: binary group. We demonstrate that for each hypercube, the group of symmetries in Class 1 is the same as the group of symmetries in Class 2. The biological implications of these findings are discussed.

Keywords:

aminoacyl-tRNA synthetases; standard genetic code; symmetry groups; origin and evolution of the genetic code; group theory

1. Introduction

Aminoacyl-tRNA synthetases (aaRSs) are key players in the genetic code of all living beings. AaRS attaches an amino acid to the cognate tRNA, and the aminoacyl-tRNA is then used for translation upon binding to mRNA according to the codon-anticodon interaction on the ribosome. The Standard Genetic Code (SGC) is the mapping of 61 codons or triplets to 20 canonical amino acids. There are 20 aaRSs, one for each of the 20 standard amino acids. AaRSs are divided into two mutually exclusive Classes, 1 and 2, based on their structural, functional, and evolutionary relatedness [1,2,3,4,5,6,7,8]. Each aaRS falls into either Class 1 or Class 2, except for lysyl-tRNA synthetase (LysRS), which has a representative in both classes. The correspondence between amino acids and synthetases is one-to-one; that is, it is a bijective, non-degenerate code. For every triplet, or codon, there is a synthetase associated with the amino acid it specifies. In a previous work [9], we outlined the group of symmetries of both Classes of synthetases in each of the 4-dimensional hypercubes of the so-called Extended Code of type II [10,11]. Herein, we rigorously determine the symmetries of aaRSs in the 4 subcodes RNY, YNY, YNR, and RNR. The article is organized as follows: First, a succinct description of the Table of the genetic code, highlighting the subcodes and the Classes of aaRSs, Next, the arithmetization of the SGC is introduced. Second, we provide the basic mathematical concepts needed to understand the derivation of the symmetries of the aaRSs in the 4 subcodes and in the whole SGC. In Appendix E, we present formal mathematical definitions and concepts. Third, we determine the symmetries in each of the four subcodes, where the mathematical derivations are explained in detail in a series of four Appendixes. We prove that the group of symmetries of both classes of synthetases in the hypercube

RNY,

is the dihedral group

D_{4};

the group of symmetries of both Classes of synthetases in the hypercube YNY is the binary group.

(Z_{2}, \oplus_{2});

The group of symmetries of both classes of synthetases in the hypercube YNR is the extended octahedral group

(O_{h}, \circ);

and the group of symmetries of the Classes of synthetases in the hypercube RNR is the group

(\{R, I\} \circ),

isomorphic to the Abelian group

(Z_{2}, \oplus_{2}),

where the reflection

R

is the only symmetry of both Classes 1 and 2, and I is the identity matrix.

Notably, we show that the group of symmetries in Class 1 is the same as the group of symmetries in Class 2 for each of the 4 subcodes. The 4 subcodes constitute the whole SGC, which displays a mirror symmetry of aaRSs. We also analyzed the 5-dimensional hypercubes NNY (all triplets that end in pyrimidine) and NNR (all triplets that end in purine) as obtained by the union of RNY with YNY and YNR with RNR, respectively. We remark that the latter step has been simply ignored in the evolution of the SGC. Finally, we discuss the biological implications of the results, in terms of the evolution of the SGC and in how the code went from managing the information by quadruples of 0’s and 1’s to sextuples of 0’1 and 1’s, where the distributions of aaRSs in the subcodes obeyed symmetrical groups.

1.1. Basic Mathematics of the SGC

The cartesian product

N^{3} = N \times N \times N,

being

N = \{C, U, A, G\}

the set of the four RNA-nucleotides, C = Cytosine, U = Uracil, A = Adenine, and G = Guanine, is the set of the 64 triplets

(X, Y, Z),

where

X, Y, Z \in N .

The standard genetic code (SGC) may be seen as a surjective function

f : N^{3} \to A_{s} = A \cup \{S\},

being

A

the set of the 20 known amino acids, and

S

the stop signal, which means the instruction of finalizing the process of synthesis of a protein.

For every

a \in A,

preimage set

f^{- 1} \{a\} = \{(X, Y, Z) |f (X, Y, Z) = a\},

is the set of triplets, also called codons, that encode the amino acid, or stop signal,

a \in A_{s} .

Since the decipherment of the genetic code [12], it is known that the number of coding triplets for any

a \in A_{s}

is one of the numbers 1, 2, 3, 4, or 6.

In Table 1, we show the table of the genetic code, highlighting the 4 subcodes RNY, YNY, YNR, and RNR, as well as the 2 Classes of synthetases. The table also indicates the subcodes NNY and NNR.

Table 1. Genetic code: Triplets and amino acids in each of the 4-, 5-, and 6-dimensional hypercubes. aaRS Class 1, one red asterisk *; aaRS Class 2, two blue asterisks **. RNY triplets in gold; YNY triplets in black; YNR triplets in blue; RNR triplets in green.

1.2. Arithmetization of the Genetic Code

The bijective correspondence

C \leftrightarrow 00, U \leftrightarrow 01, A \leftrightarrow 10, G \leftrightarrow 11,

between the set

N

and the set

Z_{2}^{2} = Z_{2} \times Z_{2},

being

Z_{2} = \{0, 1\},

induces a bijective correspondence between the set

NNN

of the 64 triplets and the set

Z_{2}^{6}

of all the sextuples of zeros and ones.

Binary operations: In the binary set

Z_{2} = \{0, 1\},

the two binary operations

\oplus_{2}, \otimes_{2},

the so-called addition and product, module 2, are defined. Their Cayley Tables (Table 2) are:

Table 2. The Cayley tables of sum and multiplication of the binary set

Z_{2}

.

They define in the set

Z_{2} = \{0, 1\},

the algebraic structure of a field, or commutative division ring. This is the smallest possible field, with only two elements: the neutral of the addition and the neutral of the product, respectively.

The addition

\oplus_{2}

is extended, component-wise, to the set

Z_{2}^{6},

which, with the natural definition of the product of any scalar

α \in Z_{2}

, by a sextuple

(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}),

becomes a 6-dimensional vector space over the binary field

O = (0, 0, 0, 0) .

This vector space is the so-called 6-dimensional binary hypercube.

The bijection between

Z_{2}^{6}

and the set

NNN

of the 64 triplets, induces in it the algebraic structure of a 6-dimensional vector space, whose canonical basis is the system: (ACC, UCC, CAC, CUC, CCA, CCU). The addition of nucleotides is shown in the following Table 3:

Table 3. Sum module 2 of nucleotide bases.

It is seen that the nucleotide C, cytosine, is the neutral element of the group. This group is isomorphic to the de group,

(Z_{2}, Z_{2}, \oplus),

which is known as the Four Klein Group. It is an Abelian group of order 4, where each element has its own inverse. It is, in the Felix Klein list of finite groups, the fourth and first that is not cyclic.

Mutations in the triplets of the genetic code: A mutation in a triplet

XYZ

is the substitution of any of its components by a nucleotide. For example, GUC→GAC, where U is replaced by A, Obviously, a mutation in a triplet may produce a change in the amino acid it encodes. In our example, valine, which is encoded by GUC, is converted into aspartic acid, encoded by GAC. Algebraically, a mutation in a triplet is performed by the addition of triplets to the canonical basis. In our example, the mutation GUC→GAC is obtained by the addition of the triplet CGC = CAC + CUC.

Classification of the nucleotides

There is a partition

\{Y, R\}

of the set

N,

being

Y = \{C, U\}

pyrimidines and

R = \{A, G\}

purines. The condition of being a pyrimidine or a purine is called the chemical type of a nucleotide.

Transitions and transversion: A mutation is called a transition if it does not change the chemical type, and it is called a transversion if the chemical type is changed. It is easy to notice that transitions are produced by the addition of pyrimidines and transversions by the addition of purines.

The primaeval genetic code. It is assumed that there was, in the RNA world, a primitive, or primaeval, genetic code of only sixteen triplets and eight amino acids: the set

RNY = \{(X, Y, Z)\},

where

X

is a purine,

Y

is any of them, and

Z

is a pyrimidine. It is a 4-dimensional hypercube, a translation of the 4-dimensional subspace

YNY,

derived from

RNY

the transversion in the first nucleotide. By transversions in the first or third component, the hypercubes

YNY, Y N R

and

RNR

are derived from the primaeval

RNY .

These four sets are pairwise disjoint, and they cover the whole set.

NNN .

Hence, the set of sets

{\{- 1, 1\}}^{4}

is a partition of

NNN .

The hypercube

YNY

determines, with the addition

\oplus_{2},

a subgroup of the additive group

(NNN, \oplus_{2})

, the other

RNY, Y N R

and

RNR

its cosets. With the addition and the product of scalars by vectors,

YNY

a 4-dimensional vector subspace

RNY, Y N R

is determined, as

RNR

are its affine subspaces, that is, translations of it, namely:

\begin{array}{l} RNY = Y N Y + \{ACC\} \\ YNR = Y N Y + \{CCA\} \\ RNR = Y N Y + \{ACA\} \end{array}

1.3. The Classes of Synthetases

Synthetases are enzymes that regulate the selection of amino acids that will be charged to tRNA molecules. A little more than 20 aaRSs are found in modern organisms. They are classified into two groups, Class 1 and Class 2, each having three subclasses (a, b, and c) based on similarity in sequences and structures [13,14]. The classification is shown in Table 4:

Table 4. Classes and subclasses of aminoacyl tRNA synthetases.

In general, aaRS consists of a catalytic domain, an anticodon-binding domain, and often an editing domain. Each class harbors class-specific characteristic motifs and structural topology in its catalytic domains [3].

According to the RO model [15,16,17,18] the table of the genetic code can be divided into the sub-codes NAN, NGN, NUN, and NCN. We have also shown that there exists an automorphism F of the cube defined piecewise, which transforms that division into the sub-codes RNR, YNR, RNY, and YNY, respectively, which is precisely our algebraic model [19].

2. Results

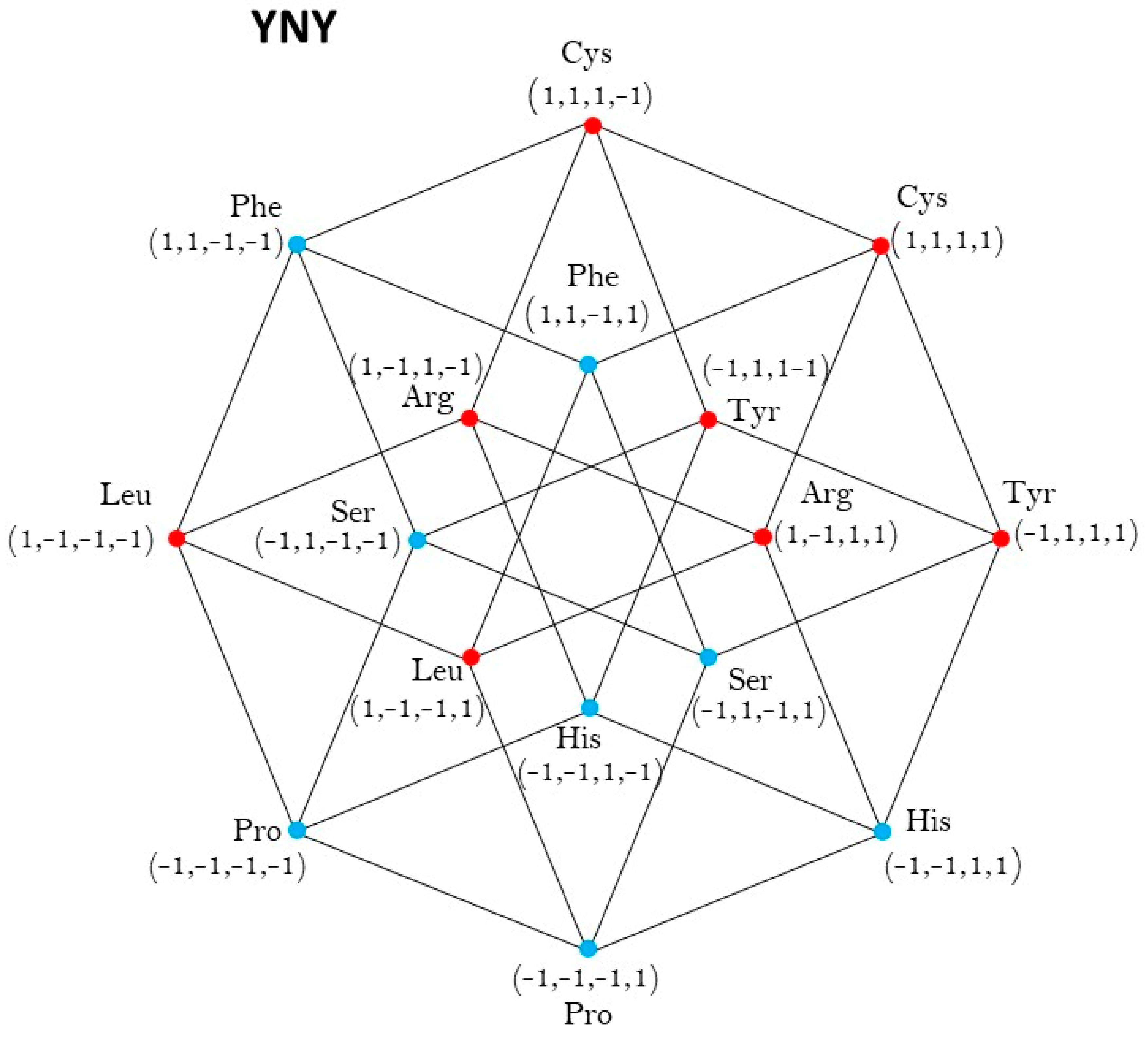
2.1. Group of Symmetries of the Classes of Synthetases in the Hypercube $RNY$

The members of Class 2 are in the vertices of a square, contained in the

{[- 1, 1]}^{4},

convex closure of the set

{\{- 1, 1\}}^{4},

taken by a suitable change of coordinates, rotations, and translations of axis as a representation of the hypercube

RNY .

See Figure 1:

Figure 1. aaRSs distribution in codes

RNY

. Class 1 (red, 2 amino acids) and Class 2 (blue, 6 amino acids). Graphic representation of the subsets

RYY

and

RRY .

The first 4-dimensional hypercube of the

RNY

code:

RNY = R Y Y \cup RYY

.

The quadruplets that belong to Class 2 of synthetases (colored black) are in the set

V_{2}

of vertexes of a square

S,

on one of the 24 faces of the hypercube.

V_{2}

is a subset of the set

{\{- 1, 1\}}^{4}

of the sixteen vertices of the hypercube

RNY .

The set of vertexes of that square is:

V_{2} = \{v_{1}, v_{2}, v_{3}, v_{4}\},

where

v₁ = (1,−1,−1,−1), v₂ = (1,−1,−1,1), v₃ = (1,1,−1,1), v₄ = (1,1,−1,1), black colored.

The center of this square is the point

c_{2} = \frac{v_{1} + v_{2} + v_{3} + v_{4}}{4} = (1, 0, - 1, 0)

.

The members of Class 1 are in the complementary set of vertexes

V_{1},

that is, the other 12 vertexes, red colored, out of the four vertexes of the square

S .

v₁ = (u₁,u₂,u₃,u₄,u₅,u₆,u₇,u₈,u₉,u₁₀,u₁₁,u₁₂) where

u₁ = (−1,−1,−1,−1), u₂ = (−1,−1,−1,1), u₃ = (−1,1,−1,1), u₄ = (−1,1,−1,−1)

u₅ = (−1,−1,−1,−1), u₆ = (−1,−1,1,1), u₇ = (−1,1,1,1), u₈ = (−1,1,1,−1)

u₉ = (1,−1,1,−1), u₁₀ = (1,−1,1,1), u₁₁ = (1,1,1,1), u₁₂ = (1,1,1,−1)

The main result of this Section 2.1 is: We have proved that the group of symmetries of both classes of synthetases, in the hypercube

RNY,

is the dihedral group

D_{4} .

Details are given in Appendix A.

Now we can state the following:

Theorem 1.

The group of symmetries of Class 1 are the same as that of Class 2.

Proof.

As the symmetry of Class 1 is a bijective isometrical function

f

from

RNY

onto itself, it preserves the set

Class 1 \in RNY .

It also preserves the square

S,

that contains the quadruples of Class 2, that is, the vertices of the square

S .

It means that both classes have the same group of symmetries. That is so because the binary set of sets

\{Class 1, Class 2\}

is a partition of the finite set

{\{- 1, 1\}}^{4}

of the 16 vertices of the hypercube

RNY .

Observation: A similar theorem takes place in any of the other hypercubes of Extended code type II and in the whole 6-dimensional hypercubes.

NNN .

In the case of the 4-dimensional YNR, the 5-dimensional NNR, and the whole 6-dimensional,

NNN,

it is valid if, for methodological reasons, we assume the stop signal as it would be an amino acid of Class 1.

2.2. Group of Symmetries of the Classes of Synthetases in the Hypercube $YNY$

In this case, the members of each class are in eight vertexes, out of the sixteen vertexes of the hypercube

YNY

(see Figure 2). They are represented by the sixteen quadruples of the set

{\{- 1, 1\}}^{4}

of ones and minus one, being the hypercube

{[- 1, 1]}^{4},

the convex closure of the set

{\{- 1, 1\}}^{4} .

The set

{[- 1, 1]}^{4}

is taken, by a suitable change of coordinates, rotations, and translations of axis, as a representation of the hypercube

YNY .

The center of this hypercube is the origin of coordinates

O = (0, 0, 0, 0) .

Figure 2. aaRSs distribution in the

YNY

code. Class 1 (red, 4 amino acids) and Class 2 (blue, 4 amino acids). Graphic representation of the subsets

YYY

and

YRY .

Second 4-dimensional hypercube of the Extended RNA-code type 2:

YNY = Y Y Y \cup YRY

.

The set of vertexes of the Class 1, colored in red, is the set:

V_{1} = \{(1, 1, - 1, - 1), (1, 1, - 1, 1), (- 1, 1, - 1, - 1), (- 1, 1, - 1, 1), (- 1, - 1, - 1, - 1), (- 1, - 1, - 1, 1), (- 1, - 1, 1, - 1), (- 1, - 1, 1, 1)\} .

The members of Class 2 are in the complementary set of vertexes, that is, the other eight vertexes, colored black, out of the eight of Class 1.

This is the set:

V_{2} = \{(1, - 1, - 1, - 1), (1, - 1, - 1, 1), (1, - 1, 1, - 1), (1, - 1, 1, 1), (1, 1, 1, - 1), (1, 1, 1, 1), (- 1, 1, 1, - 1), (- 1, 1, 1, 1)\} .

Let us consider the affine transformation:

T_{(1 / 2, 1 / 2, 1 / 2, 1 / 2)} \circ (1 / 2) I,

that converts each −1 into 0 and 1 into itself. It represents a change of coordinates, that converts the hypercube

{[- 1, 1]}^{4}

into its isometric

{[0, 1]}^{4},

whose center is the point (1/2, 1/2, 1/2, 1/2). The sets

V_{1}

and

V_{2}

are now:

V_{1} = \{(1, 1, 0, 0), (1, 1, 0, 1), (0, 1, 0, 0), (0, 1, 0, 1), (0, 0, 0, 0), (0, 0, 0, 1), (0, 0, 1, 0), (0, 0, 1, 1)\} .

V_{2} = \{(1, 0, 0, 0), (1, 0, 0, 1), (1, 0, 1, 0), (1, 0, 1, 1), (1, 1, 1, 0), (1, 1, 1, 1), (0, 1, 1, 0), (0, 1, 1, 1)\} .

Then, the group of symmetries of both Classes of synthetases in the hypercube YNY is the binary group

(Z_{2}, \oplus_{2});

Details can be found in Appendix B.

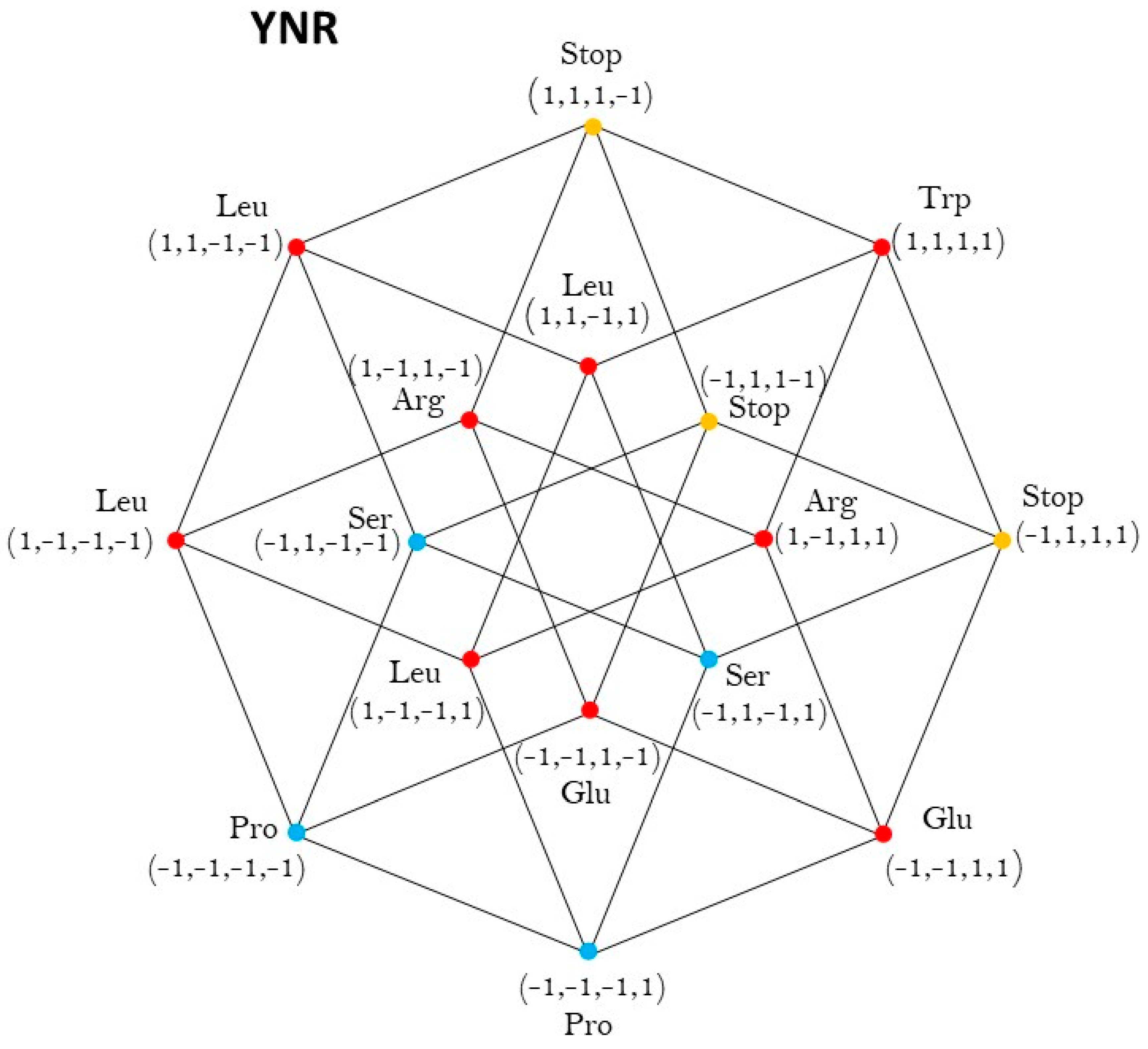
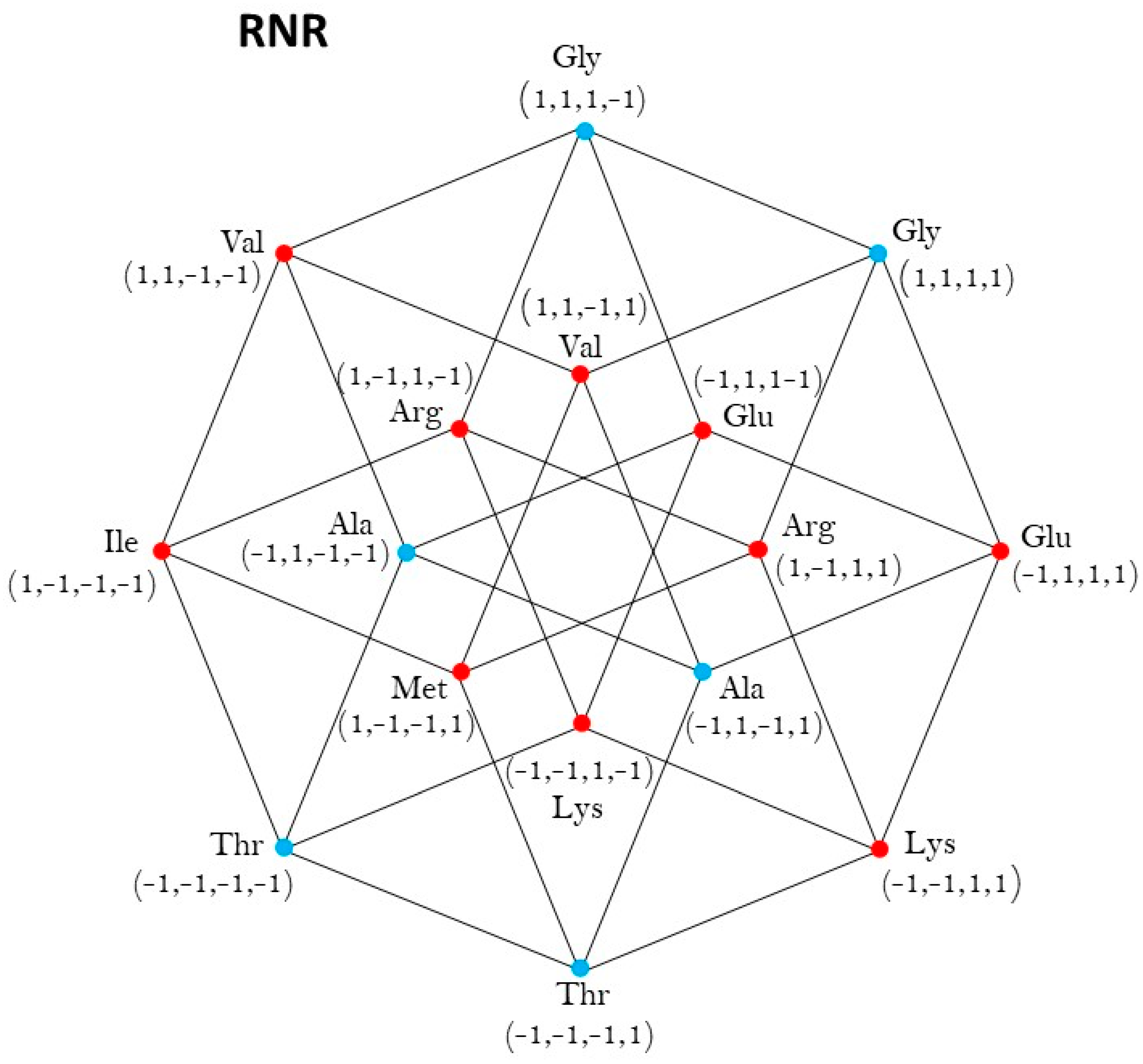
2.3. Group of Symmetries of the Synthetases in the Hypercube $YNR$

In this case there are 3 amino acids of Class 1 and 3 amino acids of Class 2 (Figure 3).

Figure 3. aaRSs distribution in the

YNR

code. Class 1 (red, 3 amino acids) and Class 2 (blue, 3 amino acids and yellow, the stop signals). Graphical representation of the subsets

YYR

and

YRR .

Third 4-dimensional hypercube of the Extended

RNA -

code type II:

YNR = Y Y R \cup YRR

.

For methodological reasons, we have assumed the three stop codons are members of Class 1. In this case, the members of each Class are on the eight vertices of a 3-dimensional cube. Both Classes coincide with the cubes

YNU

and

YNG .

The vertices

YNR

are represented by the sixteen quadruples of the set

{\{- 1, 1\}}^{4}

of ones and minus ones, being the hypercube

{[- 1, 1]}^{4},

the convex closure of the set

{\{- 1, 1\}}^{4},

The set

{[- 1, 1]}^{4}

is taken, by a suitable change of coordinates, rotation, and translations of axis, as a representation of the hypercube

YNR .

The center of this hypercube is the origin of the coordinates.

O = (0, 0, 0, 0) .

The set of vertexes of the cube, associated to Class I, colored in red, is the set:

V_{1} = \{(- 1, - 1, - 1, - 1), (- 1, - 1, - 1, 1), (- 1, 1, - 1, 1), (- 1, 1, - 1, - 1), (1, - 1, - 1, - 1), (1, - 1, - 1, 1), (1, 1, - 1, 1), (1, 1, - 1, - 1)\} .

The center of this cube is the point

- e_{1} = (0, 0, - 1, 0),

and the set of vertexes of the Class 2, colored in black, is the set:

V_{2} = \{(- 1, - 1, 1, - 1), (- 1, - 1, 1, 1), (- 1, 1, 1, 1), (- 1, 1, 1, - 1), (1, - 1, 1, - 1), (1, - 1, 1, 1), (1, 1, 1, 1), (1, 1, 1, - 1)\} .

whose center is the point

e_{3} = (0, 0, 1, 0) .

Then, we have proved that the group of symmetries of both classes of synthetases in the hypercube

YNR

is the extended octahedral group

(O_{h}, \circ) .

See Appendix C.

2.4. Group of Symmetries of the Synthetases in the Hypercube $RNR$

In this case the vertexes of Class 1, colored in red, are the set of six vectors (Figure 4):

V_{1} = \{v_{1} = (- 1, - 1, - 1, - 1), v_{2} = (- 1, - 1, - 1, 1), v_{3} = (- 1, 1, - 1, 1), v_{4} = (- 1, 1, - 1, - 1), v_{5} = (1, 1, 1, - 1), v_{6} = (1, 1, 1, 1)\},

which is the union of the square of vertexes

V_{1}, V_{2}, V_{3}, V_{4}

with the edge of vertexes

V_{5}, V_{6} .

Figure 4. aaRSs distribution in the

RNR

code. Class I (red, 3 amino acids) and Class 2 (blue, 5 amino acids). Graphic representation of the subsets

RYR

and

RRR .

Fourth 4-dimensional hypercube of the Extended RNA-code type II:

RNR = R Y R \cup RRR

.

And the set of vertexes of Class 2, colored in black, are the set of the ten vertexes (Figure 4):

V_{2} = \{\begin{array}{l} u_{1} = (1, - 1, - 1, - 1), u_{2} = (1, - 1, - 1, 1), u_{3} = (1, 1, - 1, 1), u_{4} = (1, 1, - 1, - 1), \\ u_{5} = (- 1, - 1, 1, - 1), u_{6} = (- 1, - 1, 1, 1), u_{7} = (- 1, 1, 1, 1), u_{8} = (- 1, 1, 1, - 1), \\ u_{9} = (1, - 1, 1, - 1), u_{10} = (1, - 1, 1, 1) \end{array}\}

which is he union of the squares of vertexes

u_{1}, u_{2}, u_{3}, u_{4}

and

u_{5}, u_{6}, u_{7}, u_{8}

with the edge of vertexes

u_{9}, u_{10} .

The group of symmetries of the Classes of synthetases in the hypercube RNR is

(\{R, I\} \circ),

isomorphic to the Abelian group

(Z_{2}, \oplus_{2}),

where the reflection

R

is the only symmetry of both Classes 1 and 2, and

I

is the identity matrix. A detailed derivation is given in Appendix D.

2.5. Conclusions

It has been proven that the groups of symmetries of both classes of synthetases in each of the four hypercubes are the following (Table 5):

Table 5. Summary of symmetry groups of aaRSs for each subcode.

3. The Genetic Code in 5 and 6 Dimensions

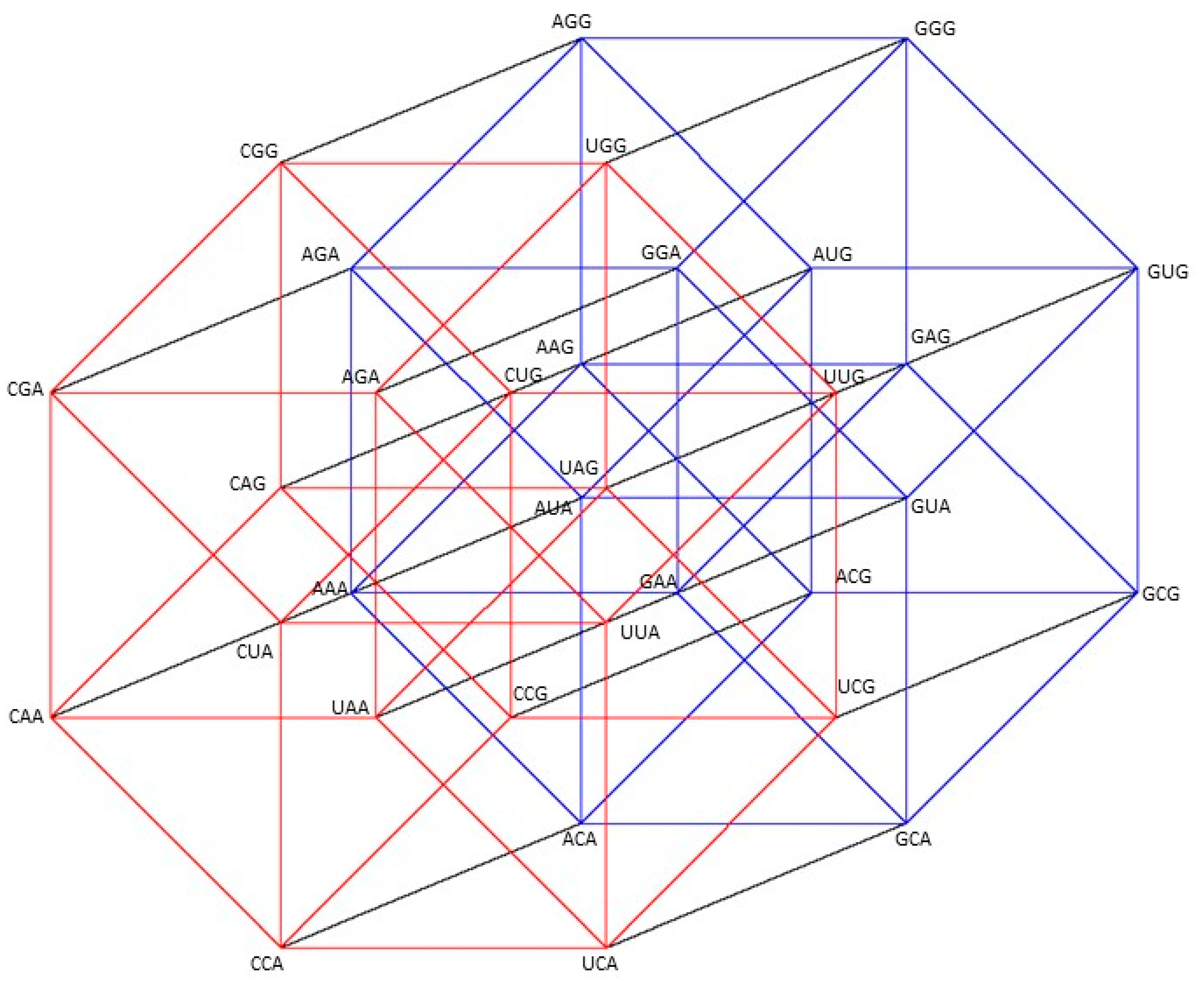
3.1. The Genetic 5-Dimensional Hypercube

The 5-dimensional hypercube

NNY

is the disjoint union of the 4-dimensional hypercubes

YNY

and

RNY .

YNY

is the subspace generated by the four unitary vectors

UCC, C A C, C U C, C C U

and

RNY

is its affine subspace

YNY + \{ACC\} .

Here, the sextuples of zeros and ones have been replaced by triplets of the letters

C, U, A, G,

with the following equivalence:

C = 00, U = 01, A = 10, G = 11 .

Y

is the binary set

\{C, U\},

R

is the also binary

\{A, G\},

and

N

is the set

\{C, U, A, G\} = \{Y, R\} .

The four triplets

UCC, C A C, C U C, C C U

are associated with the canonical unitary vectors

e_{2}, e_{3}, e_{4} . e_{6} .

In Figure 5, they are vectors initiated at the point

CCC,

colored red that generate the hypercube

YNY .

The triplet

ACC,

associated with the unitary vector

e_{1},

also initiated

CCC,

and colored blue, completes the canonical basis of the 5-dimensional hypercube

NNY .

Obviously, the translation associated with converting

YNY

into its affine subspace

RNY,

is colored blue, and the union of both

YNY

with

RNY,

is the 5-dimensional hypercube

NNY .

The vertexes

NNY

are the triplets or codons that end in a pyrimidine.

Figure 5. The five-dimensional hypercube of triplets

NNY,

which is the union of the 4-dimensional hypercubes

RNY

and

YNY .

YNY

is obtained from the

RNY

by means of transversion of each nucleotide at the left of the triplet.

YNY

is the subspace generated by the four unitary vectors CAC, CUC, CCU, UCC, and

RNY

is its affine subspace

YNY + \{ACC\} .

The translation that represents these transversions is situated at an angle of 22.5 degrees with respect to the horizontal axis generated by the canonical vector

UCC .

At this angle, none of the vertices are overlapped.

It can be seen that the translation

T_{e},

associated with the unitary vector

e_{5}

represented by the triplet

CCA,

converts the 5-dimensional subspace

NNY

into its 5-dimensional affine subspace

NNR,

whose triplets are those that end in a purine (Figure A1). It is the disjoint union of the 4-dimensional hypercubes

YNR

and

RNR .

It is clear that the 6-dimensional hypercube

NNN

is the union of the 5-dimensional hypercube

NNY

with its affine subspace, also a 5-dimensional hypercube,

NNR = NNY + \{CCA\} .

Finally, we have, that

NNN

is the disjoint union

RNY \cup YNY \cup YNR \cup RNR

of the four 4-dimensional hypercubes, derived from the primaeval

RNY

by transversions in the first or third nucleotide.

Note: The subspace (hypercube)

YNY,

is the solution set of the homogeneous system of two liner equations

x_{1} = 0, x_{5} = 0,

with the six unknowns

x_{1}, x_{2}, x_{3}, x_{4}, x_{5} . x_{6} .

Its affine subspace (hypercube)

RNY,

is the solution set of the non-homogeneous system

x_{1} = 0, x_{5} = 0,

also of rank 2, with the same six unknowns.

The 5D hypercube

NNR

(see Figure A1) is obtained by the translation

T_{CCA},

that converts every triplet that ends in pyrimidine into another that ends in purine, obtaining the hypercube

NNR .

It represents the disjoint union of the subcodes

YNR

and

RNR .

Note that this hypercube contains the stop codons

UGA, UAG

and

UAA .

The disjoint union of

NNY

them, which

NNR

is equal to the 6D hypercube

NNN

that represents the entire SGC. For the 6D genetic code, each triplet is mapped into sextuples of o’s and 1's. This hypercube is the set

NNN

isomorphic to

Z_{2}^{6},

which is the binary vector space over the binary field

Z_{2},

3.2. The Hypercube of Dimension 6 $NNN$

It is the disjoint union of the 5-dimensional

NNY

space and

NNR .

NNY

is the subspace generated by the five unitary vectors CAC, CUC, CCU, UCC, ACC, and

NNR

its affine subspace

NNY + \{CCA\} .

The vector space

NNN

is generated by the six unitary vectors CAC, CUC, CCU, UCC, ACC, and CCA. They conform to the canonical basis of

Z_{2}^{6} = NNN .

The conversion of the hypercube

{[0, 1]}^{n}

in other whose components are ones and minus ones. Multiplying by 2 all the vectors of the space, the set of the

2^{n}

vertexes is converted into the set

{\{0, 2\}}^{n},

of vertexes of the hypercube

{[0, 2]}^{n}

whose edges have length 2. Next, performing the substraction of the n-tuple

E = (1, 1, \dots, 1)

the hypercube

{\{0, 2\}}^{n}

is converted into

{[- 1, 1]}^{n},

which is another hypercube, also with edges of length 2, whose set of vertexes is the set

{\{- 1, 1\}}^{n}

of the

2^{n}

n-tuples of ones and minus ones.

Note: The n-tuple E is the opposite vertex, in the hypercube

{[0, 1]}^{n},

of the null vector

O = (0, 0 \dots 0) .

The distance between them is the real number

\sqrt{n} = |E|,

which is the diameter of that hypercube. The diameter of a hypercube is the diameter of the hypersphere that circumscribes it-Actually, the hypercube

{[- 1, 1]}^{n}

is the image of

{[0, 1]}^{n}

under the affine transformation

T_{- E} \circ 2 I

being

I

the identical automorphism. The new hypercube has its center at the origin

O = (0, 0 \dots 0) = T_{- E} \circ 2 I (\frac{1}{2}, \frac{1}{2}, \dots, \frac{1}{2})

of coordinates, and its radius is

\sqrt{n}

(Figure 6). The affine transformation

T_{- E} \circ 2 I

converts every 0 into −1 and the number 1 into itself. The linear transformation

E

is a homothetic transformation of ratio 2, which duplicates the size of every n-dimensional Figure. Its only fixed point is the origin O of the coordinates. The affine transformation

T_{- E} \circ 2 I

is also a homothety of ratio 2, whose only fixed point is the point

E .

Figure 6. The 6D representation of the Standard Genetic Code.

4. Discussion

The emergence of the first encoded processing system at the molecular level triggered the phenomenon of life. Coding systems are an inherent property of biological systems. When analyzing the origin and evolution of codes, it becomes clear that the overlap of new codes over earlier/older ones increased the complexity of the previous codes, operating to better adjust and fine-tune them. These interrelated codes started to interact to form a macrocode composed of multiple, overlapping coding systems. Therefore, an information system should be understood as any system capable of implementing the (encoded) connection between natural entities. Life should be understood as an information system that is dependent on a code (open or closed) for its processing but operates independently of other macrocode structures [20].

The distribution of aaRSs in the subcodes is not random. From the putative ancestral symmetric gene to the whole SGC, there is always a symmetrical distribution along the evolution of the genetic code.

Class aaRS I (Class aaRS II) can be converted into Class aaRS II (Class aaRS I) by means of isometric algebraic functions [19]. The fact that enzymes belonging to the two synthetase classes are grossly mirror images of each other (e.g., they approach opposite sides on tRNAs) motivated a phylogenetic analysis that indicated that these proteins were originally coded for by opposite strands of the same gene [15,16,17] in the later stages of the RNA world. This scenario was strengthened experimentally [18]. When the symmetry groups have a structure-preserving one-to-one correspondence, they are considered isomorphic [21].

All synthetases of Class II can be found in the first two 4D-hypercubes (RNY and YNY). Moreover note that Class I and II of aaRSs existed for all 20 amino acids in the Extended RNA codes 1 and 2, before the completion of the SGC. According to the symmetries found in the last step to arrive at the SGC, duplications of Lys, Arg, Glu, Gly, Pro, Leu, Ser, and Phe for the Extended RNA code type 1 and duplications of Gln, Arg, Stop, Trp, Pro, Leu, and Ser for the Extended RNA code type 2 were necessary, resulting in a simpler algebraic structure of the SGC (see Table 1).

The hypercubes consider mono-codonic, di-codonic, three-codonic, tetra-codonic, and hexa-codonic amino acids. In each code, we can observe symmetrical structures in the distribution of aaRSs. We observed that the symmetrical properties of the aaRSs distribution in the SGC are simpler than the ones observed for both Extended RNA codes. In short, there are only 20 aaRSs, one for each amino acid and, respectively, for isoacceptor tRNAs; hence, the aaRS link to the 20 coded amino acids is non-degenerate [3].

Our group-theoretical approach does not explicitly consider how the allocation of aaRSs during the evolution of the genetic code was constrained by the structural and functional properties of the interaction of aaRS, amino acids, and tRNA. Yet it permits us to determine the types of symmetries of aaRSs during the evolution of the SGC. The symmetry groups found in the RNA codes highlight intricacies in the evolution of aaRSs in conjunction with the evolution of the genetic code itself.

We have determined the type of symmetries of aaRSs in each of the 4 subcodes of the Extended RNA code type II. We used the 4D representation of each subcode. The RNY subcode has the dihedral group, with 8 symmetries, 4 rotations, and 4 reflections. The YNY subcode has

Z_{2}

symmetry with 2 symmetries; the YNR subcode exhibits octahedral amplified symmetry with 48 elements, 24 rotations, and 24 roto-reflections (the octahedral classic group contains only 24 rotations); and the RNR subcode displays the symmetry of the binary group

Z_{2} .

In each subcode, symmetrical distributions of both Classes of aaRSs were found. Indeed, we proved that for each hypercube, the group of symmetries of Class 1 is the same as the group of symmetries of Class 2. This theorem holds for both 5D hypercubes and for the whole 6D representation of the SGC. Note that the distribution of aaRSs in both Extended RNA code type I and II and the SGC is symmetrical, which is consistent with the notion that the evolution of the two aaRS classes evolved in parallel [21].

The consideration of stop codons in the determination of the type of symmetry of the subcode is not fortuitous. Mitochondrial codes present variations principally in the codons for the stop signals and unicoded amino acids. The mitochondrial genetic codes of yeast, invertebrates, and vertebrates present variations principally in the codons for the stop signals and unicoded amino acids https://www.ncbi.nlm.nih.gov/Taxonomy/Utils/wprintgc.cgi?chapter=tgencodes#SG24 (accessed on 31 July 2023). The stop codons are tricodonic in SGC, tetracodonic in vertebrate mitochondria, and dicodonic in invertebrate and yeast mitochondria.

In computer science, a byte is an octet of 0’s and 1’s, where each bit represents 0 or 1. Hence, in the genetic code, a byte would correspond to a sextuple of 0’s and 1’s, where each of them represents a triplet or codon of the nucleotides

\{C, U, A, G\} .

The presence of stop codons converts the genetic code into an algorithm that carries out protein synthesis. This means that the whole process of protein synthesis is carried out by a Turing machine, i.e., by a recursive function. Unlike the Turing machine, the genetic code has the additional property of heritability. In a forthcoming work, we will develop these concepts.

Our work can be regarded as a possible pathway for the distribution of the 2 Classes of aaRSs during the formation of the SGC. According to the model of Rodin-Ohno [15,16,17,18], there was a single gene encoding for two synthetases. They proposed a single anti-parallel complementary strand of a single base-paired nucleic acid molecule. The Rodin-Ohno model divides the table of the genetic code into two classes of aminoacyl-tRNA synthetases (Classes 1 and 2), with recognition from the minor or major groove sides of the tRNA acceptor stem [15,16,17,18]. According to the table of the genetic code, the RO model is almost symmetric. It turns out that the RO model is symmetric in a six-dimensional (6D) hypercube (José et al. 2017). Conversely, using the same automorphisms, the RO model can lead to the SGC. Class aaRS 1 (Class aaRS 2) can be converted into Class aaRS II (Class aaRS I) by means of isometric algebraic functions [19]. Notably, the 6D algebraic model is compatible with both the SGC (based upon the primeval RNY code) and the RO model [19]. Our results have implications in areas such as creating synthetic codes, astrobiology, and computer science. In astrobiology, it provides new insights into the quest for life in the Universe. In computer science, it provides a guideline for the establishment of decision criteria to define what should be considered an artificial life.

Author Contributions

Conceptualization, M.V.J. and E.R.M.; methodology, M.V.J. and E.R.M.; formal analysis, E.R.M. and M.V.J.; investigation, M.V.J. and E.R.M.; writing—original draft preparation, E.R.M. and M.V.J.; writing—review and editing, M.V.J. and E.R.M.; visualization, J.R.B.; Figures, J.R.B. All authors have read and agreed to the published version of the manuscript.

Funding

M.V.J. was funded by Dirección General de Asuntos del Personal Académico (DGAPA), the Universidad Nacional Autónoma de México, and UNAM (PAPIIT-IN200823).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Let us consider the orthogonal matrix

A = (\begin{array}{l} 1 0 0 0 \\ 0 0 0 1 \\ 0 0 1 0 \\ 0 - 1 0 0 \end{array}),

which represents a rotation of angle

\frac{3 π}{2}

in the plane

⟨e_{2}, e_{4}⟩ .

It operates over the set of vertexes of the square S in the following way:

A : (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ - 1 \end{array}) \to (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ 1 \end{array}) \to (\begin{array}{l} 1 \\ 1 \\ - 1 \\ 1 \end{array}) \to (\begin{array}{l} 1 \\ 1 \\ - 1 \\ - 1 \end{array}) \to (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ - 1 \end{array})

This means that

A

is an isometry of the square

S .

Let us now consider the orthogonal matrix

B = (\begin{array}{l} 1 0 0 0 \\ 0 1 0 0 \\ 0 0 1 0 \\ 0 0 0 - 1 \end{array}),

which represents a reflection through the 3-dimensional hyperplane

⟨e_{1}, e_{2}, e_{3}⟩,

that reverses the fourth axis

R_{e_{4}}

It operates over the set of vertexes of the square

S

in the following way:

B : (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ - 1 \end{array}) \to (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ 1 \end{array}) \to (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ - 1 \end{array})

B : (\begin{array}{l} 1 \\ 1 \\ - 1 \\ 1 \end{array}) \to (\begin{array}{l} 1 \\ 1 \\ - 1 \\ - 1 \end{array}) \to (\begin{array}{l} 1 \\ 1 \\ - 1 \\ 1 \end{array}) .

This means that

B

is an isometry of the square

S .

It is not difficult to verify the following equalities, that occur between the matrixes

A

and

B :

A^{4} = B^{2} = I; BA = A^{3} B .

They are the defining relations of the dihedral group

D_{4},

the group of all the symmetries of a square.

Now, we will see which is the action of the dihedral group

D_{4},

generated by the matrixes

A

and

B,

over the set

V_{1}

of the 12 quadruplets that represent the synthetases of Class 1.

The action of

A

over the set

V_{1}

is,

A : u_{1} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ - 1 \end{array}) \to u_{2} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ 1 \end{array}) \to u_{3} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ 1 \end{array}) \to u_{4} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ - 1 \end{array}) \to u_{1} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ - 1 \end{array})

u_{5} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ - 1 \end{array}) \to u_{6} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ 1 \end{array}) \to u_{7} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ 1 \end{array}) \to u_{8} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ - 1 \end{array}) \to u_{5} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ - 1 \end{array})

u_{9} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ - 1 \end{array}) \to u_{10} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ 1 \end{array}) \to u_{11} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}) \to u_{12} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ - 1 \end{array}) \to u_{9} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ - 1 \end{array})

It is seen that

A

is an isometry of the set of synthetases of Class 1.

The action of

B

over the set

V_{1}

is:

B : u_{1} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ - 1 \end{array}) \leftrightarrow u_{2} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ 1 \end{array}) u_{3} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ 1 \end{array}) \leftrightarrow u_{4} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ - 1 \end{array})

u_{5} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ - 1 \end{array}) \leftrightarrow u_{6} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ 1 \end{array}) u_{7} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ 1 \end{array}) \leftrightarrow u_{8} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ - 1 \end{array})

u_{9} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ - 1 \end{array}) \leftrightarrow u_{10} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ 1 \end{array}) u_{11} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}) \leftrightarrow u_{12} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ - 1 \end{array})

Note that

B

is an isometry of the set of synthetases of Class 1.

We see that

B

this is a symmetry of the set

V_{1}

vertexes of Class 1 synthetases. As

A

and

B

are symmetries of the Class 1 of synthetases, this result confirms the assertion of Theorem 1, where it was proved that both classes have the same group of symmetries.

Appendix B

The group of symmetries of both classes of synthetases is the binary group

(Z_{2}, \oplus_{2}) .

Let us consider the orthogonal matrix

A = (\begin{array}{l} 0 & 0 & 1 & 0 \\ 0 & - 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}),

which represents a rotation of angle

π = 180^{\circ}

around the vectorial plane generated by the vectors

e_{4}

and

e_{1} + e_{3} + e_{4} = (1, 0, 1, 1),

which fixes the point

e_{4}

changes the sign the vector

e_{2}

and interchanges the vectors

e_{1}

and

e_{3} .

Let us now see what the action of the rotation A over the set

V_{1}

is:

A : v_{1} = (\begin{array}{l} 1 \\ 1 \\ - 1 \\ - 1 \end{array}) \to v_{7} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ - 1 \end{array})

A : v_{2} = (\begin{array}{l} 1 \\ 1 \\ - 1 \\ 1 \end{array}) \to v_{8} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ 1 \end{array})

A : v_{3} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ - 1 \end{array}) \to v_{5} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ - 1 \end{array})

A : v_{4} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ 1 \end{array}) \to v_{6} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ 1 \end{array})

A : v_{5} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ - 1 \end{array}) \to v_{3} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ - 1 \end{array})

A : v_{6} = (\begin{array}{l} - 1 \\ - 1 \\ - 1 \\ 1 \end{array}) \to v_{4} = (\begin{array}{l} - 1 \\ 1 \\ - 1 \\ 1 \end{array})

A : v_{7} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ - 1 \end{array}) \to v_{1} = (\begin{array}{l} 1 \\ 1 \\ - 1 \\ - 1 \end{array})

A : v_{8} = (\begin{array}{l} - 1 \\ - 1 \\ 1 \\ 1 \end{array}) \to v_{2} = (\begin{array}{l} 1 \\ 1 \\ - 1 \\ 1 \end{array})

It is seen that the rotation

A

is a symmetry of the set

V_{1} .

Next, we will see the action of

A

over the set of vertexes

V_{1} :

A : u_{1} = (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ - 1 \end{array}) \to u_{7} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ - 1 \end{array})

A : u_{2} = (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ 1 \end{array}) \to u_{8} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ 1 \end{array})

A : u_{3} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ - 1 \end{array}) \to u_{5} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ - 1 \end{array})

A : u_{4} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ 1 \end{array}) \to u_{6} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array})

A : u_{5} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ - 1 \end{array}) \to u_{3} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ - 1 \end{array})

A : u_{6} = (\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}) \to u_{4} = (\begin{array}{l} 1 \\ - 1 \\ 1 \\ 1 \end{array})

A : u_{7} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ - 1 \end{array}) \to u_{1} = (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ - 1 \end{array})

A : u_{8} = (\begin{array}{l} - 1 \\ 1 \\ 1 \\ 1 \end{array}) \to u_{2} = (\begin{array}{l} 1 \\ - 1 \\ - 1 \\ 1 \end{array})

Notice that rotation

A

is a symmetry of the set

V_{2} .

The rotation

A

of an angle

π = 180^{\circ}

is an element of order two. Then, the group of symmetries of the classes of synthetases in the hypercube

YNY

contains the group generated by the rotation

A,

which is isomorphic to the binary group

(Z_{2}, \oplus_{2}) .

The isometric transformation

A

is the only symmetry of the sets,

V_{1}

and

V_{2}

in the hypercube

YNY .

Then, the group of symmetries of both classes of synthetases is the binary group

(Z_{2}, \oplus_{2}) .

Appendix C

The group of symmetries of classes of synthetases in the hypercube

YNR

is the extended octahedral group

(O_{h}, \circ) .

Let us consider the translation

T_{e 3}

associated to the point

e_{3} = (0, 0, 1, 0) .

Applying it to the set

V_{1}

we obtain:

T_{e 3} (V_{1}) = U_{1} = \{(- 1, - 1, 0, - 1), (- 1, - 1, 0, 1), (- 1, 1, 0, 1), (- 1, 1, 0, - 1), (1, - 1, 0, - 1), (1, - 1, 0, 1), (1, 1, 0, 1), (1, 1, 0, - 1)\},

which is the set of vertexes of another cube, with center in the origin

O = (0, 0, 0, 0)

of coordinates.

Analogously, applying to the set

V_{1}

the translation

T_{- e_{3}}

we obtain:

T_{- e_{3}} (V_{2}) = U_{2} = \{(- 1, - 1, 0, - 1), (- 1, - 1, 0, 1), (- 1, 1, 0, 1) (- 1, 1, 0, - 1), (1, - 1, 0, - 1), (1, - 1, 0, 1), (1, 1, 0, 1), (1, 1, 0, 1)\},

which is the same set

U_{1},

of vertexes of a cube with center in the origin

O = (0, 0, 0, 0)

of coordinates.

Let us now consider the orthogonal matrices:

A = (\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - 1 \end{array}), B = (\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & - 1 \end{array})

C = (\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}), D = (\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & - 1 \end{array})

which represent rotations,

A, B

and

D

of angles

π

radians and

C

of angle

\frac{2 π}{3}

radians. They satisfy the relations:

A^{2} = B^{2} = C^{3} = D^{2} = I,

BA = A B, C A = B C, C B = A B C, D A = B D, D B = A D, D C = A C^{2} D .

that are the defining relations of the octahedral group,

(O, \circ),

which is the group of the rotational symmetries of a cube or regular hexahedron. It is also the group of rotational symmetries of a regular octahedron, which is the dual figure of the regular hexahedron. Adding to the set of rotational matrixes

A, B, C

and

D,

the matrix

R = (\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & - 1 \end{array}),

which represents a reflection through the three-dimensional subspace

X Y Z,

generated by the unitary vectors

e_{1}, e_{2}, e_{3},

that reverses the fourth axis

ℝ e_{4},

the amplified octahedral group

(O_{h}, \circ)

is obtained, where

O_{h} = O \cup (O \circ R) .

We invite the lector to verify that these rotations, and the reflection

R,

are symmetries of the sets

V_{1}

and

V_{2}

of the vertexes of Class 1 and Class 2, respectively.

From this, it follows that the group of symmetries of classes of synthetases in the hypercube

YNR

is the extended octahedral group

(O_{h}, o) .

Appendix D

The reflection

R

is the only symmetry of both Classes 1 and 2.

Now, consider the matrix

R = (\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & - 1 \end{array}),

which represents the same reflection of Section 2.4.

Through the hyperplane

XYZ,

that reverses the axis

ℝ e_{4} .

This reflection changes the sign of the fourth component of each quadruple, and it is easy to notice that it produces the following interchange of vectors in the Class I of synthetases:

v_{1} \leftrightarrow v_{2}, v_{3} \leftrightarrow v_{4}, v_{5} \leftrightarrow v_{6}

Hence,

R

is a symmetry in the Class I of synthetases in the hypercube

RNR .

By Theorem 1, it should also be a symmetry of the set

V_{2}

of vertices in Class 2. However, it is straightforward to verify that it produces the interchange of vectors:

u_{1} \leftrightarrow u_{2}, u_{3} \leftrightarrow u_{4}, u_{5} u_{6}, u_{7} \leftrightarrow u_{8}, u_{9} \leftrightarrow u_{10} .

Then,

R

is also a symmetry of Class 2.

It is not difficult to notice that the reflection

R

is the only symmetry in both Classes 1 and 2. As it is an element of order two, the group

(\{R, I\} \circ),

isomorphic to the Abelian group

(Z_{2}, \oplus_{2})

is, as in the case of Part II, the group of symmetries of the classes of synthetases in the hypercube

RNR .

Appendix E

Mathematical background

The Euclidean n-dimensional

ℝ -

space,

(ℝ^{n}, +, \times),

being

(ℝ, +, \times)

the field of real numbers, has a basis

(e_{1}, e_{2}, \dots, e_{n}),

the so-called canonical basis, where, for each

i \in \{1, 2, \dots n\},

e_{i} = (0, 0, \dots 1, \dots, 0),

with 1 is in the place

i,

and 0 is in the remainders.

A remarkable observation: The n-dimensional vector space

(ℝ^{n}, +, \times)

is a generalization of the ordinary 3-dimensional

ℝ -

space,

(ℝ^{3}, +, \times),

where every triplet

(x_{1}, x_{2}, x_{3})

represents a point

P

of the space, endowed with a system of axis

X, Y

and

Z,

pairwise orthogonal or perpendicular, intercepted in a common point denoted as O and called the origin of coordinates, represented by the triplet (0,0,0). Usually, every point P is identified with the triplet

(x_{1}, x_{2}, x_{3})

that represents it, as if they were the same object. So, the equality

P = (x_{1}, x_{2}, x_{3})

is admitted. The axes are right lines defined as

X = ℝ e_{1} = \{(x_{1}, 0, 0) |x_{1} \in ℝ\},

Y = ℝ e_{2} = \{(0, x_{2}, 0) |x_{2} \in ℝ\}

,

Z = ℝ e_{3} = \{(0, 0, x_{3}) |x_{3} \in ℝ\}

, The addition of two points

P = (x_{1}, x_{2}, x_{3})

and

Q = (y_{1}, y_{2}, y_{3})

is defined as

P + Q = (x_{1} + y_{1}, x_{2} + y_{2}, x_{3} + y_{3}) .

This operation, therefore defined, is associative, has a neutral element,

O,

and for every point

P = (x_{1}, x_{2}, x_{3})

its additive inverse

- P = (- x_{1}, - x_{2}, - x_{3})

exists, such that

P + (- P) = O .

Then, the ordered pair

(ℝ^{3}, +)

is a group. As the addition + is also commutative, it is an Abelian group. The product of a real number

α \in ℝ

by a point

P = (x_{1}, x_{2}, x_{3})

is defined as

α \times P = (α x_{1}, α x_{2}, α x_{3}) .

This external operation of a real number by a point has the following algebraic properties:

$α \times (β \times P) = (α \times β) \times P$ for $α, β \in ℝ, P \in ℝ^{3}$ (Mixed associativity).
$1 \times P = P,$ for every $P \in ℝ^{3}$ (Existence of an external neutral element).
$α \times (P + Q) = α \times P + α \times Q,$ for all $α \in ℝ, P, Q \in ℝ^{3}$ (Distributivity of the product with respect to the addition of points, also called distributivity at the left).
$(α + β) \times P = α \times P + β \times P$ for all $α, β \in ℝ, P \in ℝ^{3}$ (Distributivity of the product with respect to the addition of numbers, also called distributivity at the right.)

The condition of the Abelian group for the addition and the four properties of the external operation completes the structure of a vector space over the field

(ℝ, +, \times)

of the real numbers, in the set

ℝ^{3}

of all the points of the space.

The concept of vector: Given two different points

P, Q \in ℝ^{3}

we call the vector of origin

P

and extreme

Q

to the oriented segment of the right line that joins

P

with

Q .

It is denoted as

\vec{PQ} .

We define the addition of two vectors

\vec{PQ}

and

PR

with common origin P as the vector

\vec{PS}

such that

S = R + Q - P .

If the points

R, Q

and

P

are not collinear, the four points are the vertices of a plane parallelogram. It means that the lines

r (P, Q)

and

r (R, S)

are parallel. If

P = O,

the null point

\{0, 0, 0\},

the function:

f : P \to \vec{PO},

where for

P = O,

\vec{OO} = 0

is defined as a vector whose initial and final points coincide, is a bijective function between the set

ℝ^{3}

of all the triplets or points of the space, and the set

V

of all the vectors with origin

O .

This correspondence induces over the set

V

the operations

+

and

\times

of addition and product of numbers by vectors and

V

is endowed the structure of a vector space over the field

\{ℝ, +, \times\}

of the real numbers.

Euclidean norm

The Euclidean norm, module, or length, of a vector

v = (x_{1}, x_{2}, \dots x_{n})

is defined as

|v| = \sqrt{x_{1}^{2} + x_{2}^{2} + \dots x_{2}^{n}},

the non-negative square root of the sum of the squares of its

n

components.

Main properties of the Euclidean norm

(N1) For every

v, |v| \geq 0,

and it is =0 if, and only if,

v = 0,

the null vector

O = (0, 0, 0 \dots 0)

, (Positivity of the norms for all the non-null vectors)

(N2) For

v \in ℝ^{n}

and

α \in ℝ,

|α \times v| = |α| |v| .

(The norm

|α|,

module, or absolute value, of the real number

α \neq 0

is the positive of the couple

\{α, - α\},

and for

α = 0, |α| = 0 .

From N₂ we have that

|- v| = |v|

for every

v \in ℝ^{n} .

(N3) For all

u, v \in ℝ^{n},

|u + v| \leq |u| + |v|

(Triangle inequality).

The Euclidean Distance between vectors

For

u, v \in ℝ^{n},

the Euclidean distance

d (u, v)

between their extremes, is defined as

|u - v .|

Main properties of the Euclidean distance

(D1) For every

v,

d (v, O) = |v| \geq 0,

being

O

the null vector

O = (0, 0, \dots 0) .

(Positivity of the distance to the origin for all the final points of the non-null vectors).

(D2) For all

u, v \in ℝ^{n},

d (u, v) = d (v, u)

(Symmetry).

(D3) For all

u, v \in ℝ^{n},

d (u, w) \leq d (u, v) + d (v, w)

(Triangle inequality).

With this distance the set

ℝ^{n},

of vectors, is a metric space and the vector space

(ℝ^{n}, +, *)

is called the n-dimensional Euclidean Vector Space.

Linear transformations

A function

f : ℝ^{n} \to ℝ^{n}

is called a linear transformation, or linear endomorphism, if it has the following property:

For all

u, v \in ℝ^{n},

and

α, β \in ℝ,

the equality

f (α * u + β * v) = α * f (u) + β * f (v)

holds.

Note: The latter condition is equivalent to the two conditions:

(L1)

f (u + v) = f (u) + f (v),

for all

u, v \in ℝ^{n} .

(This means that

f

is a group homomorphism of the additive group

(ℝ^{n}, +)

onto itself).

(L2)

f (α \times u) = α \times f (u)

for all

u \in ℝ^{n}

and

α \in ℝ .

If the function

f

is bijective, the linear transformation is a linear isomorphism, and it is called a linear automorphism of the vector space.

Matrix representation of a linear transformation

For every endomorphism

f

there is a unique square matrix

A = (a_{ij}),

such that for every j,

f (e_{j}) = (a_{1 j}, a_{2 j}, \dots a_{nj}),

being

(\begin{array}{l} a_{1 j} \\ a_{2 j} \\ \dots \\ a_{nj} \end{array})

the

j - t h

column of

A .

Then,

A

is a matrix whose columns are the column matrixes associated with the vector images of the canonical unitary vectors. It is called the matrix of

f

with respect to the canonical basis. It will be denoted as

A = [f] .

In the case of an automorphism, the matrix

A

is a non-singular or invertible matrix; hence, its determinant is different from 0.

For every vector

v = (x_{1}, x_{2}, \dots x_{n}) \in ℝ^{n}

the column matrix

[V] = [\begin{array}{l} x_{1} \\ x_{2} \\ . \\ . \\ x_{n} \end{array}]

is taken as the matrix representation of

V .

It is well known that the matrix representation of the image vector

f (V)

is the matrix product

[f] [V] .

Conversely, every square

n \times n

matrix

A

defines an endomorphism

f,

whose matrix representation

[f]

is

A .

Translations

For any vector

u

the translation defined by

u,

is the function

T_{u} : ℝ^{n} \to ℝ^{n},

such that, for all

v,

T_{u} (v) = v + u .

For every

u, T_{u}

is a bijective function that preserves the norm of each vector and the distance between different vectors of the space. Hence, it is an isometry of the Euclidean vector space. For two translations

T_{u}

and

T_{v}

the composition

T_{u} \circ T_{v}

is equal to the translations

T_{u + v} .

The correspondence

u \leftrightarrow T_{u}

between

ℝ^{n}

and the set

T,

of all the translations, is a bijective function, that induces over

T

the structure of a n-dimensional vector space, isomorphic to the Euclidean n-space

(ℝ^{n}, +, \times) .

The concept of affine transformation

An affine transformation is a function that is a composition

T_{u} \circ f

of a linear endomorphism

f,

followed by a translation

T_{u} .

It acts on every vector

v

as

(T_{u} \circ f) (v) = f (v) + u .

The affine transformation

T_{u} \circ f

is bijective if, and only if, its linear part f is an automorphism. The set of all the affine transformations of the vector space

(ℝ^{n}, +, \times)

will be denoted as

A_{ff} (ℝ^{n}) .

The composition

(T_{u} \circ f) \circ (T_{v} \circ g)

of two affine transformations

T_{u} \circ f

and

T_{v} \circ g

acts over a vector

w

in the form:

w \mapsto (T_{u} \circ f) (g (w) + v) = f (g (w) + v) + u = (f \circ g) (w) + f (v) + u = (T_{f (v) + v} \circ (f \circ g)) (w)

Then, the composition is the affine transformation

(T_{f (v) + v} \circ (f \circ g)) .

Hence, we have equality

(T_{u} \circ f) \circ (T_{v} \circ g) = T_{f (v) + v} \circ (f \circ g) .

We see that the composition of two affine transformations is an affine transformation. Then, the composition is an inner operation in the set

A_{ff} (ℝ^{n}) .

As the operation is associative and has a neutral element, the identity function

I,

it is the affine transformation

T_{\circ} \circ I,

the ordered pair

(A_{ff} (ℝ^{n}), \circ)

is a monoid or semigroup with a neutral element.

Matrix representation

The matrix representation of the affine transformation

T_{u} \circ f

is given by the composition

T_{[u]} \circ A,

being

A

the matrix of

f,

which acts over the matrix

[v]

of a vector

v

as

[v] \to A [v] + [u] .

The conjugated of a translation by a linear automorphism

The conjugated

f \circ T_{v} \circ f^{- 1}

acts over any vector

w

as

w \to (f \circ T_{v} \circ f^{- 1}) (w) = f (f^{- 1} (w) + v) = w + f (v) = T_{_{} (v)} (w) .

Then

f \circ T_{v} \circ f^{- 1} = T_{f (v)} .

The latter means that the group of translations

(T, \circ)

is a normal subgroup of the group

(A (ℝ^{n}), \circ)

being

A (ℝ^{n}) = T \circ Aut (ℝ^{n})

the set of all the invertible affine transformations, and

(Aut (ℝ^{n}), \circ)

the group of all the linear automorphisms of the space

(ℝ^{n}, +, \times) .

The group

(A (ℝ^{n}), \circ),

that is called the affine group of the space

(ℝ^{n}, +, \times) .

is a subgroup of the group of all the bijective transformation of the set

ℝ^{n} .

It contains as a normal subgroup, the group

(T, \circ)

of all the translations. In fact, it is the semidirect product of the group

(T, \circ)

with the group

(Aut (ℝ^{n}), \circ)

of all the linear automorphisms. (A group

(G, *)

is semidirect product of its subgroups

(K, *)

and

(H, *)

if

G = K * H

and

(K, *)

is a normal subgroup of

(G, *)) .

The semidirect product will be denoted as

(K ⊲ H, *) .

Then,

(A_{ff} (ℝ^{n}), \circ) = (T ⊲ Aut (ℝ^{n}), \circ) .

The affine group

(A (ℝ^{n}), \circ)

is the group of invertible elements of the monoid

(A_{ff} (ℝ^{n}), \circ) .

The n-dimensional binary hypercube

The binary vector space

(Z_{2}^{n}, \oplus_{2}, *),

vector space over the binary field

(Z_{2}, \oplus_{2}, \oplus_{2}),

is also called the n-dimensional binary hypercube. Its set of vertexes coincides with the set

{\{0, 1\}}^{n}

of the

2^{n}

n-tuples of zeros and ones. This set is a subset of the set

Z^{n}

of all the n-tuples of the whole numbers. The set

Z^{n}

determines the Abelian group

(Z^{n}, +),

subgroup of the additive group

(ℝ^{n}, +)

of the n-dimensional Euclidean n-space

(ℝ^{n}, +, \times) .

The n-dimensional hypercube, whose vertexes are the elements of the set

{\{0, 1\}}^{n}

is defined as the convex closure

{[0, 1]}^{n}

of the set

{\{0, 1\}}^{n} .

Here,

[0, 1]

denotes the closed interval of the real numbers between 0 and 1. The convex closure of a set is the minimal convex set that contains it.

A convex set is a set

C \subseteq ℝ^{n}

that, for two different elements

a

and

b

of

C,

the segment that joins them is entirely contained in

C .

The center of the hypercube

{[0, 1]}^{n}

is the point

C = \{\frac{1}{2} . \frac{1}{2}, \dots, \frac{1}{2}\}

obtained by the sum of the

2^{n}

vertexes divided by

2^{n} .

That is so because, for every place i of the n-tuples,

2^{n - 1}

of them, that is, the half, have 1, and the other

2^{n - 1}

have 0. Then, for each place i, the quotient is

\frac{2^{n - 1}}{2^{n}} = \frac{1}{2} .

A metric in the hypercube

Z_{2}^{6}

The Hamming Norm and the Hamming Distance defined in

Z_{2}^{6}

The Hamming Norm: The Hamming Norm

|u|

of a sextuple

u = (a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6})

is defined as the sum

{\sum a}_{i}

in

Z,

of its components

a_{i} .

It is equal to the number of ones it has. The only unitary sextuples, that is, of norm equal to 1, are those of the canonical basis.

The Hamming distance. The Hamming distance

H (u, v)

between two sextuples

u = (a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6})

and

v = (b_{1}, b_{2}, b_{3}, b_{4}, b_{5}, b_{6})

is defined as the norm

|u \oplus_{2} v|

of their module 2 addition. It is equal to the number of places where they differ. It is not difficult to prove that the distance so defined is actually a distance, in the mathematical sense. It means that it has the following properties:

(D1) For all

u, v,

H (u, v) \geq 0,

H (u, v) = 0 \Leftrightarrow u = v

(positivity of the distance between two different sextuples

u

and

v

), and nullity of the distance of a sextuple to itself.

(D2) For all

u, v,

H (u, v) = H (v, u)

(Symmetry)

(D3) For

u, v, w,

H (u, w) \leq H (u, v) + H (v, w)

(Triangle inequality)

The edges of the hypercube

Two vertexes are said to be neighbors if the distance between them is equal to 1. It means that they differ in only one of their n components. An edge of the hypercube is the segment that joins two neighbor vertexes. This segment has a length equal to 1. For every vertex there are

n

neighbors. As there are

2^{n}

vertexes, the product

2^{n} \times n

would count the total number of edges. However, as every edge has two extremes, it would be counted twice. Then, the actual number of edges is equal to

\frac{2^{n} \times n}{2} = 2^{n - 1} \times n

. For example, in the ordinary cube, 3-dimensional, the number of edges is

2^{2} \times 3 = 12

and, in the 4-dimensional, this number is

2^{3} \times 4 = 32 .

The faces of the hypercube

Any face of the hypercube is a plane square determined by four vertexes and four edges in such a way that two edges with a common vertex are orthogonal. If we fix

n - 2

components with values zeros and ones and leave free the other two, the four obtained vertexes are the vertexes of a plane square, then of the face of the hypercube. It may be conducted in

(\begin{array}{l} n \\ n - 2 \end{array}) \times 2^{n - 2}

ways. Hence, the total number of different faces is precisely

(\begin{array}{l} n \\ n - 2 \end{array}) \times 2^{n - 2} .

(The combinatorial number

(\begin{array}{l} n \\ k \end{array}) = \frac{n!}{k! (n - k)!}

is the number of subsets of k elements of a set of n elements, being

0 \leq k \leq n

). For example, for n = 3 the number of faces is

3 \times 2 = 6,

and for n = 4 it is 6 × 4 = 24.

Figure A1. Five-dimensional hypercube NNR. The five-dimensional hypercube of triplets

NNR,

which is the union of the 4-dimensional hypercubes

YNR

and

RNR

.

References

Ibba, M.; Söll, D. Aminoacyl-tRNA synthesis. Annu. Rev. Biochem. 2000, 69, 617–650. [Google Scholar] [CrossRef] [PubMed]
Cusack, S.; Berthet-Colominas, C.; Hartlein, M.; Nassar, N.; Leberman, R. A second class of synthetase structure revealed by X-ray analysis of Escherichia coli seryl-tRNA synthetase at 2.5 A. Nature 1990, 347, 249–255. [Google Scholar] [CrossRef] [PubMed]
Eriani, G.; Delarue, M.; Poch, O.; Gangloff, J.; Moras, D. Partition of aminoacyl-tRNA synthetases into two classes based on mutually exclusive sets of sequence motifs. Nature 1990, 347, 203–206. [Google Scholar] [CrossRef] [PubMed]
Burbaum, J.J.; Schimmel, P. Structural relationships and the classification of aminoacyl-tRNA synthetases. J. Biol. Chem. 1991, 266, 16965–16968. [Google Scholar] [CrossRef] [PubMed]
Ribas de Pouplana, L.; Schimmel, P. Two classes of tRNA synthetases suggested by sterically compatible dockings on tRNA acceptor stem. Cell 2001, 104, 191–193. [Google Scholar] [CrossRef] [PubMed]
Ribas De Pouplana, L.; Schimmel, P. Operational RNA code for amino acids in relation to genetic code in evolution. J. Biol. Chem. 2001, 276, 6881–6884. [Google Scholar] [CrossRef] [PubMed]
Ribas de Pouplana, L. The evolution of aminoacyl-tRNA synthetases: From dawn to LUCA. In Enzymes; Academic Press: Cambridge, MA, USA, 2020; Volume 48, pp. 11–37. [Google Scholar]
Schimmel, P.; Giege, R.; Moras, D.; Yokoyama, S. An operational RNA code for amino acids and possible relation to genetic code. Proc. Nat. Acad. Sci. USA 1993, 90, 8763–8768. [Google Scholar] [CrossRef] [PubMed]
José, M.V.; Bobadilla, J.R.; Zamudio, G.S.; Farías, S.T. Symmetrical Distributions of Aminoacyl-tRNA Synthetases during the evolution of the Genetic Code. Theory Biosci. 2023, 142, 211–219. [Google Scholar] [CrossRef]
José, M.V.; Morgado, E.R.; Govezensky, T. An extended RNA code and its relationship to the standard genetic code: An algebraic and geometrical approach. Bull. Math. Biol. 2007, 69, 215–243. [Google Scholar] [CrossRef] [PubMed]
José, M.V.; Morgado, E.R.; Govezensky, T. Genetic Hotels for the Standard Genetic Code: Evolutionary Analysis based upon Novel Three-dimensional Algebraic Models. Bull. Math. Biol. 2011, 73, 1443–1476. [Google Scholar] [CrossRef] [PubMed]
Nirenberg, M.W.; Matthaei, J.H. The dependance of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Natl. Acad. Sci. USA 1961, 47, 1588–1602. [Google Scholar] [CrossRef] [PubMed]
Nagel, G.M.; Doolittle, R.F. Phylogenetic analysis of the aminoacyl-tRNA synthetases. J. Mol. Evol. 1995, 40, 487–498. [Google Scholar] [CrossRef] [PubMed]
Woese, C.R.; Olsen, G.J.; Ibba, M.; Söll, D. Aminoacyl-tRNA synthetases, the genetic code, and the evolutionary process. Microbiol. Mol. Biol. Rev. 2000, 64, 202–236. [Google Scholar] [CrossRef] [PubMed]
Rodin, S.N.; Ohno, S. Two types of aminoacyl-tRNA synthetases originally encoded by complementary strands of the same nucleic acid. Orig. Life Evol. Biosph. 1995, 25, 565–589. [Google Scholar] [CrossRef] [PubMed]
Rodin, S.N.; Rodin, A.S. On the origin of the genetic code: Signatures of its primordial complementarity in tRNAs and Aminoacyl tRNA synthetases. Heredity 2008, 100, 341–355. [Google Scholar] [CrossRef] [PubMed]
Rodin, A.S.; Rodin, S.N.; Carter, C.W. On primordial sense–antisense coding. J. Mol. Evol. 2009, 69, 555–567. [Google Scholar] [CrossRef] [PubMed]
Carter, C.W., Jr.; Li, L.; Weinreb, V.; Collier, M.; Gonzalez-Rivera, K.; Jimenez-Rodriguez, M.; Erdogan, O.; Kuhlman, B.; Ambroggio, X.; Williams, T.; et al. The Rodin-Ohno hypothesis that two enzyme superfamilies descended from one ancestral gene: An unlikely scenario for the origins of translation that will not be dismissed. Biol. Direct. 2014, 9, 11. [Google Scholar] [CrossRef] [PubMed]
José, M.V.; Zamudio, G.S.; Morgado, E.R. A unified model of the standard genetic code. R Soc. Open Sci. 2017, 4, 160908. [Google Scholar] [CrossRef] [PubMed]
de Farias, S.T.; Prosdocimi, F.; Caponi, G. Organic Codes: A Unifying Concept for Life. Acta Biotheor. 2021, 69, 769–782. [Google Scholar] [CrossRef] [PubMed]
Sethuraman, B.A. Rings, Fields, and Vector Spaces; Springer: New York, NY, USA, 1997. [Google Scholar]

Figure 1. aaRSs distribution in codes

RNY

. Class 1 (red, 2 amino acids) and Class 2 (blue, 6 amino acids). Graphic representation of the subsets

RYY

and

RRY .

The first 4-dimensional hypercube of the

RNY

code:

RNY = R Y Y \cup RYY

.

Figure 2. aaRSs distribution in the

YNY

code. Class 1 (red, 4 amino acids) and Class 2 (blue, 4 amino acids). Graphic representation of the subsets

YYY

and

YRY .

Second 4-dimensional hypercube of the Extended RNA-code type 2:

YNY = Y Y Y \cup YRY

.

Figure 3. aaRSs distribution in the

YNR

code. Class 1 (red, 3 amino acids) and Class 2 (blue, 3 amino acids and yellow, the stop signals). Graphical representation of the subsets

YYR

and

YRR .

Third 4-dimensional hypercube of the Extended

RNA -

code type II:

YNR = Y Y R \cup YRR

.

Figure 4. aaRSs distribution in the

RNR

code. Class I (red, 3 amino acids) and Class 2 (blue, 5 amino acids). Graphic representation of the subsets

RYR

and

RRR .

Fourth 4-dimensional hypercube of the Extended RNA-code type II:

RNR = R Y R \cup RRR

.

Figure 5. The five-dimensional hypercube of triplets

NNY,

which is the union of the 4-dimensional hypercubes

RNY

and

YNY .

YNY

is obtained from the

RNY

by means of transversion of each nucleotide at the left of the triplet.

YNY

is the subspace generated by the four unitary vectors CAC, CUC, CCU, UCC, and

RNY

is its affine subspace

YNY + \{ACC\} .

The translation that represents these transversions is situated at an angle of 22.5 degrees with respect to the horizontal axis generated by the canonical vector

UCC .

At this angle, none of the vertices are overlapped.

Figure 6. The 6D representation of the Standard Genetic Code.

Table 1. Genetic code: Triplets and amino acids in each of the 4-, 5-, and 6-dimensional hypercubes. aaRS Class 1, one red asterisk *; aaRS Class 2, two blue asterisks **. RNY triplets in gold; YNY triplets in black; YNR triplets in blue; RNR triplets in green.

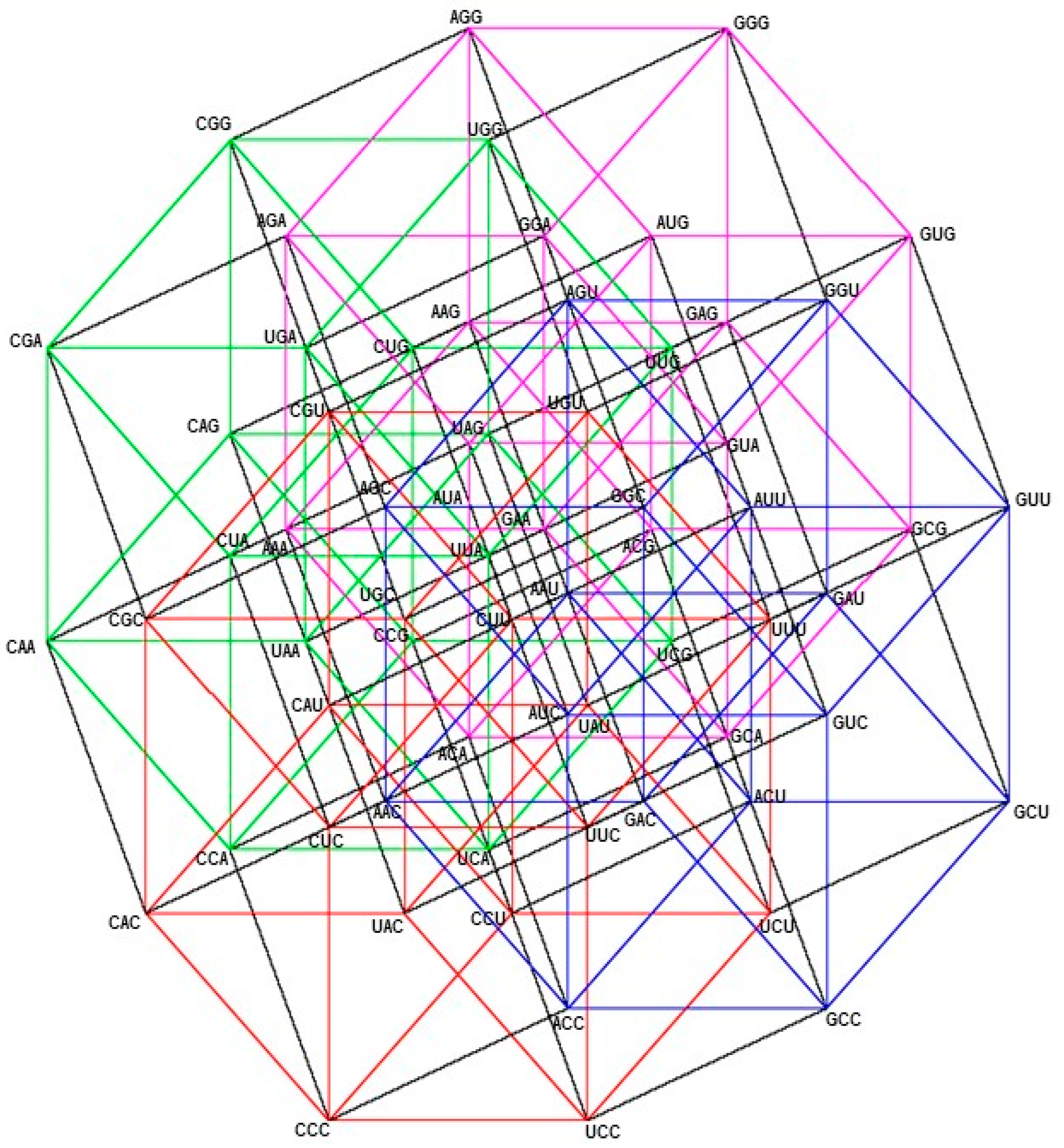
5D NNY		5D NNR
4D RNY	4D YNY	4D YNR	4D RNR
ACC	CCC	CCA	ACA
Thr **	Pro **	Pro **	Thr **
ACU	CCU	CCG	ACG
Thr **	Pro **	Pro **	Thr **
AUC	CUC	CUA	AUA
Ile *	Leu *	Leu *	Ile *
AUU	CUU	CUG	AUG
Ile *	Leu *	Leu *	Met *
AAC	CAC	CAA	AAA
Asn **	His **	Gln *	Lys *
AAU	CAU	CAG	AAG
Asn **	His **	Gln *	Lys *
AGC	CGC	CGA	AGA
Ser **	Arg *	Arg *	Arg *
AGU	CGU	CGG	AGG
Ser **	Arg *	Arg *	Arg *
GCC	UCC	UCA	GCA
Ala **	Ser **	Ser **	Ala **
GCU	UCU	UCG	GCG
Ala **	Ser **	Ser **	Ala **
GUC	UUC	UUA	GUA
Val *	Phe **	Leu *	Val *
GUU	UUU	UUG	GUG
Val *	Phe **	Leu *	Val *
GAC	UAC	UAA	GAA
Asp **	Tyr *	Stop	Glu *
GAU	UAU	UAG	GAG
Asp **	Tyr *	Stop	Glu *
GGC	UGC	UGA	GGA
Gly **	Cys *	Stop	Gly **
GGU	UGU	UGG	GGG
Gly **	Cys *	Trp *	Gly **

Table 2. The Cayley tables of sum and multiplication of the binary set

Z_{2}

.

Table 2. The Cayley tables of sum and multiplication of the binary set

Z_{2}

.

$\oplus_{2}$	0	1
0	0	1
1	1	0

$\oplus_{2}$	0	1
0	0	0
1	0	1

Table 3. Sum module 2 of nucleotide bases.

$\oplus_{2}$	C	U	A	G
C	C	U	A	G
U	U	U	G	A
A	A	G	C	U
G	G	A	U	C

Table 4. Classes and subclasses of aminoacyl tRNA synthetases.

Class 1	Class 2
1a{MetRS, ValRS, LeuRS, IleRS, CysRS, ArgRS	2a{SerRS, ThrRS, AlaRS, GlyRS-α2, ProRS, HisRS
1b{GluRS, GlnRS, LysRS	2b{AspRS, AsnRS, LysRS
1c{TyrRS, TrpRS	2c{PheRS, GlyRS-α2β2, SepRS, PylRS

Table 5. Summary of symmetry groups of aaRSs for each subcode.

Hypercube	Group of Symmetries
RNY	$D_{4}$
YNY	ℤ₂
YNR	O_h
RNR	ℤ₂

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Groups of Symmetries of the Two Classes of Synthetases in the Four-Dimensional Hypercubes of the Extended Code Type II

Abstract

1. Introduction

1.1. Basic Mathematics of the SGC

1.2. Arithmetization of the Genetic Code

1.3. The Classes of Synthetases

2. Results

2.1. Group of Symmetries of the Classes of Synthetases in the Hypercube $RNY$

2.2. Group of Symmetries of the Classes of Synthetases in the Hypercube $YNY$

2.3. Group of Symmetries of the Synthetases in the Hypercube $YNR$

2.4. Group of Symmetries of the Synthetases in the Hypercube $RNR$

2.5. Conclusions

3. The Genetic Code in 5 and 6 Dimensions

3.1. The Genetic 5-Dimensional Hypercube

3.2. The Hypercube of Dimension 6 $NNN$

4. Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Appendix A

Appendix B

Appendix C

Appendix D

Appendix E

References

Article Metrics

Citations

Article Access Statistics

Groups of Symmetries of the Two Classes of Synthetases in the Four-Dimensional Hypercubes of the Extended Code Type II

Abstract

1. Introduction

1.1. Basic Mathematics of the SGC

1.2. Arithmetization of the Genetic Code

1.3. The Classes of Synthetases

2. Results

2.1. Group of Symmetries of the Classes of Synthetases in the Hypercube RNY

2.2. Group of Symmetries of the Classes of Synthetases in the Hypercube YNY

2.3. Group of Symmetries of the Synthetases in the Hypercube YNR

2.4. Group of Symmetries of the Synthetases in the Hypercube RNR

2.5. Conclusions

3. The Genetic Code in 5 and 6 Dimensions

3.1. The Genetic 5-Dimensional Hypercube

3.2. The Hypercube of Dimension 6 NNN

4. Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Appendix A

Appendix B

Appendix C

Appendix D

Appendix E

References

Article Metrics

Citations

Article Access Statistics

2.1. Group of Symmetries of the Classes of Synthetases in the Hypercube $RNY$

2.2. Group of Symmetries of the Classes of Synthetases in the Hypercube $YNY$

2.3. Group of Symmetries of the Synthetases in the Hypercube $YNR$

2.4. Group of Symmetries of the Synthetases in the Hypercube $RNR$

3.2. The Hypercube of Dimension 6 $NNN$