Towards the First Principles in Biology and Cancer: New Vistas in Computational Systems Biology of Cancer
Abstract
1. Introduction
1.1. The Fundamental Laws of Biology/Life
1.2. Non-Equilibrium Thermodynamics in Biology (NET)
2. Brief on Systems Biology (SB) and Discovery of Emergent Properties
3. Brief on Metabolic Models and Metabolic Engineering
4. Multiscale Simulation
5. Cancer Concepts
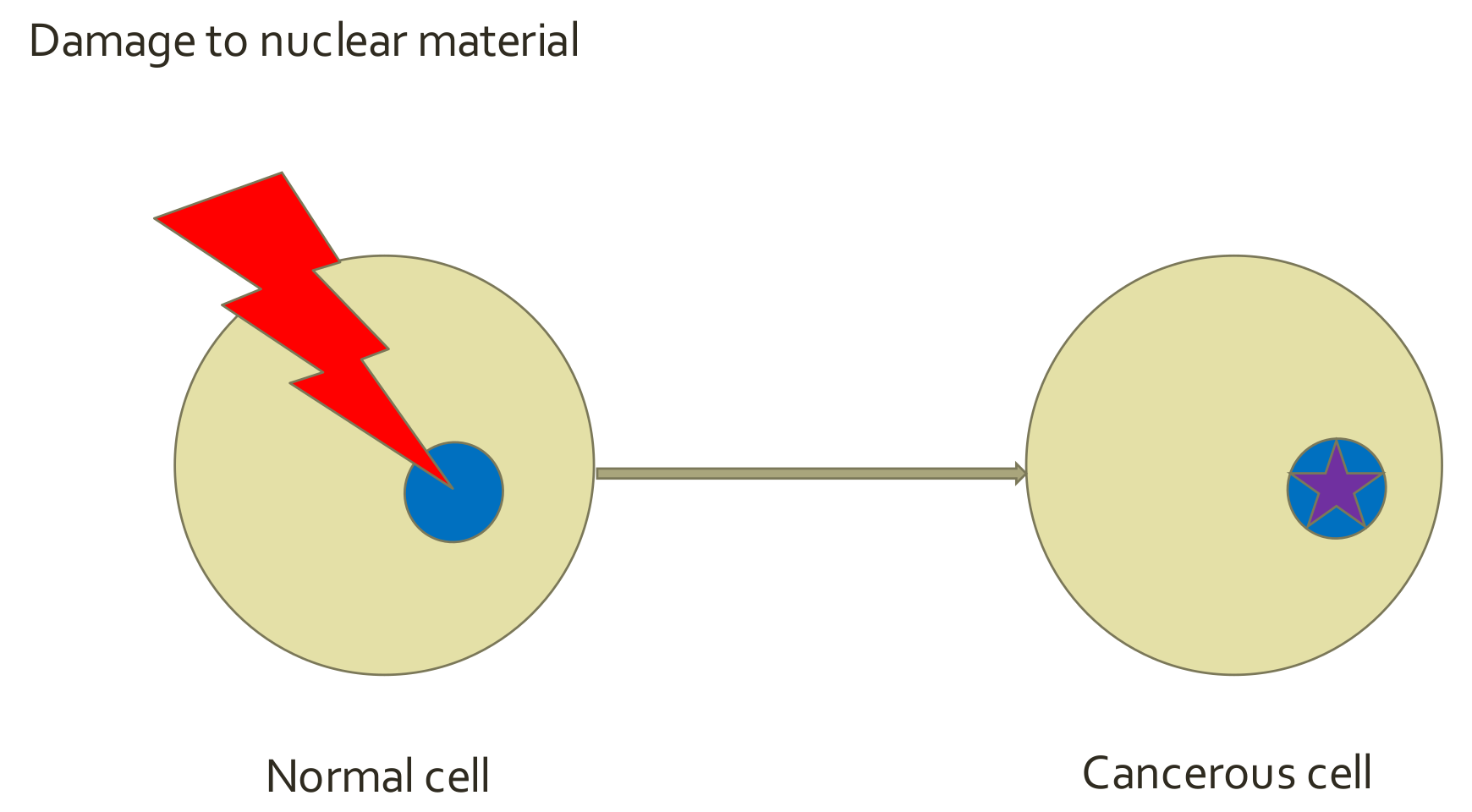
5.1. Cancer Hallmarks—SMT Paradigm
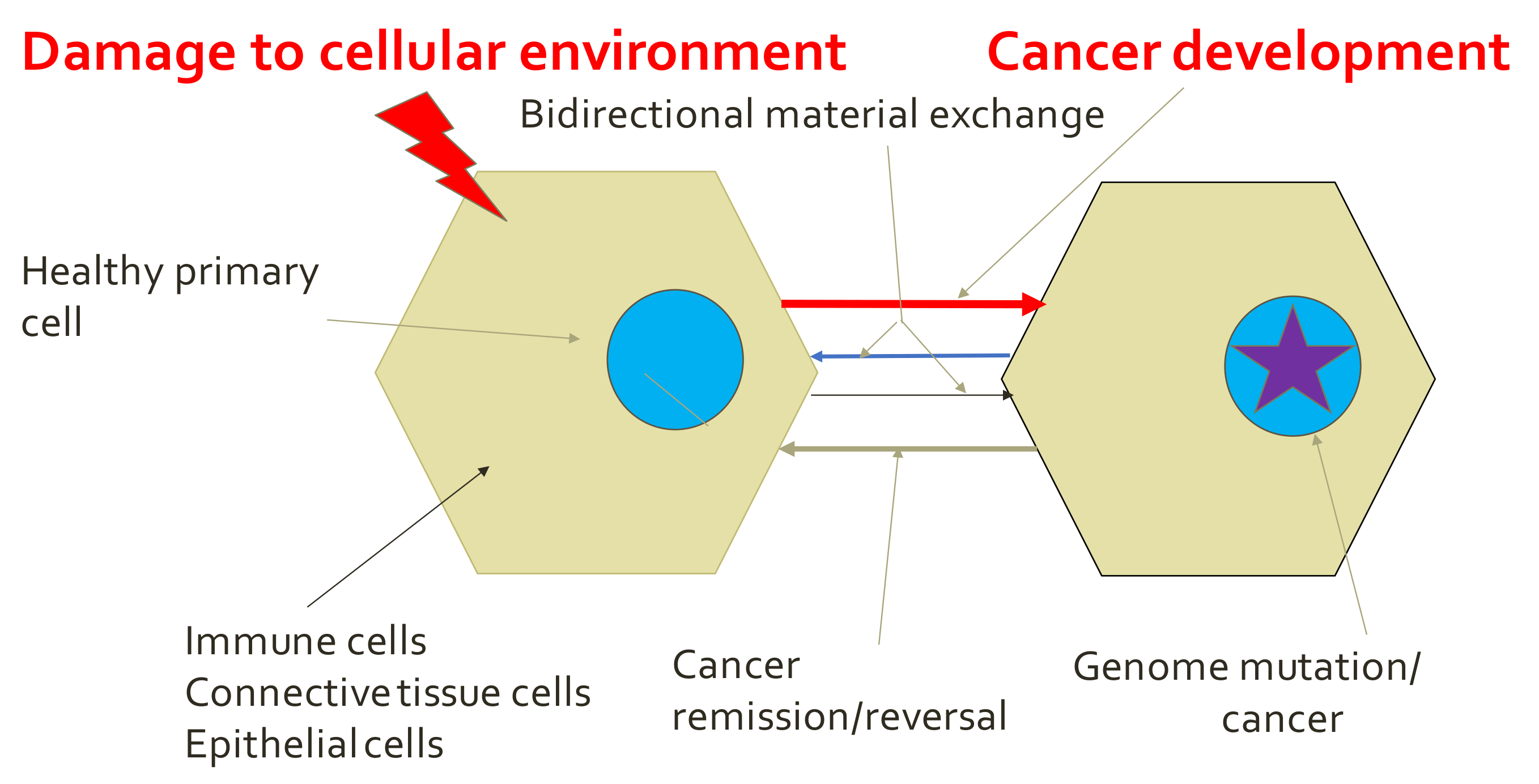
5.2. Tissue Organization Field Theory of Cancer (TOFT) and Related Concepts
5.3. Epistemological Origin of the Cancer Paradigm
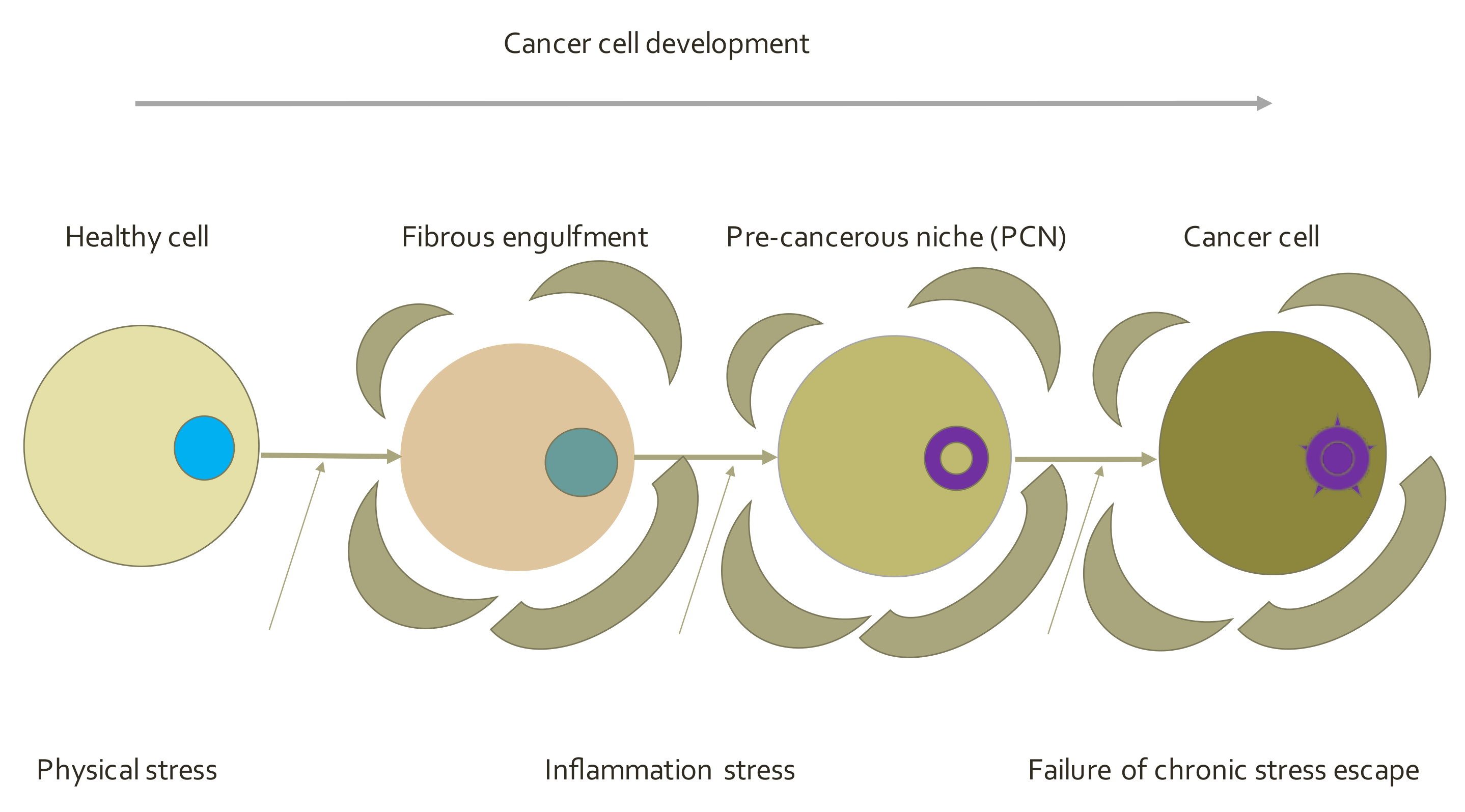
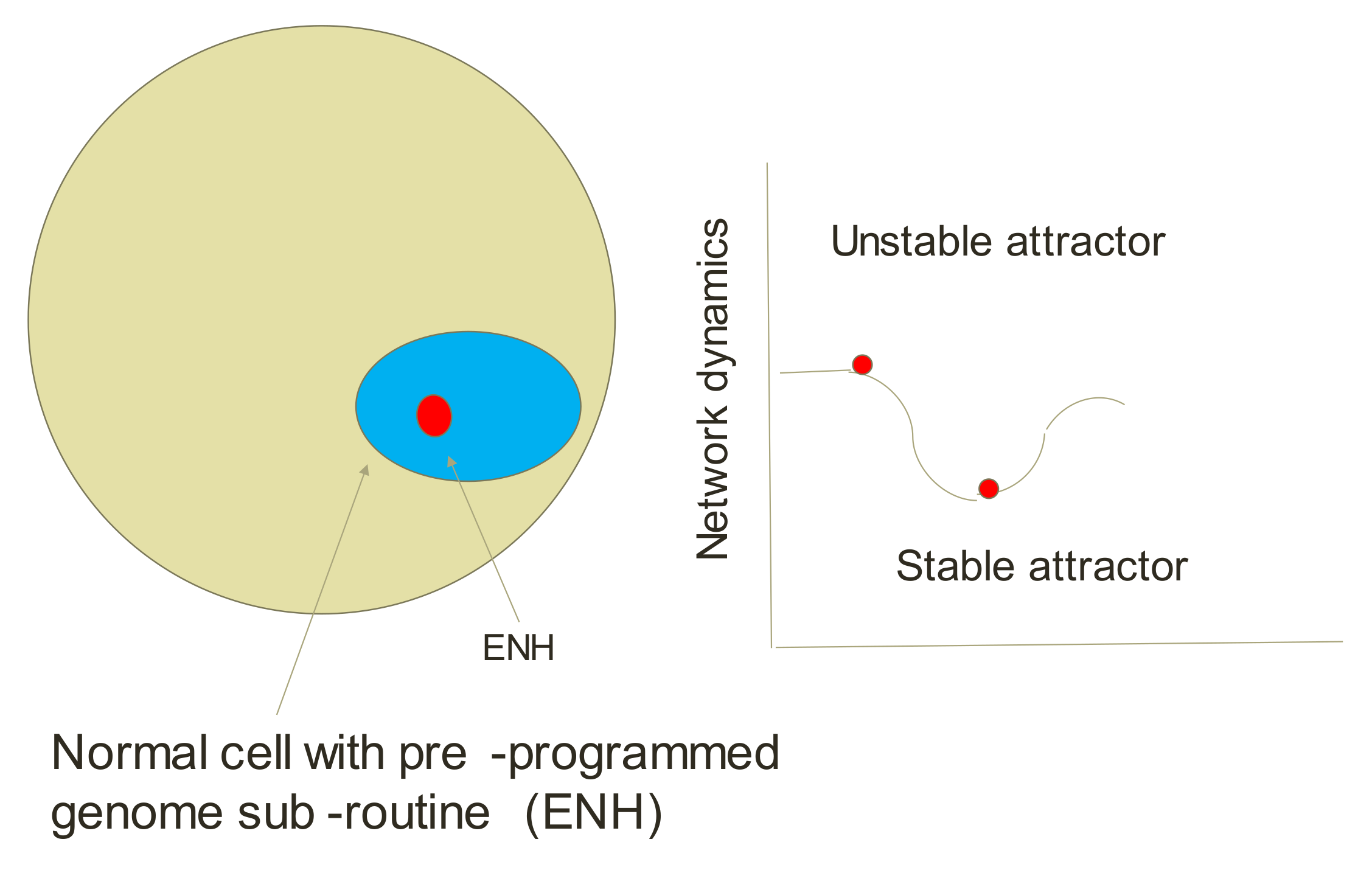
5.4. Endogenous Network Hypothesis (ENH)—Far-from Equilibrium Dynamical Systems Theory of Cancer
6. Future in Cancer Genomics by the ENH Method
7. Conclusions—An Ultimate Goal—Comprehensive E-Pharma Cancer Model
Funding
Acknowledgments
Conflicts of Interest
References
- Newman, T. Cancer as a System Hard Lessons from Physics and a Way Forward. In The Search for Progress and a New Theory Framework in Cancer Research; Bertolaso, M., Strauss, B., Eds.; The MIT Press: Cambridge, MA, USA, 2021; pp. 41–60. [Google Scholar]
- Rasmussen, S.; Baas, N.A.; Mayer, B.; Nilsson, M. M Defense of the ansatz for dynamical hierarchies. Artif. Life 2001, 7, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Andersen, P. Available online: http://www.bozemanscience.com (accessed on 15 July 2013).
- Prokop, A. Systems analysis and synthesis in biology and biotechnology. Int. J. General. Syst. 1982, 8, 7–31. [Google Scholar] [CrossRef]
- Prokop, A.; Michelson, S. Systems Biology in Biotech and Pharma; A New Paradigm for Innovation, an industrial report; Biopharm Knowledge Publishing: Sussex, UK, 2009. [Google Scholar]
- Bauer, E. Theoretical Biology; Académiai Kiadó: Budapest, Hungary, 1935/1967; pp. 19, 51. Available online: https://digital.zbmed.de/zbmed/urn/urn:nbn:de:hbz:38m:1-8460 (accessed on 30 November 2021). (In Hungarian)
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes (1955/1961/1967), 3rd ed.; Wiley Interscience: New York, NY, USA, 1967. [Google Scholar]
- Steely, A.J.E.; Macklen, P. Fractal variability: An emergent property of complex dissipative systems. Chaos 2012, 22, 013108. [Google Scholar]
- Davies PCW Emergent biological principles and computational properties of the Universe. Complexity 2004, 10, 11–15. [CrossRef]
- Schrödinger, E. What is Life? Cambridge University Press: New York, NY, USA, 1967; 96p. [Google Scholar]
- Nottale, L.; Auffray, C. Scale relativity theory and integrative systems biology: 2. Macroscopic quantum-type mechanics. Prog. Biophys. Mol. Biol. 2008, 97, 115–157. [Google Scholar] [CrossRef] [PubMed]
- Auffray, C.; Nottale, L. Scale relativity theory and integrative systems biology: 1. Founding principles and scale laws. Prog. Biophys. Mol. Biol. 2008, 97, 79–114. [Google Scholar] [CrossRef]
- Nottale, L. Fractals and the quantum theory of spacetime. Int. J. Mod. Phys. A 1989, 4, 5047–5117. [Google Scholar] [CrossRef]
- Wikswo, J.P.; Prokop, A.; Baudenbacher, F.J.; Cliffel, D.; Csukas, B.; Velkovsky, M. The engineering challenges of BioMEMS: The integration of microfluidics, micro- and nano-devices, models, and external control for systems biology. IEE Proc. Nanobiotechnol. 2006, 153, 81–101. [Google Scholar] [CrossRef] [PubMed]
- Bizzarri, M. Editor: Systems Biology; Springer: New York, NY, USA, 2018. [Google Scholar]
- Prokop, A.; Csukas, B. (Eds.) Systems Biology. In Integrative Biology and Simulation Tools; Springer: Berlin/Heidelberg, Germany, 2013; Volume 553, p. 105. [Google Scholar]
- Hornberg, J.J.; Bruggeman, F.J.; Westerhoff, H.V.; Lankelma, J. Cancer: A systems biology disease. BioSystems 2006, 83, 81–90. [Google Scholar] [CrossRef]
- Kreeger, P.K.; Lauffenburger, D.A. Cancer systems biology: A network modeling perspective. Carcinogenesis 2010, 31, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Korsunsky, I.; McGovern, K.; LaGatta, T.; Olde Loohuis, L.; Grosso-Applewhite, T.; Griffeth, N.; Mishra, B. Systems biology of cancer: A Challenging expedition for clinical and quantitative biologists. Front. Bioeng. Biotechnol. 2014, 2, 27. [Google Scholar] [CrossRef][Green Version]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally? AIChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- Buchanan, M. Nexus: The Groundbreaking Science of Networks, 2nd ed.; Norton WW: New York, NY, USA, 2006. [Google Scholar]
- Fromm, J. Ten questions about emergence. arXiv 2008, arXiv:nlin/0509049. [Google Scholar]
- Richards, K.; Bithell, M.; Dove, M.; Hodge, R. Discrete-element modelling: Methods and applications in the environmental sciences. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2004, 362, 1797–1816. [Google Scholar] [CrossRef]
- Ahmed, E.; Hashish, A.H. On modelling the immune system as a complex system. J. Theor. Biol. 2006, 124, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Barberis, M.; Klipp, E.; Vanoni, M.; Alberghina, L. Cell size at S phase initiation: An emergent property of the G1/S network. PLoS Comput. Biol. 2007, 3, e64. [Google Scholar] [CrossRef] [PubMed]
- Varma, A.; Palsson, B.O. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wildtype Escherichia coli W3110. Appl. Environ. Microbiol. 1994, 60, 2465–2473. [Google Scholar] [CrossRef] [PubMed]
- Papin, J.A.; Palsson, B.Ø. Topological analysis of mass-balanced signaling networks: A framework to obtain network properties including crosstalk. J. Theor. Biol. 2004, 227, 283–297. [Google Scholar] [CrossRef] [PubMed]
- Dada, J.O.; Mendes, M. Multi-scale modelling and simulation in systems biology. Integr. Biol. 2011, 3, 86–96. [Google Scholar] [CrossRef]
- Wolkenhauer, O.; Auffray, C.; Brass, O.; Clairambault, J.; Deutsch, A.; Drasdo, D.; Gervasio, F.; Preziosi, L.; Maini, P.; Marciniak-Czochra, A.; et al. Enabling multiscale modeling in systems medicine. Genome Med. 2014, 3, 21. [Google Scholar] [CrossRef]
- Eissing, T.; Kuepfer, L.; Becker, C.; Block, M.; Coboeken, K.; Gaub, T.; Goerlitz, L.; Jaeger, J.; Loosen, R.; Ludewig, B.; et al. A com-putational systems biology software platform for multiscale modeling and simulation: Integrating whole-body physiology, disease biology, and molecular reaction networks. Front. Physiol. 2011, 2, 4. [Google Scholar] [CrossRef]
- Chevalier, M.W.; El-Samad, H. A rigorous framework for multiscale simulation of stochastic cellular networks. J. Chem. Phys. 2009, 131, 05410. [Google Scholar] [CrossRef]
- Pérez-Velázquez, J.; Gevertz, J.L.; Karolak, A.; Rejniak, K.A. Microenvironmental Niches and Sanctuaries: A Route to Acquired Resistance. In Systems Biology of Tumor Microenvironment; Rejniak, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 936. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer. Cell 2000, 100, 5760. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2001, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Sonnenschein, C.; Soto, A.M.; Rangarajan, A.; Kulkarni, P. Competing views on cancer. J. Biosci. 2014, 39, 281–302. [Google Scholar] [CrossRef] [PubMed]
- Smythies, J. Intercellular signaling in cancer-the SMT and TOFT hypotheses, exosomes, telocytes and metastases: Is the messenger in the message? J. Cancer 2005, 6, 604–609. [Google Scholar] [CrossRef] [PubMed]
- Macklin, P.; Lowengrub, J. Nonlinear simulation of the effect of microenvironment on tumor growth. J. Theor. Biol. 2007, 245, 677–704. [Google Scholar] [CrossRef][Green Version]
- Valcz, G.; Buzás, E.; Szállási, Z.; Kalmár, A.; Krenács, T.; Tulassay, Z.; Igaz, P.; Molnár, B. Perspective: Bidirectional exosomal transport between cancer stem cells and their fibroblast-rich microenvironment during metastasis formation. Breast Cancer 2018, 164, 18. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Huang, B.; Hanasch, S.M.; Onuchica, J.N.; Ben-Jacoba, E. Modeling putative therapeutic implications of exosome exchange between tumor and immune cells. Proc. Natl. Acad. Sci. USA 2014, 111, E4165–E4174. [Google Scholar] [CrossRef] [PubMed]
- Brűcher, B.L.D.M.; Jamall, I.S. Epistemology of the origin of cancer: A new paradigm. BMC Cancer 2014, 14, 331. [Google Scholar] [CrossRef]
- Bishop, R.C. Metaphysical and epistemological issues in complex systems. In Handbook of the Philosophy of Science; Philosophy of complex systems; Hooker, C., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 10, pp. 119–151. [Google Scholar]
- Brücher, B.L.D.M.; Jamall, I.S. Cell-Cell communication in tumor microenvironment, carcinogenesis and anticancer treatment. Cell. Physiol. Biochem. 2014, 34, 213–243. [Google Scholar] [CrossRef]
- Brücher, B.L.D.M.; Li, Y.; Schnabel, P.; Daumer, M.; Wallace, T.J.; Kube, R.; Zilberstein, B.; Steele, S.; Voskuil, J.L.; Jamall, I.S. Genomics, microRNA, epigenetics, and proteomics for future diagnosis, treatment and monitoring response in upper GI cancers. Clin. Transl. Med. 2016, 5, 13. [Google Scholar] [CrossRef]
- Brücher, B.L.; Lyman, G.; van Hillegersberg, R.; Pollock, R.E.; Lordick, F.; Yang, H.K.; Ushijima, T.; Yeoh, K.G.; Skricka, T.; Polkowski, W.; et al. Imagine a world without cancer. BMC Cancer 2014, 14, 186. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jamall, I.S. Somatic mutation theory—Why it’s wrong for most cancers. Cell. Physiol. Biochem. 2016, 38, 1663–1680. [Google Scholar]
- Gao, J.; Li, S.; Xu, Q.; Zhang, X.; Huang, M.; Dai, X.; Liu, L. Exosomes promote pre-metastatic niche formation in gastric cancers. Front. Oncol. 2021, 11, 652378. [Google Scholar] [CrossRef] [PubMed]
- Ao, P.; Kwon, C.; Qian, H. On the existence of potential landscape in the evolution of complex systems. Complexity 2001, 12, 19–27. [Google Scholar] [CrossRef]
- Ao, P.; Galas, D.; Hood, L.; Zhu, X. Cancer as robust intrinsic state of endogenous molecular-cellular network shaped by evolution. Med. Hypothesis 2008, 70, 678–684. [Google Scholar] [CrossRef]
- Wright, S. The roles of mutation, inbreeding, crossbreeding, and selection in evolution. In Proceedings of the Sixth International Congress of Genetics, Ithaca, NY, USA, 24–31 August 1932; Volume 1, pp. 356–366. [Google Scholar]
- Waddington, C.H. The Strategy of the Genes; George Allen & Unwin: London, UK, 1957. [Google Scholar]
- Pe’er, D.; Hacohen, N. Principles and strategies for developing network models in cancer. Cell 2011, 144, 864–873. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Yuan, R.; Zhu, X.; Ao, P. Endogenous molecular-cellular network cancer theory: A systems biology approach. In Systems Biology, Methods in Molecular Biology; Bizzarri, M., Ed.; Humana Press: New York, NY, USA, 2018; Volume 1702, pp. 215–245. [Google Scholar]
- Huang, S.; Ernberg, I.; Kauffman, S. Cancer attractors: A systems view of tumors from a gene network dynamics and developmental perspective. Semin. Cell Dev. Biol. 2009, 20, 869–876. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Advan. Phys. 2015, 64, 1–137. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, B.; Peng, X.P.; Zhang, M.Q.; Li, Y.; Xie, Z.; Wang, X. Model-guided quantitative analysis of microRNAmediated regulation on competing endogenous RNAs using a synthetic gene circuit. Proc. Natl. Acad. Sci. USA 2015, 112, 3158–3163. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xu, L.; Wang, E.; Huang, S. The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys. J. 2010, 99, 29–39. [Google Scholar] [CrossRef]
- Kauffman, S. Differentiation of malignant to benign cells. J. Theor. Biol. 2017, 31, 429–451. [Google Scholar] [CrossRef]
- Ochsner, S.A.; Abraham, D.; Martin, K.; Ding, W.; McOwiti, A.; Kankanamge, W.; Wang, Z.; Andreano, K.; Hamilton, R.A.; Chen, Y.; et al. The Signaling Pathways Project, an integrated omics knowledge base for mammalian cellular signaling pathways. Sci. Data 2019, 6, 252. [Google Scholar] [CrossRef] [PubMed]
- Sever, R.; Brugge, J.S. Signal transduction in cancer. Cold Spring Harb. Perspect. Med. 2015, 5, a006098. [Google Scholar] [CrossRef] [PubMed]
- Staal, F.J.; Famili, F.; Garcia Perez, L.; Pike-Overzet, K. Aberrant Wnt Signaling in Leukemia. Cancers 2016, 8, 78. [Google Scholar] [CrossRef] [PubMed]
- Tocris Biosciences. Available online: https//www.tocris.com/signaling-pathways (accessed on 30 November 2021).
- ThermoFisher. Available online: https://www.thermofisher.com (accessed on 30 November 2021).
- Heng, H.H. Alternative theories to explain cancer, Chapter 3. In Debating Cancer; The Paradox in Cancer Research; World Scientific Publishing: Singapore, 2016; pp. 44–91. [Google Scholar]
- Plutynski, A.; Bertolaso, M. What and how do cancer systems biologists explain? Philos. Sci. 2018, 85, 942–954. [Google Scholar] [CrossRef]
- Ao, P.; Galas, D.; Hood, L.; Yin, L.; Zhu, X.M. Towards predictive stochastic dynamical modeling of cancer genesis and progression. Interdisc. Sci. 2010, 2, 140–144. [Google Scholar] [CrossRef]
- Ao, P. Endogenous network hypothesis for cancer genesis and progression. Eur. J. Cancer 2016, 54 (Suppl. 1), S71. [Google Scholar]
- Hanselmann, R.G.; Welter, C. Origin of cancer: An information, energy, and matter disease. Front. Cell Dev. Biol. 2016, 4, 121. [Google Scholar] [CrossRef]
- Li, C.; Wang, J. Quantifying the underlying landscape and paths of cancer. J. R. Soc. Interface 2015, 11, 20140774. [Google Scholar] [CrossRef] [PubMed]
- Hooker, C.A. Philosophy of Complex Systems, 1st ed.; Hooker, C., Ed.; Handbook of the Philosophy of Science; Elsevier: Amsterdam, The Netherlands, 2011; Volume 10. [Google Scholar]
- Anastasiadou, E.; Jacob, L.S.; Slack, F.J. Non-coding RNA networks in cancer. Nat. Rev. Cancer 2018, 18, 5–15. [Google Scholar] [CrossRef]
- Zhang, W.; Bojorquez-Gomez, A.; Velez, D.O.; Xu, G.; Sanchez, K.S.; Shen, J.P.; Chen, K.; Licon, K.; Melton, C.; Olson, K.M.; et al. A global transcriptional network connecting noncoding mutations to changes in tumor gene expression. Nat. Genet. 2018, 50, 613–620. [Google Scholar] [CrossRef]
- Shabalina, S.A.; Spiridonov, N.A. The mammalian transcriptome and the function of non-coding DNA sequences. Genome Biol. 2004, 5, 105. [Google Scholar] [CrossRef]
- Rosenfeld, S. Are the somatic mutations and tissue organization field theories of carcinogenesis compatible? Cancer Informat. 2013, 12, 221–229. [Google Scholar]
- Huang, S. Tumor progression: Chance and necessity in Darwinian and Lamarckian somatic (mutationless) evolution. Prog. Biophys. Mol. Biol. 2012, 110, 69–86. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Li, F.; Zhou, J.X.; Qian, H. Processes on the emergent landscapes of biochemical reaction network and heterogenous cell population dynamics: Differentiation in living matters. J. R. Soc. Interface 2017, 14, 20180097. [Google Scholar] [CrossRef]
- Yuan, R.; Zhu, X.; Wang, G.; Li, S.; Ao, P. Cancer as robust intrinsic state shaped by evolution: A key issues review. Rep. Prog. Phys. 2017, 80, 042701. [Google Scholar] [CrossRef]
- Remacle, F.; Zadran, S. Can Thermodynamics Help Us Better Understand Human Cancers? UCLA Newsroom: Los Angeles, CA, USA, 2013; Available online: https://newsroom.ucla.edu (accessed on 30 November 2021).
- Bertolaso, M.; Strauss, B. (Eds.) The Search for Progress and a New Theory Framework in Cancer Research. Rethinking Cancer. A New Paradigm for Postgenomics Era. In Vienna Series in Theoretical Biology; The MIT Press: Cambridge, MA, USA, 2021; 432p, ISBN 9780262045216. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prokop, A. Towards the First Principles in Biology and Cancer: New Vistas in Computational Systems Biology of Cancer. Life 2022, 12, 21. https://doi.org/10.3390/life12010021
Prokop A. Towards the First Principles in Biology and Cancer: New Vistas in Computational Systems Biology of Cancer. Life. 2022; 12(1):21. https://doi.org/10.3390/life12010021
Chicago/Turabian StyleProkop, Aleš. 2022. "Towards the First Principles in Biology and Cancer: New Vistas in Computational Systems Biology of Cancer" Life 12, no. 1: 21. https://doi.org/10.3390/life12010021
APA StyleProkop, A. (2022). Towards the First Principles in Biology and Cancer: New Vistas in Computational Systems Biology of Cancer. Life, 12(1), 21. https://doi.org/10.3390/life12010021





