Identification of Robot Joint Torsional Stiffness Based on the Amplitude of the Frequency Response of Asynchronous Data
Abstract
:1. Introduction
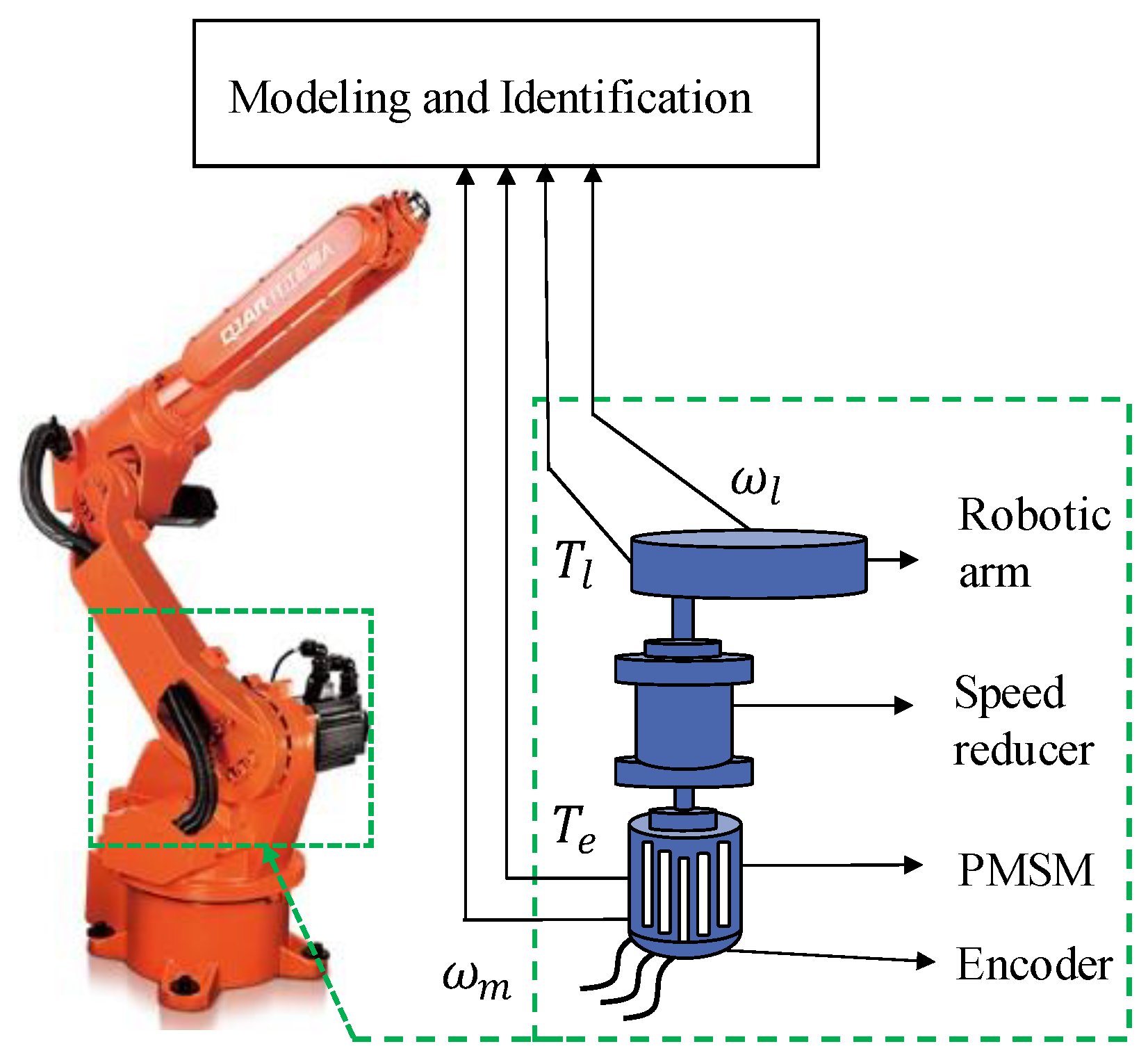
2. Dynamic Modeling of the Robot Joint with Single Degree of Freedom
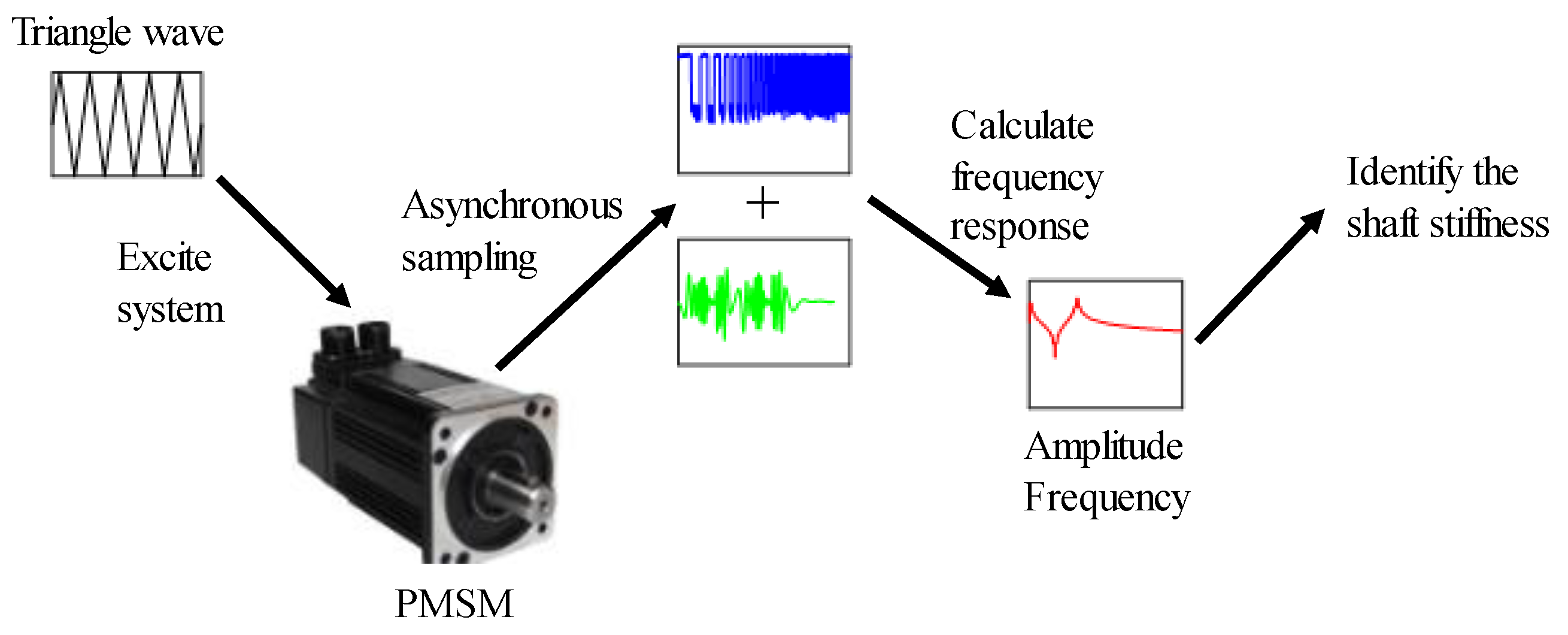
3. Proposed Parameter Identification Method
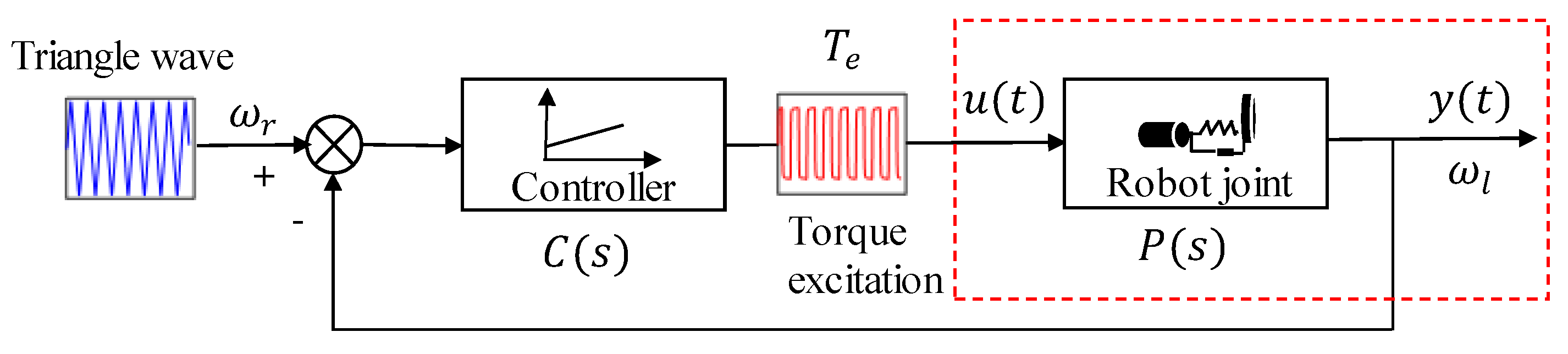
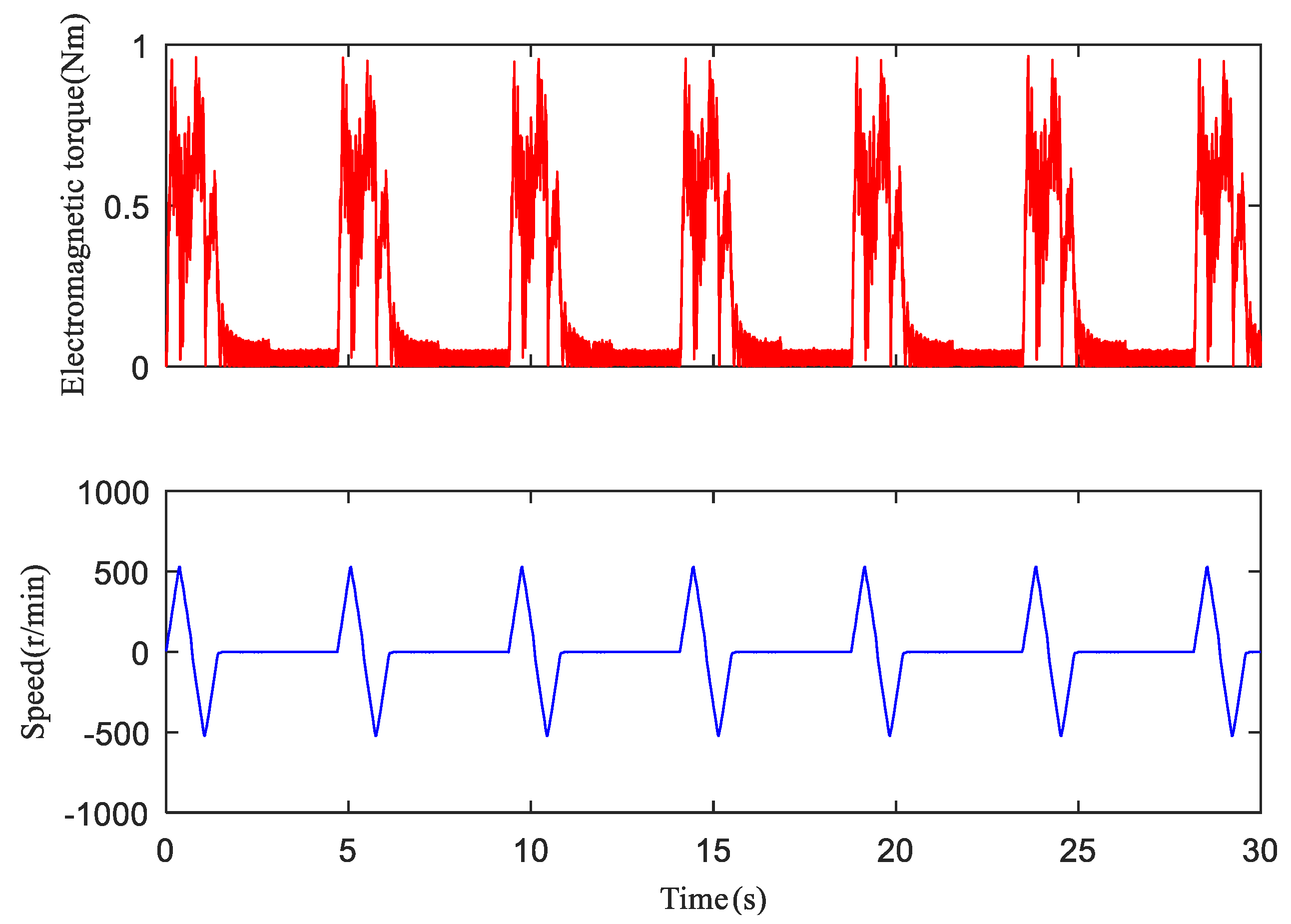
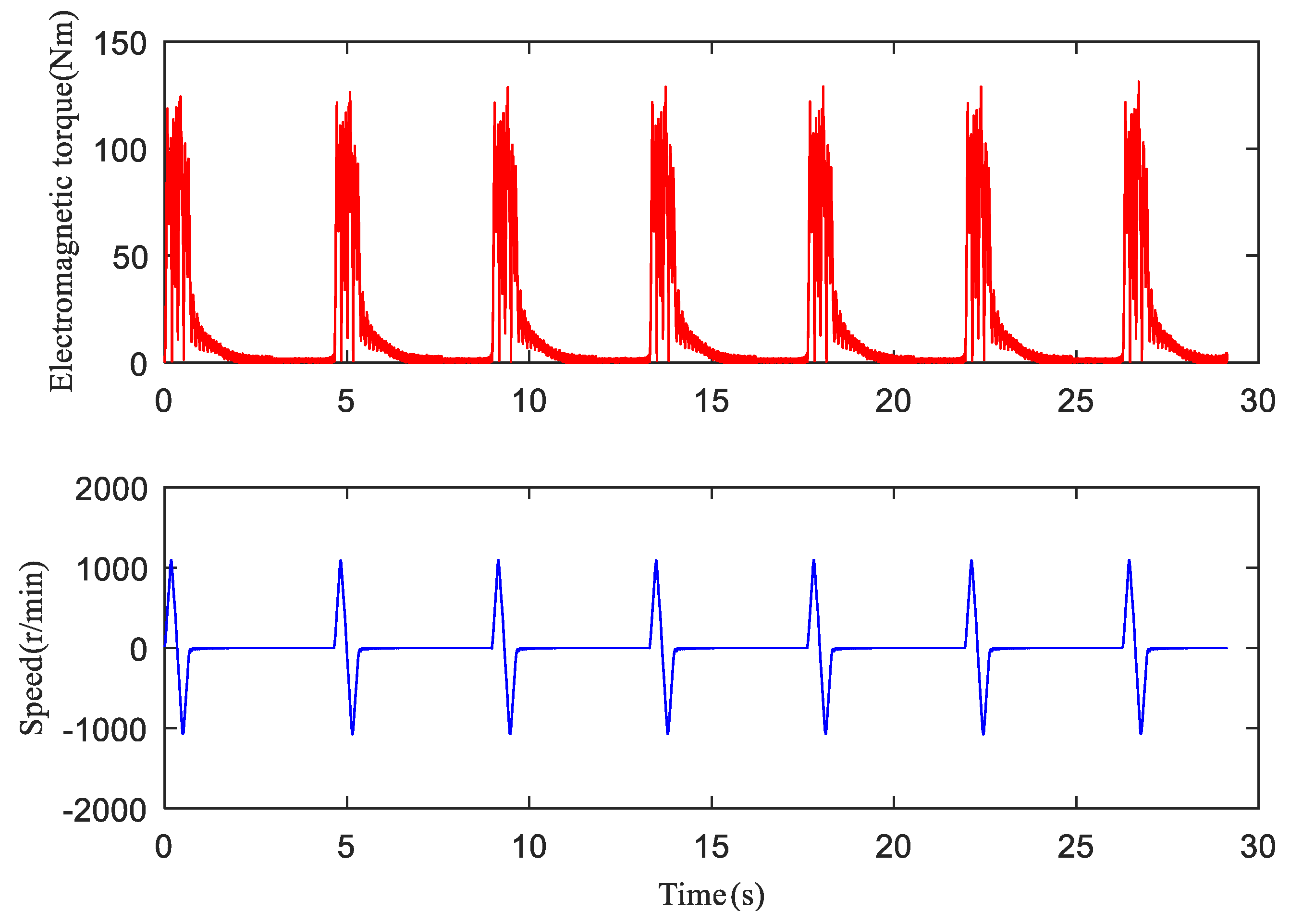
3.1. The Excitation Signal of the Swing Movement
3.2. Calculation of the Electromagnetic Torque
- (1)
- Clarke transformation can be written as follows:
- (2)
- Park transformation can be written as follows:
3.3. Error Criterion Function of the Identification Method of the Amplitude of the FRF
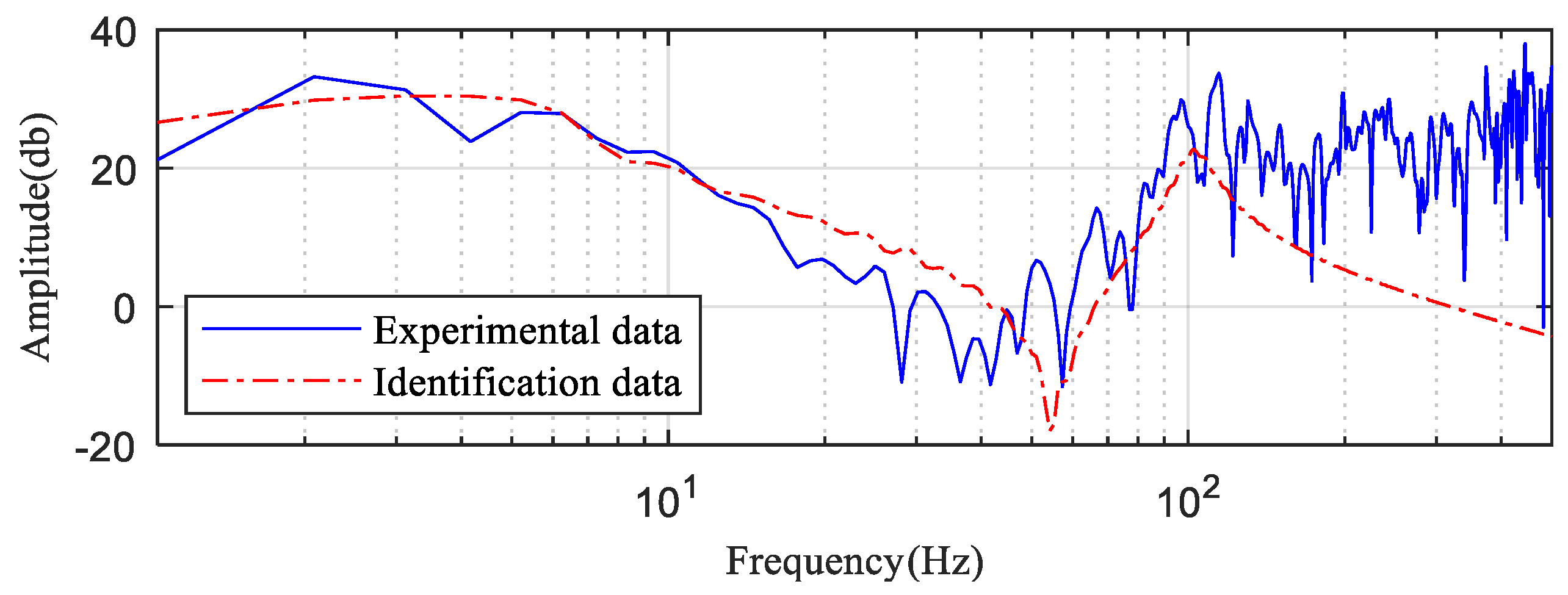
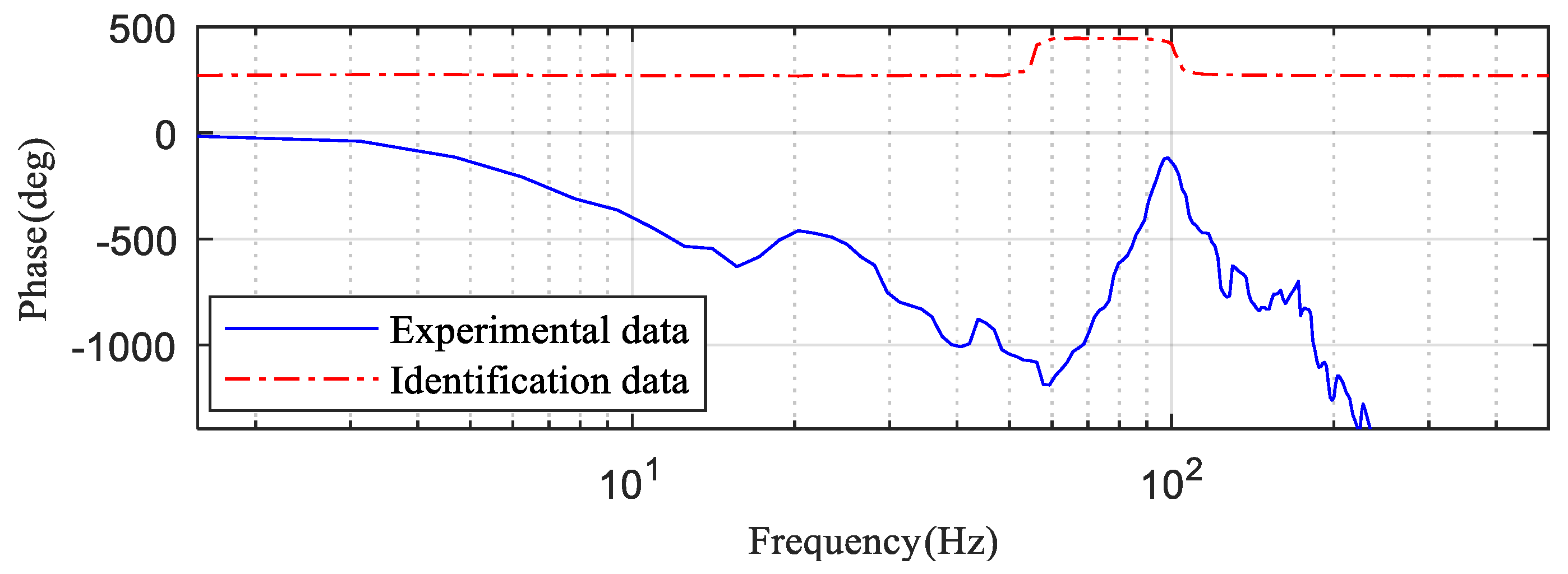
3.4. Calculation of the Frequency Response Function
3.5. Levenberg-Marquardt Algorithm
- (1)
- The dynamic model of a single robot joint is established.
- (2)
- The speed command signal is set as a triangle wave so that the electromagnetic torque follows a rectangular window to excite the system.
- (3)
- The current signal and the motor encoder signal are collected to calculate the electromagnetic torque and the motor speed.
- (4)
- The ratio between the cross-power spectrum of input and output signals and the self-power spectrum of input signals is calculated to obtain the amplitude of the FRF.
- (5)
- The L-M optimization algorithm is used to fit the experimental and theoretical amplitude of the FRF to minimize the error.
- (6)
- The shaft stiffness is identified from the amplitude of the FRF.
4. Simulations
5. Experimental Identification
5.1. Experimental System
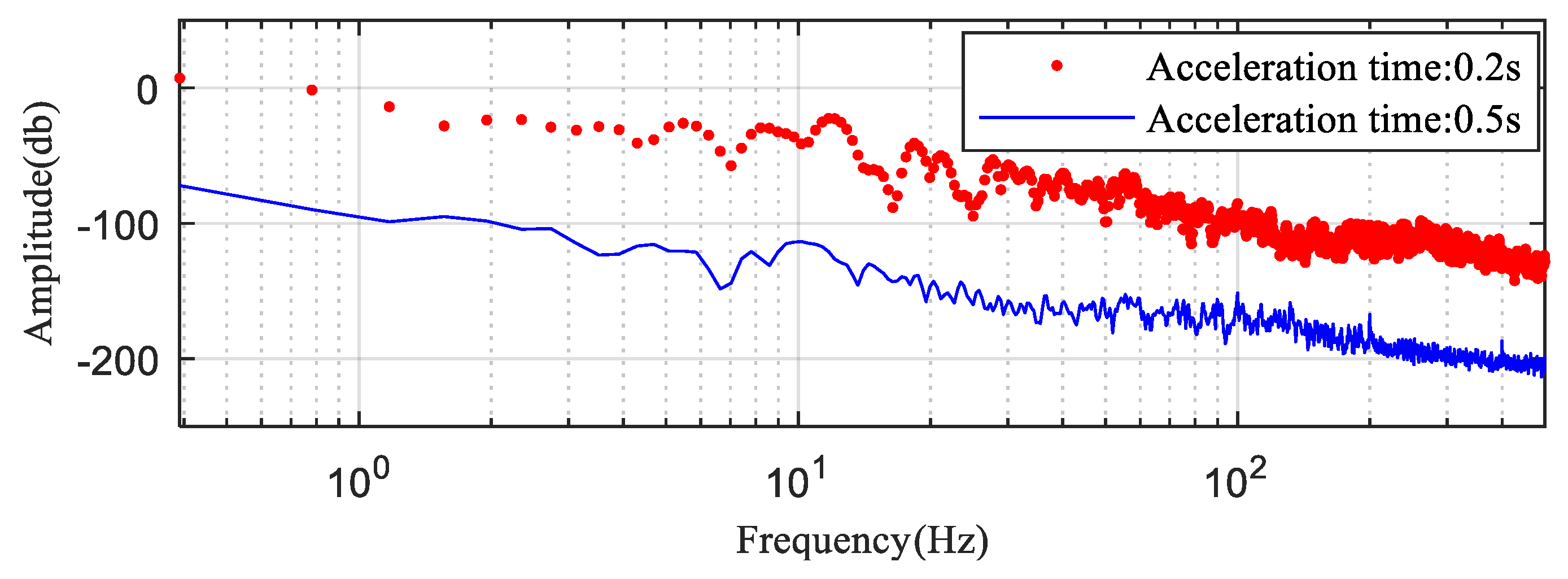
5.2. The Impact of the Acceleration Time on Excitation
5.3. Parameter Identification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Madsen, E.; Rosenlund, O.S.; Brandt, D. Comprehensive modeling and identification of nonlinear joint dynamics for collaborative industrial robot manipulators. Control Eng. Pract. 2020, 101, 104462. [Google Scholar] [CrossRef]
- Morales-Velazquez, L.; Romero-Troncoso, R.; Osornio-Rios, R.A.; Herrera-Ruiz, G.; de Santiago-Perez, J.J. Special purpose processor for parameter identification of CNC second order servo systems on a low-cost FPGA platform. Mechatronics 2010, 20, 265–272. [Google Scholar] [CrossRef]
- Choi, S.; Seong, M.; Ha, S. Accurate position control of a flexible arm using a piezoactuator associated with a hysteresis compensator. Smart Mater. Struct. 2013, 22, 045009. [Google Scholar] [CrossRef]
- Shitole, C.; Sumathi, P. Sliding DFT-based vibration mode estimator for single-link flexible manipulator. IEEE/ASME Trans. Mechatron. 2015, 20, 3249–3256. [Google Scholar] [CrossRef]
- Meng, D.; She, Y.; Xu, W. Dynamic modeling and vibration characteristics analysis of flexible-link and flexible-joint space manipulator. Multibody Syst. Dyn. 2018, 43, 321–347. [Google Scholar] [CrossRef]
- Dwivedy, S.K.; Eberhard, P. Dynamic analysis of flexible manipulators, a literature review. Mech. Mach. Theory 2006, 41, 749–777. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, J.; Wan, L. Effects of intermediate support stiffness on nonlinear dynamic response of transmission system. J. Vib. Control 2020, 26, 851–862. [Google Scholar] [CrossRef]
- Toliyat, H.A.; Levi, E.; Raina, M. A review of RFO induction motor parameter estimation techniques. IEEE Trans. Energy Convers. 2003, 18, 271–283. [Google Scholar] [CrossRef]
- Chunyu, Y.; Lingchao, B.; Bin, C. Energy modeling and online parameter identification for permanent magnet synchronous motor driven belt conveyors. Measurement 2021, 178, 109342. [Google Scholar]
- Underwood, S.J.; Husain, I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines. IEEE Trans. Ind. Electron. 2010, 57, 2435–2443. [Google Scholar] [CrossRef]
- Xiao, X.; Chen, C.; Zhang, M. dynamic permanent magnet flux estimation of permanent magnet synchronous machines. IEEE Trans. Appl. Supercond. 2010, 20, 1085–1088. [Google Scholar] [CrossRef]
- Beineke, S.; Schutte, F.; Wertz, H. Comparison of parameter identification schemes for self-commissioning drive control of nonlinear two-mass systems. In Proceedings of the IEEE Industry Applications Conference, New Orleans, LA, USA, 5–9 October 1990; pp. 493–500. [Google Scholar]
- Villwock, S.; Pacas, M. Application of the welch-method for the identification of two- and three-mass-systems. IEEE Trans. Ind. Electron. 2008, 55, 457–466. [Google Scholar] [CrossRef]
- Pacas, M.; Villwock, S.; Szczupak, P. Methods for commissioning and identification in drives. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2010, 29, 53–71. [Google Scholar] [CrossRef]
- Zoubek, H.; Pacas, M. Encoderless identification of two-mass-systems utilizing an extended speed adaptive observer structure. IEEE Trans. Ind. Electron. 2017, 64, 595–604. [Google Scholar] [CrossRef]
- Zha, F.; Sheng, W.; Guo, W.; Qiu, S.; Deng, J.; Wang, X. Dynamic parameter identification of a lower extremity exoskeleton using RLS-PSO. Appl. Sci. 2019, 9, 324. [Google Scholar] [CrossRef] [Green Version]
- Ostring, M.; Gunnarsson, S.; Norrloef, M. Closed-loop identification of an industrial robot containing flexibilities. Control Eng. Pract. 2003, 11, 291–300. [Google Scholar] [CrossRef]
- Urrea, C.; Pascal, J. Design, simulation, comparison and evaluation of parameter identification methods for an industrial robot. Comput. Electr. Eng. 2016, 67, 791–806. [Google Scholar] [CrossRef]
- Bazanellaa, S.; Gevers, M.; Miskovic, L. Closed-loop identification of MIMO systems: A new look at identifiability and experiment design. Eur. J. Control 2007, 16, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Zoubek H and Pacas, M. A method for speed-sensorless identification of two-mass-systems. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 4461–4468. [Google Scholar]
- Nevaranta, N.A.; Derammelaere, S.B.; Parkkinen, J.A. Online identification of a two-mass system in frequency domain using a Kalman filter. Modeling Identif. Control 2016, 37, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Hu, J.; Liu, W. Smooth and time-optimal S-curve trajectory planning for automated robots and machines. Mech. Mach. Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
- Mesloub, H.; Boumaaraf, R.; Benchouia, M.T. Comparative study of conventional DTC and DTC_SVM based control of PMSM motor-Simulation and experimental results. Math. Comput. Simul. 2020, 167, 296–307. [Google Scholar] [CrossRef]
- Chou, H.-H.; Kung, Y.-S.; Quynh, N.V.; Cheng, S. Optimized FPGA design, verification and implementation of a neuro-fuzzy controller for PMSM drives. Math. Comput. Simul. 2013, 90, 28–44. [Google Scholar] [CrossRef]
- Azzoug, Y.; Sahraoui, M.; Pusca, R.; Ameid, T.; Romary, R.; Cardoso, A.J.M. High-performance vector control without AC phase current sensors for induction motor drives: Simulation and real-time implementation. ISA Trans. 2021, 109, 295–306. [Google Scholar] [CrossRef]
- Zhang, Q.; Tan, L.; Xu, G. Evaluating transient performance of servo mechanisms by analysing stator current of PMSM. Mech. Syst. Signal Process. 2018, 101, 535–548. [Google Scholar] [CrossRef]
- Brancati, R.; Rocca, E.; Lauria, D. Feasibility study of the Hilbert transform in detecting the gear rattle phenomenon of automotive transmissions. J. Vib. Control 2018, 24, 2631–2641. [Google Scholar] [CrossRef]
- Montonen, J.H.; Nevaranta, N.; Lindh, T.; Alho, J.; Immonen, P.; Pyrhönen, O. Experimental identification and parameter estimation of the mechanical driveline of a hybrid bus. IEEE Trans. Ind. Electron. 2017, 65, 5921–5930. [Google Scholar] [CrossRef]
- Cárdenas-Garcia, J.F.; Ekwaro-Osire, S.; Berg, J.M. Non-linear Least-squares Solution to the Moiré Hole Method Problem in Orthotropic Materials. Part I: Residual Stresses. Exp. Mech. 2005, 45, 301–313. [Google Scholar] [CrossRef]

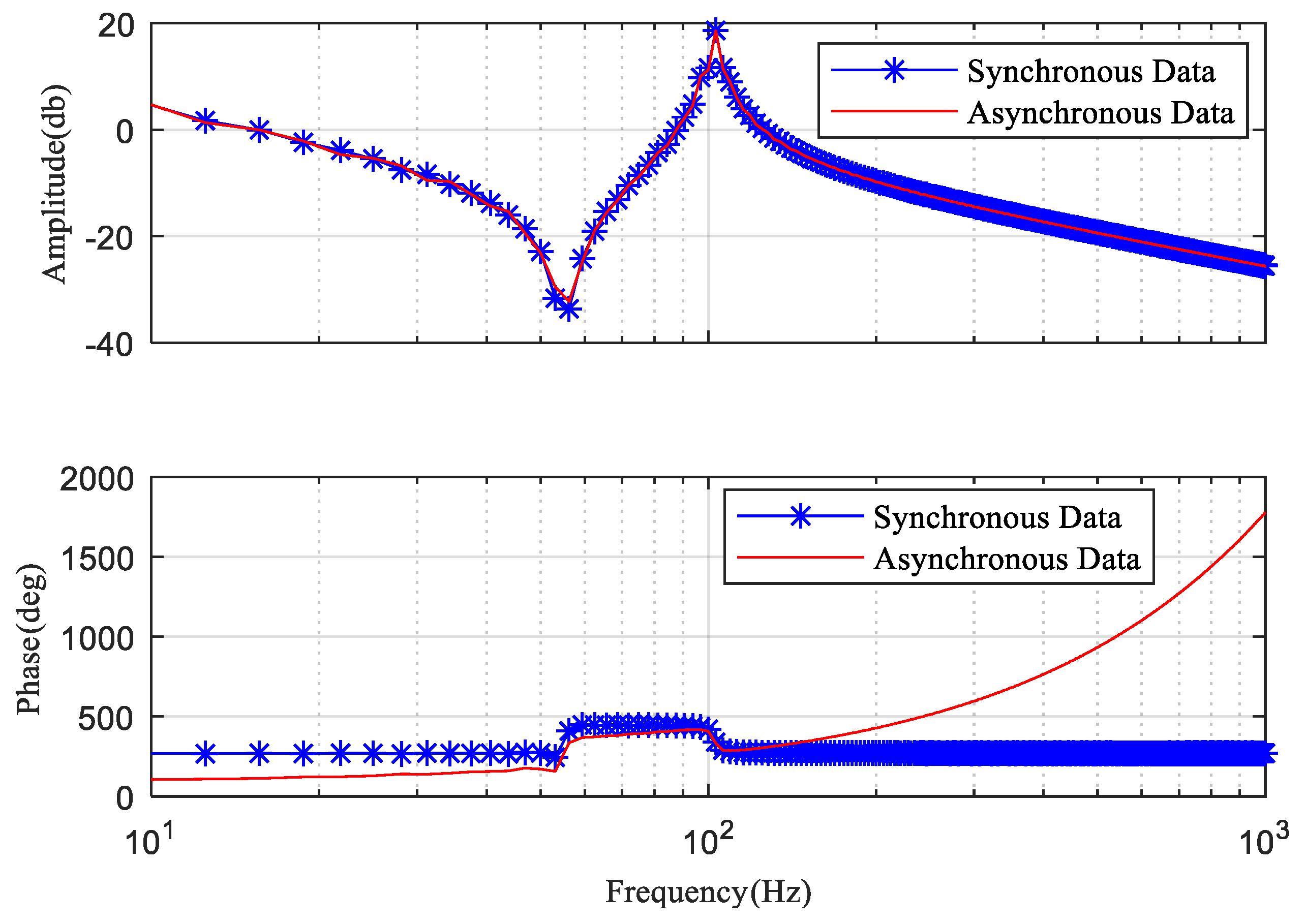


| Data | True Value | Identification Result | Error (%) |
|---|---|---|---|
| FRF of the synchronous data | 891 | 866.13 | 2.79 |
| FRF of the asynchronous data | 891 | 654.67 | 26.52 |
| amplitude of FRF of the asynchronous data | 891 | 859.93 | 3.49 |
| Parameter | Value |
|---|---|
| PMSM rated power | 2.3 |
| PMSM torque constant | 3 |
| Moment of inertia of PMSM | |
| Moment of inertia of reducer | |
| Reduction ratio | |
| Articulated arm mass | 5 |
| Articulated arm length | 75 |
| Moment of inertia of articulated arm | |
| Reducer stiffness | |
| Elastic coupling stiffness |
| Data | True Value | Identification Result | Error (%) |
|---|---|---|---|
| FRF of the asynchronous data | 891 | 1229 | 37.93 |
| amplitude of FRF of the asynchronous data | 891 | 851.9 | 4.49 |
| Parameter | True Value | Initial Value | Initial Error (%) | Identification Result | Identification Error (%) |
|---|---|---|---|---|---|
| () | 891 | 100 | 88.78 | 807.34 | 9.39 |
| () | 0.003027 | 0.001 | 66.96 | 0.00292 | 3.53 |
| () | 0.00748 | 0.005 | 33.16 | 0.00676 | 9.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Wu, X.; Liu, X.; Wang, D. Identification of Robot Joint Torsional Stiffness Based on the Amplitude of the Frequency Response of Asynchronous Data. Machines 2021, 9, 204. https://doi.org/10.3390/machines9090204
Xu K, Wu X, Liu X, Wang D. Identification of Robot Joint Torsional Stiffness Based on the Amplitude of the Frequency Response of Asynchronous Data. Machines. 2021; 9(9):204. https://doi.org/10.3390/machines9090204
Chicago/Turabian StyleXu, Kai, Xing Wu, Xiaoqin Liu, and Dongxiao Wang. 2021. "Identification of Robot Joint Torsional Stiffness Based on the Amplitude of the Frequency Response of Asynchronous Data" Machines 9, no. 9: 204. https://doi.org/10.3390/machines9090204
APA StyleXu, K., Wu, X., Liu, X., & Wang, D. (2021). Identification of Robot Joint Torsional Stiffness Based on the Amplitude of the Frequency Response of Asynchronous Data. Machines, 9(9), 204. https://doi.org/10.3390/machines9090204









