A Vibration Suppression Method for the Multistage Rotor of an Aero-Engine Based on Assembly Optimization

Abstract

The assembly quality of the multistage rotor is an essential factor affecting its vibration level. The existing optimization methods for the assembly angles of the rotors at each stage can ensure the concentricity and unbalance meet the requirements, but it cannot directly ensure its vibration responses meet the indexes. Therefore, in this study, we first derived the excitation formulas of the geometric and mass eccentricities on the multistage rotor and introduced it into the dynamics model of the multistage rotor system. Then, the coordinate transfer model of the geometric and mass eccentricities errors, including assembly angles of the rotors at all stages, was established. Moreover, the mathematical relationship between the assembly angles of the rotors at all stages and the nodal vibration responses was established by combining the error transfer model with the dynamics model of the multistage rotor system. Furthermore, an optimization function was developed, which takes the assembly angles as the optimization variables and the maximum vibration velocity at the bearings as the optimization objective. Finally, a simplified four-stage high-pressure rotor system was assembled according to the optimal assembly angles calculated in the simulations. The experimental results showed that the maximum vibration velocity at the bearings under the optimal assembly was reduced by 69.6% and 45.5% compared with that under the worst assembly and default assembly. The assembly optimization method proposed in this study has a significant effect on the vibration suppression of the multistage rotor of an aero-engine.

1. Introduction

Vibration overrun is the main reason for the failure or damage to the rotating machinery such as aero-engine and gas turbines with multistage rotors [1,2]. Rotor misalignment and unbalance are the two most common factors causing the vibration on the multistage rotor system [3,4,5]. Rotor misalignment is the geometric eccentricity caused by the accumulation of the machining errors of each single-stage rotor after assembly stage-by-stage. This accumulative error will also cause each single-stage rotor to deviate from its nominal assembly axis and form mass eccentricity, resulting in unbalance. Therefore, rotor misalignment and unbalance often exist simultaneously, and the multistage rotor of an aero-engine often needs to be repeatedly balanced and disassembled to meet vibration indexes [6,7]. Assembly optimization is to search the optimal assembly angles of the rotors at all stages to achieve the maximum vibration suppression of a multistage rotor without secondary repair. It can significantly improve the qualification rate of the one-time assembly and reduce the costs of manufacturing and test-run for an aero-engine.

Hussain et al. [8] first proposed to reduce the vibration on the stacked multistage rotor system by assembly optimization. They put forward a linear-assembly method, which means that the appropriate assembly angles of each rotor of a multistage rotor are selected to make the assembly axis as close as possible to a straight line in the assembly process. This method has the potential to reduce the vibration caused by rotor misalignment. Then, for 2-D axisymmetric rotors, Hussain et al. [9] realized the optimization of linear-assembly by minimizing the root mean square of the radial runout errors of the assembly rabbets of each rotor. Furthermore, Hussain et al. [10] proposed a method to minimize the inclination angles of the assembly rabbets of each rotor, which also aims to avoid transitional bending of the assembly axis. Zhang et al. [11] used the error transfer theory to deduce the geometric cumulative eccentricity error after assembly and used this error to represent the bending degree of the assembly axis. Zhang et al. [12] also put forward a concept of parallel-assembly: minimizing the parallelism errors of the assembly rabbets of each rotor during assembly. Comparing the linear-assembly method showed that this method could also make the assembly axis not appear too large a deflection. Moreover, Zhang et al. [13] put forward another concept of assembly optimization step-by-step, that is, for the rotors at each stage, the geometric eccentricity error of the rotor at the next stage is optimized based on the current assembly axis. In addition, Zhang et al. [14] deduced the geometric eccentricity error of the multistage rotor in [11] as a probability density function, calculated the cumulative eccentricity error under all assembly conditions, and then judged the maximum and minimum curvature of the assembly axis.

In [8,9,10,11,12,13,14], the tolerance ranges of the assembly rabbets of each rotor were given, the geometric eccentricity errors of a multistage rotor were calculated by the Monte Carlo simulation method under all possible matching relations of the assembly angles of each rotor. They could obtain the distributions of the cumulative assembly errors and the maximum and minimum values of that. However, they could not directly give the optimal assembly angles of each rotor.

Sun et al. [15] analyzed the primary and secondary relationship of the positioning datum of the rotor at different stages, transformed parts of the parallel dimension chain into the series dimension chain, established a more accurate Jacobian error transfer model, and applied it to calculate the cumulative eccentric errors. However, Sun et al. [16] pointed out that the dimension of the Jacobi matrix changes with the number of parts, which is not suitable for fast modelling. Then, they constructed a deviation propagation analysis model by homogeneous coordinate transformation. Wang et al. [17] substituted the measured orientation and positioning errors of the assembly rabbets of each rotor into the above transfer model and calculated the assembly angles of the rotors at all stages under the condition of minimum eccentricity error. They verified the optimization effect of the eccentricity error by experiments. Sun et al. [18] further combined the above transfer model with a neural network to intelligently select the optimal assembly angles of each rotor under the condition of minimizing geometric eccentricity error. The above studies only focused on optimizing rotor misalignment of multistage rotors. However, the unbalance caused by mass eccentricity is also an essential factor leading to excessive vibration on the multistage rotor. Ganine et al. [19] proposed a new parametric model order reduction algorithm for vibration analysis of rotor assemblies with variations in geometry induced by disk misalignment. However, their study focused on the dynamics model order reduction rather than the vibration suppression through optimizing the assembly angles.

Liu et al. [20] assumed that the material distribution of the rotors at all stages is uniform, estimated the mass eccentricity error through the geometric deviation of each rotor, and substituted it into the model in [17] to calculate the minimum unbalance of a three-stage rotor under all assembly possibilities, and gave the corresponding assembly angles of each rotor. Piskin et al. [21] realized the weight matching of the blades in the circumferential direction of the rotors at all stages by using an ant colony algorithm. Chen et al. [22] pointed out that the assembly datum for unbalance optimization should not be equal to that in optimization for geometric eccentricity error and proposed an optimization method for unbalance based on orientation varying-axis. Sun et al. [23] proposed an assembly optimization method for the dual objectives of concentricity and unbalance of a multistage rotor, making the concentricity and unbalance simultaneously approach their respective optimal solutions to the greatest extent. Nevertheless, for the genuine multistage rotors, the assembly angles of each rotor are discontinuous, which requires the assembly screw holes of each rotor to be aligned first and then selected. To solve this problem, Chen et al. [24] introduced the calibrated angles of screw holes into the error transfer model and proposed a reverse assembly method, which decomposed the assembly process of adjacent rotors into three steps: alignment, rotation, and translation. Chen et al. [25] further transformed the continuous variables of the assembly angles of each rotor into the discrete variables composed of assembly screw holes and obtained the corresponding optimal relationship of the screw holes directly without secondary calculation. The influence of the geometric measurement errors on the stability of assembly optimization was also investigated by the Monte Carlo method.

All the above studies aimed to reduce the misalignment and unbalance in the stacked multistage rotor by optimizing the assembly angles of each single-stage rotor. The ultimate goal is to reduce the vibration on the multistage rotor to the greatest extent during the pre-assembly stage. However, these studies have not established a direct relationship between the assembly angles of the rotors at all stages and the rotor vibration in theory. Although the optimization of the misalignment and unbalance can undoubtedly reduce the vibration to a certain extent from mechanical common sense. However, from the dynamics perspective, the vibration of different nodes on the rotor may be different under the same concentricity and unbalance of a multistage rotor. If the assembly optimization aims to reduce vibration, the vibration of the critical node caused by geometric and mass eccentricities should be taken as the optimization objective. Therefore, we summarized the existing problems in the field of assembly optimization into the following two aspects:

• The mathematical relationship between the assembly angles of the rotors at all stages and the vibration responses should be established;
• The vibration responses of the critical nodes on the rotor should be taken as the optimization objective to calculate the optimal assembly angles.

To solve the above problems, firstly, in Section 2.1, we developed a single-node dynamics model for a rotor with geometric and mass eccentricities, derived the corresponding dynamics differential equations of the elastic shaft element in Section 2.2. Moreover, in Section 2.3, we established a homogeneous coordinate transfer model of the geometric and mass eccentricities errors. Furthermore, in Section 2.4, we combined the coordinate transfer model with the rotor dynamics model to build a mathematical relationship between the assembly angles of the rotors at all stages and the nodal vibration responses. Then, the solution method of the nodal vibration responses on a multistage rotor system was introduced in Section 2.5. The objectives and variables in assembly optimization were defined in Section 2.6. Finally, a simplified four-stage high-pressure rotor system was assembled according to the optimal assembly angles calculated in the simulations. The experimental results showed that the assembly optimization method proposed in this study has a significant vibration suppression effect on multistage rotor system.

2. Methods

2.1. Single-Node Dynamics Model for a Rotor with Geometric and Mass Eccentricities

A single-node dynamics model for a rotor with geometric and mass eccentricities is shown in Figure 1. M is the center of mass of the single-disc rotor, and the mass of that is m. ε refers to the disc’s mass eccentricity, and the angle between it and the horizontal direction is φ_ε. Due to the initial bending of the rotating shaft, the geometric center of the disc deviated from the rotating center O and reached point O₀. O₁ is the geometric center of the disc after the rotation of the shaft. r_s is the initial geometric eccentricity of the center of the disc, and the angle between it and the horizontal direction is φ_s. r is the displacement vector of the center of the disc, and the angle between it and the horizontal direction is φ_r. r_d is the dynamic response vector of the center of the disc when the rotor is rotating. p is the displacement vector of the center of mass of the disc. k and c are the stiffness and damping coefficient of the shaft, respectively, and the mass of that is neglected.

According to the balanced relationship among the inertia force, the damping force and the elastic force, the dynamics differential equation of the geometric center of the disc can be expressed as in Equation (1):

$$m\ddot{p}+c\dot{r}+k{r}_d=0.$$

(1)

From the geometric relationship in Figure 1, we can obtained Equation (2):

$$\left\{\begin{array}{c}\mathit{p}=\mathit{r}+\epsilon \\ {\mathit{r}}_{\mathit{d}}=\mathit{r}-{\mathit{r}}_{\mathit{s}}\end{array}\right..$$

(2)

Equation (3) can be obtained by substituting p and r_d into Equation (1):

$$m\ddot{r}+c\dot{r}+kr=k{r}_s-m\ddot{\epsilon },$$

(3)

where r, r_s and ε can be expressed as plural forms in Equation (4):

$$\left\{\begin{array}{l}r=r\exp \left[i\left(\omega t+{\phi }_r\right)\right]=r\cos \left(\omega t+{\phi }_r\right)+jr\sin \left(\omega t+{\phi }_r\right)=x_r+j{y}_r\hfill \\ r_s=r_s\exp \left[i\left(\omega t+{\phi }_s\right)\right]=r_s\cos \left(\omega t+{\phi }_s\right)+r_{s}r\sin \left(\omega t+{\phi }_s\right)=x_s+j{y}_s\hfill \\ \epsilon =\epsilon \exp \left[i\left(\omega t+{\phi }_{\epsilon }\right)\right]=\epsilon \cos \left(\omega t+{\phi }_{\epsilon }\right)+\epsilon \sin \left(\omega t+{\phi }_{\epsilon }\right)=x_{\epsilon }+j{y}_{\epsilon }\hfill \end{array}\right..$$

(4)

Then, by substituting Equation (4) into Equation (2), the single-node dynamics differential equation can be obtained as follows:

$$\left\{\begin{array}{c}m{\ddot{x}}_r+c{\dot{x}}_r+k{x}_r=k{x}_s+m{\omega }^2{x}_{\epsilon }\\ m{\ddot{y}}_r+c{\dot{y}}_r+k{y}_r=k{y}_s+m{\omega }^2{y}_{\epsilon }\end{array}\right.,$$

(5)

where kx_s and ky_s are the nodal excitation forces caused by the geometric eccentricity, and mω²x_ε and mω²y_ε are the nodal excitation forces caused by mass eccentricity.

2.2. Dynamics Model of the Shaft Element of a Rotor

The rotor system can be divided into a finite element model composed of several shaft elements and nodes, and the dynamics differential equation of a single Timoshenko-beam element can be established as follows:

$$\left[\begin{array}{cc}{M}_{en}& 0\\ 0& M_{en}\end{array}\right]\left\{{\ddot{q}}_{en}\right\}+\left(\omega \left[\begin{array}{cc}0& G_{en}\\ -G_{en}& 0\end{array}\right]+\left[\begin{array}{cc}{C}_{en}& 0\\ 0& C_{en}\end{array}\right]\right)\left\{{\dot{q}}_{en}\right\}+\left[\begin{array}{cc}{K}_{en}& 0\\ 0& K_{en}\end{array}\right]\left\{q_{en}\right\}=\left\{R_{en}\right\}+\left\{Q_{en}\right\},$$

(6)

where {q_en} = {x_n,θ_yn, y_n, −θ_xn, x_n+1, θ_y(n+1), y_n+1, −θ_x(n+1)}^T is the displacement vector of the nth shaft element. The vectors {R_en} and {Q_en} denote the excitation forces acting on the shaft element due to the geometric and mass eccentricities, respectively, as shown in Equation (7):

$$\left\{\begin{array}{l}\left\{R_{en}\right\}=\left[\begin{array}{cc}{K}_{en}& 0\\ 0& K_{en}\end{array}\right]\left\{F_n\right\}\hfill \\ \left\{Q_{en}\right\}={\omega }^2\left\{m_n{P}_n\right\}\hfill \end{array}\right.,$$

(7)

where {F_n} is the displacement vector of the geometric eccentricity, and {P_n} is that of mass eccentricity. m_n refers to the mass of each rotor. Here, the mass-radius product of P_n and m_n can be replaced by u_nU_n, which refers to the product of the unbalanced mass u_n and its action radius U_n. The stiffness matrix K_en of the single-node was presented by Genta et al. [26] as follows:

$$K_{en}=\frac{E{I}_{dn}}{l_n^3\left(1+{\chi }_n\right)}\left[\begin{array}{cccc}12& 6l_n& -12& 6l_n\\ & \left(4+{\chi }_n\right)l_n^2& -6l_n& \left(2-{\chi }_n\right)l_n^2\\ & & 12& -6l_n\\ symm& & & \left(4+{\chi }_n\right)l_n^2\end{array}\right],$$

(8)

where E is the Elastic modulus of the rotor, and l_n is the length of the element. I_dn is the diameter moment of inertia of the circular section of the shaft element, which can be expressed as in Equation (9):

$$I_{dn}=\frac{\pi \left(D_n^4-d_n^4\right)}{64},$$

(9)

where D_n and d_n are the outer and inner diameter of the shaft element, respectively. χ_n is the dimensionless stiffness, as shown in Equation (10):

$${\chi }_n=\frac{12E_n{I}_{dn}}{G_n{A}_n{l}_n^2{\kappa }_n},$$

(10)

where G_n is the shear modulus, and A_n is the cross-sectional area of the element as shown in Equation (11). κ_n is the shear factor as shown in Equation (12):

$$A_n=\frac{\pi \left(D_n^2-d_n^2\right)}{4},$$

(11)

$${\kappa }_n=\frac{6\left(1+v_n{}^2\right)}{7+12v_n+4v_n{}^2},$$

(12)

where v_n is Poisson’s ratio. The single-node moving inertia matrix can be expressed as in Equation (13):

$$M_{Tn}=\frac{{\rho }_n{A}_n{E}_n{l}_n}{420{\left(1+{\chi }_n\right)}^2}\left[\begin{array}{cccc}{t}_1& l_n{t}_2& t_3& -l_n{t}_4\\ & l_n^2{t}_5& l_n{t}_4& -l_n^2{t}_6\\ & & t_1& -l_n{t}_2\\ symm& & & l_n^2{t}_5\end{array}\right].$$

(13)

The single-node rotational inertia matrix can be expressed as in Equation (14):

$$M_{Rn}=\frac{{\rho }_n{I}_{dn}}{30l_n{\left(1+{\chi }_n\right)}^2}\left[\begin{array}{cccc}{t}_7& l_n{t}_8& t_7& l_n{t}_8\\ & l_n^2{t}_9& -l_n{t}_8& -l_n^2{t}_{10}\\ & & t_7& -l_n{t}_8\\ symm& & & l_n^2{t}_9\end{array}\right],$$

(14)

where the expressions of t₁~t₂ are presented in Equation (15):

$$\left\{\begin{array}{l}{t}_1=156+294{\chi }_n+140{\chi }_n^2\hfill \\ t_2=22+38.5{\chi }_n+17.5{\chi }_n^2\hfill \\ t_3=54+126{\chi }_n+70{\chi }_n^2\hfill \\ t_4=13+31.5{\chi }_n+17.5{\chi }_n^2\hfill \\ t_5=4+7{\chi }_n+3.5{\chi }_n^2\hfill \\ t_6=3+7{\chi }_n+3.5{\chi }_n^2\hfill \\ t_7=36\hfill \\ t_8=3-15{\chi }_n\hfill \\ t_9=4+5{\chi }_n+10{\chi }_n^2\hfill \\ t_{10}=1+5{\chi }_n-5{\chi }_n^2\hfill \end{array}\right..$$

(15)

The single-node global mass matrix can be obtained by Equation (16):

$$M_{en}=M_{Tn}+M_{Rn}.$$

(16)

G_en is the single-node gyro matrix, which is equal to 2M_Rn. C_en is the single-node damping matrix, and the hysteretic damping model is employed (C_en = ηK_en, η = 0.001) [27].

2.3. Error Transfer Model of the Geometric and Mass Eccentricities

2.3.1. Coordinate Transfer

A multistage rotor is assembled step-by-step through the assembly rabbets of each single-stage rotor. In the assembly process, the machining error of the assembly rabbets will make the rotors at each stage deviate from their ideal assembly position and then form the geometric and mass eccentricities. In actuality, the transfer of the eccentricity errors is equivalent to transferring the coordinates of points in the rotor. If the coordinate transfer of each point in the rigid rotor during assembly is known, we can calculate the geometric and mass eccentricities errors after assembly. Figure 2 shows a coordinate transfer process of a three-stage simulated rotor. O-XYZ refers to the standard coordinate system for measuring the geometric parameters of the rotors at all stages. C_n and C_n′ are the geometric centers of the assembly rabbet of the rotor at the nth stage before and after assembly, respectively. E_n and E_n′ are the unbalanced mass points of the rotor at the nth stage before and after assembly, respectively. h_n is the axial runout error of the assembly rabbets, and the point H_n and L_n are the highest and lowest fitting points. S_n is the geometric center of the calibrated screw hole in the geometric measurement of the rotor at the nth stage, and δ_n is the angle between H_n and S_n. w_n is the diameter of the assembly rabbet of the rotor at the nth stage. Rot-axis is the nominal axis of rotation of the 3-stage rotor, connecting the front and rear supporting points. F_n and U_n are the geometric and mass eccentricity errors relative to Rot-axis, respectively.

When the rotor at the second stage is assembled on the rotor at the first stage, the coordinate transfer process of the geometric center of the assembly rabbet of the rotor at the second stage can be expressed by Equation (17):

$${\xi }_2{}^{\prime }={\xi }_{2}I{z}_{2}I{y}_1+{\xi }_1,$$

(17)

where ξ₁ is the coordinate vector of C₁, and the rotor at the first stage is fixed during assembly. ξ₂′ and ξ₂ represent the coordinate vectors of C₂ and C₂′, respectively. Iz₂ is the rotation matrix of the rotor at the second stage around Z-axis, as presented in Equation (18). Iy₁ is the rotation matrix of the rotor at the first stage around Y-axis, as presented in Equation (19).

$$I{z}_2=\left[\begin{array}{ccc}\cos \left(\theta z_2+\Delta {\delta }_2\right)& -\sin \left(\theta z_2+\Delta {\delta }_2\right)& 0\\ \sin \left(\theta z_2+\Delta {\delta }_2\right)& \cos \left(\theta z_2+\Delta {\delta }_2\right)& 0\\ 0& 0& 1\end{array}\right],$$

(18)

$$I{y}_1=\left[\begin{array}{ccc}\cos \left(\arctan \left(\frac{h_1}{w_1}\right)\right)& 0& \sin \left(\arctan \left(\frac{h_1}{w_1}\right)\right)\\ 0& 1& 0\\ -\sin \left(\arctan \left(\frac{h_1}{w_1}\right)\right)& 0& \cos \left(\arctan \left(\frac{h_1}{w_1}\right)\right)\end{array}\right],$$

(19)

where Δδ₂ = δ₂ − δ₁ is the difference between the angles of the calibrated screw holes of the rotors at the second and the first stage, which means that the angle of the rotor at the second stage needs to rotate around the Z-axis during the alignment of the rotors at the second and the first stage. θz₂ is the rotation angle of the rotor at the second stage relative to that at the first stage around the Z-axis, which is the so-called assembly angle of the rotor at the second stage to be optimized. Then, when the rotor at the third stage is assembled on the rotor at the second stage, the coordinate transfer process of the geometric center of the assembly rabbet of the rotor at the third stage can be expressed by Equation (20):

$${\xi }_3{}^{\prime }={\xi }_{3}I{z}_{3}I{y}_{2}I{z}_{2}I{y}_1+{\xi }_{2}I{z}_{2}I{y}_1+{\xi }_1,$$

(20)

where ξ₃′ and ξ₃ represent the coordinate vectors of C₃ and C₃′, respectively. Iz₃ is the rotation matrix of the rotor at the third stage around Z-axis, and Iy₂ is the rotation matrices of the rotor at the second stage around the Y-axis, and their expressions are the same as Iz₂ and Iy₁. By analogy, the assembly process of an n-stage rotor can be expressed as in Equation (21):

$${\xi }_n{}^{\prime }={\xi }_n\left[{\displaystyle \prod _{n:-1:2}\left(I{z}_{n}I{y}_{n-1}\right)}\right]+{\xi }_{n-1}{}^{\prime }\left(n\in {\mathrm{N}}^{\ast },n>1\right).$$

(21)

The assembly process of a multistage rotor is equivalent to the transfer process of multiple rigid bodies. The moving trajectory of each point in the rigid body is the same in the assembly process, so the coordinate transfer of each point in the rotors at all stages can be calculated by Equation (21).

2.3.2. Decomposition of the Geometric and Mass Eccentricities Errors

The connecting line of the geometric center of the support journals on the rotors at the first and the last stage is the nominal axis of rotation in a multistage rotor system, which is the calculation datum of the geometric and mass eccentricities errors, and its linear equation can be expressed as follows:

$$\frac{x}{{\xi }_{lx}{}^{\prime }}=\frac{y}{{\xi }_{ly}{}^{\prime }}=\frac{z}{{\xi }_{lz}{}^{\prime }}=\lambda ,$$

(22)

where ξ_l′ = (ξ_lx’, ξ_ly′, ξ_lz′) is the coordinate vector of the geometric center of the support journal on the rotor at the last stage after assembly. λ is the parameter of the linear equation. The equation of the normal plane passing through any point A in the rotor body and perpendicular to the axis of rotation can be expressed as follows:

$${\xi }_{lx}{}^{\prime }\left(x-A_x\right)+{\xi }_{ly}{}^{\prime }\left(y-A_y\right)+{\xi }_{lz}{}^{\prime }\left(z-A_z\right)=0.$$

(23)

λ can be obtained by simultaneous Equations (19) and (20) as follows:

$$\lambda =\frac{{\xi }_{lx}{}^{\prime }{A}_x+{\xi }_{ly}{}^{\prime }{A}_y+{\xi }_{lz}{}^{\prime }{A}_z}{{\left({\xi }_{lx}{}^{\prime }\right)}^2+{\left({\xi }_{ly}{}^{\prime }\right)}^2+{\left({\xi }_{lz}{}^{\prime }\right)}^2}.$$

(24)

By bringing λ into Equation (22), the coordinates of the intersection point between the axis of rotation and the normal plane can be obtained by Equation (25):

$$\left\{\begin{array}{l}{J}_x=\frac{{\left({\xi }_{lx}{}^{\prime }\right)}^2{A}_x+{\xi }_{lx}{}^{\prime }{\xi }_{ly}{}^{\prime }{A}_y+{\xi }_{lx}{}^{\prime }{\xi }_{lz}{}^{\prime }{A}_z}{{\left({\xi }_{lx}{}^{\prime }\right)}^2+{\left({\xi }_{ly}{}^{\prime }\right)}^2+{\left({\xi }_{lz}{}^{\prime }\right)}^2}\hfill \\ J_y=\frac{{\xi }_{lx}{}^{\prime }{\xi }_{ly}{}^{\prime }{A}_x+{\left({\xi }_{ly}{}^{\prime }\right)}^2{A}_y+{\xi }_{ly}{}^{\prime }{\xi }_{lz}{}^{\prime }{A}_z}{{\left({\xi }_{lx}{}^{\prime }\right)}^2+{\left({\xi }_{ly}{}^{\prime }\right)}^2+{\left({\xi }_{lz}{}^{\prime }\right)}^2}.\hfill \\ J_z=\frac{{\xi }_{lx}{}^{\prime }{\xi }_{lz}{}^{\prime }{A}_x+{\xi }_{ly}{}^{\prime }{\xi }_{lz}{}^{\prime }{A}_y+{\left({\xi }_{lz}{}^{\prime }\right)}^2{A}_z}{{\left({\xi }_{lx}{}^{\prime }\right)}^2+{\left({\xi }_{ly}{}^{\prime }\right)}^2+{\left({\xi }_{lz}{}^{\prime }\right)}^2}\hfill \end{array}\right.$$

(25)

The coordinate vector of the unbalanced mass point E₁′ in the rotor at the first stage after assembly is (E_x1′, E_y1′, E_z1′), and the coordinate vector of the intersection point J_E1 between the axis of rotation and the normal plane passing through E₁ can be obtained by Equation (25) is (J_xE1, J_yE1, J_zE1). Then, the vertical vector from E₁′ to the axis of rotation can be expressed as in Equation (26):

$$\overrightarrow{E_1{}^{\prime }{J}_{E1}}=\left\{\left(E_{x1}{}^{\prime }-J_{xE1}\right),\left(E_{y1}{}^{\prime }-J_{yE1}\right),\left(E_{z1}{}^{\prime }-J_{zE1}\right)\right\}.$$

(26)

The angles between this vector and the vertical vectors from the other unbalanced mass points to the axis of rotation can be expressed as in Equation (27):

$${\theta }_{En-1}=\arccos \left(\frac{\overrightarrow{E_1{}^{\prime }{J}_{E1}}\cdot \overrightarrow{E_n{}^{\prime }{J}_{En}}}{\left|\overrightarrow{E_1{}^{\prime }{J}_{E1}}\right|\left|\overrightarrow{E_n{}^{\prime }{J}_{En}}\right|}\right).$$

(27)

It is assumed that the angle between this vector and X-direction of the acquisition of vibration responses is Δθ. Then, the mass eccentricity error U_n of the rotor at the nth stage can be decomposed into X- and Y-directions as follows:

$$\left\{\begin{array}{l}{U}_{xn}=\left|\overrightarrow{E_n{}^{\prime }{J}_{en}}\right|\cos {\theta }_{en-1}\cos \Delta \theta +\left|\overrightarrow{E_n{}^{\prime }{J}_{en}}\right|\sin {\theta }_{en-1}\sin \Delta \theta \hfill \\ U_{yn}=\left|\overrightarrow{E_n{}^{\prime }{J}_{en}}\right|\cos {\theta }_{en-1}\sin \Delta \theta +\left|\overrightarrow{E_n{}^{\prime }{J}_{en}}\right|\sin {\theta }_{en-1}\cos \Delta \theta \hfill \end{array}\right..$$

(28)

Similarly, the geometric eccentricity error F_n of the rotor at the nth stage can also be decomposed as follows:

$$\left\{\begin{array}{l}{F}_{xn}=\left|\overrightarrow{C_n{}^{\prime }{J}_{cn}}\right|\cos {\theta }_{cn-1}\cos \Delta \theta +\left|\overrightarrow{C_n{}^{\prime }{J}_{cn}}\right|\sin {\theta }_{cn-1}\sin \Delta \theta \hfill \\ F_{yn}=\left|\overrightarrow{C_n{}^{\prime }{J}_{cn}}\right|\cos {\theta }_{cn-1}\sin \Delta \theta +\left|\overrightarrow{C_n{}^{\prime }{J}_{cn}}\right|\sin {\theta }_{cn-1}\cos \Delta \theta \hfill \end{array}\right..$$

(29)

where C_n′ refers to the coordinate vector of the geometric center of the assembly rabbet of the rotor at the nth stage after assembly. J_Cn is the intersection point between the axis of rotation and the normal plane passing through C_n′, and its solution principle is the same as that of Equation (25). θ_Cn-1 is the angle between the vertical vector from C_n′ to the axis of rotation and the vertical vector from E₁′ to the axis of rotation, which can be obtained by Equation (30) as follows:

$${\theta }_{Cn-1}=\arccos \left(\frac{\overrightarrow{E_1{}^{\prime }{J}_{E1}}\cdot \overrightarrow{C_n{}^{\prime }{J}_{Cn}}}{\left|\overrightarrow{E_1{}^{\prime }{J}_{E1}}\right|\left|\overrightarrow{C_n{}^{\prime }{J}_{Cn}}\right|}\right).$$

(30)

2.4. Dynamics Model of a Multistage Rotor System

All the shaft elements, the concentrated mass, the supporting elements and the nodal excitation forces can be superimposed to form a dynamics differential equation of a multistage rotor system as follows:

$$\left[M_s\right]\left\{{\ddot{q}}_s\right\}+\left[\omega G_s+C_s\right]\left\{{\dot{q}}_s\right\}+\left[K_s\right]\left\{q_s\right\}=\left[K_s\right]\left\{F_s\right\}+\left\{Q_s\right\},$$

(31)

where M_s is the global mass matrix with a bandwidth of 4(n + 1) × 4(n + 1), as shown in Equation (32). M_dn is the lumped mass matrix loaded at the nth node as shown in Equation (33), which can load the additional mass and the moment of inertia of a locking device. K_s and [ωG_s + C_s] are the global stiffness and damping matrices as shown in Equations (34) and (35), respectively.

$$\left[M_s\right]=\left[\begin{array}{cccccc}{M}_{e1}& & & & & 0\\ & M_{e1}+M_{e2}& & & & \\ & & M_{e2}+M_{e3}& & & \\ & & & \ddots & & \\ & & & & M_{e\left(n-1\right)}+M_{en}\left(+M_{dn}\right)& \\ 0& & & & & M_{en}\end{array}\right],$$

(32)

$$\left[M_{dn}\right]=\left[\begin{array}{cccc}{m}_n& & & 0\\ & J_{dn}& & \\ & & m_n& \\ 0& & & J_{dn}\end{array}\right],$$

(33)

$$\left[K_s\right]=\left[\begin{array}{cccccc}{K}_{e1}& & & & & 0\\ & K_{e1}+K_{e2}& & & & \\ & & K_{e2}+K_{e3}& & & \\ & & & \ddots & & \\ & & & & K_{e\left(n-1\right)}+K_{en}\left(+K_{bn}\right)& \\ 0& & & & & K_{en}\end{array}\right],$$

(34)

$$\left[\omega G_s+C_s\right]=\left[\begin{array}{cccccc}{C}_{e1}& \omega G_{e1}& & & & 0\\ -\omega G_{e1}& C_{e1}+C_{e2}& \omega G_{e2}& & & \\ & -\omega G_{e2}& C_{e2}+C_{e3}& & & \\ & & & \ddots & & \\ & & & & C_{e\left(n-1\right)}+C_{en}\left(+C_{bn}\right)& \omega G_{en}\\ 0& & & & -\omega G_{en}& C_{en}\end{array}\right].$$

(35)

where m_n and d_n refer to the lumped mass and the moment of inertia. K_bn and C_bn are the additional stiffness and damping matrices loaded at the nth node, respectively, as shown in Equations (36) and (37), which can load a supporting element such as a rolling bearing. {F_s} and {Q_s} are the excitation vectors of the geometric and mass eccentricities on the ith node, respectively, as shown in Equations (38) and (39). {q_s}, {$\dot{\mathit{q}}$_s} and {$\ddot{\mathit{q}}$_s} are the generalized displacement, velocity and acceleration vector of all nodes, as shown in Equation (40).

$$\left[K_{bn}\right]=\left[\begin{array}{cccc}{K}_{xx}& K_{xy}& & 0\\ K_{yx}& K_{yy}& & \\ & & K_{xx}& K_{xy}\\ 0& & K_{yx}& K_{yy}\end{array}\right],$$

(36)

$$\left[C_{bn}\right]=\left[\begin{array}{cccc}{C}_{xx}& C_{xy}& & 0\\ C_{yx}& C_{yy}& & \\ & & C_{xx}& C_{xy}\\ 0& & C_{yx}& C_{yy}\end{array}\right],$$

(37)

$$\left\{F_s\right\}=\left\{\dots ,F_{xi},0,F_{yi},0,F_{x(i+1)},0,F_{y(i+1)},0,\dots \right\}\left(i\in {\mathrm{N}}^{\ast },1\le i\le n+1\right),$$

(38)

$$\left\{Q_s\right\}={\omega }^2\left\{\dots ,u_i{U}_{xi},0,u_i{U}_{yi},0,u_{i+1}{U}_{x(i+1)},0,u_{i+1}{U}_{y(i+1)},0,\dots \right\}\left(i\in {\mathrm{N}}^{\ast },1\le i\le n+1\right),$$

(39)

$$\left\{q_s\right\}=\left\{x_1,{\theta }_{y1},y_1,-{\theta }_{x1},\dots ,x_{n+1},{\theta }_{y\left(n+1\right)},y_{n+1},-{\theta }_{x\left(n+1\right)}\right\}.$$

(40)

2.5. Solution Method of the Nodal Vibration Responses

The Newmark-β integration method [28] is employed to solve the nodal vibration responses step-by-step. The nodal displacement, velocity and acceleration at the time of t + Δt can be used to express that at the time of t as follows:

$$\left\{\begin{array}{l}\left\{{\dot{q}}_{t+\Delta t}\right\}=\left\{{\dot{q}}_t\right\}+\left[\left(1-\beta \right)\left\{{\ddot{q}}_t\right\}+\beta \left\{{\ddot{q}}_{t+\Delta t}\right\}\right]\Delta t\hfill \\ \left\{q_{t+\Delta t}\right\}=\left\{q_t\right\}+\left\{{\dot{q}}_t\right\}\Delta t+\left[\left(\frac{1}{2}-\gamma \right)\left\{{\ddot{q}}_t\right\}+\gamma \left\{{\ddot{q}}_{t+\Delta t}\right\}\right]\Delta t^2\hfill \end{array}\right.,$$

(41)

where β and γ are the integral parameters selected according to different expressions of the acceleration. Usually, when the value of β and γ are greater than or equal to 0.5 and 0.25(0.5 + β), respectively, the calculation is unconditionally convergent. From Equation (41), the expressions of the acceleration and velocity at the time of t + Δt can be further expressed as in Equation (42):

$$\left\{\begin{array}{l}\left\{{\ddot{q}}_{t+\Delta t}\right\}=\frac{1}{\gamma \Delta t^2}\left(\left\{q_{t+\Delta t}\right\}-\left\{{\dot{q}}_t\right\}\right)-\frac{1}{\gamma \Delta t}\left\{{\dot{q}}_t\right\}-\left(\frac{1}{2\gamma }-1\right)\left\{{\ddot{q}}_t\right\}\hfill \\ \left\{{\dot{q}}_{t+\Delta t}\right\}=\frac{\beta }{\gamma \Delta t}\left(\left\{q_{t+\Delta t}\right\}-\left\{{\dot{q}}_t\right\}\right)+\left(1-\frac{\beta }{\gamma }\right)\left\{{\dot{q}}_t\right\}+\left(1-\frac{\beta }{2\gamma }\right)\Delta t\left\{{\ddot{q}}_t\right\}\hfill \end{array}\right..$$

(42)

By substituting Equation (43) into Equation (32), the displacement vector at the time of t + Δt can be obtained as in Equation (43):

$$\left\{q_{t+\Delta t}\right\}=\left[R\right]{\left[K\right]}^{-1},$$

(43)

where the equivalent stiffness K and the equivalent load R can be expressed as in Equations (44) and (45), respectively, as follows:

$$\left[K\right]=\left[K_s\right]+\frac{1}{\gamma \Delta t^2}\left[M_s\right]+\frac{\beta }{\gamma \Delta t}\left[\omega G_s+C_s\right].$$

(44)

$$\begin{array}{l}\left[R\right]=\left(\left[K_s\right]\left\{F_s\right\}+\left\{Q_s\right\}\right)+\left(\frac{1}{\gamma \Delta t^2}\left\{q_t\right\}+\frac{1}{\gamma \Delta t}\left\{{\dot{q}}_t\right\}+\left(\frac{1}{2\gamma }-1\right)\left\{{\ddot{q}}_t\right\}\right)\left[M_s\right]\\ +\left(\frac{\beta }{\gamma \Delta t}\left\{q_t\right\}+\left(\frac{\beta }{\gamma }-1\right)\left\{{\dot{q}}_t\right\}+\left(\frac{\beta }{2\gamma }-1\right)\Delta t\left\{{\ddot{q}}_t\right\}\right)\left[\omega G_s+C_s\right]\end{array}$$

(45)

The acceleration vector $\left\{{\ddot{q}}_{t+∆t}\right\}$ and velocity vector $\left\{{\stackrel{·}{q}}_{t+∆t}\right\}$ can be obtained by substituting $\left\{q_{t+∆t}\right\}$ into Equations (41) and (42), respectively.

2.6. Optimization Objective

It can be seen from the error transfer model in Section 2.3 that the geometric and mass eccentricities errors of a multistage rotor will change with the change of the assembly angles (θz_n) of the rotors at all stages, and the excitations and the nodal vibration responses on the rotor will also change with that. The rotor system is mainly subject to the radial excitation forces, so we primarily investigate the influences of the assembly angles of each rotor on the radial vibration responses and select the optimal assembly angles to minimize that. The resultant vibration velocity of the single-node in the rotor system can be expressed as in Equation (47):

$$\left\{\begin{array}{l}{f}_i\left(\gamma \right)=\sqrt{{\left[{\dot{x}}_i\left(\gamma \right)\right]}^2+{\left[{\dot{y}}_i\left(\gamma \right)\right]}^2}\hfill \\ \mathrm{s}.\mathrm{t}.\gamma =\left\{{\theta }_{z1},{\theta }_{z2},......,{\theta }_{zk}\right\}\hfill \end{array}\right.\left(i,k\in {\mathrm{N}}^{\ast },1\le i\le n,\theta z_k\in \left[0^{\circ }~{180}^{\circ }\right]\right),$$

(46)

where n refers to the number of the nodes in the finite element model, k to the number of the single-rotor. A minimax method is used to reduce the overall vibration level of the supporting parts on both sides of the rotor caused by geometric and mass eccentricities, as shown in Equation (47). The maximum value of the vibration velocities at the left and right bearing in the rotor system is defined as the optimization objective and the assembly angles of each rotor as the optimization variables.

$$\left\{\begin{array}{l}\min V\left(\gamma \right)=\min \left(\max \left(f_l(\gamma ),f_r(\gamma )\right)\right)\hfill \\ \mathrm{s}.\mathrm{t}.\gamma =\left\{{\theta }_{z1},{\theta }_{z2},......,{\theta }_{zk}\right\}\hfill \end{array}\right.\left(\theta z_k\in \left[0^{\circ }~{180}^{\circ }\right]\right),$$

(47)

where f_l(γ) and f_r(γ) are the vibration velocities at the left and right bearings, respectively.

3. Results

3.1. Simulation

3.1.1. Finite Element Model of a 4-Stage Rotor

Figure 3 shows a sectional view of a simulated four-stage rotor, scaled to a certain scale according to the high-pressure rotor system of a real aero-engine and simplified as a multistage rotor composed of four components: Rotor-1, Rotor-2, Rotor-3 and Rotor-4. Their assembly rabbets are tightly connected by twelve, twenty-four and twelve uniformly distributed screws, respectively. There are seven optional assembly angles between Rotor-1 and Rotor-2 (${\theta z}_2\in \left\{0^{°}{,30}^{°}{,60}^{°}{,90}^{°}{,120}^{°}{,150}^{°}{,180}^{°}\right\}$), thirteen optional assembly angles between Rotor-2 and Rotor-3 (${\theta z}_3\in \left\{0^{°}{,15}^{°}{,30}^{°}{,45}^{°}{,60}^{°}{,75}^{°}{,90}^{°}{,105}^{°}{,120}^{°}{,135}^{°}{,150}^{°}{,165}^{°}{,180}^{°}\right\}$), and seven optional assembly angles between Rotor-3 and Rotor-4 $({\theta z}_4\in \left\{0^{°}{,30}^{°}{,60}^{°}{,90}^{°}{,120}^{°}{,150}^{°}{,180}^{°}\right\}$). Rotor-1 is fixed by default during assembly (${\theta z}_1=0^{°}$).

The four-stage rotor model is divided into 42 nodes, and the dimensional parameters of each element are shown in

Table A1. The dimensional parameters of each element in the finite element model.

Element	ln [mm]	Dn [mm]	dn [mm]
1	2	20	0
2	16.5	33	0
3	5	33	0
4	3.5	33	0
5	8	35	0
6	5	35	0
7	2	39	0
8	2	42	0
9	26	42	27
10	24	42	27
11	3	58	36
12	3	58	0
13	8	82	0
14	15	192	0
15	5	82	0
16	3	82	0
17	3.5	82	54
18	24	82	72
19	50	82	72
20	3.5	102	72
21	3	110	72
22	7	110	74
23	19.5	82	74
24	3.5	82	56
25	3	128	56
26	10	128	48
27	34	128	112
28	46	128	112
29	7	128	48
30	5	128	50
31	3	128	33
32	6.5	68	33
33	30	42	33
34	20.5	42	33
35	11	42	0
36	2	39	0
37	5	35	0
38	8	35	0
39	3.5	33	0
40	5	33	0
41	16.5	33	0

. The rotor’s material is aluminum alloy, its elastic modulus is 7 × 10¹⁰ Pa, and its density and Poisson’s ratio are 2700 kg/m³ and 0.3, respectively. The screws at each assembly rabbet are loaded on Node-12, -17, -22, -25, and -32 as lumped masses. The twelve uniformly distributed screws’ mass and the diameter moment of inertia are 0.014 kg and 4.89 × 10⁻⁶ kg·m², respectively, and the twenty-four uniformly distributed screws’ mass and the diameter moment of inertia are 0.028 kg and 2.92 × 10⁻⁵ kg·m². Two lock nuts and a bearing ring are installed on the front and the rear axle, and they are loaded on Node-3, -4, -5, -39, -40 and -41 as lumped masses. The masses of the lock nuts and the end ring are 0.0326 kg and 0.0093 kg, respectively, and their diameter moment of inertia are 6.82 × 10⁻⁶ kg·m² and 1.65 × 10⁻⁷ kg·m². Two angular contact bearings are selected as the support elements, which are loaded on Node-6 and -38, and the cross stiffness and damping are neglected in simulation. The linear stiffness coefficient K_xx and K_yy of the roll bearings are 8 × 10⁴ and 1 × 10⁵ N/mm at the rotational speed of 3000 rpm.

The mass eccentricities errors are set at Node-10, -19, -28 and -34, and an M5 through-hole is used to produce the unbalanced mass in the rotors at each stage, whose center is collinear with the center of the calibrated screw hole of each rotor in the axial direction. The unbalanced masses of the rotors at all stages and their coordinates in the self-measuring coordinate system produced by the M5 through-holes are shown in

Table 1. The unbalanced masses of the rotors at all stages and their coordinates produced by the M5 through-holes.

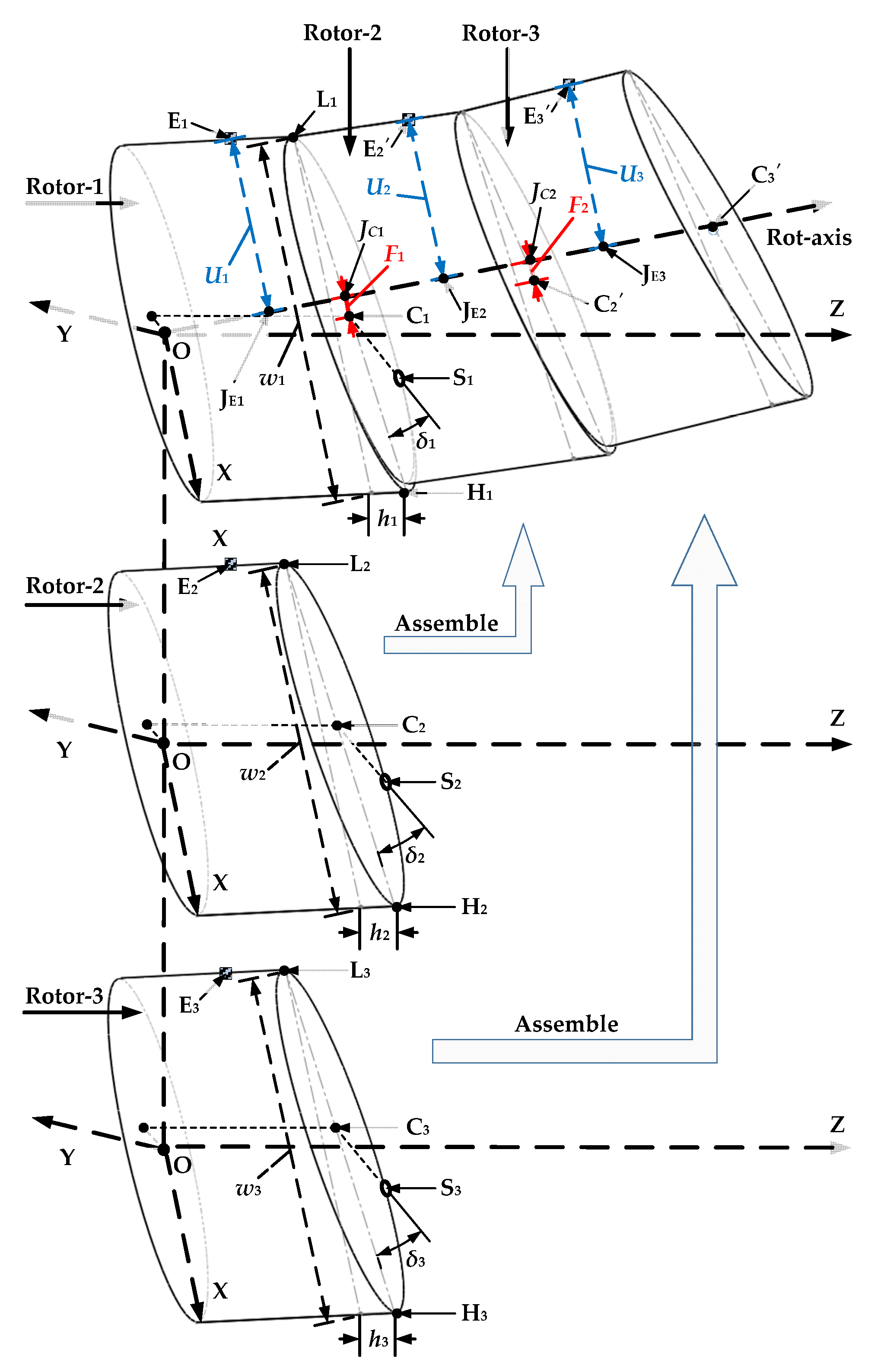
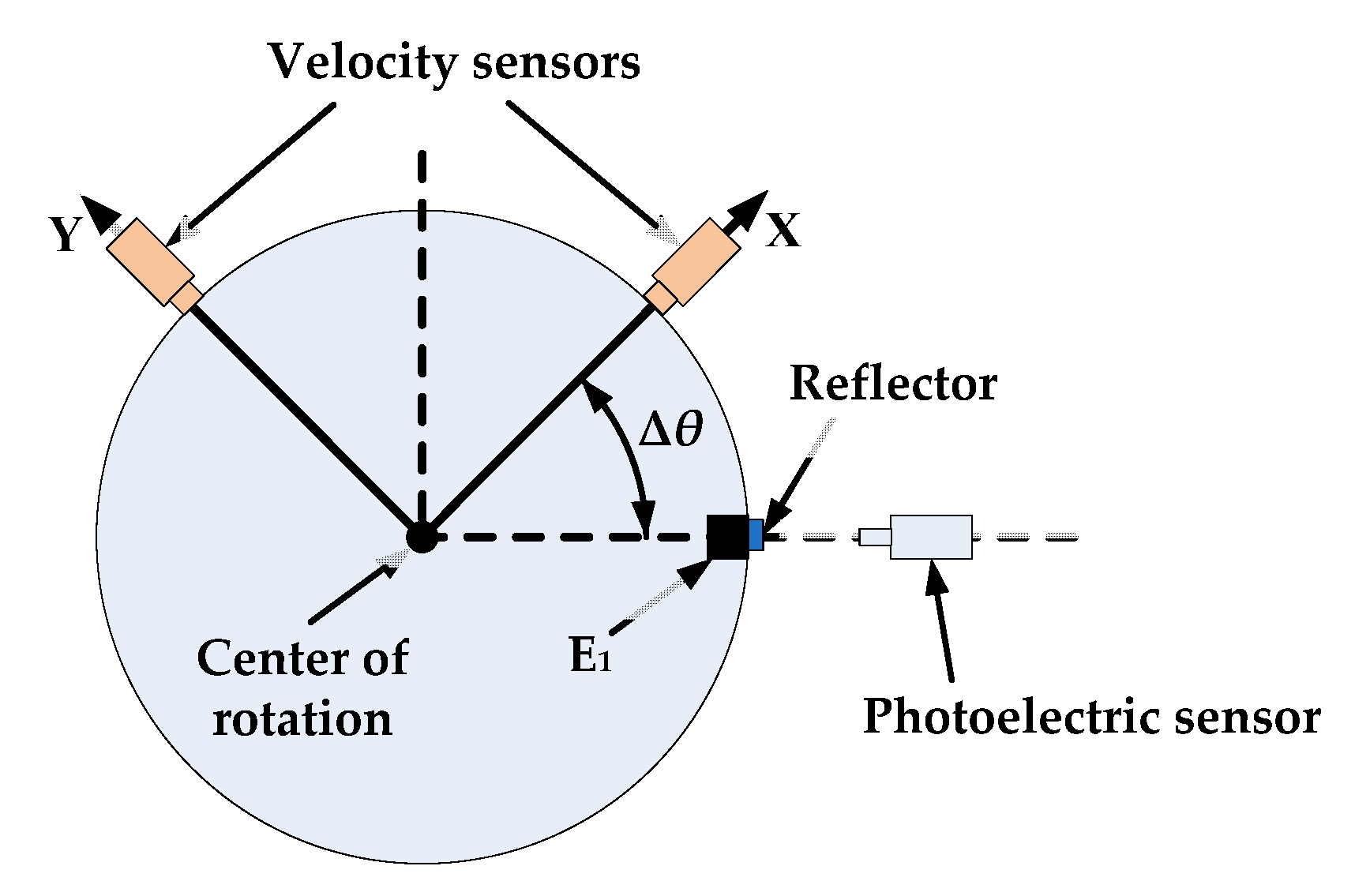
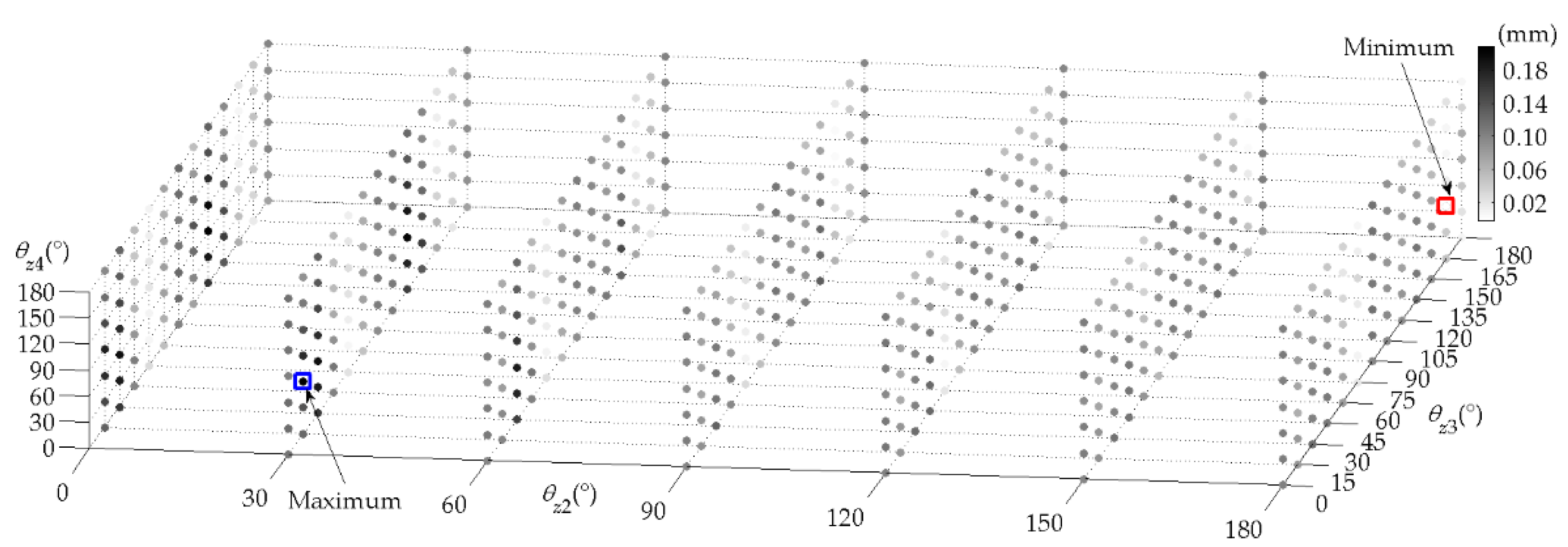
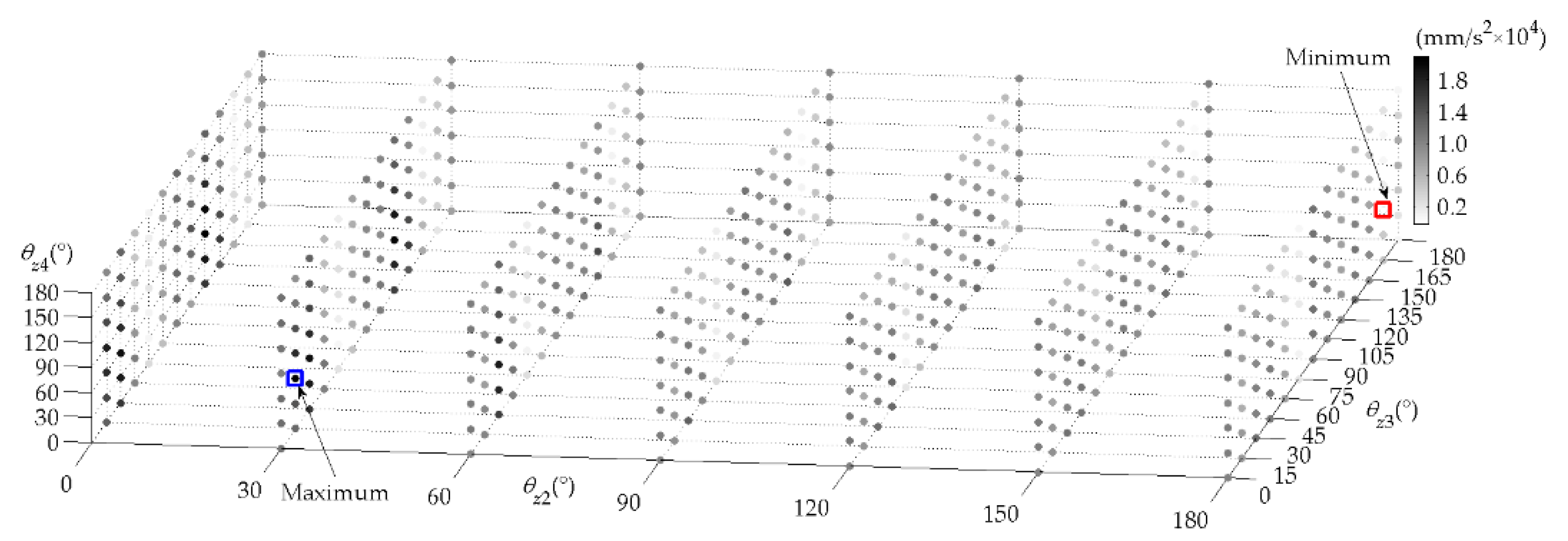
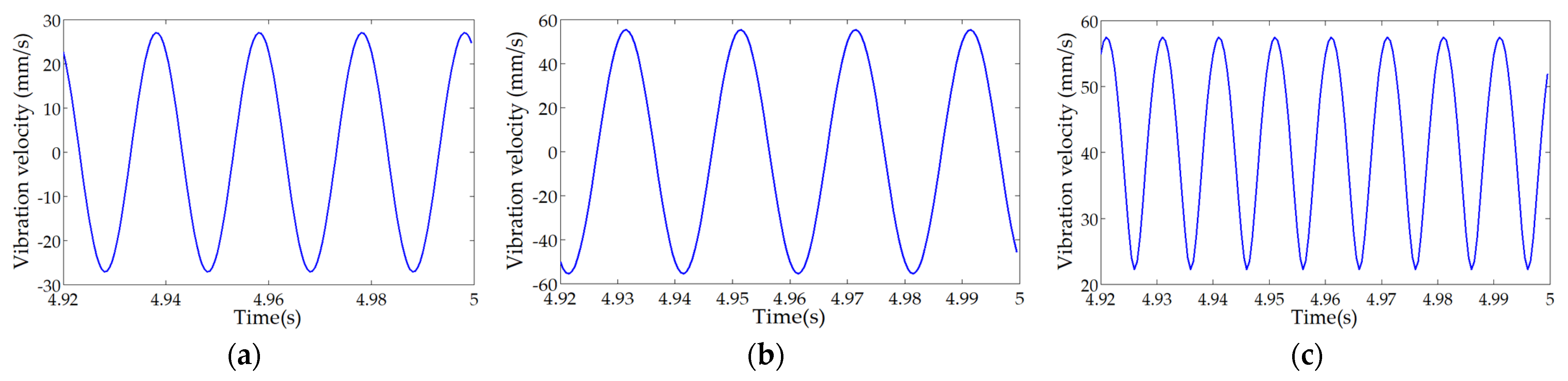
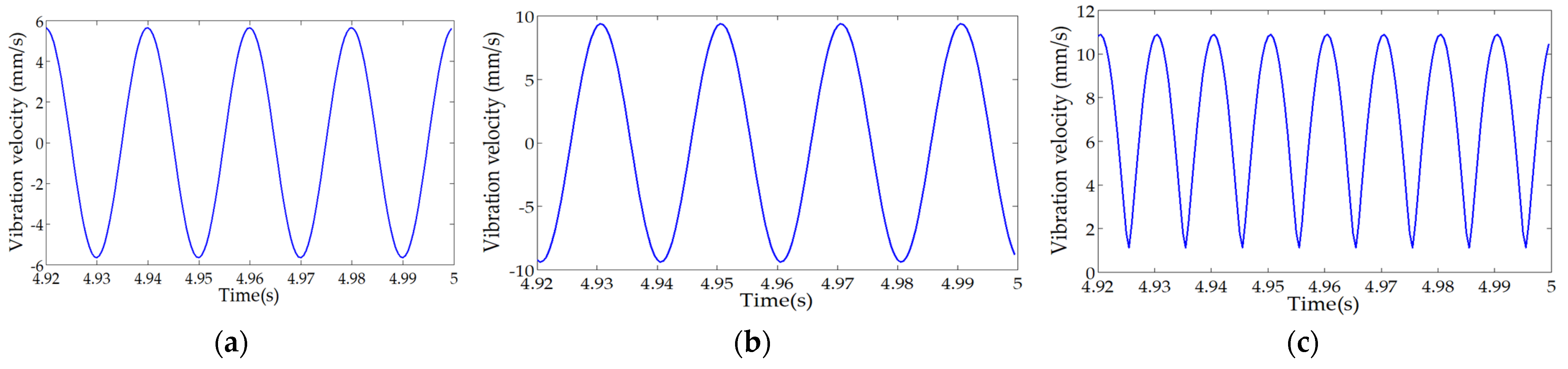
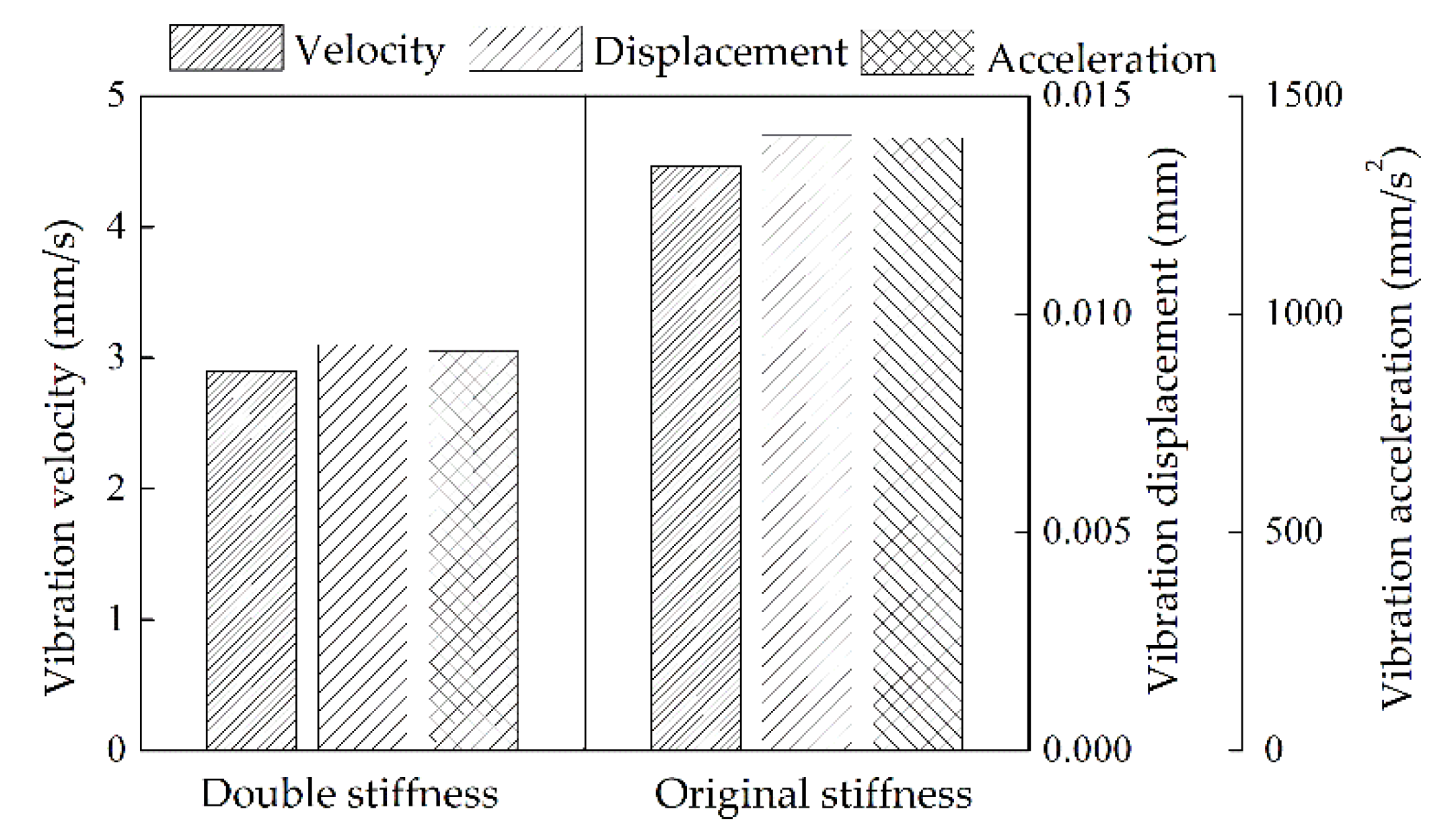
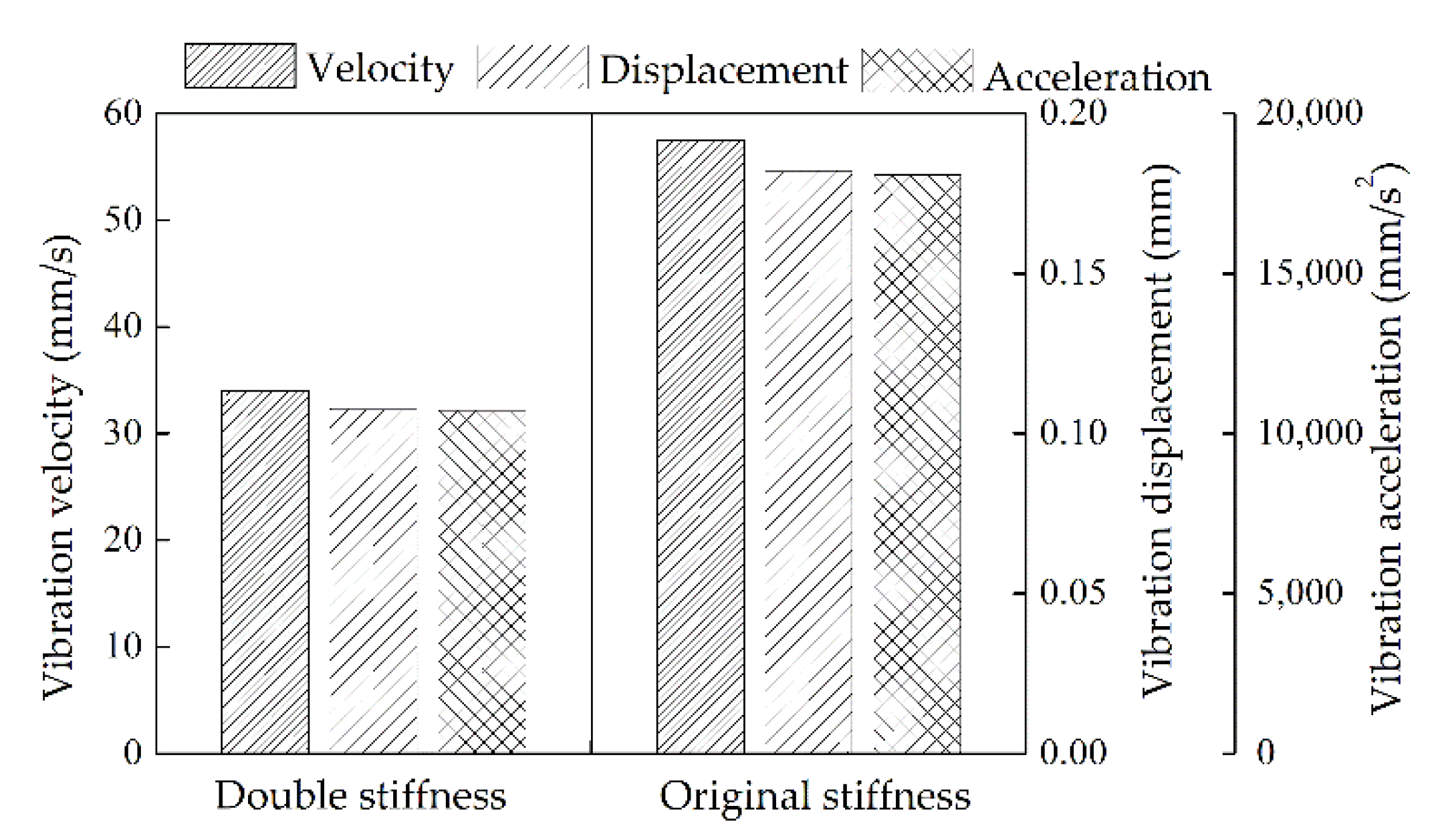
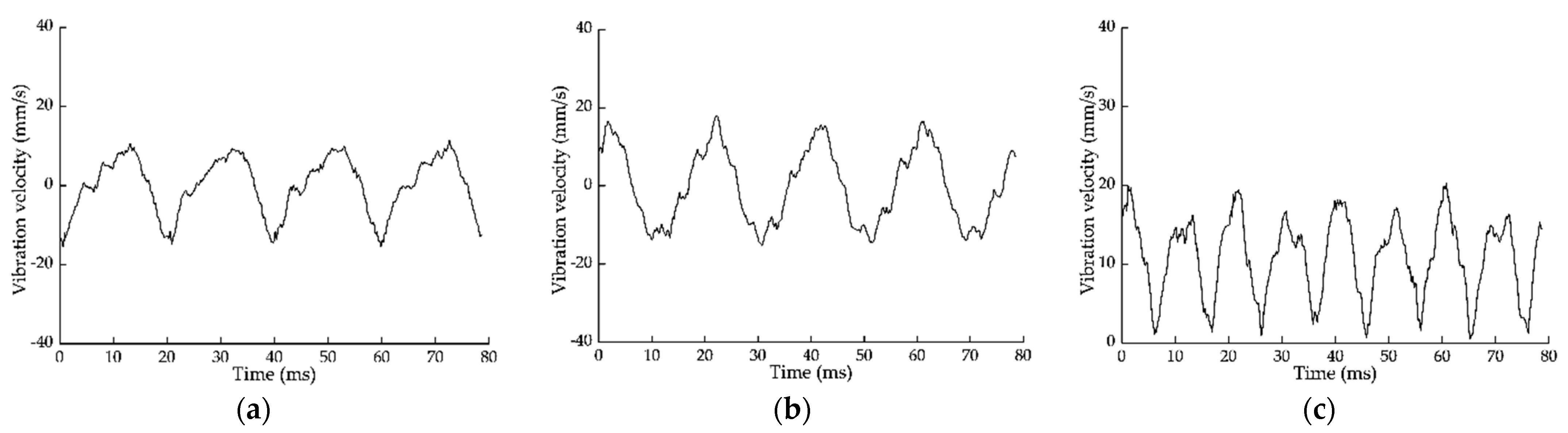
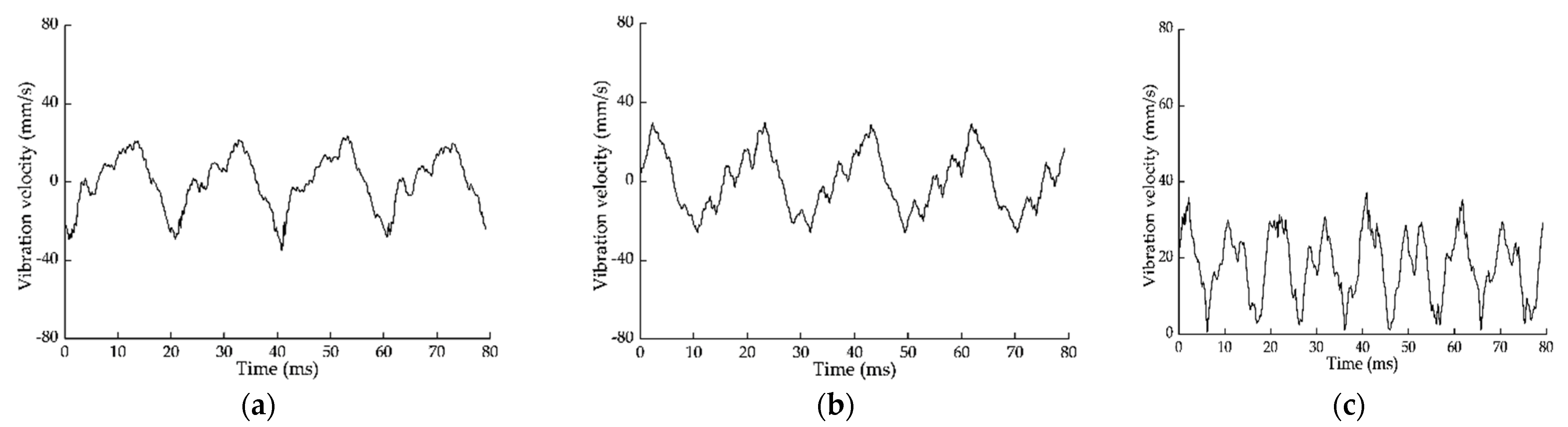
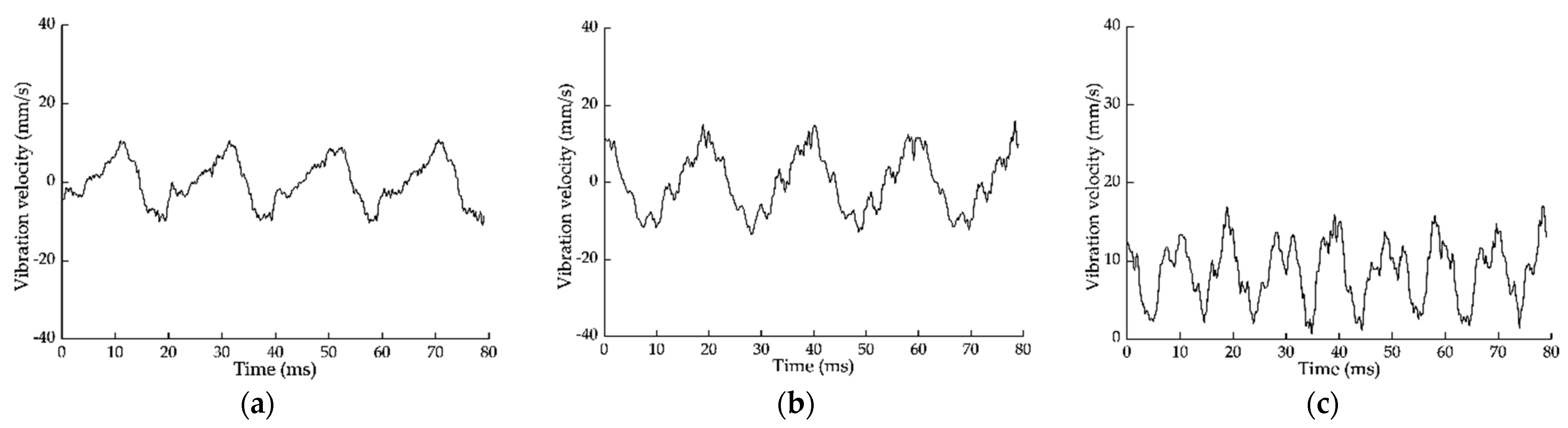
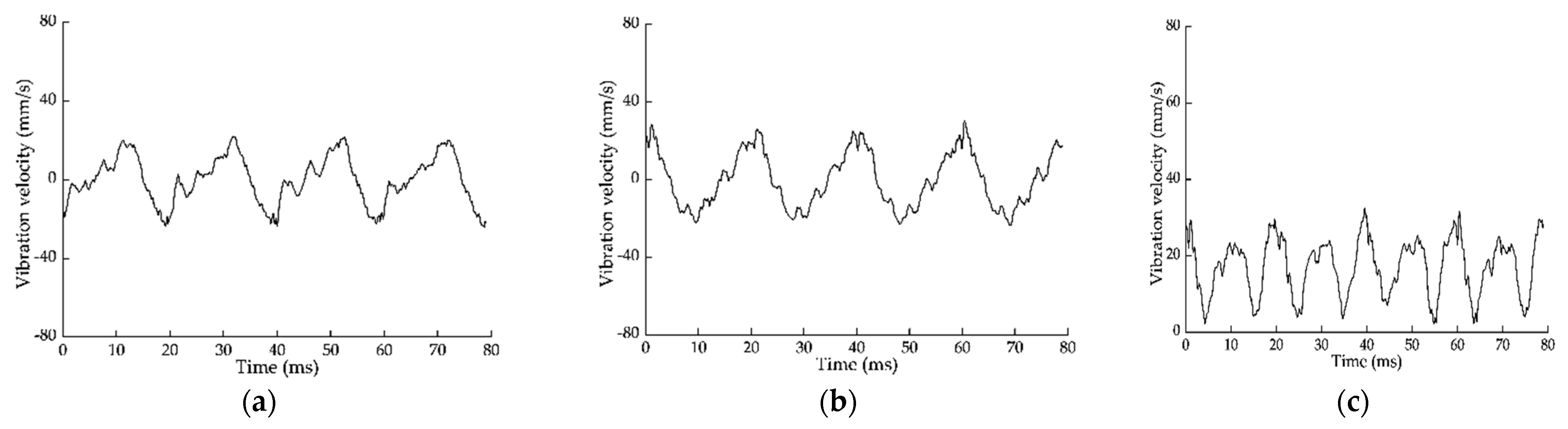
Unbalanced Mass Points	un [g]	Coordinates of En [mm]
E1	0.296	(17.25, 0, 35)
E2	0.197	(38.5, 0, 58.5)
E3	0.314	(60, 0, 77)
E4	0.178	(18.75, 0, 36.5)

. There are three combining sites in the four-stage rotor, which are Node-13, -22 and -32, respectively, that is, the excitation positions of the geometric eccentricities errors of the rotors at all stages.

3.1.2. The Machined Rotor According to the 4-Stage Rotor

The material object of the above simulated four-stage rotor was machined according to the dimensional parameters in Table A1. Figure 4 shows the measurement of the geometric parameters of each single-stage rotor by used a coordinate measuring machine (CMM).

Table 2. The measured geometric parameters of the 4-stage rotor.

Components	ξn [mm]	h1 [mm]	w1 [mm]	δn [°]
Rotor-1	(0.0181, 0.0062, 65.0152)	0.0193	36.0220	113
Rotor-2	(−0.009, −0.0223, 115.0210)	0.0235	101.9895	29
Rotor-3	(0.0056, 0.0244, 138.1047)	0.0241	50.0149	242
Rotor-4	(0.0116, 0.0124, 74.9581)	-	-	182

shows the measured geometric parameters of the four-stage rotor. By substituting the parameters in Table 1 and Table 2 into the error transfer model in Section 2.3, the geometric and mass eccentricities errors (U_n and F_n) of the rotors at each stage can be obtained, and the nodal vibration responses can be obtained by further substituting U_n and F_n into the dynamics model in Section 2.4 and Section 2.5. The unique unknown quantities are the assembly angles of the rotors at all stages (θz₁, θz₂,…, θz_n).

3.1.3. Optimization of the Assembly Angles

As the assembly angle of Rotor-1 is 0° by default, the position of the unbalanced mass point (E₁) in Rotor-1 is used as the initial acquisition direction of the photoelectric sensor. As shown in Figure 5, the acquisition angle of the vibration response in X-direction is 45° (Δθ = 45°). The rotational speed of the four-stage rotor is set at 3000 rpm. The maximum value of the vibration velocities at the left and right bearings (at Node-6 and -38) of the four-stage rotor in steady-state is taken as the optimization objective to search the optimal assembly angles of the rotors at each stage.

Figure 6, Figure 7 and Figure 8 show the maximum value of the vibration velocities, displacements and accelerations at the bearings under all possible sequences of the assembly angles (7 × 13 × 7 = 637), respectively. From

Table 3. The vibration responses at Node-6 and -38 under the optimal assembly (θz₂ = 180°, θz₃ = 165°, θz₄ = 60°).

Position	Vibration Velocity [mm/s]	Vibration Displacement [mm]	Vibration Acceleration [mm/s2]
Node-6	4.4630	0.0141	1.4044 × 103
Node-38	3.5759	0.0113	1.1259 × 103

, when the assembly angles of θz₂, θz₃ and θz₄ are 180°, 165°, and 60°, the vibration velocities at Node-6 and -38 are 4.4630 and 3.5759 mm/s, respectively. Assembling according to the above assembly sequence can also minimize the vibration displacements and accelerations at Node-6 and -38. The maximum vibration response is at Node-6 under the optimal assembly, and the vibration velocity curves of Node-6 are shown in Figure 9.

In addition, when the assembly angles of θz₂, θz₃ and θz₄ are 30°, 15°, and 60°, the vibration velocities at Node-6 and -38 are 40.5936 and 57.4941 mm/s, respectively. If the assembly is carried out according to the above assembly sequence, the vibration velocities at the bearings will reach the maximum. At the same time, the vibration displacement and acceleration can also reach the maximum (

Table 4. The vibration responses at Node-6 and -38 under the worst assembly (θz₂ = 30°, θz₃ = 15°, θz₄ = 60°).

Position	Vibration Velocity [mm/s]	Vibration Displacement [mm]	Vibration Acceleration [mm/s2]
Node-6	40.5936	0.1285	1.2785 × 104
Node-38	57.4941	0.1820	1.8076 × 104

). The maximum vibration velocity is at Node-38 under the worst assembly, and the vibration velocity curves of Node-38 are shown in Figure 10.

When θz₂, θz₃ and θz₄ are all 0°, the vibration velocity at Node-6 and -38 are 7.5441 and 10.8975 mm/s, respectively. From

Table 5. The vibration responses at Node-6 and -38 under the default assembly (θz₂ = 0°, θz₃ = 0°, θz₄ = 0°).

Position	Vibration Velocity [mm/s]	Vibration Displacement [mm]	Vibration Acceleration [mm/s2]
Node-6	7.5441	0.0239	2.3778 × 103
Node-38	10.8975	0.0345	3.4298 × 103

, the maximum vibration velocity, displacement and acceleration are all at Node-38 under the default assembly, and the vibration velocity curves of Node-38 are shown in Figure 11.

The maximum vibration velocity under the optimal assembly is reduced by 92.2% and 59.0% compared with that under the worst assembly and default assembly, respectively. The maximum vibration displacement under the optimal assembly is reduced by 89.0% and 59.1% compared with that under the worst assembly and default assembly, respectively. The maximum vibration velocity under the optimal assembly is reduced by 92.2% and 59.1% compared with that under the worst assembly and default assembly, respectively.

3.1.4. Effects of Stiffness and External Force on the Vibration Responses

The assembly angles under the optimal assembly, the worst assembly and the default assembly were obtained, respectively, in Section 3.1.3. This section will investigate the effects of the support stiffness and the external force changes on vibration response under the above three assembly states.

Firstly, the original stiffness coefficients were doubled, that is, K_xx = 1.6 × 10⁵ N/mm and K_yy = 2 × 10⁵ N/mm, and then the maximum vibration responses at the bearings (Node-6 and -38) under the new support stiffness were calculated.

Table 6. The vibration responses at Node-6 and -38 under the optimal assembly.

Position	Vibration Velocity [mm/s]	Vibration Displacement [mm]	Vibration Acceleration [mm/s2]
Node-6	2.9001	0.0093	0.9149 × 103
Node-38	2.1121	0.0074	0.8221 × 103

,

Table 7. The vibration responses at Node-6 and -38 under the worst assembly.

Position	Vibration Velocity [mm/s]	Vibration Displacement [mm]	Vibration Acceleration [mm/s2]
Node-6	25.1136	0.0795	7.9071 × 103
Node-38	34.0271	0.1077	1.0713 × 104

and

Table 8. The vibration responses at Node-6 and -38 under the default assembly.

Position	Vibration Velocity [mm/s]	Vibration Displacement [mm]	Vibration Acceleration [mm/s2]
Node-6	4.4776	0.0176	1.7205 × 103
Node-38	7.9312	0.0284	2.4682 × 103

show the vibration responses at Node-6 and -38 under the optimal assembly, the worst assembly and the default assembly. Figure 12, Figure 13 and Figure 14 show that the increase of stiffness can reduce the maximum vibration responses at the bearings under the three assembly sequences above.

In addition, considering that the belt drive will be used in the experiments and there is a very light vertical downward preload on the measured rotor, an external force was added at the contact position between the belt and the rotor (Node-34), and the vibration responses under the optimal assembly were calculated when the external force is 5 N and 10 N, respectively. From

Table 9. The vibration velocities at Node-6 and -38 under different external forces.

External Force [N]	Vibration Velocity at Node-6 [mm/s]	Vibration Velocity at Node-38 [mm/s]
0	4.4630	3.5759
5	4.3109	3.1741
10	4.1034	2.4683

,

Table 10. The vibration displacements at Node-6 and -38 under different external forces.

External Force [N]	Vibration Displacement at Node-6 [mm]	Vibration Displacement at Node-38 [mm]
0	0.0141	0.0113
5	0.0128	0.0088
10	0.0117	0.0064

and

Table 11. The vibration accelerations at Node-6 and -38 under different external forces.

External Force [N]	Vibration Acceleration at Node-6 [mm/s2]	Vibration Acceleration at Node-38 [mm/s2]
0	0.9149 × 103	0.8221 × 103
5	0.8058 × 103	0.6072 × 103
10	0.7129 × 103	0.4305 × 103

, because the external force was applied closer to the right bearing, the vibration response at Node-38 is significantly affected by the external force than that at Node-6.

3.2. Experimental Verification

The experimental setup is shown in Figure 15. The measured rotor was placed on a dynamic balancing machine driven by a belt, and the original rollers support on both sides were refitted into two fixed bearings. The four single-stage rotors in Figure 4 were assembled according to the three assembly sequences (optimal, worst and default) obtained in Section 3.1.3, respectively. Then, the corresponding three vibration tests were carried out on the assembled four-stage rotor system at the rotational speed of 3000 rpm. The sensitivity of the velocity sensors in Figure 15 are all 20 mv/mm/m. The eight channel signal collector was manufactured by National Instruments Co., Ltd. (Austin, TX, USA).

The vibration velocity curves of the left bearing under the optimal assembly, worst assembly and default assembly are shown in Figure 16, Figure 17 and Figure 18, respectively, and that of the right bearing under the same assembly conditions are shown in Figure 19, Figure 20 and Figure 21. From

Table 12. The vibration velocities at the left and right bearings.

State	Maximum of fl(γ) [mm/s]	Maximum of fr(γ) [mm/s]
Optimal assembly	20.2505	17.1042
Worst assembly	66.5348	55.5799
Default assembly	37.1793	32.4968

, the maximum vibration velocities at the bearings in the four-stage rotor system under the optimal assembly, worst assembly and default assembly are 20.2505, 66.5348 and 37.1793 mm/s, respectively. The maximum vibration velocity under the optimal assembly is reduced by 69.6% and 45.5% compared with that under the worst assembly and default assembly, respectively. Although the reduction rate of the vibration velocities at the bearings after optimized assembly is lower than the simulation results, the optimization effect is still significant. The difference in support stiffness may cause the difference between the simulated and measured vibration velocities. It can be seen from the simulation results in Section 3.1.4 that the actual support stiffness in the experiments may be slightly lower than that in the simulations.

The experimental results verified the effectiveness of assembly optimization to a certain extent. However, unlike the simulation results, the maximum vibration velocities under the worst and default assembly appeared at the left bearing. This is because the belt applied a slight preload evenly distributed force to the rotor, which generates friction to drive the rotor to rotate, and this preload was closer to the right bearing, which may inhibit the vibration at the right bearing. Therefore, the vibration response at right bearing is significantly affected by the external force than that at left bearing.

4. Discussion

The aero-engine is composed of multistage rotors, and its primary function is to realize the pressurization of air step-by-step, thus providing an enormous power source. The vibration index of the multistage rotor system directly affects the safe operation and working efficiency of the aero-engine. However, the assembly process of the multistage rotor is complex. The traditional assembly process mainly depends on manual experiences matching the assembly angles, which often needs repeated disassembly to meet the vibration index. The existing assembly optimization methods only optimize the concentricity and unbalance of the multistage rotor, not directly optimize the vibration responses of the rotor. Therefore, to solve this problem, we established the direct relationship between the assembly angles of the rotors at each stage and the vibration responses of the rotor. The nodal vibration responses could be directly obtained by inputting the geometric and mass characteristic parameters of the rotor into the calculation model. In the simulation, we took the maximum vibration velocities at the left and right bearings of a scaled high-pressure rotor system as the optimization objective, and obtained the optimal assembly angles, making the maximum vibration velocities to the minimum. Although the optimization effect of the experiments was not as significant as that of the simulations, the vibration velocities at the bearings of the four-stage rotor could be significantly reduced by assembling according to the optimal assembly angles obtained by the simulation. As each test needs to be reassembled and clamped, the absolute consistency of the boundary conditions for each test cannot be fully guaranteed. Moreover, the support stiffness used in the simulation was also challenging to be entirely consistent with the actual support stiffness, which can only ensure that the boundary conditions of the three simulations and experiments are consistent. In the follow-up research, we plan to use a coupling drive instead of a belt-drive, which can eliminate the interference of the belt preload on the one hand, and investigate the suppression effect of the assembly optimization method proposed in this study on rotor vibration at higher rotational speed on the other hand.

5. Conclusions

In this study, we proposed a vibration suppression method for the multistage rotor of an aero-engine based on assembly optimization. The main contributions of this study can be summarized as follows:

• The mathematical relationship between the assembly angles of the rotors at all stages and the nodal vibration responses was established by combining the error transfer model of the geometric and mass eccentricities with the dynamics model of the multistage rotor system.
• An optimization function was developed, which takes the assembly angles as the optimization variables and the maximum vibration velocity at the bearings as the optimization objective. Then, the optimal assembly angles that can minimize the maximum vibration velocity at the bearings were calculated in the simulation.
• The experimental results showed that the maximum vibration velocity at the bearings of the four-stage rotor system under the optimal assembly was reduced by 69.6% and 45.5% compared with that under the worst assembly and default assembly.