Abstract
For mechanical compound fault, it is of great significance to employ the vibration signal of a single-channel compound fault to analyze and realize the separation of multiple fault sources, which is essentially the problem of single-channel blind source separation. Shift invariant K-means singular value decomposition (shift invariant K-SVD) dictionary learning is suitable to extract the periodic and repeated fault features of a rotating machinery fault, hence in this article a single-channel compound fault analysis method is put forward which combines shift invariant K-SVD with improved fast independent component analysis (improved FastICA) algorithm. Firstly, based on single-channel compound fault signal, the shift invariant K-SVD algorithm can be used for learning multiple latent components that can be constructed as a virtual multi-channel signal. Then the improved FastICA algorithm is utilized to realize the separation of multiple fault source signals. With regard to the FastICA algorithm, the third-order convergence Newton iteration method is adopted to improve convergence speed. Moreover, in order to address the problem that FastICA is very sensitive to initialization, a steepest descent method can be applied. The experimental analysis of the compound fault of rolling bearing verifies that the presented method is effective to separate multiple fault source signals and the improved FastICA algorithm can increase convergence rate and overcome the problem of sensitivity to initialization.
1. Introduction
Recently in the field of mechanical fault diagnosis, sparse representation has been extensively employed [1,2,3,4,5]. Sparse representation mainly includes two parts: sparse coefficient solving and dictionary learning. With regard to dictionary learning, K-means singular value decomposition (K-SVD) [6] can be utilized. In the shift invariant case, some patterns appear periodically and repeatedly in the long signal, and shift invariant dictionary learning algorithms can be adopted, e.g., shift invariant sparse coding [7] and shift invariant K-SVD [8], etc. There are periodic repetitive shocks in the vibration signals of a rotating machinery fault, therefore shift invariant dictionary learning algorithm is especially available to extract fault feature of a rotating machine and then fault diagnosis can be carried out. In recent years in the area of fault diagnosis of rotating machinery, shift invariant dictionary learning algorithms have been introduced [9,10,11,12,13,14,15,16,17,18]. In [11,13,18], shift invariant K-SVD was implemented. In this article, we utilized shift invariant K-SVD to acquire basis functions, then their corresponding latent components can be obtained and constructed as virtual multi-channel signal.
In engineering practice the vibration signal of a machinery fault is usually generated by multiple vibration sources, however the contribution of each vibration source to the mixed signal is unknown. For the diagnosis of a mechanical compound fault, it is very meaningful to effectively separate multiple unknown vibration source signals from a mixed signal, which is called blind source separation (BSS). To address this issue, blind source separation methods, e.g., independent component analysis (ICA), have been broadly applied to machinery fault diagnosis [19,20,21,22]. BSS usually needs to collect multi-channel signals. However, considering the installation conditions and cost of sensors, the number of sensors is required to be as small as possible in engineering practice, and sometimes only one channel signal can be utilized to separate different vibration source signals, which is called single-channel BSS. For this kind of underdetermined BSS problem, ICA cannot solve it directly. Therefore, we usually transform a single-channel signal to a multi-channel signal through some methods, and then ICA can be carried out using the transformed multi-channel signal. For example, based on a single-channel signal we can adopt empirical mode decomposition (EMD) [23] and ensemble empirical mode decomposition (EEMD) [24], etc. to obtain multiple intrinsic mode functions [25,26], and then perform ICA to realize blind source separation [27,28,29,30,31,32,33,34,35,36,37,38]. EMD does not need to construct basis functions and realizes adaptive decomposition of the signal in the time scale. However, there exists mode aliasing in EMD. Although EEMD can effectively suppress mode aliasing, the added white noise finally needs to be compensated by increasing the number of ensemble averaging, hence the calculation is time-consuming and the reconstruction error is large. In this article, we implemented shift invariant K-SVD to transform a single-channel signal into multi-channel signal.
As for ICA, fast independent component analysis (FastICA) is a frequently used algorithm, which employs fixed point and Newton iteration, thus possessing a fast convergence rate [39]. However, the FastICA algorithm is very sensitive to the initial value that leads to unstable convergence. In this paper, we employed the steepest descent method to solve this problem. Additionally, third-order convergence Newton iteration method is implemented to further accelerate convergence [40].
In this article, we propose a new mechanical compound fault analysis method combining shift invariant K-SVD and improved FastICA based on the steepest descent method and third-order convergence Newton iteration method to achieve single-channel blind source separation. Firstly, shift invariant K-SVD is conducted for a single-channel mechanical compound fault signal to learn multiple basis functions and corresponding latent components that can be constructed as a virtual multi-channel signal. Subsequently, based on a virtual multi-channel signal improved FastICA is carried out to separate different source signals that are statistically independent.
The rest of this paper is shown below: in Section 2 shift invariant K-SVD algorithm and the relationship between single-channel blind source separation and shift invariant K-SVD are introduced. Section 3 describes the improved FastICA algorithm using steepest descent and third-order convergence Newton iteration. Afterwards, in Section 4 the proposed single-channel compound fault analysis method combining shift invariant K-SVD with improved FastICA is summarized. Next, Section 5 presents the experiment of rolling bearing compound fault, which verified the validity of the developed method. Finally, the conclusions are obtained in Section 6.
2. Single-Channel Blind Source Separation (BSS) Based on Shift Invariant K-Means Singular Value Decomposition (K-SVD)
The proposed single-channel BSS method based on shift invariant K-SVD is divided into two stages: shift invariant dictionary learning and ICA. Firstly, the shift invariant K-SVD dictionary learning algorithm is employed to obtain basis functions and their corresponding latent components and the multiple latent components can constitute virtual multi-channel signals. Then, ICA is conducted to separate multiple source signals using the constructed virtual multi-channel signal.
2.1. Shift Invariant K-SVD Algorithm
Shift invariant K-SVD algorithm is based on a long signal and suppose there are K basis functions . Then the objective function is [8]:
where is shift operator that shifts the basis function to time τ and extends it by setting the rest to 0 to get a dictionary atom with the same length as the long signal. is the sparse coefficient corresponding to the dictionary atom . s indicates the sparse coefficient of the long signal while T denotes sparsity prior.
In the shift invariant K-SVD algorithm, there are two steps: sparse coefficient solving and dictionary updating stage. During dictionary updating, with respect to the basis function , the set of activated sparse coefficients is and the definition of signal without contribution from other basis functions can be made:
where r represents residual signal. According to Equation (1), the basis function can be optimized by:
The above objective function can be rewritten:
where is the operator that can extract a segment with the same length as the basis function from the long signal and the start time of the segment is τ.
Based on the activation coefficients corresponding to the basis function , the sparse coefficients and the basis functions can be jointly estimated. Through Equation (4), a matrix can be formed by segment , and singular value decomposition is carried out on it while only the maximum singular value is kept, that is, the best basis function and the corresponding sparse coefficient can be obtained by taking the first principal component:
In summary, the steps of shift invariant K-SVD algorithm are:
- (1)
- For a long signal x, set the parameters including the length q and number K of basis functions and the sparsity prior T. The basis functions are initialized through randomly intercepting on the signal x and be normalized afterwards. Let the iteration number t = 1 and set tolerance error ;
- (2)
- Sparse coefficient solving. The fast matching pursuit algorithm [41] is employed to solve sparse coefficient s;
- (3)
- Dictionary update. The basis functions are updated sequentially and if it is updated to , the set of sparse coefficients activated by can be obtained, then new and corresponding sparse coefficients are computed through Equations (5) and (6);
- (4)
- Let and decide whether the algorithm reaches the termination condition. When the ratio of reconstruction error of two adjacent iterations is less than , the iterations stop, if not repeat (2)–(4).
2.2. Single-Channel BSS with Shift Invariant K-SVD
Shift invariant K-SVD does not need to truncate the original long signal to obtain training samples, while directly using the original long signal for self-learning to obtain a series of basis functions. Each basis function is translated and extended to the length of the original signal to obtain the sub-dictionary corresponding to the basis function . Through the shift invariant dictionary learning, K self-learned basis functions in total are obtained, and each basis function represents the fault characteristic mode implicit in the original signal.
After the basis functions and corresponding sub-dictionaries are learned, a total over-complete dictionary can be constructed. Then, based on dictionary D, matching pursuit can be employed to calculate sparse coefficient of the original single-channel signal x, and the latent component corresponding to basis function can be reconstructed by:
where represents corresponding sparse coefficient of sub-dictionary . These latent components are obtained by the reconstruction of the basis functions that capture different fault characteristic modes hidden in the long signal, therefore multiple latent components can be constructed as a virtual multi-channel signal, namely observation signal .
In this study, the single-channel BSS is a linear mixed model. Suppose there are n independent source signals, then observation signal acquired through only one sensor is a linear superposition of the source signals, as shown below:
where indicates the i-th source signal and mixing coefficient represents the contribution of to the mixed signal.
For the virtual multi-channel signals (K indicates the number of channels), the above equation can be rewritten:
where A means mixing matrix, which can be estimated by ICA and thus the estimation of the source signals can be acquired:
where W corresponding to mixing matrix A stands for demixing matrix, namely separating matrix. represents the estimated source signals separated by ICA.
3. Improved Fast Independent Component Analysis (FastICA) Algorithm
3.1. FastICA
Suppose that the observation signal X is preprocessed to obtain a new signal z, w denotes a row vector in demixing matrix W. The FastICA algorithm maximizes the non-Gaussianity of vector (where T denotes transpose) through a fixed point iterative algorithm. The most commonly used evaluation function for non-Gaussianity is the approximation of negative entropy. The objective function of the FastICA algorithm is [39]:
where G indicates an arbitrary non-quadratic function and v represents Gaussian random variable with zero mean and unit variance. Optimal w can be obtained through maximizing . It can be seen that under the constraints of , the negative entropy is maximized means that is maximized, then using Lagrange multiplier algorithm the objective function of the fixed point algorithm can be acquired as follows:
where β signifies a constant. The above optimization problem can be solved via:
where the function g represents derivative of G. In order to get solution of w in the above equation, the principle of FastICA algorithm is similar to Newton iterative. Let the left of the above equation be:
The gradient of is:
where T denotes transpose. Through the above equations and approximate treatment, the final iterative form of FastICA algorithm can be obtained:
The weight vector w needs to be normalized after each iteration by the following equation:
In general, the steps of FastICA algorithm are:
- (1)
- Firstly, remove the mean value of the observation signal X, and then whiten it to get the variable z. Set the maximum number of iterations N and tolerance error ε;
- (2)
- Set initial weight vector w and let the iteration number t = 1;
- (3)
- Update w by Equation (16) and normalize it after each iteration by Equation (17);
- (4)
- Let . If it does not converge, namely and , go back to step (3).
3.2. Improved FastICA
The FastICA algorithm is generally a relatively good learning algorithm, but the algorithm is easily affected by the selection of the initial value, resulting in unstable convergence. To solve the problem, the steepest descent whose performance is not affected by the initial value can be employed to initialize w. Moreover, a third-order convergence Newton iteration method can improve convergence speed.
3.2.1. Steepest Descent Method
The iteration steps of steepest descent include:
- (1)
- The initialization matrix is randomly selected and transformed into an orthogonal matrix (where T denotes transpose);
- (2)
- Compute negative gradient of (where T denotes transpose) at W:
The function drops faster in the negative gradient direction, so negative gradient can be brought in as a relaxation factor:
- (3)
- If it does not converge, namely , go back to step (2).
3.2.2. Third-Order Convergence Newton Iteration
The conventional Newton iteration has a second-order convergence rate, while the third-order convergence Newton iteration method is on the basis of the conventional Newton iteration, which has a third-order convergence rate. In the FastICA algorithm with third-order convergence, the iteration of w is as follows [40]:
3.2.3. Improved FastICA
The improved FastICA combines the steepest descent method and third-order convergence Newton iteration method, whose steps are:
- (1)
- Firstly, remove mean value of observation signal X, and then whiten the zero-mean signal to obtain the variable z. Set the maximum number of iterations N and tolerance error ε;
- (2)
- Using steepest descent method to solve initial weight vector w and let the iteration number t = 1;
- (3)
- Update w by Equation (20);
- (4)
- Let . If it does not converge, namely and , go back to step (3).
4. Single-Channel Compound Fault Analysis Method Using Shift Invariant K-SVD and Improved FastICA
In this study, a single-channel mechanical compound fault analysis method combining shift invariant dictionary learning with an improved FastICA algorithm is presented. Figure 1 describes the whole process of the method and the description with regard to each stage is as follows:
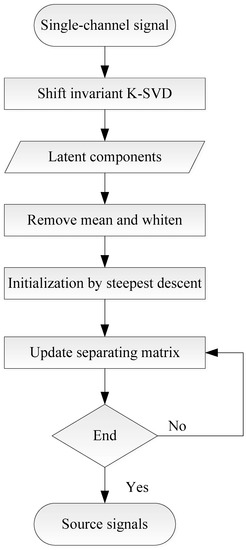
Figure 1.
Diagram of the presented method.
- (1)
- Dictionary learning with shift invariant K-SVD. Using the single-channel vibration signal, an over-complete dictionary is obtained with shift invariant K-SVD.
- (2)
- Construct a virtual multi-channel signal through latent components. Using the learned over-complete dictionary, latent components can be obtained and constructed as a virtual multi-channel signal.
- (3)
- Blind source separation using improved FastICA. The improved FastICA algorithm combining steepest descent method and third-order convergence Newton iteration can be conducted to achieve BSS and obtain estimated source signals.
5. Experiment and Analysis
5.1. Description of the Experiment
To validate the proposed method, an experiment of a compound fault of rolling bearings was carried out on the QPZZ II test bench that can simulate faults in rotating machinery, including compound faults of outer and inner races, outer race and rolling element, and outer race, inner race and rolling element. The experiment rig is demonstrated in Figure 2a. In rolling bearing, the inner race revolves with the main drive shaft at 800 r/min, while the outer race is installed on the bearing housing. An acceleration sensor is respectively installed on the horizontal and vertical positions of bearing housing to synchronously collect the vibration signals of the bearing in two directions. The data acquisition system is shown in Figure 2b, whose sampling frequency is 8192 Hz. The type of experiment bearing is NU205, and the main geometric parameters and theoretical fault characteristic frequencies are described in Table 1 and Table 2, respectively. Among them, Z, d, D, θ represent number of rolling elements, rolling element diameter, pitch diameter and contact angle individually. fr, fc, fi, fo and fb separately denotes rotation frequency of drive shaft, rotation frequency of cage, characteristic frequency of bearing inner race fault, outer race fault and rolling element fault. In total 26 sets of signal are collected under each compound fault state of the rolling bearing. Each signal has 8192 points and the duration is 1 s.

Figure 2.
The experiment rig of rolling bearings with compound fault: (a) experiment rig; (b) data acquisition system.

Table 1.
The main parameters of rolling bearing.

Table 2.
The characteristic frequencies of rolling bearing (Hz).
5.2. Compound Fault of Rolling Bearing with Outer and Inner Race Fault
The time waveform and envelope spectrum of the first set of vibration signals of a compound fault of a rolling bearing with outer and inner race faults are shown in Figure 3. As can be seen from the envelope spectrum, the peak values under the characteristic frequency of the bearing outer race fault and its multiplier frequencies are obvious, which means that an outer race fault has occurred, but the peak value under the characteristic frequency of inner race fault is not obvious.
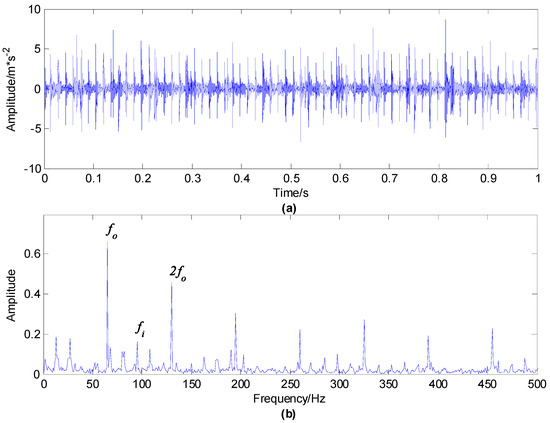
Figure 3.
Rolling bearing signal with outer and inner race compound fault: (a) time waveform; (b) envelope spectrum.
Firstly, shift invariant K-SVD was utilized to analyze the first set of vibration signals of the compound fault of a rolling bearing with outer and inner race faults. The main parameters of shift invariant K-SVD are: the length of basis function is 128, the basis function number is 8, and the signal length is 8192 so the sparsity is set to 1.2 × 8192/128 ≈ 77 [11]. The learned eight basis functions are exhibited in Figure 4. It can be seen that these basis functions can successfully capture the fault characteristics in the mixed signal.
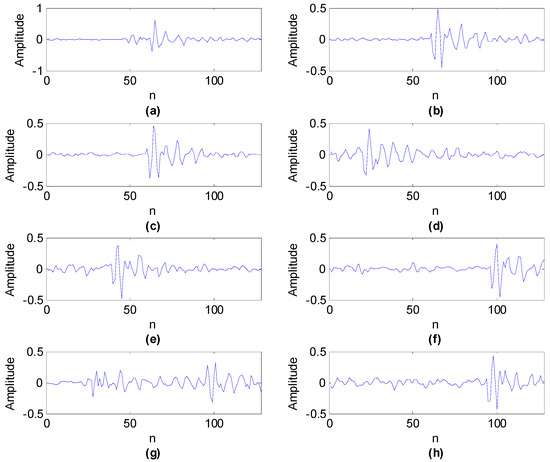
Figure 4.
The eight learned basis functions using shift invariant K-SVD algorithm corresponding to outer and inner race compound fault.
After that the multiple latent components can be obtained and constructed as a virtual 8-channel signal. Then, original FastICA and improved FastICA were employed to separate the source signals, respectively. The source number is 2 and tanh function is utilized as nonlinear function. Through a large number of repeated runs of 26 sets of vibration signals using original FastICA and improved FastICA algorithms, respectively, it can be found that the separation effect of the improved FastICA algorithm and original FastICA is basically the same. The estimated source signals and their corresponding envelope spectra of the first set of vibration signals using improved FastICA are demonstrated in Figure 5. From Figure 5, we can see that improved FastICA can successfully separate mixed signals. Besides that for source signal , in the envelope spectrum the peak values under and its multiplier frequencies are obvious, indicating that it is the source signal of outer race fault, while for source signal , the peak value under is obvious, and there are side frequencies on both sides of with the interval of rotation frequency , indicating that it is the source signal of the inner race fault. The energy of the inner race fault source signal in the original mixed signal is small. Hence, if the envelope spectrum of the original signal is directly analyzed, is easily ignored. However, the proposed method using shift invariant K-SVD dictionary learning and improved FastICA can successfully separate signals from different fault sources.
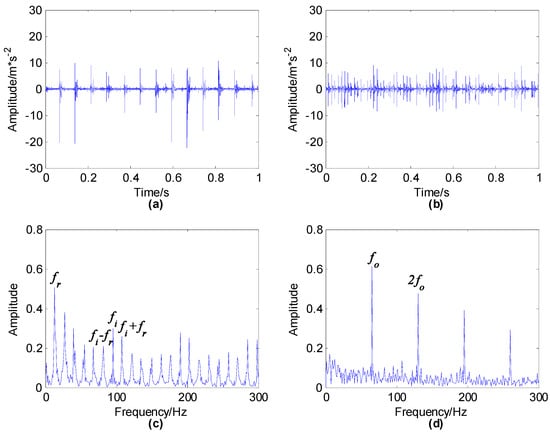
Figure 5.
Estimated source signal using improved fast independent component analysis (FastICA): (a) source signal ; (b) source signal ; (c) envelope spectrum of ; (d) envelope spectrum of .
Although the separation effect of original FastICA and improved FastICA is basically the same, the convergence performance of the two algorithms is quite different. Based on the first set of vibration signals, each algorithm is run 10 times respectively. The number of iterations corresponding to the separated two source signals in a certain run is illustrated in Table 3 and the total number of iterations (sum of the number of iterations of two source signals) in each run is revealed in Figure 6. From the table and figure we can see that improved FastICA can reduce the number of iterations. As shown in the figure, using original FastICA the number of iterations fluctuates greatly which is caused by the algorithm being sensitive to initialization, while the iteration number is relatively stable in improved FastICA. The results indicate that the improved FastICA algorithm can not only speed up the convergence speed significantly, but also solve the problem of unstable convergence.

Table 3.
The number of iterations corresponding to the separated two source signals in a certain run.
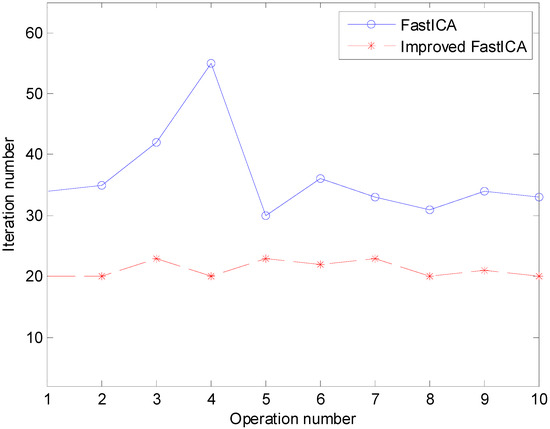
Figure 6.
Iteration number under 10 runs using FastICA and improved FastICA.
5.3. Compound Fault of Rolling Bearing with Outer Race and Rolling Element Fault
The time waveform and envelope spectrum of the first set of the vibration signal of the compound fault of the rolling bearing with an outer race and rolling element fault are displayed in Figure 7. As can be observed from Figure 7b that the peak values under the characteristic frequency of bearing outer race fault and its multiplier frequencies are obvious, indicating that the bearing has outer race fault, however the characteristic frequency of the rolling element fault cannot be seen.
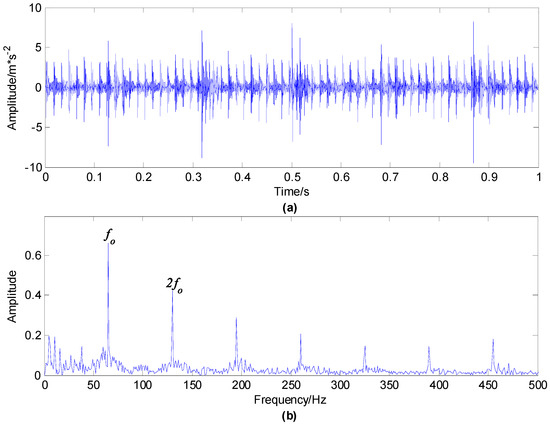
Figure 7.
Rolling bearing signal with outer race and rolling element compound fault: (a) time waveform; (b) envelope spectrum.
As in the previous subsection, firstly based on the first set of vibration signal, a shift invariant K-SVD dictionary learning algorithm was employed and the parameters of the algorithms are consistent with the previous subsection. The learned eight basis functions are manifested in Figure 8. The estimated source signals and their envelope spectrums with improved FastICA are shown in Figure 9.
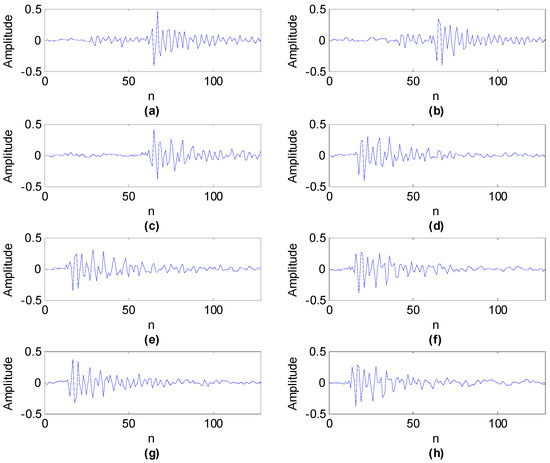
Figure 8.
The eight learned basis functions using shift invariant K-SVD algorithm corresponding to outer race and rolling element compound fault.
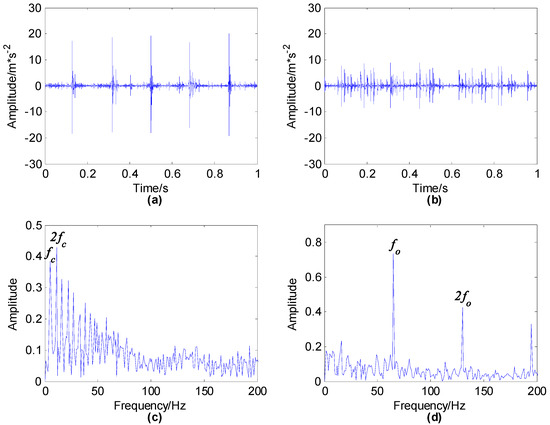
Figure 9.
Estimated source signal using improved FastICA: (a) source signal ; (b) source signal ; (c) envelope spectrum of ; (d) envelope spectrum of .
Figure 9 shows that improved FastICA can succeed in isolating the source signals. For source signal in the envelope spectrum the peak values under and its multiplier frequencies are obvious, indicating that represents the source signal of the outer race fault. The source signal is actually the impulse signal produced by the rolling element fault and in the envelope spectrum is not obvious, yet the peak values under the rotation frequency of cage and its multiplier frequencies are obvious, which is because the impact signal caused by a rolling element fault is modulated by the rotation frequency of the cage. When the failed rolling element runs to the load-bearing area, the load is the largest and the impact energy is also large, while once it leaves the load area, the load on it decreases rapidly and thus the impact energy is also rapidly reduced, especially when running to the top when the load is very small or there is even no load, hence there is no obvious impact signal. Therefore, in the envelope spectrum the rotation frequency of cage and its multiplier frequencies are obvious.
As in the above subsection, the convergence performance of original FastICA and improved FastICA is also compared, which is demonstrated in Table 4 and Figure 10. The comparison results indicate that the improved FastICA algorithm possesses stable convergence and faster convergence speed.

Table 4.
The number of iterations corresponding to the separated two source signals in a certain run.
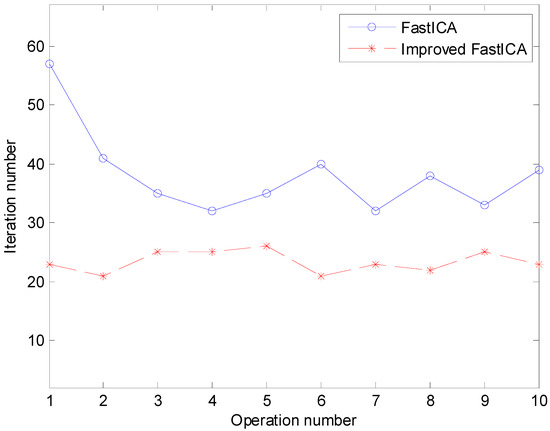
Figure 10.
Iteration number under 10 runs using FastICA and improved FastICA.
5.4. Compound Fault of Rolling Bearing with Outer Race, Inner Race and Rolling Element Fault
The time waveform and envelope spectrum of the first set of vibration signals of the compound fault of a rolling bearing with an outer race, inner race and rolling element fault are demonstrated in Figure 11. As shown in Figure 11b, and its multiplier frequencies have obvious peaks. Besides, obvious peaks under can be found and there are side frequencies on both sides of with the interval of rotation frequency , however cannot appear. The analysis of the mixed signal demonstrates that there are obvious outer and inner race faults, but it is easy to ignore the weak rolling element fault.
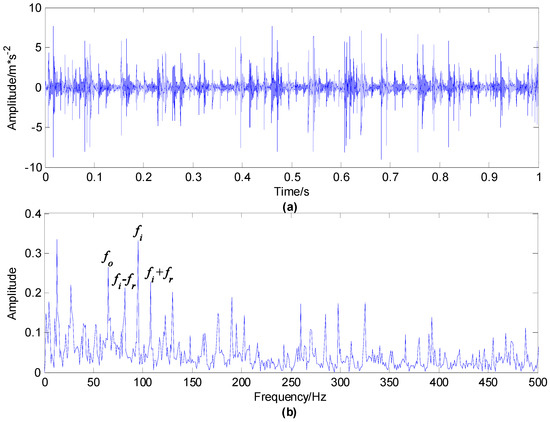
Figure 11.
Rolling bearing signal with outer race, inner race and rolling element compound fault: (a) time waveform; (b) envelope spectrum.
Firstly, the shift invariant K-SVD dictionary learning algorithm was conducted to analyze the first set of vibration signals. The parameters of the algorithms are the same as the previous subsection except that the source number is 3. The learned eight basis functions are illustrated in Figure 12.
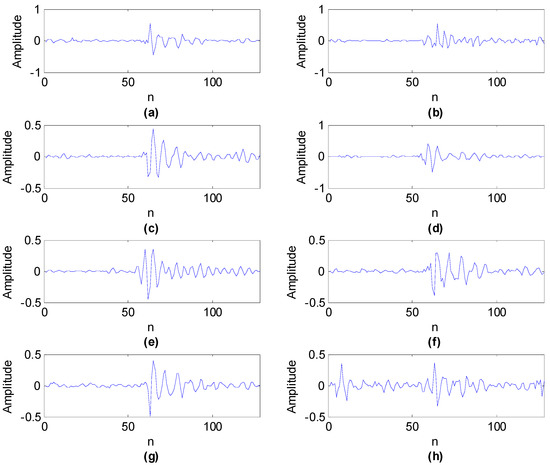
Figure 12.
The eight learned basis functions using shift invariant K-SVD corresponding to outer race, inner race and rolling element compound fault.
The estimated source signals and their envelope spectrums with improved FastICA are demonstrated in Figure 13, which proves that the mixed signals can be separated effectively by improved FastICA. Moreover, from the envelope spectrum of the source signal we can find that there is an obvious peak at , and near there exist side frequencies with the interval of the rotation frequency , which suggests that it is the source signal of inner race fault. With regard to source signal , there are obvious peaks in and its multiplier frequencies, indicating that it is the source signal of outer race fault, while for source signal , the peak value on the rotation frequency of cage is obvious and according to the analysis in the previous subsection, it actually represents the impact signal generated by the rolling element fault. Therefore, the proposed method successfully achieved the separation of the complex mixed signal containing three fault sources.
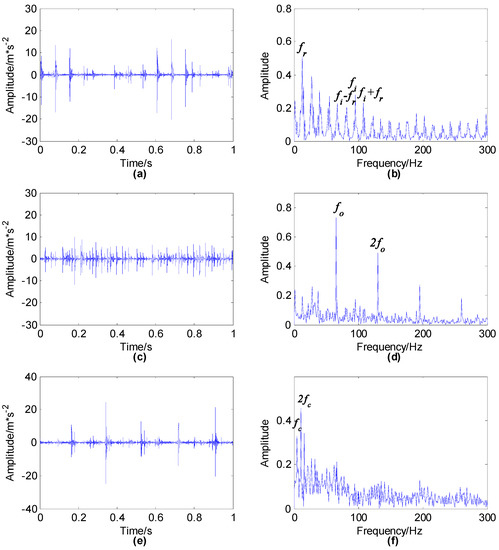
Figure 13.
Estimated source signal using improved FastICA: (a) source signal ; (b) envelope spectrum of ; (c) source signal ; (d) envelope spectrum of ; (e) source signal ; (f) envelope spectrum of .
Furthermore, the iteration numbers of the original FastICA and improved FastICA are presented in Table 5 and Figure 14, which prove that the improved FastICA algorithm outperforms original FastICA in convergence speed and stability.

Table 5.
The number of iterations corresponding to the separated two source signals in a certain run.
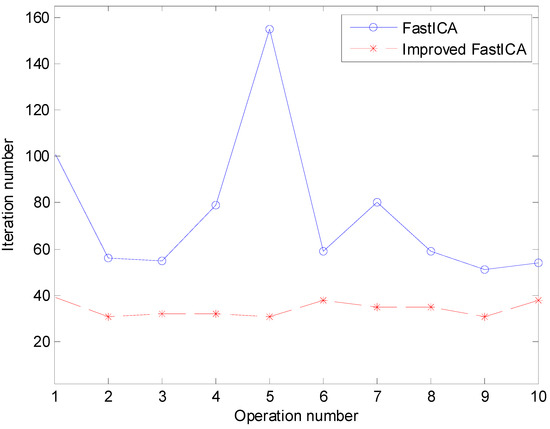
Figure 14.
Iteration number under 10 runs using FastICA and improved FastICA.
6. Conclusions
A single-channel compound fault analysis method combining shift invariant K-SVD with improved FastICA is proposed. First of all, shift invariant K-SVD is employed to obtain multiple latent components and then constructed as a virtual multi-channel signal. After that, improved FastICA is utilized to separate multiple fault source signals. The experimental results indicate that with respect to a single-channel compound fault signal, the multiple fault source signals can be successfully separated based on the proposed method. Besides that, the improved FastICA algorithm can improve convergence speed and deal with the problem that original FastICA is sensitive to initialization thus making the convergence more stable. In future research, other shift invariant dictionary learning algorithms and further improvement methods of FastICA including the improvement of convergence stability and speed will be exploited.
Author Contributions
Conceptualization, H.Y. and N.W.; methodology, H.Y.; software, H.Y.; validation, N.W. and H.Y.; formal analysis, N.W.; investigation, H.Y. and N.W.; resources, H.Y. and N.W.; data curation, H.Y.; writing–original draft preparation, H.Y.; writing–review and editing, H.Y. and N.W.; visualization, X.C.; supervision, H.Y. and N.W.; project administration, H.Y. and N.W.; funding acquisition, H.Y. and N.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The research carried out in this paper was supported by the Fundamental Research Funds for the Central Universities (2232019D3-61) as well as the initial research fund for the young teachers of Donghua University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, J.; Peng, Y.; Yang, Y.; Wu, Z. Adaptive Sparsest Narrow-Band Decomposition Method and Its Applications to Rolling Element Bearing Fault Diagnosis. Mech. Syst. Signal. Process. 2017, 85, 947–962. [Google Scholar] [CrossRef]
- Ding, Y.; He, W.; Chen, B.; Zi, Y.; Selesnick, I.W. Detection of Faults in Rotating Machinery Using Periodic Time-Frequency Sparsity. J. Sound Vib. 2016, 382, 357–378. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Chen, X.; Du, Z.; Yang, B. Sparsity-Aware Tight Frame Learning with Adaptive Subspace Recognition for Multiple Fault Diagnosis. Mech. Syst. Signal. Process. 2017, 94, 499–524. [Google Scholar] [CrossRef]
- Zhao, C.; Feng, Z.; Wei, X.; Qin, Y. Sparse Classification Based on Dictionary Learning for Planet Bearing Fault Identification. Expert Syst. Appl. 2018, 108, 233–245. [Google Scholar] [CrossRef]
- Feng, Z.; Zhou, Y.; Zuo, M.J.; Chu, F.; Chen, X. Atomic Decomposition and Sparse Representation for Complex Signal Analysis in Machinery Fault Diagnosis: A Review with Examples. Measurement 2017, 103, 106–132. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Grosse, R.; Raina, R.; Kwong, H.; Ng, A.Y. Shift-Invariant Sparse Coding for Audio Classification. In Proceedings of the Proceedings of the Twenty-Third Conference on Uncertainty in AI, Vancouver, BC, Canada, 19–22 July 2007; pp. 149–158. [Google Scholar]
- Bimbot, F.; Gribonval, R.; Lesage, S.; Mailhé, B.; Vandergheynst, P. Shift-Invariant Dictionary Learning for Sparse Representations: Extending K-SVD. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Huang, Y. Adaptive Feature Extraction Using Sparse Coding for Machinery Fault Diagnosis. Mech. Syst. Signal. Process. 2011, 25, 558–574. [Google Scholar] [CrossRef]
- Tang, H.; Chen, J.; Dong, G. Sparse Representation Based Latent Components Analysis for Machinery Weak Fault Detection. Mech. Syst. Signal. Process. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M. Complex Signal Analysis for Planetary Gearbox Fault Diagnosis via Shift Invariant Dictionary Learning. Measurement 2016, 90, 382–395. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, J.; Dong, G.; Wang, R. Detection and Diagnosis of Bearing Faults Using Shift-Invariant Dictionary Learning and Hidden Markov Model. Mech. Syst. Signal. Process. 2016, 72–73, 65–79. [Google Scholar] [CrossRef]
- Yang, B.; Liu, R.; Chen, X. Fault Diagnosis for a Wind Turbine Generator Bearing via Sparse Representation and Shift-Invariant K-SVD. IEEE Trans. Ind. Inf. 2017, 13, 1321–1331. [Google Scholar] [CrossRef]
- Ding, J. Fault Detection of a Wheelset Bearing in a High-Speed Train Using the Shock-Response Convolutional Sparse-Coding Technique. Measurement 2018, 117, 108–124. [Google Scholar] [CrossRef]
- Li, Q.; Ding, X.; Huang, W.; He, Q.; Shao, Y. Transient Feature Self-Enhancement via Shift-Invariant Manifold Sparse Learning for Rolling Bearing Health Diagnosis. Measurement 2019, 148, 106957. [Google Scholar] [CrossRef]
- He, L.; Yi, C.; Lin, J.; Tan, A.C. Fault Detection and Behavior Analysis of Wheelset Bearing Using Adaptive Convolutional Sparse Coding Technique Combined with Bandwidth Optimization. Shock. Vib. 2020, 2020, 1–27. [Google Scholar] [CrossRef]
- Ding, C.; Zhao, M.; Lin, J. Sparse Feature Extraction Based on Periodical Convolutional Sparse Representation for Fault Detection of Rotating Machinery. Meas. Sci. Technol. 2020, 32, 015008. [Google Scholar] [CrossRef]
- Zheng, K.; Li, T.; Su, Z.; Wen, J.; Zhang, B.; Zhang, Y. Faults Diagnosis of Rolling Bearings Based on Shift Invariant K-Singular Value Decomposition with Sensitive Atom Nonlocal Means Enhancement. Measurement 2019, 135, 836–851. [Google Scholar] [CrossRef]
- Mahvash, A.; A Lakis, A. Independent Component Analysis as Applied to Vibration Source Separation and Fault Diagnosis. J. Vib. Control. 2014, 22, 1682–1692. [Google Scholar] [CrossRef]
- Yu, G. Fault Feature Extraction Using Independent Component Analysis with Reference and Its Application on Fault Diagnosis of Rotating Machinery. Neural Comput. Appl. 2014, 26, 187–198. [Google Scholar] [CrossRef]
- Li, Z.X.; Yan, X.P.; Yuan, C.Q.; Li, L. Gear Multi-Faults Diagnosis of a Rotating Machinery Based on Independent Component Analysis and Fuzzy K-Nearest Neighbor. Adv. Mater. Res. 2010, 108–111, 1033–1038. [Google Scholar] [CrossRef]
- Ye, H.X.; Yang, S.X.; Yang, J.X.; Ji, H.W. Vibration Sources Identification with Independent Component Analysis. In Proceedings of the WCICA 2006: Sixth World Congress on Intelligent Control and Automation, Dalian, China, 20–24 June 2006; pp. 5814–5818. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A: Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, T. Single-Channel Blind Source Separation for Vibration Signals Based on TVF-EMD and Improved SCA. IET Signal Proc. 2020, 14, 259–268. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, T. An Analysis Approach for Multivariate Vibration Signals Integrate HIWO/BBO Optimized Blind Source Separation with NA-MEMD. IEEE Access 2019, 7, 87233–87245. [Google Scholar] [CrossRef]
- Miao, Q.; Wang, D.; Pecht, M. Rolling Element Bearing Fault Feature Extraction Using EMD-Based Independent Component Analysis. In Proceedings of the 2011 IEEE Conference on Prognostics and Health Management, Denver, CO, USA, 20–23 June 2011. [Google Scholar] [CrossRef]
- Wang, H.; Li, R.; Tang, G.; Yuan, H.; Zhao, Q.; Cao, X. A Compound Fault Diagnosis for Rolling Bearings Method Based on Blind Source Separation and Ensemble Empirical Mode Decomposition. PLoS ONE 2014, 9, e109166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taralunga, D.D.; Gussi, I.; Strungaru, R. A New Method for Fetal Electrocardiogram Denoising Using Blind Source Separation and Empirical Mode Decomposition. Rev. Roum. Sci Tech. El. 2016, 61, 94–98. [Google Scholar]
- Tsai, Y.T.; Huang, J.H. Discrimination Method for Spindle Vibration Analysis Based on Empirical Mode Decomposition and Independent Component Analysis Algorithm. In Proceedings of the 23rd International Congress on Sound and Vibration 2016 (ICSV 23): From Ancient to Modern Acoustics, Athens, Greece, 10–14 July 2016; pp. 593–600. [Google Scholar]
- Yang, Q.; Yang, Q.; Yan, W.J.; Huang, M.Y.; Hu, C.Z. On Prognosis of Wind Turbine Faults Based on Nonlinear Mixed Vibration Signals: A PSO Based EMD and KICA Combined Approach. In Proceedings of the Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–17 June 2016; pp. 571–576. [Google Scholar]
- Yi, C.; Lv, Y.; Xiao, H.; You, G.; Dang, Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Appl. Sci. 2017, 7, 414. [Google Scholar] [CrossRef]
- Sun, H.; Wang, H.; Guo, J. A Single-Channel Blind Source Separation Technique Based on AMGMF and AFEEMD for the Rotor System. IEEE Access 2018, 6, 50882–50890. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, M.; Yan, W. Particle Swarm Optimization-Based Empirical Mode Decomposition-Kernel Independent Component Analysis Joint Approach for Diagnosing Wind Turbine Gearbox with Multiple Faults. Trans. Inst. Meas. Control. 2017, 40, 1836–1845. [Google Scholar] [CrossRef]
- Li, H.Y.; Lin, W.; Zhao, D. A Single-Channel BSS Method Based on ICEEMDAN and FastICA and Its Application in EMI Analysis. In Proceedings of the 14th International Conference on Computer Science and Education (ICCSE 2019), Toronto, ON, Canada, 19–21 August 2019; pp. 780–784. [Google Scholar]
- Li, S.-G.; Li, Z.-H.; Wang, Y.-L.; Liu, Y.; Chen, T.-T.; Tan, S.-L.; Su, Z.; Gao, M.; Jiang, F.; Li, H.-L. Single Channel Blind Source Separation for Gas Regulators’ Acoustic Signal Using EEMD-FastICA. In Proceedings of the 2019 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA19), Shijiazhuang, China, 1–4 November 2019. [Google Scholar] [CrossRef]
- Ma, S.X.; Yang, L.Y.; Meng, X. Single Channel Blind Source Separation Based on Dual-Tree Complex Wavelet Transform and Ensemble Empirical Mode Decomposition. In Proceedings of the 2019 IEEE 9th International Conference on Electronics Information and Emergency Communication (ICEIEC 2019), Beijing, China, 12–14 July 2019; pp. 359–362. [Google Scholar]
- Xiong, F.; Chen, D. CEEMDAN-IMFX-PCA-CICA: An Improved Single-Channel Blind Source Separation in Multimedia Environment for Motion Artifact Reduction in Ambulatory ECG. Complex Intell. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.; Yang, Y.; Peng, Y. A New FastICA Algorithm of Newton’s Iteration. In Proceedings of the ICETC, Shanghai, China, 22–24 June 2010; pp. 481–484. [Google Scholar]
- Krstulovic, S.; Gribonval, R. MPTK: Matching Pursuit Made Tractable. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; pp. 496–499. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).