Abstract
Although a two-dimensional (2D) valve has excellent performance, the processing of its spiral groove has a high cost and is time-consuming. This paper proposes a novel torque motor based on an annulus air gap (TMAAG) to replace the negative feedback function of the spiral groove to reduce the machining difficulty. In order to study the torque change law of the TMAAG, the air gap permeance was analyzed, and then a qualitative analytical model was established. Orthogonal tests were carried out to initially select the crucial parameters, which were further optimized through a back propagation (BP) neural network and genetic algorithm. The prototype of TMAAG was machined, and a special experimental platform was built, and experiment results are similar to the simulation values, which verifies the accuracy of the air gap analysis and qualitative model. For torque-angle characteristics, the output torque increases with both current and rotation angle and reaches about 0.754 N·m with 2 A and 1.5°. While for torque-displacement characteristics, due to the negative feedback mechanism, the output torque decreases with increasing armature displacement, which is about 0.084 N·m with 2 A and 1 mm. The research validates the unique negative feedback mechanism of the TMAAG and indicates that it can be potentially used as an electro-mechanical converter of a 2D valve.
1. Introduction
The electro-hydraulic servo control system is widely used in crucial fields such as aerospace and mobile engineering equipment due to its high power-to-weight ratio, large output force, and excellent static and dynamic performance. As a key component, the electro-hydraulic servo valve has the functions of energy conversion and signal amplification, which determine the overall performance of the system [1,2,3,4]. After World War II, low-cost and robust electro-hydraulic control technology has grown rapidly in the civil industry, and proportional valves that use proportional solenoid as electro-mechanical converters (EMCs) appeared [5,6]. With the integration of the servo valve and proportional valve, so-called industrial servo valves have emerged, which use high-performance linear force motors to directly drive the valve and incorporate a linear variable differential transformer (LVDT) sensor to form a closed-loop control of the spool position [7,8]. Compared with the proportional valve, it has better static and dynamic response while retaining stability and simplicity [9,10,11,12].
Limited by the linear EMC output force, the servo valve usually needs to be designed as a multi-stage structure with a pilot-operated mechanism to overcome the Bernoulli force and friction force. Typical pilot-operated servo valves include a flapper-nozzle pilot valve, jet pipe valve, and two-dimensional (2D) valve. The flapper-nozzle pilot valve has a complicated structure, high machining and assembly precision requirements, and potential pollution ability due to the pilot control stage structure [13,14,15]; the jet pipe valve does not cause pollution, but the jet characteristics are not easy to predict [16,17].
A 2D valve is a novel pilot-operated valve based on the principle of the hydraulic servo-screw mechanism, which was first proposed by Ruan in 1989. The spool can move in two degrees of freedom similar to a mechanical screw, with a predetermined proportional relationship between the rotation and linear displacement. This is the key to the operation of the negative feedback mechanism [18,19,20]. It is also because of the servo screw mechanism that the 2D valve integrates the separated pilot stage and the power stage onto one single spool, featuring a simple structure, high power-to-weight ratio, and excellent anti-pollution ability [21,22]. Nevertheless, the machining of spiral grooves on 2D valve sleeves usually requires electric discharge machining (EDM) machine tools with at least three axes, which is not only expensive but also time consuming. This shortcoming greatly influences the further promotion of 2D valves for civil industry areas that are more sensitive to cost and relatively less sensitive in terms of performance [23]. Thus, in order to reduce machining costs, necessary structural changes should be considered.
It is a feasible solution to transfer the negative feedback function from the spool-sleeve to the EMC. Due to the characteristics of the 2D valve, linear EMC cannot be used directly. 2D valves need a rotary electro-mechanical converter (REMC) to rotate the spool firstly to actuate the so-called “2D” mechanism. Common REMCs can be divided into a step motor, rotary proportional solenoid (RPS), and torque motor. Step motors can nearly achieve continuous angular displacements by using a multipole-pair structure and large gear ratio, but they are not appropriate for servo valves due to structural complexity and large volumes. The RPS features flat torque-angle characteristics. It has large output torque and is easy to be designed as a “wet type” actuator with high-pressure oil resistant ability [24]. The main difficulty of RPS designs is that there is no perfect universal method to obtain proportional control characteristic. Torque motors have advantages of high control accuracy, bidirectional capability, and fast dynamic response, which have been widely used as EMCs for nozzle-flapper valves, jet pipe valves, and deflector jet pipe valves. Zhang et al. proposed a novel torque motor with hybrid-magnetization pole arrays, whose output torque can be increased by range of 47–52% compared with traditional designs, while maintaining the original size and mass [25]. In order to solve self-excited high frequency oscillations and noise, Li et al. added magnetic fluid to the working air gap of torque motors and found that magnetic fluids can improve the stability of servo valves owing to their damping and resistant effects [26,27]. Considering the torque motors might have unequal air gaps due to production errors, Urata studied the influence of such unequal thickness on the output torque of torque motors [28]. Liu et al. proposed a novel mathematical model of torque motors. From the comparisons of results, the magnetic reluctances of the magnetic elements cannot be neglected if the permeability is small [29]. Zhu et al. proposed a set of theoretical models to describe the entire magnetization and demagnetization process of torque motors [30]. Besides, several studies have been carried out on functional materials such as piezoelectric crystals [31], giant magnetostrictive materials [32], magnetorheological fluid, and shape memory alloys, which are used for EMC for novel servo valves [33,34]. Despite its extremely fast dynamic response, the material’s sensitivity to temperature and hysteresis, and material deformation characteristics make it unsuitable as a REMC for 2D valves.
Many studies of torque motor have been carried out, but so far, it can only drive the armature to rotate; there is no torque motor with both drive and negative feedback functions. This paper presents a novel torque motor based on the annular air gap (TMAAG), which integrates negative feedback mechanism. For a 2D valve driven by TMAAG, a simple rectangular sensing groove can be used to replace the complicated spiral sensing groove, which can greatly reduce manufacturing costs.
For novel electro-mechanical converters, parameter determination and optimization are indispensable. Using algorithms can speed up this process and improve accuracy. As an adaptive global optimization search algorithm, the genetic algorithm has the characteristics of high efficiency, practicality, and strong robustness. It has been used in the parameter optimization of various electro-mechanical converters. Diao et al. simultaneously employed sensitivity analysis, approximate models, and a genetic algorithm to reduce the computation cost [35]. In order to improve the performance of the surface-mounted permanent-magnet (SMPM), Jing et al. combined the analytical model with the genetic algorithm to optimize some parameters of the motor [36]. Xu et al. studied the influence of the slot parameters. The genetic algorithm-based optimization method is proposed to maximize the torque density of the dual redundant permanent magnet synchronous motor (PMSM) [37]. El-Nemr et al. proposed an optimal design methodology for switched reluctance motor (SRM) using the non-dominated sorting genetic algorithm (NSGA-II) optimization technique [38]. Yang et al. proposed an active disturbance rejection control (ADRC) strategy based on the improved particle swarm optimization-genetic algorithm (IPSO-GA) for a bearing less induction motor (BIM) [39]. Wang et al. proposed a multi-objective optimization method based on the genetic algorithm and magnetostatic FEA 2D model to optimize the shape design parameters of linear proportional solenoids [40]. Shen et al. proposed an effective optimization method for mechanical structure of a bearing less permanent magnet slice motor (BPMSM), which uses the gradient descent method to obtain a linear regression model, and the genetic algorithm was used to solve it [41]. For the research of TMAAG in this paper, the method where a regression model is obtained through neural network and then solved by genetic algorithm is selected, which considers both simplicity and accuracy simultaneously.
The rest of this paper is organized as follows: In Section 2, the structure and working principle of TMAAG are introduced. In Section 3, the air gap permeance of TMAAG is analyzed, and a novel analytical model is established by using the equivalent magnetic circuit method. In Section 4, the orthogonal test, BP neural network, and genetic algorithm are used to study the influence of crucial parameters on the performance of TMAAG. In Section 5, a prototype of TMAAG is designed and manufactured, and a specialized experiment platform is built to measure its torque-angle and torque-displacement characteristics. The experiment results are then compared with the finite element method (FEM) simulation. Finally, some conclusions of this work are drawn in Section 6.
2. Structure and Working Principle
As shown in Figure 1, the structure of TMAAG consists of yokes, an armature, permanent magnets (PMs), and coils. The PMs are installed in upper and lower grooves of the yokes, and the coils are wound on the left and right sides of the yokes. Both the yoke and the armature are made of a soft magnetic material, DT4, the armature is located in the middle of the yokes, its two wings are centered symmetrical, and there is a pitch angle between the wing surface and the axis. The inner annulus surface of the yoke is also designed with a slope groove of the pitch angle.
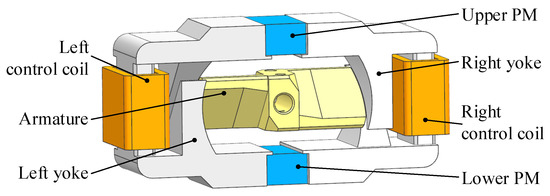
Figure 1.
Schematic of the structure of TMAAG.
The schematic of the magnetic circuit of TMAAG is shown in Figure 2. When the coils are not electrified, due to the symmetrical structure, the armature is in the neutral position and there is no output torque. When the coils are electrified, the control magnetic flux , generated by the coils and the polarized magnetic flux , generated by the PMs are differentially superimposed at the air gap , , and , thereby generating torque. In addition, since both the armature and the yoke have an annulus structure, there will be no touching in any case. This ensures that the armature can be greatly rotated or moved in the axial direction.
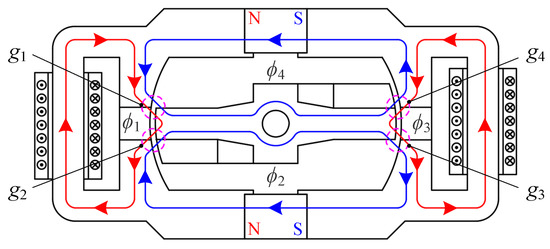
Figure 2.
Schematic of the magnetic circuit of TMAAG.
Due to the pitch angle of TMAAG, either the rotation or axial movement of the armature can vary the four air gaps, resulting in corresponding torque variation. When the coils are electrified, a magnetic force is generated. The circumferential component force generates a driving torque to drive the armature to rotate a certain angle . As shown in Figure 3, the armature moves from position 1 to position 2. The upper and lower air gaps vary accordingly, and therefore the magnetic force and its circumferential component force and axial component force further increase. At this time, if an external force pulls the armature to move axially with displacement , the air gaps will vary again. Then, the armature will be acted on by a feedback torque whose value is proportional to the armature displacement . The feedback torque is opposite to the driving torque and counteracts the latter. Therefore, the armature can return to initial position, and the so-called “negative feedback mechanism” can be realized.
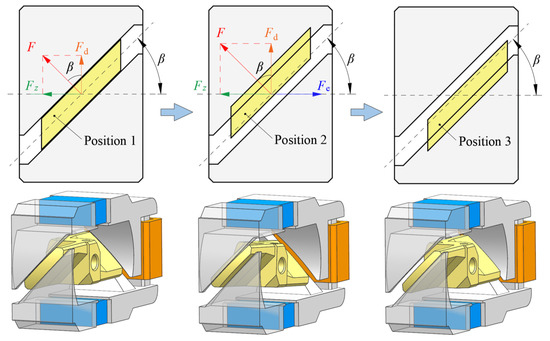
Figure 3.
Schematic of the armature movement and force.
Figure 4 shows the novel 2D valve driven by TMAAG. The armature of TMAAG is fixed on the spool by a pin. In the sleeve, the spool forms a high-pressure chamber and a sensitive chamber with the concentric ring and the end cap, respectively. Two pairs of symmetrical high-pressure and low-pressure grooves are machined on the inner peripheral surface of the spool close to the sensitive chamber. Hole a, hole b, and an internal channel in the spool can pilot the high-pressure oil into the high-pressure groove and high-pressure chamber, and the low-pressure groove is directly connected to the oil return port. The internal surface of the sleeve is also machined with a centrally symmetrical straight groove. One end of the straight groove communicates with the sensitive chamber, and the other end forms a resistance half bridge with the high-pressure and the low-pressure groove to control the pressure in the sensitive chamber. In this way, the pressure difference between the two ends of the spool is controlled to realize the axial movement of the spool.
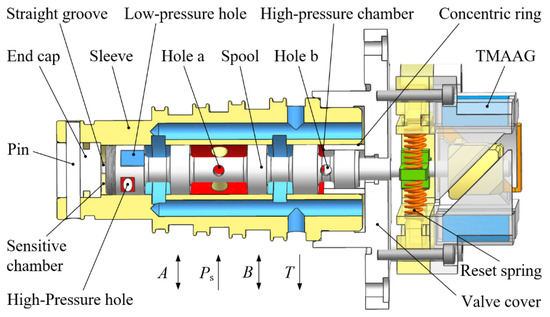
Figure 4.
Schematic of the 2D valve driven by TMAAG.
When TMAAG is electrified, the armature drives the spool to rotate; this rotary motion varies the two overlapping openings differentially, so that the pressure in the sensitive chamber is changed. The hydrostatic force balance is broken, and the spool begins to moves axially. Due to this axial external force ( in Figure 3) and the slope structure of the armature, the armature generates a feedback torque during the axial movement, which continuously counteracts the driving torque until the output torque decreases to zero. The angle returns to zero, and two overlapping openings are restored to equal, which re-establish the spool force balance; at this time, the spool stops moving and is in a new equilibrium position.
3. Analytical Modeling
3.1. Air Gap Analysis
TMAAG needs to achieve the goal of rapid variation of feedback torque with displacement. Therefore, it is necessary to study the air gap structure of TMAAG and the law of torque changes.
TMAAG with overlapping parts between the yoke and the armature (the opening is negative) was selected as the analysis object, and its air gaps were divided into four parts, where the thin lines with arrows represent the magnetic flux lines, as shown in Figure 5. In the initial position, part 1 and 2 are symmetrical to part 3 and 4. When electrified, owing to the negative feedback mechanism, the armature realizes the conversion of torque to displacement, which is uniformly shown as the center section after movement. At this time, because of displacement , part 1 disappeared, part 2 and 3 did not change significantly, and part 4 increased. From displacement to , part 1 and 4 changed, and the magnetic force on part 1 and 4 is in the radial direction. Therefore, changes in part 1 and 4 do not affect the variation of torque. From displacement to , part 4 continues to increase but basically does not affect the torque, part 3 remains the same, while part 2 changes significantly; the air path passing by is increased, which greatly reduces the permeance. The changes in part 2 and 3 are the main factors for the variation of torque. If the feedback torque needs to be changed rapidly with the armature displacement, the opening should not be designed to be negative.
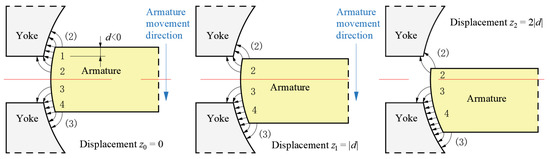
Figure 5.
Air gap permeance variation of TMAAG.
The magnetization curve of DT4 is shown in Figure 6. Using Maxwell 2D, the magnetic flux lines of TMAAG are simulated in Figure 7. The working principle is in line with expectations. When electrified, the magnetic flux on one side is strengthened, and the other side is weakened. After the armature is rotated or displaced, the change in the magnetic flux lines is also consistent with Figure 5, which verifies the above-mentioned discussion.
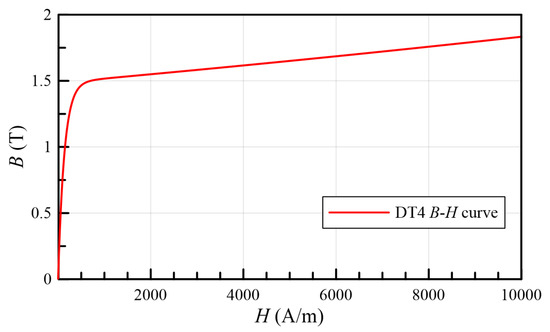
Figure 6.
The magnetization curve of DT4.
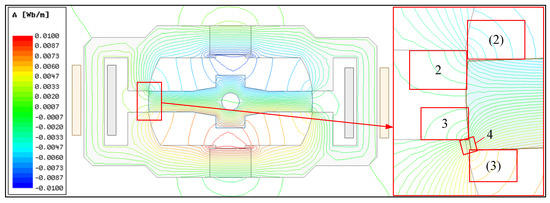
Figure 7.
Magnetic flux line diagram of TMAAG.
The basic form of the permeance formula can be written as Equation (1), where, represents the permeability of the material, represents the area perpendicular to the direction of the magnetic flux line (magnetic equipotential plane), and represents the path distance along the direction of the magnetic flux line [42]. Therefore, the choice of the plane where the magnetic flux path is located is very important when analyzing the permeance.
The permeance model of the magnetic-flux-strengthened side is shown in Figure 8b. According to (1), we can obtain:
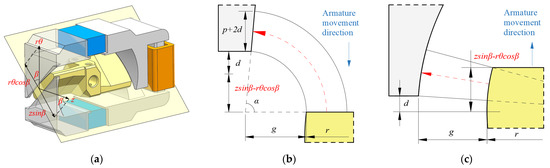
Figure 8.
Air gap permeance. (a) Selected plane for analysis; (b) permeance of the magnetic-flux-strengthened side; (c) permeance of the magnetic-flux-weakened side.
Here, is 0, is the parameter related to the width of the magnetic equipotential plane, is the opening between the yoke and the armature, is the length of armature wing, represents the permeability of the air, represents the linear displacement of armature, represents the pitch angle, represents the radius of armature, represents the rotation angle of armature. The value of is equal to in Figure 8b; it is related to the ellipse cut by the cylinder along the pitch angle. Since changes little, the given value is 1.52 rad.
The main permeance on the magnetic-flux-weakened side is shown in Figure 8c. In addition, there is also other permeance on the magnetic-flux-weakened side that will not change. Since the two are connected in parallel, the total permeance can be written as:
3.2. Magnetic Circuit and Torque Analysis
The equivalent magnetic circuit diagram of TMAAG is shown in Figure 9.
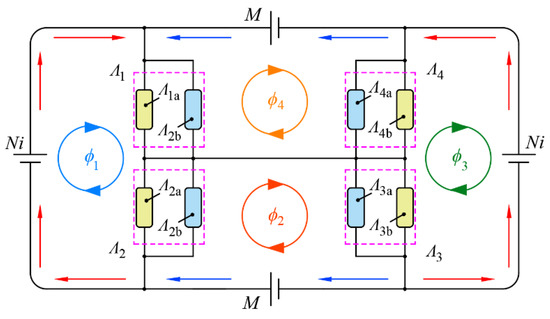
Figure 9.
Equivalent magnetic circuit diagram.
According to Kirchhoff’s law of magnetic circuit, we can have:
represents the magnetic potential of PMs, represents the turns of coil, and represents the current. Since , , it can be obtained from Equation (5) that , thus, the following Equation can be obtained:
The magnetic potential drop in the air gap can be written as:
The magnetic co-energy can be written as:
Equation (8) can be further expanded as:
Taking the partial derivative of , we get:
where
Equation (11) is obtained under the condition that no torque is generated when there is no movement. Equation (10) is a function of the torque inversely proportional to the square of the movement. When the armature movement is very small, the torque change will be obvious. When the armature movement is large, the torque change is basically invisible.
When the armature movement is very small, the torque change is approximately a straight line. The above Equation (10) can be further processed as:
The denominator extracts , leaving . Because , this part is omitted.
the molecule is extracted, and it is compared with the bottom . Because , this part is omitted again and the formula is obtained:
If is much less than , , the first term of Equation (14) can be written as:
Therefore, Equation (14) can be finally simplified as:
where
It can be seen that the output torque of TMAAG consists of three terms, where the terms of and represent the sum of driving torque while represents feedback torque. represents the electromagnetic torque coefficient, which will increase with and yet decrease with and . and represent rotary magnetic spring stiffness and linear magnetic spring stiffness, respectively. They both increase with , and decreases with , and . The highlight is that is negative spring stiffness, which makes the feedback torque and the driving torque in the opposite direction. Therefore, is the key of the negative feedback mechanism. Besides, Equation (17) indicates that will have the maximum value when = 45°.
4. Parameter Optimization
In order to verify the trend of the analytical model, an orthogonal test was designed. Five structural variables including the pitch angle , air gap , opening , wing length , and radius were selected as the five factors of the orthogonal test. Among them, the pitch angle is an essential research parameter, thus three levels were selected, and the other factors were set as two levels, as shown in Table 1.

Table 1.
Factor level table of the orthogonal test.
Based on the principle of selecting fewer tests, was selected as the appropriate orthogonal array, which means 12 sets of tests need to be conducted by using the Maxwell 3D. The test results of FEM simulation are shown in Figure 10. Therefore, 12 groups of tests were analyzed, and the analysis results are shown in Table 2.

Figure 10.
Orthogonal array test results.

Table 2.
Results analysis of the orthogonal test.
The target represents the torque value that changes every 0.1 mm. The test results show that the optimal levels of pitch angle, air gap, opening, length, and radius are 45°, 0.4 mm, 0.1 mm, 20 mm, and 28 mm, respectively. Among these factors, the air gap has the greatest influence, followed by the pitch angle. From the orthogonal test, the same trend as the analytical model can be drawn.
The trend of the opening is opposite to the analytical model. This is because the opening of 0 is the limiting condition in the model. If the opening is 0, the permeance tends to infinity. In fact, the transition between the positive and the negative of the opening is continuous. Therefore, according to the orthogonal test, when the size of the opening is near 0, the proper opening to avoid the limiting position is beneficial to the feedback torque, while too large an opening is disadvantageous.
The optimal design based on the intelligent algorithm needs enough samples. However, it is time-consuming and laborious to obtain samples only by FEM simulation. Here, a three-layer BP neural network was constructed on the platform of Matlab in order to approximate the FEM results of TMAAG, where the number of input layer nodes is 5, the number of hidden layer nodes is 8, and the number of output layer nodes is 1. The BP network is trained by gradient descent with momentum and adaptive lr algorithm, where the target error goal = 1 × 10−3, learning rate lr = 0.035, and the maximum number of iterations epochs = 2000. The fitting orthogonal test curve is shown in Figure 11, which indicates the BP neural network has very high fitting accuracy.
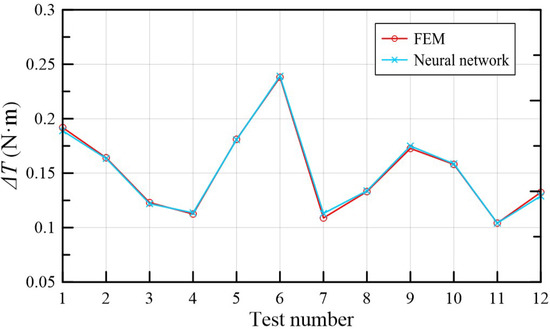
Figure 11.
Neural network fitting curve.
A genetic algorithm is used to obtain the optimal parameters of TMAAG. Here, the number of the initial population NP = 100, the length of the chromosome binary code is 20, the maximum evolution algebra G = 100, the crossover probability is = 0.8, and the mutation probability = 0.1. The initial population was generated first, then the binary code was converted into decimal system, and the individual fitness value was calculated and normalized. The selection operation based on roulette, crossover, and mutation operation based on probability are used to generate new populations, and the optimal individuals of previous generations are retained in the new species group for the next genetic operation. During this process, the termination condition will be judged, and if the termination condition is met, the optimization value will be output, otherwise the iterative optimization continues. The fitness evolution curve is shown in Figure 12. After 100 iterations, the algorithm has approached the optimal solution, and the result = 0.24. The optimization results are as follows: pitch angle = 45.001, air gap = 0.403, opening = 0.1, wing length = 20, radius = 27.615, which basically conforms to the previous conclusions. Finally, according to the optimized results, the key parameters of the TMAAG prototype are determined, as shown in Table 3.
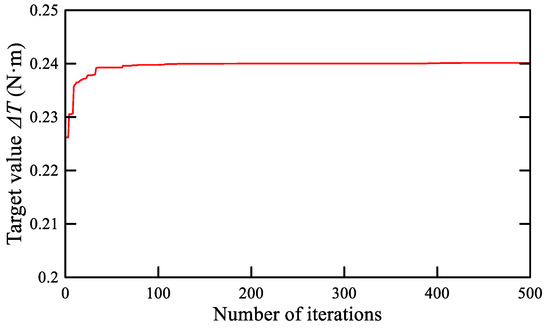
Figure 12.
Fitness evolution curve.

Table 3.
Key parameters of the TMAAG prototype.
Before the experiment, a 3D model was established to perform FEM simulation in Maxwell 3D. The simulation cloud diagrams are shown in Figure 13. When TMAAG is not electrified, the magnetic flux is symmetrical. From Figure 13a,b after electrification, the magnetic flux in one side is strengthened and the other side is weakened. Figure 13c,d show magnetic flux variation after rotation and axial movement, respectively. The axial movement obviously plays a role of negative feedback and make two sides of the magnetic flux gradually closer.
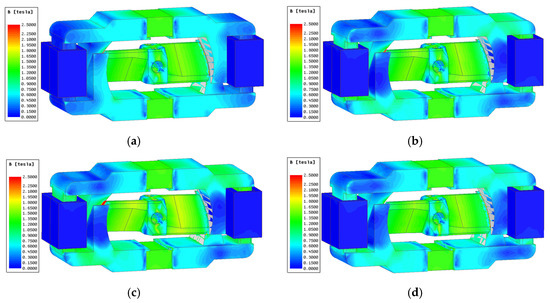
Figure 13.
Cloud diagram of TMAAG. (a) = 0 A, = 0°, = 0 mm; (b) = 2 A, = 0°, = 0 mm; (c) = 2 A, = 1.5°, = 0 mm; (d) = 2 A, = 0°, = 1 mm.
5. Experiment
In order to further verify the analytical and simulation results, a prototype of TMAAG was machined, and an experiment platform was built, as shown in Figure 14a,c. The experiment platform includes the prototype, direct current (DC) power supply, torque sensor, controller, and linear and rotary micrometers. As shown in Figure 14b, the angular and linear displacement of the yoke relative to the armature can be changed by using the linear and rotary micrometer, respectively. The armature is fixedly connected to the torque sensor through the shaft, and thereby the torque of TMAAG at any position can be measured. Finally, the torque-angle and the torque-displacement characteristic curves can be obtained, which reflect driving torque and feedback torque, respectively.

Figure 14.
Experiment device. (a) Prototype; (b) Linear micrometer and rotary micrometer; (c) Experiment platform.
Torque-angle characteristics were measured when the current was 0, 1, and 2 A. The results were then compared with the corresponding FEM simulation, as shown in Figure 15. Table 4 summarizes the comparison data. With the increase in current and rotation angle, the torque presented an increasing trend, which is consistent with the analysis of and in Equation (17). When = 2 A and = 1.5°, the FEM and experiment results were 0.859, and 0.754 N·m, respectively. As the current gradually increased, the experimental result was smaller than the simulation value. The reason for such deviation might be that compared with the BH curve in the finite element model, the real soft magnetic material tends to be saturated more easily under high current excitation.
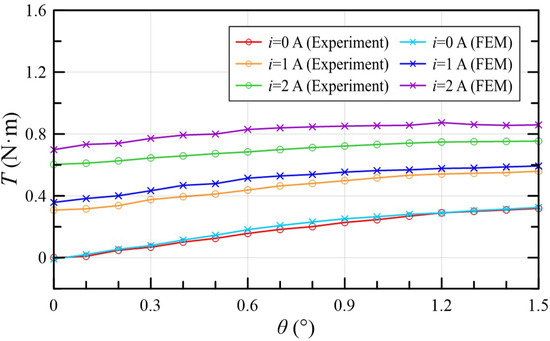
Figure 15.
Torque-angle characteristic curve with different currents.

Table 4.
Comparison of torque-angle characteristics.
In order to validate the negative feedback mechanism of TMAAG, the torque-displacement characteristics were also measured when the current was 0, 1, and 2 A. The results were then compared with the corresponding FEM simulation, as shown in Figure 16. Table 5 summarizes the comparison data. With the increase in armature displacement, the feedback torque increased. Note that here the measured torque is the sum of the driving torque and feedback torque. Since the direction of driving torque and feedback torque is opposite, the measured overall torque is influenced by the increasing feedback torque and thus presents a downward trend, which is consistent with the analysis of in Equation (17) and verifies the negative feedback mechanism of TMAAG. When = 2 A, = 1 mm, the torque was 0.175 and 0.084 N·m. Similarly, when the current gradually increased, the experimental result was smaller than the simulation value. The reason of such deviation can also be attributed to the different material characteristics between the FEM model and real situation, as discussed for the torque-angle characteristics.
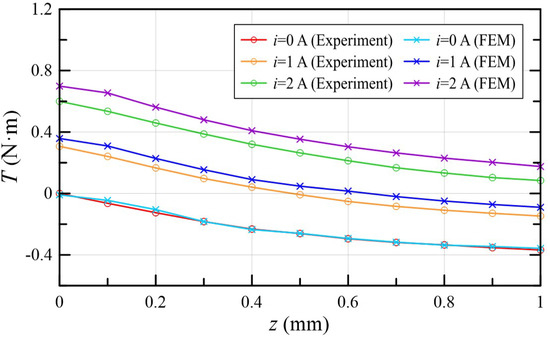
Figure 16.
Torque-displacement characteristic curve with different currents.

Table 5.
Comparison of torque-displacement characteristics.
6. Conclusions
- (1)
- In order to reduce machining difficulty and costs of 2D valves, a novel TMAAG is proposed in this paper, which has a negative feedback mechanism to replace the original spiral groove of traditional 2D valves.
- (2)
- Aiming at the annulus air gap structure of TMAAG, the air gap change law is analyzed and verified by FEM simulation. A qualitative analytical model that can intuitively reflect the torque change law of TMAAG is proposed, which shows that the output torque consists of three parts: electromagnetic torque, driving torque, and feedback torque.
- (3)
- Using the method of orthogonal test, the significance of the factors affecting the torque change was analyzed, and the optimization results were obtained through neural network learning and genetic algorithm verification.
- (4)
- A prototype of TMAAG was machined, and the experiment proved the consistency of the analytical analysis and experiment. For torque-angle characteristics, the output torque increased with increasing current and rotary angle, which reached about 0.754 N·m with 2 A and 1.5°. While for torque-displacement characteristics, due to the negative feedback mechanism, the output torque decreased with armature displacement, which was about 0.084 N·m with 2 A and 1 mm. The research validates the unique negative feedback mechanism of the TMAAG and indicates that it can be potentially used as an electro-mechanical converter of 2D valves.
- (5)
- In order to improve the optimization effect, more factors and levels in orthogonal tests will be considered in future work. A robust design optimization based on space reduction strategy might be used for the optimization algorithm.
Author Contributions
Conceptualization, B.M.; methodology, M.D.; formal analysis, M.D.; investigation, M.D.; resources, B.M.; software, M.D. and C.Z.; validation, M.D.; data curation, S.L.; writing—original draft preparation, M.D. and H.X.; writing—review and editing, B.M.; supervision, B.M. and W.J.; project administration, S.L., W.J. and B.M.; funding acquisition, S.L., W.J. and B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51975524, the National Key Research and Development Program of China, grant number 2019YFB2005200 and the Natural Science Foundation of Zhejiang Province, grant number LY21E050015.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Pitch angle | |
| Air gap | |
| Magnetic flux | |
| Magnetic force | |
| Circumferential component force | |
| Driving torque | |
| Rotation angle | |
| Axial component force | |
| External force | |
| Feedback torque | |
| Axial displacement | |
| Opening between the yoke and the armature | |
| Permeance | |
| Permeability of the material | |
| Magnetic equipotential plane aera | |
| The path distance along the direction of the magnetic flux line | |
| Air gap permeance of magnetic strengthened side | |
| Air gap permeance of magnetic weakened side | |
| Permeability of air | |
| A parameter related to the width of the magnetic equipotential plane | |
| A parameter related to the ellipse cut by the cylinder along the pitch angle | |
| Armature radius | |
| Armature wing length | |
| Permanent magnet magnetic potential | |
| Coil turns | |
| Current | |
| Air gap magnetic potential | |
| Magnetic co-energy | |
| Output torque | |
| Electromagnetic torque coefficient | |
| Rotary magnetic spring stiffness | |
| Linear magnetic spring stiffness | |
| Torque change value every 0.1 mm |
References
- Yang, H.Y. Review of Intelligent Manufacturing and Intelligent Hydraulic Components. Chin. Hydraul. Pneum. 2020, 1, 1–9. [Google Scholar]
- Tamburrano, P.; Plummer, A.R.; Distaso, E.; Amirante, R. A review of electro-hydraulic servovalve research and development. Int. J. Fluid. Power. 2018, 1–23. [Google Scholar] [CrossRef]
- Tamburrano, P.; Plummer, A.R.; Distaso, E. A review of direct drive proportional electrohydraulic spool valves: Industrial state-of-the-art and research advancements. J. Dyn. Syst. Meas. Control 2019, 141, 020801. [Google Scholar] [CrossRef]
- Vyas, J.J.; Gopalsamy, B.; Joshi, H. Electro-Hydraulic Actuation Systems: Design, Testing, Identification and Validation; Springer: Singapore, 2018; ISBN 9789811325465. [Google Scholar]
- Huang, L.; Ji, H.; Zhu, Y. Analysis of effective working characteristic of the proportional solenoid. In Proceedings of the 2017 International Conference on Green Energy and Applications (ICGEA), Singapore, 11 May 2017; pp. 35–38. [Google Scholar]
- Meng, B.; Lai, Y.J.; Qiu, X.G. Regulation method for torque–angle characteristics of rotary electric–mechanical converter based on hybrid air gap. Chin. J. Mech. Eng. 2020, 33, 35. [Google Scholar] [CrossRef]
- Li, Y.; Ding, F.; Cui, J. Low power linear actuator for direct drive electrohydraulic valves. J. Zhejiang Univ. Sci. A 2008, 9, 940–943. [Google Scholar] [CrossRef]
- Direct Drive Servo Valves D633/D634. Available online: https://www.heash-tech.com/uploads/59ba1fb5e65b8717954917.pdf (accessed on 31 May 2021).
- Xu, B.; Shen, J.; Liu, S.H.; Zhang, J.H. Research and Development of Electro-hydraulic Control Valves Oriented to Industry 4.0: A Review. Chin. J. Mech. Eng. 2020, 33, 29. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.B. Electro Hydraulic Control Theory and Its Applications Under Extreme Environment; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Amirante, R.; Distaso, E.; Tamburrano, P. Sliding spool design for reducing the actuation forces in direct operated proportional directional valves: Experimental validation. Energy Conv. Manag. 2016, 119, 399–410. [Google Scholar] [CrossRef]
- Meng, B.; Xu, H.; Ruan, J. Theoretical and experimental investigation on novel 2D maglev servo proportional valve. Chin. J. Aeronaut. 2021, 34, 416–431. [Google Scholar] [CrossRef]
- Zhang, S.Z.; Aung, N.Z.; Li, S.J. Reduction of undesired lateral forces acting on the flapper of a flapper–nozzle pilot valve by using an innovative flapper shape. Energy Conv. Manag. 2015, 106, 835–848. [Google Scholar] [CrossRef]
- Aung, N.Z.; Yang, Q.J.; Chen, M.; Li, S.J. CFD analysis of flow forces and energy loss characteristics in a flapper–nozzle pilot valve with different null clearances. Energy Conv. Manag. 2014, 83, 284–295. [Google Scholar] [CrossRef]
- Yang, H.; Wang, W.; Lu, K.Q.; Chen, Z.F. Cavitation reduction of a flapper-nozzle pilot valve using continuous microjets. Int. J. Heat Mass Transf. 2019, 133, 1099–1109. [Google Scholar] [CrossRef]
- Yan, H.; Wang, F.J.; Li, C.C. Research on the jet characteristics of the deflector–jet mechanism of the servo valve. Chin. Phys. B 2017, 26, 252–260. [Google Scholar] [CrossRef]
- Li, C.M.; Yin, Y.B.; Wang, M.Y. Influence of high temperature on couples matching and characteristics of jet pipe electrohydraulic servovalve. J. Mech. Eng. 2018, 54, 251–261. [Google Scholar] [CrossRef]
- Ruan, J.; Burton, R.; Ukrainetz, P.R. An investigation into the characteristics of a two dimensional “2D” flow control valve. J. Dyn. Syst. Meas. Control 2002, 124, 214–220. [Google Scholar] [CrossRef]
- He, J.F.; Chen, X.; Lu, P.Y.; Ruan, J.; Chang, L. Theoretical analysis and experimental study on two-dimensional cartridge servo valve. Acta Aeronaut. Astronaut. Sin. 2019, 40, 422590. [Google Scholar]
- Ren, Y.; Ruan, J. Theoretical and experimental investigations of vibration waveforms excited by an electro-hydraulic type exciter for fatigue with a two-dimensional rotary valve. Mechatronics 2016, 33, 161–172. [Google Scholar] [CrossRef] [Green Version]
- Zuo, X.Q.; Ruan, J.; Liu, G.W.; Yu, Z.Q. Characteristics of direct-acting airborne 2D electro-hydraulic pressure servo valve. Acta Aeronaut. Astronaut. Sin. 2017, 38, 421294. [Google Scholar]
- Zhang, Q.H.; Xiong, W.; Ruan, J. Research on 2D Digital Buffering Valve for Vehicle Shift. J. Mech. Eng. 2018, 54, 206–212. [Google Scholar] [CrossRef]
- Li, S.; Ruan, J.; Meng, B. Two-dimensional electro-hydraulic proportional directional valve. J. Mech. Eng. 2016, 52, 202–212. [Google Scholar] [CrossRef]
- Cui, J.; Ding, F.; Li, Q.P. Novel bidirectional rotary proportional actuator for electrohydraulic rotary valves. IEEE Trans. Magn. 2007, 43, 3254–3258. [Google Scholar]
- Zhang, Q.F.; Yan, L.; Duan, Z.H.; Jiao, Z.X. High torque density torque motor with hybrid magnetization pole arrays for jet pipe servo valve. IEEE Trans. Ind. Electron. 2019, 67, 2133–2142. [Google Scholar] [CrossRef]
- Li, S.; Song, Y. Dynamic response of a hydraulic servo-valve torque motor with magnetic fluids. Mechatronics 2007, 17, 442–447. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, J.; Li, S. Damping force modeling and suppression of self-excited vibration due to magnetic fluids applied in the torque motor of a hydraulic servovalve. Energies 2017, 10, 749. [Google Scholar] [CrossRef] [Green Version]
- Urata, E. Influence of unequal air-gap thickness in servo valve torque motors. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 1287–1297. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, H. Influence of magnetic reluctances of magnetic elements on servo valve torque motors. Chin. J. Mech. Eng. 2016, 29, 136–144. [Google Scholar] [CrossRef]
- Tai, M.H.; Jiang, Y.L.; Chen, L. Theoretical research on magnetization and demagnetization process of electrohydraulic servo valve with permanent magnet torque motor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Han, C.; Choi, S.B.; Han, Y.M. A piezoelectric actuator-based direct-drive valve for fast motion control at high operating temperatures. Appl. Sci. 2018, 8, 1806. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; He, Z.; Yang, F.; Rong, C.; Cui, X. Design and Analysis of a Voltage Driving Method for Electro-Hydraulic Servo Valve Based on Giant Magnetostrictive Actuator. Int. J. Appl. Electromagn. Mech. 2018, 57, 439–456. [Google Scholar] [CrossRef]
- Hu, G.L.; Zheng, K.Y. Pressure drop and response time analysis of magnetorheological valve with mosquito-plate fluid flow channels. Trans. Chin. Soc. Agric. Mach. 2019, 50, 401–409. [Google Scholar]
- Shi, H.; He, B.; Wang, Z. Magneto-mechanical behavior of magnetic shape memory alloy and its application in hydraulic valve actuator. J. Mech. Eng. 2018, 54, 235–244. [Google Scholar] [CrossRef]
- Diao, K.K.; Sun, X.D.; Lei, G. Multiobjective System Level Optimization Method for Switched Reluctance Motor Drive Systems Using Finite-Element Model. IEEE Trans. Ind. Electron. 2020, 67, 10055–10064. [Google Scholar] [CrossRef]
- Jing, L.B.; Gong, J. Analytical model and optimisation design of surface-mounted PM motors with Halbach arrays accounting for semi-closed slots. IET Electr. Power Appl. 2020, 14, 2074–2081. [Google Scholar] [CrossRef]
- Xu, J.Q.; Zhang, B.Y.; Kuang, X.L. Influence analysis of slot parameters and high torque density optimisation for dual redundant permanent magnet motor in aerospace application. IET Electr. Power Appl. 2020, 14, 1263–1273. [Google Scholar] [CrossRef]
- El-Nemr, M.; Afifi, M.; Rezk, H.; Ibrahim, M. Finite Element Based Overall Optimization of Switched Reluctance Motor Using Multi-Objective Genetic Algorithm (NSGA-II). Mathematics 2021, 9, 576. [Google Scholar] [CrossRef]
- Yang, Z.B.; Lu, C.L.; Sun, X.D.; Ji, J.L.; Ding, Q.F. Study on Active Disturbance Rejection Control of a Bearingless Induction Motor Based on an Improved Particle Swarm Optimization-Genetic Algorithm. IEEE Trans. Transp. Electrif. 2021, 7, 694–705. [Google Scholar] [CrossRef]
- Wang, S.J.; Weng, Z.D.; Jin, B.; Cai, H.X. Multi-objective genetic algorithm optimization of linear proportional solenoid actuator. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 60. [Google Scholar] [CrossRef]
- Shen, H.M.; Bian, F.; Yue, Y. Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell. Appl. Sci. 2021, 11, 4740. [Google Scholar] [CrossRef]
- Wang, B.L. Design Basis of Electromagnetic Appliances; National Defense Industry Press: Beijing, China, 1989. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).