High-Efficient Calculation Method for Sensitive PDGEs of Five-Axis Reconfigurable Machine Tool
Abstract
1. Introduction
2. Theoretical Basis of the High-Efficient Calculation Method
2.1. Morris Global Sensitivity Analysis Method
2.2. Discovery of Mapping Relationships
3. Mapping Expressions
3.1. The Defined Symbols and Expressions
- (1)
- represents the sensitive PDGEs of the motion axis (Axis) in the identification direction (Dir). is the type of sensitive geometric error to be calculated and is divided into the following four categories: represents the sensitive linear PDGEs of the translational axis. represents the sensitive linear PDGEs of the rotational axis. represents the sensitive angular PDGEs of the translational axis. represents the sensitive angular PDGEs of rotational axis.
- (2)
- The defined mapping expressions is used to calculate the error items in Table 1, taking for an example, where = x and = X.
- (3)
- Combined with the relevant definitions in (1) and (2), the relevant calculation forms of Equation (6) are illustrated with examples as follows:
- If Equation (6) is = , then = ;
- If Equation (6) is = , then = ;
- If Equation (6) is = , then = {, };
- If Equation (6) is = , then = {, }.
3.2. Calculation Method of RTTTR-Type Five-Axis Machine Tools
3.2.1. Sensitive Linear PDGEs for Translational Axes
3.2.2. Sensitive Linear PDGEs for Rotational Axes
3.2.3. Sensitive Angular PDGEs of Translational Axis
- (1)
- When belongs to the workpiece chain
- (2)
- When belongs to the tool chain
3.2.4. Sensitive Angular PDGEs of Rotational Axis
- (1)
- When = R1
- (2)
- When = R2
- If sensitivity PDGE in x direction is identified, (), then = = {, , } can be obtained;
- If sensitivity PDGE in y direction is identified, (), then = = {, , } can be obtained;
- If sensitivity PDGE in z direction is identified, = ( = ), then = = {, } can be obtained.
- If sensitivity PDGE in x direction is identified, (, then = = can be obtained;
- If sensitivity PDGE in y direction is identified, (), then = = can be obtained;
- If sensitivity PDGE in z direction is identified, = ( = ), then = = can be obtained.
3.3. Calculation Method of TTTRR-Type five-Axis Machine Tools
3.3.1. Sensitive Linear PDGEs of Translational Axis
3.3.2. Sensitive Linear PDGEs of Rotational Axes
- (1)
- When
- (2)
- When
3.3.3. Sensitive Angular PDGEs of Translational Axis
3.3.4. Sensitive Angular PDGEs of Rotational Axis
- (1)
- When
- (2)
- When
3.4. Summary of Mapping Expressions
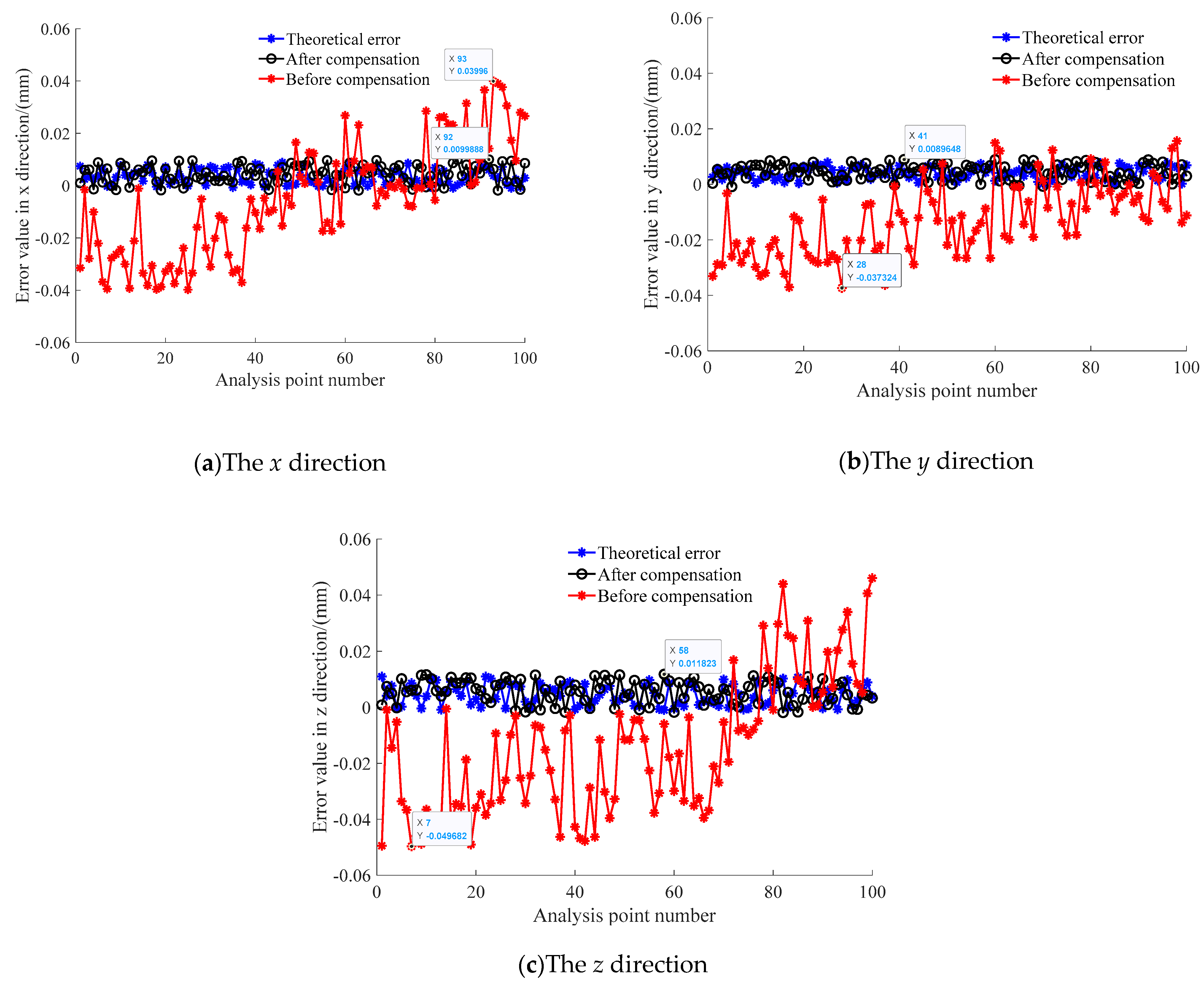
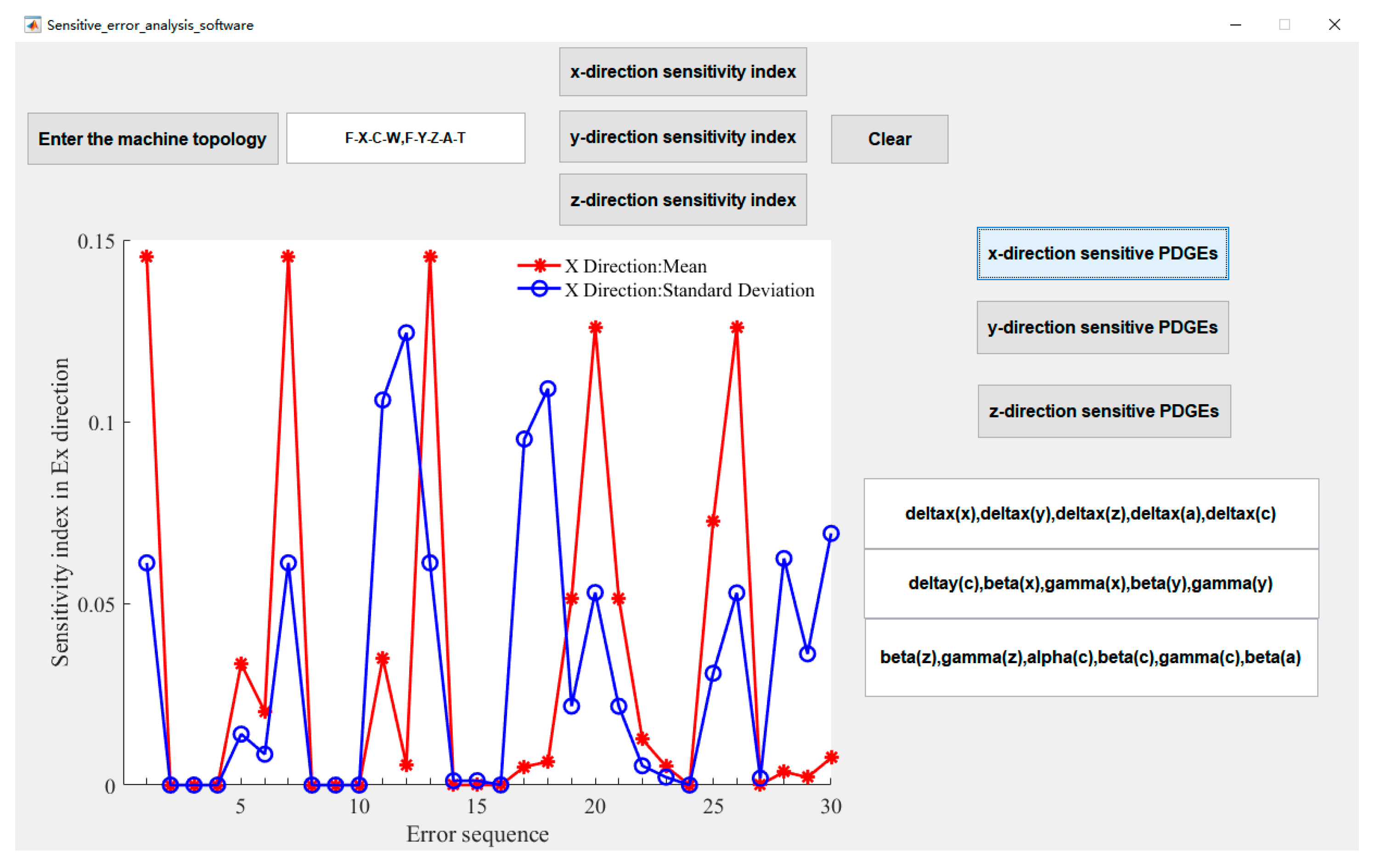
4. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Linear PDGEs | Angular PDGEs | ||
|---|---|---|---|
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
} | } | ||
| } | } | ||
| } | } | ||
| } | } | } | } |
} | } | } | } |
| } | } | ||
| } | } | ||
| } | } | ||
| } | } | ||
References
- Ni, J. CNC Machine Accuracy Enhancement Through Real-Time Error Compensation. J. Manuf. Sci. Eng. 1997, 119, 717–725. [Google Scholar] [CrossRef]
- Koren, Y.; Heisel, U.; Jovane, F.; Moriwaki, T.; Pritschow, G.; Ulsoy, G.; Van Brussel, H. Reconfigurable Manufacturing System. Ann. CIRP 1999, 48, 527–540. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, M.; Du, J.; Zhou, L. Design of a machine tool control system for function reconfiguration and reuse in network environment. Robot. Comput. Manuf. 2019, 56, 117–126. [Google Scholar] [CrossRef]
- Gadalla, M.; Xue, D.Y. Recent advances in research on reconfigurable machine tools: A literature review. Int. J. Prod. Res. 2017, 55, 1440–1454. [Google Scholar] [CrossRef]
- Álvarez, Á.; Calleja, A.; Ortega, N.; López de Lacalle, L.N. Five-axis milling of large spiral bevel gears: Tool path definition, finishing, and shape errors. Metals 2018, 8, 353. [Google Scholar] [CrossRef]
- McCulloch, A. Sensitivity analysis in practice: A guide to assessing scientific models. J. R. Stat. Soc. Ser. Stat. Soc. 2005, 168, 466. [Google Scholar] [CrossRef]
- Fan, K.-C.; Wang, H.; Zhao, J.-W.; Chang, T.-H. Sensitivity analysis of the 3-PRS parallel kinematic spindle platform of a serial-parallel machine tool. Int. J. Mach. Tools Manuf. 2003, 43, 1561–1569. [Google Scholar] [CrossRef]
- Li, D.; Feng, P.; Zhang, J.; Yu, D.; Wu, Z. An identification method for key geometric errors of machine tool based on matrix differential and experimental test. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 3141–3155. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Y.; Sun, Y.; Chen, W.; Wang, B. Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2013, 68, 2525–2534. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, G.; Liu, Z.; Xuan, D.; Chang, W. An identification approach for key geometric error sources of machine tool based on sensitivity analysis. J. Mech. Eng. 2012, 48, 171–179. (In Chinese) [Google Scholar] [CrossRef]
- Yao, H.; Li, Z.; Zhao, X.; Sun, T.; Dobrovolskyi, G.; Li, G. Modeling of kinematics errors and alignment method of a swing arm ultra-precision diamond turning machine. Int. J. Adv. Manuf. Technol. 2016, 87, 165–176. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, H.; Zhang, G.; Gu, P.; Cai, L. An analytical approach for crucial geometric errors identification of multi-axis machine tool based on global sensitivity analysis. Int. J. Adv. Manuf. Technol. 2014, 75, 107–121. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, D.; Xi, Y. Global Quantitative Sensitivity Analysis and Compensation of Geometric Errors of CNC Machine Tool. Math. Probl. Eng. 2016, 2016, 2834718. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, B.; Liu, Z.; Li, J.; Dong, X.; Gu, P. Key geometric error extraction of machine tool based on extended Fourier amplitude sensitivity test method. Int. J. Adv. Manuf. Technol. 2017, 90, 3369–3385. [Google Scholar] [CrossRef]
- Cheng, Q.; Feng, Q.; Liu, Z.; Gu, P.; Zhang, G. Sensitivity analysis of machining accuracy of multi-axis machine tool based on POE screw theory and Morris method. Int. J. Adv. Manuf. Technol. 2016, 84, 2301–2318. [Google Scholar] [CrossRef]
- Fu, G.; Gong, H.; Fu, J.; Gao, H.; Deng, X. Geometric error contribution modeling and sensitivity evaluating for each axis of five-axis machine tools based on POE theory and transforming differential changes between coordinate frames. Int. J. Mach. Tools Manuf. 2019, 147, 103455. [Google Scholar] [CrossRef]
- Changjiu, X.; Shilong, W.; Shouli, S.; Xiaochuan, L.; Xiaodiao, H. Geometric error to tooth surface error model and identification of crucial errors in five-axis CNC gear profile grinding machines. Comput. Integr. Manuf. Syst. 2020, 26, 1191–1201. (In Chinese) [Google Scholar]
- Guo, S.; Jiang, G.; Mei, X. Investigation of sensitivity analysis and compensation parameter optimization of geometric error for five-axis machine tool. Int. J. Adv. Manuf. Technol. 2017, 93, 3229–3243. [Google Scholar] [CrossRef]
- Li, Q.; Wang, W.; Jiang, Y.; Li, H.; Zhang, J.; Jiang, Z. A sensitivity method to analyze the volumetric error of five-axis machine tool. Int. J. Adv. Manuf. Technol. 2018, 98, 1791–1805. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Pandey, M.D. Global sensitivity analysis of a CNC machine tool: Application of MDRM. Int. J. Adv. Manuf. Technol. 2015, 81, 159–169. [Google Scholar] [CrossRef]
- Zou, X.; Zhao, X.; Li, G.; Li, Z.; Sun, T. Sensitivity analysis using a variance-based method for a three-axis diamond turning machine. Int. J. Adv. Manuf. Technol. 2017, 92, 4429–4443. [Google Scholar] [CrossRef]
- Fan, J.; Tao, H.; Pan, R.; Chen, D. An approach for accuracy enhancement of fifive-axis machine tools based on quantitative interval sensitivity analysis. Mech. Mach. Theory 2020, 148, 103806. [Google Scholar] [CrossRef]
- Li, Z.; Sato, R.; Shirase, K.; Ihara, Y.; Milutinovic, D.S. Sensitivity analysis of relationship between error motions and machined shape errors in five-axis machining center-Peripheral milling using squareend mill as test case. Precis. Eng. 2019, 60, 28–41. [Google Scholar] [CrossRef]
- Li, J.; Xie, F.; Liu, X.-J. Geometric error modeling and sensitivity analysis of a five-axis machine tool. Int. J. Adv. Manuf. Technol. 2016, 82, 2037–2051. [Google Scholar] [CrossRef]
- Okafor, A.C.; Ertekin, Y.M. Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics. Int. J. Mach. Tools Manuf. 2000, 40, 1199–1213. [Google Scholar] [CrossRef]
- Fan, J.W.; Guan, J.L.; Wang, W.C.; Luo, Q.; Zhang, X.; Wang, L. A universal modeling method for enhancement the volumetric accuracy of CNC machine tools. J. Mater. Process. Technol. 2002, 129, 624–628. [Google Scholar] [CrossRef]
- Crosetto, M.; Tarantola, S. Uncertainty and sensitivity analysis: Tools for GIS-based model implementation. Int. J. Geogr. Inf. Sci. 2001, 15, 415–437. [Google Scholar] [CrossRef]
- Ding, S.; Huang, X.; Yu, C.; Wang, W. Actual inverse kinematics for position-independent and position-dependent geometric error compensation of five-axis machine tools. Int. J. Mach. Tools Manuf. 2016, 111, 55–62. [Google Scholar] [CrossRef]
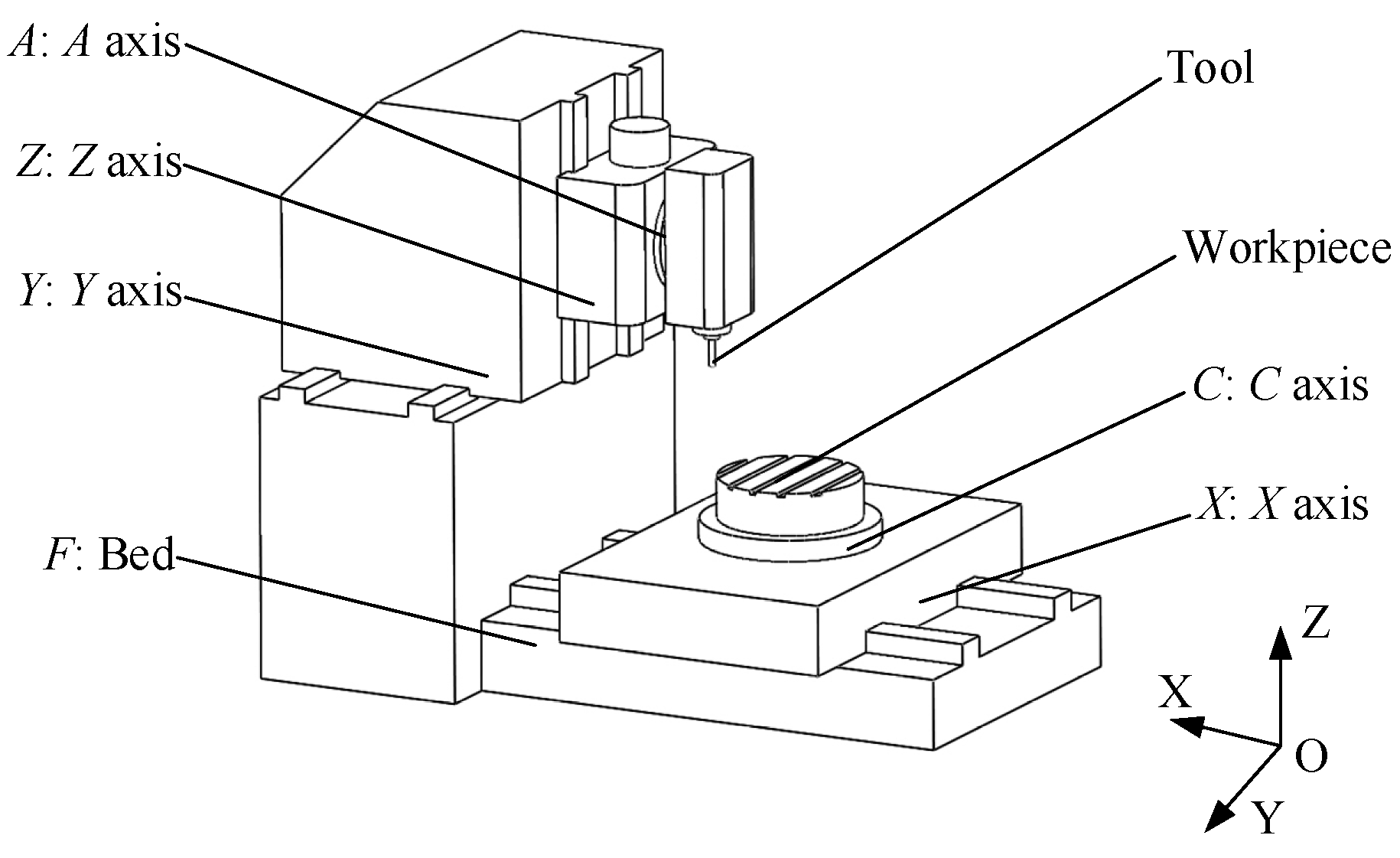





| The Name of the Linear Error Term | The Geometric Meaning of the Error Term | The Name of the Angular Error Term | The Geometric Meaning of the Error Term |
|---|---|---|---|
| Positioning error of the X axis in the x direction | Rolling error of X axis in x direction | ||
| Straightness error of X axis in y direction | X axis angular error in y direction | ||
| Straightness error of X axis in z direction | X axis angular error in z direction | ||
| Straightness error of Y axis in x direction | Y axis angular error in x direction | ||
| Positioning error of Y axis in y direction | Rolling error of Y axis in y direction | ||
| Straightness error of Y axis in z direction | Y axis angular error in z direction | ||
| Straightness error of Z axis in x direction | Z axis angular error in x direction | ||
| Straightness error of Z axis in y direction | Z axis angular error in y direction | ||
| Positioning error of Z axis in z direction | Rolling error of Z axis in z direction | ||
| Positioning error of the A axis in the x direction | Rolling error of A axis in x direction | ||
| Straightness error of A axis in y direction | A axis angular error in y direction | ||
| Straightness error of A axis in z direction | A axis angular error in z direction | ||
| Straightness error of B axis in x direction | B axis angular error in x direction | ||
| Positioning error of B axis in y direction | Rolling error of B axis in y direction | ||
| Straightness error of B axis in z direction | B axis angular error in z direction | ||
| Straightness error of C axis in x direction | C axis angular error in x direction | ||
| Straightness error of C axis in y direction | C axis angular error in y direction | ||
| Positioning error of C axis in z direction | Rolling error of C axis in z direction |
| Error Direction | Sensitive PDGEs |
|---|---|
| x | |
| y | , |
| z |
| Sensitive Linear PDGEs | Sensitive Angular PDGEs | |
|---|---|---|
| Translational axis in the workpiece chain | ||
| Translational axis in the tool chain | ||
| Rotational axis in the workpiece chain | ||
| Rotational axis in the tool chain |
| Sensitive Linear PDGEs | Sensitive Angular PDGEs | |
|---|---|---|
| Translational axis in the workpiece chain | ||
| Translational axis in the tool chain | ||
| Rotational axis in the tool chain | : : | : : |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Ding, S.; Chen, Z.; Lu, Z.; Wang, Z. High-Efficient Calculation Method for Sensitive PDGEs of Five-Axis Reconfigurable Machine Tool. Machines 2021, 9, 84. https://doi.org/10.3390/machines9050084
Song Z, Ding S, Chen Z, Lu Z, Wang Z. High-Efficient Calculation Method for Sensitive PDGEs of Five-Axis Reconfigurable Machine Tool. Machines. 2021; 9(5):84. https://doi.org/10.3390/machines9050084
Chicago/Turabian StyleSong, Zhanqun, Shuang Ding, Zhiwei Chen, Zhongwang Lu, and Zhouzhou Wang. 2021. "High-Efficient Calculation Method for Sensitive PDGEs of Five-Axis Reconfigurable Machine Tool" Machines 9, no. 5: 84. https://doi.org/10.3390/machines9050084
APA StyleSong, Z., Ding, S., Chen, Z., Lu, Z., & Wang, Z. (2021). High-Efficient Calculation Method for Sensitive PDGEs of Five-Axis Reconfigurable Machine Tool. Machines, 9(5), 84. https://doi.org/10.3390/machines9050084





