Numerical and Experimental Investigation of Flow and Heat Transfer in Heat Exchanger Channels with Different Dimples Geometries
Abstract
:1. Introduction
2. Model and Numerical Method
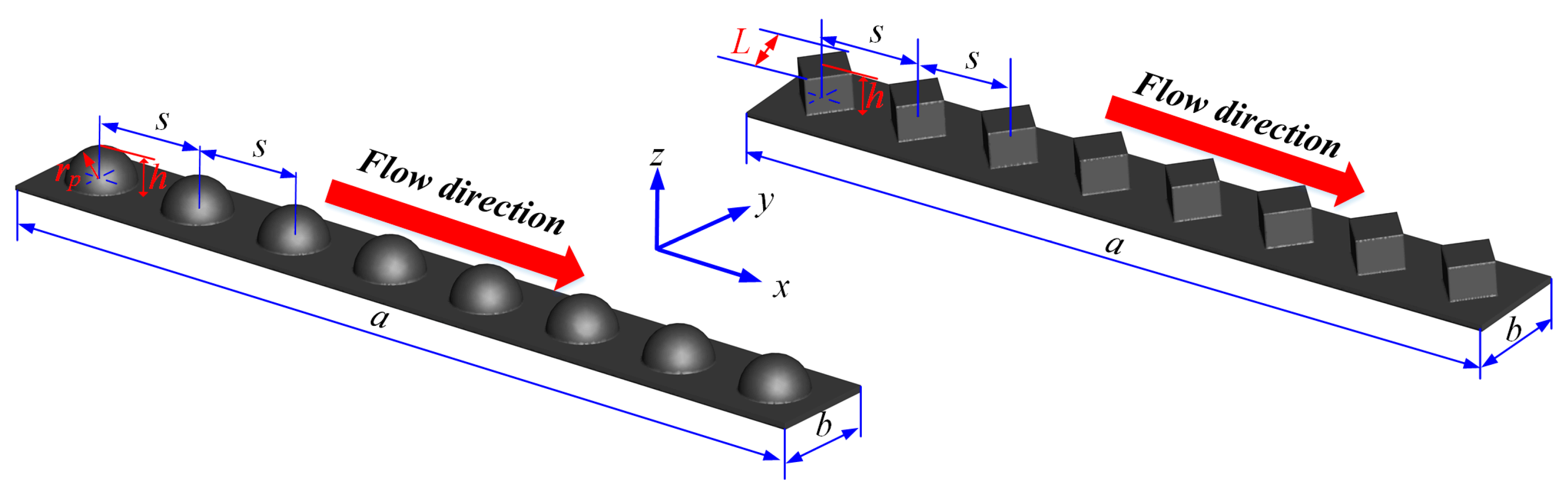
2.1. Geometrical Model
2.2. Mathematical Model and Governing Equations
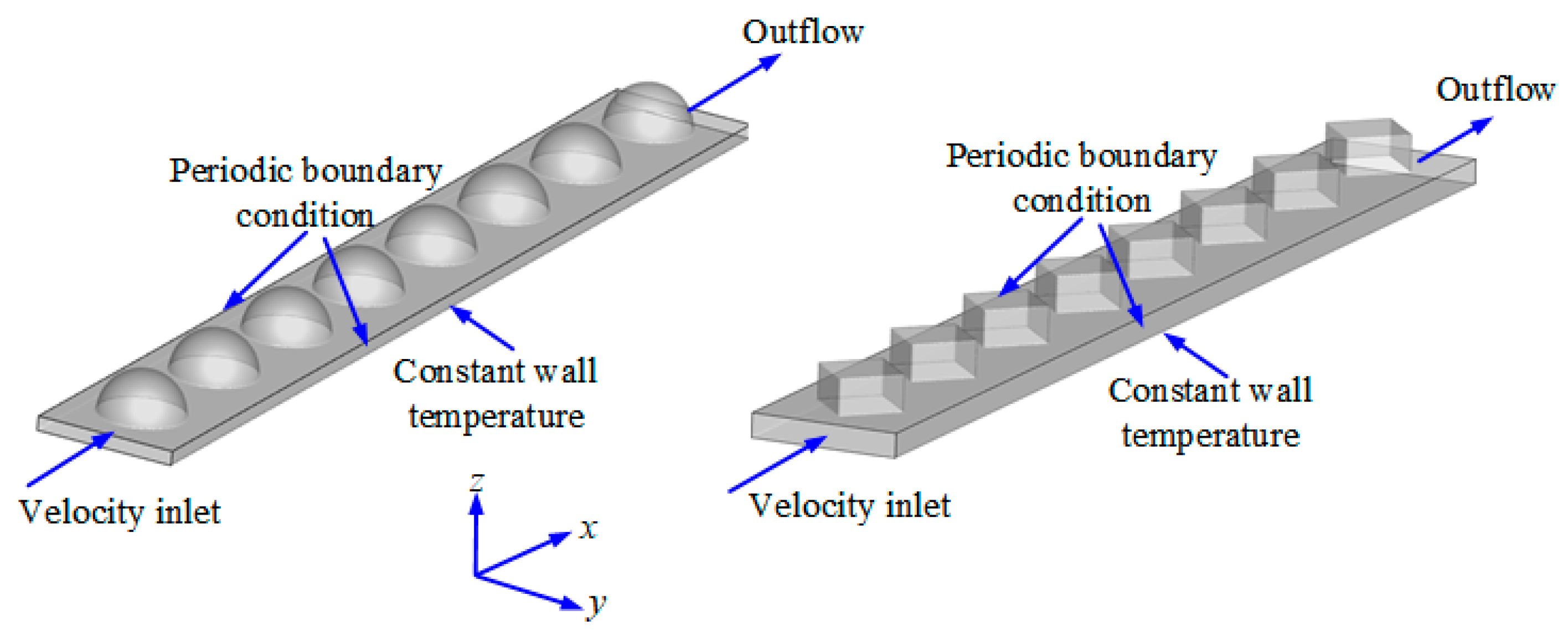
2.3. Boundary Conditions
2.4. Data Reduction
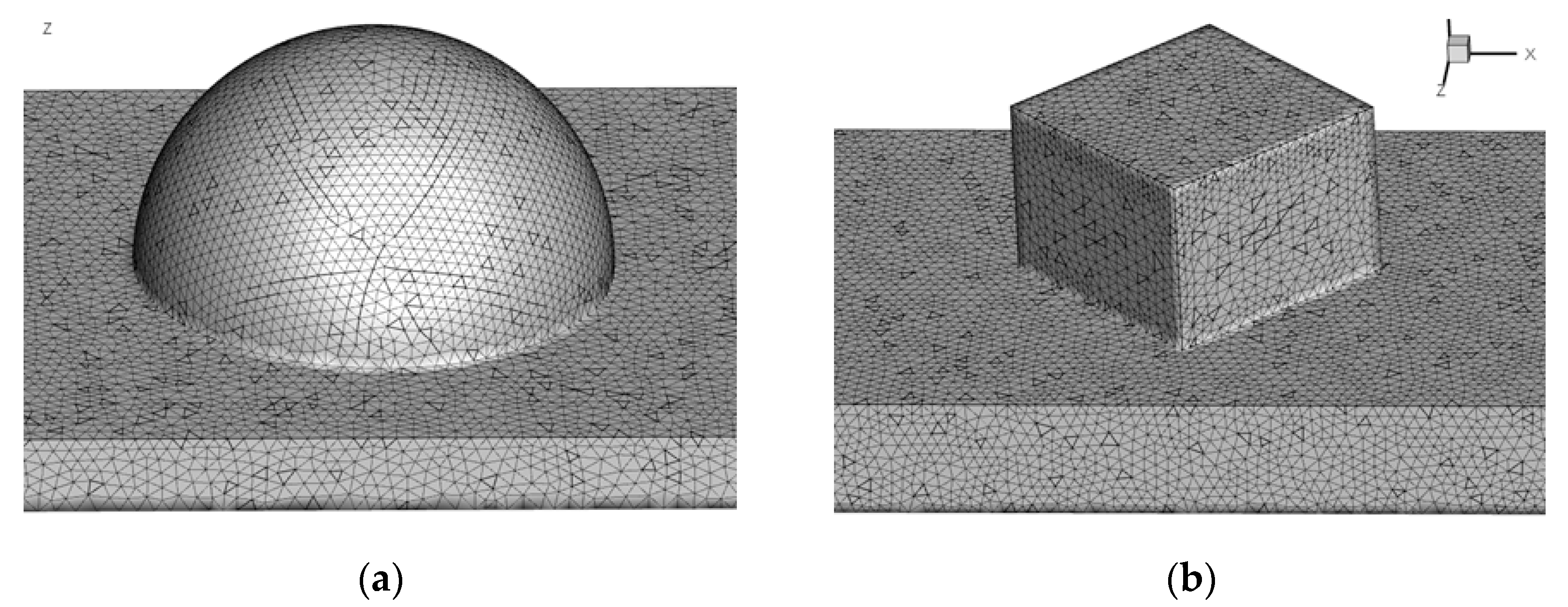
3. Grid Independence Study
4. Experimental Apparatus
5. Results and Discussion
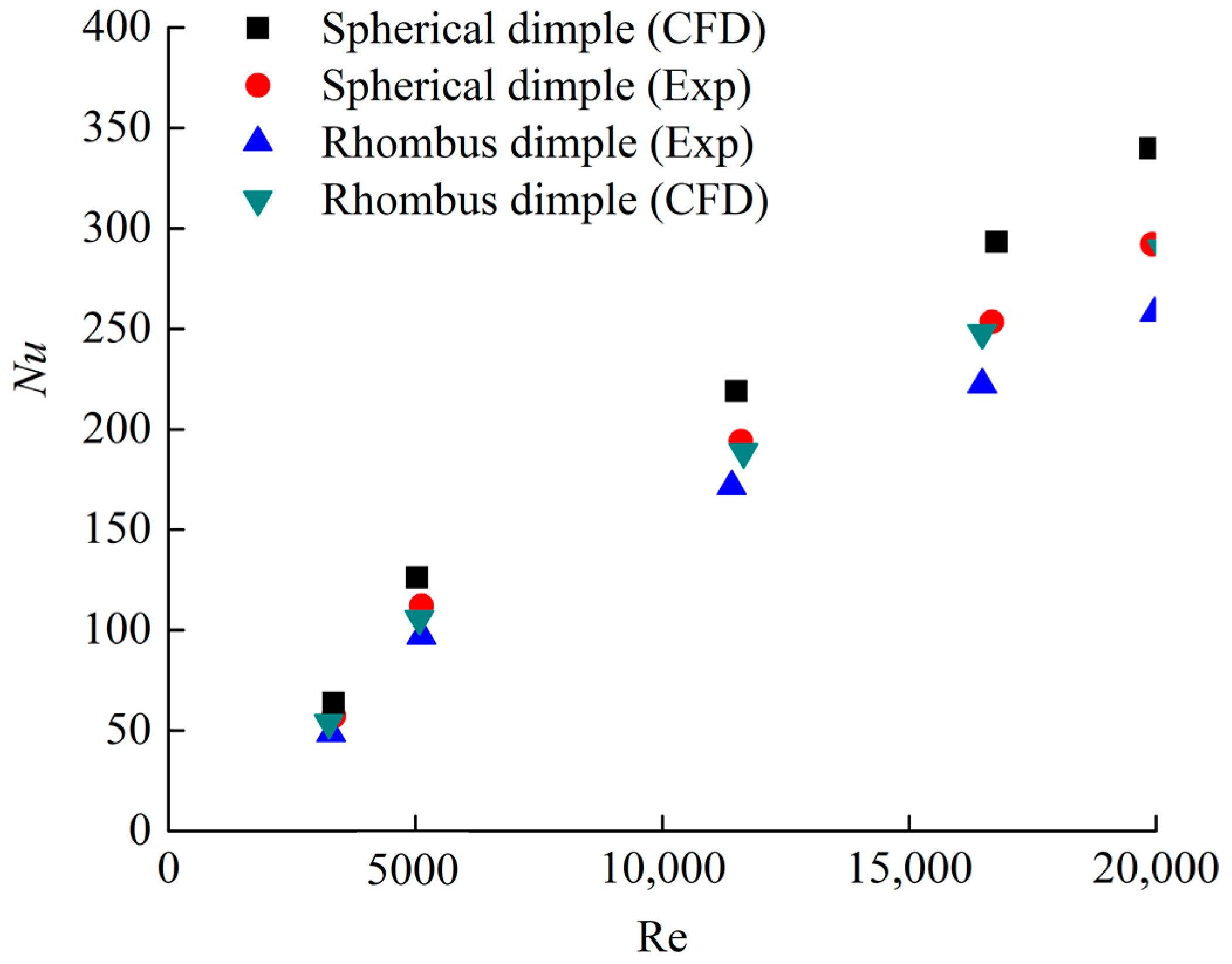
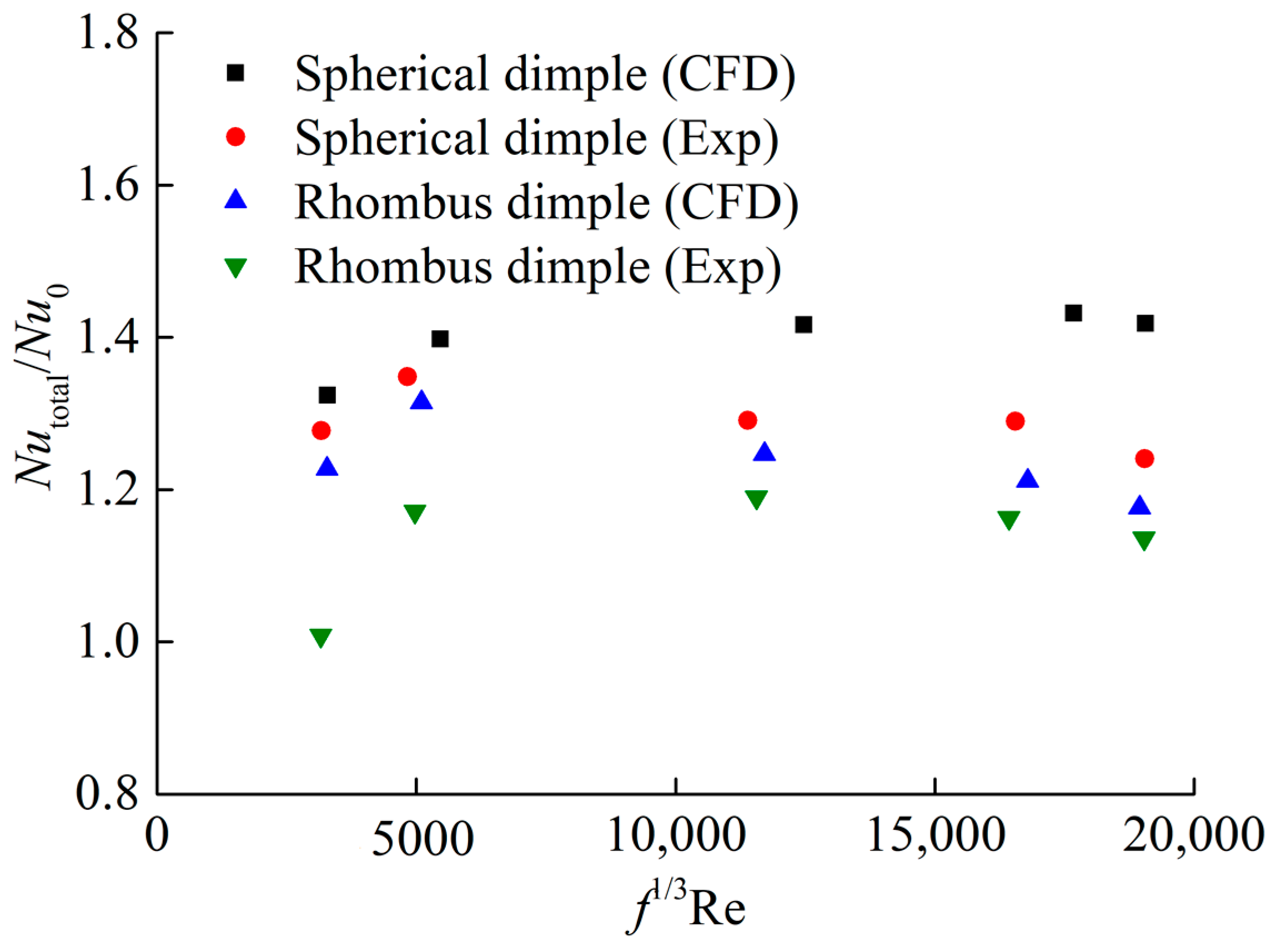
5.1. Validation with Empirical Equations
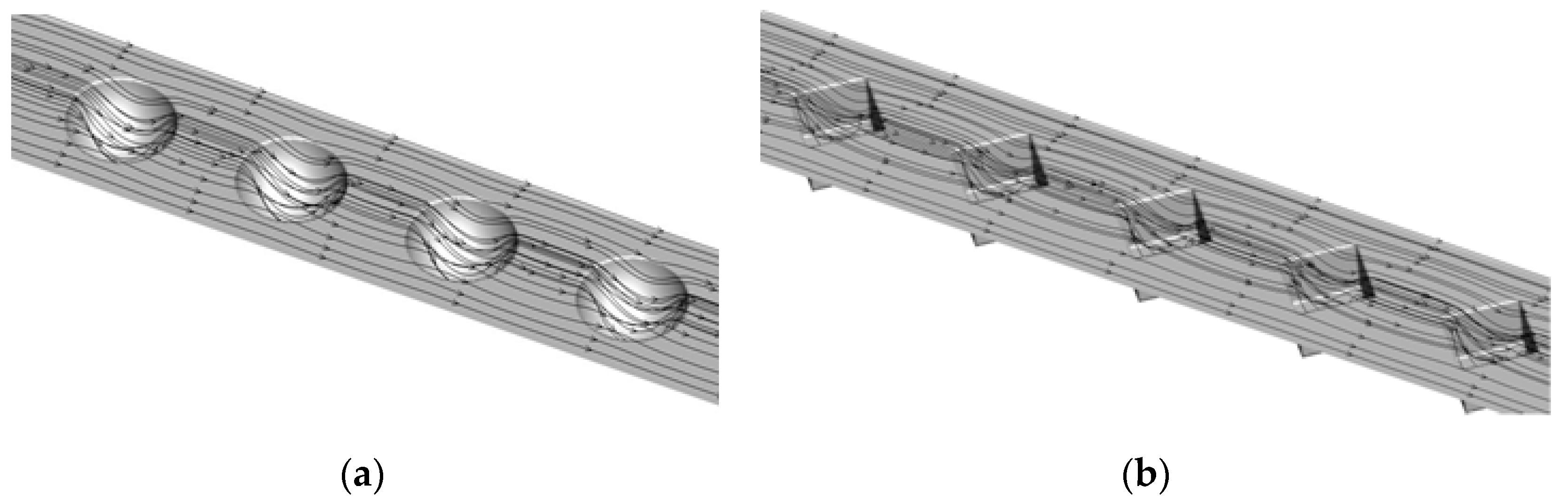
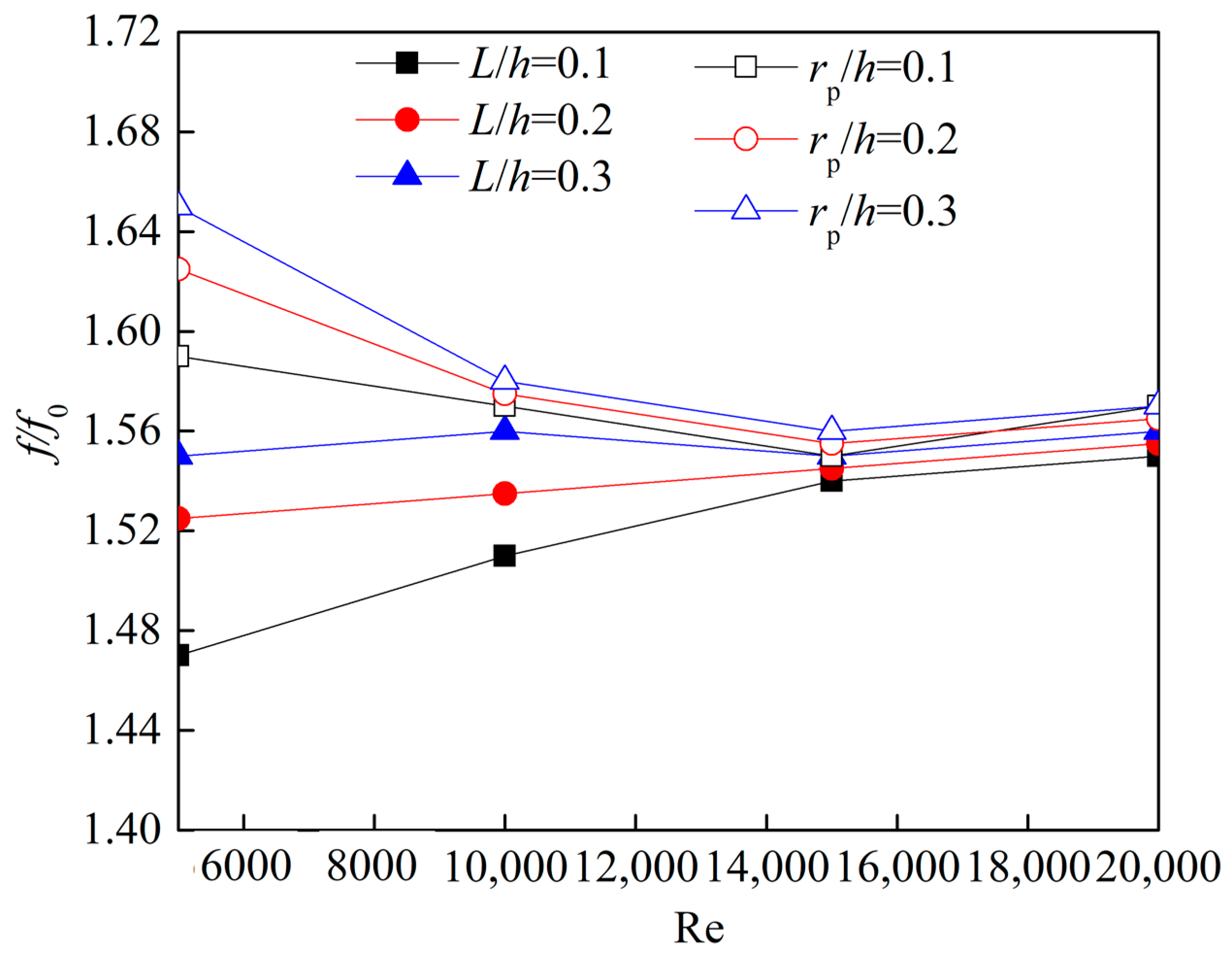
5.2. Flow Characteristics
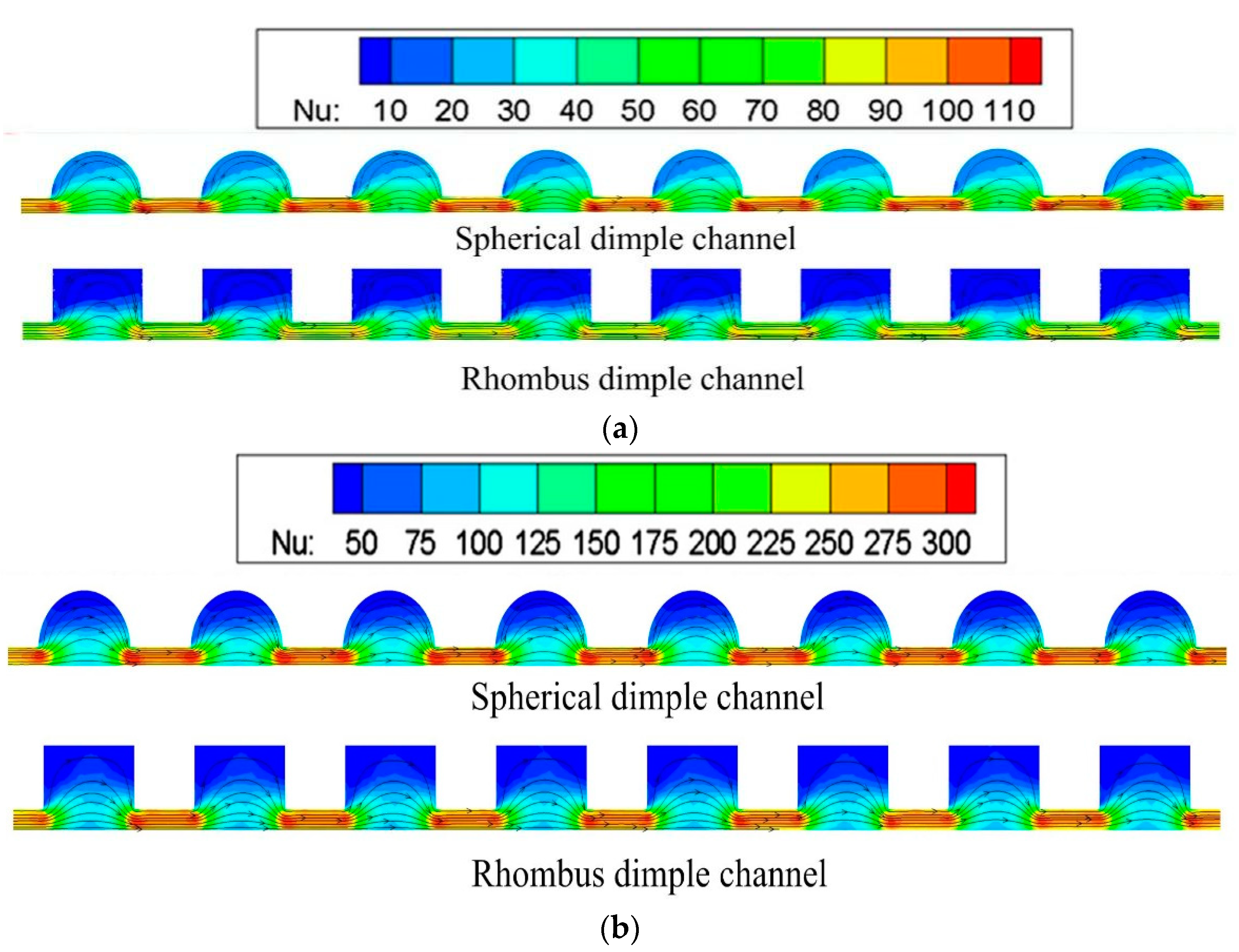
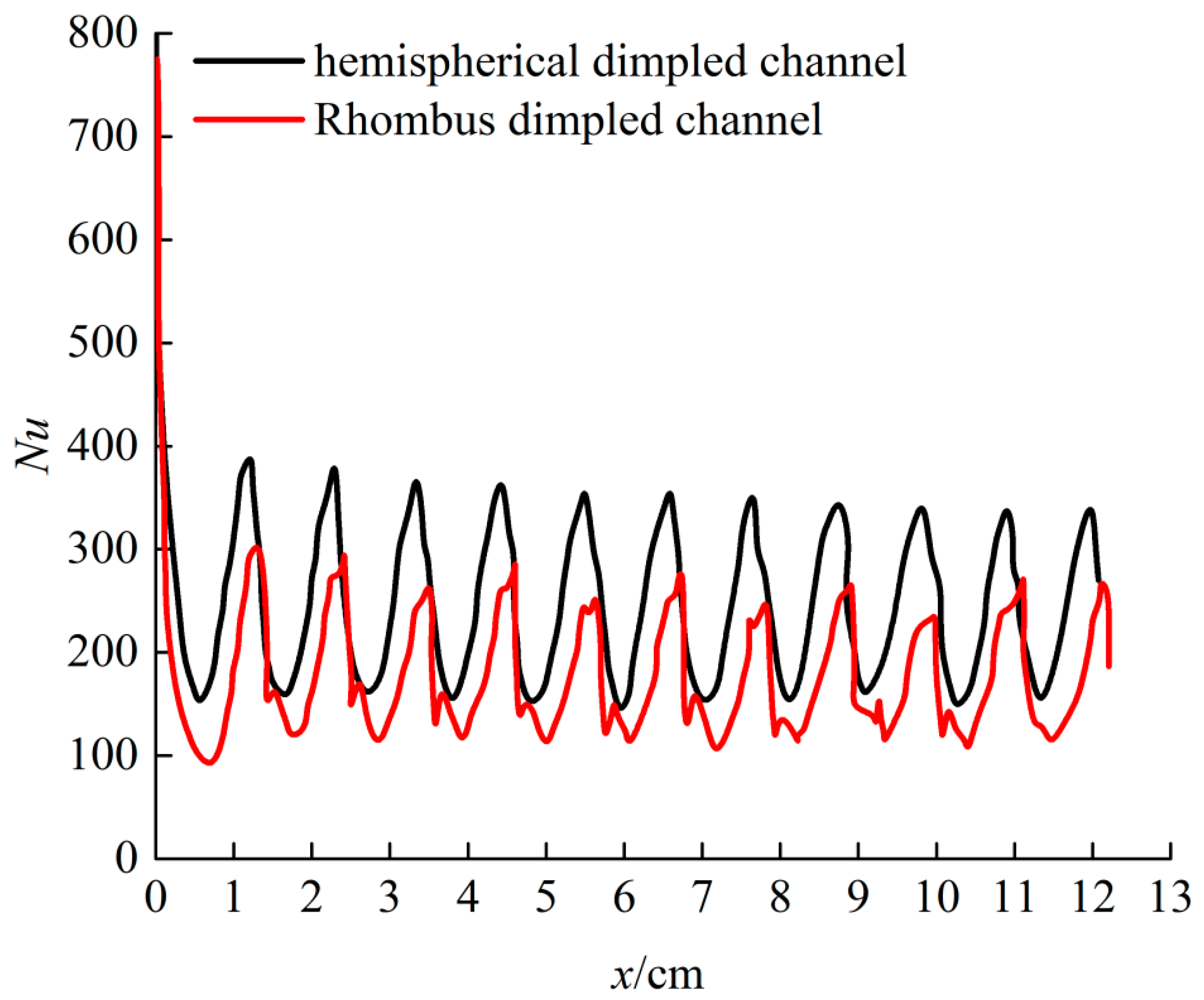
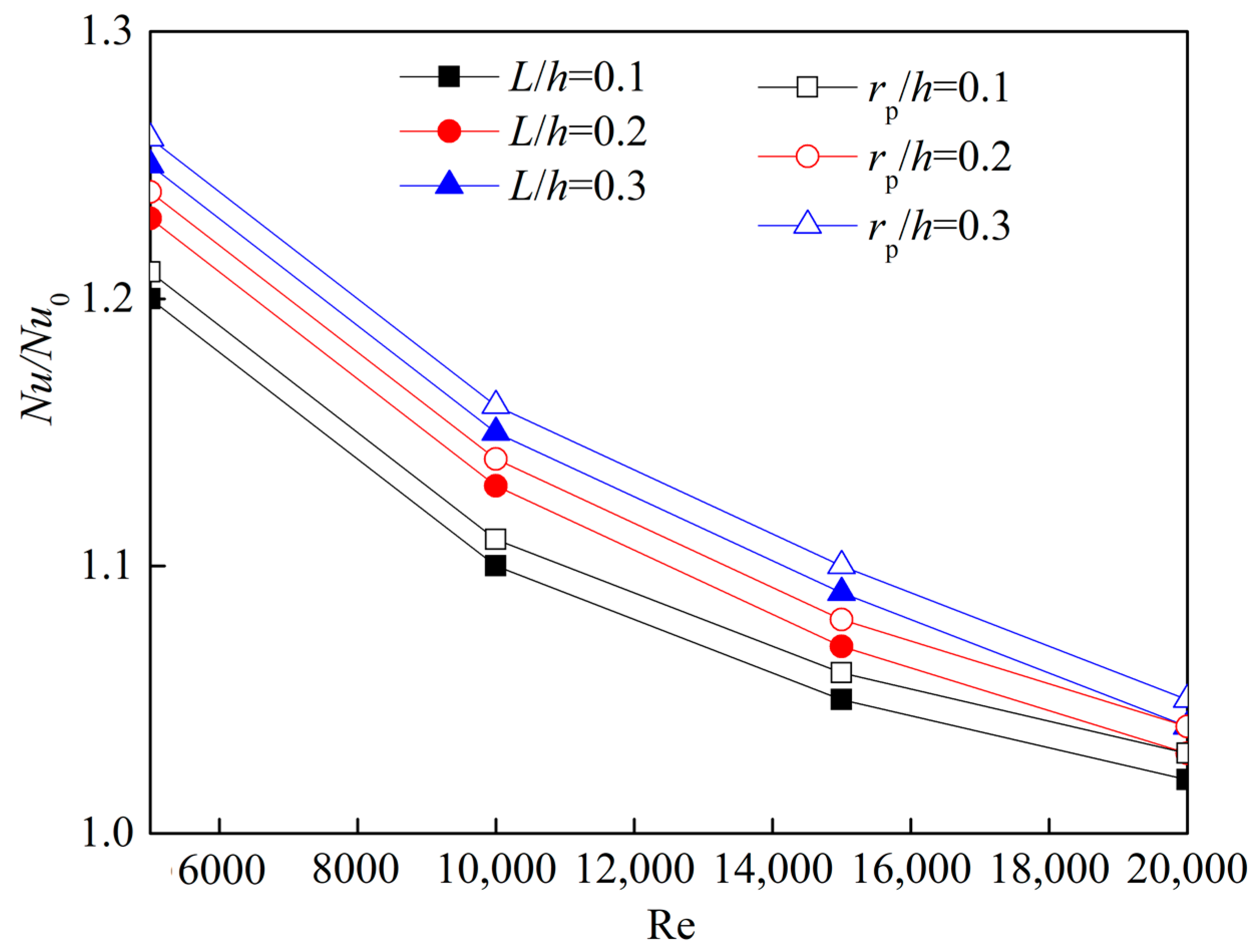
5.3. Heat Transfer
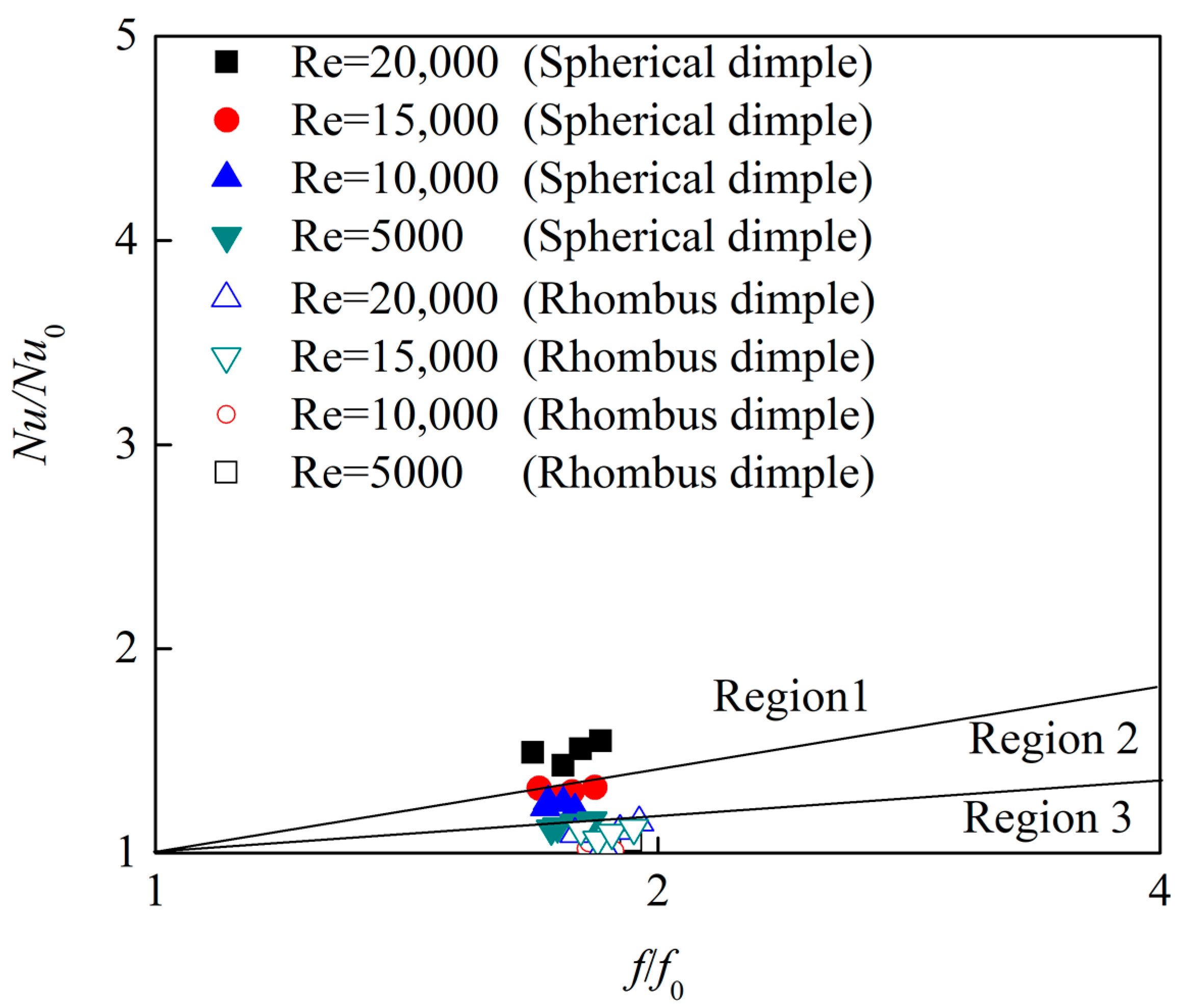
5.4. Thermal Performance Evaluation
6. Conclusions
- (1)
- The Nusselt number enhancement of the hemispherical dimple channel increases with the increasing of Reynolds number. The Nusselt number enhancement of a hemispherical dimpled channel with higher radius–depth ratio is noticed to be more than the rhombus dimpled channel.
- (2)
- The flow friction performance depends on the dimple radius depth ratio of hemispherical dimple channels. The friction coefficient increment of hemispherical dimple channel increases with increasing of the dimple radius depth ratio, but it decreases with the increase of Reynolds number.
- (3)
- The fluid flows smoothly and easily on the hemispherical dimple surface, and the hemispherical dimples can improve the flow mixing, interrupt the boundary layer and forms periodic impinge flows, thus realized the enhancement of thermal–hydraulic performance.
- (4)
- The hemispherical dimpled channel present better overall thermal performance because the strength and extent of the recirculation flow is significant decreased compared with the rhombus dimpled channel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| p | Fluid pressure | Pa |
| vi | Fluid velocity | m/s |
| ρ | Fluid property | kg/m3 |
| F | Body force | N |
| cp | Specific heat | J/(kg·K) |
| λ | Thermal conductivity | W/(m·K) |
| τ | Time | ms |
| μ | Oil viscosity | Pa·s |
| i,j,w | Direction of coordinate | - |
| μt | Turbulent viscosity ratio | - |
| σk | Turbulent kinetic energy | K |
| k | Turbulent kinetic energy ratio | - |
| Gk | Turbulent viscosity | - |
| ε | Dissipation rate | - |
| mtest | Mass flow rate measurement | kg/s |
| Tw | wall temperature | °C |
| Q | Total heat absorbed by heat transfer fluid | J |
| mout | Outlet mass flow rate | kg/s |
| d | Channel diameter | mm |
| Re | Reynold number | - |
| Tin | Inlet temperature | °C |
| A | Flow area | m2 |
| Tave | Average fluid temperature | °C |
| Heat transfer rate | W | |
| Tout | Outlet temperature | °C |
| qm | Heat flux | W/m2 |
| △Tm | Mean temperature difference | °C |
| de | Equivalent diameter of channel | mm |
| L | Channel length | mm |
| f | Friction factor | - |
| △p | Pressure difference between inlet and outlet | Pa |
| Nu0 | Nusselt number in the fully developed fluid region | - |
| f0 | Darcy friction factor in the corresponding fully developed fluid region | - |
| Pr | Prandtl number | - |
| Φ | Temperature measurement | °C |
| Qh | Heat exchange rate of hydraulic oil | W/(m2·K) |
| Qc | Heat exchange rate of water | W/(m2·K) |
| mh | Heat fluid mass | kg/s |
| ph | Heat fluid density | kg/m3 |
| A0 | Initial heating area | m2 |
| Thi | Oil inlet temperature | °C |
| Tho | Oil exit temperature | °C |
| Tci | Inlet exit temperature of cold water | °C |
| Tco | Exit temperature of cold water | °C |
| x | Measurement | - |
| xav | Mean of a set of measurements | - |
| ψ | Deviation | - |
| Nutotal | Total Nusselt number | - |
| Awet | Total wetted heat area | m2 |
| Abase | Base heating area | m2 |
References
- Zhang, J.H.; Li, Y.; Xu, B.; Pan, M.; Chao, Q. Experimental study of an insert and its influences on churning losses in a high-speed electro-hydrostatic actuator pump of an aircraft. Chin. J. Aeronaut. 2019, 32, 2028–2036. [Google Scholar] [CrossRef]
- Ashif, P.; Shreyak, K.; Rakesh, K. Forced convection based heat transfer analysis of spherical dimple and protrusion surface in turbulent flow. Trans. Can. Soc. Mech. Eng. 2017, 41, 771–786. [Google Scholar]
- Wang, Y.; He, Y.L.; Lei, Y.G.; Zhang, J. Heat transfer and hydrodynamics analysis of a novel dimpled tube. Exp. Therm. Fluid Sci. 2010, 34, 1273–1281. [Google Scholar] [CrossRef]
- Bi, C.; Tang, G.H.; Tao, W.Q. Heat transfer enhancement in mini-channel heat sinks with dimples and cylindrical grooves. Appl. Therm. Eng. 2013, 55, 121–132. [Google Scholar] [CrossRef]
- Xie, S.; Liang, Z.; Zhang, L.; Wang, Y.; Ding, H.; Zhang, J. Numerical investigation on heat transfer performance and flow characteristics in enhanced tube with dimples and protrusions. Int. J. Heat Mass Transf. 2018, 122, 602–613. [Google Scholar] [CrossRef]
- Wang, Y.; He, Y.; Lei, Y.; Li, R. Heat transfer and friction characteristics for turbulent flow of dimpled tubes. Chem. Eng. Technol. 2009, 32, 956–963. [Google Scholar] [CrossRef]
- Chang, S.W.; Chiang, K.F.; Chou, T.C. Heat transfer and pressure drop in hexagonal ducts with surface dimples. Exp. Thermal Fluid Sci. 2010, 34, 1172–1181. [Google Scholar] [CrossRef]
- Zheng, N.; Liu, W.; Liu, Z.; Liu, P.; Shan, F. A numerical study on heat transfer enhancement and the flow structure in a heat exchanger tube with discrete double inclined ribs. Appl. Therm. Eng. 2015, 90, 232–241. [Google Scholar] [CrossRef]
- Wei, X.J.; Joshi, Y.K.; Ligrani, P.M. Numerical simulation of flow and heat transfer inside a micro-channel with one dimpled surface. In Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition, New York, NY, USA, 1–2 March 2007; pp. 149–156. [Google Scholar]
- Suvanjan, B. Fluid flow and heat transfer in a heat exchanger channel with shortlength twisted tape turbulator inserts. Iran J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 217–227. [Google Scholar]
- Afanasyev, V.N.; Chudnovsky, Y.P.; Leontiev, A.I.; Roganov, P.S. Turbulent flow friction and heat transfer characteristics for spherical cavities on a flat plate. Exp. Therm. Fluid Sci. 1993, 7, 1–8. [Google Scholar] [CrossRef]
- Bunker, R.S.; Donnellan, K.F. Heat transfer and friction factors for flows inside circular tubes with concavity surfaces. J. Turbomach. 2003, 125, 665–670. [Google Scholar] [CrossRef]
- Coy, E.B.; Danczyz, S.A. Measurements of the effectiveness of concave spherical dimples for enhancement heat transfer. J. Propuls. Power 2011, 27, 955–958. [Google Scholar] [CrossRef]
- Rao, Y.; Li, B.; Feng, Y. Heat transfer of turbulent flow over surfaces with spherical dimples and teardrop dimples. Exp. Therm. Fluid Sci. 2015, 61, 201–209. [Google Scholar] [CrossRef]
- Turnow, J.; Kornev, N.; Zhdanov, V.; Hassel, E. Flow structures and heat transfer on dimples in a staggered arrangement. Int. J. Heat Fluid Flow 2012, 35, 168–175. [Google Scholar] [CrossRef]
- Turnow, J.; Kornev, N.; Isaev, S.; Hassel, E. Vortex mechanism of heat transfer enhancement in a channel with spherical and oval dimples. Heat Mass Transf. 2011, 47, 301–313. [Google Scholar] [CrossRef]
- Xie, G.; Liu, J.; Ligrani, P.M.; Zhang, W.H. Numerical analysis of flow structure and heat transfer characteristics in square channels with different internal-protruded dimple geometries. Int. J. Heat Mass Transf. 2013, 67, 81–97. [Google Scholar] [CrossRef]
- Shchukin, A.V.; Il’inkov, A.V.; Takmovtsev, V.V.; Khabibullin, I.I. Specifics of heat and mass transfer in spherical dimples under the effect of external factors. Therm. Eng. 2017, 64, 450–457. [Google Scholar] [CrossRef]
- Leontiev, A.I.; Kiselev, N.A.; Burtsev, S.A.; Strongin, M.M.; Vinogradov, Y.A. Experimental investigation of heat transfer and drag on surfaces with spherical dimples. Exp. Therm. Fluid Sci. 2016, 79, 74–84. [Google Scholar] [CrossRef]
- Zhou, F.; Acharya, S. Experimental and computational study of heat/mass transfer and flow structure for four dimple shapes in a square internal passage. J. Turbomach. 2012, 136, 061028. [Google Scholar]
- Isaev, S.A.; Leont’ev, A.I.; Baranov, P.A. Simulating tornado-like enhancement of heat transfer for low-velocity motion of air in a rectangular channel with cavities. Part 1: Selection and justification of calculation methods. Therm. Eng. 2007, 54, 193–199. [Google Scholar] [CrossRef]
- Isaev, S.A.; Leont’ev, A.I.; Baranov, P.A. Simulating tornado-like enhancement of heat transfer under low-velocity motion of air in a rectangular dimpled channel. Part 2: Results of parametric studies. Therm. Eng. 2007, 54, 655–663. [Google Scholar] [CrossRef]
- Kim, K.Y.; Moon, M.A.; Kim, H.M. Shape optimization of inclined elliptic dimples in a cooling channel. J. Thermophys. Heat Transf. 2011, 25, 472–476. [Google Scholar] [CrossRef]
- Yoon, H.S.; Park, S.H.; Choi, C.; Ha, M.Y. Numerical study on characteristics of flow and heat transfer in a cooling passage with a tear-drop dimple surface. Int. J. Therm. Sci. 2015, 89, 121–135. [Google Scholar] [CrossRef]
- Park, J.; Ligrani, P.M. Numerical predictions of heat transfer and fluid flow characteristics for seven different dimpled surfaces in a channel. Numer. Heat Transf. Part A Appl. 2005, 47, 209–232. [Google Scholar] [CrossRef]
- Ge, M.W.; Xu, C.X.; Cui, G.X. Study on flow structures due to a dimple in channel flow by direct numerical simulation. Int. J. Flow Control 2013, 4, 67–82. [Google Scholar] [CrossRef]
- Lan, J.; Xie, Y.; Zhang, D. Flow and heat transfer in microchannels with dimples and protrusions. J. Heat Transf. 2012, 134, 021901. [Google Scholar] [CrossRef]
- Haque, M.R.; Rahman, M.A. Numerical investigation of convective heat transfer characteristics of circular and oval tube banks with vortex generators. J. Mech. Sci. Technol. 2020, 34, 457–467. [Google Scholar] [CrossRef]
- Xie, S.; Liang, Z.; Zhang, L.; Wang, Y. A numerical study on heat transfer enhancement and flow structure in enhanced tube with cross ellipsoidal dimples. Int. J. Heat Mass Transf. 2018, 125, 434–444. [Google Scholar] [CrossRef]
- Xie, S.; Liang, Z.; Zhang, J.; Zhang, L.; Wang, Y.L.; Ding, H. Numerical investigation on flow and heat transfer in dimpled tube with teardrop dimples. Int. J. Heat Mass Transf. 2019, 131, 713–723. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.J.; Li, J. Flow and heat transfer characteristics in rectangular channels using combination of convex-dimples with grooves. Appl. Therm. Eng. 2017, 113, 926–936. [Google Scholar] [CrossRef]
- Kaood, A.; Abou-Deif, T.; Eltahan, H.; Yehia, M.; Khalil, E. Numerical investigation of heat transfer and friction characteristics for turbulent flow in various corrugated tubes. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 233, 457–475. [Google Scholar] [CrossRef]
- Gnielinski, V. New equations for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Rao, Y.; Feng, Y.; Li, B.; Weigand, B. Experimental and numerical study of heat transfer and flow friction in channels with dimples of different shapes. J. Heat Transf. 2015, 37, 031901. [Google Scholar] [CrossRef]
- Bergman, T.; Lavine, A.; Incropera, F.K.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; Wiley: Hoboken, NJ, USA, 2011; pp. 256–279. [Google Scholar]
- Gee, D.L.; Webb, R.L. Forced Convection Heat Transfer in Helically Rib-Roughened Tubes. Int. J. Heat Mass Transf. 1980, 23, 1127–1136. [Google Scholar] [CrossRef]
- Fan, J.F.; Ding, W.K.; He, Y.L.; Tao, W.Q. Three-dimensional numerical study of fluid and heat transfer characteristics of dimpled fin surfaces. Numer. Heat Transf. Part A Appl. 2012, 62, 271–294. [Google Scholar] [CrossRef]

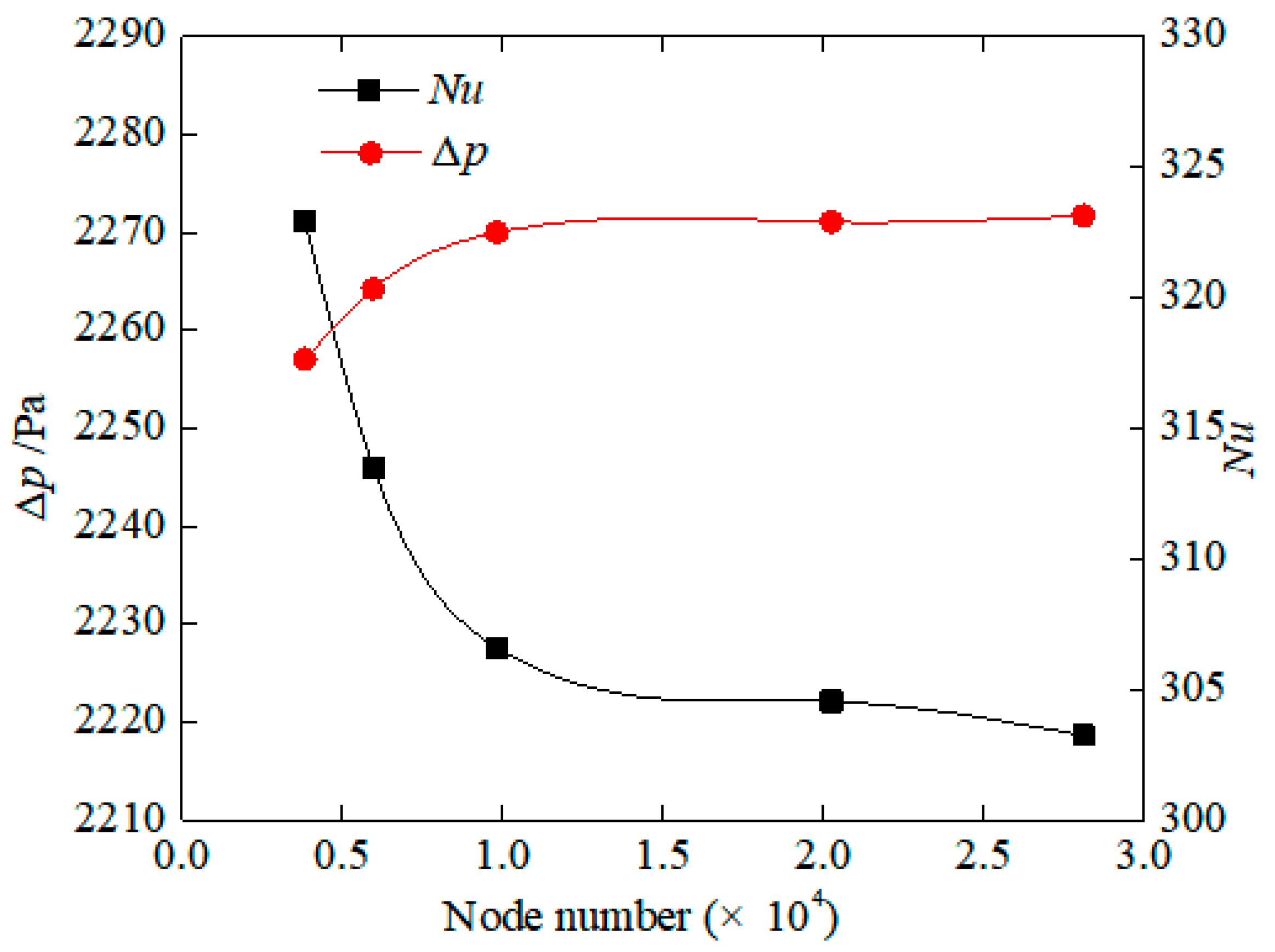
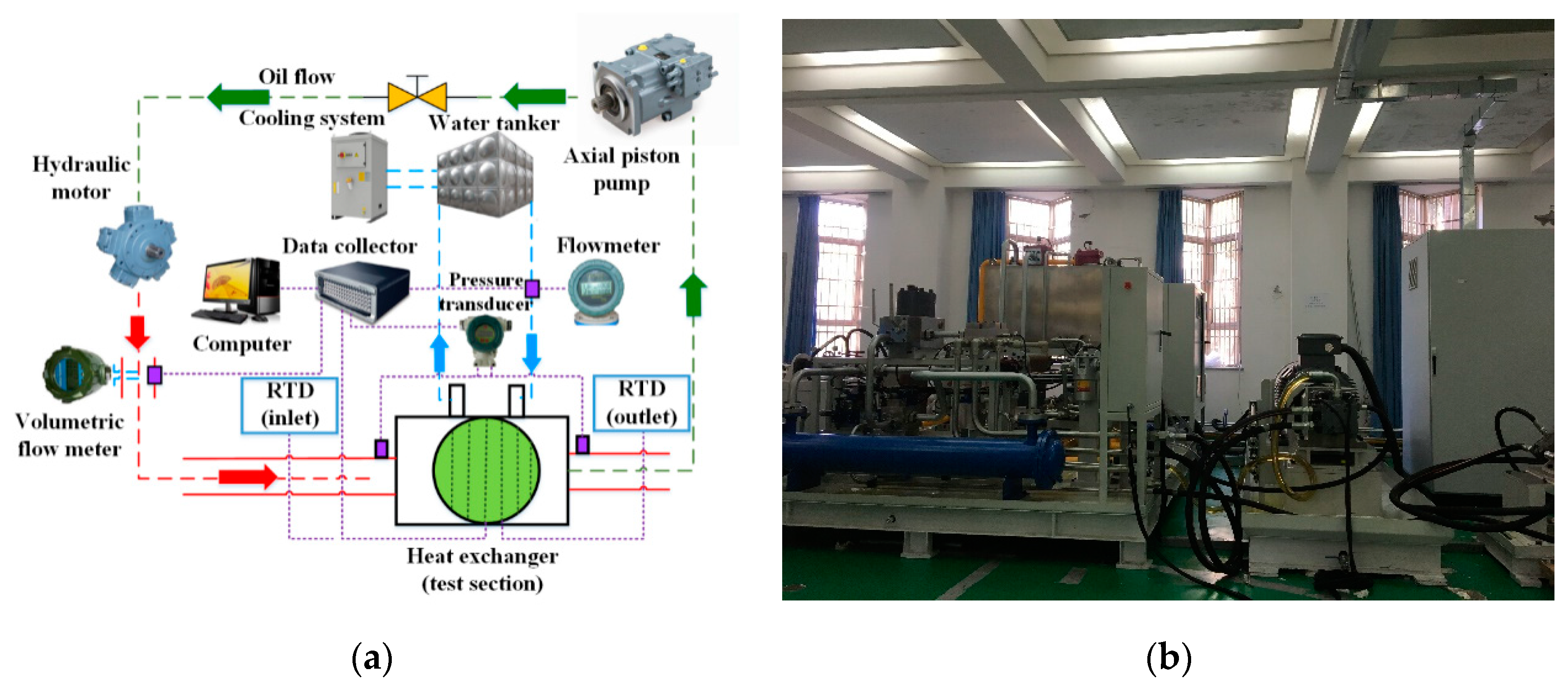
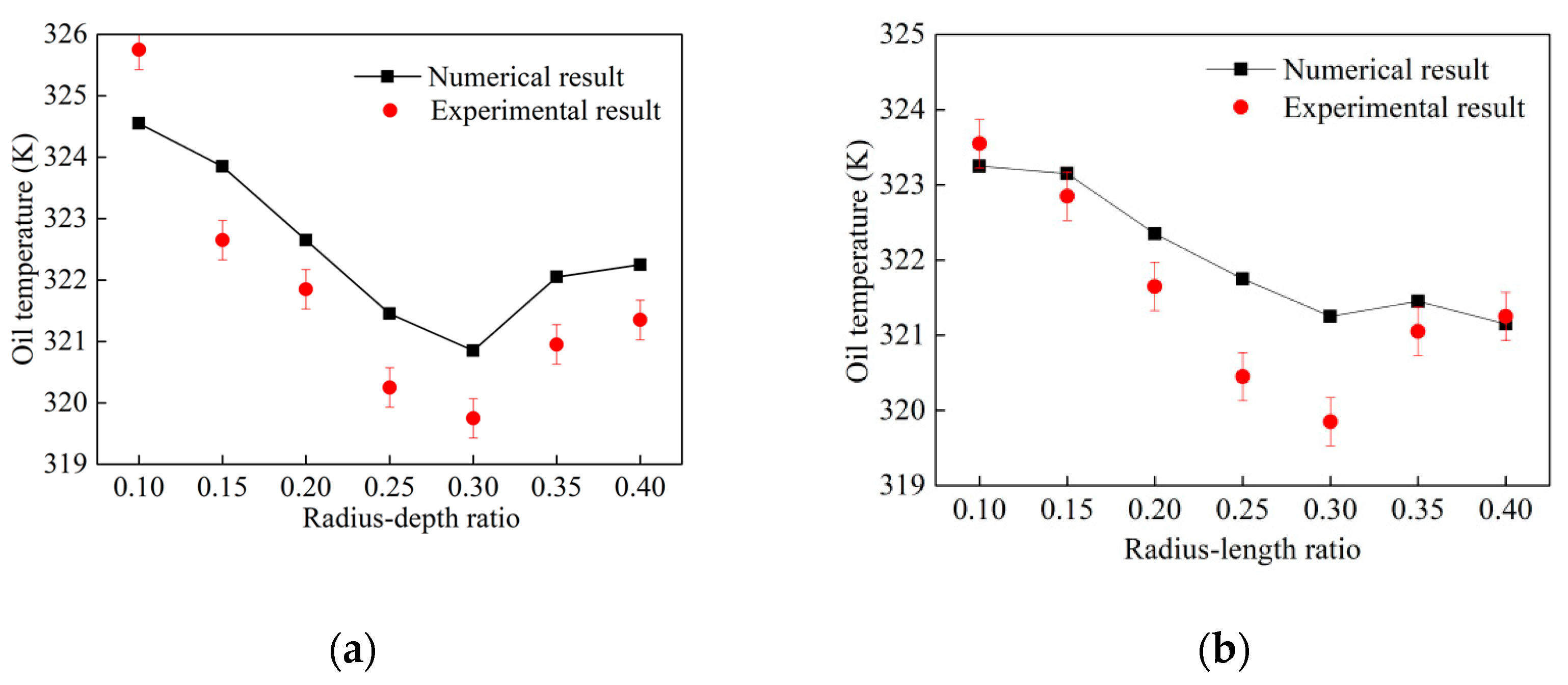
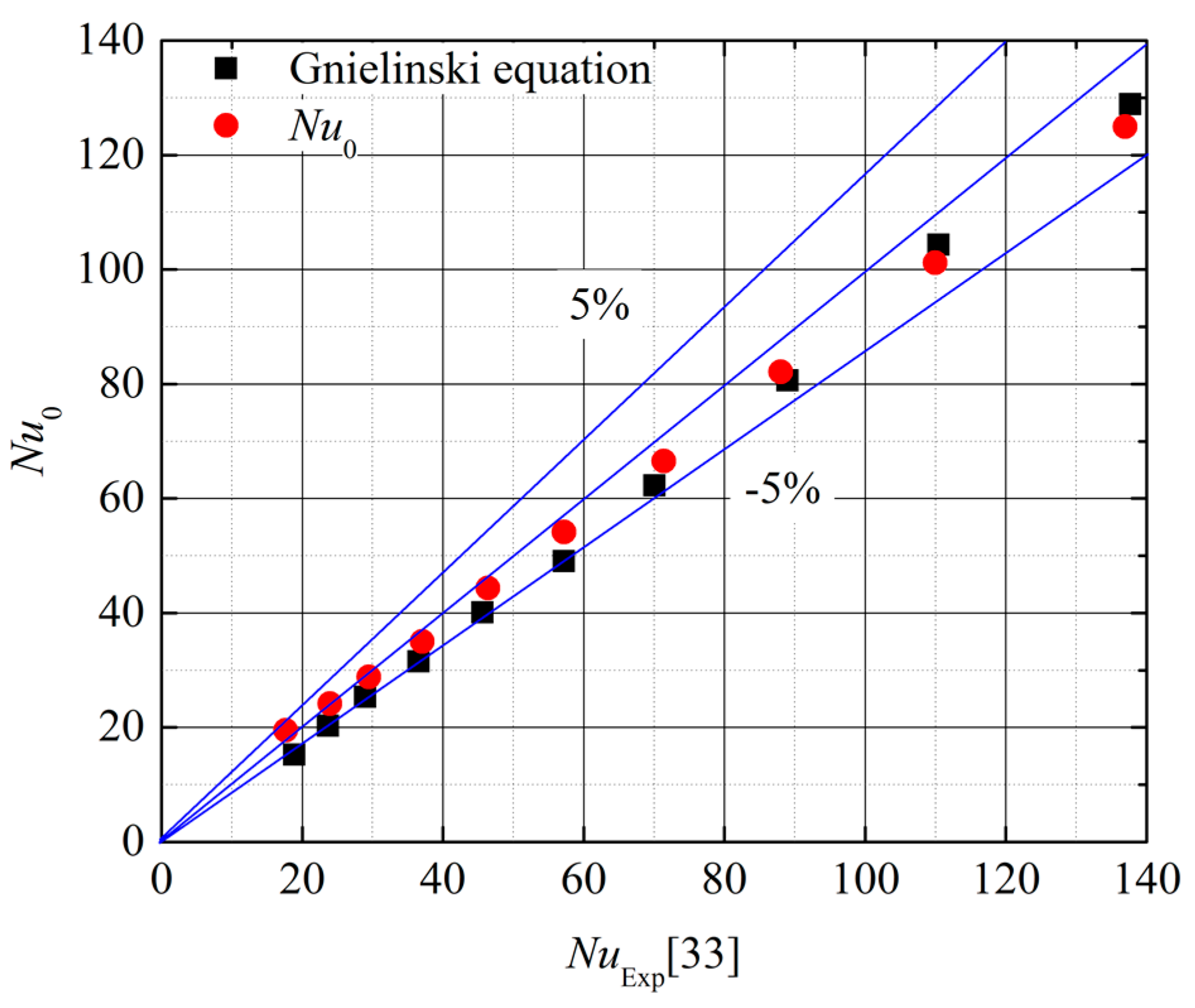
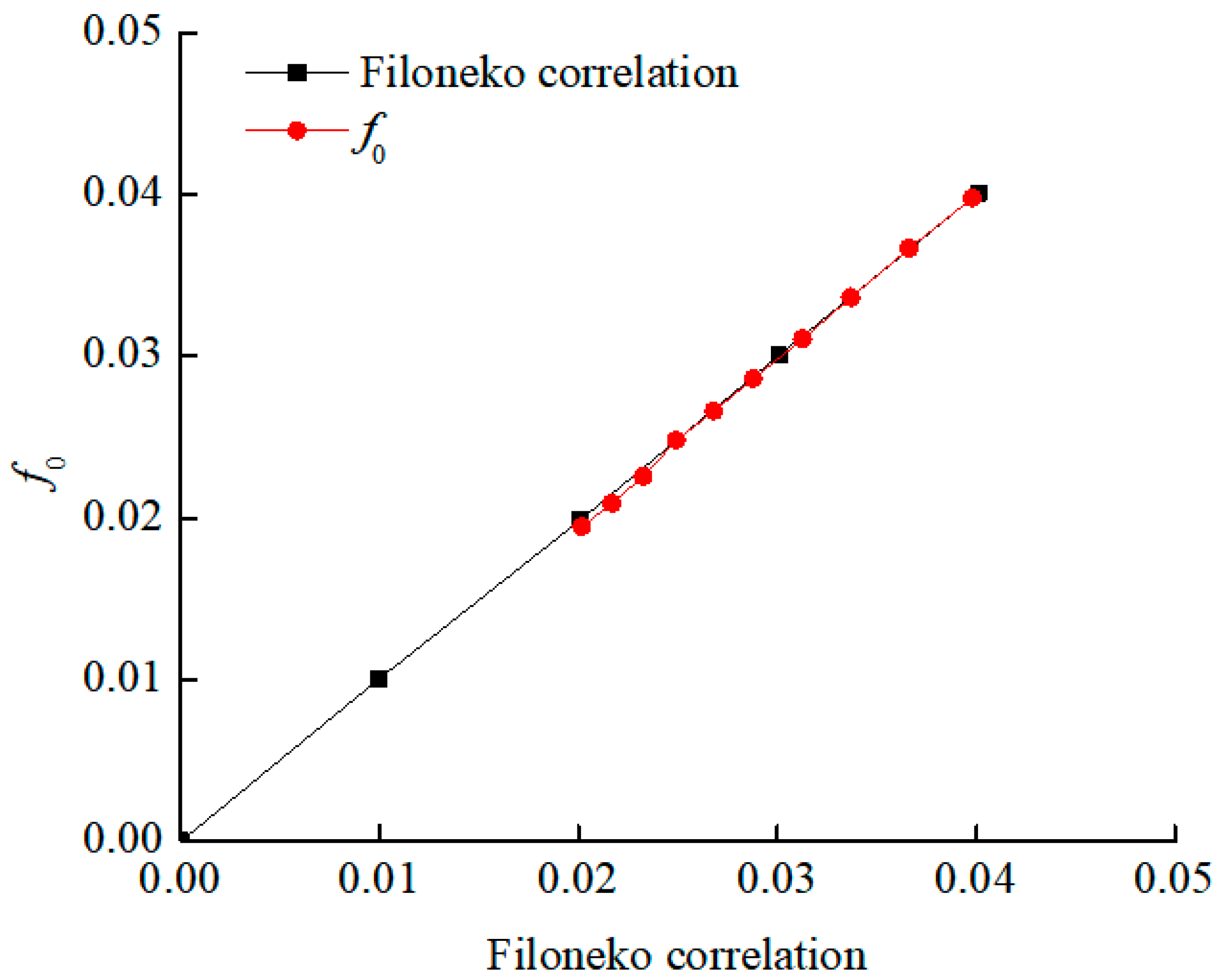



| Grid Number | ∆p | ∆p-Difference, % | Nμ | Nμ-Difference, % |
|---|---|---|---|---|
| 4682 | 2271 | 2.361 | 323.13 | 1.725 |
| 5325 | 2246 | 1.235 | 322.9 | 1.652 |
| 9634 | 2227.6 | 0.406 | 322.49 | 1.523 |
| 20,488 | 2222.1 | 0.017 | 320.35 | 0.094 |
| 28,320 | 2218.61 | Reference | 317.65 | Reference |
| Measured Parameters | Instruments | Brand | Error | Measuring Range |
|---|---|---|---|---|
| Oil temperature | RTD | PT100 | ±0.05%FS | 0–200 °C |
| Tube wall and water temperature | Thermocouple | OMEGA | ±0.05%FS | 0–200 °C |
| Pressure difference | Differential pressure transmitter | ABB | ±0.04%FS | 0–1000 Pa |
| Oil volume flow rate | Volumetric flowmeter | ABB | ±0.2%FS | 0–2000 m3/h |
| Water mass flow rate | Electromagnetic flow meter | ABB | ±0.25%FS | 0–4 m3/h |
| Parameters | Deviation |
|---|---|
| Tin | 3.9 K |
| Tout | 1.5 K |
| Tci | 3.6 K |
| Tco | 1.5 K |
| ∆Tm | 3.7 K |
| Pressure drop | 25 bar |
| Reh | Rec | Qh (W) | Qc (W) | Difference (%) |
|---|---|---|---|---|
| 7500 | 2720 | 1287.5 | 1201.3 | 6.7 |
| 3920 | 1906.2 | 1879.5 | 1.4 | |
| 10,500 | 2720 | 2518.3 | 2447.8 | 2.8 |
| 3920 | 3176.8 | 3125.9 | 1.6 | |
| 5213 | 3765.2 | 3723.8 | 1.1 | |
| 7836 | 4782.1 | 4676.9 | 2.2 | |
| 15,000 | 3920 | 3931.5 | 3829.3 | 2.6 |
| 5213 | 5375.7 | 5273.6 | 1.9 | |
| 7836 | 5872.3 | 5737.2 | 2.3 | |
| 10,980 | 6473.4 | 6330.9 | 2.2 | |
| 17,500 | 2720 | 3495.2 | 3388.7 | 2.7 |
| 5213 | 5162.4 | 5037.5 | 2.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, P.; He, Y.; Tang, H.; Ren, Y. Numerical and Experimental Investigation of Flow and Heat Transfer in Heat Exchanger Channels with Different Dimples Geometries. Machines 2021, 9, 72. https://doi.org/10.3390/machines9040072
Ying P, He Y, Tang H, Ren Y. Numerical and Experimental Investigation of Flow and Heat Transfer in Heat Exchanger Channels with Different Dimples Geometries. Machines. 2021; 9(4):72. https://doi.org/10.3390/machines9040072
Chicago/Turabian StyleYing, Pingting, You He, Hesheng Tang, and Yan Ren. 2021. "Numerical and Experimental Investigation of Flow and Heat Transfer in Heat Exchanger Channels with Different Dimples Geometries" Machines 9, no. 4: 72. https://doi.org/10.3390/machines9040072
APA StyleYing, P., He, Y., Tang, H., & Ren, Y. (2021). Numerical and Experimental Investigation of Flow and Heat Transfer in Heat Exchanger Channels with Different Dimples Geometries. Machines, 9(4), 72. https://doi.org/10.3390/machines9040072





