Research of a Flexible Space-Vector-Based Hybrid PWM Transition Algorithm between SHEPWM and SHMPWM for Three-Level NPC Inverters
Abstract
1. Introduction
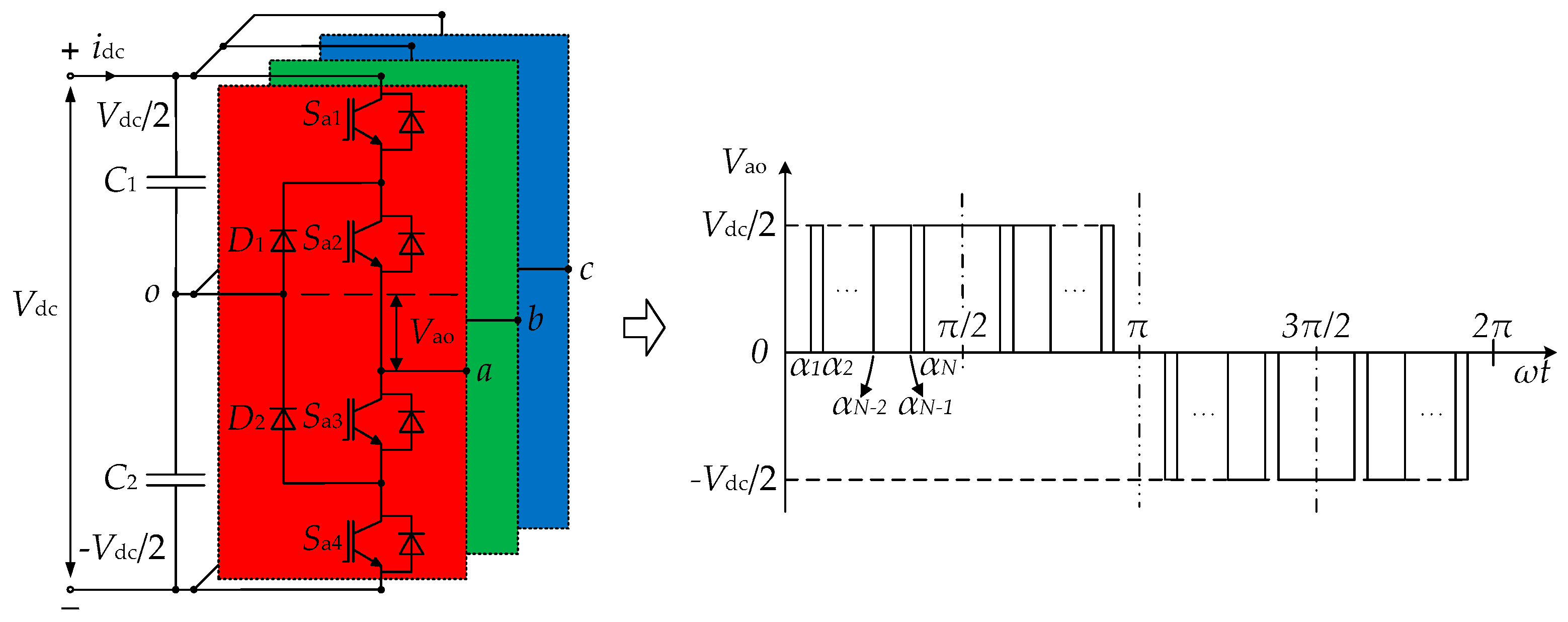
2. Formulation of SHEPWM and SHMPWM for 3L-NPC Inverters
2.1. Basis of SHEPWM
2.2. Basis of SHMPWM
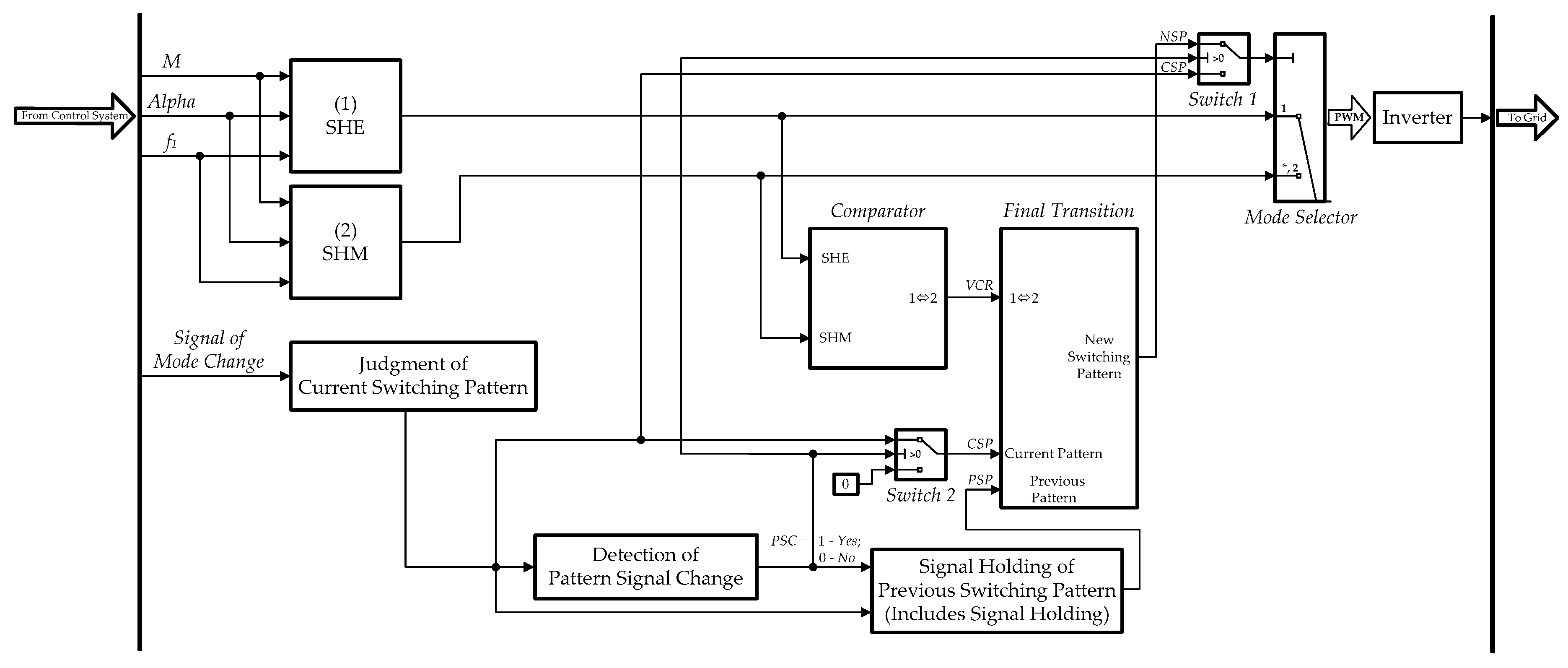
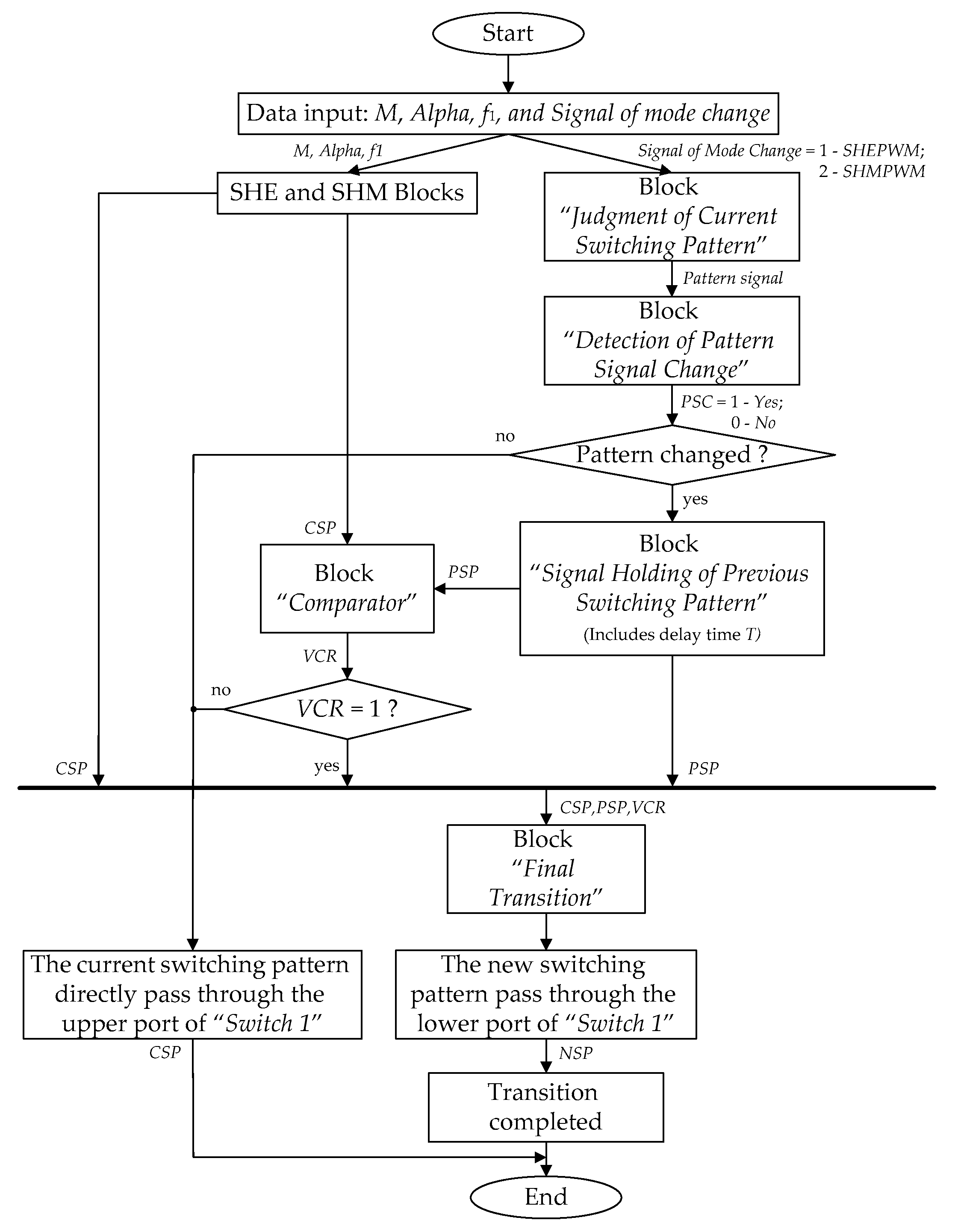
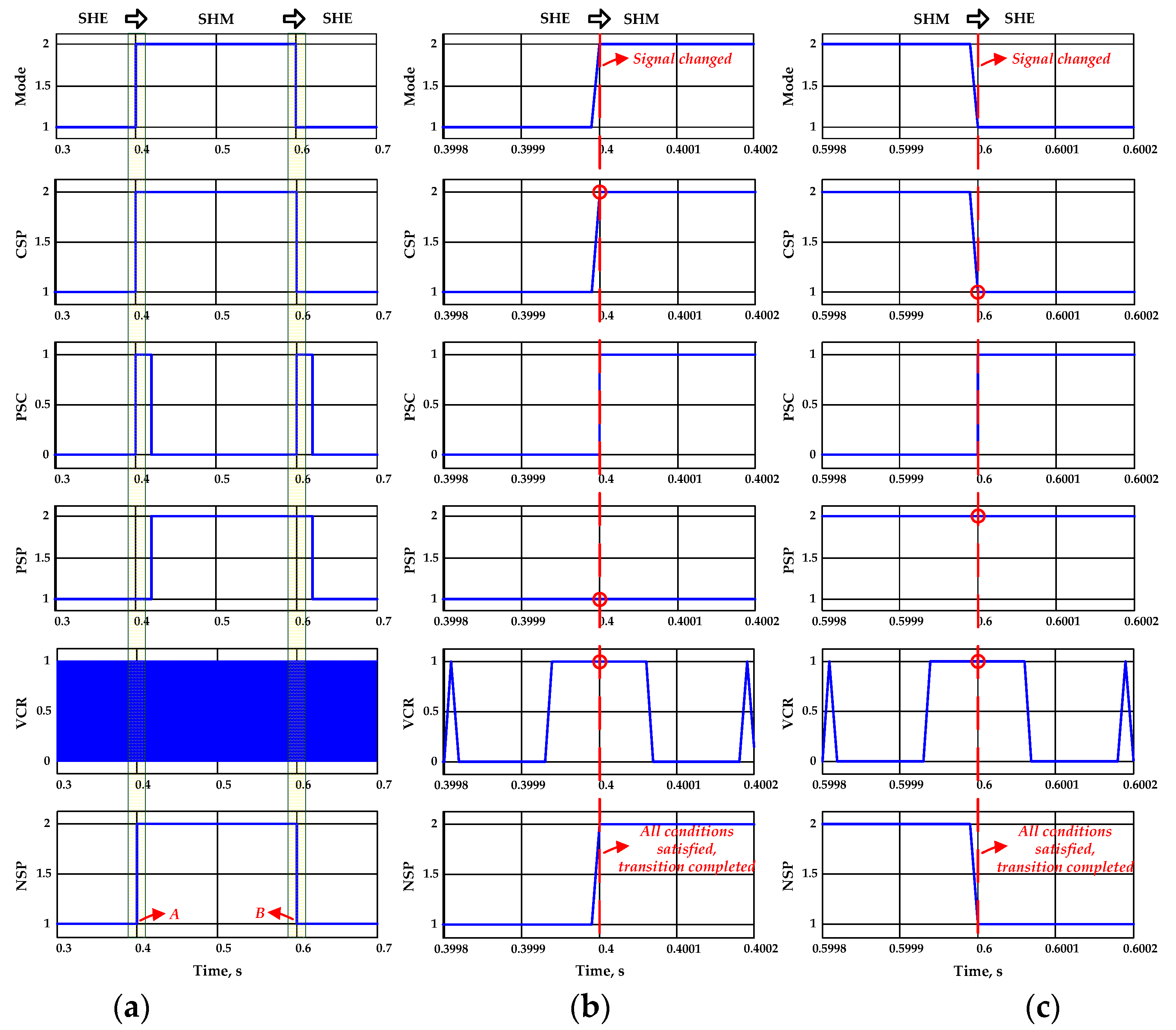
3. Principle of Proposed Flexible Space-Vector-Based HPWM Transition Algorithm between SHEPWM and SHMPWM
- When the power system starts running, the SHE and SHM blocks produce their own switching patterns according to M, Alpha and f1, which are obtained from the closed-loop control system;
- First, the block “Judgment of Current Switching Pattern” starts to detect the current switching pattern based on the “Signal of Mode Change” (here, the mode is SHEPWM or SHMPWM);
- Then, the next block “Detection of Pattern Signal Change” starts to detect the change of the pattern signal in the meantime, and output “the signal of the pattern signal change, PSC” (here, 1—Yes, 0—No);
- If the pattern signal is changed, the block “Signal Holding of Previous Switching Pattern (Includes Signal Holding)” starts to hold the signal of the previous switching pattern for some time (here, delay time T is determined by the specific object);
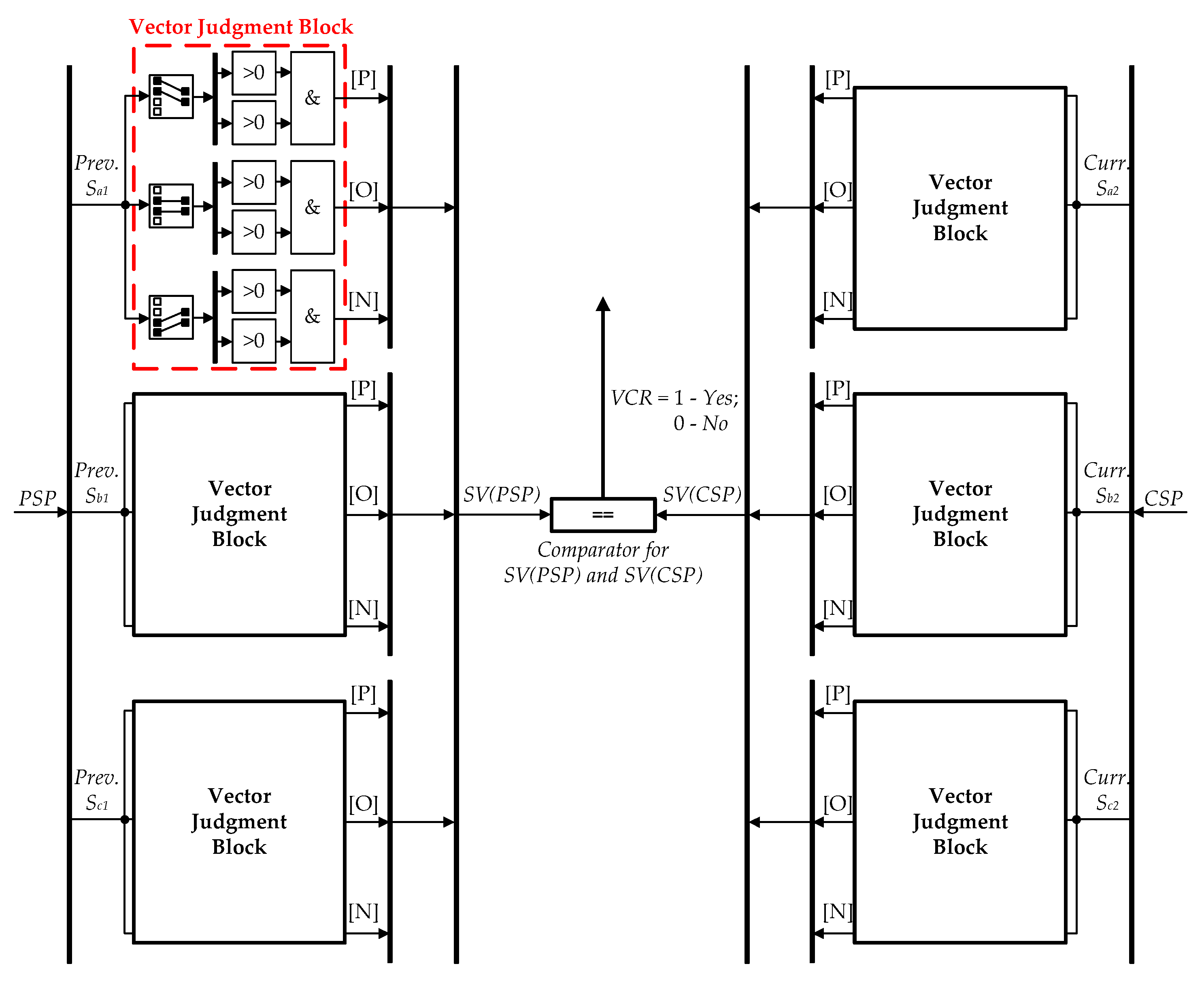
- The block “Comparator” is used for the real-time comparison of the output space vectors (SV) of each pair of phase legs between SHEPWM and SHMPWM, as shown in Figure 5;
- Finally, three types of signals, namely “the signal of the previous switching pattern, PSP”, “the signal of the current switching pattern, CSP” and “the signal of the vector comparison result, VCR”, are fed to the block “Final Transition”. The block “Final Transition” outputs “the new switching pattern, NSP” through the lower port of “Switch 1” if all three conditions above are satisfied; Otherwise, the current switching pattern will directly pass through the upper port of “Switch 1”.
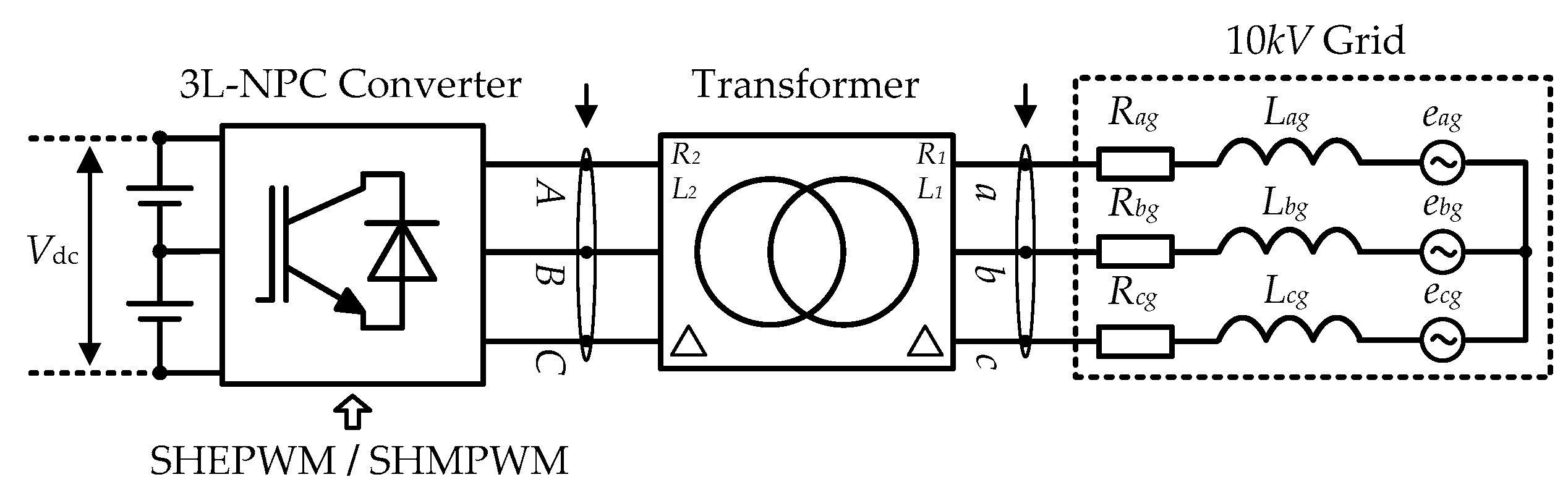
4. Simulation Results and Analysis
4.1. Algorithm Verification
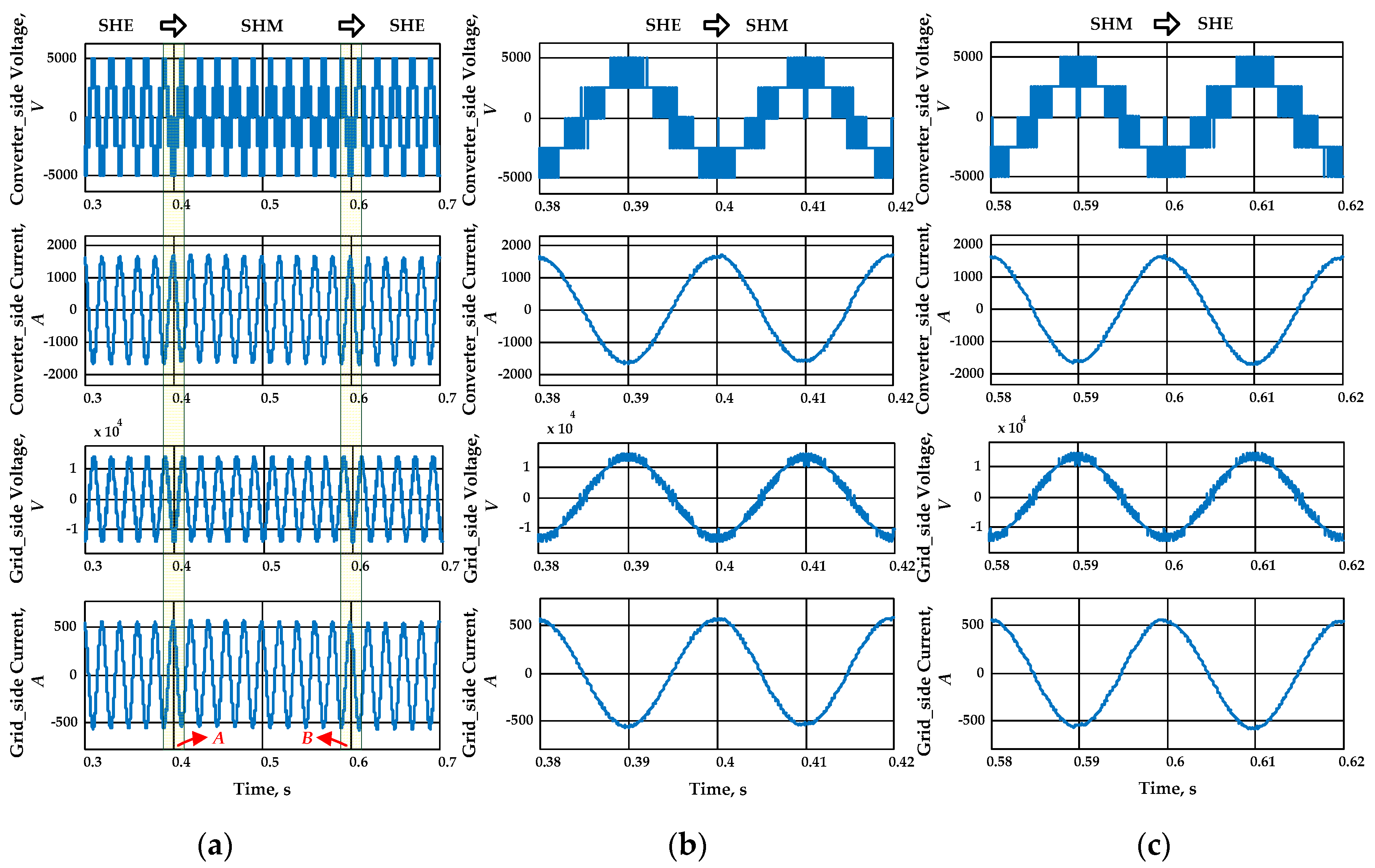
4.2. Analysis of Output Voltage and Current
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bose, B.K. Global warming: Energy, environmental pollution and the impact of power electronics. IEEE Trans. Ind. Electron. 2010, 4, 6–17. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Holtz, J.; Rodriguez, J.; Baoming, G. Medium voltage multilevel converters—state of the art, challenges and requirements in industrial applications. IEEE Trans. Ind. Electron. 2010, 57, 2581–2596. [Google Scholar] [CrossRef]
- van Wyk, J.D.; Lee, F.C. On a future for power electronics. IEEE Trans. Emerg. Sel. Topics Power Electron. 2013, 1, 59–72. [Google Scholar] [CrossRef]
- Jing, T.; Maklakov, A.S. A review of voltage source converters for energy applications. In Proceedings of the International Ural Conference on Green Energy (UralCon), Chelyabinsk, Russia, 4–6 October 2018. [Google Scholar]
- Teodorescu, R.; Liserre, M.; RodrÕguez, P. Grid Converters for Photovoltaic and Wind Power Systems; Wiley-IEEE Press: New York, NY, USA, 2011. [Google Scholar]
- Wang, H.; Jia, H.; He, J. Parallel interlinking PWM current source converter for hybrid AC/DC microgrids. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Radionov, A.A.; Gasiyarov, V.R.; Maklakov, A.S. Hybrid PWM on the basis of SVPWM and SHEPWM for VSI as part of 3L-BtB-NPC converter. In Proceedings of the IECON—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Wang, H.; Liserre, M.; Blaabjerg, F. Toward reliable power electronics: Challenges, design tools, and opportunities. IEEE Ind. Electron. Mag. 2013, 7, 17–26. [Google Scholar] [CrossRef]
- Mohammed, S.A.; Abdel-Moamen, M.A.; Hasanin, B. A review of the state-of-the-art of power electronics for power system applications. JECER 2013, 1, 43–52. [Google Scholar]
- Abu-Rub, H.; Malinowski, M.; Al-Haddad, K. Power Electronics for Renewable Energy Systems, Transportation and Industrial Applications; Wiley-IEEE Press: New York, NY, USA, 2014. [Google Scholar]
- Leon, J.I.; Kouro, S.; Franquelo, L.G.; Rodriguez, J.; Wu, B. The essential role and the continuous evolution of modulation techniques for voltage-source inverters in the past, present, and future power electronics. IEEE Trans. Ind. Electron. 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Yan, C.; Zou, S. Hybrid PWM scheme for the grid inverter. IEEE Trans. Emerg. Sel. Top. Power Electron. 2015, 3, 1151–1159. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Vahedi, H.; Sheikholeslami, A.; Labbé, P.; Al-Haddad, K. Hybrid SHM–SHE modulation technique for a four-leg NPC inverter with DC capacitor self-voltage balancing. IEEE Trans. Ind. Electron. 2015, 62, 4890–4899. [Google Scholar] [CrossRef]
- Moeini, A.; Zhao, H.; Wang, S. Improve control to output dynamic response and extend modulation index range with hybrid selective harmonic current mitigation-PWM and phase-shift PWM for four-quadrant cascaded H-bridge converters. IEEE Trans. Ind. Electron. 2017, 64, 6854–6863. [Google Scholar] [CrossRef]
- Portillo, R.; Sharifzadeh, M.; Vahedi, H.; Franquelo, L.G.; Al-Haddad, K. Improved hybrid SHM-SHE modulation technique for four-leg three-level NPC inverters. In Proceedings of the IECON—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Wang, Y.; Wen, X.; Guo, X.; Zhao, F.; Cong, W. The smooth transition research of different PWM modulations for vector control of induction motor in medium voltage high power. In Proceedings of the International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar]
- Zaragoza, J.; Pou, J.; Ceballos, S.; Robles, E.; Ibanez, P.; Villate, J.L. A comprehensive study of a hybrid modulation technique for the neutral-point-clamped converter. IEEE Trans. Ind. Electron. 2009, 56, 294–304. [Google Scholar] [CrossRef]
- Jing, T.; Maklakov, A.; Radionov, A.; Baskov, S.; Kulmukhametova, A. Research on hybrid SHEPWM based on different switching patterns. IJPEDS 2019, 10, 1875–1884. [Google Scholar]
- Jing, T.; Maklakov, A.; Radionov, A.; Gasiyarov, V. A flexible hybrid selective harmonic elimination transition algorithm to provide variable frequency of output voltage in 3L-NPC inverter. In Proceedings of the IECON—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Narayanan, G.; Zhao, D.; Krishnamurthy, H.K.; Ayyanar, R.; Ranganathan, V.T. Space vector based hybrid PWM techniques for reduced current ripple. IEEE Trans. Ind. Electron. 2008, 55, 1614–1627. [Google Scholar] [CrossRef]
- Hari, V.P.K.; Narayanan, G. Space-vector-based hybrid PWM technique to reduce peak-to-peak torque ripple in induction motor drives. IEEE Trans. Ind. Appl. 2016, 52, 1489–1499. [Google Scholar]
- Jing, T.; Maklakov, A.; Radionov, A. Two selective harmonic control techniques applied in 10 kV grid with three-level NPC inverter. In Proceedings of the IEEE Russian Workshop on Power Engineering and Automation of Metallurgy Industry: Research & Practice (PEAMI), Magnitogorsk, Russia, 14–17 October 2019. [Google Scholar]
- CENELEC. Voltage Characteristics of Electricity Supplied by Public Distribution Systems, EN 50160; CENELEC: Brussels, Belgium, 2001. [Google Scholar]
- CIGRE. Harmonics, Characteristic Parameters, Methods of Study, Estimates of Existing Values in the Network, Electra No. 77; CIGRE WG 36–05; CIGRE: Paris, France, 1981. [Google Scholar]

| Odd Non-Triplen Harmonics | Odd Triplen Harmonics | Even Harmonics | |||
|---|---|---|---|---|---|
| Harmonic Order (n) | Relative Voltage (Li) | Harmonic Order (n) | Relative Voltage (Li) | Harmonic Order (n) | Relative Voltage (Li) |
| 5 7 11 13 17 19 23 25 >25 | 6% 5% 3.5% 3% 2% 1.5% 1.5% 1.5% 0.2 + 32.5/n | 3 9 15 21 >21 | 5% 1.5% 0.5% 0.5% 0.2% | 2 4 6…10 >10 | 2% 1% 0.5% 0.2% |
| Space Vector | Gate Signal |
|---|---|
| [P] | [1 1 0 0] |
| [O] | [0 1 1 0] |
| [N] | [0 0 1 1] |
| Parameter, Symbol | Value |
|---|---|
| Switching frequency, N | 15 |
| Switching frequency, fs | 750 Hz |
| Delay time, T | 0.02 s |
| AC voltage, Vac | 10 kV |
| DC-link voltage, Vdc | 5020 V |
| AC voltage frequency, f | 50 Hz |
| Resistance value in winding 1, R1 | 0.080533 Ω |
| Inductance value in winding 1, L1 | 0.0055304 H |
| Resistance value in winding 2, R2 | 0.042809 Ω |
| Inductance value in winding 2, L2 | 0.0022477 H |
| Source resistance, Rxg (x=a,b,c) | 0.000347 Ω |
| Source inductance, Lxg (x=a,b,c) | 0.00347 H |
| Harm. Order | Harm. Limits (%) | SHEPWM | SHMPWM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Voltage (%) | Current (%) | Voltage (%) | Current (%) | ||||||
| 5 | 6 | 0.35 | ✓ | 0.24 | - | 0.3 | ✓ | 0.25 | - |
| 7 | 5 | 0.06 | ✓ | 0.07 | - | 3.37 | ✓ | 2.19 | - |
| 11 | 3.5 | 0.08 | ✓ | 0.07 | - | 2.43 | ✓ | 1.04 | - |
| 13 | 3 | 0.5 | ✓ | 0.12 | - | 1.68 | ✓ | 0.81 | - |
| 17 | 2 | 0.42 | ✓ | 0 | - | 1.85 | ✓ | 0.21 | - |
| 19 | 1.5 | 0.36 | ✓ | 0.04 | - | 0.55 | ✓ | 0.01 | - |
| 23 | 1.5 | 0.58 | ✓ | 0.02 | - | 0.02 | ✓ | 0.01 | - |
| 25 | 1.5 | 0.28 | ✓ | 0.03 | - | 0.75 | ✓ | 0.18 | - |
| 29 | 1.32 | 0.46 | ✓ | 0.03 | - | 0.54 | ✓ | 0.18 | - |
| 31 | 1.25 | 0.14 | ✓ | 0 | - | 0.01 | ✓ | 0.02 | - |
| 35 | 1.13 | 0.38 | ✓ | 0.03 | - | 0.05 | ✓ | 0.04 | - |
| 37 | 1.08 | 0.55 | ✓ | 0.03 | - | 0.67 | ✓ | 0.03 | - |
| 41 | 0.99 | 0.36 | ✓ | 0.01 | - | 0.21 | ✓ | 0 | - |
| 43 | 0.96 | 0.35 | ✓ | 0.01 | - | 0.18 | ✓ | 0.03 | - |
| 47 | 0.89 | 17.8 | ✕ | 1.11 | - | 0.09 | ✓ | 0 | - |
| 49 | 0.86 | 11.14 | ✕ | 0.67 | - | 0.4 | ✓ | 0.02 | - |
| THD40 | 8 | 2.06 | ✓ | 0.7 | - | 5.08 | ✓ | 2.65 | - |
| THD50 | - | 21.1 | ✕ | 1.47 | - | 5.1 | ✓ | 2.65 | - |
| Harm. Order | Harm. Limits (%) | SHEPWM | SHMPWM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Voltage (%) | Current (%) | Voltage (%) | Current (%) | ||||||
| 5 | 6 | 0.08 | ✓ | 0.24 | - | 0.06 | ✓ | 0.25 | - |
| 7 | 5 | 0.01 | ✓ | 0.07 | - | 0.73 | ✓ | 2.13 | - |
| 11 | 3.5 | 0.02 | ✓ | 0.07 | - | 0.53 | ✓ | 1.01 | - |
| 13 | 3 | 0.11 | ✓ | 0.12 | - | 0.37 | ✓ | 0.79 | - |
| 17 | 2 | 0.1 | ✓ | 0 | - | 0.4 | ✓ | 0.2 | - |
| 19 | 1.5 | 0.08 | ✓ | 0.04 | - | 0.12 | ✓ | 0.01 | - |
| 23 | 1.5 | 0.13 | ✓ | 0.02 | - | 0 | ✓ | 0.02 | - |
| 25 | 1.5 | 0.06 | ✓ | 0.03 | - | 0.16 | ✓ | 0.18 | - |
| 29 | 1.32 | 0.11 | ✓ | 0.03 | - | 0.12 | ✓ | 0.18 | - |
| 31 | 1.25 | 0.03 | ✓ | 0 | - | 0 | ✓ | 0.01 | - |
| 35 | 1.13 | 0.09 | ✓ | 0.03 | - | 0.01 | ✓ | 0.04 | - |
| 37 | 1.08 | 0.12 | ✓ | 0.03 | - | 0.14 | ✓ | 0.03 | - |
| 41 | 0.99 | 0.08 | ✓ | 0.01 | - | 0.04 | ✓ | 0 | - |
| 43 | 0.96 | 0.08 | ✓ | 0.01 | - | 0.04 | ✓ | 0.03 | - |
| 47 | 0.89 | 4.06 | ✕ | 1.08 | - | 0.02 | ✓ | 0 | - |
| 49 | 0.86 | 2.54 | ✕ | 0.65 | - | 0.08 | ✓ | 0.02 | - |
| THD40 | 8 | 0.47 | ✓ | 0.69 | - | 1.11 | ✓ | 2.58 | - |
| THD50 | - | 4.81 | ✓ | 1.44 | - | 1.11 | ✓ | 2.58 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, T.; Radionov, A.; Maklakov, A.; Gasiyarov, V. Research of a Flexible Space-Vector-Based Hybrid PWM Transition Algorithm between SHEPWM and SHMPWM for Three-Level NPC Inverters. Machines 2020, 8, 57. https://doi.org/10.3390/machines8030057
Jing T, Radionov A, Maklakov A, Gasiyarov V. Research of a Flexible Space-Vector-Based Hybrid PWM Transition Algorithm between SHEPWM and SHMPWM for Three-Level NPC Inverters. Machines. 2020; 8(3):57. https://doi.org/10.3390/machines8030057
Chicago/Turabian StyleJing, Tao, Andrey Radionov, Alexander Maklakov, and Vadim Gasiyarov. 2020. "Research of a Flexible Space-Vector-Based Hybrid PWM Transition Algorithm between SHEPWM and SHMPWM for Three-Level NPC Inverters" Machines 8, no. 3: 57. https://doi.org/10.3390/machines8030057
APA StyleJing, T., Radionov, A., Maklakov, A., & Gasiyarov, V. (2020). Research of a Flexible Space-Vector-Based Hybrid PWM Transition Algorithm between SHEPWM and SHMPWM for Three-Level NPC Inverters. Machines, 8(3), 57. https://doi.org/10.3390/machines8030057







