Abstract
This paper presents an extensive literature review on the field of condition-based maintenance (CBM). The paper encompasses over 4000 contributions, analysed through bibliometric indicators and meta-analysis techniques. The review adopts Factor Analysis as a dimensionality reduction, concerning the metric of the co-citations of the papers. Four main research areas have been identified, able to delineate the research field synthetically, from theoretical foundations of CBM; (i) towards more specific implementation strategies (ii) and then specifically focusing on operational aspects related to (iii) inspection and replacement and (iv) prognosis. The data-driven bibliometric results have been combined with an interpretative research to extract both core and detailed concepts related to CBM. This combined analysis allows a critical reflection on the field and the extraction of potential future research directions.
1. Introduction
The complicated nature of modern engineering systems and manufacturing processes is increasing rapidly. Consequently, managing the reliability of the systems becomes challenging in modern dynamic operational settings [1]. In this context, condition-based maintenance (CBM) is a leading strategy for the scheduling of maintenance interventions, in contrast to more traditional solutions relying on time-based maintenance (TBM) [2]. Reflections on CBM implementation can be found since the 1970s [3,4,5]. Since its early implementations, the need for collecting information when the system is in operating conditions has been recognized (i.e., Condition Monitoring, CM) [6]. Such information generally ensures a reduced number of interventions, if compared to TBM. CM is defined as the monitoring of one or more meaningful parameters to model the performance of the considered systems and to identify changes potentially linked to future failures. This is a crucial step for ensuring proactive monitoring and resource optimization of repair interventions, to limit performance losses. CBM is considered as the optimal maintenance strategy to be adopted when a failure or the degradation process can cause important economic losses [7].
An optimal CBM strategy has the potential to generate important benefits for the competitiveness of industrial companies, even in the modern industrial systems (e.g., increasing system availability and consequent benefits for safety management [8], reducing maintenance costs [9], increasing product quality [10]).
Since CBM is a well-established research field, the presence of previous literature reviews is not surprising. One of them reviews worldwide CBM industrial practices, introducing basic concepts such as the necessity for planned maintenance, the role of CM and the difference between prediction and diagnosis up to 1994 [11]. Other papers review the techniques commonly adopted to monitor the condition of mechanical systems and the decision models up to 1993 [12] as well as a more modern state-of-the-art about data integration for CBM [13] or the statistical data-driven approaches for the prediction of remaining useful life (RUL) [14], respectively dated 2009 and 2011. Further papers review a specific area of CBM implementation, such as prognostics and health management [15,16,17,18], aircraft engine health management [19], vehicle health management [18], punching/blanking of sheet metal [20], CBM strategies for multi-component systems [21] or the prognostics of the rotating machines [22].
Nowadays, there is a lack of a global analytical review that analyses the field of CBM in its entirety from a thematical and temporal perspective. As far as the authors know, this manuscript proposes the first meta-analysis in the context of CBM.
This article investigates available research on CBM, by an extensive review of the literature published over more than 40 years (first considered contribution dated back to 1976 [3]). The meta-analytic perspective adopted in this study allows reducing the number of subjective choices to those requested just for pragmatical reasons—restriction to Scopus database, the largest available academic repository; the definition of parameters for bibliometric analyses; and the interpretative labelling of the research areas.
In summary, this paper aims to explore literature in the field to provide an overview of the most relevant research themes and potential future research directions.
For clarity purposes, a homogenous terminology has been adopted throughout the document. Main terms and respective definitions are as follows:
- MAINTENANCE POLICY—all management activities that set requirements, objectives, strategies and responsibilities for maintenance and implement them using management approach (i.e., planning, control, supervision and improvement). Policies refer to a set of rules made by the organization to ensure rational decision making.
- MAINTENANCE STRATEGY—management direction used to achieve maintenance objectives, achieving a competitive and effective position in the market.
- MAINTENANCE PLAN—structured and documented set of commitments including activities, procedures, resources and time required to perform maintenance activities.
These definitions are based on the UNI EN 13306:2018 [23]. Specifically, maintenance policy follows the definition of maintenance management but maintenance strategy and maintenance plan refer to the same concepts in the standard.
Structure of the Paper
Before getting to the core of the paper, to make it easier to read and understand the review, the authors consider it appropriate to explain in detail the structure of the paper. The rationale behind the structure given to the paper can be ascribed to two macro-motivations:
- the overall structure of the paper reflects the actual path followed by the authors for the implementation of the presented literature review
- the presentation of the extracted research factors (RFs) follows what the authors consider to be the logical path within CBM.
Detailing the sections of the paper, Section 2, that is, methodology, firstly describes in detail how the papers were searched, as well as the database from which the papers were extracted. Secondly, it describes the technique used to circumscribe the areas of interest within the CBM field and the reasons for this choice.
In Section 3 instead, that is, findings from a systematic literature search and factor analysis, the authors can primarily explain to readers the path taken for the selection and screening of the papers. According to the selected papers, in this section the extracted factors and therefore the sub-areas in the context of CBM reality, are stated.
Section 4, that is, research factors, retraces the logical flow of thematic areas covered by the identified RFs.
Finally, Section 5 and Section 6 present the discussion of the conclusions drawn from the analysis of the main areas of CBM. Based on these considerations, possible and desirable future research developments on the topic are presented.
To summarize, the remainder of the paper is organized as follows. Section 2 details the bibliometric approach adopted in this study; Section 3 presents a brief descriptive summary of the results, which are extensively discussed in Section 4. Section 5 proposes critical reflections on the field and proposes potential future research directions. Lastly, the conclusions summarize the outcome of the study.
2. Methodology
The literature search of this study considered the Scopus database, the largest abstract and citation database of peer-reviewed literature [24]. The selected key-search was set to include all the documents proposing “condition-based maintenance” in the title, abstract or keywords, that is, TITLE-ABS-KEY (“condition based maintenance”). The query has been run-up in July 2019.
The query results 4292 documents, that refer to different subject areas, mainly “Engineering,” “Computer Science,” “Energy,” “Mathematics,” “Material Science,” “Physics and Astronomy,” “Business, Management and Accounting” and “Decisions Sciences.”
Due to the multiplicity and the large number of contributions on CBM, it remains challenging to understand and delineate the main areas of this research field by a priori choice. For this reason, the authors decided to implement a meta-analysis approach based on bibliometric indicators. The analysis of the co-citations of the papers is a common approach in this context since it enables the comprehension of the connections between two or more papers [25]. Its main assumption is that if two contributions are often co-cited, the same contributions most likely share a thematic concept [26]. This analysis is developed through an explorative Principal Component Analysis (PCA), that is, a multivariate technique used for dimensionality reduction and the metric used for analytical proximity is the count of the co-citations. The output of PCA is a set of factors or even “research factors” (RF)—a set of documents that explore a shared thematic value. PCA is used to define the sub-fields of research on CBM.
3. Findings from a Systematic Literature Search and Factor Analysis
Among the starting 4292 contributions, 465 contributions (10.83%) are never cited by other papers, while 2619 of the cited contributions (61.02%) are never co-cited with other papers of the dataset. Therefore, just 1208 papers in the dataset have been co-cited at least once.
The authors have decided to further refine the dataset, inserting a threshold of co-citations for inclusion in text analysis. The threshold has been calculated based on the ratio between the papers considered and the percentage of citations preserved. The 1208 considered papers share 66,130 co-citations. Considering only the documents with at least 3 co-citations (i.e., using a threshold of 2), the dataset can be reduced up to 386 hits. In this scenario, the obtained dataset contains 31.2% of the 1208 documents but keeping about 86% of total co-citations. Documents in the final dataset have 69.92 average citations, which confirm the significance of the filtered contributions across the research field.
In operational terms, a 386 × 386 co-citation matrix has been defined. This matrix constitutes the input for a PCA with VariMax rotation to extract the minimum number of factors. Analytically, a factor represents a linear combination of optimally weighted observed variables that account for a maximal amount of variance in the observed variables, not accounted for by the preceding components and uncorrelated with all of the preceding components [27]. The first ten factors include 378 papers and explain 86.4% of the total variance (see Table 1), while the first four factors economically describe the same phenomenon (75%).

Table 1.
Results of the Principal Component Analysis (PCA) for the first ten factors.
Based on previous research [27], the authors have chosen 0.3 as a threshold for significant factor loading.
At this step, it is necessary to assign each document to the highest loaded factor (factor with the highest value of factor loading, above the threshold). Subsequently, the authors read independently the title, abstract and full text of the records to identify common themes of papers, as grouped in factors. This step allows re-assigning some papers with multiple loadings to the more suitable factor and shifting to the notion of research factors (cf. Section 2). Assessing thematical aspects, the authors isolated 4 research factors covering different and complementary areas of CBM (cf. Section 5):
- Research factor 1: The fundamentals of CBM and its implementation
- Research factor 2: CBM strategies
- Research factor 3: Replacement and inspections management and plan and actual machinery health state
- Research factor 4: Prognosis management and plan
The reduction of the number of research factors compared to the starting 10 PCA factor is justified considering the reduced number of documents (as well as the minor explained variance, see Table 1). The structure of the factors excluded from an in-depth thematical analysis has been kept summarizing minor research contributions, where relevant (cf. Other, Section 4.5).
For the sake of completeness, it is necessary to better explain the management of the factors not included in the 4 RFs presented:
- Factor 5, factor 7 and factor 9 are presented in Section 4.5 respectively as CBM for electrical components, Maintenance scheduling for wind farms and Lot-sizing optimization for maintenance
- Factor 8 and factor 10 were relocated within one of the four RFs presented in the paper, that is, RF1, RF2, RF3 and RF4. Factor 6 has been excluded due to the lack of articles attributed to this factor.
Figure 1 summarizes the proposed research methodology.
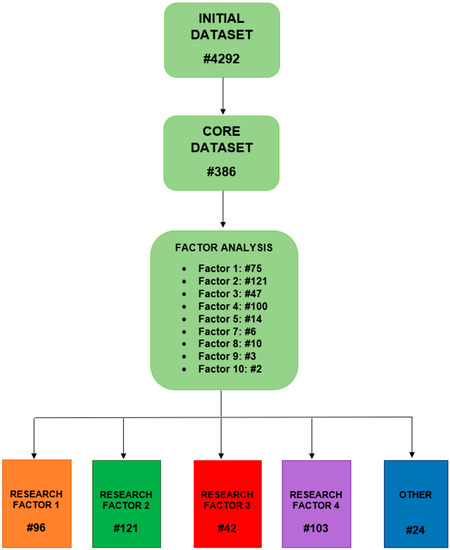
Figure 1.
Research methodology.
The temporal distribution of RFs clearly explains the trend of interest in the CBM field, providing some observations. To simplify this analysis, Figure 2 shows the trend of contributions attributable to each RF over the years. One can observe that the first included year is 1994 and the last is 2018.
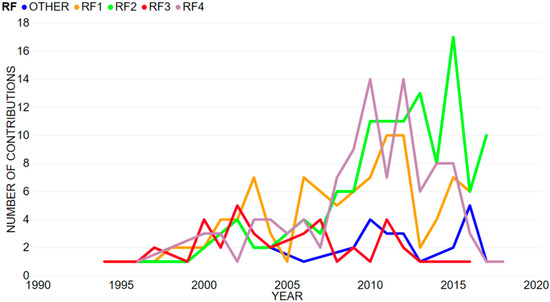
Figure 2.
Temporal distribution of research factors (RF) using a histogram.
- Besides the initial interest on standard themes about CBM (RF1 and RF3), there is a common ground interest on these topics over the years
- RF2 is one of the most examined research themes, with a significant increase around 2008 and 2015 and opposite tendency over more recent years
- RF3 can be considered a saturated RF, as for only three contributions belong to it over the last three years
- After 2008, RF4 raised significantly, becoming one of the most investigated CBM research areas in terms of number of contributions
- “Other” research topics seem to be attracting increasing interest in recent years
Table 2 summarizes some bibliometric aspects of each research factor.

Table 2.
Analysis of the citations trend by RF.
4. Research Factors
Figure 3 represents the logical flow of thematic areas covered by the 4 identified RFs. RF1 introduces CBM, its theoretical fundamentals and main differences with other policies, as a support for policy selection. Moreover, it defines the main steps to be carried out for its implementation, discussing all of them except for prognosis, presented in RF4.
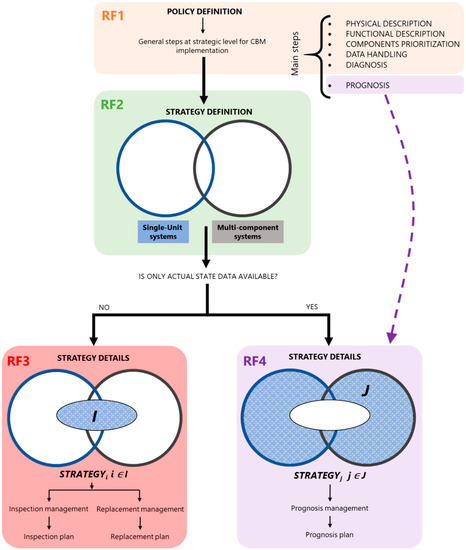
Figure 3.
Main research area in condition-based maintenance (CBM).
RF2 further explores CBM at a more strategic level. Once CBM has been chosen as the organization maintenance policy, it is necessary to select the best strategy which ensures its proper implementation. Based on these considerations, the contributions in RF2 deal with such an issue, dividing substantially between single-unit and multi-component systems. RF3 and RF4 deal with the planning phase of maintenance. RF3 deals with maintenance strategies based only on the actual health state of the machinery and related activities of replacement and inspections. RF4 deals with strategies where future state and useful life of the machinery are also modeled, that is, prognosis.
The following Section 4.1, Section 4.2, Section 4.3, Section 4.4 and Section 4.5 present each RF, specifying its contributions, outcomes and limitations.
4.1. The Fundamentals of CBM and Its Implementation
This research factor includes 96 (of 386) contributions. Most contributions in this RF discuss the fundamentals of CBM and its implementation, following either a theoretical or an operational approach. The RF includes comparison studies between CBM and other maintenance strategies.
The contributions in this RF span over more than 20 years of research—1994 [11]–2016 [28,29,30]. The oldest one [11] reviews worldwide industrial practices on CBM, introducing basic concepts such as the necessity of planned maintenance, the role of CM and the difference between prediction and diagnosis. It also introduces the state of the art on automatic monitoring devices for industrial machines.
A temporal evolution remains relevant within this factor. This latter starts with more general contributions about performance indicators to be considered for building a maintenance strategy [31] or the main techniques used for item monitoring [12]. Early research focused on general industrial settings, without a specific machine-oriented contextualization. Later on, research interest in the construction industry emerged [32,33].
4.1.1. Domain-Based CBM Fundamentals
The interest of the field enlarged in recent years including mainly but not limited to, (i) railway, (ii) naval operations, (iii) nuclear plants, (iv) aviation.
The interest in railway maintenance is recently increasing due to the necessity to guarantee both safety and availability of lines [28,34]. It is possible to differentiate between railway vehicle, that is made up of several components and the identification of a failure root is neither obvious nor unique [34] and railway infrastructure, that is difficult to maintain, due to the number of stakeholders involved, the effects of weather or the designed for previous operating conditions [28]. The recent increment in rail traffic causes more rapid degradation of railway tracks, that have a crucial role in railway maintenance [28,34,35]. Railway tracks can affect maintenance costs, comfort, safety and overall performance [28]. Despite the high costs of investment, the return in terms of reliability and maintenance costs justifies the application of CBM in the railway area [36].
CBM in the naval field has to consider the impossibility of causing failures and considerable difficulty in data collection [37]. Nowadays, interest for CBM in naval settings is primarily about very expensive equipment such as propulsion systems [30] or more specifically on gas turbines or coolers, compressors and fuel injection systems [37,38,39]. In this context, machine learning is reaching valuable results for condition monitoring [30], especially through neural networks [37]. The main areas of intervention for gas turbines, which can affect fuel consumption and pollution emissions [39], are internal crank wash, fuel nozzles and lube oil filter replacement.
An outdated nuclear power plant has a higher cost for maintenance if compared to modern generation ones because their decommission at the end of the licensing lives is cherished and the high costs to satisfy energy demand and generate the required capacity [40]. Considering their characteristics, the natural degradation phenomena of materials inside them and their correlation with the specific driving stressors, that are the root cause of the degradation process [40,41], must be monitored and controlled. Monitoring vibration signals may be helpful, for example, for the management of motor position indication, the accelerator response and the dynamic force loading on the bearings [41].
CBM has been widely applied within the aviation domain. The first challenge is the integration of data, distinguishing between onboard and offboard data sources [42]. In general, aviation health monitoring systems are separated, generating costs and complexity [42]. Based on this, the integration between model-based diagnosis and prognosis could be useful, to synthesize them within the system design [43]. Gas turbines are important components of the aviation systems, composed by a large number of items and various levels of subsystems, that can be affected by hostile environments and that show promising responses with artificial neural networks [44]. The relationships between prognostics and health management technologies and servitization for aviation components should be considered [18] because it can deeply reduce the risk connected with the latter [45].
Besides the previously mentioned contributions on CBM for turbines, further contributions refer to their application for thermal plants as a response to the expansion of renewable energy market [46], also for offshore wind farms [47]. Traditional CBM models developed for steady-state situations should be revisited to consider the intermittence of the respective parameters [46], caused by the necessity to compensate intermittent renewable energy sources. Over the years, these settings proofed the superiority of data-driven approaches rather than physical-based ones [47,48], considering, for example, neural networks for the diagnosis, especially when designed individually for specific failure modes [44].
4.1.2. Meta-Dimensions of CBM Fundamentals
In addition to the proposed domain-based perspective, this RF encompasses contributions ranging from pure theoretical papers towards more practical models for diagnosis implementation, besides reviews that consider only specific sub-topic related to CBM, as mentioned in Section 1.
CBM implementation relies on four main steps, that is, physical description, functional description, components prioritization, data handling, diagnosis and prognosis. Regarding data handling, it is relevant to consider data collection, data analysis, decision-making and implementation, as collected through eight relevant postulates [49]. The first steps refer to the comprehension of information sources, subordinated to physical structure and functional aspects [29]. These latter constitute necessary outputs for analyzing the symptoms and making interpretative sense out of them. The selection of the most important systems and the most critical components precede the description of maintenance tasks and general actions, that is, diagnosis and prognosis [50], which require periodic updates for optimal setting [50,51]. The analysis of critical components connects CBM with the concept of Reliability Centered Maintenance (RCM), which enhances CBM with a specific focus on failure modes analysis [29,52]. Based on these considerations, data fusion levels remain relevant [51]—starting from signal-level fusion, including feature-level fusion up to decision-level fusion. Decision-making refers to the prioritization of maintenance activities [53]. Every equipment has different reliability requirements, safety levels and failure effects and needs different maintenance policies and strategies [54]. The decision making process is a multi-criteria problem, acknowledging costs, safety, added-value, feasibility [54] and risk [55]. The literature proposes the Analytic Hierarchy Process (AHP) for decision-making [54,56], sometimes combined with different algorithms [55]. A fuzzy version of the AHP has been proposed as well to include uncertainty analysis [54]. About diagnosis, some papers present practical suggestions for its implementation concerning data mining and data processing. Four main areas can be identified, that is, Bayesian models [57], Logical Analysis of Data (LAD) [58,59,60], Fuzzy model [61,62] and Neural Networks [44,63,64,65]. The Hierarchical Bayesian approach helps with the uncertainty of degradation data and maintenance activities, providing its quantification. Moreover, the Bayesian theory is the basis for the particle filtering, that can powerfully process sequential signals, facilitating the prognosis [57]. LAD is a supervised learning data mining technique, based on combinatory and Boolean theory, to find patterns in a binary database and generate decision functions without any statistical theory [59]. LAD affects the process of handling missing data and noise since it provides structured approaches for the replacement of missing values by the Min-Max method [59]. LAD has been successfully applied for the diagnosis of rotor bearings [58], as well as for the systemic identification of rogue components [60]. Finally, LAD is completely transparent [59,60], with the possibility to find the root causes for the categorization of each observation. Fuzzy models have been adopted for both diagnosis and prognosis. Starting from traditional fuzzy inference systems based on if-then rules requiring manual tuning of parameters [61], more advanced approaches including fuzzy inference systems and neural networks can enhance performance, simplifying the interaction with other business functions [61]. The neuro-fuzzy approach overcomes the non-transparency of neural networks, which involves a difficult interpretation of the resulting control law [62], as proved for CBM applications in bearings management. Neural networks have been largely applied in CBM, even in terms of decentralized artificial neural networks. These latter involve the use of a hierarchical approach based on multiple neural networks, each of them specialized for a specific task [44]. The digression in Fuzzy models can be improved with a neuro-fuzzy approach, also including self-organizing map techniques. These latter are able to learn without having the corresponding class labels for the input pattern and with unknown conditions can be activated where the previous neural classifier lose its validity [64].
An interest in data gathering and data management, with associated data quality problems, can be observed [66]. Poor raw data management can affect CBM implementation, as proved by a set of wide reviews about data-driven approaches (from data preparation to sensitivity analysis) [47,66]. CM is central for ensuring correct data management [67] and relates to ICT (Information Communication Technology) application, specifically of web and agent technologies [13]. After the data integration, a correspondent technological support development is required, especially in contexts where assets are geographically dislocated [13,68]. Even considering the publishing years of [13,67], respectively 2009 and 2008, one can assert that data management and its correlation with technologies is still an open challenge. Sensor technologies have an important role for CM and they have been developed widely in response to the monitoring of specific parameters (particularly for vibration, a largely used parameter for CBM) and usability challenges (portability, non-contact and reduced size) [69]. The evolution in sensor technologies is tightly linked to prognostics and health management, facilitating a more powerful and cheaper data acquisition [67]. Prognostics and health management are defined as methods and technologies to analyze the reliability of a product and understand potential failures, mitigating risks. They represent a complex research area on CBM, affecting CBM effectiveness from raw data gathering to item behavior forecasts [15,70]. Recently, they have been enhanced by artificial intelligence [17]. One can observe that implementing maintenance correctly implies integrating three policies, that is, corrective, preventive and CBM, depending on the role of items and associated cost-effectiveness [32]. Focusing on CBM, it is essential to understand that it involves—and requires integrated management of—various disciplines like data mining, artificial intelligence and statistics [71]. Production contexts must be considered for the effectiveness of CBM since they are differently affected by CBM implementation [72]. The main areas of CBM are diagnosis and prognosis and the systematic explorative integration of different data sources is the most challenging task [70].
4.2. CBM Strategies
This research factor includes 121 (of 386) contributions, which discuss CBM strategies through practical examples, explaining the ones previously available or proposing variations of them. As a complementary perspective to RF1, RF2 defines more details for CBM policy implementation, with a distinction between single-unit systems and multi-component systems. The term single-unit is used to depict a system with a unique unit or even a system with a unique critical component able to sufficiently represent the entire system [73]. Multi-component systems refer to either a system with more than one unit or a unit with multiple sub-components to be analyzed jointly [74]. Literature is mainly focused on single-unit systems [75,76,77,78,79], even if recently multi-component systems are increasingly investigated since they represent a more realistic setting [80,81,82,83]. Multi-component system analysis is usually more demanding since it involves dependencies analysis between the various components and even environmental settings [21,84,85,86,87]. Reproducing the strategy for a single-component system to a multi-component system does not usually represent an optimal solution [88], that is, the superposition property does not remain valid [80,89]—a single-unit strategy can be applied to a multi-unit system only if there are no dependencies inside it.
4.2.1. Single-Unit Systems
For single-unit systems, parameters are usually optimized as a primary function of maintenance costs. This latter should be precisely assessed since production rate and capacity or availability could be aspects to be prioritized under specific circumstances [90,91,92]. For this purpose, a dynamic maintenance structure can be preferred to reduce uncertainty on measurements [93]. The most applied strategy for single-unit systems refers to opportunistic maintenance, in which maintenance decisions usually follow control-limit rules [90,94]. The presented strategy ensures that inspection time is optimized to guarantee that the failure probability before the next inspection remains lower than an imposed limit Q (0 < Q < 1), also considering environmental conditions [95].
4.2.2. Multi-Component Systems
This subsection refers to those components which require more sophisticated approaches, in light of their numerosity and respective functionally intertwined properties [96].
Multi-component systems can be analyzed either at the system—or at a component-level. In the first case, the predictive reliability of the system is determined as a function of the reliability of its components and it drives preventive maintenance interventions. On the other hand, the component-level analysis drives the identification of an optimal components grouping to ensure the optimal implementation of the triggered systemic preventive intervention [86]. An intertwined perspective on these two levels should encompass multi-level decision-making [97]. In this context, a two-stages approach has been proposed as well—the first stage determines the maintenance strategy for each component, based on the nature and the urgency of the problem; the second stage considers pre-determined maintenance strategies for the individual components and aggregates them at the system level to minimize total costs in light of risk tolerance of degradation behavior [98]. CBM is often compared with the ABR (Age-Based Replacement), usually in terms of cost-savings [99]. A comparison of the difference for these strategies in serial and parallel configuration reported how CBM outperforms ABR in parallel configurations and vice versa for serial configurations, due to starving and blocking effects [100]. Further observations remain relevant when comparing CBM and ABR, (e.g.,) maintenance worker constraints, external maintenance workers with response time and a limited number of internal maintenance workers [100]. Such aspects pave the way to human-oriented analyses focused on human error during maintenance interventions [101]. A proper CBM strategy development for multi-component systems profits in prognostics and RUL information analysis [84,85,97,102,103,104]. In this context, the degradation level of any component may affect the RUL of any other component in the system [85]. More specifically, a relevant property of the RUL (i.e., monotonicity) allows converting the events of RUL associated with quantity in degradation levels [103]. As such, RUL represents a valuable condition index to make the maintenance actions more reliable [97], also ensuring dynamic information update [102]. Degradation processes acquire a central role for CBM implementation—required planning time, imprecise conditional information and uncertainty of failure levels have a strong influence on the strategy cost-benefit [105]. In this way, CBM optimization can be modeled either as a Markov [80,106] or a semi-Markov decision process [96]. It can also refer to the proportional hazards model [75]. Alternatively, Monte Carlo simulation represents a valuable approach since it enables modeling a large set of realistic scenarios [107,108]. In large multi-component systems, analytical models are indeed less effective than simulation models, as proven by Markov models [109,110], continuous-time Markov, time hidden-Markov chains [111,112], gamma processes [113,114] or competition/cooperative heuristic hybrid games [115]. The genetic algorithm has been used as well in combination with Monte Carlo simulation [107] or for risk management associated with strategy selection [116]. The computation of relevant thresholds is a central issue for CBM, especially in multi-component settings. Their calculation is usually based on costs [108] or failure probability [84]. In practical terms, one can imagine that there is no single optimum strategy, especially considering imperfect maintenance actions and short-run availability constraints [113]. In this context, CBM should be linked to inventory, as for the (s, S) strategy (i.e., variable spare part order quantity to reach the maximum stock level S to be scheduled only below a certain level of the inventory s) [80]. Such inventory strategy can be further improved if combined with the condition-based replacement strategy, named as the (T, S, s, Lp) strategy, where T is the inspection interval, S is the maximum stock level, s is the reorder level and Lp is the preventive replacement threshold [117]. For multi-component systems, multiple competing failure modes should be considered to correctly design a CBM strategy [118]. A preliminary distinction refers to internal degradation and external shocks [119,120,121], which can include human-induced ones [101]. Another distinction is on failure type—hard (i.e., abrupt) and soft failures (i.e., gradual) [122]. One advantage of CBM is its capability of being independent from the failure mode, that is, being able to consider jointly multiple failures modes (at least expect abrupt failure, where there is no evidence of a detectable precursor signal) [123]. An example is represented by wind turbines, which can be affected by types of failure even in relation to external operating conditions [109].
4.2.3. About Dependencies
A multi-component system involves some dependencies that cannot be neglected between different components as well as with the environment. These dependencies are the main difference between a single-unit strategy and a multi-component strategy. Based on this, in multi-component systems the optimal maintenance and inventory decisions depend on the complete system. As asserted before, these dependencies are the reason why reproducing the strategy for a single-component system to a multi-component system could not be optimal [80,89] and a single-unit strategy can be applied to a multi-unit system only if there are no dependencies inside it.
Based on this assumption, an important amount of contributions focuses on these dependencies, their role and their management.
The most considered dependencies in literature are economical-oriented or structure-based, with research also referring to stochastic dependencies [21]. The biggest part of the analyzed papers agrees about the importance of the economical dependencies [21,75,84,85,86,89,94,97,98,102,116,124,125,126,127]. This kind of dependence can be approached in two main ways, that is, grouping maintenance and opportunistic maintenance. The former is suitable in those settings when reliability is less important than economic requirements or when the multi-component system has a high level of structural dependencies. The latter is more suitable when there are several stochastically failing parts or high-reliability requirements [85]. Structural dependencies represent the structural and static relationships between different components, mainly represented by technical dependencies or performance dependencies [98,124]. Considering structural dependencies, component repair or replacement may require or inhibit additional components to be maintained. The literature presents rather limited contributions referred to the investigation of this dependency [97,125], with some attempts aimed at interfacing economical and structural dependencies, modeling the latter based on the former [102]. Stochastic dependencies entail the deterioration or failure processes of components that are partially or totally dependent, for failure-induced damage, load sharing or common-mode deterioration [89,102,116]. Further types of dependencies include resources management, that is, maintenance activities can be performed only if the required resources are available (i.e., maintenance worker restrictions, tool restrictions, spares restrictions, transport restrictions and budget restrictions) [128]. In this context, spare parts acquire a central role, since they have to be available for the actual CBM implementation [128].
Different approaches have been proposed for the definition and the management of dependencies in a system, required for a full comprehension of their influence on CBM implementation. Risk-attitude becomes relevant for the optimization of the parameters—when a subject is risk-neutral, the optimal strategy should consider the minimization of the cost rate; when a subject is risk-adverse or risk-seeking, the strategy should consider the stochastic dominant rules [129]. For economic dependencies, the most frequent strategies are complete clustering [130], inspection-driven clustering [99], opportunistic clustering and optimal clustering [124]. For structural dependencies, thresholds for opportunistic replacement and preventive replacement or threshold for preventive replacement and probability thresholds for grouping replacements [89]. Finally, for what concern the stochastic dependencies, the most applied strategies are the threshold for preventive replacement and the thresholds for preventive imperfect repair and preventive replacement [131], as well as copulas, motivated by their particular flexibility and simplicity in modeling multi-dimensional variables [129,132].
4.3. Replacement and Inspections Management and Plan and Actual Machinery Health State
This research factor includes 42 (of 386) contributions. It explores maintenance strategies that rely only on the actual state of the machinery, discussing specific inspection and replacement strategies and respective maintenance plans. As a premise, it is worth separating the two ways state information can be collected from a machine, that is, directly (the measured parameter that directly determines a failure process) or indirectly (provides associated information, which is influenced by the component condition but is not a direct measure of the failure process) [133,134].
4.3.1. About Inspection
Common practices for inspection management start from the development of a model for machine reliability based on its historical failure data [135]. Nowadays, it has been recognized the need to integrate such static data with real-time ones, as proved (e.g.,) by the adoption of the Kalman filter where even a shorter increment time for every step can improve model accuracy [136]. The evidence of the condition of one or more components can be correlated both with efficiency and inspection intervals [137]. Nevertheless, considering the computational efforts of the method, it should be used only for those elements in a minimum cut set as obtained from a fault tree analysis or a Petri net model failure [136]. The inspection interval is strictly correlated with the typology of deterioration to consider [138].
For Markovian or semi-Markovian deterioration models, the effectiveness of a multi-variate process capability index supports the integration of equipment multiple parameters into a synthetic equipment health index [135]. The LAD ensures reasonable performance to evaluate the health state and consequently to predict the survivability of a machine [139]. Risk factors should be considered and integrated through proportional hazards models to extract information from the signals obtained during CM [134]. A correct signal estimation is essential to the proper implementation of replacement and inspection policies [140,141]. Nevertheless, since the validity of the results can be compromised by an excessive number of variables compared to available instances, it becomes necessary to reduce, if possible, their number (e.g., through PCA, principal components analysis) [142]. PCA has been combined with the proportional hazards model for time-dependent stochastic covariates in real settings [143]. Parameter estimation can be implemented online and offline, with an increasing interest in real-time online settings [141].
4.3.2. About Replacement
Replacement strategy should refer to a precise machinery health state assessment and aim at minimizing the expected total discounted cost, especially in partially observable systems [140,141,144,145,146]. Costs minimization can be modelled as a Markov decision process whose state contains the probability distribution of system deterioration levels [144]. In theoretical terms, a component can be preventively replaced if its associated risk of failure exceeds a pre-determined threshold, as for the data obtained from inspections, which have a non-negligible cost [133,147]. The role of the interval for an inspection is linked even with the development of a significant critical level about an objective function for replacement, (e.g.,) expected cost per unit time, the expected downtime per unit time or other reliability measures [148]. In simpler approaches, the maintenance threshold is usually fixed, while it could be of interest to link it to other parameters related to costs, downtime and reliability [149,150]. On these assumptions, replacement becomes tightly related to inspections to trade-off the cost associated with inspection frequency and potential induced failure costs due to non-replaced components [147,151,152]. More frequent inspections provide detailed information about the system conditions and avoid unnecessary replacements. A two stages approach can be applied to model this trade-off—the first stage assumes inspections costs as negligible in a partial replacement strategy; the second stage relaxes the assumption through an A * heuristic algorithm to refine the replacement strategy [133]. The application of the Weibull proportional-hazards model for determining the optimal replacement strategy provided relevant results [143,153]. It has been used as a Weibull baseline hazard combined with a Markov process for modeling equipment lifetime [153] and in combination with time-dependent stochastic covariates to describe the system failure rate [143].
4.4. Prognosis Management and Plan
This RF includes 103 (of 386) contributions that discuss RUL or future health state prediction for a machine. RF4 is complementary to RF3 because it is integrated with maintenance strategies that consider both the actual and the future health state, integrating prognostics both at a management and at a plan level.
From a theoretical perspective, four main steps constitute a prognostics process—data acquisition, health indicator construction, health stage division and RUL prediction [154]. A major challenge in predicting RUL is the uncovering of the relationships between quantitative measures and damage states [155], exploring direct or indirect state variables. Direct state variables are usually analyzed via regression-based models, Brownian motion with drift (Wiener processes [156]), gamma processes and Markovian-based models; indirect ones via stochastic filtering-based models, covariate based hazard models and Hidden Markov model (HMM) and hidden semi-Markov model (HSMM) based methods [14]. Another distinction consists of model-based approaches and data-driven approaches [157]. The former relies on developing physics models of failure or degradation, while the latter is based on data transformation directly from sensor outputs into models, especially valuable if adopting artificial intelligence [2,155]. Experience-based prognostics (or reliability-based prognostics) can be considered as a hybrid approach based on using knowledge from experience feedbacks gathered during a significant period (maintenance data, operating data, failure times, etc.) to adjust the parameters of some predefined reliability models [158].
From a methodological point of view, some methods have been largely used within prognostics, that is, fuzzy logic, Monte Carlo simulation, neural networks, Kalman filters, Wavelet methods, Bayesian models, Support Vector Machines, Markov and semi-Markov models. All these techniques are rarely used standalone since their integration usually provides more advantageous results [159]. The fuzzy process has been investigated especially on bearings [160,161,162,163]. In combination with the Weibull distribution and neural networks, fuzzy logic can manage nonlinear time series [160]. Similarly, it is possible to mix fuzzy c-means (a user-friendly method for pattern recognition) with the lifting wavelet packet decomposition, that is, the most used time-frequency analysis method [161]. This composed method assures the user a simplified set of parameters and it has been further expanded including a support vector data description to increase robustness to outliers and degradation assessment [162]. Adaptive neuro-fuzzy inference systems can also be mixed with high-order particle filtering [163]. Monte Carlo simulation is particularly relevant for modern applications since it remains valid in nonlinear systems [164]. It can be effectively combined with Hidden Markov models [159] or Bayesian networks [165,166,167]. Kalman filter has been used to increase prediction accuracy, even if it requires a large amount of data to be implemented [168]. Some extensions of Kalman filter have been tested to relax the assumption on the linear system dynamics model with Gaussian noise [169,170]. The wavelet packet–empirical mode decomposition has been applied for feature extraction in combination with the self-organization mapping to evaluate performance degradation [171]. To extract system features, the wavelet transform has been combined with support vector regression [172,173]. The wavelet decomposition has been also used as a basis for the development of health indexes [174]. In this regard, it is important to note that the decomposition level of the wavelet has generally an impact on prediction accuracy [173]. The effectiveness of support vector machines for RUL prediction has been confirmed standalone [175] or even if applied in a Cox proportional hazard model for the estimation of the survival function of a system [176]. Bayesian logic guarantees correct uncertainty management, especially in light of parameter estimation dynamic updates [177]. A dynamic Bayesian approach enables more flexible Hidden Markov models [178] and remains effective even if combined with a particle filter algorithm [179]. A Bayesian model can be used to iteratively evaluate the probability of failure of a component, mainly in the case of individual failure modes [180]. Neural networks and especially deep neural networks, are applicable for dimensionality reduction problems [181,182] In data management context, self-organizing map neural networks can be applied as a feature-level fusion algorithm [183]. Additional neural network based approaches include a Weibull failure rate function to reduce the noise effect [184,185] or the adoption of a recurrent two layers structure, that is, the Elman context layer and the Jordan context layer [186]. Interesting considerations can be done even about the use of wavelet neural networks in prognostics [187]. They can also be combined with wavelets to produce a joint approach particularly flexible for non-linear failure modes analyses [187]. Markov and semi-Markov models have been largely adopted due to their flexibility for both diagnosis and prognosis which counterbalances their challenging design and training [188,189,190,191,192,193,194,195,196]. Hidden Markov models ensure effective results even without data pre-processing and remain valuable to reduce the computational complexity in multi-sensor systems [189], especially in case of no knowledge on previous failure states [190] or to include environmental factors via belief rule-based methodologies [191]. In general, hidden semi-Markov models are preferable since they guarantee more realistic applicability if compared to Markov chains [193].
The performance of any prognosis model should be assessed based on different metrics referring to three major categories—algorithm performance metrics, computational performance metrics and cost-benefit metrics [197]. The most frequent metrics are accuracy, precision, mean square error and mean absolute percentage error [198]. When human experts are involved, it becomes necessary to provide a measure of the consistency of the judgments and their influence on the entire process [199]. Similar observations remain valid for the reliability of the sensors networks [200]. In this context, the 5S methodology can be used to convert raw data in prognostics information [201] via 5 steps, that is, streamline, smart processing, synchronize & see, standardize and sustain.
4.5. Other
Besides the major factors previously discussed, it is possible to isolate some minor sub-factors referred to very specific domains, inductively identified after full-text reading—(i) maintenance scheduling for wind farms, (ii) lot-sizing optimization for maintenance, (iii) CBM for electrical components.
4.5.1. Maintenance Scheduling for Wind Farms
The 6 papers in this area deal with scheduling of maintenance tasks, evolving traditional time-based maintenance [202], as discussed (e.g.,) through a risk-based model for offshore wind turbines [203]. The approach relies on the pre-posterior Bayesian decision theory to quantify indirect information about the damage state of critical components [203]. Alternative approaches for wind turbines rely on Markov decision process models to develop an optimal cost-effective maintenance strategy [204] or discrete event simulation to include stochastic hourly and seasonal loading [205]. An innovative mixed-integer optimization model for maintenance scheduling is proposed to rely on sensor-driven interventions, via a Bayesian prognostic model [206]. The approach has been further extended considering the effects of maintenance on network operation [207].
4.5.2. Lot-Sizing Optimization for Maintenance
This minor sub-factor including just 3 documents refers to contributions dealing with the integration of maintenance with production aspects linked to lot-sizing.
Sampling models do not consider interactions with production, inventory and maintenance aspects [208].
One of these models suggests the minimization of an objective function defined by costs constrained on production quality. Through the proposed numerical examples, several functional inter-connections are defined between maintenance, production, inventory and quality.
A similar contribution adopting a slightly different objective function in this context is the long-run expected average cost per unit time, acknowledging multiple costs such as shortage, set-up, maintenance, inventory holding and lost production costs [209]. Relying on the same costs, another research presents a joint optimization model of production lot-sizing and CBM for a multi-component production system to meet in a finite time horizon demand schedule [210].
4.5.3. CBM for Electrical Components
This sub-factor includes 15 contributions which deal with CBM for electrical components, as investigated by Chinese scholars. These contributions encompass maintenance decision-making aspects and risk-based strategies [211,212,213], mostly concerning very specific technical issues, (e.g.,) electrical transmission equipment and the power transmission system [214,215] or electrical substation [216]. In this case, the minimization of an integrated risk cost function including equipment failure risk and grid operation risk factors has been solved via a Tabu search algorithm [215]. Another document adopts the Marquardt method in combination with Weibull distribution fitting and refers to how post-failure statistical analysis has low significance for electrical failure rate estimation [217]. The same method has been combined with a fuzzy analytic hierarchy process to prioritize events and reliability levels for life cycle failure rates of electrical power transformers [218].
5. Discussion
This section aims to discuss and critically reflect on the results of the literature review. Firstly, a bibliometric discussion is proposed, as a complementary explorative dimension to the detailed analysis of RFs proposed in Section 4. Then, the topics of each RFs are critically re-discussed to give a synthetic overview of the current status of the literature.
5.1. Bibliometric-Driven Discussion
An analysis of the citations of each RF offers some tangible measures on the topic being investigated (see Figure 4). Note that Figure 4 excludes a highly cited paper ascribed to RF4 ([2], 2271 citations, while average citations are 85.57) which reviews both diagnosis and prognosis, with a focus on RUL prediction.
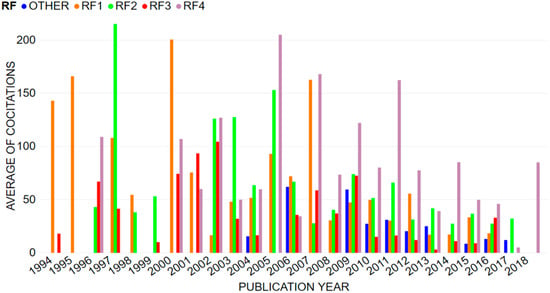
Figure 4.
Temporal analysis of RFs, excluding [2].
Figure 4 clarifies that the most relevant RFs in recent years are RF2 and RF4. Such results can be explained by two main reasons—the increasing interest in multi-component systems as for RF2 [21,98,124]; the evolution of sensors technologies as well as the evolution of machine learning and data management techniques as for RF4 [154,160,169,219].
A peak in the citations graph referred to RF2 can be easily observed (1997), followed by a substantial decrease in citations for the following papers. 1997 includes a contribution dealing with the application of multiple mathematical models in maintenance [220]. This latter represents a milestone for CBM since it emphasizes topics that remain largely relevant even today, that is, inspection maintenance, maintenance for multi-component systems and maintenance management information systems.
Analysing RF4, one can note that there is a peak of citations and published contributions from 2005 to 2012, which is reflected also by an increase in the number of contributions—11 documents per year (2009–2012), 2 contributions per year (2005–2009), 4 contributions per year (2012 onwards). Contributions over these years are highly cited since they refer to important reviews on topics considerably debated in the CBM field, (e.g., prognostics and rotating machines [14,132]). Specifically, the peak in 2005 can be ascribed to References [188,221]—the former suggests the application of a large-scale hidden Markov model for both diagnosis and prognosis, demonstrating how it can improve RUL prediction; the latter critically reflects on diagnosis and prognosis. In 2007, two further highly-cited contributions present the applicability of hidden semi-Markov models in prognostics and confirm their effectiveness [193,222]. The most relevant document in 2009 is the review of prognostics for rotating machines, which remains a topic of large interest in industrial settings [22]. This review is then integrated by the paper published in 2011 including data-driven approaches, which have been progressively investigated over recent years [14].
The analysis of contributions in RF3 reveals how its early contributions have received considerable research interest over the years, with a decreasing trend for more recent contributions. Documents published until 2002 collect about 40% of the total citations of this RF, proving its recent saturation. Most recognized research in RF3 spans over replacement policy management [153], actual machinery health state assessment [136] and inspections interval management [137].
Citations analysis of RF1 reveals three peaks, that is, 1995, 2000 and 2007, respectively due to References [12,54,56]. The first document [12] is a milestone document summarizing different maintenance settings, including CBM, while the other ones [54,56] discuss optimization of maintenance policy selection using the analytic hierarchy process, a well-known and consolidated technique.
In conclusion, one can observe how RF4 and RF2 appear as the RFs with the largest overall number of citations, with a higher trend for RF4 over recent years, proving its attractiveness for contemporary scholars.
5.2. Future Research
For what concerns RF1, 50% of its contributions have been published by 2010. It is, therefore, a RF including essential contributions used as references (and thus highly co-cited) for many aspects of CBM, such as its theoretical fundamentals and its main steps. This observation implies that RF1 is the most various RF, dealing mostly with abstract topics. The importance of CBM for cost management has been clearly underlined and specified in all papers analysed in this review. Cost-effectiveness is one of the basic criteria for proper maintenance and the reduction of maintenance costs can help increasing enterprise profit [51], to compete in the modern global business landscape [223]. Nevertheless, the equipment is becoming more complicated and sophisticated, with a consequent growth of maintenance costs [63], starting from the decision-making process [53]. In conclusion, the continuous pressure on companies to reduce costs and improve customer satisfaction motivated increasingly detailed examinations of maintenance practices and strategies [224]. Such observations become considerably relevant for equipment or plants with a higher cost and high availability constraints, such as marine propulsion plants. A typical example is represented by propulsion systems, because several propulsion components are periodically subjected to expensive maintenance works to restore, as far as possible, their original design characteristics [39].
The relationship between CBM and the evolution of technologies has been widely discussed. The correct choice about technologies can be fundamental for the implementation of a suitable prognosis, nowadays recognized as a key feature for any successful maintenance strategy [17]. This area relies on sensor and information system technologies [225,226], whose technical progress enabled significant evolution in CBM, mainly linked to remote dynamic data collection [99,227,228]. The use of machine learning is still an open topic concerning such advancements especially for RUL and future health state prediction. Examples in this sense are represented by the application of support vector machine [175,176] or neural networks [62,65] and their derived self-organizing maps [64,171]. A large number of papers suggests the application of hidden semi-Markov model [159,189,196] or hidden Markov model [112,190,229] for diagnosis or prognosis.
Data management for CBM appears still as an immature research area, with several open challenges at different levels. Several CBM approaches are data-driven [47,230] and as such scarcity, incompleteness or miss of data require a dedicated approach for its compensation [231]. The handling of missing data is a crucial aspect for modern CBM implementation and in general for the management of asset-related maintenance, to support CBM decision analysis [66]. Due to the different properties of processed CBM data [42], the conversion and integration of multiple data from sensors are usually challenging [201,232]. Due to the growth of new technologies [67] and the widespread application of machine learning in the field of CBM, a deeper investigation in this direction seems necessary.
Another promising research area, not deeply investigated, refers to the effects of human factors for CBM. Research should analyze human-induced failure scenarios emergent from erroneous functional dependencies, including human reliability and functional characteristics of human error, as well as its main performance influencing factors [101]. It is important to clarify the need for integrating technical, human and organizational aspects of maintenance activities [21,100,101].
RUL prediction is another largely discussed research area, which involves aspects of the degradation processes that affect a system—different degradation processes need different RUL prediction approaches [85,167,168,184]. As such, a proper comprehension of the degradation processes is a cornerstone for this research area, with even more research desirable to develop more accurate models for several of their effects [124,233].
When referring to real operating settings, research on multi-component systems become fundamental, forcing to model both economic, stochastic, structural and resource dependencies [97,125]. Future research should encompass mainly the resource dependencies, which are less investigated so far [21].
Finally, more systemic approaches linked to CBM should be investigated within industrial settings, such as the integration of lot-sizing and maintenance actions [208,209,210] or the optimization of a maintenance strategy considering economic manufacturing quantity [234].
6. Conclusions
CBM is a wide research area. Its effectiveness and impact on industrial settings have been largely recognized and proved via multiple empirical research projects in a variety of contexts. This research aimed at uncovering the structure of the field, epitomizing its main streams of research. The proposed bibliometric approach defined 4 main research areas, able to capture synthetically the domain.
The field has been investigated in terms of policy, strategies and implementation plans, compared with traditional ones. In this regard, research contributions have been differentiated between simpler single-unit systems and more realistic multi-component ones. This distinction presents different perspectives both at theoretical and operational levels for inspection, replacement and prognosis.
A large set of methods have been used standalone or integrated for CBM different steps, with a promising tendency over recent years towards artificial intelligence and machine learning. Nevertheless, new challenges are already open in front of contemporary and future technological developments—more specific component degradation models, the integration of CBM in multi-component multi-sensor systems, in light of global optimization functions and the analysis of humans and machine interactions in a progressively more digitalized era.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
In this section are summarized all the abbreviations encountered in the various sections of the paper. Abbreviations are presented in alphabetical order.
| Abbreviation | Meaning |
| ABR | Age-Based Replacement |
| AHP | Analytic Hierarchy Process |
| CBM | Condition-Based Maintenance |
| CM | Condition Monitoring |
| HMM | Hidden Markov Model |
| HSMM | Hidden Semi-Markov Model |
| ICT | Information And Communication Technology |
| LAD | Logical Analysis Of Data |
| PCA | Principal Component Analysis |
| RCM | Reliability-Centered Maintenance |
| RF | Research Factor |
| RUL | Remaining Useful Life |
| TBM | Time-Based Maintenance |
References
- Lee, J.; Ghaffari, M.; Elmeligy, S. Self-maintenance and engineering immune systems: Towards smarter machines and manufacturing systems. Annu. Rev. Control 2011, 35, 111–122. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Baldin, A.E. Global approach to plant maintenance. In Proceedings of the AIPE Conference, Montreal, QC, Cananda, 1 June 1976. [Google Scholar]
- Baldin, A.E. Condition based maintenance: A powerful tool for modern plant management. Terotechnica 1979, 1, 119–129. [Google Scholar]
- Hirani, J.A.; Varadrajan, R. Condition-Based Maintenance. Indian Text. J. 1985, 95, 43–50. [Google Scholar]
- Henry, T.A. The simple approach to condition monitoring. Terotechnical 1979, 1, 131. [Google Scholar]
- Baldin, A.E. Condition-based maintenance. Chem. Eng. 1981, 88, 89–95. [Google Scholar]
- Harrou, F.; Sun, Y.; Madakyaru, M. Kullback-Leibler distance-based enhanced detection of incipient anomalies. J. Loss Prev. Process Ind. 2016, 44, 73–87. [Google Scholar] [CrossRef]
- Wiboonrat, M. Developing diagnostics and prognostics of data center systems implementing with condition-based maintenance. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4901–4906. [Google Scholar]
- Harrou, F.; Sun, Y.; Khadraoui, S. Amalgamation of anomaly-detection indices for enhanced process monitoring. J. Loss Prev. Process Ind. 2016, 40, 365–377. [Google Scholar] [CrossRef]
- Martin, K.F. A review by discussion of condition monitoring and fault diagnosis in machine tools. Int. J. Mach. Tools Manuf. 1994, 34, 527–551. [Google Scholar] [CrossRef]
- Tsang, A.H.C. Condition-based maintenance: Tools and decision making. J. Qual. Maint. Eng. 1995, 1, 3–17. [Google Scholar] [CrossRef]
- Campos, J. Development in the application of ICT in condition monitoring and maintenance. Comput. Ind. 2009, 60, 1–20. [Google Scholar] [CrossRef]
- Si, X.-S.; Wang, W.; Hu, C.-H.; Zhou, D.-H. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Guillén, A.J.; Crespo, A.; Macchi, M.; Gómez, J. On the role of Prognostics and Health Management in advanced maintenance systems. Prod. Plan. Control 2016, 27, 991–1004. [Google Scholar] [CrossRef]
- Kothamasu, R.; Huang, S.H.; Verduin, W.H. System health monitoring and prognostics—A review of current paradigms and practices. Int. J. Adv. Manuf. Technol. 2006, 28, 1012–1024. [Google Scholar] [CrossRef]
- Dragomir, O.E.; Gouriveau, R.; Dragomir, F.; Minca, E.; Zerhouni, N. Review of prognostic problem in condition-based maintenance. In Proceedings of the 2009 European Control Conference, ECC 2009, Budapest, Hungary, 23–26 August 2009; pp. 1587–1592. [Google Scholar]
- Benedettini, O.; Baines, T.S.; Lightfoot, H.W.; Greenough, R.M. State-of-the-art in integrated vehicle health management. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 157–170. [Google Scholar] [CrossRef]
- Jaw, L.C. Recent advancements in aircraft Engine Health Management (EHM) technologies and recommendations for the next step. In Proceedings of the ASME Turbo Expo, Reno-Tahoe, NV, USA, 6–9 June 2005; Volume 1, pp. 683–695. [Google Scholar]
- Klingenberg, W.; de Boer, T.W. Condition-based maintenance in punching/blanking of sheet metal. Int. J. Mach. Tools Manuf. 2008, 48, 589–598. [Google Scholar] [CrossRef]
- Olde Keizer, M.C.A.; Flapper, S.D.P.; Teunter, R.H. Condition-based maintenance policies for systems with multiple dependent components: A review. Eur. J. Oper. Res. 2017, 261, 405–420. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.C.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- UNI EN 13306:2018 - Maintenance—Maintenance Terminology. 2018. Available online: http://store.uni.com/catalogo/uni-en-13306-2018?josso_back_to=http://store.uni.com/josso-security-check.php&josso_cmd=login_optional&josso_partnerapp_host=store.uni.com (accessed on 7 June 2020).
- Elsevier, Scopus, An Eye on Global Research. 2018. Available online: https://www.elsevier.com/solutions/scopus (accessed on 7 June 2020).
- Shafique, M. Thinking inside the box? Intellectual structure of the knowledge base of innovation research (1988–2008). Strateg. Manag. J. 2013, 34, 62–93. [Google Scholar] [CrossRef]
- Di Stefano, G.; Gambardella, A.; Verona, G. Technology push and demand pull perspectives in innovation studies: Current findings and future research directions. Res. Policy 2012, 41, 1283–1295. [Google Scholar] [CrossRef]
- Patriarca, R.; Bergström, J.; Di Gravio, G.; Costantino, F. Resilience engineering: Current status of the research and future challenges. Saf. Sci. 2018, 102, 79–100. [Google Scholar] [CrossRef]
- Al-Douri, Y.K.; Tretten, P.; Karim, R. Improvement of railway performance: A study of Swedish railway infrastructure. J. Mod. Transp. 2016, 24, 22–37. [Google Scholar] [CrossRef]
- Guillén, A.J.; Crespo, A.; Gómez, J.F.; Sanz, M.D. A framework for effective management of condition based maintenance programs in the context of industrial development of E-Maintenance strategies. Comput. Ind. 2016, 82, 170–185. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Ghio, A.; Savio, S.; Anguita, D.; Figari, M. Machine learning approaches for improving condition-based maintenance of naval propulsion plants. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 230, 136–153. [Google Scholar] [CrossRef]
- Arts, R.H.P.M.; Knapp, G.M.; Mann, L. Some aspects of measuring maintenance performance in the process industry. J. Qual. Maint. Eng. 1998, 4, 6–11. [Google Scholar] [CrossRef]
- Horner, R.M.W.; El-Haram, M.A.; Munns, A.K. Building maintenance strategy: A new management approach. J. Qual. Maint. Eng. 1997, 3, 273–280. [Google Scholar] [CrossRef]
- Edwards, D.J.; Holt, G.D.; Harris, F.C. Predictive maintenance techniques and their relevance to construction plant. J. Qual. Maint. Eng. 1998, 4, 25–37. [Google Scholar] [CrossRef]
- Galar, D.; Kumar, U.; Villarejo, R.; Johansson, C.-A. Hybrid prognosis for railway health assessment: An information fusion approach for PHM deployment. Chem. Eng. Trans. 2013, 33, 769–774. [Google Scholar]
- Su, Z.; Núñez, A.; Jamshidi, A.; Baldi, S.; Li, Z.; Dollevoet, R.; De Schutter, B. Model Predictive Control for Maintenance Operations Planning of Railway Infrastructures. In Proceedings of the 6th International Conference on Computational Logistics, ICCL 2015, Delft, The Netherlands, 23–25 September 2015; Volume 9335, ISBN 9783319242637. [Google Scholar]
- Berdinyazov, A.; Camci, F.; Baskan, S.; Sevkli, M.; Eldemir, F. Economic analysis of condition based maintenance. Int. J. Ind. Eng. Theory Appl. Pract. 2011, 18, 386–403. [Google Scholar]
- Basurko, O.C.; Uriondo, Z. Condition-based maintenance for medium speed diesel engines used in vessels in operation. Appl. Therm. Eng. 2015, 80, 404–412. [Google Scholar] [CrossRef]
- Kacprzynski, G.J.; Gumina, M.; Roemer, M.J.; Caguiat, D.E.; Galie, T.R.; McGroarty, J.J. A prognostic modeling approach for predicting recurring maintenance for shipboard propulsion systems. In Proceedings of the ASME Turbo Expo, New Orleans, LA, USA, 4–7 June 2001; Volume 1. [Google Scholar]
- Altosole, M.; Campora, U.; Martelli, M.; Figari, M. Performance decay analysis of a marine gas turbine propulsion system. J. Ship Res. 2014, 58, 117–129. [Google Scholar] [CrossRef]
- Bond, L.J.; Doctor, S.R.; Griffin, J.W.; Hull, A.B.; Malik, S.N. Damage assessment technologies for prognostics and proactive management of materials degradation. Nucl. Technol. 2011, 173, 46–55. [Google Scholar] [CrossRef]
- Jarrell, D.B.; Sisk, D.R.; Bond, L.J. Prognostics and condition-based maintenance: A new approach to precursive metrics. Nucl. Technol. 2004, 145, 275–286. [Google Scholar] [CrossRef]
- Dunsdon, J.; Harrington, M. The application of Open system architecture for condition based maintenance to complete IVHM. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar]
- Luo, J.; Namburu, M.; Pattipati, K.; Qiao, L.; Kawamoto, M.; Chigusa, S. Model-based Prognostic Techniques. In Proceedings of the AUTOTESTCON (Proceedings), Anaheim, CA, USA, 22–25 September 2003; pp. 330–340. [Google Scholar]
- Ogaji, S.O.T.; Singh, R. Advanced engine diagnostics using artificial neural networks. Appl. Soft Comput. J. 2003, 3, 259–271. [Google Scholar] [CrossRef]
- Greenough, R.M.; Grubic, T. Modelling condition-based maintenance to deliver a service to machine tool users. Int. J. Adv. Manuf. Technol. 2011, 52, 1117–1132. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. A dynamic prognosis scheme for flexible operation of gas turbines. Appl. Energy 2016, 164, 686–701. [Google Scholar] [CrossRef]
- Wiggelinkhuizen, E.; Verbruggen, T.; Braam, H.; Rademakers, L.; Xiang, J.; Watson, S. Assessment of condition monitoring techniques for offshore wind farms. J. Sol. Energy Eng. Trans. ASME 2008, 130, 0310041–0310049. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, H.; Weng, S. A novel prognostic model of performance degradation trend for power machinery maintenance. Energy 2014, 78, 740–746. [Google Scholar] [CrossRef]
- Veldman, J.; Klingenberg, W.; Wortmann, H. Managing condition-based maintenance technology: A multiple case study in the process industry. J. Qual. Maint. Eng. 2011, 17, 40–62. [Google Scholar] [CrossRef]
- Waeyenbergh, G.; Pintelon, L. Maintenance concept development: A case study. Int. J. Prod. Econ. 2004, 89, 395–405. [Google Scholar] [CrossRef]
- Niu, G.; Yang, B.-S.; Pecht, M. Development of an optimized condition-based maintenance system by data fusion and reliability-centered maintenance. Reliab. Eng. Syst. Saf. 2010, 95, 786–796. [Google Scholar] [CrossRef]
- Lehtonen, M. On the optimal strategies of condition monitoring and maintenance allocation in distribution systems. In Proceedings of the 2006 9th International Conference on Probabilistic Methods Applied to Power Systems, PMAPS, Stockholm, Sweden, 11–15 June 2006. [Google Scholar]
- Moore, W.J.; Starr, A.G. An intelligent maintenance system for continuous cost-based prioritisation of maintenance activities. Comput. Ind. 2006, 57, 595–606. [Google Scholar] [CrossRef]
- Wang, L.; Chu, J.; Wu, J. Selection of optimum maintenance strategies based on a fuzzy analytic hierarchy process. Int. J. Prod. Econ. 2007, 107, 151–163. [Google Scholar] [CrossRef]
- Arunraj, N.S.; Maiti, J. Risk-based maintenance policy selection using AHP and goal programming. Saf. Sci. 2010, 48, 238–247. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Braglia, M. Analytic hierarchy process applied to maintenance strategy selection. Reliab. Eng. Syst. Saf. 2000, 70, 71–83. [Google Scholar] [CrossRef]
- Ly, C.; Tom, K.; Byington, C.S.; Patrick, R.; Vachtsevanos, G.J. Fault diagnosis and failure prognosis for engineering systems: A global perspective. In Proceedings of the 2009 IEEE International Conference on Automation Science and Engineering, CASE 2009, Bangalore, India, 22–25 August 2009; pp. 108–115. [Google Scholar]
- Mortada, M.-A.; Yacout, S.; Lakis, A. Diagnosis of rotor bearings using logical analysis of data. J. Qual. Maint. Eng. 2011, 17, 371–397. [Google Scholar] [CrossRef]
- Bennane, A.; Yacout, S. LAD-CBM; New data processing tool for diagnosis and prognosis in condition-based maintenance. J. Intell. Manuf. 2012, 23, 265–275. [Google Scholar] [CrossRef]
- Mortada, M.-A.; Carroll III, T.; Yacout, S.; Lakis, A. Rogue components: Their effect and control using logical analysis of data. J. Intell. Manuf. 2012, 23, 289–302. [Google Scholar] [CrossRef]
- Kothamasu, R.; Huang, S.H. Adaptive Mamdani fuzzy model for condition-based maintenance. Fuzzy Sets Syst. 2007, 158, 2715–2733. [Google Scholar] [CrossRef]
- Ciarapica, F.E.; Giacchetta, G. Managing the condition-based maintenance of a combined-cycle power plant: An approach using soft computing techniques. J. Loss Prev. Process Ind. 2006, 19, 316–325. [Google Scholar] [CrossRef]
- Yam, R.C.M.; Tse, P.W.; Li, L.; Tu, P. Intelligent predictive decision support system for condition-based maintenance. Int. J. Adv. Manuf. Technol. 2001, 17, 383–391. [Google Scholar] [CrossRef]
- Wu, F.; Wang, T.; Lee, J. An online adaptive condition-based maintenance method for mechanical systems. Mech. Syst. Signal Process. 2010, 24, 2985–2995. [Google Scholar] [CrossRef]
- Garga, A.K.; McClintic, K.T.; Campbell, R.L.; Yang, C.-C.; Lebold, M.S.; Hay, T.A.; Byington, C.S. Hybrid reasoning for prognostic learning in CBM systems. IEEE Aerosp. Conf. Proc. 2001, 6, 62957–62969. [Google Scholar]
- Tsang, A.H.C.; Yeung, W.K.; Jardine, A.K.S.; Leung, B.P.K. Data management for CBM optimization. J. Qual. Maint. Eng. 2006, 12, 37–51. [Google Scholar] [CrossRef]
- Fumagalli, L.; Macchi, M.; Rapaccini, M. Computerized maintenance management systems in SMEs: A survey in Italy and some remarks for the implementation of Condition Based Maintenance. IFAC Proc. Vol. (IFAC-PapersOnline) 2009, 13, 1615–1619. [Google Scholar] [CrossRef]
- Campos, J.; Jantunen, E.; Prakash, O. A web and mobile device architecture for mobile e-maintenance. Int. J. Adv. Manuf. Technol. 2009, 45, 71–80. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B.S. Condition based maintenance of machine tools–A review. CIRP J. Manuf. Sci. Technol. 2015, 10, 24–35. [Google Scholar] [CrossRef]
- Galar, D.; Palo, M.; Van Horenbeek, A.; Pintelon, L. Integration of disparate data sources to perform maintenance prognosis and optimal decision making. Insight Non-Destr. Test. Cond. Monit. 2012, 54, 440–445. [Google Scholar] [CrossRef]
- Prajapati, A.; Bechtel, J.; Ganesan, S. Condition based maintenance: A survey. J. Qual. Maint. Eng. 2012, 18, 384–400. [Google Scholar] [CrossRef]
- Koochaki, J.; Bokhorst, J.; Wortmann, H.; Klingenberg, W. Evaluating condition based maintenance effectiveness for two processes in series. J. Qual. Maint. Eng. 2011, 17, 398–414. [Google Scholar] [CrossRef]
- Do, P.; Voisin, A.; Levrat, E.; Iung, B. A proactive condition-based maintenance strategy with both perfect and imperfect maintenance actions. Reliab. Eng. Syst. Saf. 2015, 133, 22–32. [Google Scholar] [CrossRef]
- Rasmekomen, N.; Parlikad, A.K. Condition-based maintenance of multi-component systems with degradation state-rate interactions. Reliab. Eng. Syst. Saf. 2016, 148, 1–10. [Google Scholar] [CrossRef]
- Tian, Z.; Liao, H. Condition based maintenance optimization for multi-component systems using proportional hazards model. Reliab. Eng. Syst. Saf. 2011, 96, 581–589. [Google Scholar] [CrossRef]
- Huynh, K.T.; Barros, A.; Bérenguer, C.; Castro, I.T. A periodic inspection and replacement policy for systems subject to competing failure modes due to degradation and traumatic events. Reliab. Eng. Syst. Saf. 2011, 96, 497–508. [Google Scholar] [CrossRef]
- Deloux, E.; Castanier, B.; Bérenguer, C. Predictive maintenance policy for a gradually deteriorating system subject to stress. Reliab. Eng. Syst. Saf. 2009, 94, 418–431. [Google Scholar] [CrossRef][Green Version]
- Berrade, M.D.; Scarf, P.A.; Cavalcante, C.A.V.; Dwight, R.A. Imperfect inspection and replacement of a system with a defective state: A cost and reliability analysis. Reliab. Eng. Syst. Saf. 2013, 120, 80–87. [Google Scholar] [CrossRef]
- Liu, B.; Liang, Z.; Parlikad, A.K.; Xie, M.; Kuo, W. Condition-based maintenance for systems with aging and cumulative damage based on proportional hazards model. Reliab. Eng. Syst. Saf. 2017, 168, 200–209. [Google Scholar] [CrossRef]
- Olde Keizer, M.C.A.; Teunter, R.H.; Veldman, J. Joint condition-based maintenance and inventory optimization for systems with multiple components. Eur. J. Oper. Res. 2017, 257, 209–222. [Google Scholar] [CrossRef]
- Bouvard, K.; Artus, S.; Bérenguer, C.; Cocquempot, V. Condition-based dynamic maintenance operations planning & grouping. Application to commercial heavy vehicles. Reliab. Eng. Syst. Saf. 2011, 96, 601–610. [Google Scholar]
- Alaswad, S.; Xiang, Y. A review on condition-based maintenance optimization models for stochastically deteriorating system. Reliab. Eng. Syst. Saf. 2017, 157, 54–63. [Google Scholar] [CrossRef]
- Flage, R.; Coit, D.W.; Luxhøj, J.T.; Aven, T. Safety constraints applied to an adaptive Bayesian condition-based maintenance optimization model. Reliab. Eng. Syst. Saf. 2012, 102, 16–26. [Google Scholar] [CrossRef]
- Tian, Z.; Jin, T.; Wu, B.; Ding, F. Condition based maintenance optimization for wind power generation systems under continuous monitoring. Renew. Energy 2011, 36, 1502–1509. [Google Scholar] [CrossRef]
- Shi, H.; Zeng, J. Real-time prediction of remaining useful life and preventive opportunistic maintenance strategy for multi-component systems considering stochastic dependence. Comput. Ind. Eng. 2016, 93, 192–204. [Google Scholar] [CrossRef]
- Nguyen, K.-A.; Do, P.; Grall, A. Multi-level predictive maintenance for multi-component systems. Reliab. Eng. Syst. Saf. 2015, 144, 83–94. [Google Scholar] [CrossRef]
- Shafiee, M.; Finkelstein, M.; Bérenguer, C. An opportunistic condition-based maintenance policy for offshore wind turbine blades subjected to degradation and environmental shocks. Reliab. Eng. Syst. Saf. 2015, 142, 463–471. [Google Scholar] [CrossRef]
- Castanier, B.; Grall, A.; Bérenguer, C. A condition-based maintenance policy with non-periodic inspections for a two-unit series system. Reliab. Eng. Syst. Saf. 2005, 87, 109–120. [Google Scholar] [CrossRef]
- Li, H.; Deloux, E.; Dieulle, L. A condition-based maintenance policy for multi-component systems with Lévy copulas dependence. Reliab. Eng. Syst. Saf. 2016, 149, 44–55. [Google Scholar] [CrossRef]
- Van, P.D.; Bérenguer, C. Condition based maintenance model for a production deteriorating system. In Proceedings of the Conference on Control and Fault-Tolerant Systems, SysTol’10—Final Program and Book of Abstracts, Nice, France, 6–8 October 2010; pp. 424–429. [Google Scholar]
- Van, P.D.; Bérenguer, C. Condition-based maintenance with imperfect preventive repairs for a deteriorating production system. Qual. Reliab. Eng. Int. 2012, 28, 624–633. [Google Scholar] [CrossRef]
- Wang, L.; Chu, J.; Mao, W. A condition-based order-replacement policy for a single-unit system. Appl. Math. Model. 2008, 32, 2274–2289. [Google Scholar] [CrossRef]
- Huynh, K.T.; Barros, A.; Bérenguer, C. Maintenance decision-making for systems operating under indirect condition monitoring: Value of online information and impact of measurement uncertainty. IEEE Trans. Reliab. 2012, 61, 410–425. [Google Scholar] [CrossRef][Green Version]
- Huynh, T.K.; Barros, A.; Bérenguer, C. A reliability-based opportunistic predictive maintenance model for k-out-of-n deteriorating systems. Chem. Eng. Trans. 2013, 33, 493–498. [Google Scholar]
- Chouikhi, H.; Khatab, A.; Rezg, N. A condition-based maintenance policy for a production system under excessive environmental degradation. J. Intell. Manuf. 2014, 25, 727–737. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Sun, Y.; Ma, L. Condition-based maintenance optimisation without a predetermined strategy structure for a two-component series system | Optymalizacja zależnego od stanu technicznego utrzymania urza{ogonek}dzeń dla dwuskładnikowego systemu szeregowego nie wymagaja{ogonek}. Eksploat. Niezawodn. 2012, 14, 120–129. [Google Scholar]
- Huynh, K.T.; Barros, A.; Bérenguer, C. Multi-level decision-making for the predictive maintenance of k-out-of-n:F deteriorating systems. IEEE Trans. Reliab. 2015, 64, 94–117. [Google Scholar] [CrossRef]
- Verbert, K.; De Schutter, B.; Babuška, R. Timely condition-based maintenance planning for multi-component systems. Reliab. Eng. Syst. Saf. 2017, 159, 310–321. [Google Scholar] [CrossRef]
- Zhu, Q.; Peng, H.; van Houtum, G.-J. A condition-based maintenance policy for multi-component systems with a high maintenance setup cost. OR Spectr. 2015, 37, 1007–1035. [Google Scholar] [CrossRef]
- Koochaki, J.; Bokhorst, J.A.C.; Wortmann, H.; Klingenberg, W. The influence of condition-based maintenance on workforce planning and maintenance scheduling. Int. J. Prod. Res. 2013, 51, 2339–2351. [Google Scholar] [CrossRef]
- Asadzadeh, S.M.; Azadeh, A. An integrated systemic model for optimization of condition-based maintenance with human error. Reliab. Eng. Syst. Saf. 2014, 124, 117–131. [Google Scholar] [CrossRef]
- Van Horenbeek, A.; Pintelon, L. A dynamic predictive maintenance policy for complex multi-component systems. Reliab. Eng. Syst. Saf. 2013, 120, 39–50. [Google Scholar] [CrossRef]
- Huynh, K.T.; Castro, I.T.; Barros, A.; Berenguer, C. On the use of mean residual life as a condition index for condition-based maintenance decision-making. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 877–893. [Google Scholar] [CrossRef]
- Huynh, K.T.; Grall, A.; Bérenguer, C. Assessment of diagnostic and prognostic condition indices for efficient and robust maintenance decision-making of systems subject to stress corrosion cracking. Reliab. Eng. Syst. Saf. 2017, 159, 237–254. [Google Scholar] [CrossRef]
- de Jonge, B.; Teunter, R.; Tinga, T. The influence of practical factors on the benefits of condition-based maintenance over time-based maintenance. Reliab. Eng. Syst. Saf. 2017, 158, 21–30. [Google Scholar] [CrossRef]
- Kim, M.J.; Makis, V. Joint optimization of sampling and control of partially observable failing systems. Oper. Res. 2013, 61, 777–790. [Google Scholar] [CrossRef]
- Marseguerra, M.; Zio, E.; Podofillini, L. Condition-based maintenance optimization by means of genetic algorithms and Monte Carlo simulation. Reliab. Eng. Syst. Saf. 2002, 77, 151–165. [Google Scholar] [CrossRef]
- Barata, J.; Soares, C.G.; Marseguerra, M.; Zio, E. Simulation modelling of repairable multi-component deteriorating systems for “on condition” maintenance optimisation. Reliab. Eng. Syst. Saf. 2002, 76, 255–264. [Google Scholar] [CrossRef]
- Byon, E.; Ding, Y. Season-dependent condition-based maintenance for a wind turbine using a partially observed markov decision process. IEEE Trans. Power Syst. 2010, 25, 1823–1834. [Google Scholar] [CrossRef]
- Zhao, X.; Fouladirad, M.; Bérenguer, C.; Bordes, L. Condition-based inspection/replacement policies for non-monotone deteriorating systems with environmental covariates. Reliab. Eng. Syst. Saf. 2010, 95, 921–934. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, E.; Li, Y.; Wang, B.; Wu, J. Maintenance optimization of generating equipment based on a condition-based maintenance policy for multi-unit systems. In Proceedings of the 2009 Chinese Control and Decision Conference, CCDC 2009, Guilin, China, 17–19 June 2009; pp. 2440–2445. [Google Scholar]
- Naderkhani, Z.G.F.; Makis, V. Optimal condition-based maintenance policy for a partially observable system with two sampling intervals. Int. J. Adv. Manuf. Technol. 2015, 78, 795–805. [Google Scholar] [CrossRef]
- Liao, H.; Elsayed, E.A.; Chan, L.-Y. Maintenance of continuously monitored degrading systems. Eur. J. Oper. Res. 2006, 175, 821–835. [Google Scholar] [CrossRef]
- Tan, L.; Cheng, Z.; Guo, B.; Gong, S. Condition-based maintenance policy for gamma deteriorating systems. J. Syst. Eng. Electron. 2010, 21, 57–61. [Google Scholar] [CrossRef]
- Feng, Q.; Bi, X.; Zhao, X.; Chen, Y.; Sun, B. Heuristic hybrid game approach for fleet condition-based maintenance planning. Reliab. Eng. Syst. Saf. 2017, 157, 166–176. [Google Scholar] [CrossRef]
- Camci, F. System maintenance scheduling with prognostics information using genetic algorithm. IEEE Trans. Reliab. 2009, 58, 539–552. [Google Scholar] [CrossRef]
- Wang, L.; Chu, J.; Mao, W. A condition-based replacement and spare provisioning policy for deteriorating systems with uncertain deterioration to failure. Eur. J. Oper. Res. 2009, 194, 184–205. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. On the development of condition based maintenance strategy for offshore wind farm: Requirement elicitation process. Energy Procedia 2012, 24, 328–339. [Google Scholar] [CrossRef]
- Caballé, N.C.; Castro, I.T.; Pérez, C.J.; Lanza-Gutiérrez, J.M. A condition-based maintenance of a dependent degradation-threshold-shock model in a system with multiple degradation processes. Reliab. Eng. Syst. Saf. 2015, 134, 98–109. [Google Scholar] [CrossRef]
- Castro, I.T.; Caballé, N.C.; Pérez, C.J. A condition-based maintenance for a system subject to multiple degradation processes and external shocks. Int. J. Syst. Sci. 2015, 46, 1692–1704. [Google Scholar] [CrossRef]
- Li, W.; Pham, H. An inspection-maintenance model for systems with multiple competing processes. IEEE Trans. Reliab. 2005, 54, 318–327. [Google Scholar] [CrossRef]
- Chen, D.; Trivedi, K.S. Closed-form analytical results for condition-based maintenance. Reliab. Eng. Syst. Saf. 2002, 76, 43–51. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Al-Khalifa, K.N.; Hamouda, A.S.; Coit, D.W.; Elsayed, E.A. Condition-based maintenance for continuously monitored degrading systems with multiple failure modes. IIE Trans. 2013, 45, 422–435. [Google Scholar] [CrossRef]
- Olde Keizer, M.C.A.; Teunter, R.H.; Veldman, J. Clustering condition-based maintenance for systems with redundancy and economic dependencies. Eur. J. Oper. Res. 2016, 251, 531–540. [Google Scholar] [CrossRef]
- Do, P.; Scarf, P.; Lung, B. Condition-based maintenance for a two-component system with dependencies. IFAC-PapersOnLine 2015, 28, 946–951. [Google Scholar] [CrossRef]
- Nguyen, K.-A.; Do, P.; Grall, A. Condition-based maintenance for multi-component systems using importance measure and predictive information. Int. J. Syst. Sci. Oper. Logist. 2014, 1, 228–245. [Google Scholar] [CrossRef]
- Qian, X.; Wu, Y. Dynamic control-limit policy of condition based maintenance for the hydroelectricity generating unit. Int. J. Secur. Appl. 2014, 8, 95–106. [Google Scholar] [CrossRef]
- De Smidt-Destombes, K.S.; Van der Heijden, M.C.; Van Harten, A. On the availability of a k-out-of-N system given limited spares and repair capacity under a condition based maintenance strategy. Reliab. Eng. Syst. Saf. 2004, 83, 287–300. [Google Scholar] [CrossRef]
- Hong, H.P.; Zhou, W.; Zhang, S.; Ye, W. Optimal condition-based maintenance decisions for systems with dependent stochastic degradation of components. Reliab. Eng. Syst. Saf. 2014, 121, 276–288. [Google Scholar] [CrossRef]
- Shafiee, M.; Finkelstein, M. A proactive group maintenance policy for continuously monitored deteriorating systems: Application to offshore wind turbines. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2015, 229, 373–384. [Google Scholar] [CrossRef]
- Liang, Z.; Parlikad, A.K. A tiered modelling approach for condition-based maintenance of industrial assets with load sharing interaction and fault propagation. IMA J. Manag. Math. 2015, 26, 125–144. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, S.; Lee, S.; Ni, J. Modified iterative aggregation procedure for maintenance optimisation of multi-component systems with failure interaction. Int. J. Syst. Sci. 2014, 45, 2480–2489. [Google Scholar] [CrossRef]
- Golmakani, H.R. Optimal age-based inspection scheme for condition-based maintenance using A* search algorithm. Int. J. Prod. Res. 2012, 50, 7068–7080. [Google Scholar] [CrossRef]
- Jardine, A.K.S. Optimizing condition based maintenance decisions. In Proceedings of the Annual Reliability and Maintainability Symposium, Seattle, WA, USA, 28–31 January 2002; pp. 90–97. [Google Scholar]
- Chen, A.; Wu, G.S. Real-time health prognosis and dynamic preventive maintenance policy for equipment under aging Markovian deterioration. Int. J. Prod. Res. 2007, 45, 3351–3379. [Google Scholar] [CrossRef]
- Yang, S.K. An experiment of state estimation for predictive maintenance using Kalman filter on a DC motor. Reliab. Eng. Syst. Saf. 2002, 75, 103–111. [Google Scholar] [CrossRef]
- Saranga, H.; Knezevic, J. Reliability prediction for condition-based maintained systems. Reliab. Eng. Syst. Saf. 2001, 71, 219–224. [Google Scholar] [CrossRef]
- Hontelez, J.A.M.; Burger, H.H.; Wijnmalen, D.J.D. Optimum condition-based maintenance policies for deteriorating systems with partial information. Reliab. Eng. Syst. Saf. 1996, 51, 267–274. [Google Scholar] [CrossRef]
- Ghasemi, A.; Esmaeili, S.; Yacout, S. Development of equipment failure prognostics model based on Logical Analysis of Data (LAD). Eng. Lett. 2013, 21, 256–263. [Google Scholar]
- Lin, D.; Makis, V. Filters and parameter estimation for a partially observable system subject to random failure with continuous-range observations. Adv. Appl. Probab. 2004, 36, 1212–1230. [Google Scholar] [CrossRef]
- Lin, D.; Makis, V. On-line parameter estimation for a failure-prone system subject to condition monitoring. J. Appl. Probab. 2004, 41, 211–220. [Google Scholar] [CrossRef]
- Lin, D.; Banjevic, D.; Jardine, A.K.S. Using principal components in a proportional hazards model with applications in condition-based maintenance. J. Oper. Res. Soc. 2006, 57, 910–919. [Google Scholar] [CrossRef]
- Banjevic, D.; Jardine, A.K.S.; Makis, V.; Ennis, M. A control-limit policy and software for condition-based maintenance optimization. INFOR 2001, 39, 32–50. [Google Scholar] [CrossRef]
- Ohnishi, M.; Morioka, T.; Ibaraki, T. Optimal minimal-repair and replacement problem of discrete-time Markovian deterioration system under incomplete state information. Comput. Ind. Eng. 1994, 27, 409–412. [Google Scholar] [CrossRef]
- Makis, V.; Jiang, X. Optimal replacement under partial observations. Math. Oper. Res. 2003, 28, 382–394. [Google Scholar] [CrossRef]
- Grall, A.; Bérenguer, C.; Dieulle, L. A condition-based maintenance policy for stochastically deteriorating systems. Reliab. Eng. Syst. Saf. 2002, 76, 167–180. [Google Scholar] [CrossRef]
- Golmakani, H.R.; Pouresmaeeli, M. Optimal replacement policy for condition-based maintenance with non-decreasing failure cost and costly inspection. J. Qual. Maint. Eng. 2014, 20, 51–64. [Google Scholar] [CrossRef]
- Wang, W. A model to determine the optimal critical level and the monitoring intervals in condition-based maintenance. Int. J. Prod. Res. 2000, 38, 1425–1436. [Google Scholar] [CrossRef]
- Li, L.; You, M.; Ni, J. Reliability-based dynamic maintenance threshold for failure prevention of continuously monitored degrading systems. J. Manuf. Sci. Eng. Trans. ASME 2009, 131, 0310101–0310109. [Google Scholar] [CrossRef]
- Castanier, B.; Bérenguer, C.; Grall, A. A sequential condition-based repair/replacement policy with non-periodic inspections for a system subject to continuous wear. Appl. Stoch. Model. Bus. Ind. 2003, 19, 327–347. [Google Scholar] [CrossRef]
- Golmakani, H.R. Condition-based inspection scheme for condition-based maintenance. Int. J. Prod. Res. 2012, 50, 3920–3935. [Google Scholar] [CrossRef]
- Golmakani, H.R.; Fattahipour, F. Age-based inspection scheme for condition-based maintenance. J. Qual. Maint. Eng. 2011, 17, 93–110. [Google Scholar] [CrossRef]
- Vlok, P.J.; Coetzee, J.L.; Banjevic, D.; Jardine, A.K.S.; Makis, V. Optimal component replacement decisions using vibration monitoring and the proportional-hazards model. J. Oper. Res. Soc. 2002, 53, 193–202. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Ray, A.; Tangirala, S. Stochastic modeling of fatigue crack dynamics for on-line failure prognostics. IEEE Trans. Control Syst. Technol. 1996, 4, 443–451. [Google Scholar] [CrossRef]
- Le Son, K.; Fouladirad, M.; Barros, A.; Levrat, E.; Lung, B. Remaining useful life estimation based on stochastic deterioration models: A comparative study. Reliab. Eng. Syst. Saf. 2013, 112, 165–175. [Google Scholar] [CrossRef]
- Medjaher, K.; Tobon-Mejia, D.A.; Zerhouni, N. Remaining useful life estimation of critical components with application to bearings. IEEE Trans. Reliab. 2012, 61, 292–302. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N.; Tripot, G. A data-driven failure prognostics method based on mixture of gaussians hidden markov models. IEEE Trans. Reliab. 2012, 61, 491–503. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, M.; Peng, Y. A novel method for online health prognosis of equipment based on hidden semi-Markov model using sequential Monte Carlo methods. Mech. Syst. Signal Process. 2012, 32, 331–348. [Google Scholar] [CrossRef]
- Ben Ali, J.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56, 150–172. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, J.; Li, X. Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means. Mech. Syst. Signal Process. 2010, 24, 559–566. [Google Scholar] [CrossRef]
- Pan, Y.N.; Chen, J.; Dong, G.M. A hybrid model for bearing performance degradation assessment based on support vector data description and fuzzy c-means. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 2687–2695. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Vachtsevanos, G.; Orchard, M. Machine condition prediction based on adaptive neuro-fuzzy and high-order particle filtering. IEEE Trans. Ind. Electron. 2011, 58, 4353–4364. [Google Scholar] [CrossRef]
- Caesarendra, W.; Niu, G.; Yang, B.-S. Machine condition prognosis based on sequential Monte Carlo method. Expert Syst. Appl. 2010, 37, 2412–2420. [Google Scholar] [CrossRef]
- Barraza-Barraza, D.; Tercero-Gómez, V.G.; Beruvides, M.G.; Limón-Robles, J. An adaptive ARX model to estimate the RUL of aluminum plates based on its crack growth. Mech. Syst. Signal Process. 2017, 82, 519–536. [Google Scholar] [CrossRef]
- Camci, F.; Chinnam, R.B. Health-state estimation and prognostics in machining processes. IEEE Trans. Autom. Sci. Eng. 2010, 7, 581–597. [Google Scholar] [CrossRef]
- Sun, J.; Zuo, H.; Wang, W.; Pecht, M.G. Application of a state space modeling technique to system prognostics based on a health index for condition-based maintenance. Mech. Syst. Signal Process. 2012, 28, 585–596. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Lin, J. A New Method Based on Stochastic Process Models for Machine Remaining Useful Life Prediction. IEEE Trans. Instrum. Meas. 2016, 65, 2671–2684. [Google Scholar] [CrossRef]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. Extended kalman filtering for remaining-useful-life estimation of bearings. IEEE Trans. Ind. Electron. 2015, 62, 1781–1790. [Google Scholar] [CrossRef]
- Carr, M.J.; Wang, W. An approximate algorithm for prognostic modelling using condition monitoring information. Eur. J. Oper. Res. 2011, 211, 90–96. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z.; Zio, E.; Hong, K. Condition assessment for the performance degradation of bearing based on a combinatorial feature extraction method. Digit. Signal Process. A Rev. J. 2014, 27, 159–166. [Google Scholar] [CrossRef]
- Loutas, T.H.; Roulias, D.; Georgoulas, G. Remaining useful life estimation in rolling bearings utilizing data-driven probabilistic E-support vectors regression. IEEE Trans. Reliab. 2013, 62, 821–832. [Google Scholar] [CrossRef]
- Yaqub, M.F.; Gondal, I.; Kamruzzaman, J. Multi-step support vector regression and optimally parameterized wavelet packet transform for machine residual life prediction. JVC/J. Vib. Control 2013, 19, 963–974. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Kang, R. Robust health evaluation of gearbox subject to tooth failure with wavelet decomposition. J. Sound Vib. 2009, 324, 1141–1157. [Google Scholar] [CrossRef]
- Kim, H.-E.; Tan, A.C.C.; Mathew, J.; Choi, B.-K. Bearing fault prognosis based on health state probability estimation. Expert Syst. Appl. 2012, 39, 5200–5213. [Google Scholar] [CrossRef]
- Tran, V.T.; Thom Pham, H.; Yang, B.-S.; Tien Nguyen, T. Machine performance degradation assessment and remaining useful life prediction using proportional hazard model and support vector machine. Mech. Syst. Signal Process. 2012, 32, 320–330. [Google Scholar] [CrossRef]
- Tang, S.-J.; Guo, X.-S.; Yu, C.-Q.; Zhou, Z.-J.; Zhou, Z.-F.; Zhang, B.-C. Real time remaining useful life prediction based on nonlinear Wiener based degradation processes with measurement errors. J. Cent. South Univ. 2014, 21, 4509–4517. [Google Scholar] [CrossRef]
- Camci, F.; Chinnam, R.B. Hierarchical HMMs for autonomous diagnostics and prognostics. In Proceedings of the IEEE International Conference on Neural Networks—Conference Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 2445–2452. [Google Scholar]
- Dong, M.; Yang, Z.-B. Dynamic Bayesian network based prognosis in machining processes. J. Shanghai Jiaotong Univ. 2008, 13E, 318–322. [Google Scholar] [CrossRef]
- Carr, M.J.; Wang, W. Modeling failure modes for residual life prediction using stochastic filtering theory. IEEE Trans. Reliab. 2010, 59, 346–355. [Google Scholar] [CrossRef]
- Heng, A.; Tan, A.C.C.; Mathew, J.; Montgomery, N.; Banjevic, D.; Jardine, A.K.S. Intelligent condition-based prediction of machinery reliability. Mech. Syst. Signal Process. 2009, 23, 1600–1614. [Google Scholar] [CrossRef]
- Guo, L.; Gao, H.; Huang, H.; He, X.; Li, S. Multifeatures Fusion and Nonlinear Dimension Reduction for Intelligent Bearing Condition Monitoring. Shock Vib. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Niu, G.; Yang, B.-S. Intelligent condition monitoring and prognostics system based on data-fusion strategy. Expert Syst. Appl. 2010, 37, 8831–8840. [Google Scholar] [CrossRef]
- Tian, Z. An artificial neural network method for remaining useful life prediction of equipment subject to condition monitoring. J. Intell. Manuf. 2012, 23, 227–237. [Google Scholar] [CrossRef]
- Mahamad, A.K.; Saon, S.; Hiyama, T. Predicting remaining useful life of rotating machinery based artificial neural network. Comput. Math. Appl. 2010, 60, 1078–1087. [Google Scholar] [CrossRef]
- Tian, Z.; Zuo, M.J. Health condition prediction of gears using a recurrent neural network approach. IEEE Trans. Reliab. 2010, 59, 700–705. [Google Scholar] [CrossRef]
- Wang, P.; Vachtsevanos, G. Fault prognostics using dynamic wavelet neural networks. Artif. Intell. Eng. Des. Anal. Manuf. AIEDAM 2001, 15, 349–365. [Google Scholar] [CrossRef]
- Baruah, P.; Chinnam, R.B. HMMs for diagnostics and prognostics in machining processes. Int. J. Prod. Res. 2005, 43, 1275–1293. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, M.; Lv, W.; Geng, X.; Li, Y. A novel method using adaptive hidden semi-Markov model for multi-sensor monitoring equipment health prognosis. Mech. Syst. Signal Process. 2015, 64–65, 217–232. [Google Scholar] [CrossRef]
- Yu, J. Health condition monitoring of machines based on hidden markov model and contribution analysis. IEEE Trans. Instrum. Meas. 2012, 61, 2200–2211. [Google Scholar] [CrossRef]
- Zhou, Z.-J.; Hu, C.-H.; Xu, D.-L.; Chen, M.-Y.; Zhou, D.-H. A model for real-time failure prognosis based on hidden Markov model and belief rule base. Eur. J. Oper. Res. 2010, 207, 269–283. [Google Scholar] [CrossRef]
- Chinnam, R.B.; Baruah, P. Autonomous diagnostics and prognostics in machining processes through competitive learning-driven HMM-based clustering. Int. J. Prod. Res. 2009, 47, 6739–6758. [Google Scholar] [CrossRef]
- Dong, M.; He, D. A segmental hidden semi-Markov model (HSMM)-based diagnostics and prognostics framework and methodology. Mech. Syst. Signal Process. 2007, 21, 2248–2266. [Google Scholar] [CrossRef]
- Dong, M.; He, D. Hidden semi-markov models for machinery health diagnosis and prognosis. Trans. N. Am. Manuf. Res. Inst. SME 2004, 32, 199–206. [Google Scholar]
- Jiang, R.; Kim, M.J.; Makis, V. Maximum likelihood estimation for a hidden semi-markov model with multivariate observations. Qual. Reliab. Eng. Int. 2012, 28, 783–791. [Google Scholar] [CrossRef]
- Dong, M.; Peng, Y. Equipment PHM using non-stationary segmental hidden semi-Markov model. Robot. Comput. Integr. Manuf. 2011, 27, 581–590. [Google Scholar] [CrossRef]
- Saxena, A.; Celaya, J.; Balaban, E.; Goebel, K.; Saha, B.; Saha, S.; Schwabacher, M. Metrics for evaluating performance of prognostic techniques. In Proceedings of the 2008 International Conference on Prognostics and Health Management, PHM 2008, Denver, CO, USA, 6–9 October 2008. [Google Scholar]
- Saxena, A.; Celaya, J.; Saha, B.; Saha, S.; Goebel, K. Evaluating algorithm performance metrics tailored for prognostics. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 7–14 March 2009. [Google Scholar]
- Wang, W.; Zhang, W. An asset residual life prediction model based on expert judgments. Eur. J. Oper. Res. 2008, 188, 496–505. [Google Scholar] [CrossRef]
- Elghazel, W.; Bahi, J.; Guyeux, C.; Hakem, M.; Medjaher, K.; Zerhouni, N. Dependability of wireless sensor networks for industrial prognostics and health management. Comput. Ind. 2015, 68, 1–15. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Andrawus, J.A.; Watson, J.F.; Kishk, M.; Adam, A. The selection of a suitable maintenance strategy for wind turbines. Wind Eng. 2006, 30, 471–486. [Google Scholar] [CrossRef]
- Sørensen, J.D. Framework for risk-based planning of operation and maintenance for offshore wind turbines. Wind Energy 2009, 12, 493–506. [Google Scholar] [CrossRef]
- Wu, Y.-R.; Zhao, H.-S. Optimization maintenance of wind turbines using Markov decision processes. In Proceedings of the 2010 International Conference on Power System Technology: Technological Innovations Making Power Grid Smarter, POWERCON2010, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Byon, E.; Pérez, E.; Ding, Y.; Ntaimo, L. Simulation of wind farm operations and maintenance using discrete event system specification. Simulation 2011, 87, 1093–1117. [Google Scholar] [CrossRef]
- Yildirim, M.; Sun, X.A.; Gebraeel, N.Z. Sensor-Driven Condition-Based Generator Maintenance Scheduling—Part I: Maintenance Problem. IEEE Trans. Power Syst. 2016, 31, 4253–4262. [Google Scholar] [CrossRef]
- Yildirim, M.; Sun, X.A.; Gebraeel, N.Z. Sensor-Driven Condition-Based Generator Maintenance Scheduling—Part II: Incorporating Operations. IEEE Trans. Power Syst. 2016, 31, 4263–4271. [Google Scholar] [CrossRef]
- Bouslah, B.; Gharbi, A.; Pellerin, R. Joint economic design of production, continuous sampling inspection and preventive maintenance of a deteriorating production system. Int. J. Prod. Econ. 2016, 173, 184–198. [Google Scholar] [CrossRef]
- Jafari, L.; Makis, V. Optimal lot-sizing and maintenance policy for a partially observable production system. Comput. Ind. Eng. 2016, 93, 88–98. [Google Scholar] [CrossRef]
- Cheng, G.Q.; Zhou, B.H.; Li, L. Joint optimization of lot sizing and condition-based maintenance for multi-component production systems. Comput. Ind. Eng. 2017, 110, 538–549. [Google Scholar] [CrossRef]
- Xu, B.; Han, X.; Li, Y.; Zhang, Y.; Li, M.; Huang, H. Opportunistic maintenance decision-making model for power equipment. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2016, 36, 6379–6388. [Google Scholar]
- Yuan, Z.; Sun, C.; Li, J.; Du, L.; Liao, R. Study on condition-based maintenance policy of transformer based on fuzzy multiple expert and multiple attribute group decision making. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2004, 28, 66–70. [Google Scholar]
- Tian, L.; Xing, J.-G. Discussion on making decision about electric equipment for condition based maintenance. Power Syst. Technol. 2004, 28, 60–63. [Google Scholar]
- Li, M.; Han, X.; Yang, M.; Guo, Z. Basic concept and theoretical study of condition-based maintenance for power transmission system. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2011, 31, 43–52. [Google Scholar]
- Pan, L.; Lu, G.; Zhang, Y.; Yu, G.; Zhu, D. Decision-making optimization of equipment condition-based maintenance according to risk comprehensive evaluation. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2010, 34, 28–32. [Google Scholar]
- Li, M.; Han, X.; Wang, Y.; Guo, Z.; Liu, G. Decision-making model and solution of condition-based maintenance for substation. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2012, 32, 196–202. [Google Scholar]
- Pan, L.; Zhang, Y.; Yu, G.; Du, C. Prediction of electrical equipment failure rate for condition-based maintenance decision-making. Dianli Zidonghua Shebei/Electr. Power Autom. Equip. 2010, 30, 91–94. [Google Scholar]
- Sun, P.; Chen, S.-H.; Zhang, C.-Q. Assessment of failure rate for substation equipment life cycle based on Marquardt parameter estimation method. Dianli Xitong Baohu yu Kongzhi/Power Syst. Prot. Control 2012, 40, 85–90. [Google Scholar]
- Meeker, W.Q.; Hong, Y. Reliability meets big data: Opportunities and challenges. Qual. Eng. 2014, 26, 102–116. [Google Scholar] [CrossRef]
- Scarf, P.A. On the application of mathematical models in maintenance. Eur. J. Oper. Res. 1997, 99, 493–506. [Google Scholar] [CrossRef]
- Katipamula, S.; Brambley, M.R. Review article: Methods for fault detection, diagnostics, and prognostics for building systems—A review, part I. HVAC R Res. 2005, 11, 3–25. [Google Scholar] [CrossRef]
- Wang, W. A two-stage prognosis model in condition based maintenance. Eur. J. Oper. Res. 2007, 182, 1177–1187. [Google Scholar] [CrossRef]
- Goh, K.M.; Tjahjono, B.; Baines, T.; Subramaniam, S. A review of research in manufacturing prognostics. In Proceedings of the 2006 IEEE International Conference on Industrial Informatics, INDIN’06, Singapore, 16–18 August 2006; pp. 417–422. [Google Scholar]
- Mechefske, C.K.; Wang, Z. Using fuzzy linguistics to select optimum maintenance and condition monitoring strategies. Mech. Syst. Signal Process. 2001, 15, 1129–1140. [Google Scholar] [CrossRef]
- De Jonge, B.; Klingenberg, W.; Teunter, R.; Tinga, T. Reducing costs by clustering maintenance activities for multiple critical units. Reliab. Eng. Syst. Saf. 2016, 145, 93–103. [Google Scholar] [CrossRef]
- Peng, H.; Van Houtum, G.-J. Joint optimization of condition-based maintenance and production lot-sizing. Eur. J. Oper. Res. 2016, 253, 94–107. [Google Scholar] [CrossRef]
- Shin, J.-H.; Jun, H.-B. On condition based maintenance policy. J. Comput. Des. Eng. 2015, 2, 119–127. [Google Scholar] [CrossRef]
- Wang, W. Condition-Based Maintenance Modelling. Springer Ser. Reliab. Eng. 2008, 8, 111–131. [Google Scholar]
- Neves, M.L.; Santiago, L.P.; Maia, C.A. A condition-based maintenance policy and input parameters estimation for deteriorating systems under periodic inspection. Comput. Ind. Eng. 2011, 61, 503–511. [Google Scholar] [CrossRef]
- Ji, G.; Wu, W.; Zhang, B.; Liu, S.; Jiang, W. A time-varying component outage model for power system condition-based maintenance. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2013, 33, 139–146. [Google Scholar]
- Zuashkiani, A.; Banjevic, D.; Jardine, A.K.S. Estimating parameters of proportional hazards model based on expert knowledge and statistical data. J. Oper. Res. Soc. 2009, 60, 1621–1636. [Google Scholar] [CrossRef]
- Galar, D.; Gustafson, A.; Tormos, B.; Berges, L. Maintenance decision making based on different types of data fusion | Podejmowanie decyzji eksploatacyjnych w oparciu o fuzje{ogonek} różnego typu danych. Eksploat. Niezawodn. 2012, 14, 135–144. [Google Scholar]
- Creveling, C.J. Increasing the Reliability of Electronic Equipment by the Use of Redundant Circuits. Proc. IRE 1956, 44, 509–515. [Google Scholar] [CrossRef]
- Jafari, L.; Makis, V. Joint optimal lot sizing and preventive maintenance policy for a production facility subject to condition monitoring. Int. J. Prod. Econ. 2015, 169, 156–168. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).