Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model †
Abstract
1. Introduction
2. Specifications of the Analyzed Forklift Truck
3. Experimental Measurements
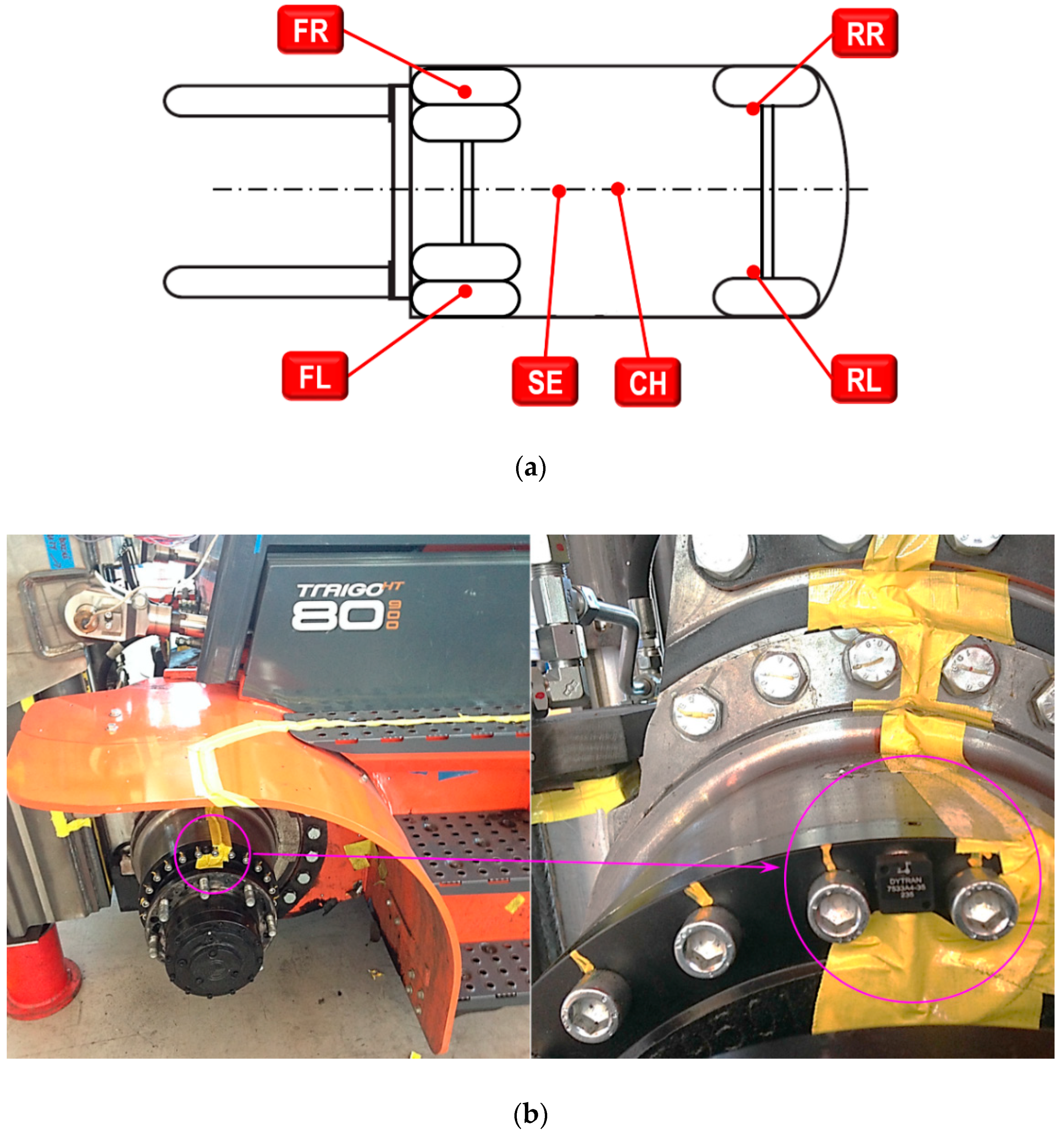
3.1. Sensor Setup and Test Protocols
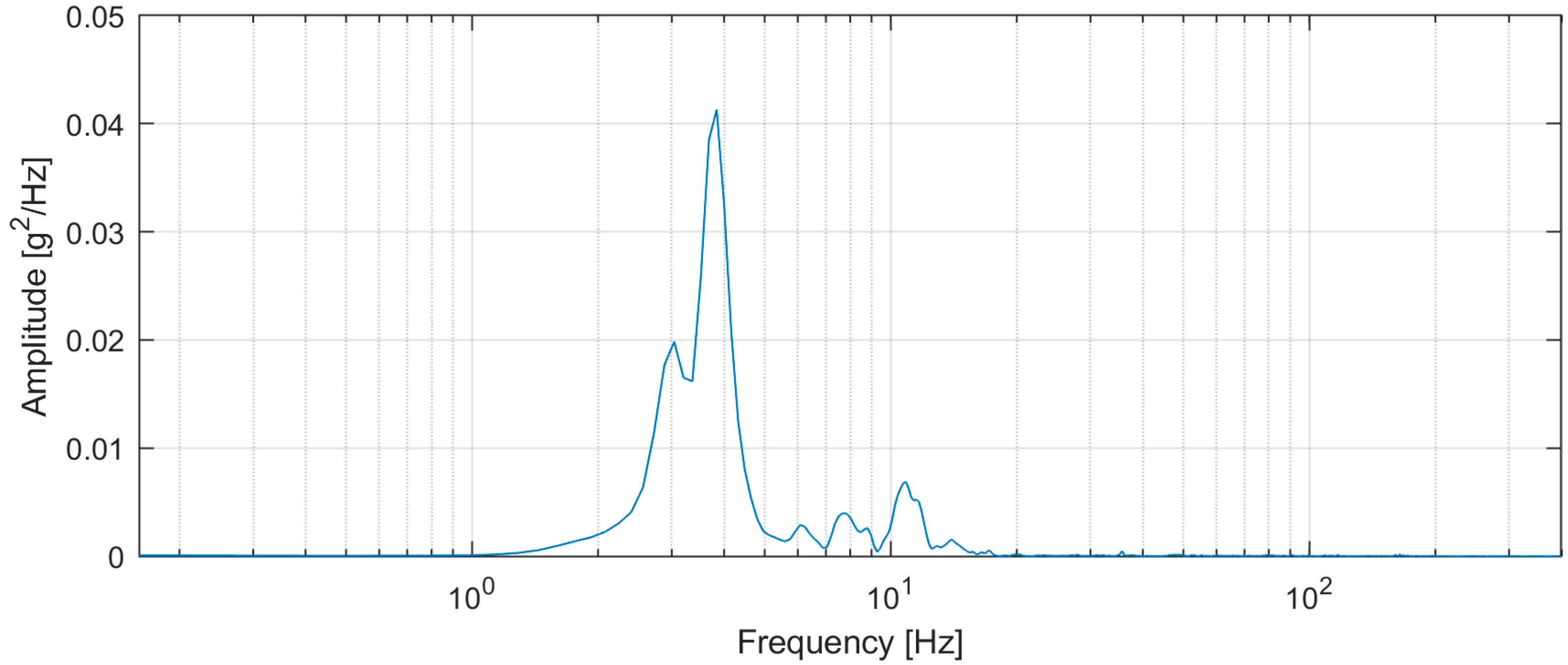
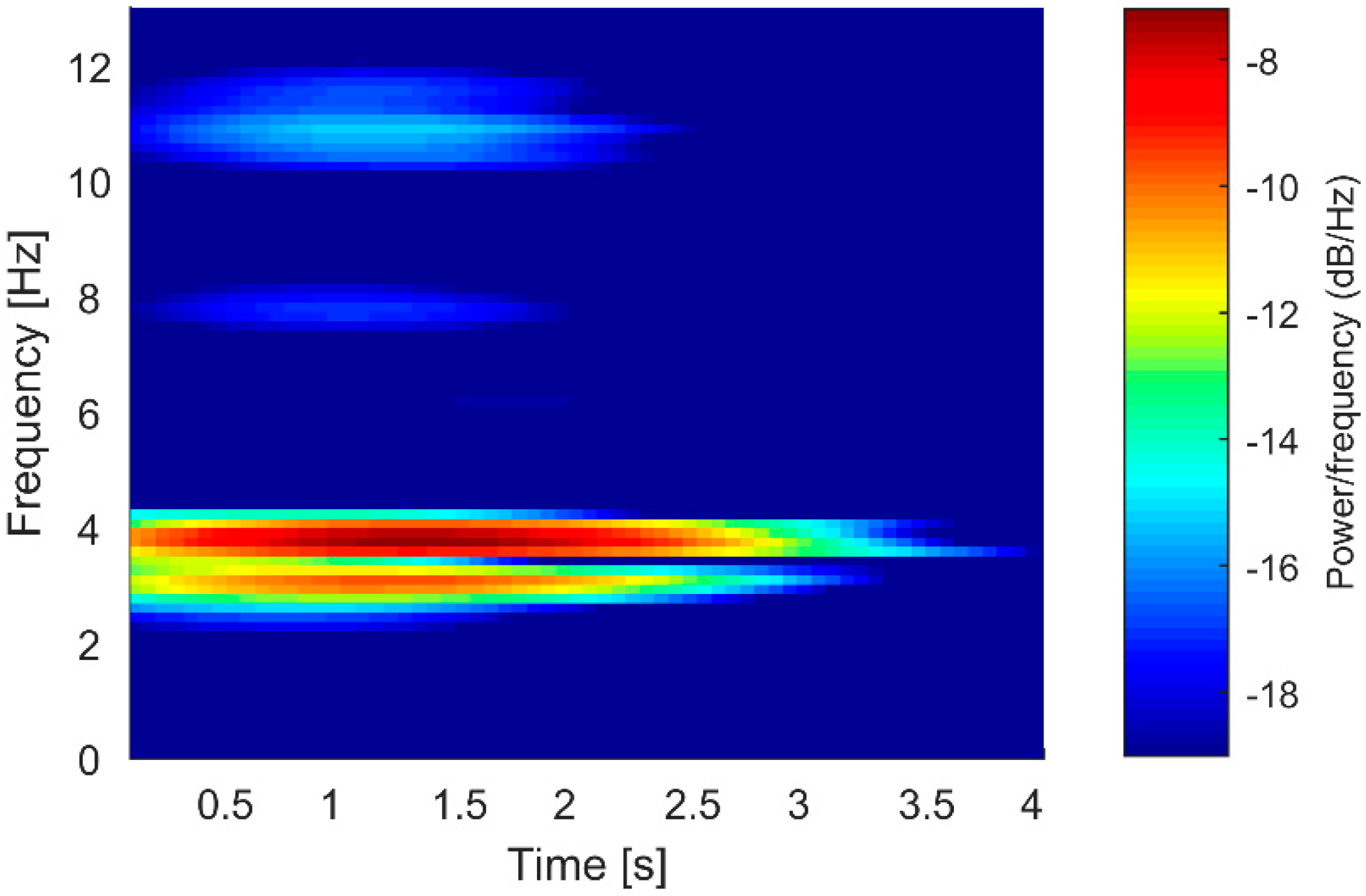
3.2. Experimental Results
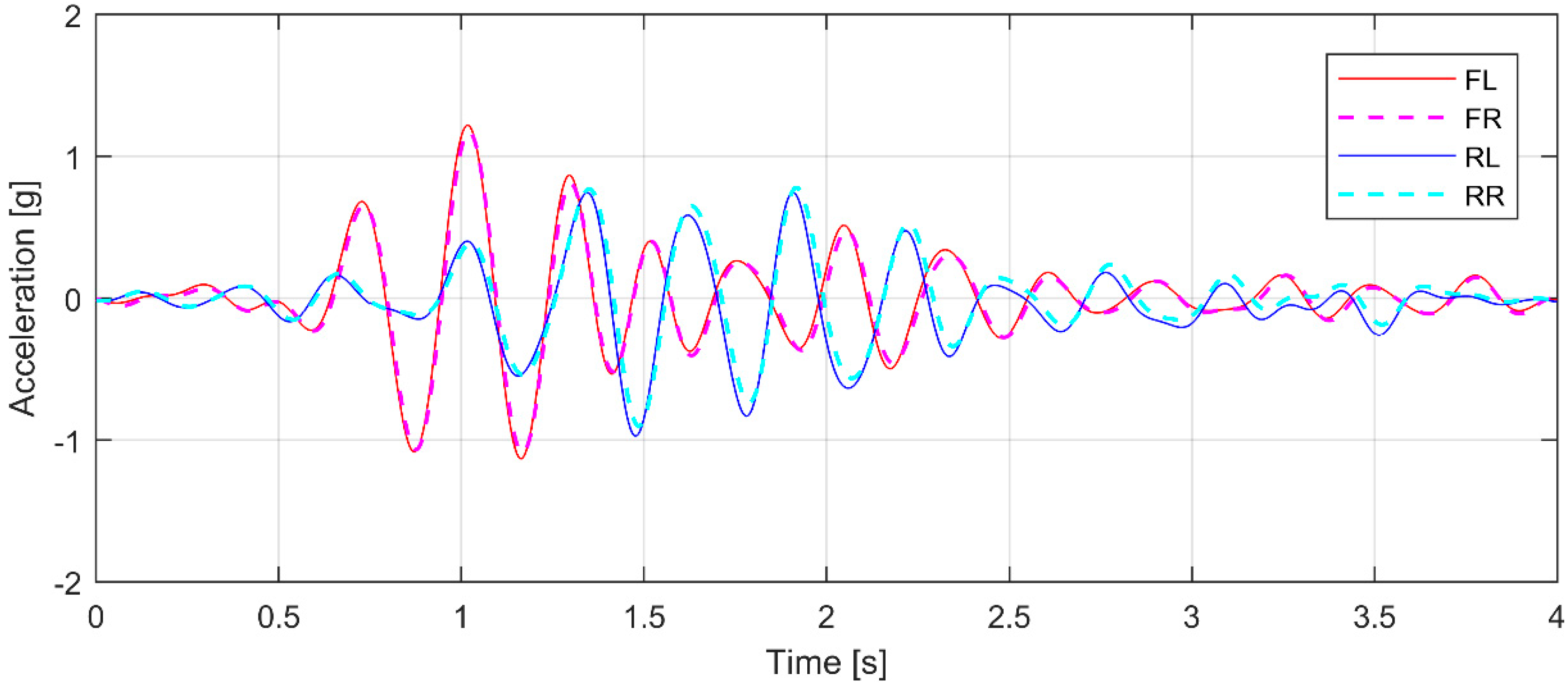
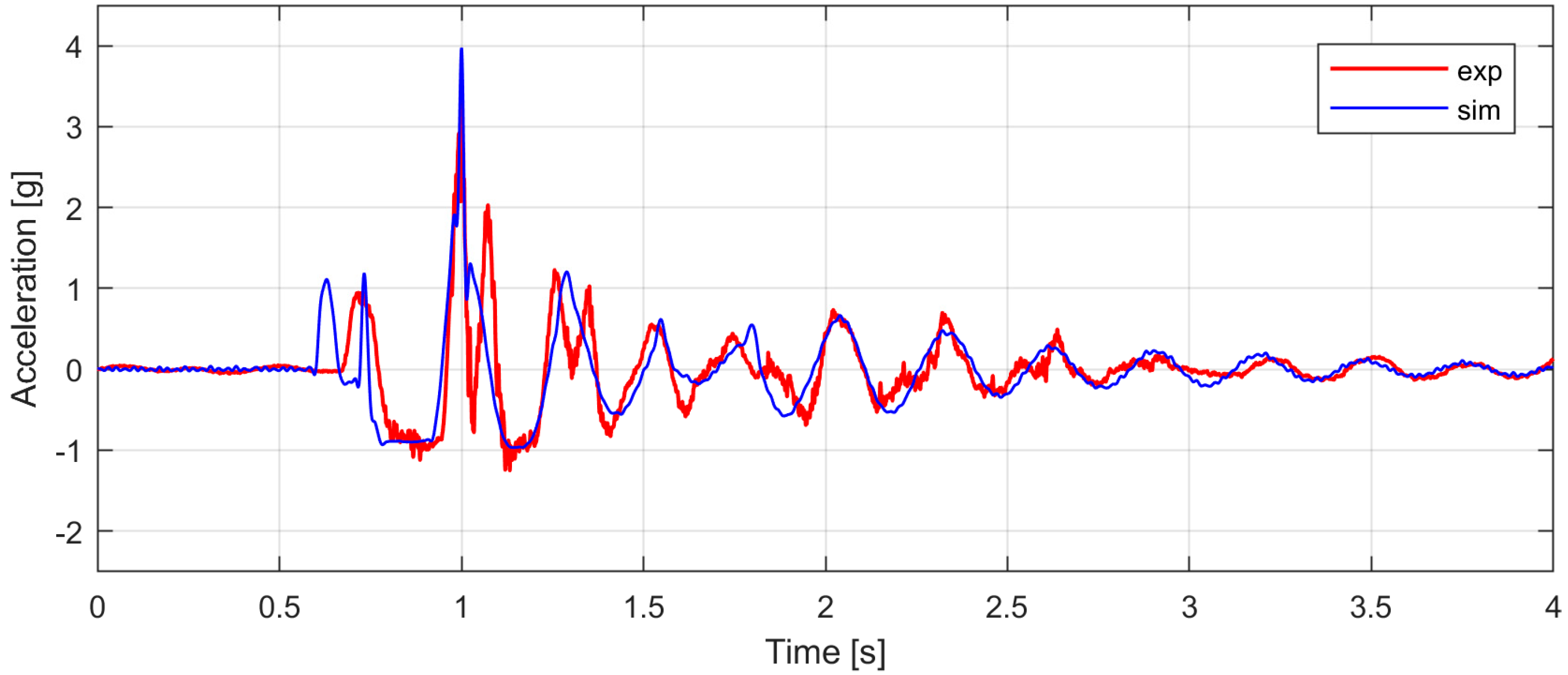
- A high acceleration peak (namely, the maximum value of the signal, referred to as ) occurs when the front wheels jump over the obstacle and rebound on the ground (time 1.00 s).
- Two lift-off phases are apparently present before and after the main rebound, respectively. Indeed, an almost constant acceleration of −1 g can be observed (except for minor oscillation at high frequency), reasonably indicating that the front axle is undergoing free fall (it is worth recalling that the gravitational component has been subtracted from the signals).
- The rear wheels impact on the obstacle with a delay of about 0.75 s. This event generates a second remarkable peak at time 2.02 s (referred to as ).
- Oscillations are present over the whole time history; the first collision with the obstacle causes their amplitude to increase sizably.
- The accelerations of the front wheels are always in phase;
- The accelerations of the rear wheels are always in phase as well;
- After the first impact with the obstacle, the signals of the front and the rear wheels are in antiphase for a longer time interval.
4. Numerical Model and Simulations
4.1. Model Implementation
- The static equilibrium of the forklift lying on the ground in steady state is solved.
- The vehicle natural frequencies and vibration modes are determined through linearization of the system around the static equilibrium configuration computed at the previous step.
- Inverse dynamics simulation is carried out by starting from the static equilibrium condition computed at step 1. The forklift is driven from null velocity to a constant forward speed of 11 km/h by defining analytical laws of motion for the front wheels (namely cubic polynomial velocity functions). Then, after a proper time interval to let transient phenomena dampen, the vehicle crosses over the obstacle. The steering angle on the rear wheels is kept constantly equal to zero during the simulations. Hence, the simulated conditions replicate the experimental ones.
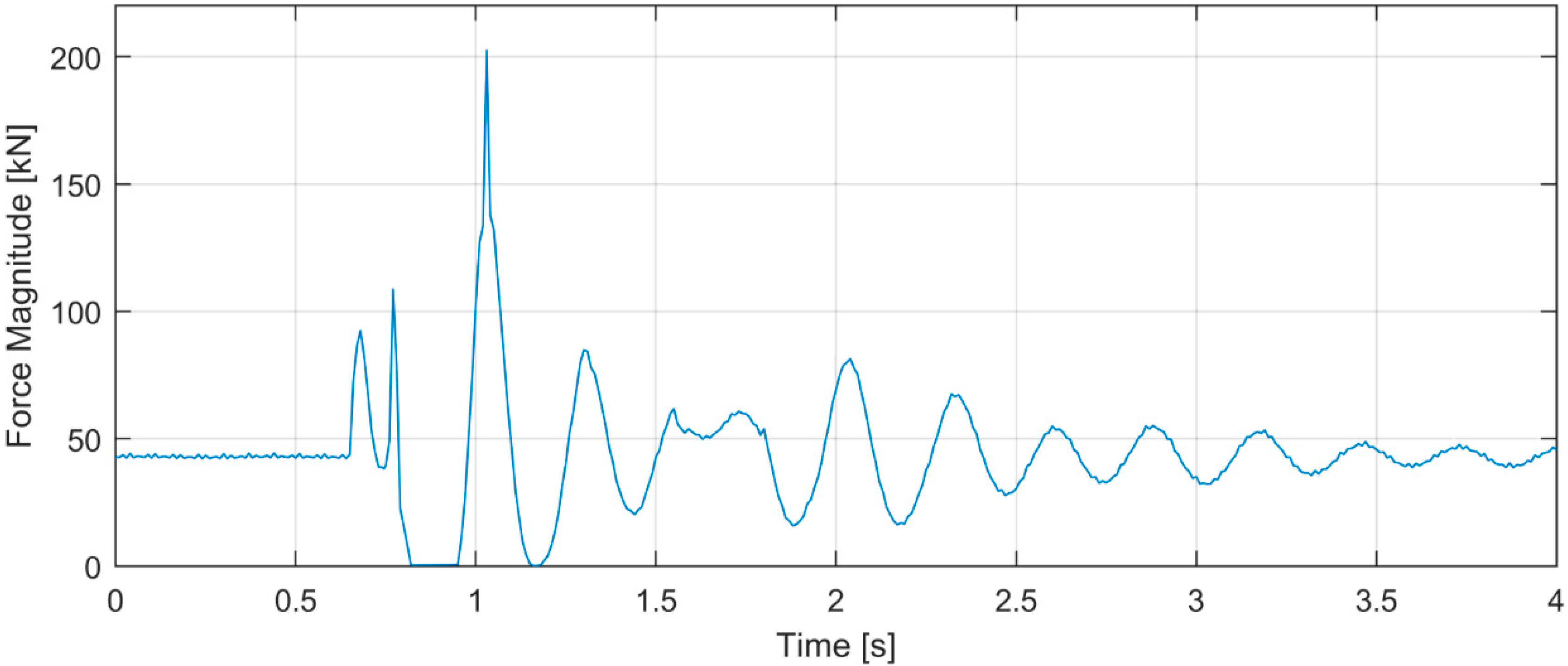
4.2. Model Validation and Results Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Industrial Truck Association. Lifting America—The Economic Impact of Industrial Truck Manufacturers, Distributors and Dealers. Available online: https://www.oxfordeconomics.com/recent-releases/lifting-america (accessed on 12 March 2020).
- Cao, D.; Song, X.; Ahmadian, M. Editors’ perspectives: Road vehicle suspension design, dynamics, and control. Veh. Syst. Dyn. 2011, 49, 3–28. [Google Scholar] [CrossRef]
- Azraai, M.R.; Priyandoko, G.; Yusoff, A.R.; Rashid, M.F.F.A. Parametric optimization of magneto-rheological fluid damper using particle swarm optimization. Int. J. Automot. Mech. Eng. 2015, 11, 2591–2599. [Google Scholar] [CrossRef]
- Martini, A.; Bellani, G.; Fragassa, C. Numerical assessment of a new hydro-pneumatic suspension system for motorcycles. Int. J. Automot. Mech. Eng. 2018, 15, 5308–5325. [Google Scholar] [CrossRef]
- Rebelle, J.; Mistrot, P.; Poirot, R. Development and validation of a numerical model for predicting forklift truck tip-over. Veh. Syst. Dyn. 2009, 47, 771–804. [Google Scholar] [CrossRef]
- Larsson, T.J.; Oldertz, C. Hazardous Exposures and Injury Types Associated with the Use of Industrial Lift Trucks in Sweden 2005–2007. Available online: http://www.diva-portal.org/smash/get/diva2:433870/FULLTEXT01.pdf (accessed on 13 May 2020).
- Saric, S.; Bab-Hadiashar, A.; Hoseinnezhad, R.; Hocking, I. Analysis of forklift accident trends within Victorian industry (Australia). Saf. Sci. 2013, 60, 176–184. [Google Scholar] [CrossRef]
- Yang, M.; Xu, G.; Dong, Q.; Han, X. Vibration study of fork-lift truck based on the virtual prototype technology. Sens. Transducers 2014, 170, 177–183. [Google Scholar]
- Strandberg, L. Danger, rear wheel steering. J. Occup. Accid. 1983, 5, 39–58. [Google Scholar] [CrossRef]
- Frazer-Nash Consultancy Limited. Fork Lift Truck Validation and Trials. Available online: http://www.hse.gov.uk/research/rrhtm/rr456.htm (accessed on 12 March 2020).
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Popescu, S.; Nastase, S.; Csatlos, C. Contributions to theoretical and experimental study of the dynamic stability of the forklift trucks. J. Eng. Stud. Res. 2012, 18, 115–121. [Google Scholar]
- International Organization for Standardization. Industrial Trucks—Verification of Stability—Part 2: Counterbalanced Trucks with Mast; Standard ISO 22915-2; International Organization for Standardization: Geneva, Switzerland, 2018. [Google Scholar]
- Milanowicz, M.; Budziszewski, P.; Kedzior, K. Numerical analysis of passive safety systems in forklift trucks. Saf. Sci. 2018, 101, 98–107. [Google Scholar] [CrossRef]
- Gardella, M.; Martini, A. Multibody models and simulations to assess the stability of counterbalance forklift trucks. In Multibody Dynamics 2019—ECCOMAS 2019. Computational Methods in Applied Sciences; Kecskeméthy, A., Geu Flores, F., Eds.; Springer: Cham, Switzerland, 2020; Volume 53, pp. 526–533. [Google Scholar]
- Larsson, T.J.; Lambert, J.; Wilde, M.; Tully, G.; Askew, H.; Skinner, W.; Carter, B.; Martin, T.; Kenningham, L. Industrial Forklift Trucks-Dynamic Stability and the Design of Safe Logistics. Available online: http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A430110&dswid=-6079 (accessed on 13 May 2020).
- International Organization for Standardization. Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration-Part 1: General Requirements; Standard ISO 2631-1; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Malchaire, J.; Piette, A.; Mullier, I. Vibration exposure on fork-lift trucks. Ann. Occup. Hyg. 1996, 40, 79–91. [Google Scholar] [CrossRef]
- Lemerle, P.; Mistrot, P. A new tire model to predict vibration emission of counterbalance trucks. Tire Sci. Technol. 2000, 28, 119–137. [Google Scholar] [CrossRef]
- De Man, P.; Lemerle, P.; Mistrot, P.; Verschueren, J.-P.; Preumont, A. An investigation of a semiactive suspension for a fork lift truck. Veh. Syst. Dyn. 2005, 43, 107–119. [Google Scholar] [CrossRef]
- Doçi, I.; Bajraktari, M.; Imeri, V. Studying Dynamic Effects on Warehouse Forklift During Forward Movement with Full Loading. In Proceedings of the 16th International Research/Expert Conference Trends in the Development of Machinery and Associated Technology-TMT 2012, Dubai, UAE, 10–12 September 2012. [Google Scholar]
- Doçi, I.; Imeri, V. Dynamic analysis of forklift during load lifting using modeling and simulations. Int. J. Curr. Eng. Technol. 2013, 3, 342–347. [Google Scholar]
- Martini, A.; Troncossi, M. Upgrade of an automated line for plastic cap manufacture based on experimental vibration analysis. Case Stud. Mech. Syst. Signal Process. 2016, 3, 28–33. [Google Scholar] [CrossRef]
- Challener, S.A.; Wylie, A.F. Development of Theoretical Model for Simulating FLT Overturn-Rate of Steering Response-Fixed Geometry Vehicle; Health and Safety Executive Research Report 291; HSE Books: Sudbury, UK, 2004. [Google Scholar]
- Stepanyuk, S.; Bruns, R.; Krivenkov, K. Empirical lateral-force-model for forklift tires. Logist. Res. 2017, 10, 1–12. [Google Scholar]
- Gipser, M. FTire—The tire simulation model for all applications related to vehicle dynamics. Veh. Syst. Dyn. 2007, 45, 139–151. [Google Scholar] [CrossRef]
- MSC Software Corporation. Adams/Solver: Software User Manual; MSC Software Corporation: Newport Beach, CA, USA, 2009. [Google Scholar]



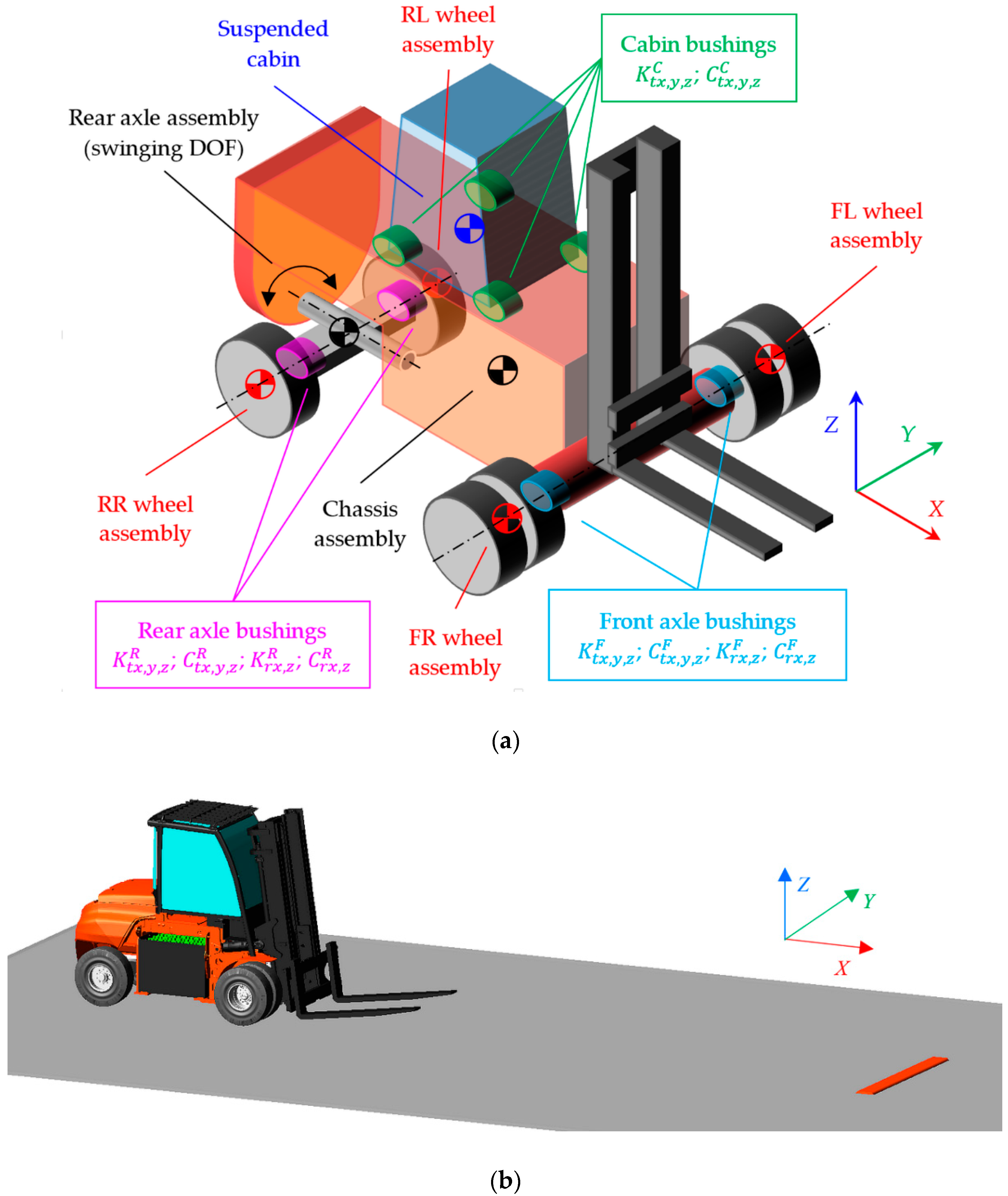
| Parameter | Value | Unit |
|---|---|---|
| overall mass (with operator) 1 | 17,280 | kg |
| front | rear mass distribution (unloaded) 1 | 9355 | 7925 | kg |
| load capacity | 8000 | kg |
| battery mass 1 | 2824 | kg |
| cabin mass 1 | 497 | kg |
| wheelbase | 2300 | mm |
| lift height | 3300 | mm |
| turning radius | 3207 | mm |
| overall width | 2141 | mm |
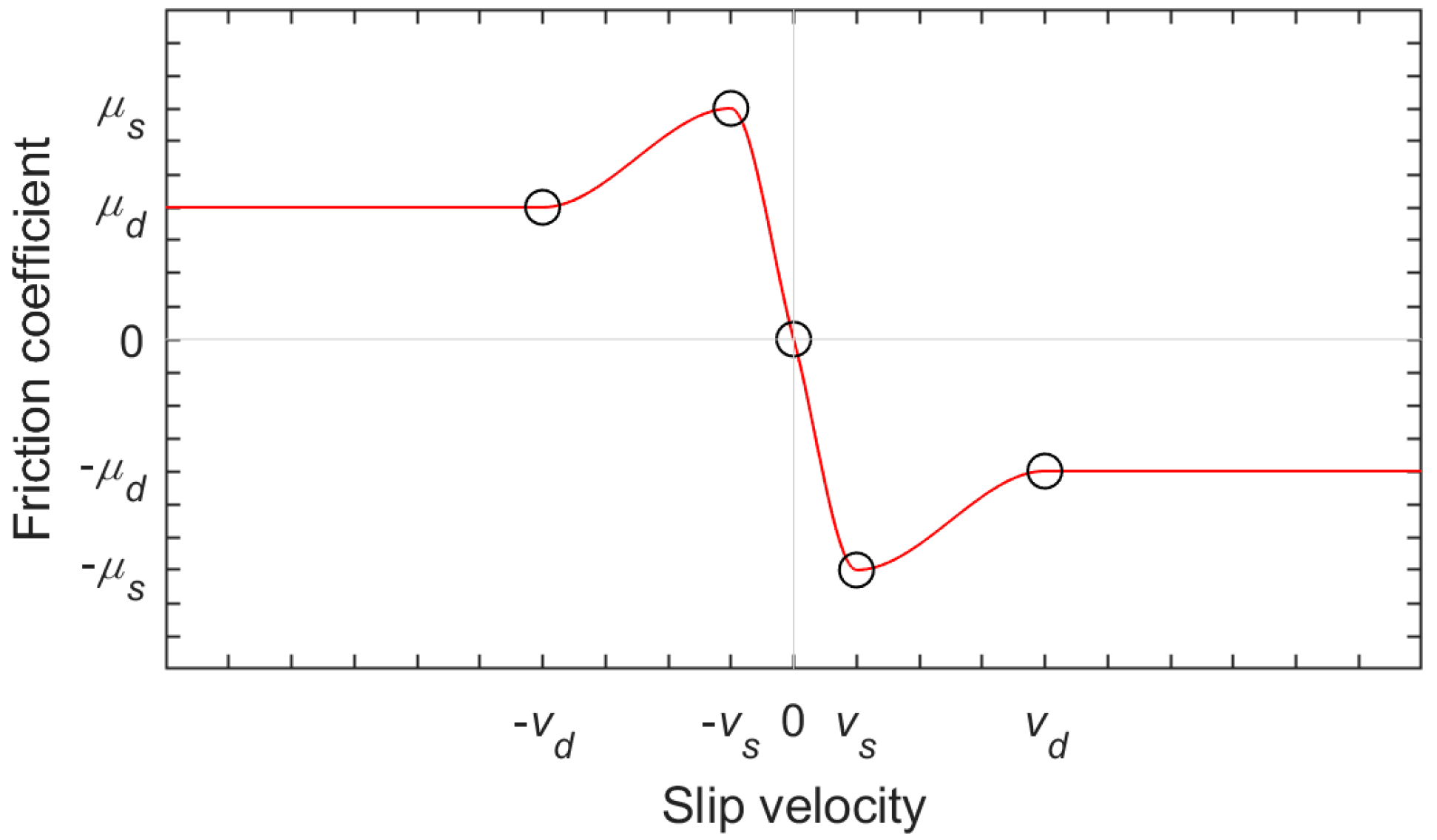
| Contact | KTR [N/m] | Cmax [N·s/m] | m | μs | μd |
|---|---|---|---|---|---|
| tire-road, front | 6.0·106 | 5.0·103 | 1.5 | 0.6 | 0.5 |
| tire-road, rear | 6.0·106 | 5.0·103 | 1.5 | 0.6 | 0.5 |
| tire-obstacle, front | 4.0·106 | 7.5·103 | 1.5 | 1.0 | 0.8 |
| tire-obstacle, rear | 7.2·106 | 7.5·103 | 1.5 | 1.0 | 0.8 |
| Linear Bushing 1 | [N/m] | [N/m] | [N/m] | [N·s/m] | [N·s/m] | [N·s/m] | [Nm/rad] | [Nm·s/rad] |
|---|---|---|---|---|---|---|---|---|
| front axle | 7.8·107 | 9.1·108 | 7.8·107 | 5.0·105 | 5.8·106 | 5.0·105 | 2.3·1010 | 5.7·105 |
| rear axle | 2.5·107 | 3.0·108 | 2.5·107 | 1.7·105 | 1.9·106 | 1.7·105 | 5.0·109 | 1.3·105 |
| cabin | 1.4·106 | 1.4·106 | 4.8·105 | 1.0·104 | 1.0·104 | 5.0·103 | – | – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martini, A.; Bonelli, G.P.; Rivola, A. Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model. Machines 2020, 8, 26. https://doi.org/10.3390/machines8020026
Martini A, Bonelli GP, Rivola A. Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model. Machines. 2020; 8(2):26. https://doi.org/10.3390/machines8020026
Chicago/Turabian StyleMartini, Alberto, Giovanni Paolo Bonelli, and Alessandro Rivola. 2020. "Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model" Machines 8, no. 2: 26. https://doi.org/10.3390/machines8020026
APA StyleMartini, A., Bonelli, G. P., & Rivola, A. (2020). Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model. Machines, 8(2), 26. https://doi.org/10.3390/machines8020026





