Comparative Machine-Learning Approach: A Follow-Up Study on Type 2 Diabetes Predictions by Cross-Validation Methods
Abstract
1. Introduction
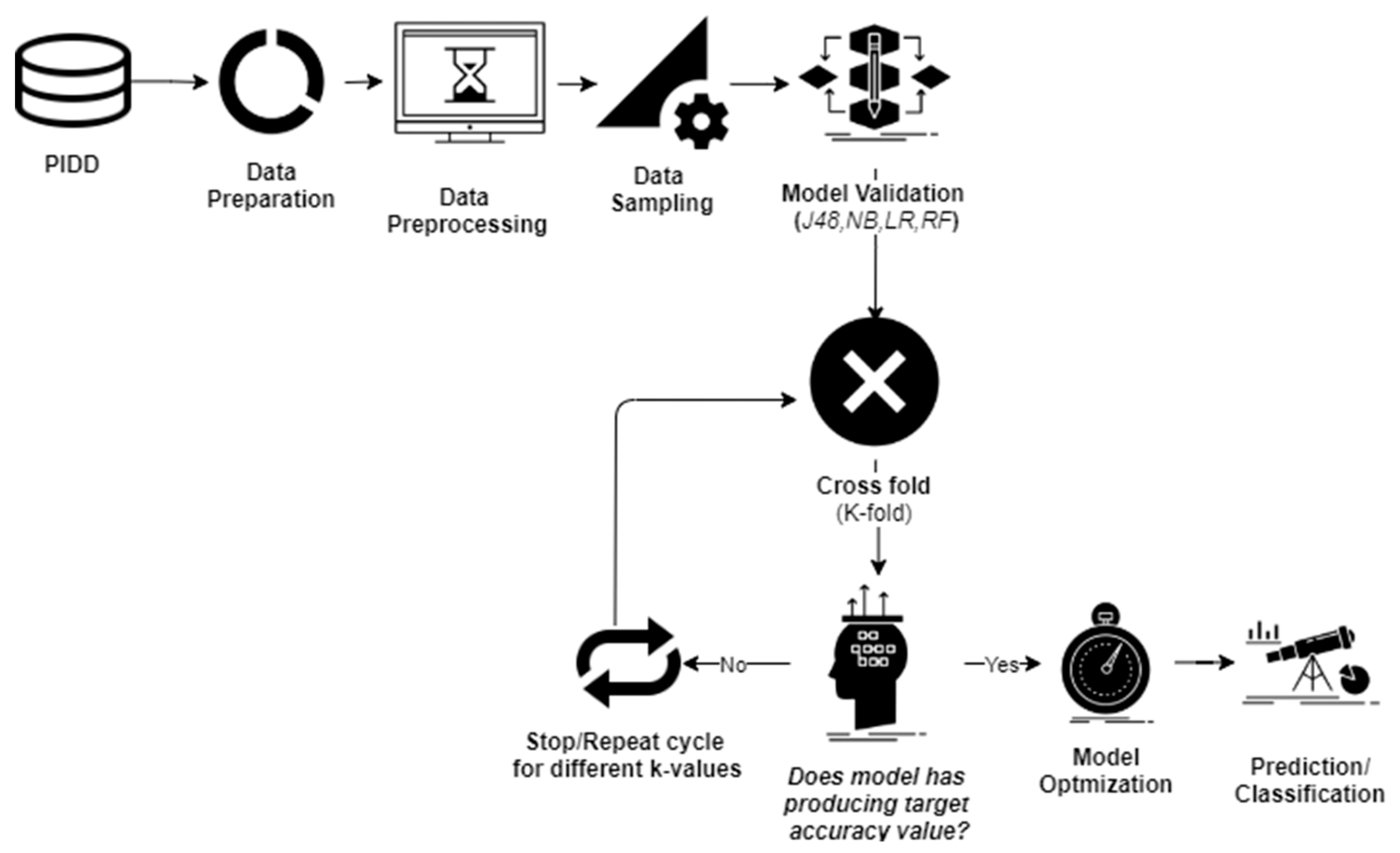
2. Methods and Materials
2.1. Data Sampling
2.2. Cross-Validation
2.3. Naïve Bayes (NB)
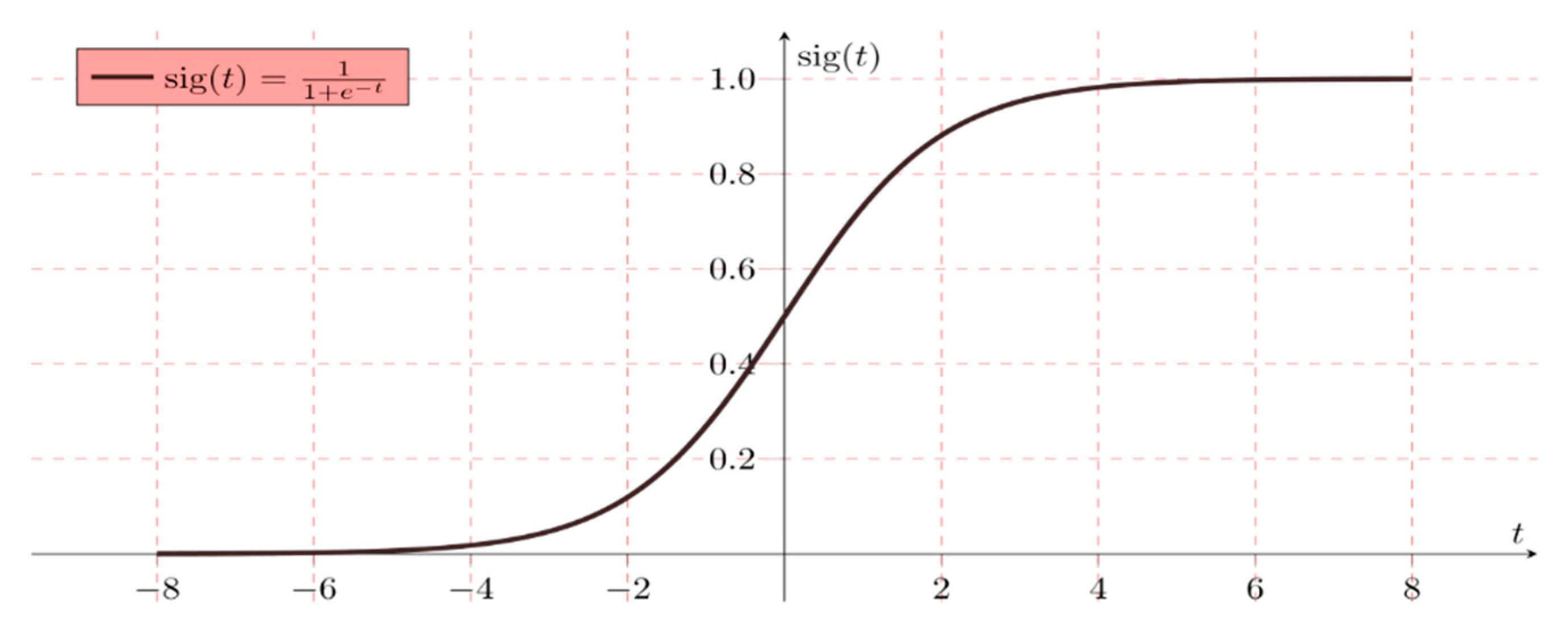
2.4. Logistic Regression (LR)
2.5. Random Forest (RF)
2.6. J48 (Decision Tree Algorithm)
2.7. Performance Measures
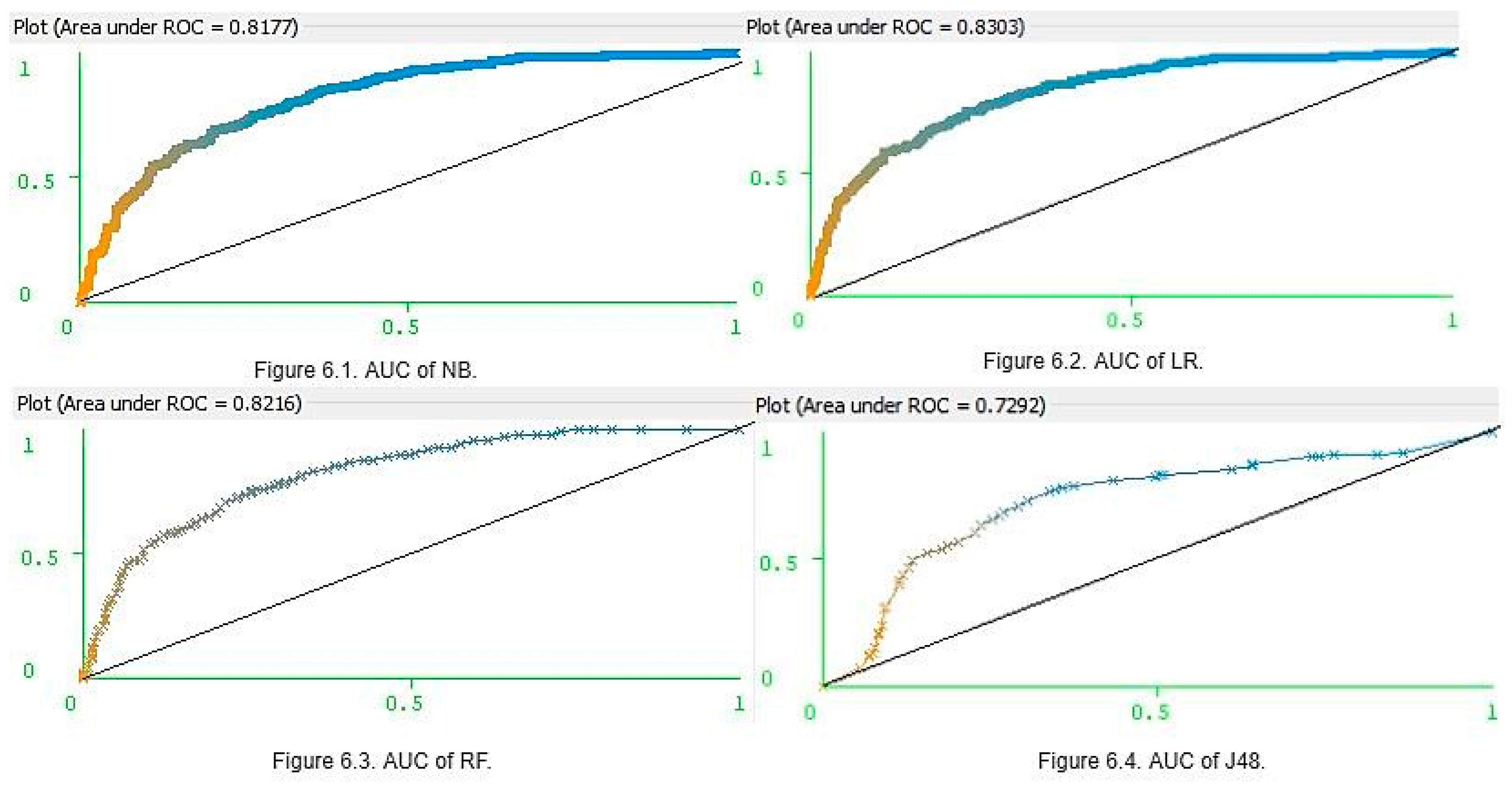
3. Results
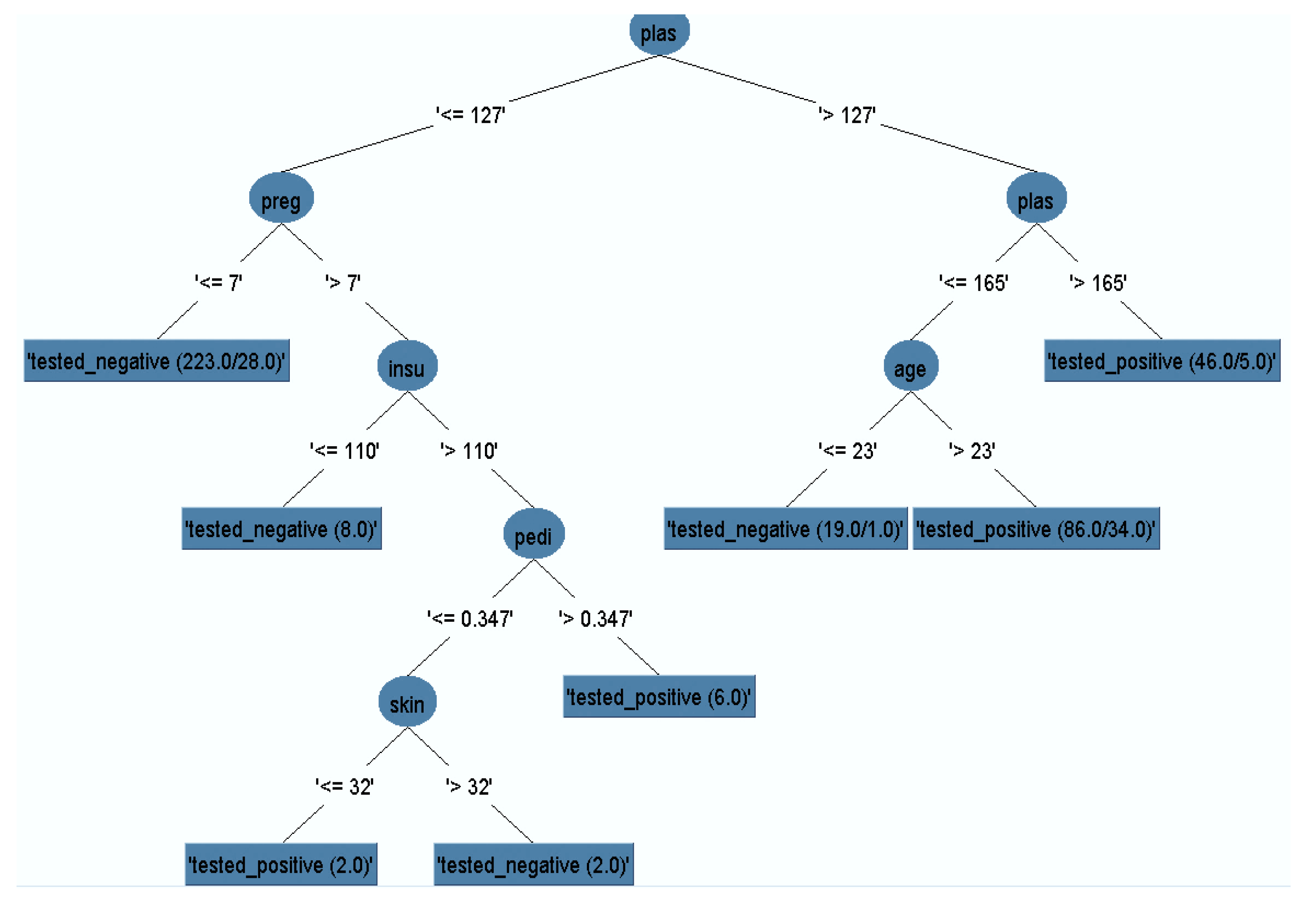
3.1. Pruned Decision Tree
3.2. Confusion Matrix
3.3. Model Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seshasai, S.R.K.; Kaptoge, S.; Thompson, A.; Di Angelantonio, E.; Gao, P.; Sarwar, N.; Whincup, P.H.; Mukamal, K.J.; Gillum, R.F.; Holme, I.; et al. Diabetes mellitus, fasting glucose, and risk of cause-specific death. N. Engl. J. Med. 2011, 364, 829–841. [Google Scholar]
- Chatterjee, S.; Khunti, K.; Davies, M.J. Type 2 diabetes. Lancet 2017, 389, 2239–2251. [Google Scholar] [CrossRef]
- Kaur, H.; Kumari, V. Predictive modelling and analytics for diabetes using a machine learning approach. Appl. Comput. Inform. 2018, in press. [Google Scholar] [CrossRef]
- Baştanlar, Y.; Özuysal, M. Introduction to Machine Learning. In miRNomics: MicroRNA Biology and Computational Analysis; Humana Press: Totowa, NJ, USA, 2014. [Google Scholar]
- Battineni, G.; Chintalapudi, N.; Amenta, F. Machine learning in medicine: Performance calculation of dementia prediction by support vector machines (SVM). Inform. Med. Unlocked 2019, 16, 100200. [Google Scholar] [CrossRef]
- Rajkomar, A.; Dean, J.; Kohane, I. Machine learning in medicine. N. Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef]
- Methods, D.P. Data Preprocessing Techniques for Data Mining. Science 2011, 80, 80–120. [Google Scholar]
- Cawley, G.C.; Talbot, N.L.C. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Mathotaarachchi, S.; Pascoal, T.A.; Shin, M.; Benedet, A.L.; Kang, M.S.; Beaudry, T.; Fonov, V.S.; Gauthier, S.; Rosa-Neto, P. Identifying incipient dementia individuals using machine learning and amyloid imaging. Neurobiol. Aging 2017, 59, 80–90. [Google Scholar] [CrossRef]
- Parmar, C.; Grossmann, P.; Rietveld, D.; Rietbergen, M.M.; Lambin, P.; Aerts, H.J.W.L. Radiomic machine-learning classifiers for prognostic biomarkers of head and neck cancer. Front. Oncol. 2015, 5, 272. [Google Scholar] [CrossRef]
- Nirala, N.; Periyasamy, R.; Singh, B.K.; Kumar, A. Detection of type-2 diabetes using characteristics of toe photoplethysmogram by applying support vector machine. Biocybern. Biomed. Eng. 2019, 39, 38–51. [Google Scholar] [CrossRef]
- Giger, M.L. Machine Learning in Medical Imaging. J. Am. Coll. Radiol. 2018, 15, 512–520. [Google Scholar] [CrossRef] [PubMed]
- Forouhi, N.G.; Wareham, N.J. Epidemiology of diabetes. Medicine 2010, 38, 602–606. [Google Scholar] [CrossRef]
- Forouhi, N.G.; Misra, A.; Mohan, V.; Taylor, R.; Yancy, W. Dietary and nutritional approaches for prevention and management of type 2 diabetes. BMJ 2018, 361, k2234. [Google Scholar] [CrossRef] [PubMed]
- Barakat, N.; Bradley, A.P.; Barakat, M.N.H. Intelligible support vector machines for diagnosis of diabetes mellitus. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1114–1120. [Google Scholar] [CrossRef]
- Zou, Q.; Qu, K.; Luo, Y.; Yin, D.; Ju, Y.; Tang, H. Predicting Diabetes Mellitus With Machine Learning Techniques. Front. Genet. 2018, 9, 1–10. [Google Scholar] [CrossRef]
- Sisodia, D.; Sisodia, D.S. Prediction of Diabetes using Classification Algorithms. Procedia Comput. Sci. 2018, 132, 1578–1585. [Google Scholar] [CrossRef]
- Wei, S.; Zhao, X.; Miao, C. A comprehensive exploration to the machine learning techniques for diabetes identification. In Proceedings of the 2018 IEEE 4th World Forum on Internet of Things (WF-IoT), Singapore, 5–8 February 2018. [Google Scholar]
- Frank, E.; Hall, M.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Workbench Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: New York, NY, USA, 2016. [Google Scholar]
- Watanabe, S. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Patil, T.R.; Sherekar, S.S. Performance Analysis of Naive Bayes and J48 Classification Algorithm for Data Classification. Int. J. Comput. Sci. Appl. 2013, 6, 256–261. [Google Scholar]
- Schein, A.I.; Ungar, L.H. Active learning for logistic regression: An evaluation. Mach. Learn. 2007, 68, 235–265. [Google Scholar] [CrossRef]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed]
- Tsang, S.; Kao, B.; Yip, K.Y.; Ho, W.S.; Lee, S.D. Decision trees for uncertain data. IEEE Trans. Knowl. Data Eng. 2011, 23, 64–78. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Lingenfelter, D.J.; Fessler, J.A.; Scott, C.D.; He, Z. Predicting ROC curves for source detection under model mismatch. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Knoxville, TN, USA, 30 October–6 November 2010. [Google Scholar]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]

| Attribute Number | Risk Factor | Acronym | Variable Type | Range (Min-Max) |
|---|---|---|---|---|
| 1 | Number of times pregnant | Preg | Integer | 0–17 |
| 2 | Plasma glucose concentration a 2 h in an oral glucose tolerance test | Plus | Integer | 44–199 |
| 3 | Diastolic blood pressure (mm Hg) | Pres | Integer | 24–122 |
| 4 | Triceps skinfold thickness (mm) | Skin | Integer | 7–99 |
| 5 | 2-Hour serum insulin (mu U/mL) | Insu | Integer | 14–846 |
| 6 | Body mass index (weight in kg/(height in m)^2) | Mass | Real | 18.2–67.1 |
| 7 | Diabetes pedigree function | Pedi | Real | 0.07–2.42 |
| 8 | Age (years) | Age | Integer | 21-81 |
| 9 | Class | - | Binary | 1-Tested Positive (268) 0-Tested Negative (500) |
| Statistics | Dataset | Preg | Plas | Pres | Skin | Insu | BMI | Pedi | Age |
|---|---|---|---|---|---|---|---|---|---|
| Count | Original | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 |
| Preprocess | 392 | 392 | 392 | 392 | 392 | 392 | 392 | 392 | |
| Under-sampling | 536 | 536 | 536 | 536 | 536 | 536 | 536 | 536 | |
| Oversampling | 1036 | 1036 | 1036 | 1036 | 1036 | 1036 | 1036 | 1036 | |
| Mean | Original | 3.84 | 121.6 | 72.40 | 29.15 | 155.54 | 32.45 | 0.472 | 33.241 |
| Preprocess | 3.301 | 122.62 | 70.66 | 29.14 | 156.05 | 33.08 | 0.523 | 30.86 | |
| Under-sampling | 4 | 126.228 | 69.095 | 20.403 | 84.981 | 32.553 | 0.488 | 33.944 | |
| Oversampling | 4.084 | 126.123 | 69.593 | 20.818 | 84.894 | 32.765 | 0.494 | 34.2 | |
| SD | Original | 3.37 | 30.43 | 12.09 | 8.79 | 85.02 | 6.87 | 0.331 | 11.76 |
| Preprocess | 3.211 | 30.86 | 12.49 | 10.51 | 118.84 | 7.028 | 0.345 | 10.201 | |
| Under-sampling | 3.464 | 33.335 | 20.378 | 16.515 | 124.84 | 7.877 | 0.351 | 11.684 | |
| Oversampling | 3.349 | 32.443 | 19.378 | 16.062 | 121.33 | 7.522 | 0.332 | 11.43 | |
| Min | Original | 0 | 0 | 0 | 0 | 0 | 0 | 0.07 | 21 |
| Preprocess | 0 | 56 | 24 | 7 | 14 | 18.2 | 0.085 | 21 | |
| Under-sampling | 0 | 0 | 0 | 0 | 0 | 0 | 0.078 | 21 | |
| Oversampling | 0 | 0 | 0 | 0 | 0 | 0 | 0.078 | 21 | |
| Max | Original | 17 | 199 | 122 | 99 | 846 | 67.1 | 2.42 | 81 |
| Preprocess | 17 | 198 | 110 | 63 | 846 | 67.1 | 2.42 | 81 | |
| Under-sampling | 17 | 199 | 114 | 99 | 846 | 67.1 | 2.42 | 81 | |
| Oversampling | 17 | 199 | 122 | 99 | 846 | 67.1 | 2.42 | 81 |
| Parameter | Definition | Formulation |
|---|---|---|
| Accuracy | Rate of correctly classified instances from total instances | |
| PRECISION (P) | Rate of correct predictions | |
| RECALL (R) | True positive rate | |
| F-Measure | Used to measure the accuracy of the experiment |
| A | B | <-- Classified as | Model |
|---|---|---|---|
| 427 | 73 | A = Tested negative | Naïve Bayes (NB) |
| 122 | 146 | B = Tested positive | |
| 450 | 50 | A = Tested negative | Logistic Regression (LR) |
| 129 | 139 | B = Tested positive | |
| 431 | 69 | A = Tested negative | Random Forest (RF) |
| 118 | 152 | B = Tested positive | |
| 427 | 73 | A = Tested negative | J48 |
| 122 | 146 | B = tested positive |
| N | Model | Tuning Parameters |
|---|---|---|
| 1 | J48 | C = 0.25 |
| 2 | NB | - |
| 3 | RF | Number of trees—100, Number of features to construct each tree—4, and out of bag error—0.237 |
| 4 | LR | R = 1.0E-8 |
| K | Classifier | Accuracy | Precision | Recall | F-Score | AUC |
|---|---|---|---|---|---|---|
| 5 | J48 | 0.71 | 0.71 | 0.71 | 0.71 | 0.72 |
| NB | 0.76 | 0.76 | 0.76 | 0.76 | 0.81 | |
| RF | 0.75 | 0.75 | 0.75 | 0.75 | 0.82 | |
| LR | 0.77 | 0.77 | 0.77 | 0.76 | 0.83 | |
| 10 | J48 | 0.73 | 0.73 | 0.73 | 0.73 | 0.75 |
| NB | 0.76 | 0.75 | 0.76 | 0.76 | 0.81 | |
| RF | 0.74 | 0.74 | 0.74 | 0.74 | 0.81 | |
| LR | 0.77 | 0.76 | 0.77 | 0.76 | 0.83 | |
| 15 | J48 | 0.76 | 0.75 | 0.76 | 0.76 | 0.74 |
| NB | 0.76 | 0.75 | 0.76 | 0.75 | 0.81 | |
| RF | 0.76 | 0.76 | 0.76 | 0.76 | 0.82 | |
| LR | 0.77 | 0.77 | 0.77 | 0.76 | 0.83 | |
| 20 | J48 | 0.75 | 0.74 | 0.75 | 0.74 | 0.74 |
| NB | 0.76 | 0.75 | 0.76 | 0.75 | 0.81 | |
| RF | 0.75 | 0.74 | 0.75 | 0.74 | 0.82 | |
| LR | 0.77 | 0.77 | 0.77 | 0.76 | 0.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battineni, G.; Sagaro, G.G.; Nalini, C.; Amenta, F.; Tayebati, S.K. Comparative Machine-Learning Approach: A Follow-Up Study on Type 2 Diabetes Predictions by Cross-Validation Methods. Machines 2019, 7, 74. https://doi.org/10.3390/machines7040074
Battineni G, Sagaro GG, Nalini C, Amenta F, Tayebati SK. Comparative Machine-Learning Approach: A Follow-Up Study on Type 2 Diabetes Predictions by Cross-Validation Methods. Machines. 2019; 7(4):74. https://doi.org/10.3390/machines7040074
Chicago/Turabian StyleBattineni, Gopi, Getu Gamo Sagaro, Chintalapudi Nalini, Francesco Amenta, and Seyed Khosrow Tayebati. 2019. "Comparative Machine-Learning Approach: A Follow-Up Study on Type 2 Diabetes Predictions by Cross-Validation Methods" Machines 7, no. 4: 74. https://doi.org/10.3390/machines7040074
APA StyleBattineni, G., Sagaro, G. G., Nalini, C., Amenta, F., & Tayebati, S. K. (2019). Comparative Machine-Learning Approach: A Follow-Up Study on Type 2 Diabetes Predictions by Cross-Validation Methods. Machines, 7(4), 74. https://doi.org/10.3390/machines7040074









