1. Introduction
Chip removal processes are still crucial for the manufacturing sector since they are able to reach a high accuracy, productivity, and versatility. Thanks to efforts on improving machining processes, it is possible to obtain high quality components even with hard-to-cut materials thanks to the use of high-performance tool materials such as PCBN (Polycrystalline Cubic Boron Nitride), as reported by Pan and Li [
1,
2] for turning hardened bearing steel GCr15. At present, the most crucial aspects that limit machining process performance are related to the flexibility of the elements that make up the cutting system. Therefore, the most critical operations are the ones that involve the use of slender tools or thin-walled workpieces. From a static point of view, the forces that the workpiece and the tool exchange during the cutting process may cause relative displacements between them, resulting in geometrical errors [
3,
4,
5]. In order to reduce these, strategies to compensate the relative displacement by modifying the toolpath were developed both in real time [
6] and offline [
7].
The most important dynamic issue is the onset of unstable vibrations (i.e., chatter [
8]) that compromise workpiece surface quality and drastically reduce tool life. One of the most interesting results for chatter prediction is represented by the estimation of a stability lobe diagram (SLD) [
9] that shows the stability region in terms of cutting velocity and depth of cut values that ensure stable machining. SLDs may be predicted using different models [
9] and can be used to select cutting parameters that can maximize productivity while guaranteeing stability.
Estimating the static and dynamic behavior of tool and workpiece (i.e., relative frequency response functions) is essential in order to obtain the aforementioned results, and this is particularly critical in the case of thin-wall component machining where workpiece behavior changes during machining due to local stiffness and material removal [
10,
11,
12]. In such cases, many authors use the simulation as the best approach to predict and improve the process [
13]. In addition, different approaches for cutting parameter selection [
14] and toolpath optimization [
15] have been developed using Finite Element (FE) solvers to take into account the effects of workpiece static and dynamic variation during the chip removal process. However, the workpiece high compliance stability area may be very limited, which compromises the maximum productivity rate.
In such cases, the most effective way to guarantee the required tolerances and surface quality is to improve workpiece response. In particular, since the fixturing system has been demonstrated to have a great impact on workpiece response [
16],part of the research was focused on the development of a fixturing framework able to significantly improve workpiece response. These approaches include both optimization strategies for optimal fixturing and support point placing and the development of active fixturing systems [
17]. Due to the rotational workpiece in the turning process, the use of active fixtures that require external power can be very complicated. For this reason, a strategy for support optimization is more promising. Thanks to the spread of modeling techniques for the chip removal process, in the last few decades, several computer aided fixture design (CAFD) approaches have been presented [
18,
19]. These integrate a streamlined approach that includes process modeling and optimization algorithms and several strategies to optimize fixtures. Some of these approaches are aimed at finding the fixturing configuration that allows the minimization of geometrical errors [
20,
21] and the evaluation of the effects of additional supports [
22,
23,
24]. Clamping systems also affect workpiece dynamics [
25] and additional supports may have a mitigating effect on chatter onset [
26,
27]. Fixture design in turning must also consider the necessity of an axisymmetric framework for the fixturing system in order to avoid unbalances during workpiece rotation.
In this paper, a new fixture design methodology for thin-wall component turning is presented. By means of an integration of models for geometrical error and chatter stability prediction, an additional support configuration that guarantees both the required tolerances and stability, while minimizing the fixture system complexity, is found. The proposed method can be easily adapted to different cutting conditions, whose change is required for a preliminary optimization of the process [
28], and workpiece geometries. In this paper, a numerical example for an Inconel 718 external finishing turning is presented using the MSC Nastran
® FE solver.
2. Geometrical Errors and Chatter Onset Prediction
Diametral error is the difference between the nominal and the real diameter of a machined component, and it is due to the difference between the nominal and real relative positions between tool and component in relation to the cutting area during the turning process. In the case of thin-walled component machining, that difference is mainly due to workpiece local deformations caused by clamping forces, cutting forces, and thermal aspects. In order to take into account both static and thermal aspects, an FE approach for geometrical error prediction was proposed by Izamshah [
29]. In this work, only the contribution given by workpiece static deflection (i.e., the most compliant element of the cutting system) under cutting force was considered. According to the approach proposed by Polini and Prisco [
30], the cutting area is assumed to be point-like, and in correlation with it, both workpiece stiffness and cutting forces are estimated in order to predict geometrical error. Since static and dynamic workpiece behavior changes along the toolpath, this procedure must be repeated for all of the tool positions. Concerning workpiece stiffness computation, the finite element method (FEM) represents the best compromise between functional requirements (i.e., adaptability to different geometries, ease of implementation, and computational costs) and accuracy. In particular, in the case of thin parts, two-dimensional shell elements can be used proficiently. Actually, the material removal process can be easily implemented in shell elements just by modifying element thickness according to the local real depth of cut. Moreover, the computational effort required to perform the FE analysis is lower, due to the reduced degree of freedoms of the model. Therefore, several simulations in different load conditions and constraints may be carried out, and different configurations may be easily compared.
In the case of axial symmetric components, as in the case of the turning processes, the generation of the FE model can be easily automatized, starting from a workpiece two-dimensional draft, without the need of pre-post FE software. A Matlab® code has been realized that is able to extract the midline and local thickness (see
Figure 1), starting from the two-dimensional workpiece CAD section (exported in .dxf standard format).
For the sake of simplicity, workpiece in this work is considered fully constrained (all degrees of freedom blocked) in the clamping area (near to the spindle) and subjected to cutting forces. The presence of additional supports was modeled considering CGAP elements in order to realize unilateral constraints, taking into account the local stiffness provided by the additional clamping elements.
For the evaluation of the cutting forces, in this study, the empirical model proposed by Yao et al. [
31] for Inconel 718 was used (Equation (1)). By means of the following relations, cutting forces may be predicted, given the cutting parameters (i.e., radial depth of cut
ap, feed per revolution
f and spindle speed
vc):
However, the dependence of cutting forces on the radial depth of cut is crucial in case of compliant parts, since part deflection may produce a real depth of cut (apR) which is significantly different from the nominal ones (apN). Therefore, local workpiece deflection prediction is included in the estimation of the cutting force.
Chatter stability models [
32] allow predicting if machining is stable for given cutting parameters, knowing the relative frequency response functions (FRFs) between workpiece and tool in correspondence of cutting point (i.e., workpiece FRFs, in cases of thin-wall components). In the finishing operation, due to the small depth of cut, the cutting tool geometry deeply influences machining stability. For this reason, the model by Eynian et al. [
33] was used in this work.
Since workpiece FRF varies along the toolpath and is influenced by material removal, as well as in the static case, workpiece dynamics is predicted by means of the FE approach.
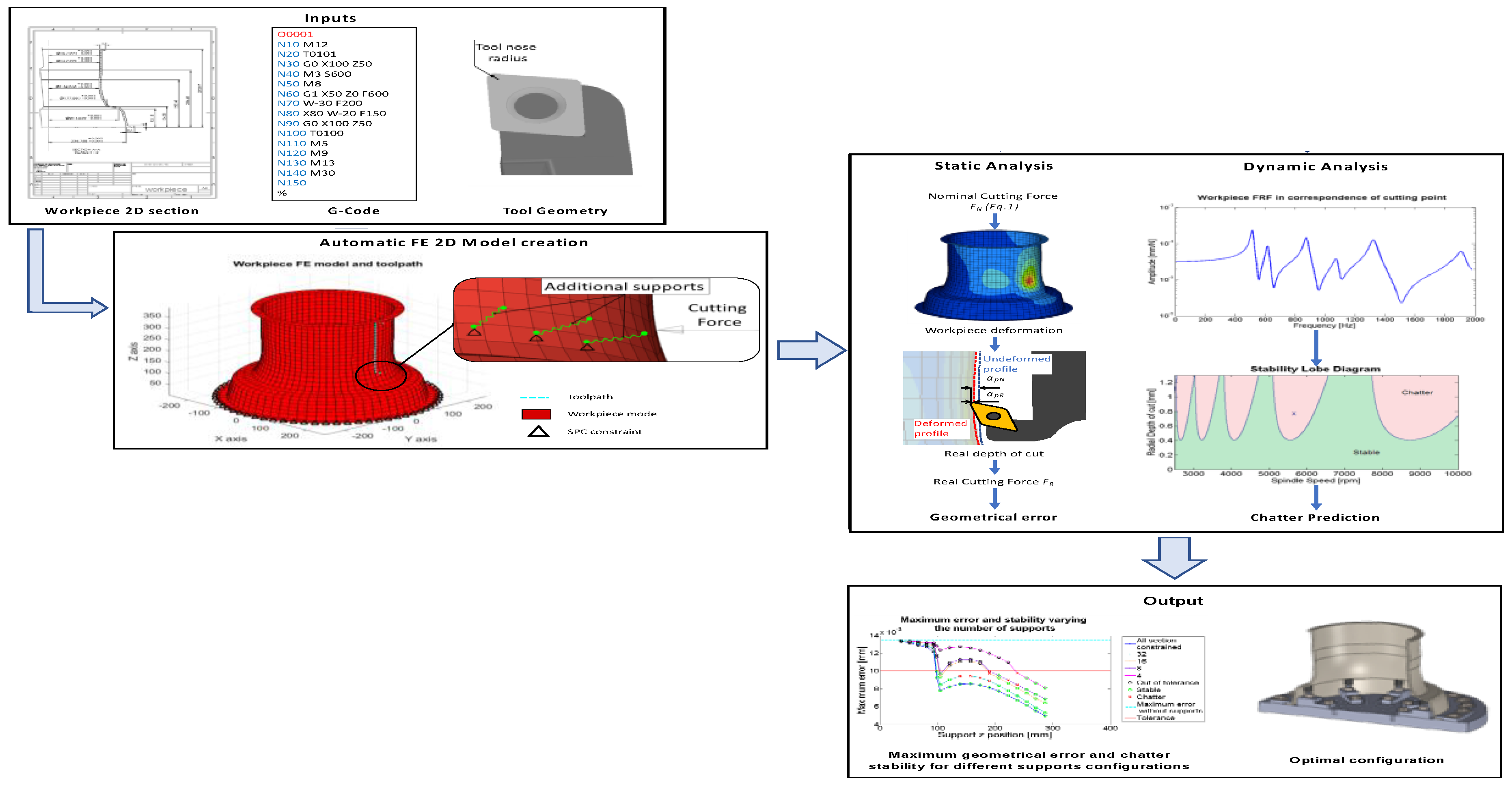
3. Proposed Methodology
The proposed methodology, schematized in
Figure 1, aims at finding an optimal fixture configuration that allows guaranteeing both tolerances required and dynamically stable machining, for a given toolpath: Just the last machining step (i.e., the finishing process) is considered. A Matlab
® code was implemented for this purpose.
The required input data are: stock midline and thickness, the G-Code produced by the CAM software, tolerance required, and tool geometry. In addition, information on zones in which supports cannot be mounted may be provided. The FE model is automatically generated from the stock geometry, while the toolpath is extracted by the G–code.
A preliminary analysis was carried out without considering additional supports: For each node laying on the toolpath, the geometrical error and chatter stability were predicted, and the FE model was updated in order to consider material removal. In cases where at least one requirement is not satisfied in any point, the algorithm proceeds to find optimal support configuration following a two-step approach.
First, a selection of possible configurations is carried out. Geometrical errors and chatter onset are predicted varying support position along the z-axis. CGap elements are placed in correspondence of all nodes laying on each given z-axis position to simulate the presence of a continuum annular support. Only configurations that guarantee both tolerances required and chatter stability along the toolpath are considered in the second step, where the number of supports is gradually decreased. As a result, for each axial position of the supports, the minimum number of additional supports can be found. Based on the obtained results, the optimal fixture position can be chosen as the most effective in terms of costs and easiness of mounting.
4. Numerical Example
In order to numerically validate the entire procedure, the presented algorithm was applied to evaluate the optimal fixturing configuration for a finishing turning operation of an Inconel 718 component, performed on a vertical lathe using a CNMG 12 04 08-23 1105 cutting insert. Material, additional supports, and cutting parameters are summarized in
Table 1.
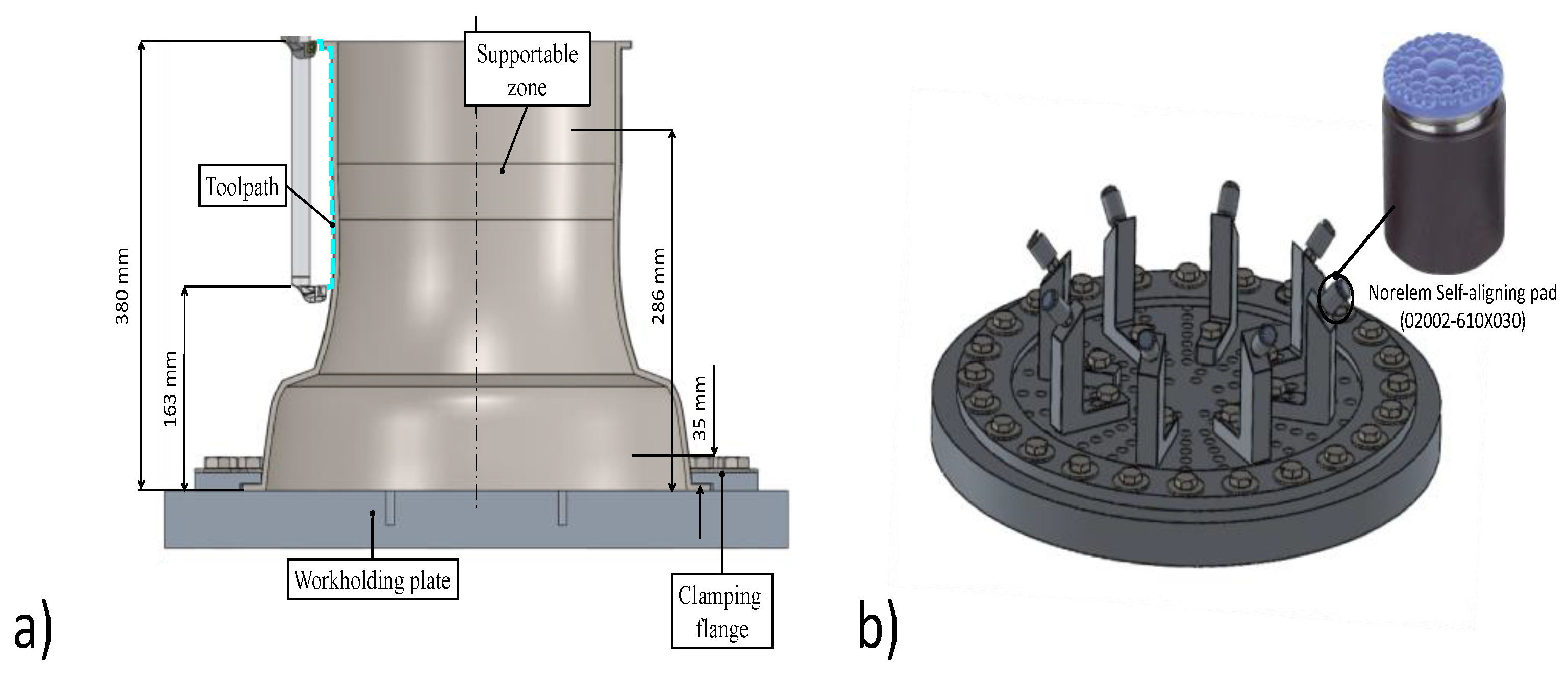
The stock, featuring a constant thickness of 6.8 mm, is fixed to the lathe by means of a flange screwed on an additional workholding plate (
Figure 2b) fixed to the spindle. Using this framework is possible to realize different support configurations. Setting the radial position of supports and pin height, it is possible to place supports in different positions, while self-aligning pads guarantee the correct contact, adapting to local workpiece curvature. A total of 32 nodes were used for the discretization of the midline, obtaining a FE model with a 9280 degree of freedom. This allows performing static simulation in 4 s and dynamic simulations in 20 s on a standard PC (INTEL
® CORE
™ i7-2600 CPU 3.4 Hz).
The schematized geometry of the component is shown in
Figure 2a, in which the zone considered for additional supports is highlighted, located between 35 and 286 mm from the workholding plate, the geometry of the additional workplate and a picture of the additional supports considered.
In the first step of optimization, errors and stability are evaluated for each additional support layer position, assuming the entire circumference supported. In the second step, the number of supports is reduced from 64 (number of nodes along each section) to 4. For each configuration, FE analysis was carried out, estimating local static stiffness and FRFs in the angular position correspondent to the middle point between two supports (i.e., where local stiffness is lower).
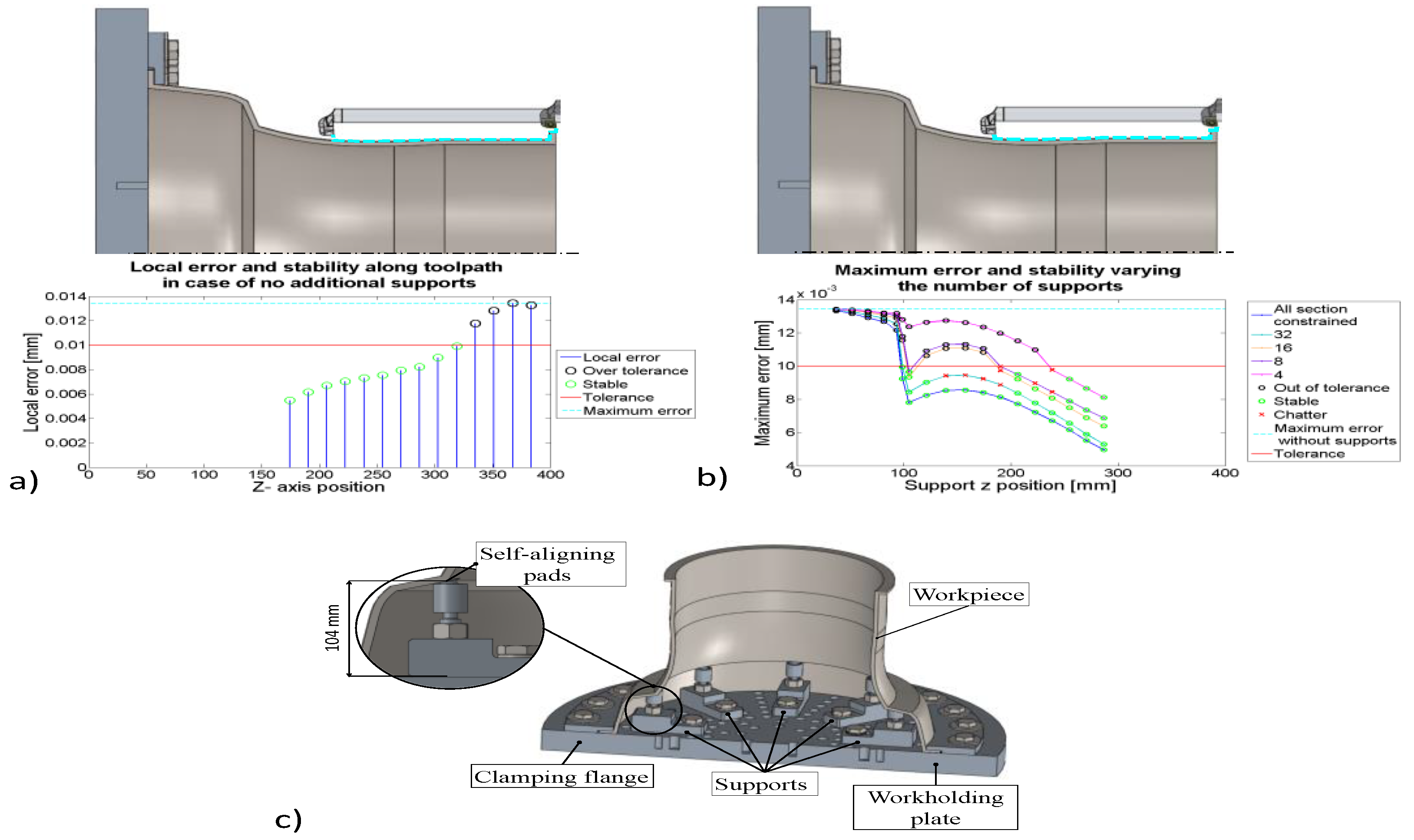
As a result, all possible configurations (in terms of axial position and relative minimum number of supports) can be deduced from the graph in
Figure 3, in which the geometrical error and chatter onset along the toolpath is reported in the absence of supports (
Figure 3a), and maximum diametral error and chatter prediction along the toolpath varying the number and position of support (
Figure 3b). For the test case presented, 8 supports at 104 mm from workholding (
Figure 3c) have been chosen. Compared with other options that allow reducing the minimum number of supports, this arrangement is preferable for its setup simplicity.
5. Conclusion
The paper presents a general methodology for fixture optimization in cases of turning of a thin-walled component. Starting from the workpiece geometry and toolpath, by means of the combination of the FE model, geometrical error model, and chatter model, the optimal fixture configuration is computed, as the one able to guarantee the imposed tolerance and stable cutting with the minimum number of additional supports. The proposed method was applied to an Inconel component to guarantee a diameter tolerance of 0.01 mm and a stable machining. Using eight supports at a distance of 104 mm from the clamping section, the maximum error was reduced by about 35%, tolerances were respected, and machining was stable. The following conclusions can be drawn:
The modeling approach used in this work, based on 2D finite elements, can be efficiently used to predict static and dynamic behavior of the thin-walled part;
In thin-walled turning, static and dynamic issues depend mainly on component flexibility. A comprehensive strategy considering both geometrical errors arising by static deflection and the occurrence of unstable vibrations, such as the one proposed here, should be adopted to tackle these issues and achieve quality components.
The use of additional supports in holding the thin-walled part can reduce static and dynamic issues, and depending on component geometry and boundary conditions, an optimized number of supports can be found;
The employment of the proposed method gives an aim to fixture design, avoiding time-consuming trial and error approaches.
Experimental tests are planned to be carried out in order to validate the workpiece FE model and prove the effectiveness of the entire approach.
Author Contributions
Conceptualization, G.C. and A.S.; methodology, A.S., N.G., and L.C.; software, A.S. and L.C.; validation, L.C. and N.G.; formal analysis, G.C.; investigation, L.C.; resources, G.C.; data curation, N.G.; writing—original draft preparation, L.C. and N.G.; writing—review and editing, G.C. and A.S.; visualization, N.G.; supervision, A.S.; project administration, A.S.; funding acquisition, G.C.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the DMG Mori Seiki Co. and the Machine Tool Technology Research Foundation (MTTRF) for the loaned machine tool.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, C.; Li, Q.; Hu, K.; Jiao, Y.; Song, Y. Study on Surface Roughness of Gcr15 Machined by Micro-Texture PCBN Tools. Machines 2018, 6, 42. [Google Scholar] [CrossRef]
- Li, Q.; Pan, C.; Jiao, Y.; Hu, K. Research on PCBN tool dry cutting GCr15. Machines 2018, 6, 28. [Google Scholar] [CrossRef]
- Mayer, J.R.R.; Phan, A.V.; Cloutier, G. Prediction of diameter errors in bar turning: A computationally effective model. Appl. Math. Model. 2000, 24, 943–956. [Google Scholar] [CrossRef]
- Carrino, L.; Giorleo, G.; Polini, W.; Prisco, U. Dimensional errors in longitudinal turning based on the unified generalized mechanics of cutting approach. Part I: Three-dimensional theory. Int. J. Mach. Tools Manuf. 2002, 42, 1509–1515. [Google Scholar] [CrossRef]
- Benardos, P.G.; Mosialos, S.; Vosniakos, G.C. Prediction of workpiece elastic deflections under cutting forces in turning. Robot. Comput. Integr. Manuf. 2006, 22, 505–514. [Google Scholar] [CrossRef]
- Yang, S.; Yuan, J.; Ni, J. Real-time cutting force induced error compensation on a turning center. Int. J. Mach. Tools Manuf. 1997, 37, 1597–1610. [Google Scholar] [CrossRef]
- Ratchev, S.; Liu, S.; Becker, A.A. Error compensation strategy in milling flexible thin-wall parts. J. Mater. Process. Technol. 2005, 162–163, 673–681. [Google Scholar] [CrossRef]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Altintans, Y. Manufacturing Automation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012; ISBN 9780521172479. [Google Scholar]
- Mehdi, K.; Rigal, J.F.; Play, D. Dynamic behavior of a thin-walled cylindrical workpiece during the turning process, Part 1: Cutting process simulation. J. Manuf. Sci. Eng. Trans. ASME 2002, 124, 562–568. [Google Scholar] [CrossRef]
- Mehdi, K.; Rigal, J.F.; Play, D. Dynamic behavior of a thin-walled cylindrical workpiece during the turning process, Part 2: Eperimental approach and validation. J. Manuf. Sci. Eng. Trans. ASME 2002, 124, 569–580. [Google Scholar] [CrossRef]
- Gerasimenko, A.; Guskov, M.; Duchemin, J.; Lorong, P.; Gouskov, A. Variable compliance-related aspects of chatter in turning thin-walled tubular parts. Procedia CIRP 2015, 31, 58–63. [Google Scholar] [CrossRef]
- Urbikain, G.; Alvarez, A.; de Lacalle, L.N.L.; Arsuaga, M.; Alonso, M.A.; Veiga, F. A reliable turning process by the early use of a deep simulation model at several manufacturing stages. Machines 2017, 5, 15. [Google Scholar] [CrossRef]
- Scippa, A.; Grossi, N.; Campatelli, G. FEM based cutting velocity selection for thin walled part machining. Procedia CIRP 2014, 14, 287–292. [Google Scholar] [CrossRef]
- Grossi, N.; Scippa, A.; Croppi, L.; Morelli, L.; Campatelli, G. Adaptive toolpath for 3-axis milling of thin walled parts. MM Sci. J. 2019. HSM 2019 Special Issue. [Google Scholar]
- Sölter, J.; Grote, C.; Brinksmeier, E. Influence of clamping strategies on roundness deviations of turned rings. Mach. Sci. Technol. 2011, 15, 338–355. [Google Scholar] [CrossRef]
- Sallese, L.; Innocenti, G.; Grossi, N.; Scippa, A.; Flores, R.; Basso, M.; Campatelli, G. Mitigation of chatter instabilities in milling using an active fixture with a novel control strategy. Int. J. Adv. Manuf. Technol. 2017, 89, 2771–2787. [Google Scholar] [CrossRef]
- Wang, H.; Rong, Y.; Li, H.; Shaun, P. Computer aided fixture design: Recent research and trends. CAD Comput. Aided Des. 2010, 42, 1085–1094. [Google Scholar] [CrossRef]
- Boyle, I.; Rong, Y.; Brown, D.C. A review and analysis of current computer-aided fixture design approaches. Robot. Comput. Integr. Manuf. 2011, 27, 1–12. [Google Scholar] [CrossRef]
- Kurnadi, M.S.; Morehouse, J.; Melkote, S.N. A workholding optimization model for turning of ring-shaped parts. Int. J. Adv. Manuf. Technol. 2007, 32, 656–665. [Google Scholar] [CrossRef]
- Krishnakumar, K.; Melkote, S.N. Machining fixture layout optimization using the genetic algorithm. Int. J. Mach. Tools Manuf. 2000, 40, 579–598. [Google Scholar] [CrossRef]
- Liu, S.G.; Zheng, L.; Zhang, Z.H.; Li, Z.Z.; Liu, D.C. Optimization of the number and positions of fixture locators in the peripheral milling of a low-rigidity workpiece. Int. J. Adv. Manuf. Technol. 2007, 33, 668–676. [Google Scholar] [CrossRef]
- Jianliang, G.; Rongdi, H. A united model of diametral error in slender bar turning with a follower rest. Int. J. Mach. Tools Manuf. 2006, 46, 1002–1012. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Xiao, J.; Ding, M.; Yan, S.; Zhang, X.; Zhang, J. Investigation of moving fixture on deformation suppression during milling process of thin-walled structures. J. Manuf. Process. 2018, 32, 403–411. [Google Scholar] [CrossRef]
- Zeng, S.; Wan, X.; Li, W.; Yin, Z.; Xiong, Y. A novel approach to fixture design on suppressing machining vibration of flexible workpiece. Int. J. Mach. Tools Manuf. 2012, 58, 29–43. [Google Scholar] [CrossRef]
- Wan, X.J.; Zhang, Y. A novel approach to fixture layout optimization on maximizing dynamic machinability. Int. J. Mach. Tools Manuf. 2013, 70, 32–44. [Google Scholar] [CrossRef]
- Matsubara, A.; Taniyama, Y.; Wang, J.; Kono, D. Design of a support system with a pivot mechanism for suppressing vibrations in thin-wall milling. CIRP Ann. Manuf. Technol. 2017, 66, 381–384. [Google Scholar] [CrossRef]
- Kundrak, J.; Molnar, V.; Deszpoth, I. Comparative Analysis of Machining Procedures. Machines 2018, 6, 13. [Google Scholar] [CrossRef]
- Izamshah, R.A.; Mo, J.; Ding, S. Finite Element Analysis of Machining Thin-Wall Parts. Key Eng. Mater. 2011, 458, 283–288. [Google Scholar] [CrossRef]
- Polini, W.; Prisco, U. The estimation of the diameter error in bar turning: A comparison among three cutting force models. Int. J. Adv. Manuf. Technol. 2003, 22, 465–474. [Google Scholar] [CrossRef]
- Yao, C.; Zhou, Z.; Zhang, J.; Wu, D.; Tan, L. Experimental study on cutting force of face-turning Inconel718 with ceramic tools and carbide tools. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Siddhpura, M.; Paurobally, R. A review of chatter vibration research in turning. Int. J. Mach. Tools Manuf. 2012, 61, 27–47. [Google Scholar] [CrossRef]
- Eynian, M.; Altintas, Y. Chatter Stability of General Turning Operations with Process Damping. J. Manuf. Sci. Eng. 2009, 131, 041005. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).