Design and Testing of a 3-DOF Robot for Studying the Human Response to Vibration
Abstract
1. Introduction
1.1. Effects of Vibrations on the Human Body
1.2. Linear Delta Robot Selection
1.3. Functional Requirements
2. Materials and Methods
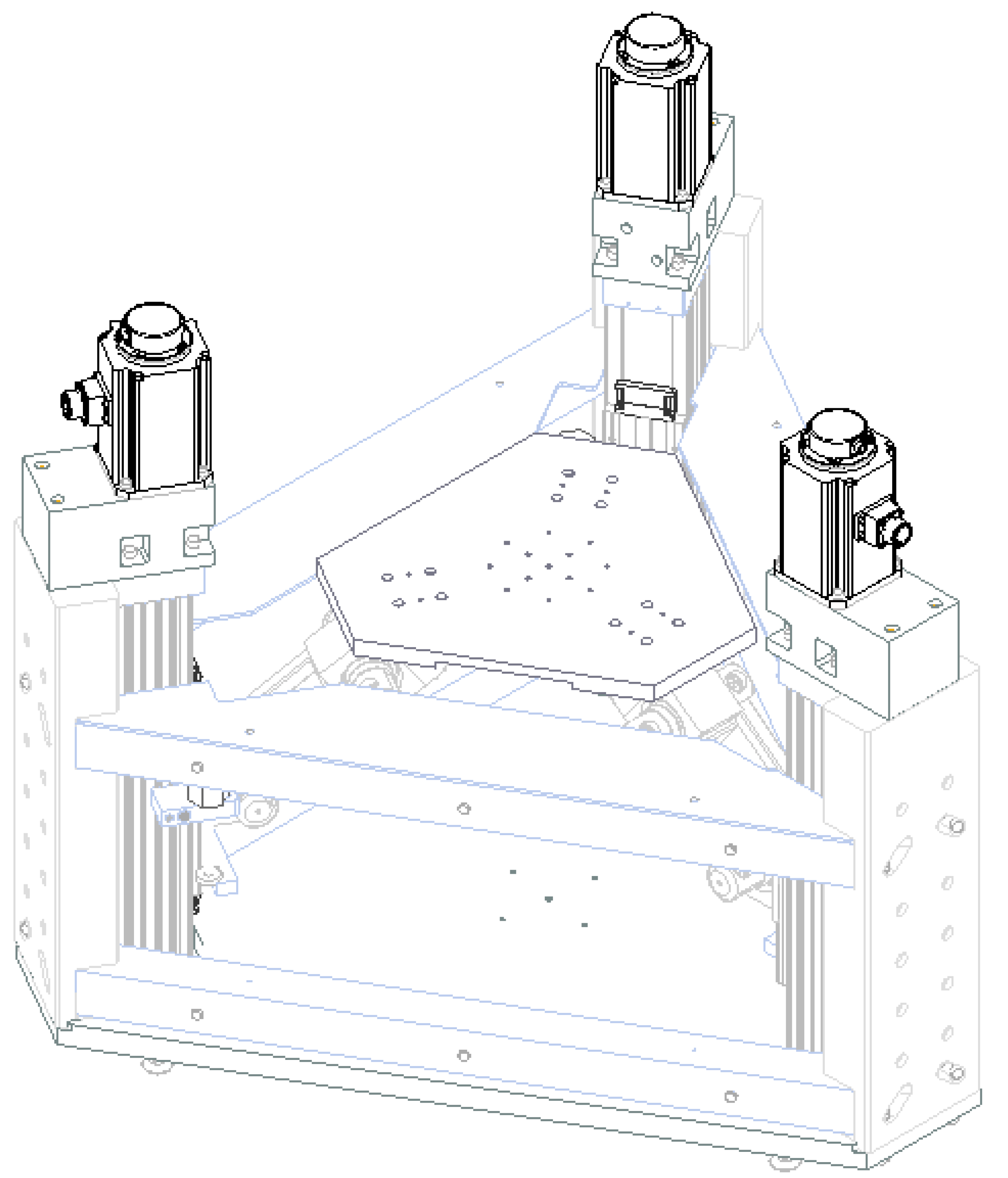
2.1. Design of the Delta Shaker
2.1.1. Kinematic Optimization
2.1.2. Actuator Selection
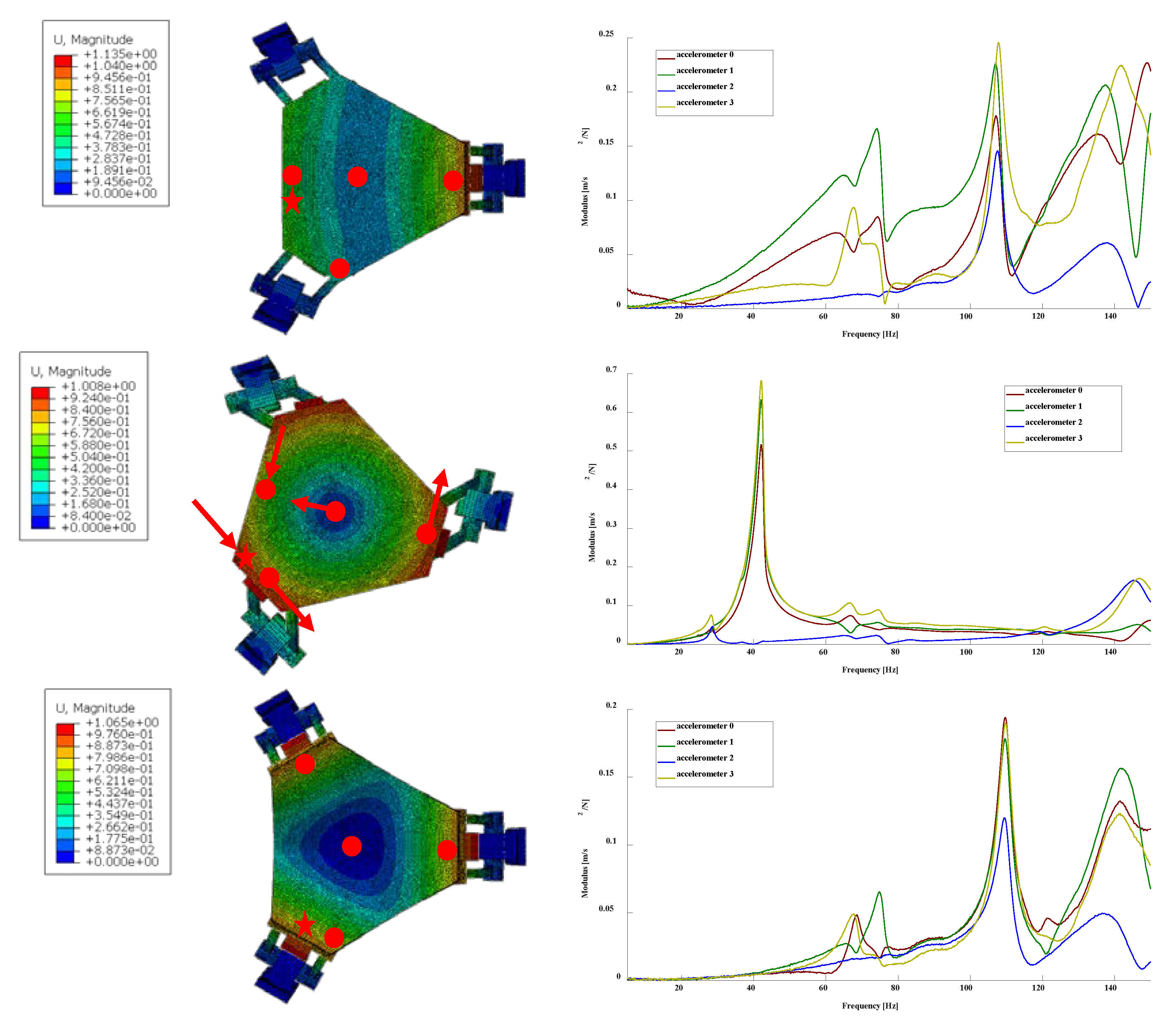
2.1.3. FEM Modal Analysis
2.1.4. Experimental Modal Analysis
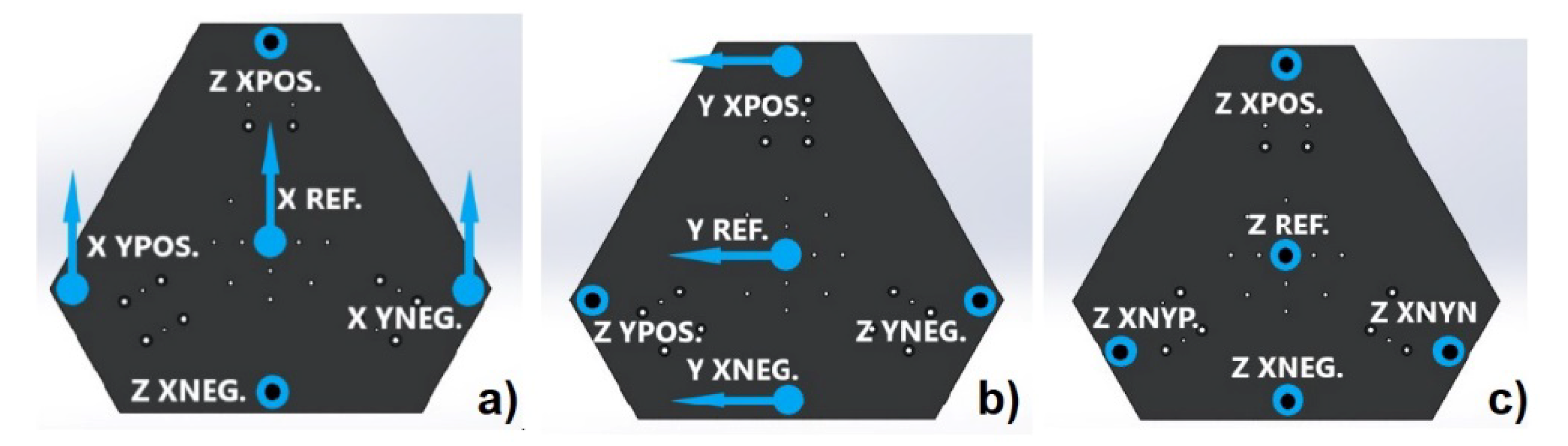
2.2. Performance Tests
3. Results
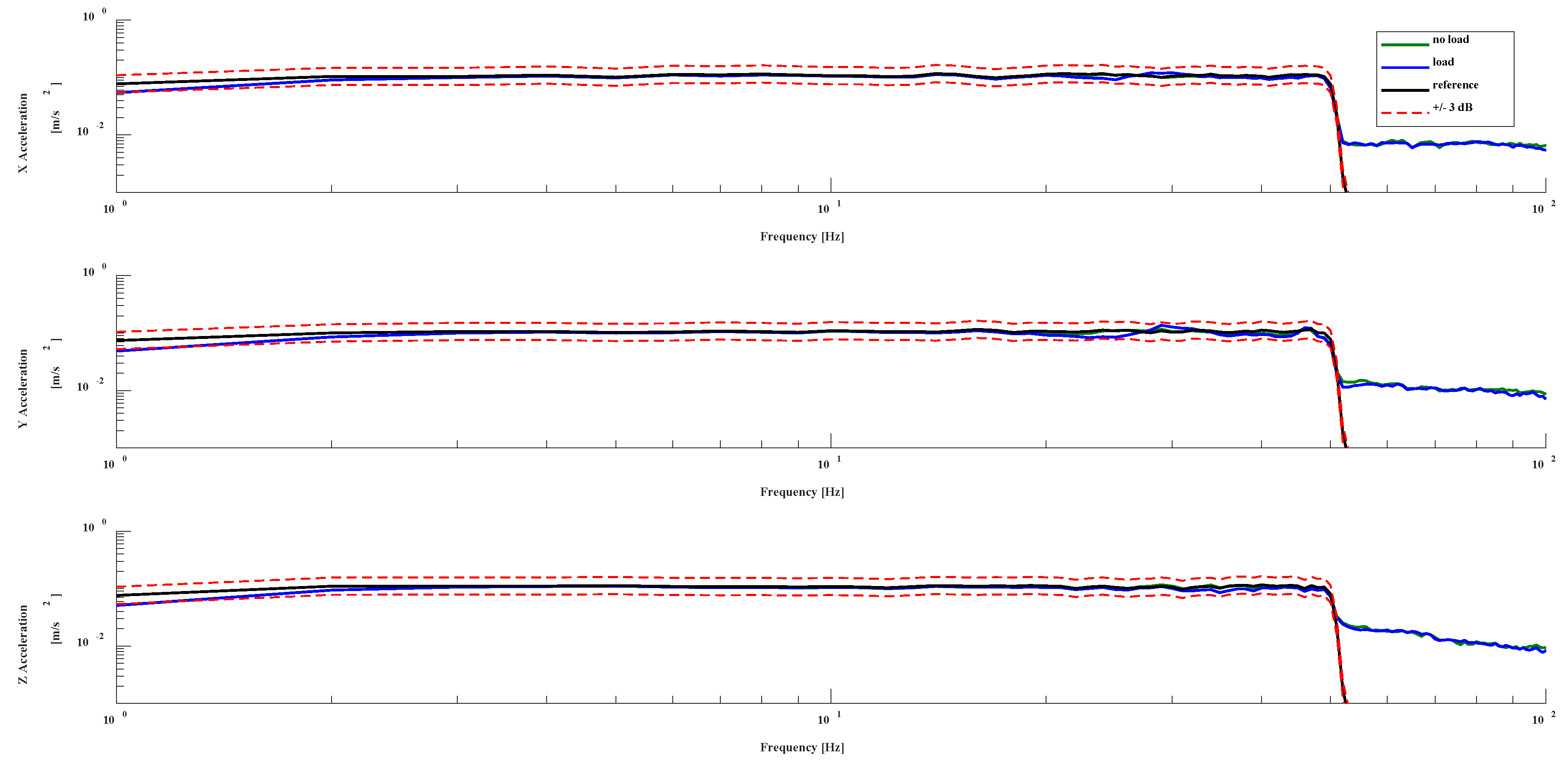
3.1. Experimental Modal Analysis
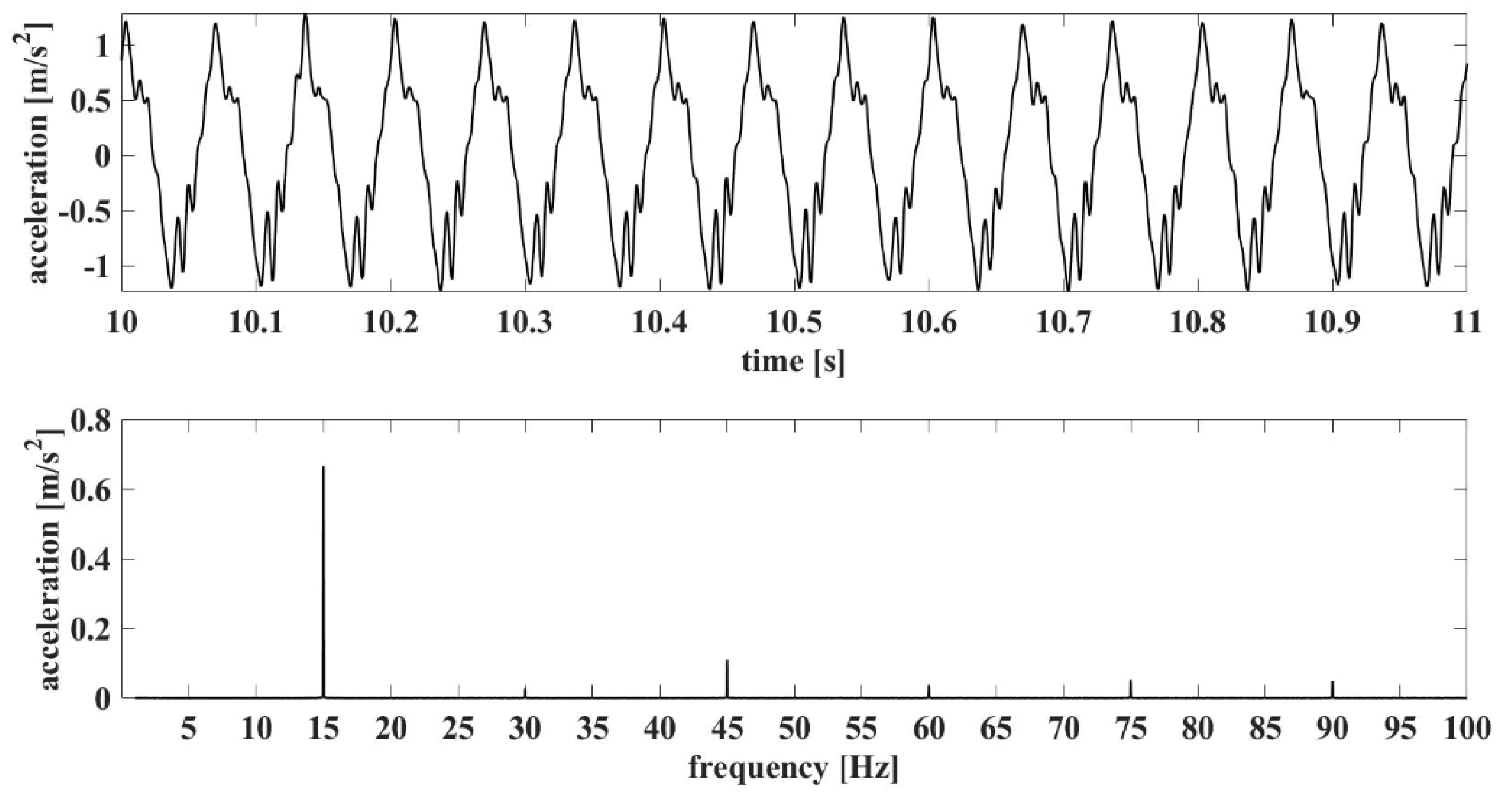
3.2. Measured Performances
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
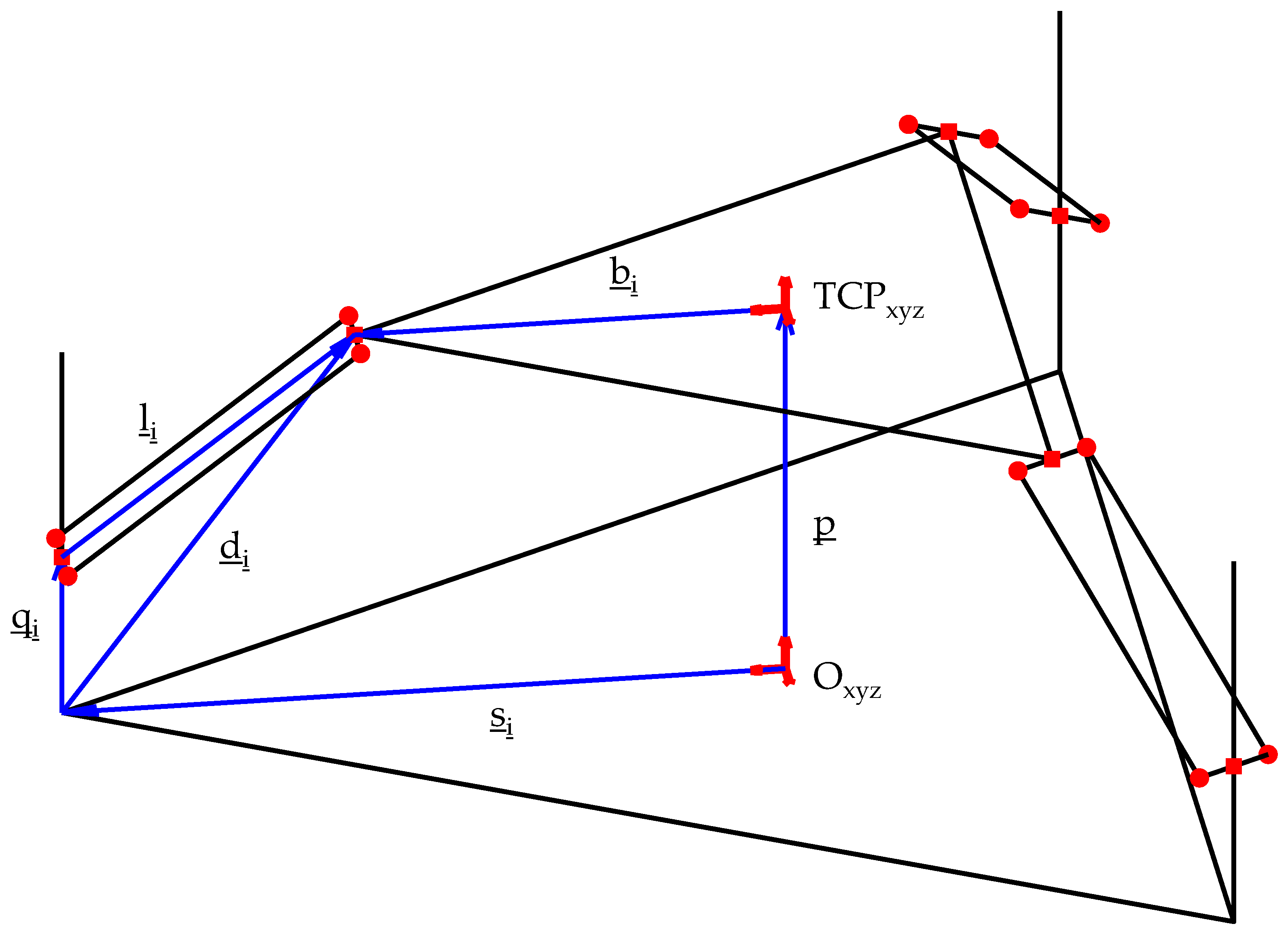
Appendix A
- Reference coordinate system: Oxyz;
- Unit vectors of the reference coordinate system Oxyz: ;
- Reference system integral with the moving platform: TCPxyz. Due to the linear delta kinematic constraints, this reference system is always parallel to Oxyz;
- Unit vectors of the moving platform coordinate system TCPxyz: ;
- Position vector of TCPxyz: p;
- Components of p along the reference coordinates system Oxyz:
- Linear actuator and joint index: i;
- Distance between Oxyz and the projection of the linear actuators along the plane defined by : s;
- Position vector of the projection of the ith linear actuator along the plane : si. Given the radial symmetry of the linear delta, its components are
- Distance between TCPxyz and the joints attached to the platform: b;
- Position vector of the ith joint attached to the platform in the reference system TCPxyz: bi. As stated before, its components can be immediately computed:
- Vector of the distance between the position of the ith linear actuator end and its projection along the plane qi. Its components are defined as
- Length of the linear delta links: l;
- Vector connecting the joint of the ith linear actuator to the ith joint of the moving platform: li;
- Unit vector of li: Vector connecting the projection of the ith linear actuator on the plane and the ith joint of the moving platform: di;
References
- Smith, D.R.; Leggat, P.A. Whole-Body Vibration. Prof. Saf. 2005, 50, 35. [Google Scholar]
- Bovenzi, M.; Hulshof, C. An updated review of epidemiologic studies on the relationship between exposure to whole-body vibration and low back pain. J. Sound Vib. 1998, 215, 595–611. [Google Scholar] [CrossRef]
- Seidel, H.; Bluethner, R.; Hinz, B. Effects of sinusoidal whole-body vibration on the lumbar spine: The stress-strain relationship. Int. Arch. Occup. Environ. Health 1986, 57, 207–223. [Google Scholar] [CrossRef]
- Bovenzi, M.; Hulshof, C. An updated review of epidemiologic studies on the relationship between exposure to whole-body vibration and low back pain (1986–1997). Int. Arch. Occup. Environ. Health 1999, 72, 351–365. [Google Scholar] [CrossRef] [PubMed]
- Palmer, K.T.; Griffin, M.J.; Syddall, H.E.; Pannett, B.; Cooper, C.; Coggon, D. The relative importance of whole body vibration and occupational lifting as risk factors for low-back pain. Occup. Environ. Med. 2003, 60, 715–721. [Google Scholar] [CrossRef]
- Nordlund, M.; Thorstensson, A. Strength training effects of whole-body vibration. Scand. J. Med. Sci. Sports 2007, 17, 12–17. [Google Scholar] [CrossRef]
- Orsini, F.; Rossi, A.; Botta, F.; Scorza, A.; Sciuto, S.A.; Marzaroli, P.; Chadefaux, D.; Tarabini, M.; Scalise, L. A case study on the characterization of whole body vibration platforms for medical applications. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar]
- Orsini, F.; Rossi, A.; Scorza, A.; Botta, F.; Sciuto, S.A. A comparison between a commercial WBV platform and an experimental prototype. In Proceedings of the 22nd IMEKO TC4 International Symposium & 20th International Workshop on ADC Modelling and Testing Supporting World Development through Electrical&electronic Measurements Iasi, Rome, Italy, 14–15 September 2017. [Google Scholar]
- Mansfield, N.J.; Griffin, M.J. Non-Linearities in apparent mass and transmissibility during exposure to whole-body vertical vibration. J. Biomech. 2000, 33, 933–941. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Griffin, M. The horizontal apparent mass of the standing human body. J. Sound Vib. 2011, 330, 3284–3297. [Google Scholar] [CrossRef]
- Paddan, G.; Griffin, M. The transmission of translational floor vibration to the heads of standing subjects. J. Sound Vib. 1993, 160, 503–521. [Google Scholar] [CrossRef]
- Tarabini, M.; Saggin, B.; Scaccabarozzi, D.; Gaviraghi, D.; Moschioni, G. Apparent mass distribution at the feet of standing subjects exposed to whole-body vibration. Ergonomics 2013, 56, 842–855. [Google Scholar] [CrossRef]
- Tarabini, M.; Solbiati, S.; Moschioni, G.; Saggin, B.; Scaccabarozzi, D. Analysis of non-linear response of the human body to vertical whole-body vibration. Ergonomics 2014, 57, 1711–1723. [Google Scholar] [CrossRef]
- Tarabini, M.; Solbiati, S.; Saggin, B.; Scaccabarozzi, D. Apparent mass matrix of standing subjects exposed to multi-axial whole-body vibration. Ergonomics 2016, 59, 1038–1049. [Google Scholar] [CrossRef]
- Mansfield, N.; Griffin, M.J. Effects of posture and vibration magnitude on apparent mass and pelvis rotation during exposure to whole-body vertical vibration. J. Sound Vib. 2002, 2253, 93–107. [Google Scholar] [CrossRef]
- Dickey, J.P.; Eger, T.R.; Oliver, M.L.; Boileau, P.E.; Trick, L.M.; Edwards, A.M. Multi-axis sinusoidal whole-body vibrations: Part II—Relationship between Vibration Total Value and discomfort varies between vibration axes. J. Low Freq. Noise Vib. Act. Control 2007, 26, 195–204. [Google Scholar] [CrossRef]
- Welcome, D.E.; Dong, R.G.; Xu, X.S.; Warren, C.; McDowell, T.W.; Wu, J.Z. An examination of the vibration transmissibility of the hand-arm system in three orthogonal directions. Int. J. Ind. Ergon. 2015, 45, 21–34. [Google Scholar] [CrossRef]
- Boileau, P.; Rakheja, S. Whole-body vertical biodynamic response characteristics of the seated vehicle driver: Measurement and model development. Int. J. Ind. Ergon. 1998, 22, 449–472. [Google Scholar] [CrossRef]
- Tarabini, M.; Solbiati, S.; Saggin, B.; Scaccabarozzi, D. Setup for the measurement of apparent mass matrix of standing subjects. IEEE Trans. Instrum. Meas. 2016, 65, 1856–1864. [Google Scholar] [CrossRef]
- Subashi, G.; Matsumoto, Y.; Griffin, M. Modelling resonances of the standing body exposed to vertical whole-body vibration: Effects of posture. J. Sound Vib. 2008, 317, 400–418. [Google Scholar] [CrossRef]
- Merlet, J. Parallel manipulators: State of the art and perspectives. Adv. Rob. 1993, 8, 589–596. [Google Scholar] [CrossRef]
- Patel, Y.; George, P. Parallel manipulators applications—a survey. Mod. Mech. Eng. 2012, 2, 57. [Google Scholar] [CrossRef]
- Clavel, R. A fast robot with parallel geometry. In Proceedings of the 18th International Symposium on Industrial Robots, New York, NY, USA, 26–28 April 1988; pp. 91–100. [Google Scholar]
- Liu, X.; il Jeong, J.; Kim, J. A three translational DoFs parallel cube-manipulator. Robotica 2003, 21, 645–653. [Google Scholar] [CrossRef]
- Bouri, M.; Clavel, R. The linear delta: Developments and applications. In Proceedings of the Robotics (ISR), 2010 41st International Symposium on and 2010 6th German Conference on Robotics (ROBOTIK), Munich, Germany, 7–9 June 2010; pp. 1–8. [Google Scholar]
- Giberti, H.; Cinquemani, S.; Legnani, G. Effects of transmission mechanical characteristics on the choice of a motor-reducer. Mechatronics 2010, 20, 604–610. [Google Scholar]
- Ucar, H.; Basdogan, I. Dynamic characterization and modeling of rubber shock absorbers: A comprehensive case study. J. Low Freq. Noise Vib. Act. Control 2018, 37, 509–518. [Google Scholar] [CrossRef]
- Pastor, M.; Binda, M.; Harčarik, T. Modal assurance criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Egusquiza, M.; Bossio, M. Accurate determination of the frequency response function of submerged and confined structures by using PZT-patches. Sensors 2017, 17, 660. [Google Scholar] [CrossRef]
- Giberti, H.; Sbaglia, L.; Silvestri, M. Mechatronic design for an extrusion-based additive manufacturing machine. Machines 2017, 5, 29. [Google Scholar] [CrossRef]

| Parameter | Lower Bound (mm) | Step (mm) | Upper Bound (mm) |
|---|---|---|---|
| Base radius | 250 | 10 | 500 |
| Link length | 150 | 5 | 250 |
| Fx (N) | Fy (N) | Fz (N) | Mx (Nm) | My (Nm) | Mz (Nm) |
|---|---|---|---|---|---|
| 1916 | 1908 | 282 | 148 | 181 | 320 |
| C10 | C20 | C30 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| 0.9636 | −0.6213 | 0.3265 | 0 | 0 | 0 |
| ax (mm/s2) | ay (mm/s2) | az (mm/s2) | |
|---|---|---|---|
| No load | 5.7 | 8.2 | 6.3 |
| Loaded | 9.6 | 14.0 | 9.8 |
| ax (mm/s2) | ay (mm/s2) | az (mm/s2) | |
|---|---|---|---|
| No load | 4.9 | 6.5 | 8.2 |
| Loaded | 4.6 | 6.0 | 7.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzaroli, P.; Albanetti, A.; Negri, E.; Giberti, H.; Tarabini, M. Design and Testing of a 3-DOF Robot for Studying the Human Response to Vibration. Machines 2019, 7, 67. https://doi.org/10.3390/machines7040067
Marzaroli P, Albanetti A, Negri E, Giberti H, Tarabini M. Design and Testing of a 3-DOF Robot for Studying the Human Response to Vibration. Machines. 2019; 7(4):67. https://doi.org/10.3390/machines7040067
Chicago/Turabian StyleMarzaroli, Pietro, Alessandro Albanetti, Edoardo Negri, Hermes Giberti, and Marco Tarabini. 2019. "Design and Testing of a 3-DOF Robot for Studying the Human Response to Vibration" Machines 7, no. 4: 67. https://doi.org/10.3390/machines7040067
APA StyleMarzaroli, P., Albanetti, A., Negri, E., Giberti, H., & Tarabini, M. (2019). Design and Testing of a 3-DOF Robot for Studying the Human Response to Vibration. Machines, 7(4), 67. https://doi.org/10.3390/machines7040067







