A Soft Sensor for Estimation of In-Flow Rate in a Flow Process Using Pole Placement and Kalman Filter Methods
Abstract
1. Introduction
2. Problem Description
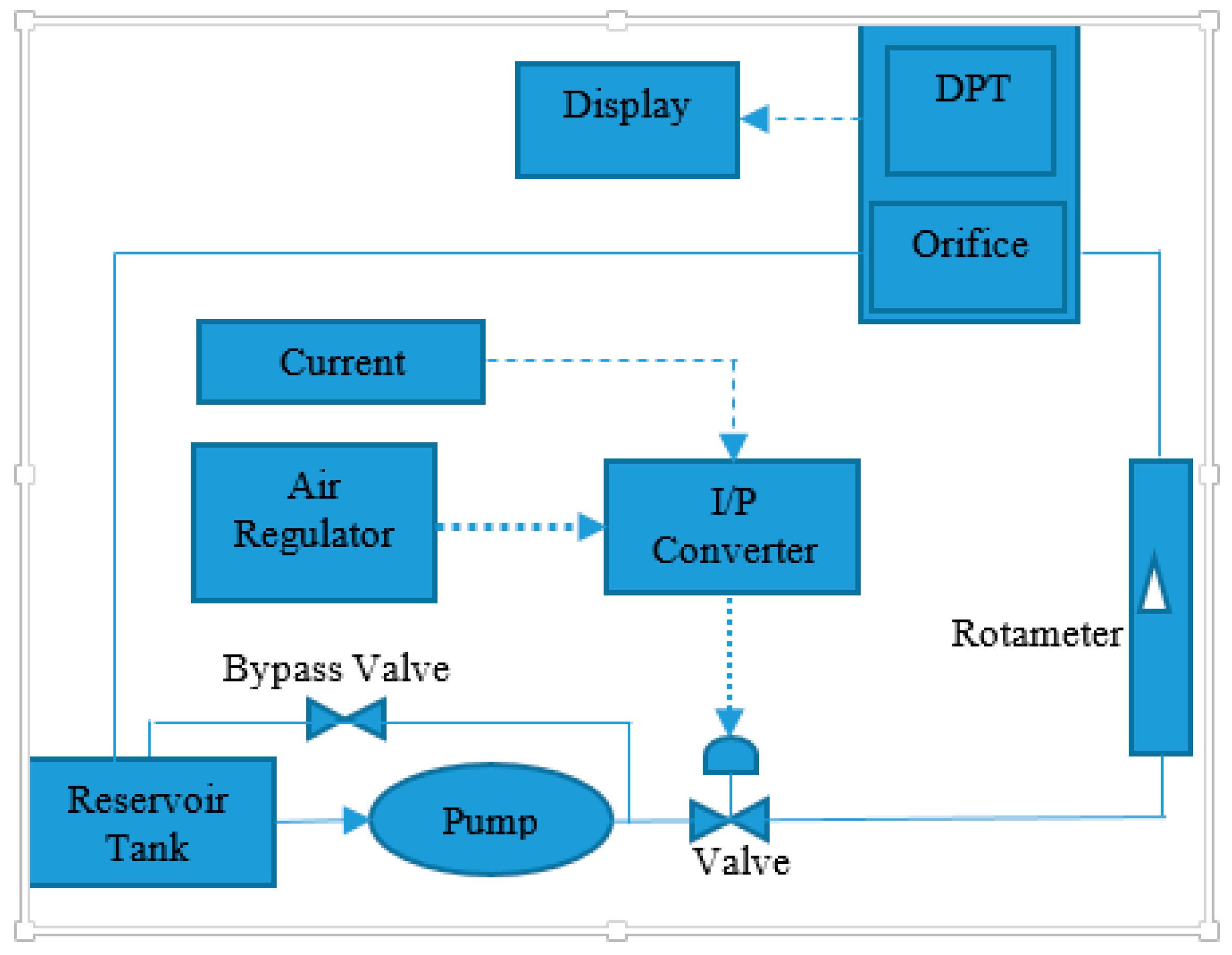
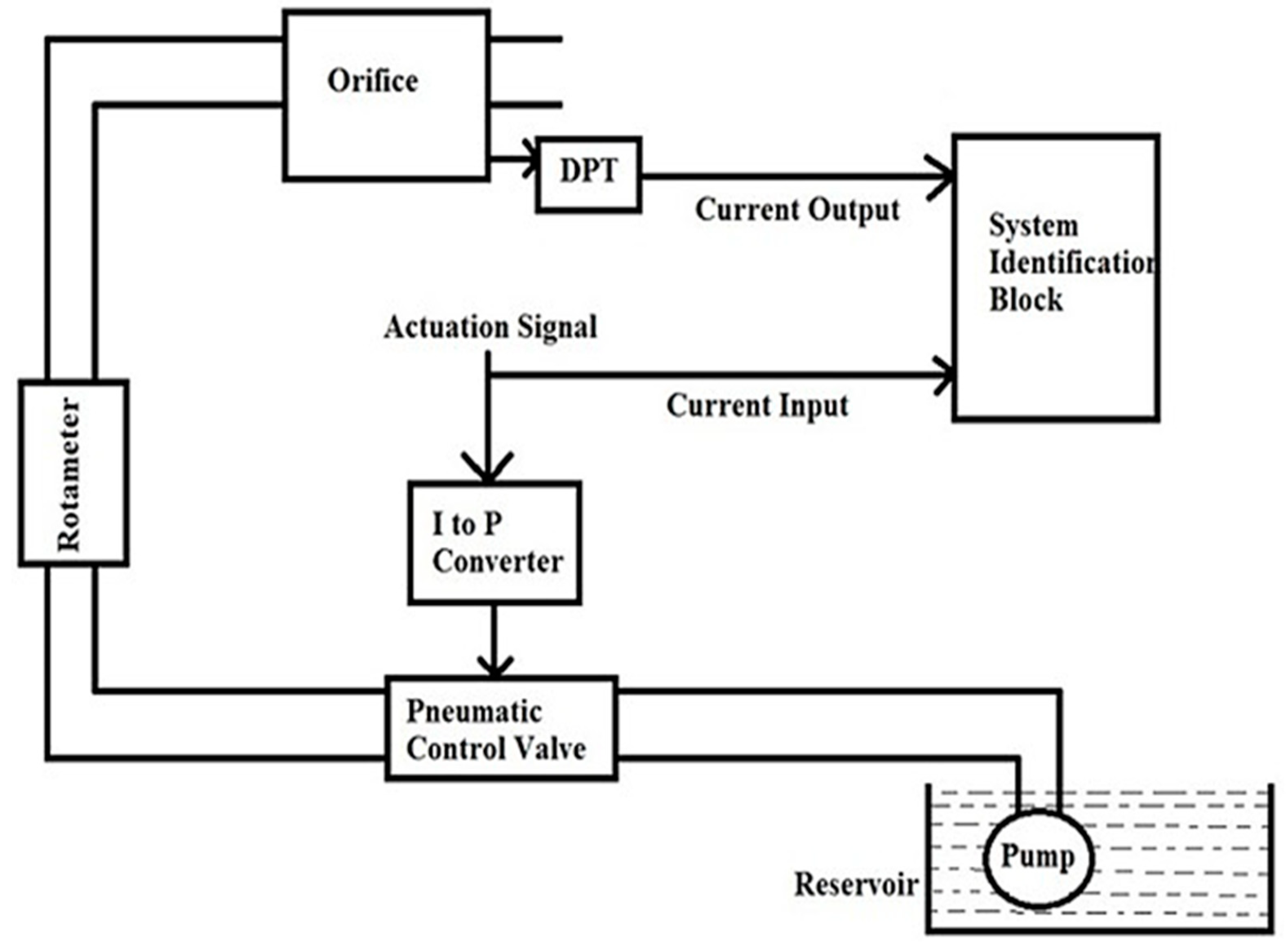
2.1. Flow Process Experimental Setup
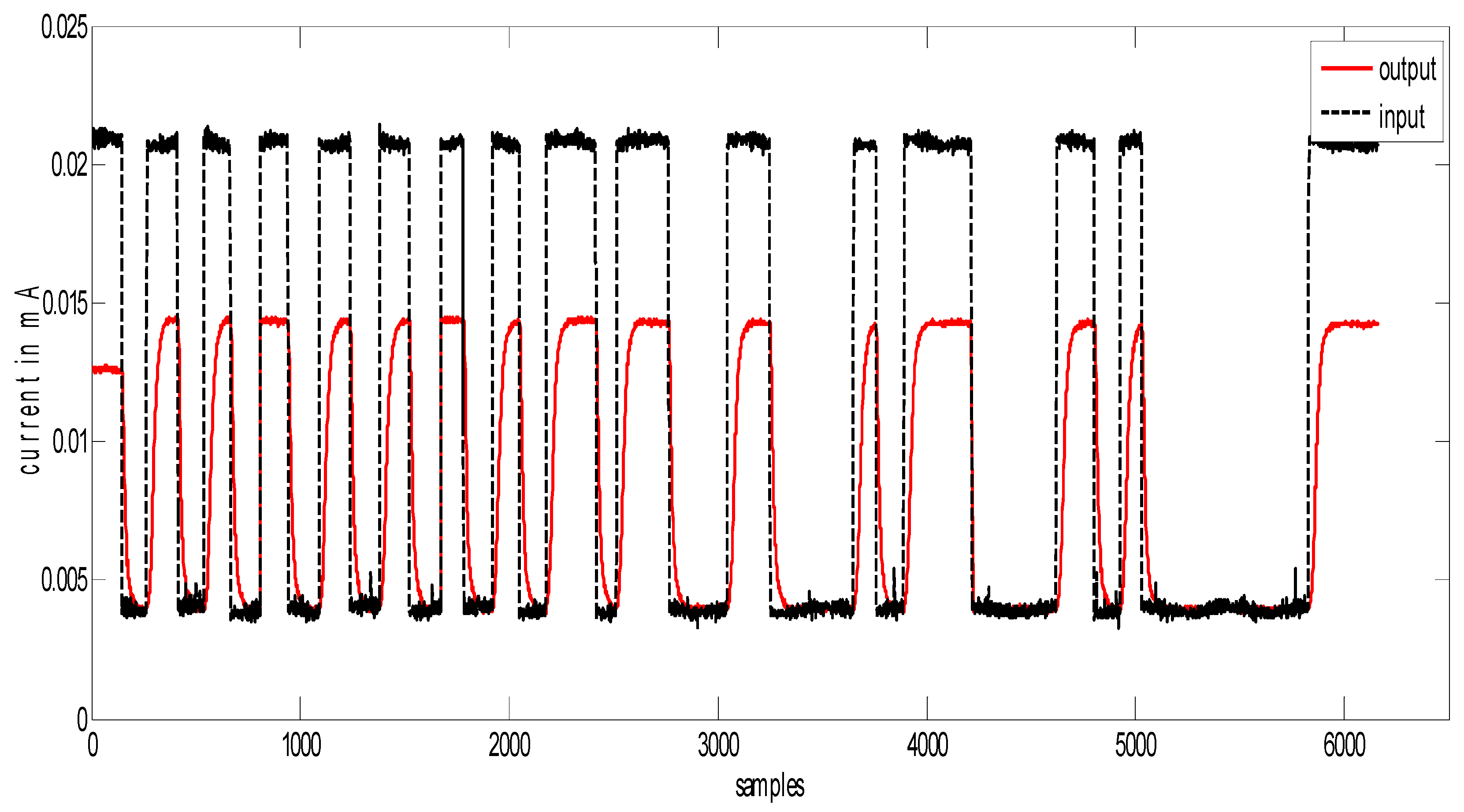
2.2. Identification of the Control Valve Model
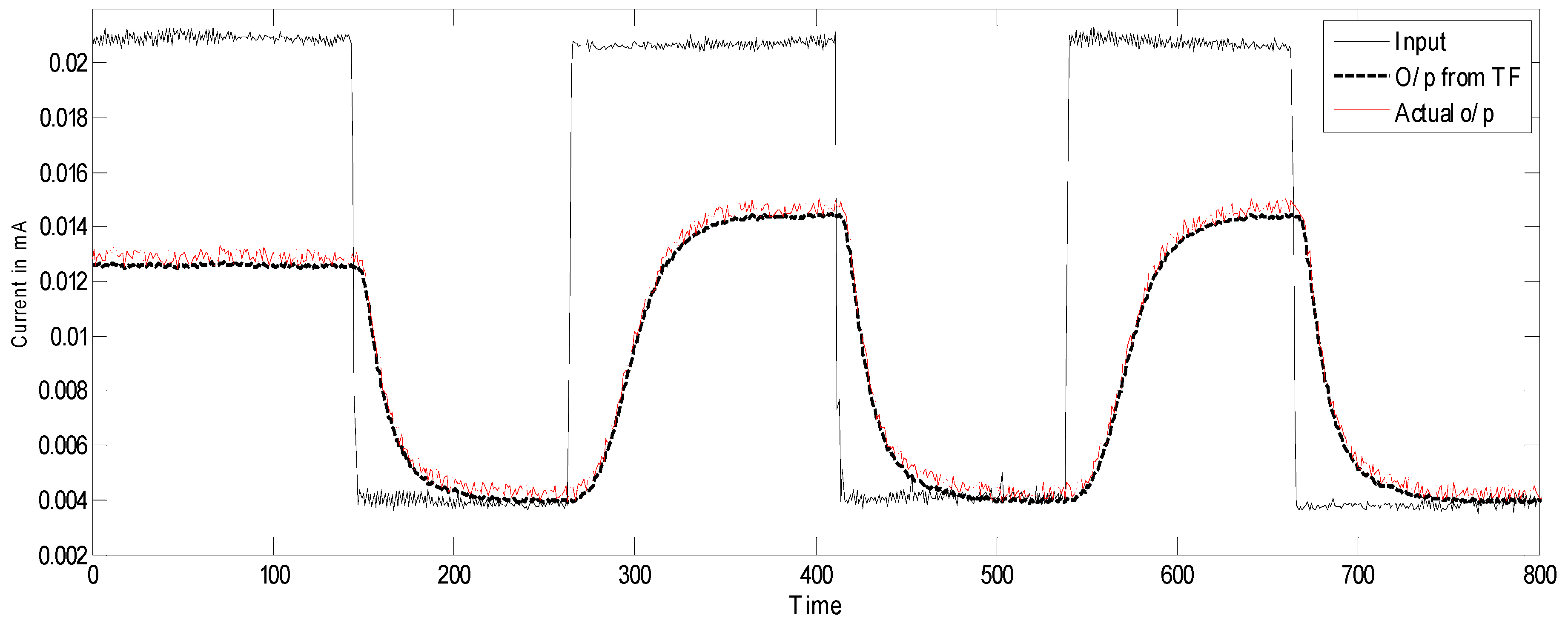
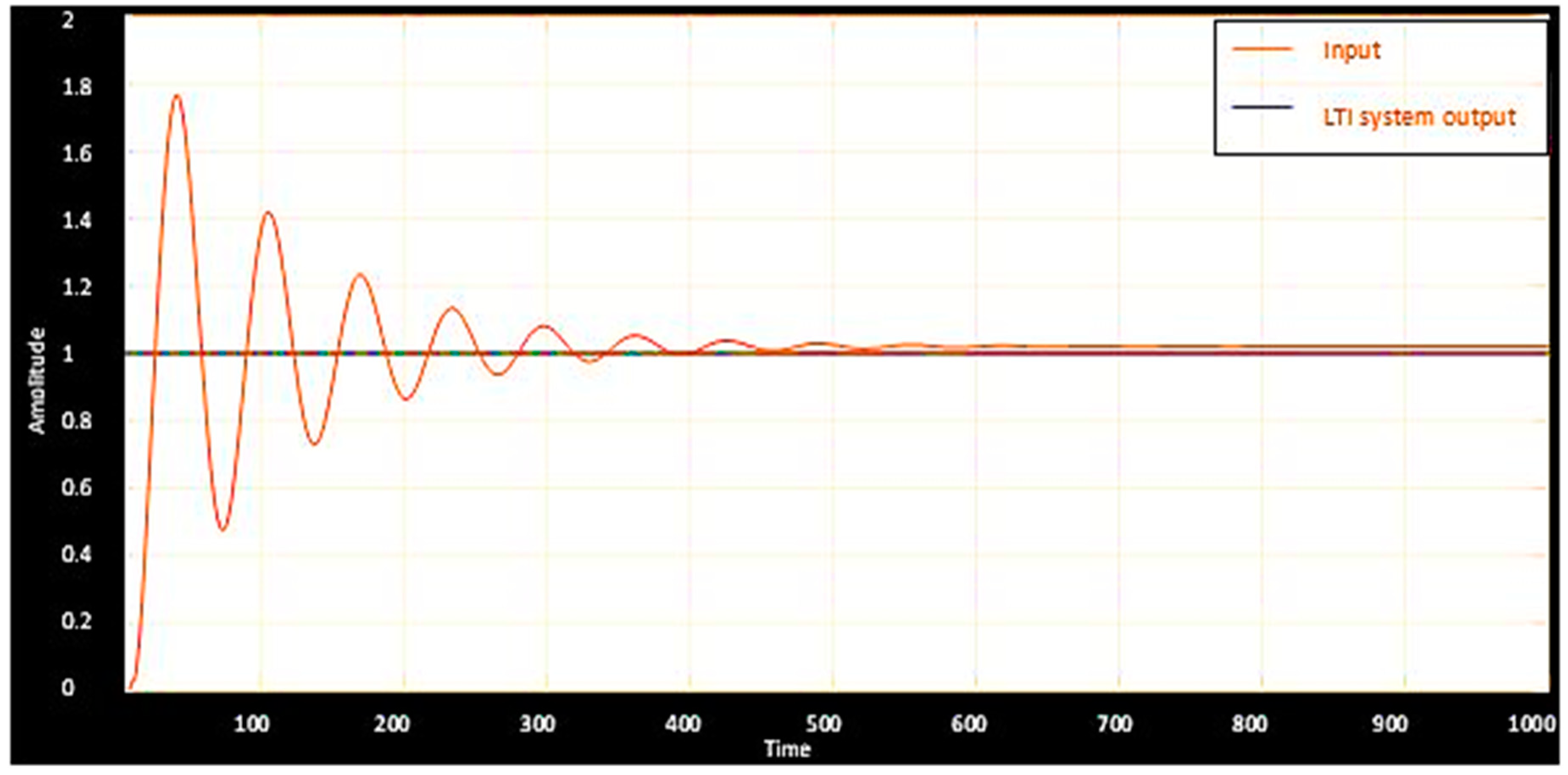
Pseudo Random Signal Response
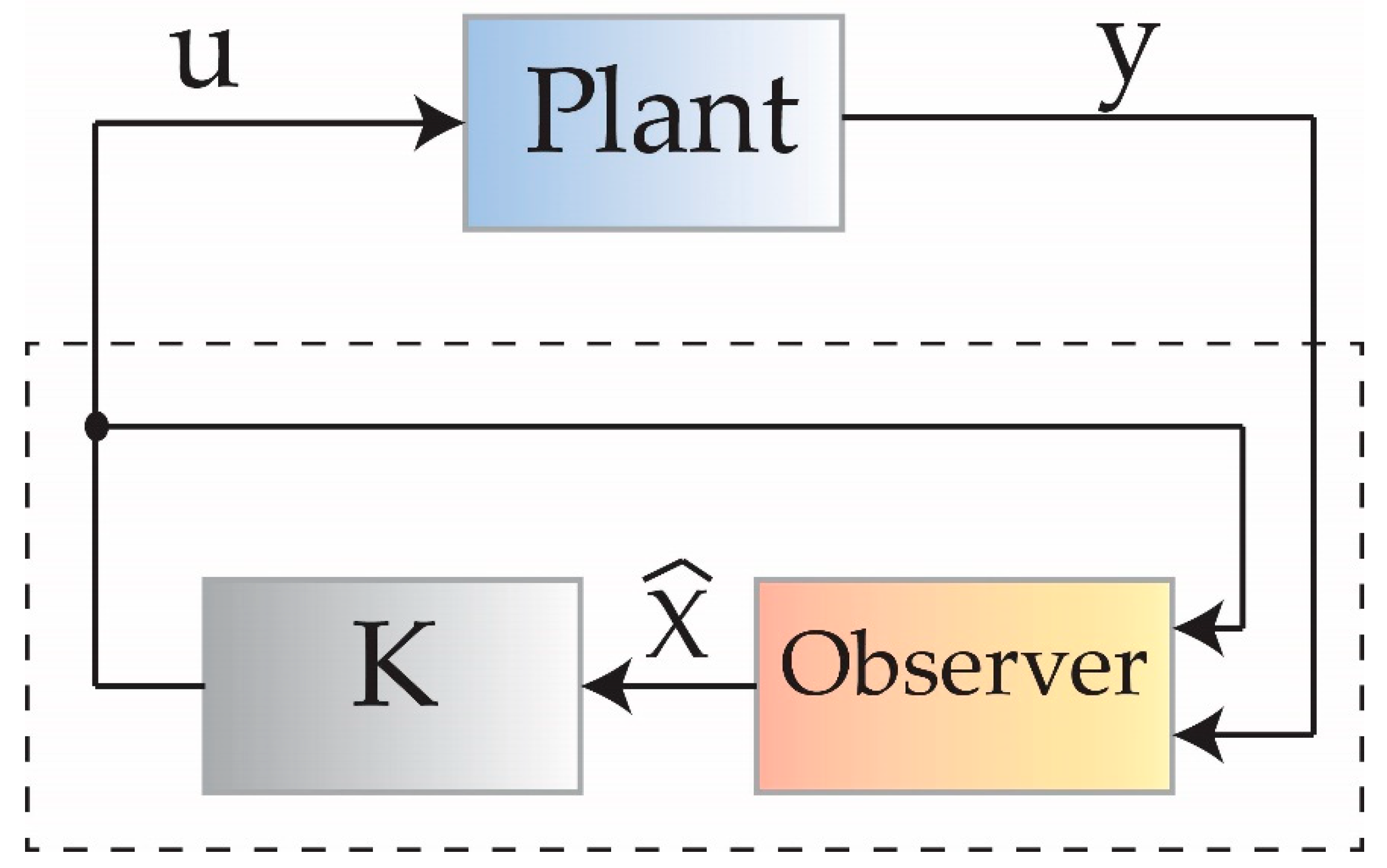
3. Design of Observers
3.1. Pole Placement Technique
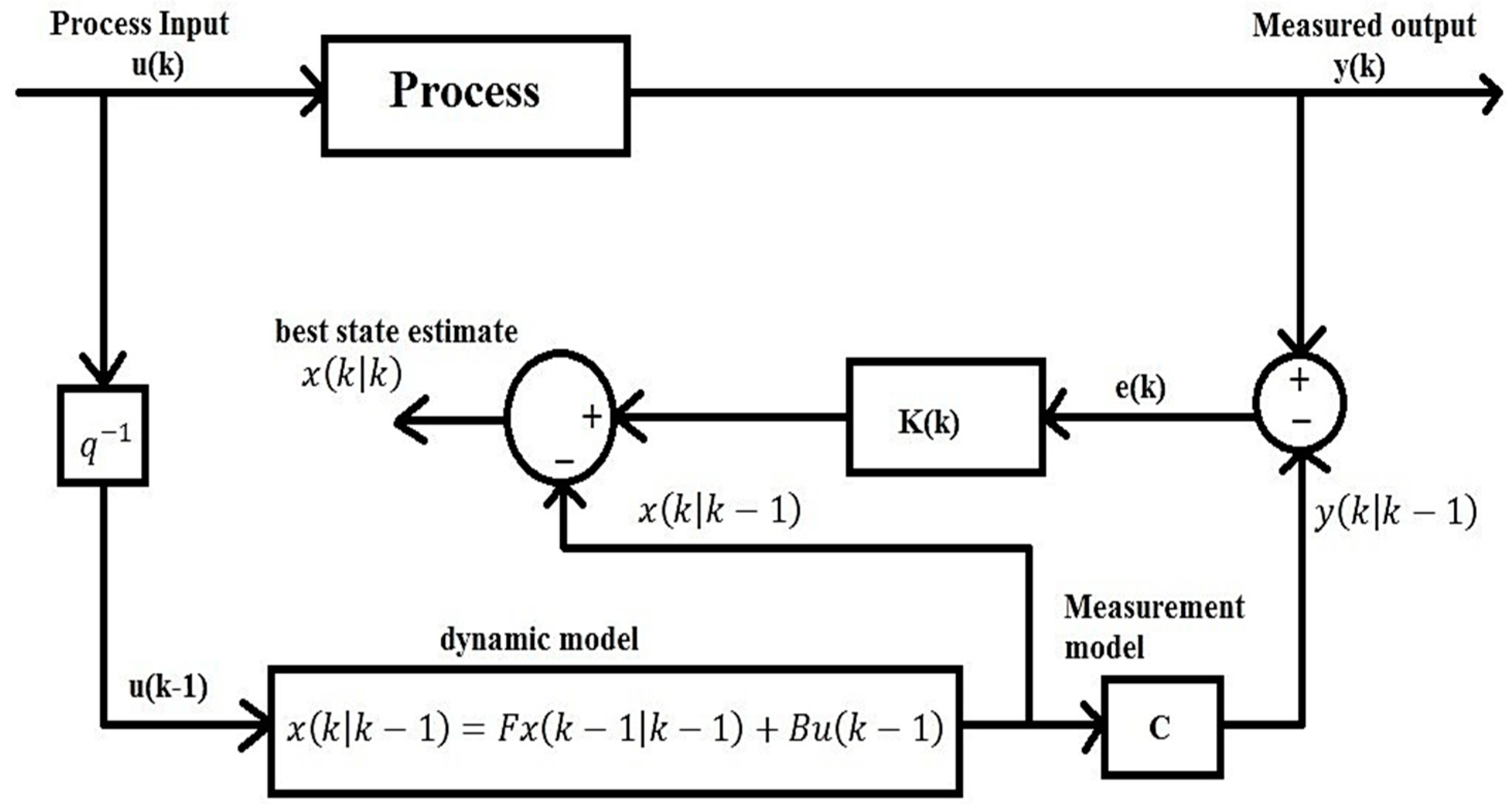
3.2. Kalman Filter Technique
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shah, M.S.; Joshi, J.B.; Kalsi, A.S.; Prasad, C.S.; Shukla, D.S. Analysis of flow through an orifice meter: CFD simulation. Chem. Eng. Sci. 2012, 26, 300–309. [Google Scholar] [CrossRef]
- Bentley, J.P. Principles of Measurement Systems; Pearson Education: London, UK, 2005. [Google Scholar]
- Manshoor, B.B.; Nicolleau, F.C.; Beck, S.B. The fractal flow conditioner for orifice plate flow meters. Flow Meas. Instrum. 2011, 22, 208–214. [Google Scholar] [CrossRef]
- Haddad, S.; Benghanem, M.; Mellit, A.; Daffallah, K.O. ANNs-based modeling and prediction of hourly flow rate of a photovoltaic water pumping system: Experimental validation. Renew. Sustain. Energy Rev. 2015, 1, 635–643. [Google Scholar] [CrossRef]
- Norgia, M.; Pesatori, A.; Donati, S. Compact laser-diode instrument for flow measurement. IEEE Trans. Instrum. Meas. 2016, 65, 1478–1483. [Google Scholar] [CrossRef]
- Liu, W.; Hu, J.; Zhao, X.; Pan, H.; Lakhiar, I.A.; Wang, W. Development and experimental analysis of an intelligent sensor for monitoring seed flow rate based on a seed flow reconstruction technique. Comput. Electron. Agric. 2019, 164, 104899. [Google Scholar] [CrossRef]
- Arlit, M.; Schroth, C.; Schleicher, E.; Hampel, U. Flow rate measurement in flows with asymmetric velocity profiles by means of distributed thermal anemometry. Flow Meas. Instrum. 2019, 68, 101570. [Google Scholar] [CrossRef]
- Langford, S.; Wiggins, C.; Tenpenny, D.; Ruggles, A. Positron emission particle tracking (PEPT) for fluid flow measurements. Nucl. Eng. Des. 2016, 302, 81–89. [Google Scholar] [CrossRef]
- Venkata, S.K.; Roy, B.K. A practically validated intelligent calibration circuit using optimized ANN for flow measurement by venture. J. Inst. Eng. Ser. B 2016, 97, 31–39. [Google Scholar] [CrossRef]
- Kim, Y.S. Overview of geometrical effects on the critical flow rate of sub-cooled and saturated water. Ann. Nucl. Energy 2015, 76, 12–18. [Google Scholar] [CrossRef]
- Lannes, D.P.; Gama, A.L.; Bento, T.F. Measurement of flow rate using straight pipes and pipe bends with integrated piezoelectric sensors. Flow Meas. Instrum. 2018, 60, 208–216. [Google Scholar] [CrossRef]
- Lay-Ekuakille, A.; Vergallo, P.; Griffo, G.; Morello, R. Pipeline flow measurement using real-time imaging. Measurement 2014, 47, 1008–1015. [Google Scholar] [CrossRef]
- Sinha, S.; Banerjee, D.; Mandal, N.; Sarkar, R.; Bera, S.C. Design and implementation of real-time flow measurement system using Hall probe sensor and PC-based SCADA. IEEE Sens. J. 2015, 15, 5592–5600. [Google Scholar] [CrossRef]
- Hussain, A.; Ahmad, Z.; Ojha, C.S. Flow through lateral circular orifice under free and submerged flow conditions. Flow Meas. Instrum. 2016, 52, 57–66. [Google Scholar] [CrossRef]
- Schena, E.; Cecchini, S.; Silvestri, S. An orifice meter for bidirectional air flow measurements: Influence of gas thermo-hygrometric content on static response and bidirectionality. Flow Meas. Instrum. 2013, 34, 105–112. [Google Scholar] [CrossRef]
- Peters, F.; Groß, T.F. Flow rate measurement by an orifice in a slowly reciprocating gas flow. Flow Meas. Instrum. 2011, 22, 81–85. [Google Scholar] [CrossRef]
- Shan, F.; Liu, Z.; Liu, W.; Tsuji, Y. Effects of the orifice to pipe diameter ratio on orifice flows. Chem. Eng. Sci. 2016, 152, 497–506. [Google Scholar] [CrossRef]
- Jaiswal, S.K.; Yadav, S.; Agarwal, R. Design and development of a novel water flow measurement system. Measurement 2017, 105, 120–129. [Google Scholar] [CrossRef]
- Edwards, J.E.; Otterson, D.W. Tech Talk (6) Flow Measurement Basics (Part 1). Meas. Control 2015, 48, 18–25. [Google Scholar] [CrossRef]
- Xing, L.; Hua, C.; Zhu, H.; Drahm, W. Flow Measurement Model of Ultrasonic Flowmeter for Gas-Liquid Two-Phase Stratified and Annular Flows. Adv. Mech. Eng. 2014, 6, 194871. [Google Scholar] [CrossRef]
- Wang, X.; Sun, X.; Doup, B.; Zhao, H. Dynamic modeling strategy for flow regime transition in gas-liquid two-phase flows. J. Comput. Multiph. Flows 2012, 4, 387–397. [Google Scholar] [CrossRef]
- Medeiros, K.A.; de Oliveira, F.L.; Barbosa, C.R.; de Oliveira, E.C. Optimization of flow rate measurement using piezoelectric accelerometers: Application in water industry. Measurement 2016, 91, 576–581. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, L.; Wang, T.; Wang, X.; Hu, Y.; Duan, Q. Application of soft computing techniques to multiphase flow measurement: A review. Flow Meas. Instrum. 2018, 60, 30–43. [Google Scholar] [CrossRef]
- Tsukada, K.; Kikura, H. Study on Velocity Profile Measurement of Saturated Jet Flow by Air-coupled Ultrasound. Energy Procedia 2017, 131, 436–443. [Google Scholar] [CrossRef]
- Krejčí, J.; Ježová, L.; Kučerová, R.; Plička, R.; Broža, Š.; Krejčí, D.; Ventrubová, I. The measurement of small flow. Sens. Actuators A Phys. 2017, 266, 308–313. [Google Scholar] [CrossRef]
- Boushaki, T.; Koched, A.; Mansouri, Z.; Lespinasse, F. Volumetric velocity measurements (V3V) on turbulent swirling flows. Flow Meas. Instrum. 2017, 54, 46–55. [Google Scholar] [CrossRef]
- Li, Q.; Xing, J.; Shang, D.; Wang, Y. A Flow Velocity Measurement Method Based on a PVDF Piezoelectric Sensor. Sensors 2019, 19, 1657. [Google Scholar] [CrossRef]
- Formato, G.; Romano, R.; Formato, A.; Sorvari, J.; Koiranen, T.; Pellegrino, A.; Villecco, F. Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations. Machines 2019, 7, 50. [Google Scholar] [CrossRef]
- Chen, S.; Yu, M.; Kan, J.; Li, J.; Zhang, Z.; Xie, X.; Wang, X. A Dual-Chamber Serial–Parallel Piezoelectric Pump with an Integrated Sensor for Flow Rate Measurement. Sensors 2019, 19, 1447. [Google Scholar] [CrossRef]
- Silva, W.L.; Lima, V.S.; Fonseca, D.A.; Salazar, A.O.; Maitelli, C.W.; Echaiz, E.; German, A. Study of Flow Rate Measurements Derived from Temperature Profiles of an Emulated Well by a Laboratory Prototype. Sensors 2019, 19, 1498. [Google Scholar] [CrossRef]
- Rad, C.R.; Hancu, O. An improved nonlinear modelling and identification methodology of a servo-pneumatic actuating system with complex internal design for high-accuracy motion control applications. Simul. Model. Pract. Theory 2017, 75, 29–47. [Google Scholar] [CrossRef]
- Metwally, M.; Aly, A.A.; Ola, M. Effect of spool side chambers on dynamic response of contactless electro-operated pneumatic directional control valve. Comput. Fluids 2013, 86, 125–132. [Google Scholar] [CrossRef]
- Topçu, E.E.; Yüksel, İ.; Kamış, Z. Development of electro-pneumatic fast switching valve and investigation of its characteristics. Mechatronics 2006, 16, 365–378. [Google Scholar] [CrossRef]
- Li, S.; Wu, P.; Cao, L.; Wu, D.; She, Y. CFD simulation of dynamic characteristics of a solenoid valve for exhaust gas turbocharger system. Appl. Therm. Eng. 2017, 110, 213–222. [Google Scholar] [CrossRef]
- Tlisov, A.A.; Mitrishkin, Y.V. Adaptive control system for pipeline valve pneumatic actuator. IFAC Proc. Vol. 2009, 42, 373–378. [Google Scholar] [CrossRef]
- Chinyaev, I.R.; Fominykh, A.V.; Pochivalov, E.A. Method for Determining of the Valve Cavitation Characteristics. Procedia Eng. 2016, 150, 260–265. [Google Scholar] [CrossRef]
- Righettini, P.; Giberti, H.; Strada, R. A novel in field method for determining the flow rate characteristics of pneumatic servo axes. J. Dyn. Syst. Meas. Control 2013, 135, 041013. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, L.; Zhao, T.; Fan, W.; Kagawa, T. Determination of Flow Rate Characteristics for Pneumatic Components During Isothermal Discharge by Integral Algorithm. J. Dyn. Syst. Meas. Control 2012, 134, 061005. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes; Springer-Verlag: London, UK, 31 May 2007. [Google Scholar]
- Pappalardo, C.; Guida, D. System identification algorithm for computing the modal parameters of linear mechanical systems. Machines 2018, 6, 12. [Google Scholar] [CrossRef]
- Astrom, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: New Jersey, NJ, USA, 2010; pp. 201–219. [Google Scholar]
- Grewal, M.S. Kalman Filtering; Springer: Berlin/Heidelberg, Germany, 2011; pp. 705–708. [Google Scholar]



| References | Technique/Method | Findings |
|---|---|---|
| [4] | Artificial neural network | It is reported that the models developed using artificial neural networks are for forecasting of flow rate. Lesser computational effort |
| [5] | Doppler shift | Accuracy of 0.1 L/min for a 0–6 L/min range. Limited to laminar flow measurement. |
| [6] | Particle Counting method Mass estimation method | Suitable for measurement in common and large seed flow rate with accuracy greater than 95%. |
| [7] | Thermal anemometry grid sensor | Flow rate deviation of less than 2% for 83% of tested data. |
| [8] | Positron emission particle tracking algorithm | Majorly used for turbulent flow rates. |
| [11] | Integrated piezoelectric sensor | Integrated piezoelectric sensor placed in straight and bent pipes, with high sensitivity towards 900 bends. |
| [12] | Image flow measurement | The flow rate was measured through real-time video acquisition. This is a non-contact technique. |
| [13] | Hall probe sensor | The flow rate was measured through a hall probe sensor connected to the rotameter with a magnetic float. Limited range due to magnetic float size. |
| Kalman Filter Observer | Pole Placement | |
|---|---|---|
| IAE | 0.4896 | 0.165 |
| ISE | 0.038 | 0.053 |
| ITAE | 6.732 | 11.745 |
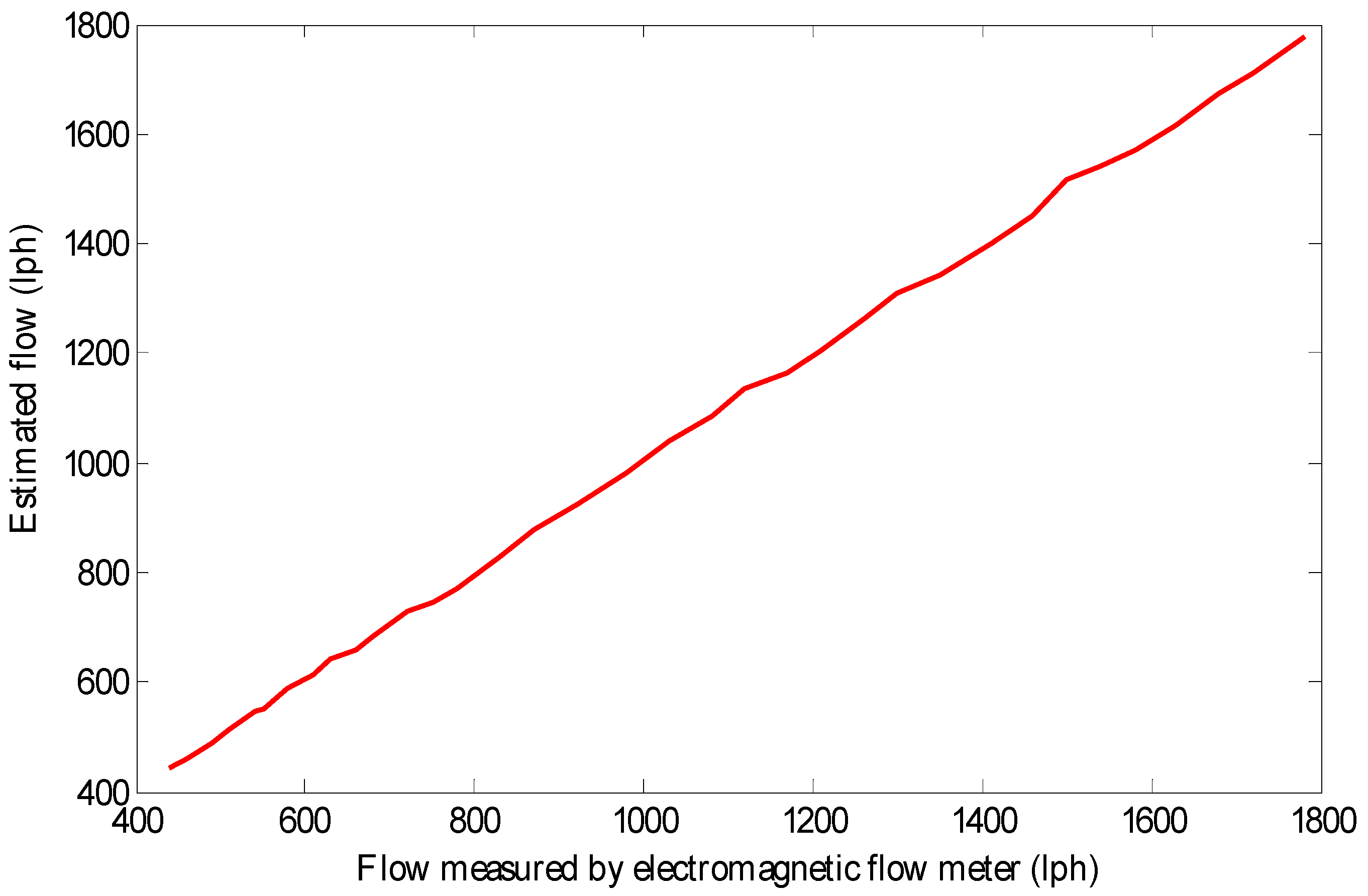
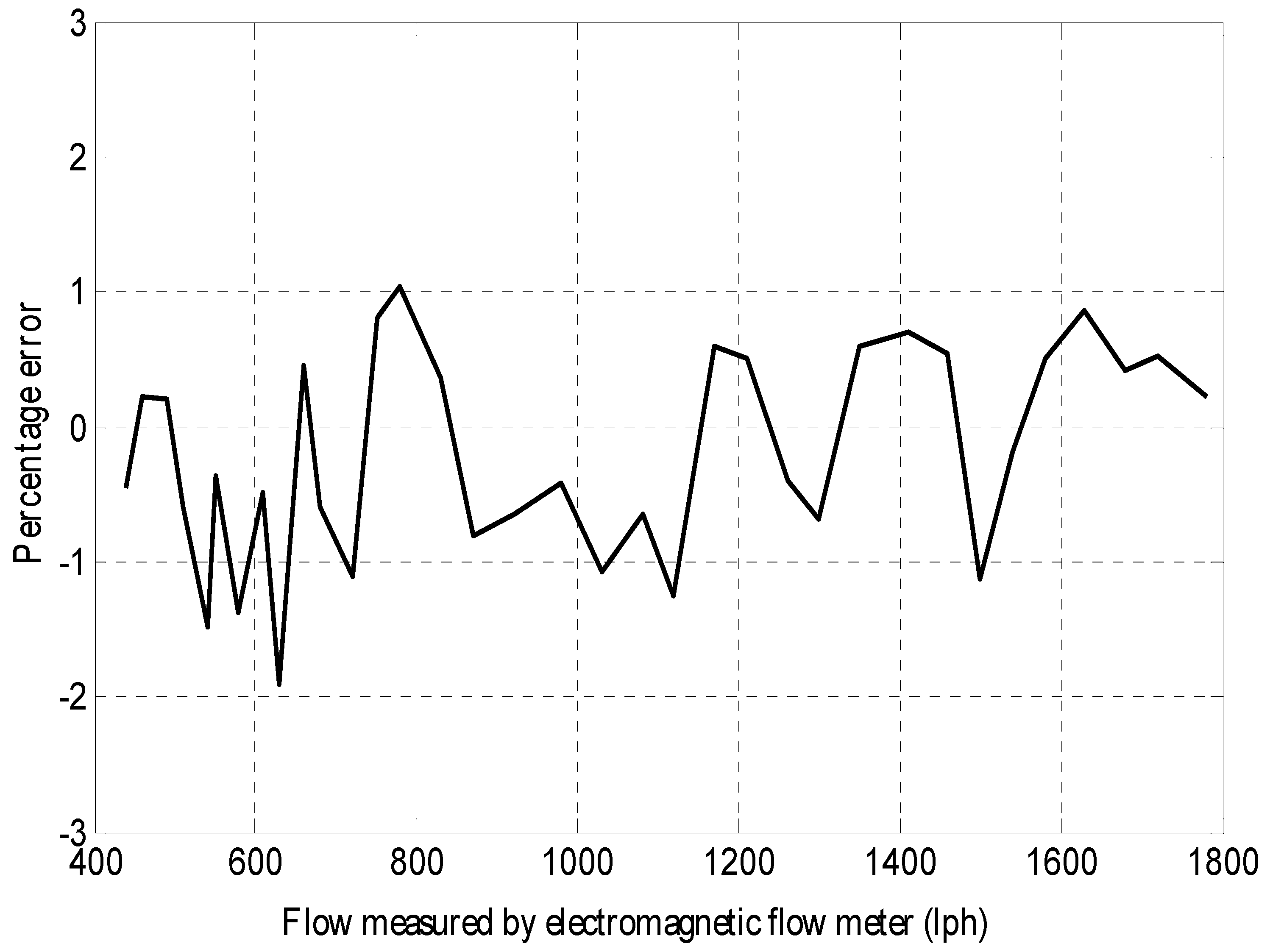
| Actual Flow Rate (lph) | Estimated Flow Rate (lph) | Percentage Error |
|---|---|---|
| 440 | 442 | −0.45 |
| 460 | 459 | 0.22 |
| 490 | 489 | 0.20 |
| 510 | 513 | −0.59 |
| 540 | 548 | −1.48 |
| 550 | 552 | −0.36 |
| 580 | 588 | −1.38 |
| 610 | 613 | −0.49 |
| 630 | 642 | −1.90 |
| 660 | 657 | 0.45 |
| 680 | 684 | −0.59 |
| 720 | 728 | −1.11 |
| 750 | 744 | 0.80 |
| 780 | 772 | 1.03 |
| 830 | 827 | 0.36 |
| 870 | 877 | −0.80 |
| 920 | 926 | −0.65 |
| 980 | 984 | −0.41 |
| 1030 | 1041 | −1.07 |
| 1080 | 1087 | −0.65 |
| 1120 | 1134 | −1.25 |
| 1170 | 1163 | 0.60 |
| 1210 | 1204 | 0.50 |
| 1260 | 1265 | −0.40 |
| 1300 | 1309 | −0.69 |
| 1350 | 1342 | 0.59 |
| 1410 | 1400 | 0.71 |
| 1460 | 1452 | 0.55 |
| 1500 | 1517 | −1.13 |
| 1540 | 1543 | −0.19 |
| 1580 | 1572 | 0.51 |
| 1630 | 1616 | 0.86 |
| 1680 | 1673 | 0.42 |
| 1720 | 1711 | 0.52 |
| 1780 | 1776 | 0.22 |
| Parameters | Proposed Method Using Kalman Filter | Nonlinear Autoregressive Exogenous Model Reported in Reference [4] |
|---|---|---|
| MAE | 8.6 × 10−4 | 0.2041 |
| MSE | 5.96 × 10−5 | 0.1111 |
| RMSE | 0.0077 | 0.3332 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navada, B.R.; Venkata, S.K.; Rao, S. A Soft Sensor for Estimation of In-Flow Rate in a Flow Process Using Pole Placement and Kalman Filter Methods. Machines 2019, 7, 63. https://doi.org/10.3390/machines7040063
Navada BR, Venkata SK, Rao S. A Soft Sensor for Estimation of In-Flow Rate in a Flow Process Using Pole Placement and Kalman Filter Methods. Machines. 2019; 7(4):63. https://doi.org/10.3390/machines7040063
Chicago/Turabian StyleNavada, Bhagya R., Santhosh K. Venkata, and Swetha Rao. 2019. "A Soft Sensor for Estimation of In-Flow Rate in a Flow Process Using Pole Placement and Kalman Filter Methods" Machines 7, no. 4: 63. https://doi.org/10.3390/machines7040063
APA StyleNavada, B. R., Venkata, S. K., & Rao, S. (2019). A Soft Sensor for Estimation of In-Flow Rate in a Flow Process Using Pole Placement and Kalman Filter Methods. Machines, 7(4), 63. https://doi.org/10.3390/machines7040063





