Non-Rectangular Dynamic Range of the Drive System: A New Approach for the Choice of Motor and Transmission
Abstract
:1. Introduction
- -
- The feasibility analysis allows the designer to exclude all the drive system-transmission couples that are not able to drive the given load from the point of view of their operating ranges, i.e., of their torque and speed characteristics. In this phase, one (or more than one) reference task is taken into consideration, assuming that the machine executes it perfectly, i.e., with no control error. It is clear that a drive system-reducer couple can be excluded because of either the thermal problem or the torque peak problem. The feasibility analysis permits the designer to rapidly limit the number of admissible motor-transmission couples and, if convenient, to apply his experience to them to further restrict this set, in order to proceed with the optimization phase.
- -
- Then, the optimization phase allows the designer to find the motor-transmission pair that best meets some additional criteria (minimum cost, weight, volume etc.).
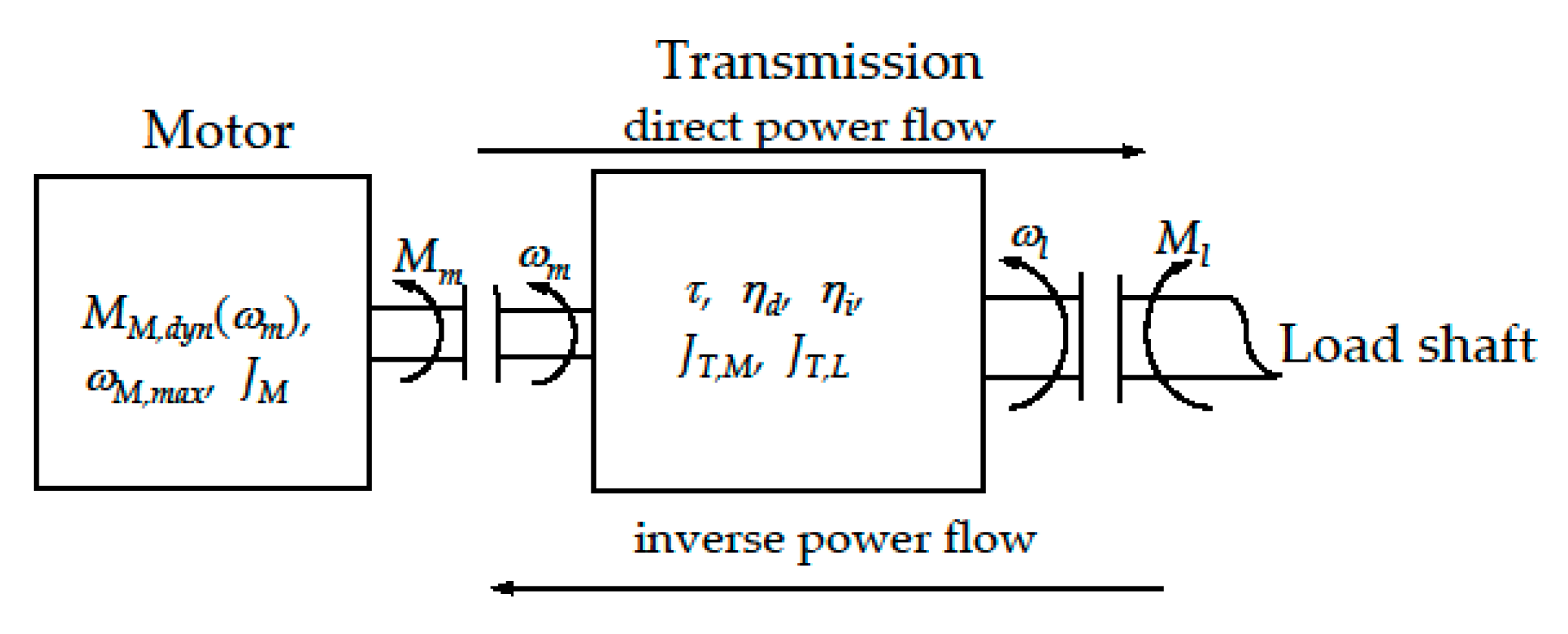
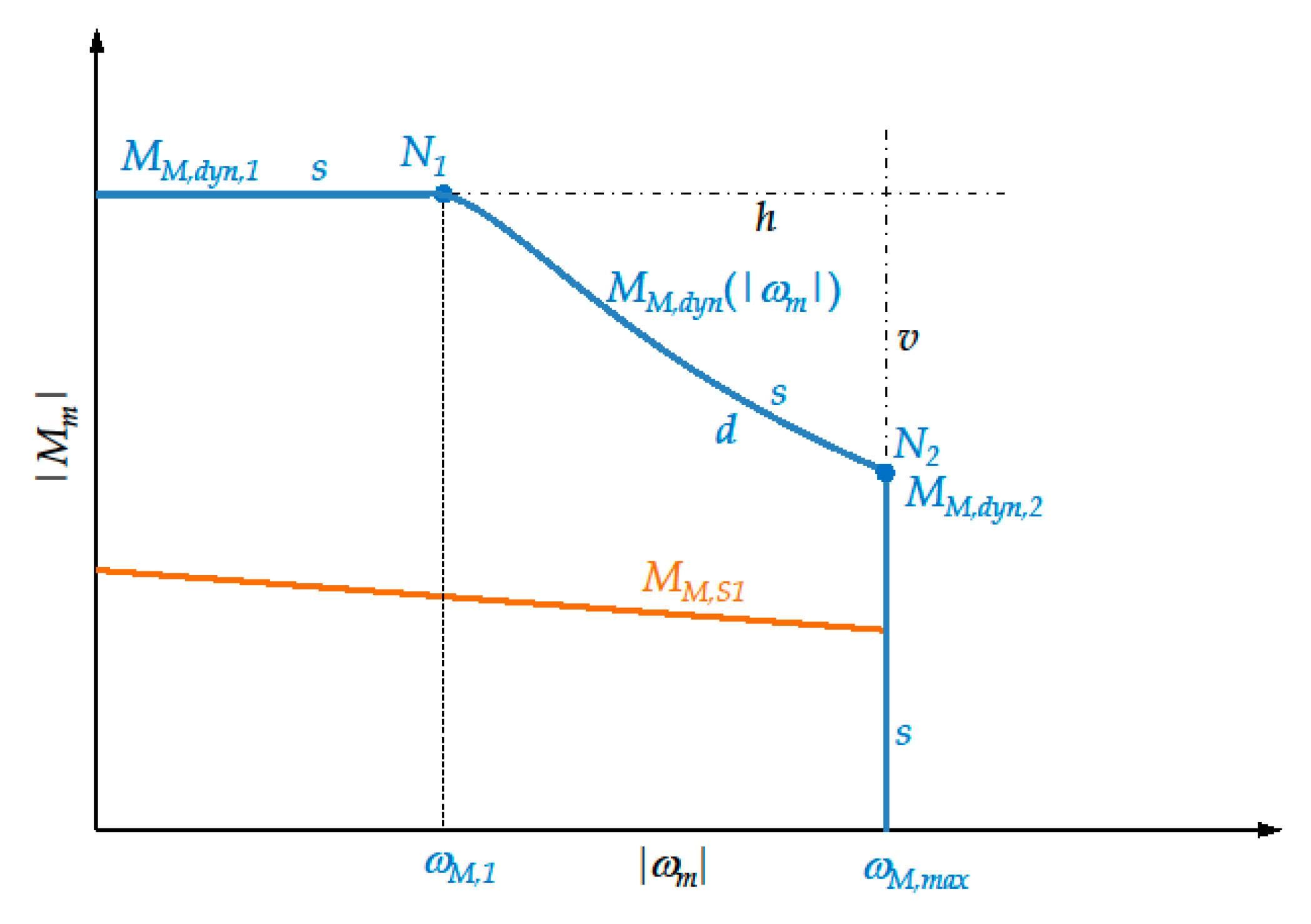
2. Drive System and Transmission Characterization
- -
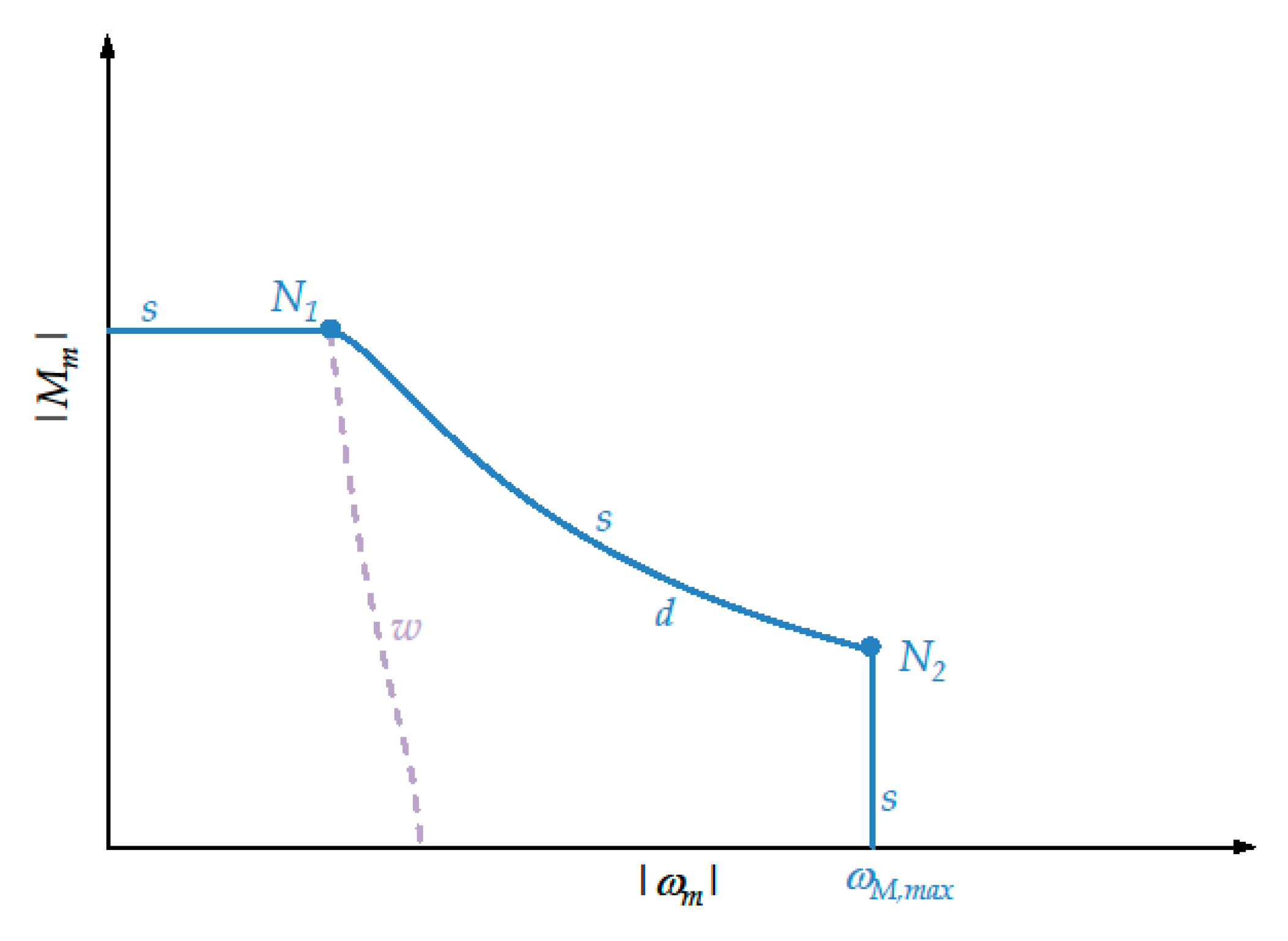
- A horizontal segment belonging to the straight-line h, with a constant torque equal to , due to current saturation;
- -
- A descending arc d (arc), which is the limit curve of the dynamic operating range of the drive system corresponding to the saturation of both current and voltage;
- -
- A vertical segment belonging to the straight-line v, with a constant speed equal to , which is electronically fixed by the drive system.
- -
- The transmission efficiencies are often quite high and the introduction of a certain safety margin maintains the validity of the choices made with reference to the ideal case.
- -
- The moments of inertia of the transmission, on motor side and on load side, are often negligible compared to the moments of inertia of motor and load, respectively.
3. Task Specifications and Inequalities due to the Dynamic Operating Range
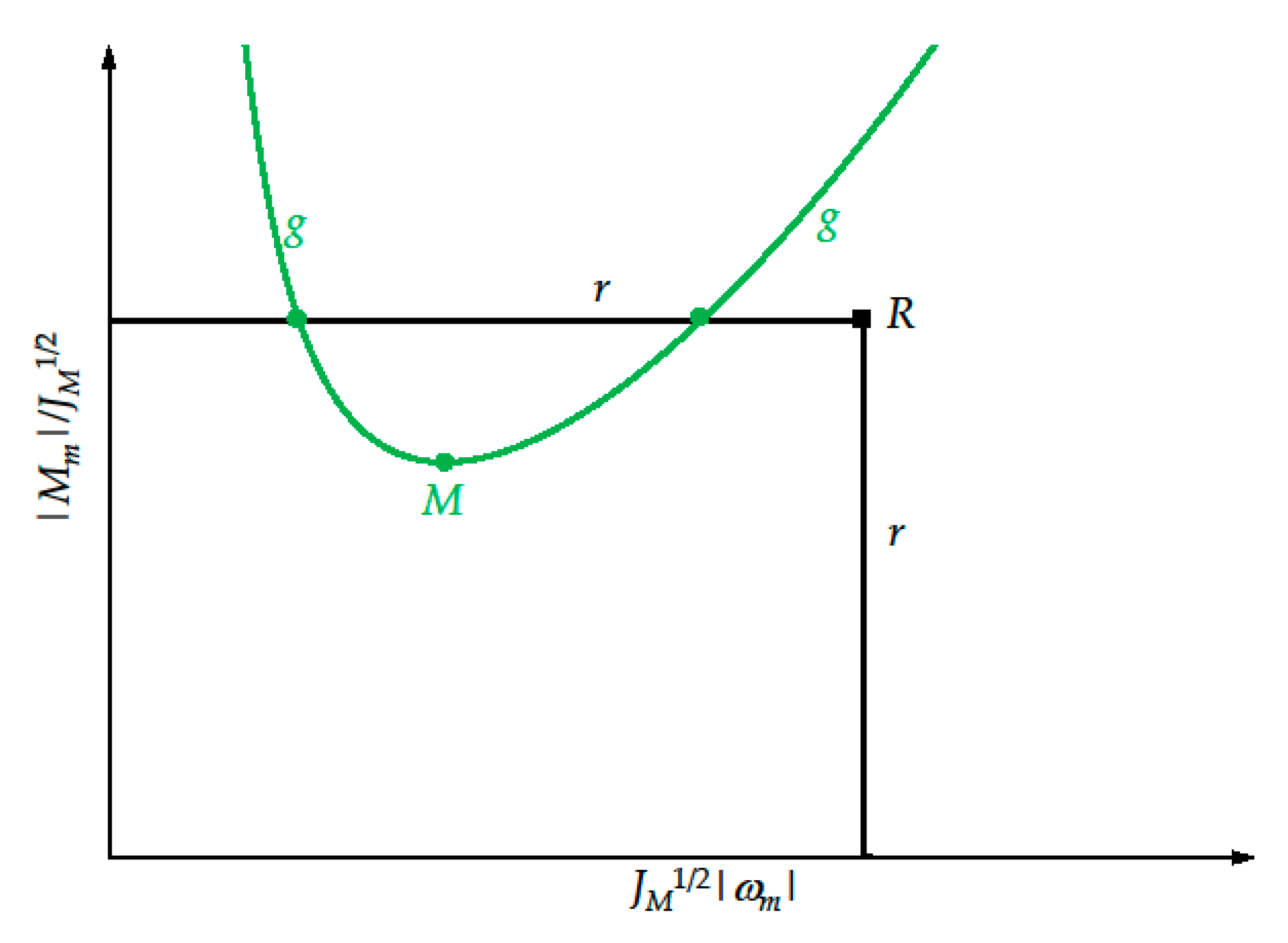
4. Classical Approach
- -
- A global load torque curve g is taken into consideration, i.e., a curve that depends on the global reference task; this curve depends on the load speed only through its maximum value , whereor is a specification independent of the reference task and greater than the value given by Equation (5).
- -
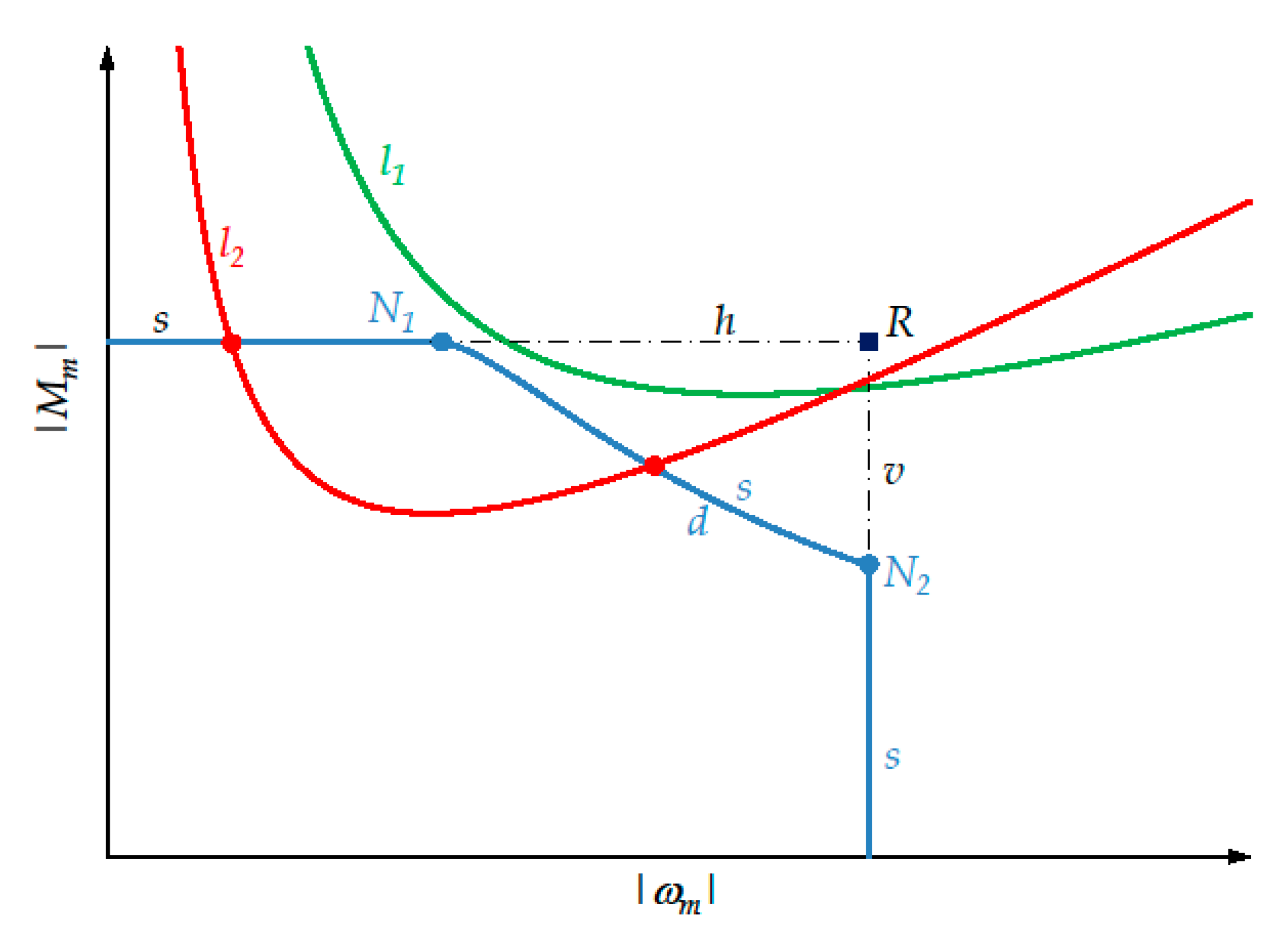
- Each drive system is represented by a corresponding point, i.e., the vertex R of the rectangular dynamic operating range, whose limit curve is denoted by r.
- -
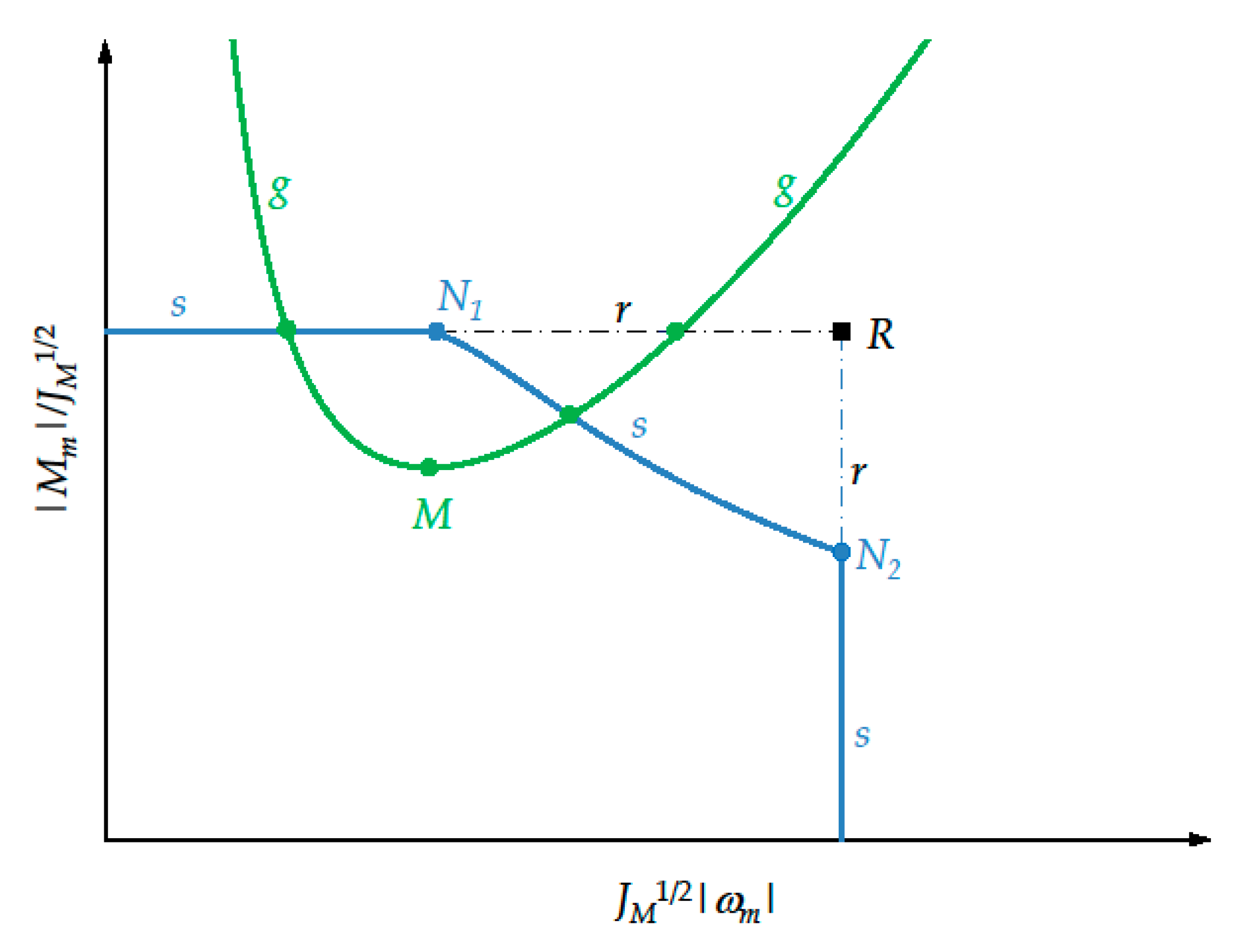
- The same global load torque curve g as before.
- -
- Each drive system not only by means of the corresponding non-rectangular dynamic operating range, whose limit curve is denoted by s, but also by means of the corresponding rectangular operating range, denoted by r. Its vertex is denoted by R.
- (1)
- The drive system must surely be excluded;
- (2)
- The transmission ratio range in correspondence to which the motor can be adopted is perfectly defined.
- (1)
- To ascertain if they are admissible or not;
- (2)
- To completely determine the corresponding transmission ratio range for motors whose admissibility is already known.
5. The New Approach
5.1. Outlines of the New Approach
5.2. New Approach for a Non-Rectangular Dynamic Operating Range
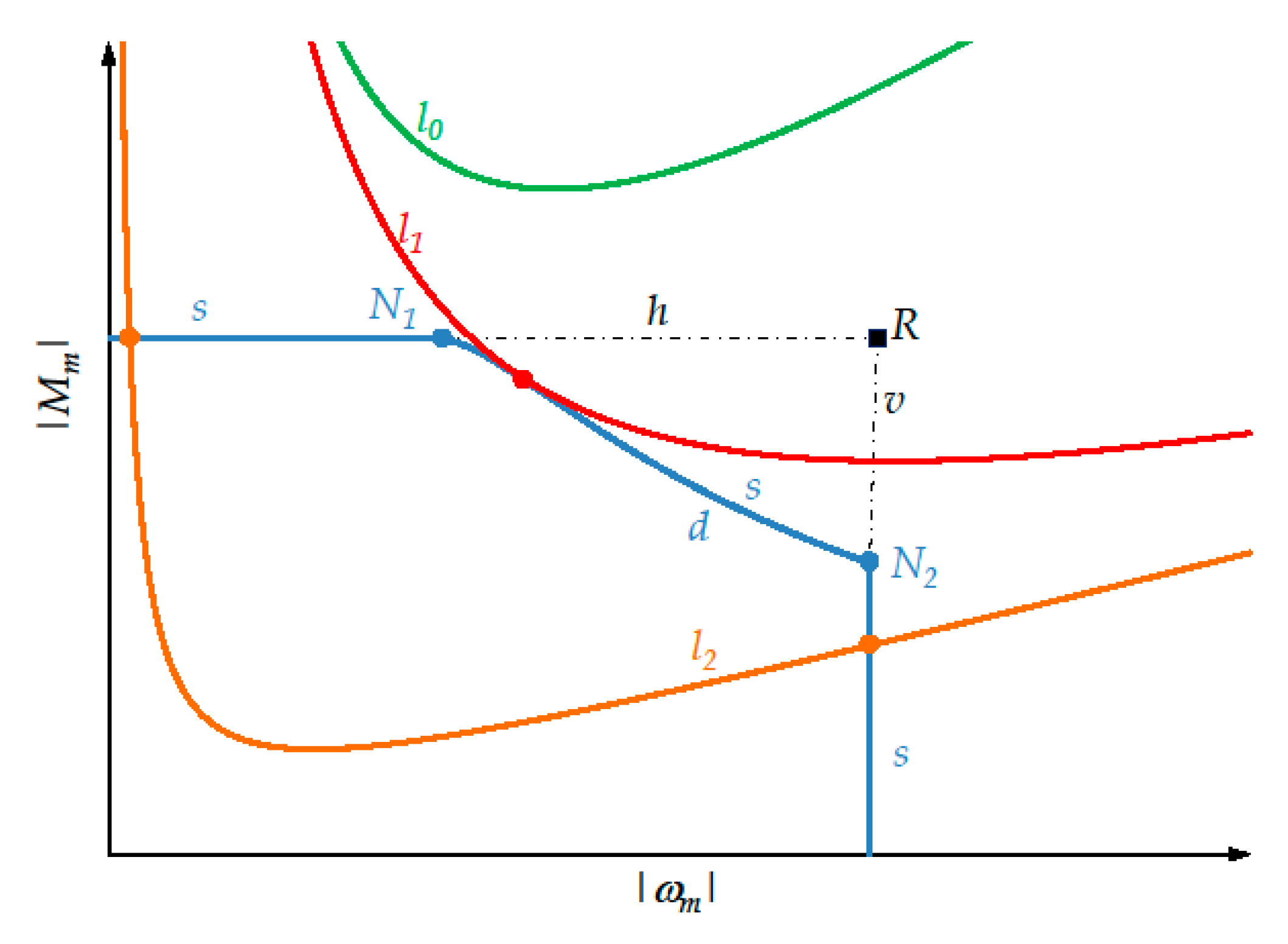
- Curve l can intersect the curvilinear triangle , but not the limit curve s of the dynamic operating range (curve ): in this case the drive system must be excluded.
- Curve l can intersect the limit curve of the dynamic operating range in correspondence to arc d (curve ).
6. Limit Curve of a Non-Rectangular Dynamic Operating Range
6.1. Limit Curve Equation in Ideal Conditions
6.2. Polynomial Interpolation
- -
- Some required electrical parameters of the drive system are not provided by the catalog.
- -
- At high current, there is not linearity between torque and current.
- -
- The resistances are not constant and, in particular, at high motor speed they increase with speed because of the skin and proximity effect, which determine a non-uniform distribution of current density in the wire section.
7. Procedure to Find the Transmission Ratio Range Corresponding to the Given Motor
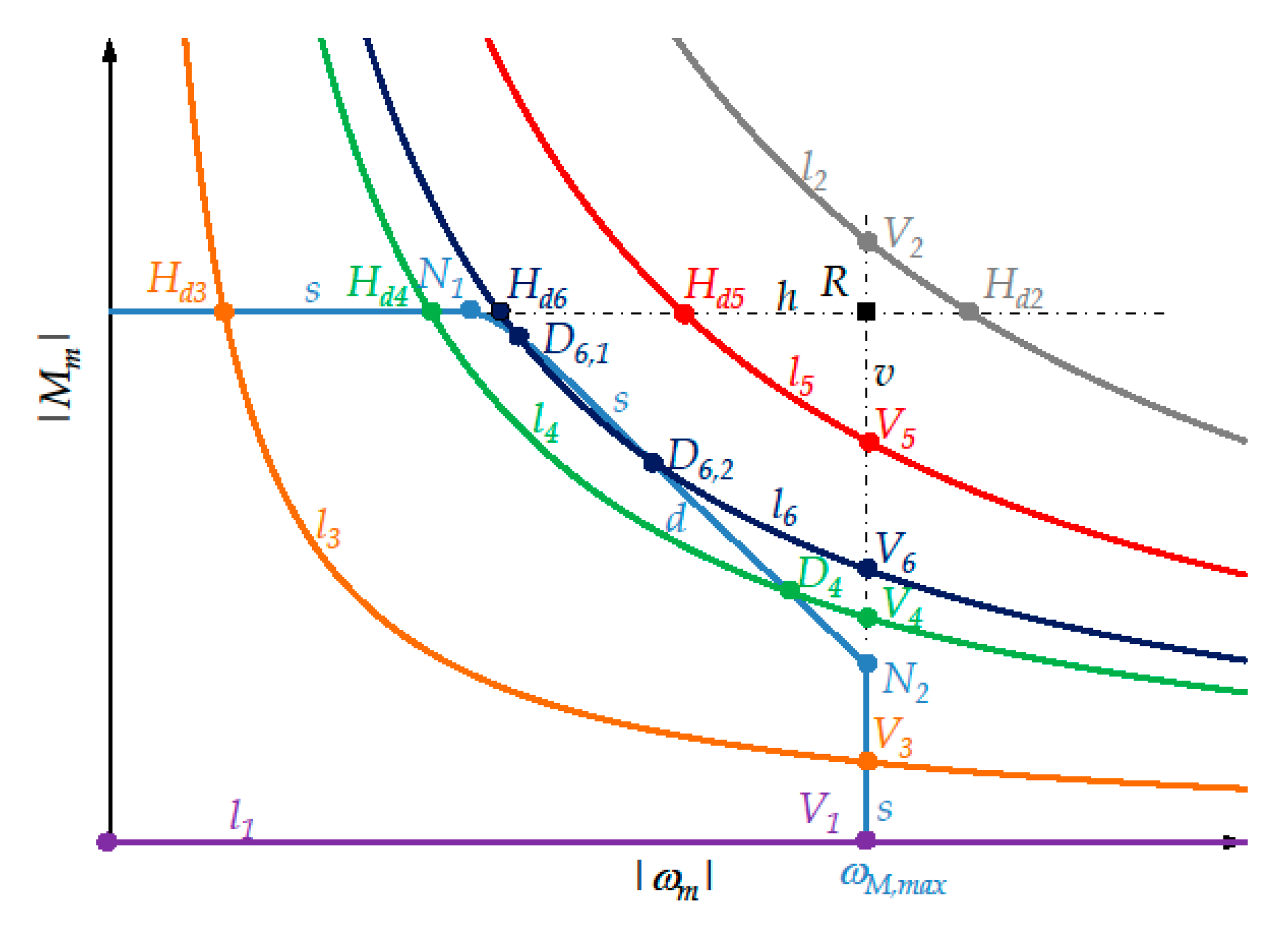
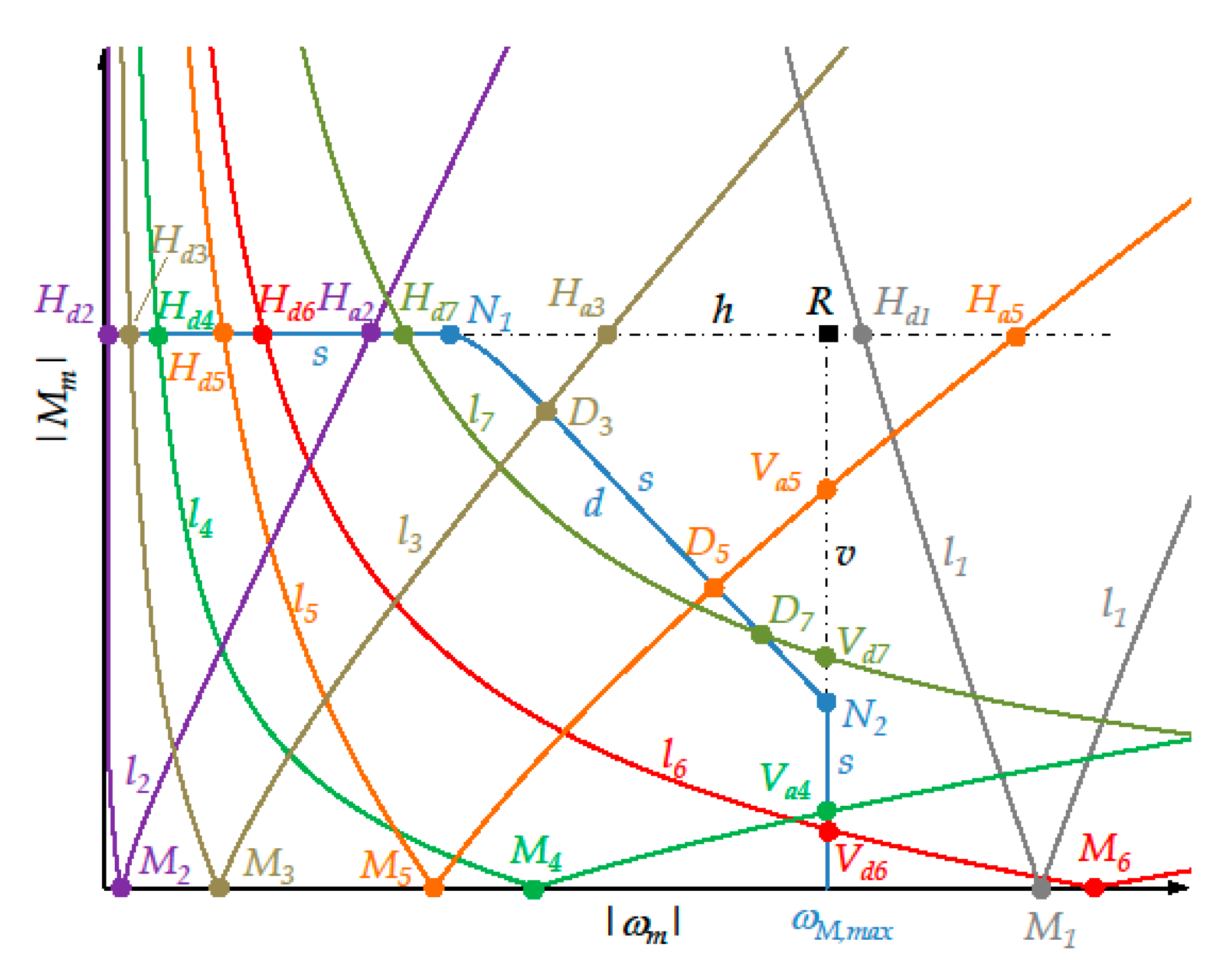
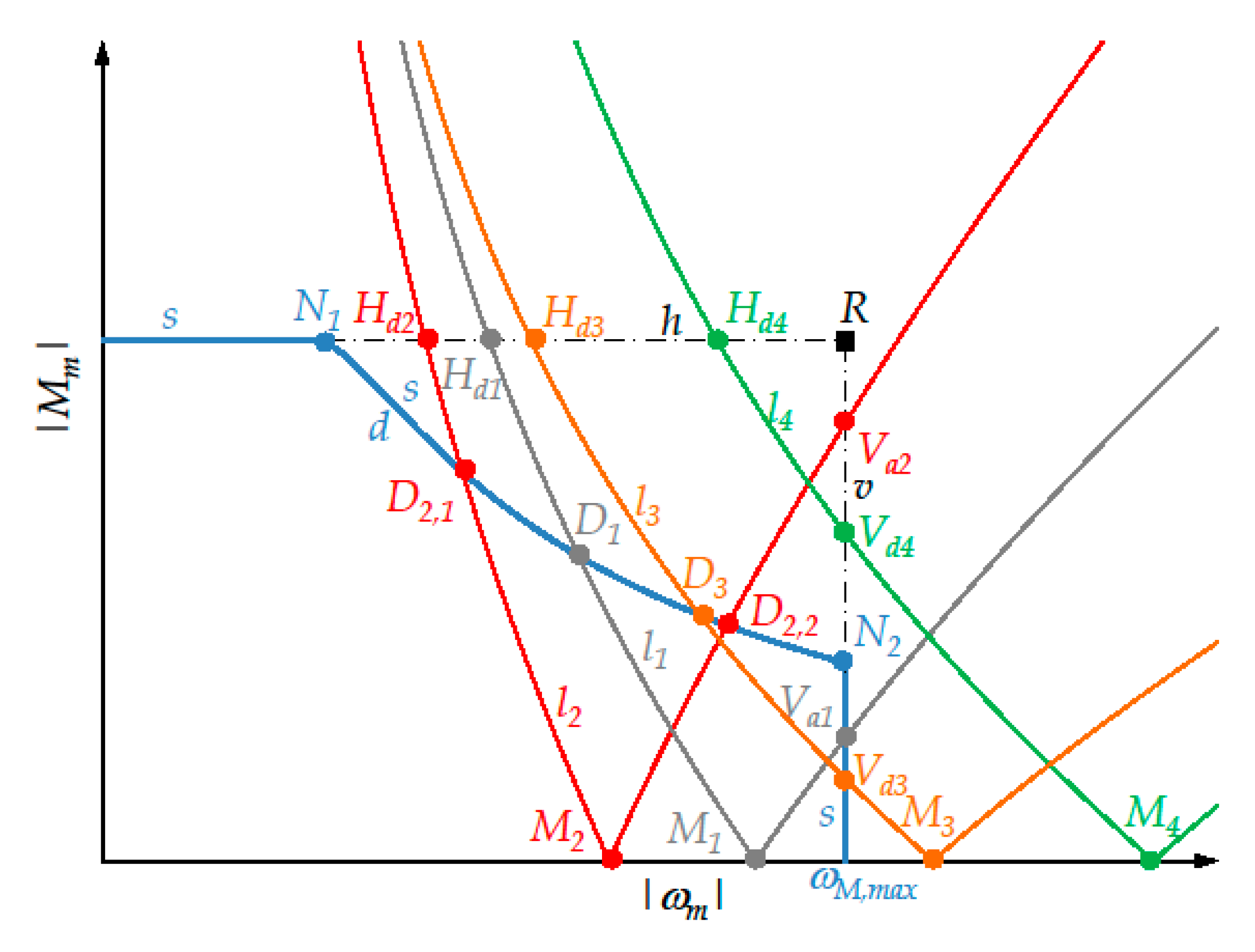
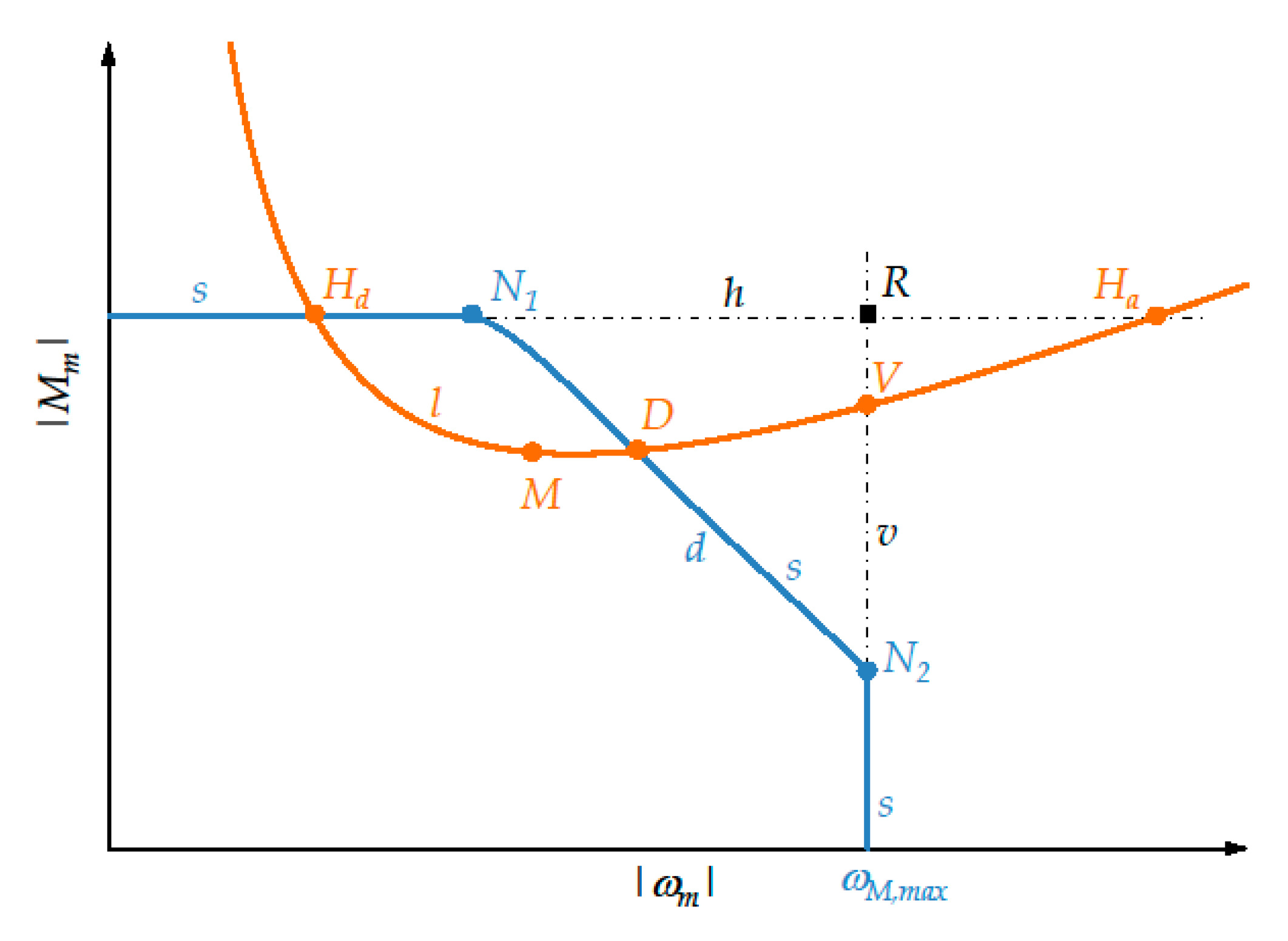
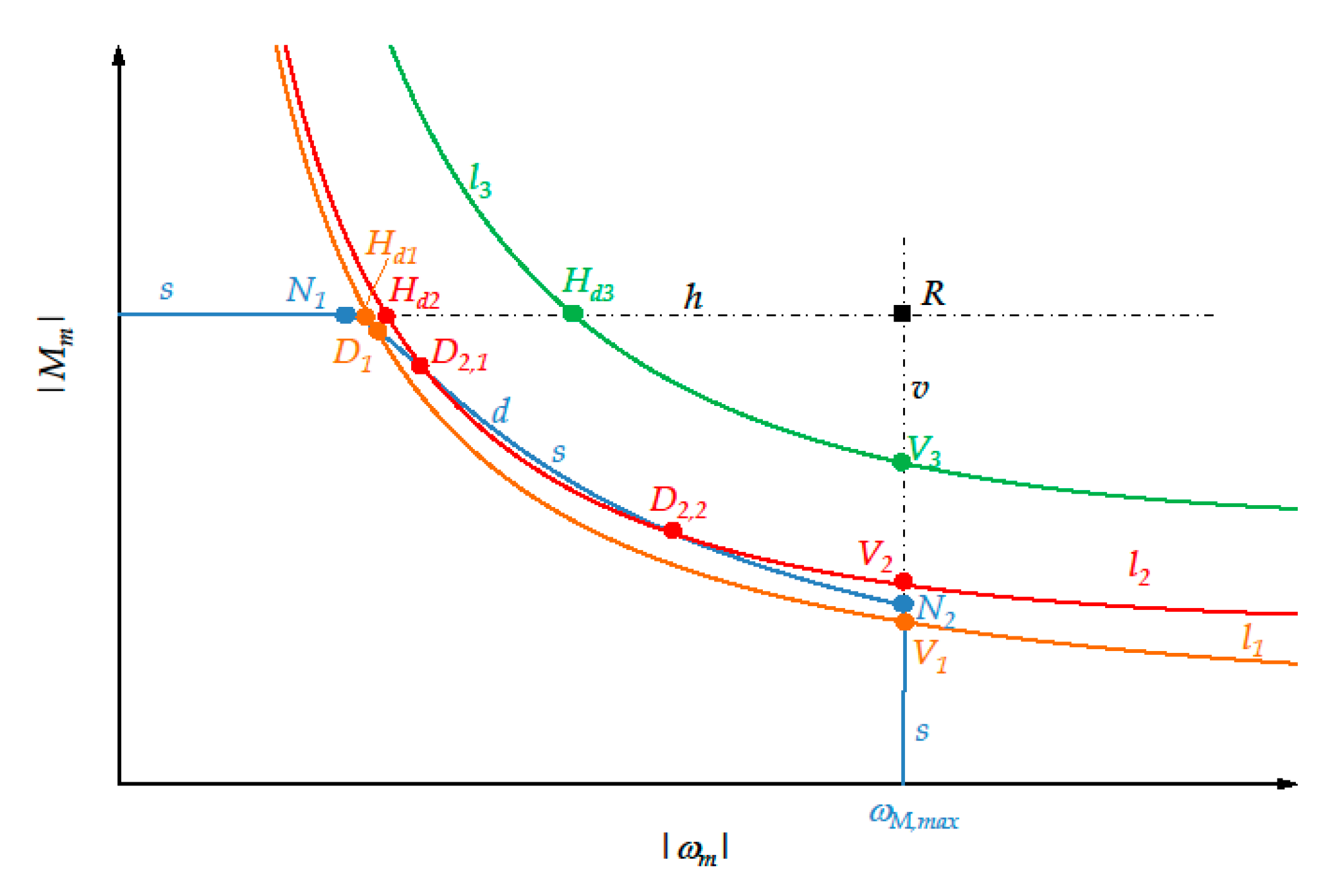
7.1. Significant Points for the New Approach
- -
- and denote the intersections, if exist, between the instantaneous load torque curve l and the horizontal straight-line h (see Figure 2) whose ordinate is . In particular, is the intersection of the descending arc of l, while is that of the ascending arc. Obviously, lies to the left of .
- -
- D denotes any intersection of l with the descending arc d of the limit curve of the dynamic operating range of the motor.
- -
- V denotes the only intersection of l with the vertical straight-line v whose abscissa is
7.2. Brief Explanation of the New Approach
- If the exclusion of the motor is possible without calculating the intersections between curve l and arc d.
- Otherwise, if both the intersections between curves l and s do not belong to arc d.
8. Effect of Efficiency and Inertia of the Transmission
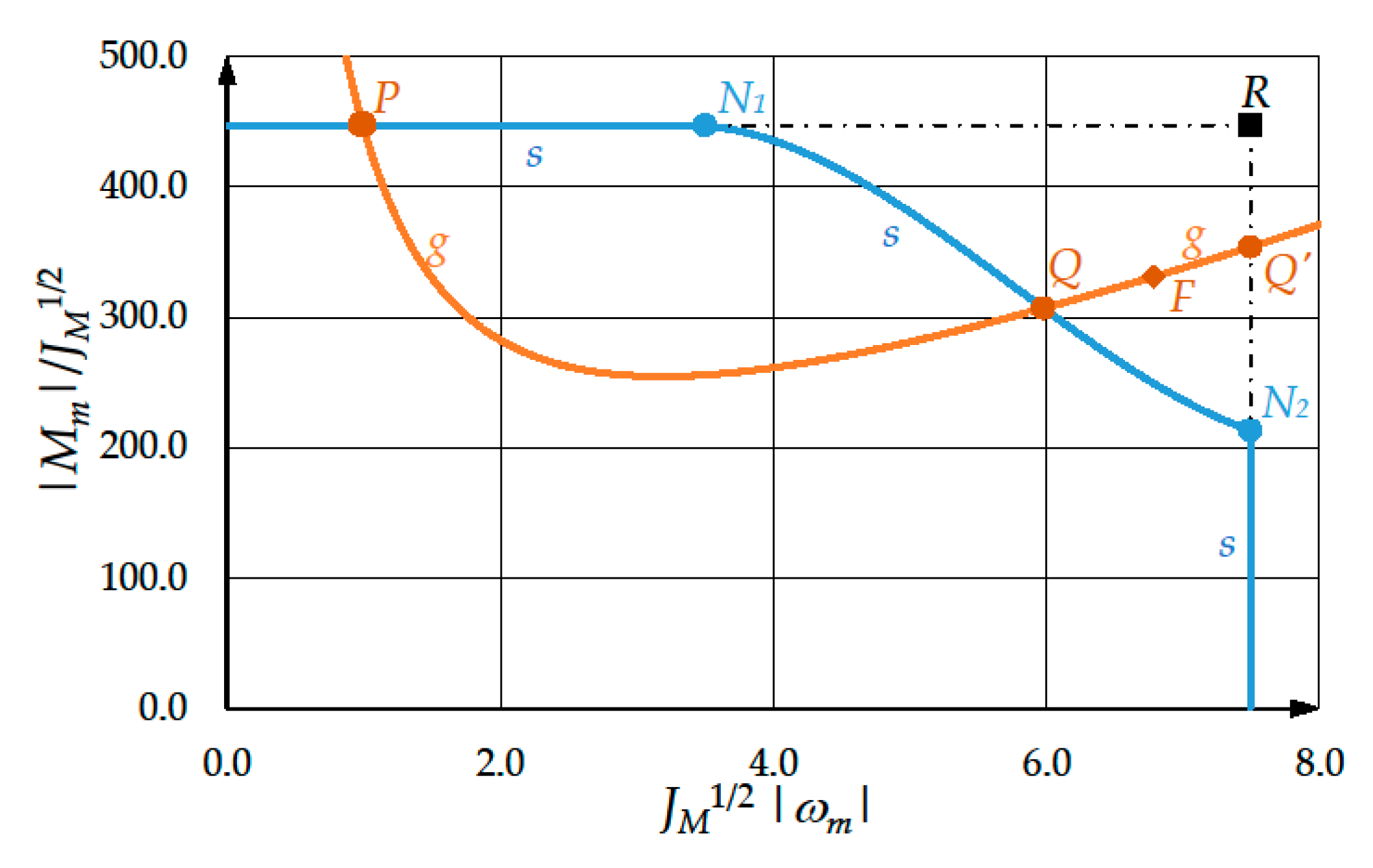
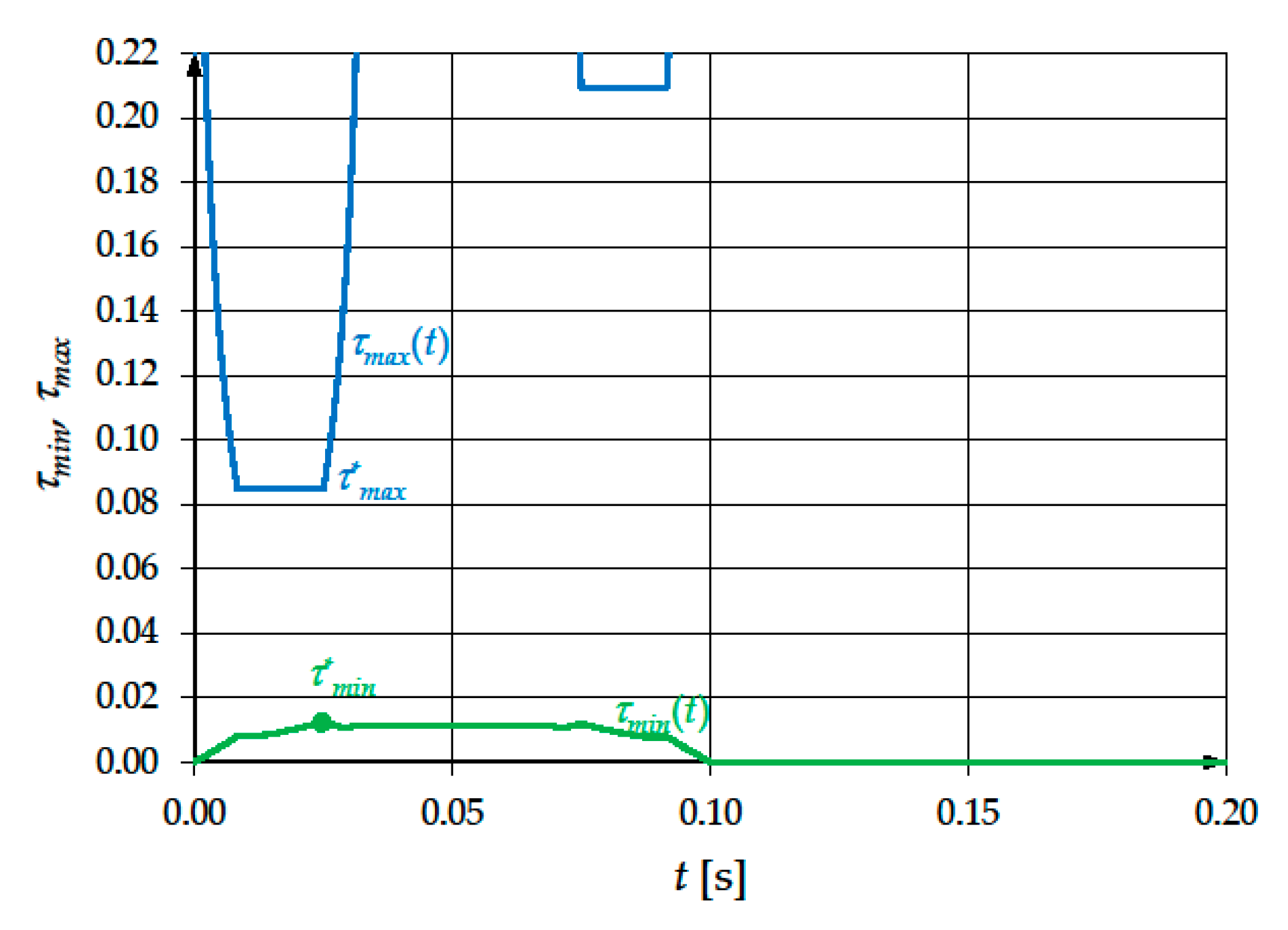
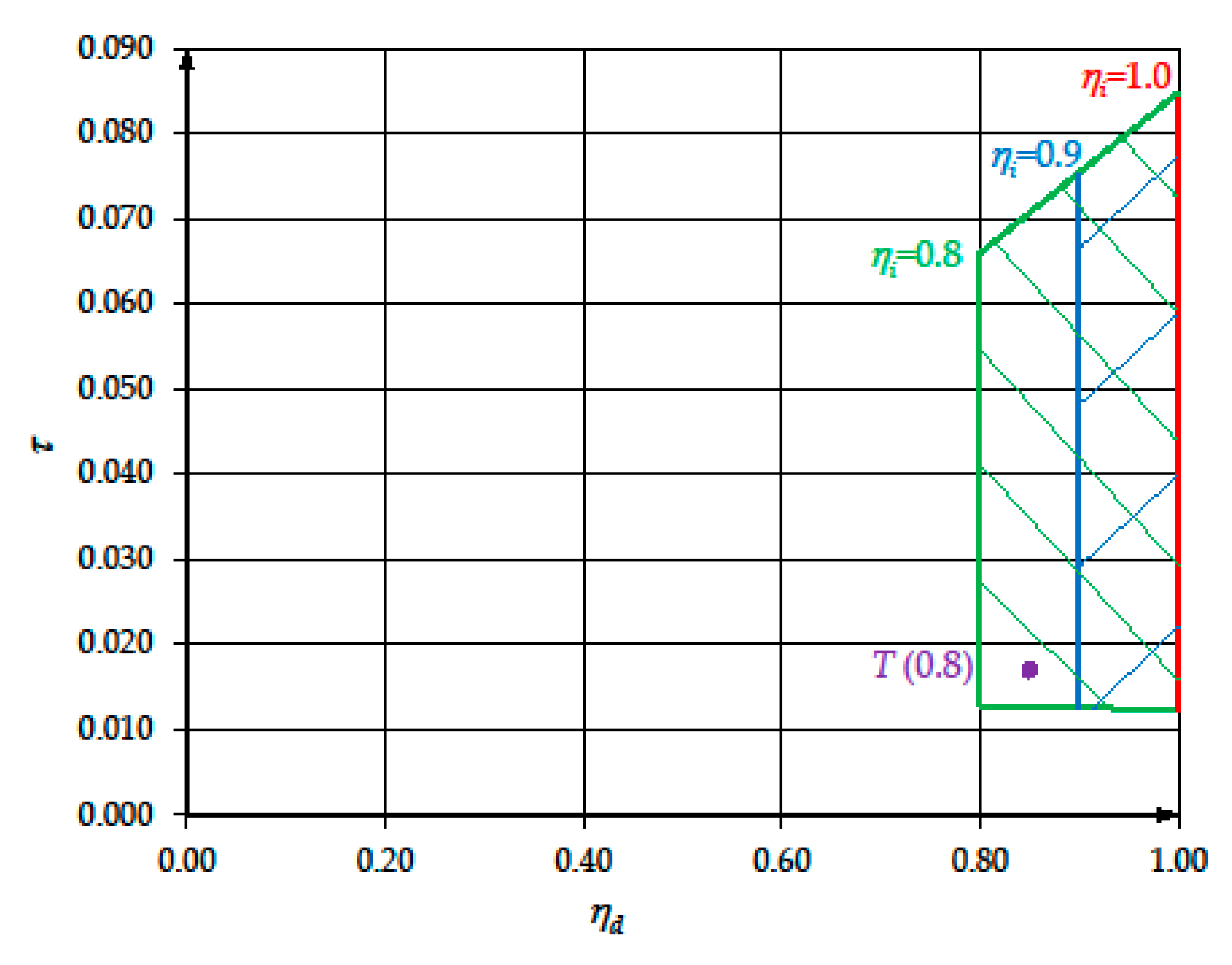
9. Case Study
- -
- Arc PQ is a feasibility arc and corresponds to the transmission ratio range . This means that the motor is admissible and can surely be coupled with an ideal reducer whose transmission ratio lies in this range.
- -
- Arc QQ’ is an uncertainty arc and corresponds to the transmission ratio range This means that, according to the method described in [15], the designer cannot ascertain if the motor can be coupled with an ideal reducer whose transmission ratio lies in this range. Therefore, this is a case for which the method proposed in this paper is particularly effective.
10. Conclusions
Funding
Conflicts of Interest
Nomenclature
| [A] | current phasor in the equivalent two-phase motor | |
| [A] | direct component of current in the equivalent two-phase motor | |
| [A] | quadrature component of current in the equivalent two-phase motor | |
| [A] | saturation value of current in the equivalent two-phase motor | |
| [A] | saturation value of current in the drive system (maximum rms current in the three-phase motor) | |
| [V/rad/s] | voltage constant of the motor (rms line to line voltage in the three-phase motor) | |
| [V/rad/s] | voltage constant of the equivalent two-phase motor | |
| [Nm/A] | torque constant of the equivalent two-phase motor | |
| [kg m2] | moment of inertia of the motor | |
| [kg m2] | moment of inertia of the transmission on load side | |
| [kg m2] | moment of inertia of the transmission on motor side | |
| [H] | synchronous inductance | |
| [Nm] | load torque | |
| [Nm] | current motor torque | |
| [Nm] | limit torque of the dynamic operating range | |
| [Nm] | limit torque of the continuous duty operating range | |
| [-] | number of pole pairs | |
| [Ω] | phase resistance | |
| [s] | time | |
| [V] | voltage phasor in the equivalent two-phase motor | |
| [V] | direct component of voltage in the equivalent two-phase motor | |
| [V] | quadrature component of voltage in the equivalent two-phase motor | |
| [V] | saturation value of voltage in the equivalent two-phase motor (rms line to line voltage in the three-phase motor) | |
| [Ω] | absolute value of the phase impedance in the equivalent two-phase motor | |
| [rad/s2] | load angular acceleration | |
| [-] | direct efficiency of transmission | |
| [-] | inverse efficiency of transmission | |
| [-] | transmission ratio | |
| [Wb] | permanent magnet flux | |
| [s−1] | electrical frequency | |
| [rad/s] | load angular speed | |
| [rad/s] | motor angular speed |
Appendix A
Appendix B
Appendix C
- (A)
- (B)
- Otherwise
- (1)
- If does not lie to the right of , i.e., ifthen the first intersection between curves l and s coincides with , andAs regards the second intersection, there are two sub-cases:
- (a)
- If point V does not lie above (Figure A1, curve ), i.e., ifthen the second intersection coincides with V, and is given by (Equation (32))
- (b)
- Otherwise (Figure A1, curve ) the second intersection of curve l with curve s belongs to arc d and the corresponding transmission ratio, i.e., , must be calculated by solving Equation (31) and lies in the range .
- (2)
- Otherwise lies to the right of and to the left of R, i.e.,Two sub-cases are possible:
- (a)
- If point V does not lie above , i.e., if inequality (A40) is met, the second intersection coincides with V and is given by Equation (A41), while the first intersection of curve l with curve s belongs to arc d. The corresponding transmission ratio, i.e., , must be calculated by solving Equation (31) and lies in the range .
- (b)
- Otherwise the intersections between curves l and d that lie along arc d must be calculated by solving Equation (31):

- (A)
- If does not lie to the right of (Figure A2, curve ), i.e., ifthen the second intersection coincides with and is given by
- (B)
- Otherwise ( lies to the right of )
- (1)
- If V does not lie above (Figure A2, curve ), i.e., if inequality (A40) is met, then the second intersection between curves l and s coincides with V and is given by Equation (A41).
- (2)
- Otherwise lies to the right of and V lies above (Figure A2, curve ), i.e.and the second intersection of curves l and s belongs to arc d. The corresponding transmission ratio must be calculated by solving Equation (31) and lies in the range .that is eitheror
- (A)
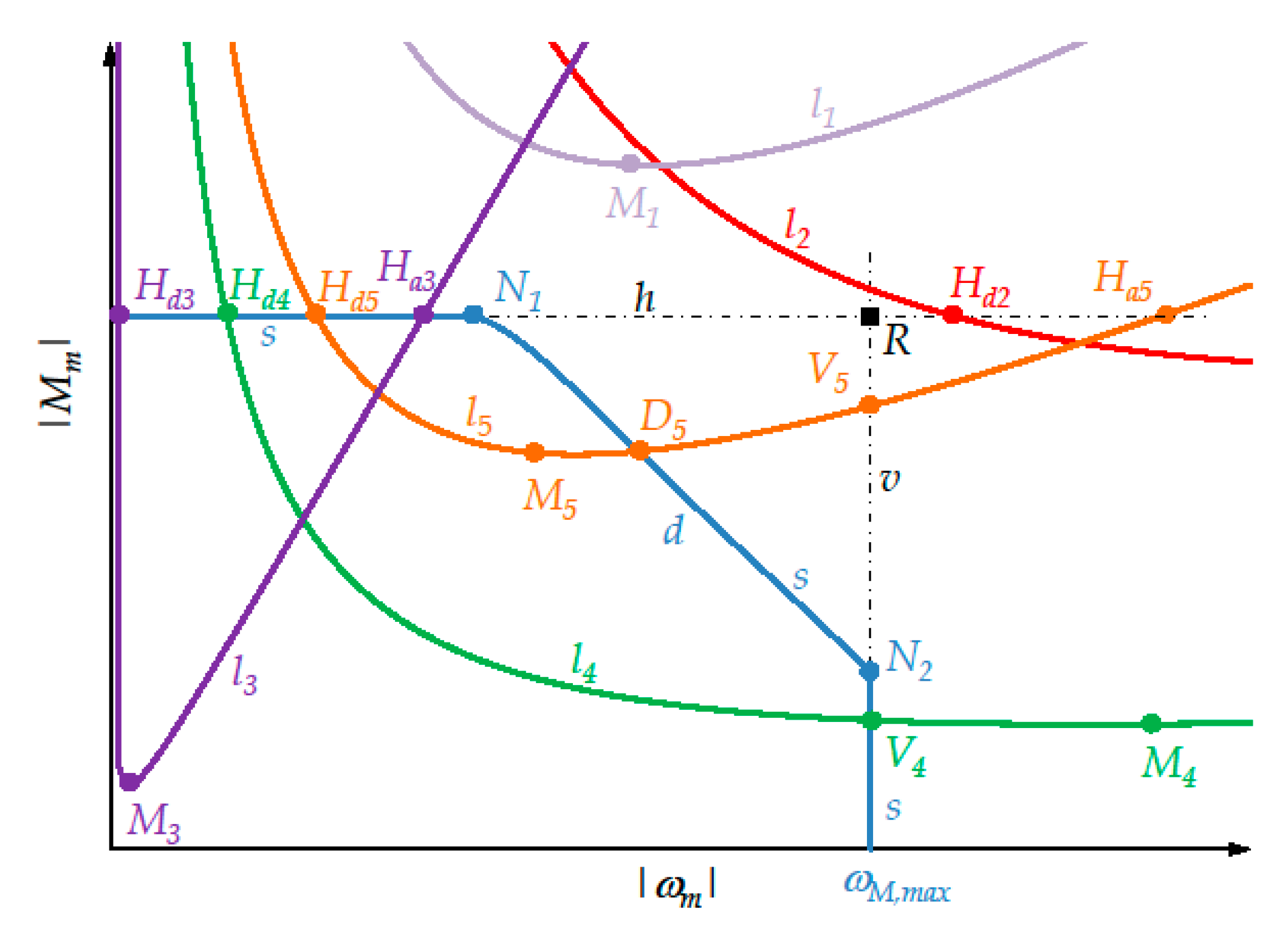
- If the minimum point M of curve l lies above the horizontal straight-line h, i.e., ifthe motor must be excluded (Figure 9, curve ).
- (B)
- Otherwise
- (1)
- If does not lie to the left of R, i.e., if inequality (A37) is met, the motor must be excluded (Figure 9, curve ).
- (2)
- Otherwise if does not lie to the right of , i.e., if inequality (A38) is met, at the instant considered the motor is admissible and is the first intersection between curves l and s, so thatAs regards the second intersection of curves l and s:
- (a)
- If does not lie to the right of , i.e., if Equation (A46) is met, the second intersection coincides with (Figure 9, curve ) and
- (b)
- Otherwise (if lies to the right of ) there are two sub-cases:
- If point V does not lie above (Figure 9, curve ), i.e., if inequality (A40) is met, the second intersection coincides with V and is given by Equation (A41).
- Otherwise (Figure 9, curve ) the second intersection belongs to arc d and the corresponding transmission ratio must be calculated by solving Equation (31) and lies in the range .
- (3)
- Otherwise lies to the right of , i.e., inequalities (A42) are met. Some subcases are possible:
- (a)
- If point V does not lie above (Figure 10, curve ), i.e., if inequality (A40) is met, then the second intersection of curves l and s coincides with V and is given by Equation (A41), while the first intersection belongs to arc d. The corresponding transmission ratio must be calculated by solving Equation (31) and lies in the range .
- (b)
- Otherwise the intersections between curve l and arc must be calculated by solving Equation (31):
- (A)
- If does not lie to the left of R, i.e., if inequality (A37) is met, then the motor must be excluded (Figure A3, curve ).
- (B)
- Otherwise
- (1)
- If does not lie to the right of , i.e., if inequality (A38) is met, then at the instant considered the motor is admissible and the first intersection between curves l and s coincides with , so thatgiven by Equation (A69).As regards the second intersection of curves l and s:
- (a)
- If does not lie to the right of , i.e., if Equation (A46) is met, the second intersection coincides with (Figure A3, curve ), andgiven by Equation (A72).
- (b)
- Otherwise, if does not lie to the right of R (Figure A3, curve ), i.e., ifthe second intersection coincides with the intersection between the ascending curve and arc d. Its transmission ratio, i.e., , must be calculated by solving Equation (31) and lies in the range .
- (c)
- Otherwise ( lies to the right of R) there are some sub-cases:
- (1)
- If the edge-point M does not lie to the right of R, i.e., ifthe second intersection belongs to the ascending curve , with two sub-cases:
- (a)
- If point does not lie above , i.e., ifthe second intersection coincides with V (Figure A3, curve ) and is given by Equation (A41).
- (b)
- Otherwise (Figure A3, curve ) the second intersection coincides with the intersection between the ascending curve and arc d. Its transmission ratio, i.e., , must be calculated by solving Equation (31) and lies in the range .
- (2)
- Otherwise (the edge point M lies to the right of R), the second intersection belongs to the descending curve with two sub-cases:
- (a)
- If point does not lie above , i.e., ifthe second intersection coincides with V (Figure A3, curve ) and is given by Equation (A41).
- (b)
- Otherwise the second intersection coincides with the intersection between the descending curve and arc d (Figure A3, curve ). Its transmission ratio, i.e., , must be calculated by solving Equation (31) and lies in the range .
- (2)
- Otherwise, lies to the right of (Figure A4), i.e., inequalities (A42) are met.
- (a)
- If the edge-point M does not lie to the right of R, i.e., if inequality (A79) is met, curve l intersects curve s and the first intersection coincides with the intersection between the descending curve and arc d. Its transmission ratio, i.e., , must be calculated by solving Equation (31) and lies in the range . The second intersection belongs to the ascending curve , with two sub-cases:
- (1)
- If point does not lie above (Figure A4, curve ), i.e., if inequality (A79) is met, the second intersection coincides with V, and is given by Equation (A41).
- (2)
- Otherwise (Figure A4, curve ) the second intersection coincides with the intersection between the ascending curve and arc d. Its transmission ratio, i.e., must be calculated by solving Equation (31) and lies in the range .
- (b)
- Otherwise (if the edge point M lies to the right of R) there are two sub-cases:
- (1)
- If point does not lie above (Figure A4, curve ), i.e., if inequality (A80) is met, curve l intersects curve s and the first intersection coincides with the intersection between the descending curve and arc d. Its transmission ratio, i.e., must be calculated by solving Equation (31) and lies in the range . The second intersection coincides with , and is given by Equation (A41).
- (2)
References
- Pettersson, M.; Ölvander, J. Drive train optimization for industrial robots. IEEE Trans. Robot. 2009, 25, 1419–1424. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, S.; Hansen, M.R. Design optimization on the drive train of a light-weight robotic arm. Mechatronics 2011, 21, 560–569. [Google Scholar] [CrossRef]
- Ge, L.; Chen, J.; Li, R.; Liang, P. Optimization design of drive system for industrial robots based on dynamic performance. Ind. Robot Int. J. 2017, 44, 765–775. [Google Scholar] [CrossRef]
- Padilla-Garcia, E.A.; Rodriguez-Angeles, A.; Reéndiz, J.R.; Cruz-Villar, C.A. Concurrent optimization for the selection and control of ac servomotors on the powertrain of industrial robots. IEEE Access 2018, 6, 27923–27938. [Google Scholar] [CrossRef]
- Roos, F.; Johansson, H.; Wikander, J. Optimal selection of motor and gearhead in mechatronic application. Mechatronics 2006, 16, 63–72. [Google Scholar] [CrossRef]
- Van de Straete, H.J.; De Schutter, J.; Degezelle, P.; Belmans, R. Servo motor selection criterion for mechatronic applications. IEEE/ASME Trans. Mechatron. 1998, 3, 43–50. [Google Scholar] [CrossRef]
- Pasch, K.A.; Seering, W.P. On the drive systems for high performance machines. J. Mech. Trans. Autom. Des. 1984, 106, 102–108. [Google Scholar] [CrossRef]
- Cusimano, G. Choice of electrical motor and transmission for mechatronic applications: The torque peak. Mech. Mach. Theory 2011, 46, 1207–1235. [Google Scholar] [CrossRef]
- Cusimano, G. Influence of the reducer efficiencies on the choice of motor and transmission: Torque peak of the motor. Mech. Mach. Theory 2013, 67, 122–151. [Google Scholar] [CrossRef]
- Giberti, H.; Cinquemani, S.; Legnani, G. Effects of transmission mechanical characteristics on the choice of a motor-reducer. Mechatronics 2010, 20, 604–610. [Google Scholar] [CrossRef]
- Cusimano, G.; Casolo, F. An almost comprehensive approach for the choice of motor and transmission in mechatronic applications: Motor thermal problem. Mechatronics 2016, 40, 96–105. [Google Scholar] [CrossRef]
- Cusimano, G. Optimization of the choice of the system electric drive-transmission for mechatronic applications. Mech. Mach. Theory 2007, 42, 48–65. [Google Scholar] [CrossRef]
- Nicolescu, A.; Avram, C.; Ivan, M. Optimal servomotor selection algorithm for industrial robots and machine tools NC axis. Proc. Manuf. Sys. 2014, 9, 105–114. [Google Scholar]
- Van de Straete, H.J.; De Schutter, J.; Belmans, R. An efficient procedure for checking performance limits in servo drive selection and optimization. IEEE/ASME Trans. Mechatron. 1999, 4, 378–386. [Google Scholar] [CrossRef]
- Cusimano, G. Choice of motor and transmission in mechatronic applications: Non-rectangular dynamic range of the drive system. Mech. Mach. Theory 2015, 85, 35–52. [Google Scholar] [CrossRef]
- De Doncker, R.; Pulle, D.W.J.; Veltman, A. Advanced Electrical Drives, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 165–237. [Google Scholar]
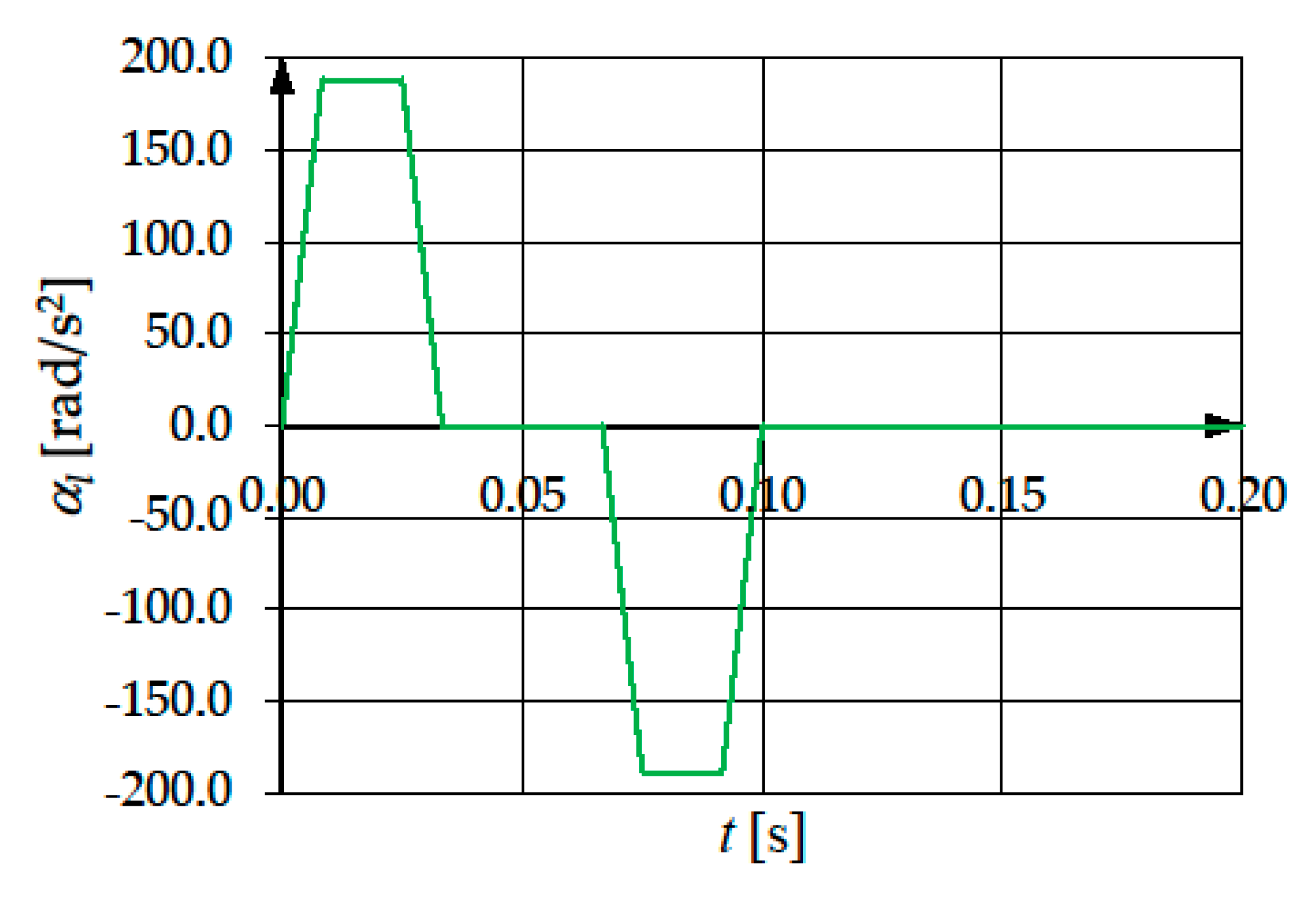
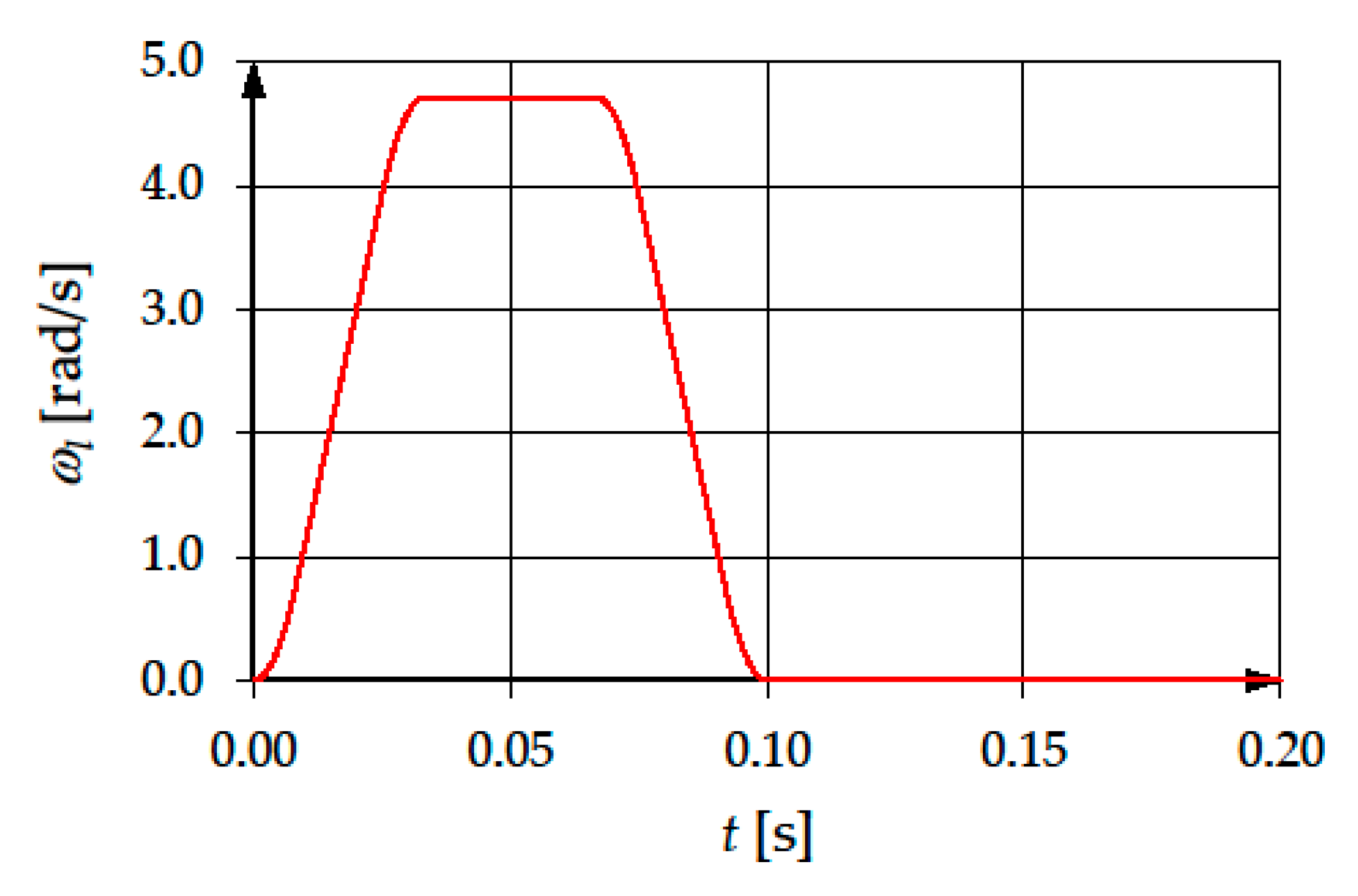
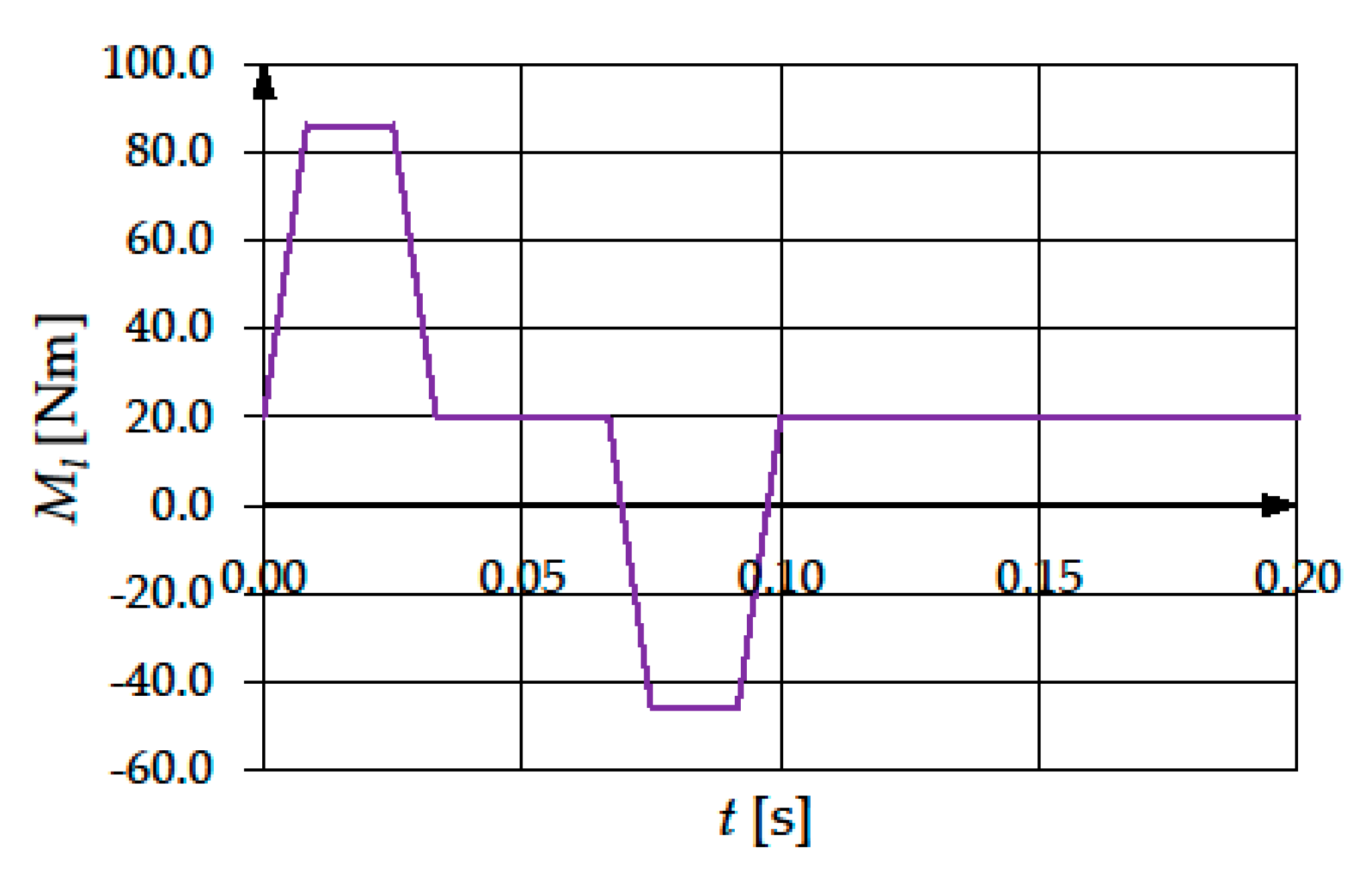
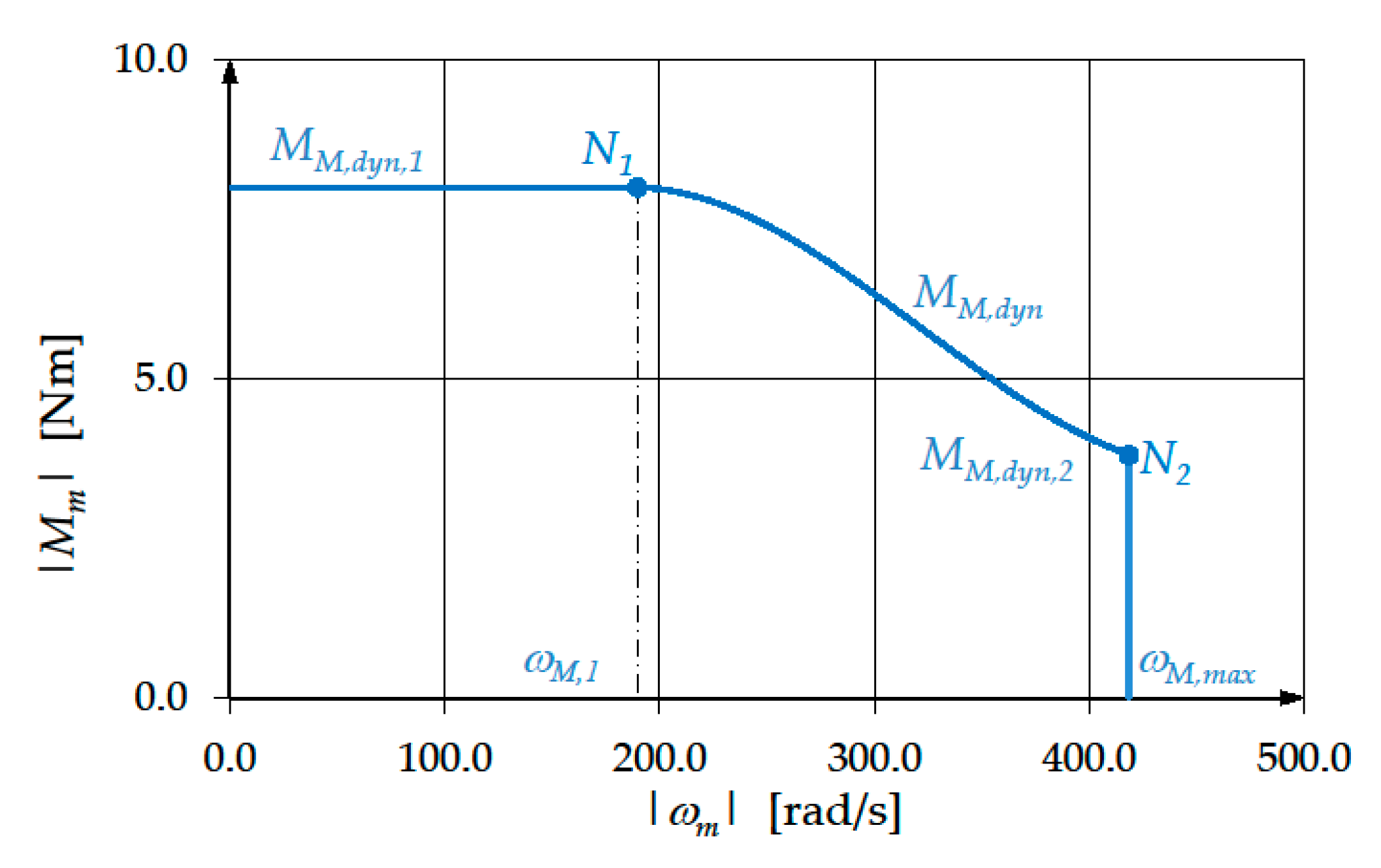

(Nm) | ||||
|---|---|---|---|---|
| 3.2·10−4 | 8.0 | 3.8 | 188.50 | 418.90 |
| 1/59.00 | 1.34·10−4 | 0.85 | 0.80 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cusimano, G. Non-Rectangular Dynamic Range of the Drive System: A New Approach for the Choice of Motor and Transmission. Machines 2019, 7, 54. https://doi.org/10.3390/machines7030054
Cusimano G. Non-Rectangular Dynamic Range of the Drive System: A New Approach for the Choice of Motor and Transmission. Machines. 2019; 7(3):54. https://doi.org/10.3390/machines7030054
Chicago/Turabian StyleCusimano, Giancarlo. 2019. "Non-Rectangular Dynamic Range of the Drive System: A New Approach for the Choice of Motor and Transmission" Machines 7, no. 3: 54. https://doi.org/10.3390/machines7030054
APA StyleCusimano, G. (2019). Non-Rectangular Dynamic Range of the Drive System: A New Approach for the Choice of Motor and Transmission. Machines, 7(3), 54. https://doi.org/10.3390/machines7030054





