Design and Development of a New Press for Grape Marc
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Tests
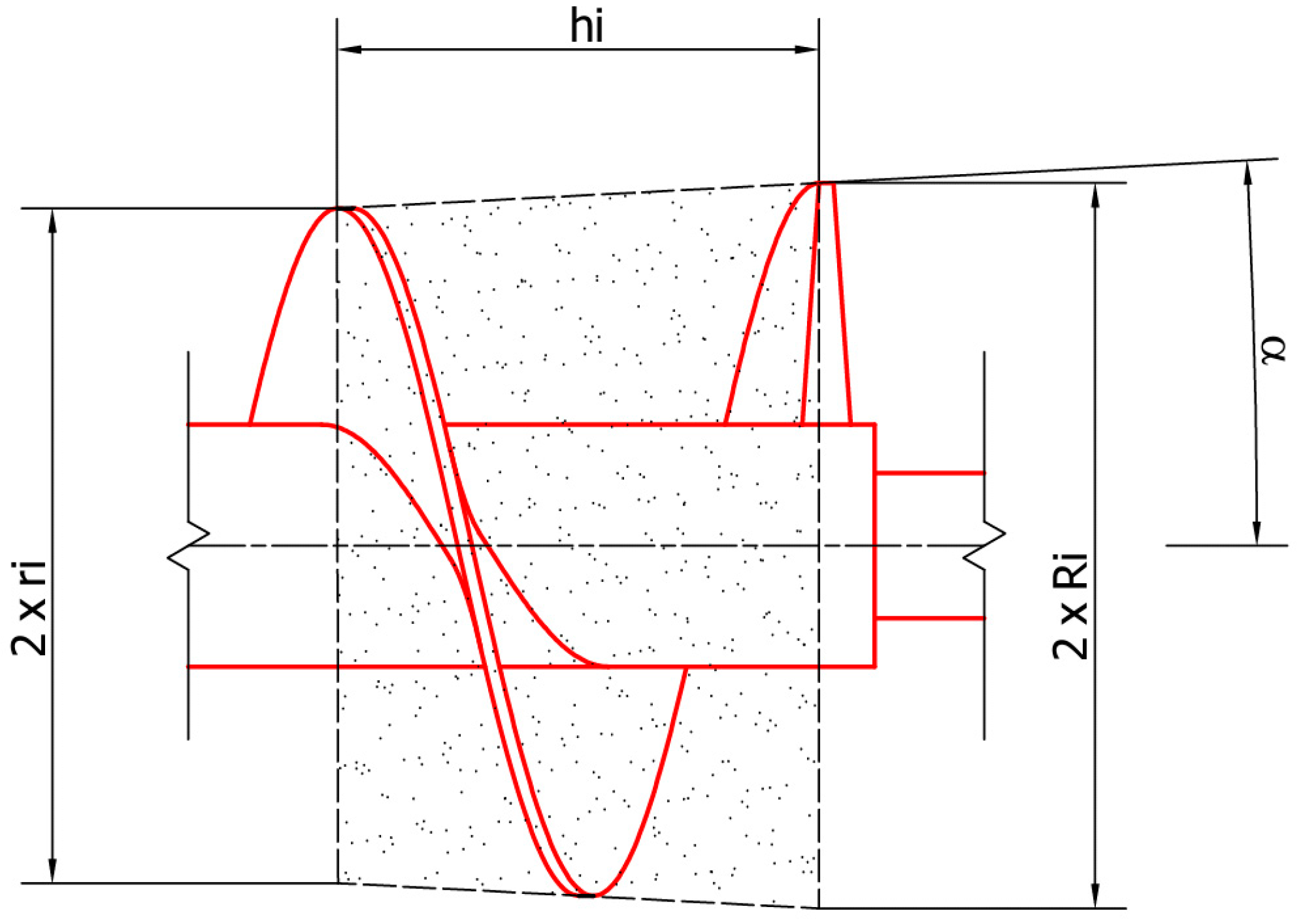
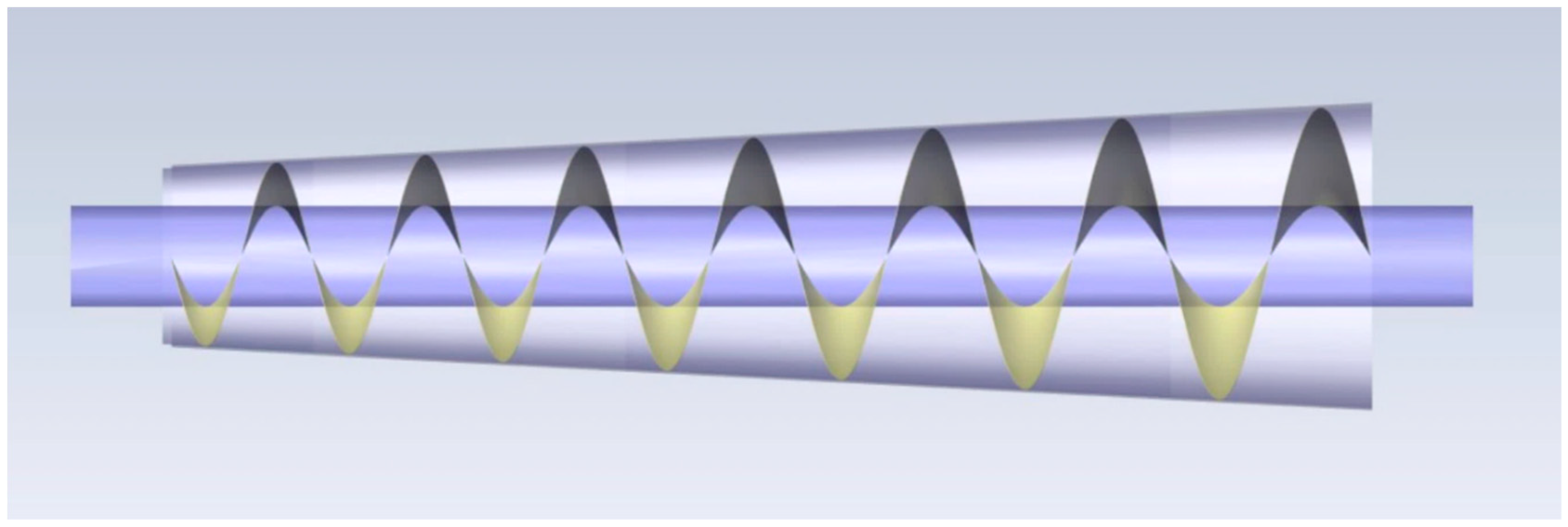
2.2. Helicoidal Screw Press Geometry
3. Discussion
3.1. Specific Energy Consumption
3.2. Quality of Wine
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Vita, P. Corso di Meccanica Enologica, 1st ed.; Hoepli: Milano, Italy, 1997; pp. 100–125. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Use of the adjoint method in the optimal control problem for the mechanical vibrations of nonlinear systems. Machines 2018, 6, 19. [Google Scholar] [CrossRef]
- De Simone, M.C.; Rivera, Z.B.; Guida, D. Obstacle avoidance system for unmanned ground vehicles by using ultrasonic sensors. Machines 2018, 6, 18. [Google Scholar] [CrossRef]
- Shimizu, Y.; Cundall, P.A. Three dimensional DEM simulation of bulk handling screw conveyors. J. Eng. Mech. 2001, 127, 864–872. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. Dynamic analysis of planar rigid multibody systems modelled using natural absolute coordinates. Appl. Comput. Mech. 2018, 12, 73–110. [Google Scholar] [CrossRef]
- Belladonna, U. Elementi di Oleodinamica, 3rd ed.; Hoepli: Milano, Italy, 2001; pp. 90–120. [Google Scholar]
- Cammarata, A. A novel method to determine position and orientation errors in clearance-affected overconstrained mechanisms. Mech. Mach. Theory 2017, 118, 247–264. [Google Scholar] [CrossRef]
- Cleary, P.W. DEM modelling of particulate flow in a screw feeder. Prog. Comput. Fluid Dyn. 2007, 7, 128–138. [Google Scholar] [CrossRef]
- Iannone, V.; De Simone, M.C.; Guida, D. Modelling of a DC gear motor for feed-forward control law design for unmanned ground vehicles. Actuators 2019. (In Press)
- Cammarata, A.; Angeles, J.; Sinatra, R. Kinetostatic and inertial conditioning of the McGill Schönflies-motion generator. Adv. Mech. Eng. 2010, 2, 186203. [Google Scholar] [CrossRef]
- De Simone, M.C.; Russo, S.; Rivera, Z.B.; Guida, D. Multibody model of a UAV in presence of wind fields. In Proceedings of the 2017 International Conference on Control, Artificial Intelligence, Robotics and Optimization (ICCAIRO 2017), Prague, Czech Republic, 20–22 May 2018; pp. 83–88. [Google Scholar] [CrossRef]
- De Vita, P.; De Vita, G. Corso di Meccanica Enologica, 3rd ed.; Hoepli: Milano, Italy, 2004; pp. 70–90. [Google Scholar]
- Owen, P.J.; Cleary, P.W. Prediction of screw conveyor performance using the Discrete Element Method (DEM). Powder Technol. 2009, 193, 274–288. [Google Scholar] [CrossRef]
- Roberts, A.W. Design and performance criteria for screw conveyors in bulk solids operation. Bulk Sol. Hand 2002, 22, 436–444. [Google Scholar]
- Cammarata, A. Unified formulation for the stiffness analysis of spatial mechanisms. Mech. Mach. Theory 2016, 105, 272–284. [Google Scholar] [CrossRef]
- Firdaus, M.; Salleh, S. M.; Nawi, I.; Ngali, Z.; Siswanto, W.A.; Yusup, E.M. Preliminary Design on Screw Press Model of Palm Oil Extraction Machine. Colloquium of Advanced Mechanics (CAMS2016). IOP Conf. Ser. Mater. Sci. Eng. 2017, 165, 012029. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Dry friction influence on structure dynamics. In Proceedings of the 2015 5th Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Hersonissos, Greece, 25–27 May 2015; pp. 4483–4491. [Google Scholar]
- Pappalardo, C.M.; Guida, D. On the Lagrange multipliers of the intrinsic constraint equations of rigid multibody mechanical systems. Arch. Appl. Mech. 2018, 88, 419–451. [Google Scholar] [CrossRef]
- Fu, Y.F.; Gong, J.; Peng, Z.; Li, J.H.; Li, S.D.; Li, P.W.; Yang, Z.M. Optimization design for screw wash-sand machine based on fruit fly optimization algorithm. J. Appl. Sci. Eng. 2016, 19, 149–161. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. On the Computational Methods for the Dynamic Analysis of Rigid Multibody Mechanical Systems. Machines 2018, 6, 20. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Modal coupling in presence of dry friction. Machines 2018, 6, 8. [Google Scholar] [CrossRef]
- Milosavljevic, B.; Pesic, R.; Dasic, P. Binary Logistic Regression Modeling of Idle CO Emissions in order to Estimate Predictors Influences in Old Vehicle Park. Math. Prob. Eng. 2015, 2015, 463158. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. Control of nonlinear vibrations using the adjoint method. Meccanica 2017, 52, 2503–2526. [Google Scholar] [CrossRef]
- Owen, P.J.; Cleary, P.W.; McBride, B. Simulated granular flow in screw feeders using 3D Discrete Element Method (DEM). CHEMECA 2003, 1, 10–15. [Google Scholar]
- Dasic, P.; Franek, F.; Assenova, E.; Radovanovicville, M. International standardization and organizations in the field of tribology. Ind. Lubr. Tribol. 2003, 55, 287–291. [Google Scholar] [CrossRef]
- Cleary, P.W. Large scale industrial DEM modelling. Eng. Comput. 2004, 21, 169–204. [Google Scholar] [CrossRef]
- Callegari, M.; Cammarata, A.; Gabrielli, A.; Sinatra, R. Kinematics and dynamics of a 3-CRU spherical parallel robot. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, Las Vegas, NV, USA, 4–7 September 2007; pp. 933–941. [Google Scholar]
- Naviglio, D.; Formato, A.; Scaglione, G.; Montesano, D.; Pellegrino, A.; Villecco, F.; Gallo, M. Study of the grape cryo-maceration process at different temperatures. Foods 2018, 7, 107. [Google Scholar] [CrossRef] [PubMed]
- Cammarata, A.; Lacagnina, M.; Sinatra, R. Dynamic simulations of an airplane-shaped underwater towed vehicle marine. In Proceedings of the Computational Methods in Marine Engineering V—5th International Conference on Computational Methods in Marine Engineering, Hamburg, Germany, 29–31 May 2013. [Google Scholar]
- Barbagallo, R.; Sequenzia, G.; Cammarata, A.; Oliveri, S.M. An integrated approach to design an innovative motorcycle rear suspension with eccentric mechanism. In Proceedings of the Advances on Mechanics Design Engineering and Manufacturing—Lecture Notes in Mechanical Engineering Catania, Catania, Italy, 14–16 September 2016; Springer: Cham, Swizerland, 2017; pp. 609–619. [Google Scholar]
- De Simone, M.C.; Guida, D. Control design for an under-actuated UAV model. FME Trans. 2018, 46, 443–452. [Google Scholar] [CrossRef]
- Villecco, F. On the Evaluation of Errors in the Virtual Design of Mechanical Systems. Machines 2018, 6, 36. [Google Scholar] [CrossRef]
- Barbagallo, R.; Sequenzia, G.; Cammarata, A.; Oliveri, S.M.; Fatuzzo, G. Redesign and multibody simulation of a motorcycle rear suspension with eccentric mechanism. Int. J. Interact. Des. Manuf. 2018, 12, 517–524. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Identification and control of a Unmanned Ground Vehicle by using Arduino. UPB Sci. Bull. Ser. D Mech. Eng. 2018, 80, 141–154. [Google Scholar]
- Quatrano, A.; De Simone, M.C.; Rivera, Z.B.; Guida, D. Development and implementation of a control system for a retrofitted CNC machine by using Arduino. FME Trans. 2017, 45, 565–571. [Google Scholar] [CrossRef]
- Dasic, P.; Dasic, J.; Crvenkovic, B. Applications of Access Control as a Service for Software Security. Int. J. Ind. Eng. Manag. 2016, 7, 111–116. [Google Scholar]
- Barbagallo, R.; Sequenzia, G.; Oliveri, S.M.; Cammarata, A. Dynamics of a high-performance motorcycle by an advanced multibody/control co-simulation. Proc. Inst. Mech. Eng. Part. K J. Multi-Body Dyn. 2016, 230, 207–221. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. System identification algorithm for computing the modal parameters of linear mechanical systems. Machines 2018, 6, 12. [Google Scholar] [CrossRef]
- Cammarata, A. Optimized design of a large-workspace 2-DOF parallel robot for solar tracking systems. Mech. Mach Theory 2015, 83, 175–186. [Google Scholar] [CrossRef]
- Villecco, F.; Pellegrino, A. Evaluation of uncertainties in the design process of complex mechanical systems. Entropy 2017, 19, 475. [Google Scholar] [CrossRef]
- Formato, A.; Guida, D.; Ianniello, D.; Villecco, F.; Lenza, T.L.; Pellegrino, A. Design of delivery valve for hydraulic pumps. Machines 2018, 6, 44. [Google Scholar] [CrossRef]
- Pappalardo, C.M. A Natural Absolute Coordinate Formulation for the Kinematic and Dynamic Analysis of Rigid Multibody Systems. Nonlinear Dyn. 2015, 81, 1841–1869. [Google Scholar] [CrossRef]
- Cammarata, A.; Lacagnina, M.; Sequenzia, G. Alternative elliptic integral solution to the beam deflection equations for the design of compliant mechanisms. Int. J. Interact. Des. Manuf. 2018, 1–7. [Google Scholar] [CrossRef]
- Sena, P.; Attianese, P.; Pappalardo, M.; Villecco, F. FIDELITY: Fuzzy Inferential Diagnostic Engine for on-LIne supporT to phYsicians. In 4th International Conference on Biomedical Engineering in Vietnam; Springer: Berlin/Heidelberg, Germany, 2013; pp. 396–400. [Google Scholar]
- Muscat, M.; Cammarata, A.; Maddio, P.D.; Sinatra, R. Design and development of a towfish to monitor marine pollution. Euro-Mediterr. J. Environ. Integr. 2018, 11. [Google Scholar] [CrossRef]
- Carillo, M.; Formato, A.; Fabiani, A.; Scaglione, G.; Pucillo, G.P. An inertizing and cooling process for grapes cryomaceration. Electron. J. Biotechnol. 2011. [Google Scholar] [CrossRef]

| Solutions Proposed | Advantages | Disadvantages |
|---|---|---|
| Membrane press | Optimized pressing process | Non-continuous process |
| Press with Archimedes’ screw | Continuous process | Non-optimized pressing process |
| Press with conical helicoid with variable pitch | Continuous process optimized pressing process | More studies to optimize the pressing process for different types of marc |
| n. phase | p1 (105 Pa) | DVp (%) |
|---|---|---|
| 1 | 0.20 | 4 |
| 2 | 0.40 | 16 |
| 3 | 0.80 | 26 |
| 4 | 1.20 | 34 |
| 5 | 1.50 | 39 |
| 6 | 1.80 | 45 |
| 7 | 2.0 | 51 |
| h | Pitch (m) | i | Radius Ri (m) |
|---|---|---|---|
| 1 | 1 | 1 | 0.75 |
| 2 | 0.95 | 2 | 0.73 |
| 3 | 0.90 | 3 | 0.70 |
| 4 | 0.85 | 4 | 0.68 |
| 5 | 0.80 | 5 | 0.67 |
| 6 | 0.75 | 6 | 0.66 |
| 7 | 0.70 | 7 | 0.65 |
| 8 | 0.64 |
| Cochlea after Pitch h | DVc % | Membrane Press Phase | Optimized Volume Changing DVp % |
|---|---|---|---|
| h1 | 5 | 1 | 4 |
| h2 | 14 | 2 | 16 |
| h3 | 24 | 3 | 26 |
| h4 | 32 | 4 | 34 |
| h5 | 39 | 5 | 39 |
| h6 | 47 | 6 | 45 |
| h7 | 51 | 7 | 51 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Formato, A.; Ianniello, D.; Romano, R.; Pellegrino, A.; Villecco, F. Design and Development of a New Press for Grape Marc. Machines 2019, 7, 51. https://doi.org/10.3390/machines7030051
Formato A, Ianniello D, Romano R, Pellegrino A, Villecco F. Design and Development of a New Press for Grape Marc. Machines. 2019; 7(3):51. https://doi.org/10.3390/machines7030051
Chicago/Turabian StyleFormato, Andrea, Domenico Ianniello, Raffaele Romano, Arcangelo Pellegrino, and Francesco Villecco. 2019. "Design and Development of a New Press for Grape Marc" Machines 7, no. 3: 51. https://doi.org/10.3390/machines7030051
APA StyleFormato, A., Ianniello, D., Romano, R., Pellegrino, A., & Villecco, F. (2019). Design and Development of a New Press for Grape Marc. Machines, 7(3), 51. https://doi.org/10.3390/machines7030051






