Dynamic Performance of a Squeeze Film Damper with a Cylindrical Roller Bearing under a Large Static Radial Loading Range
Abstract
:1. Introduction
2. Oil-Damped Rotor Support—Squeeze Film Dampers
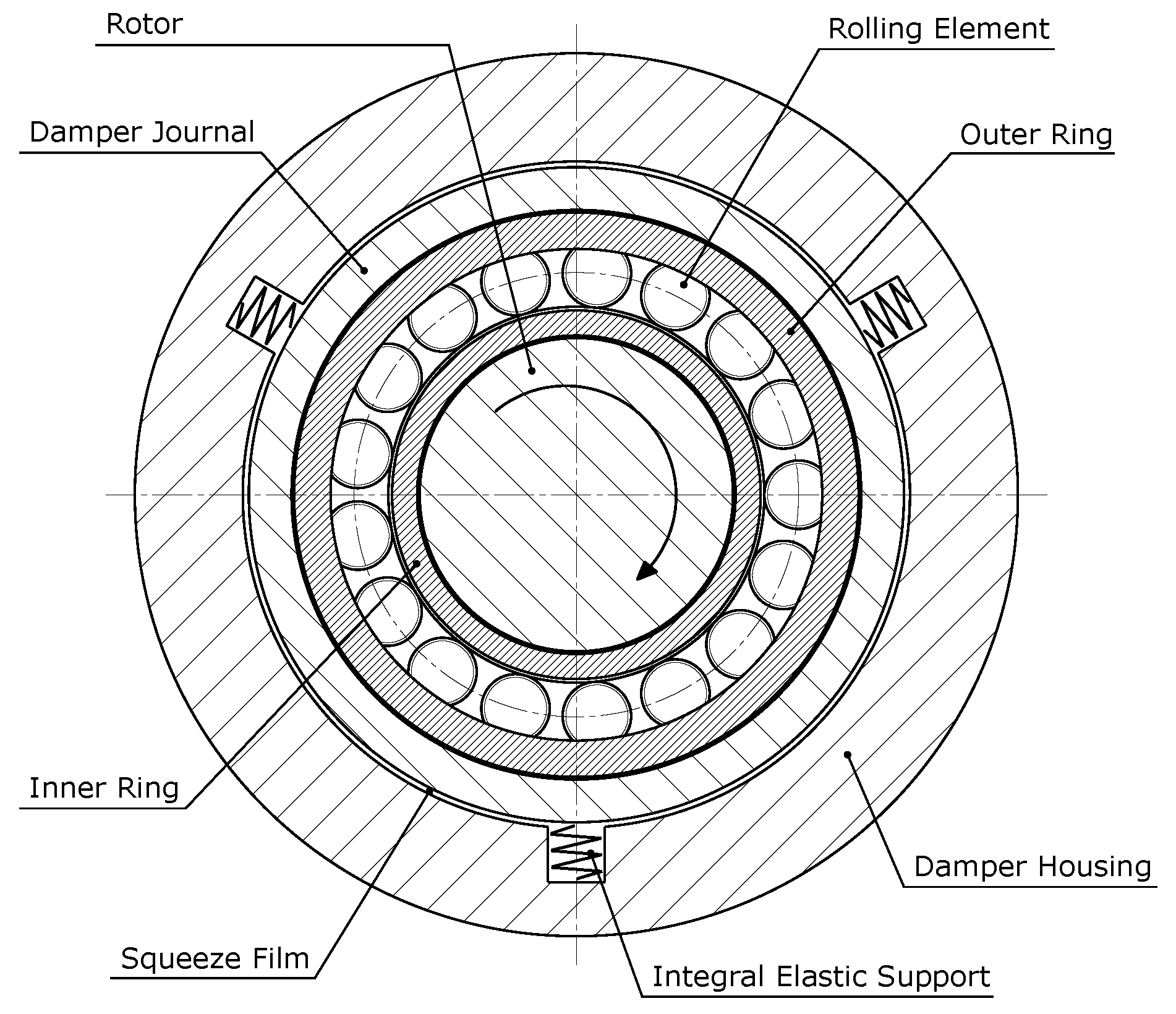
2.1. Description of a Squeeze Film Damper
2.2. Brief Review of Squeeze Film Damper Technology
3. Numerical Simulations of the Rotor-Bearing System
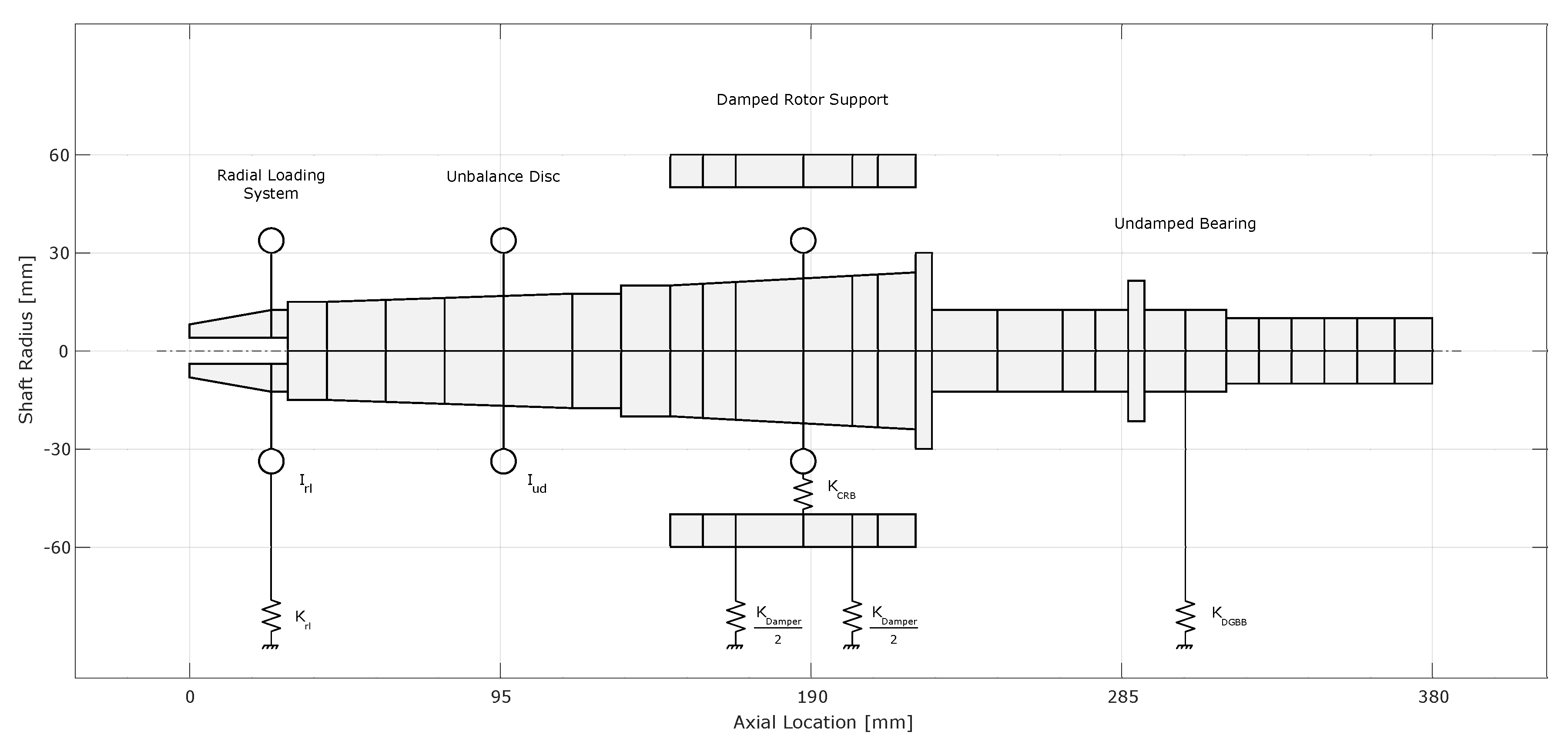
3.1. Rotor Geometry
3.2. Squeeze Film Damper Properties
3.3. Bearing Properties: Load Cases and Results
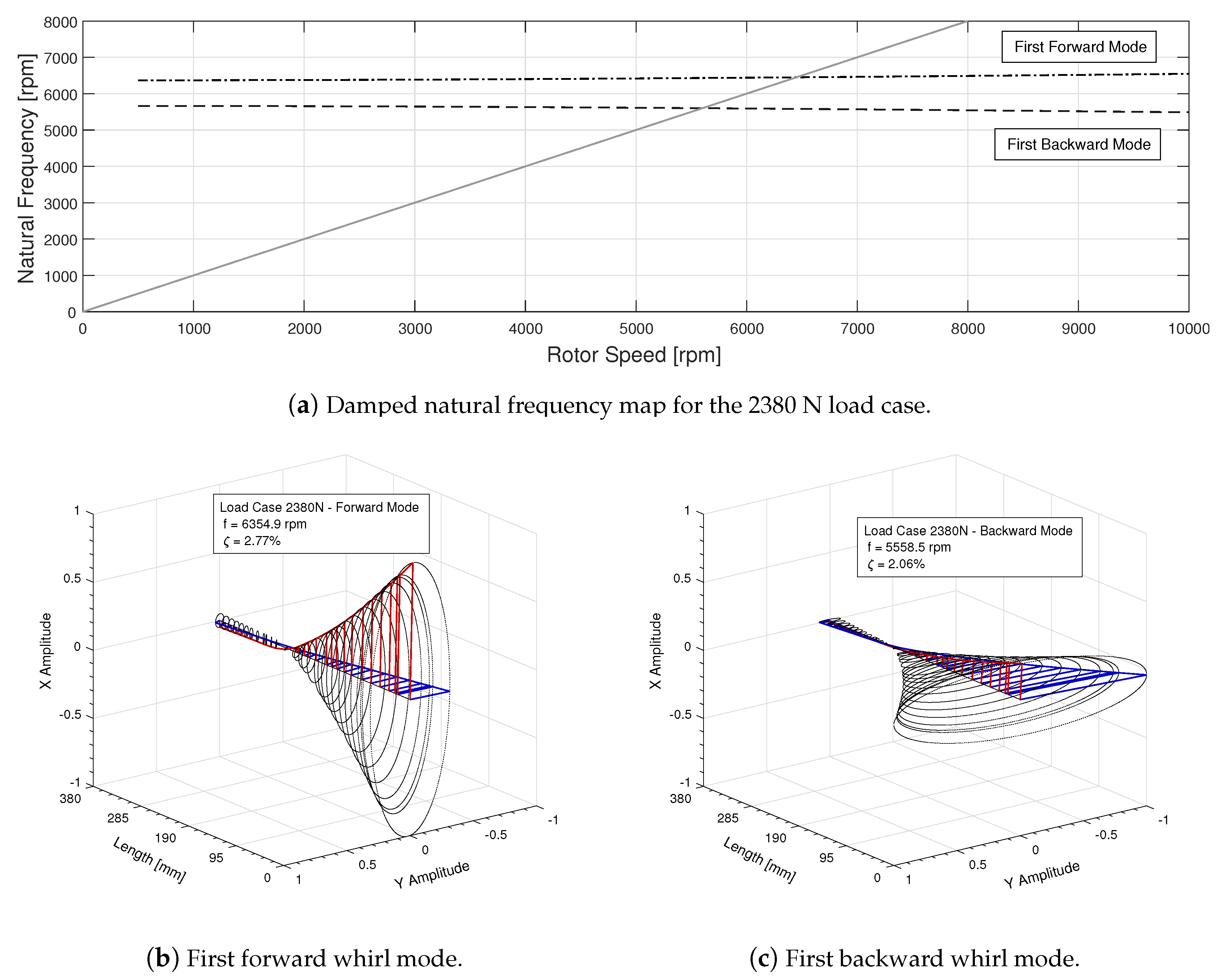
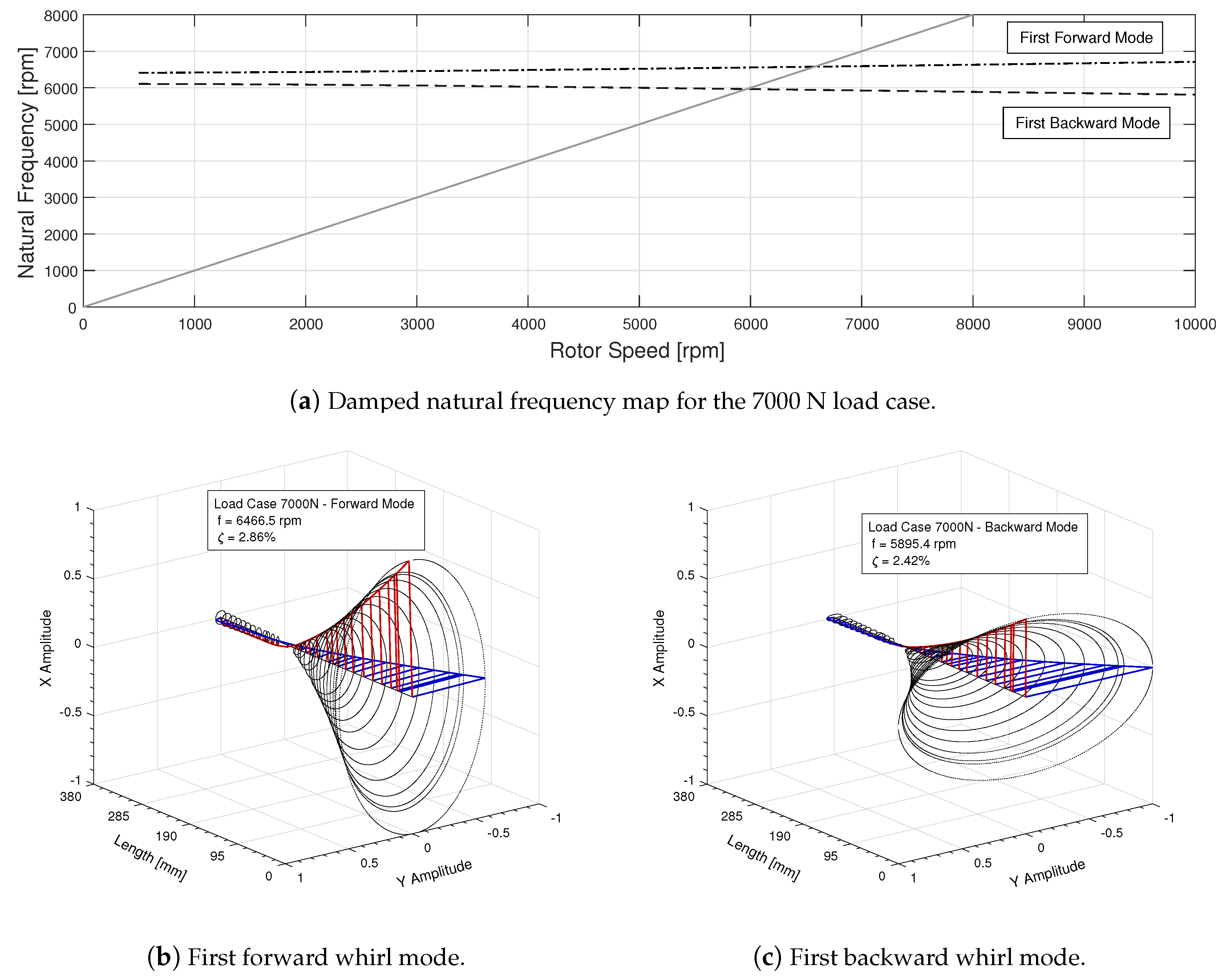
3.4. Damped Eigenvalue Analysis
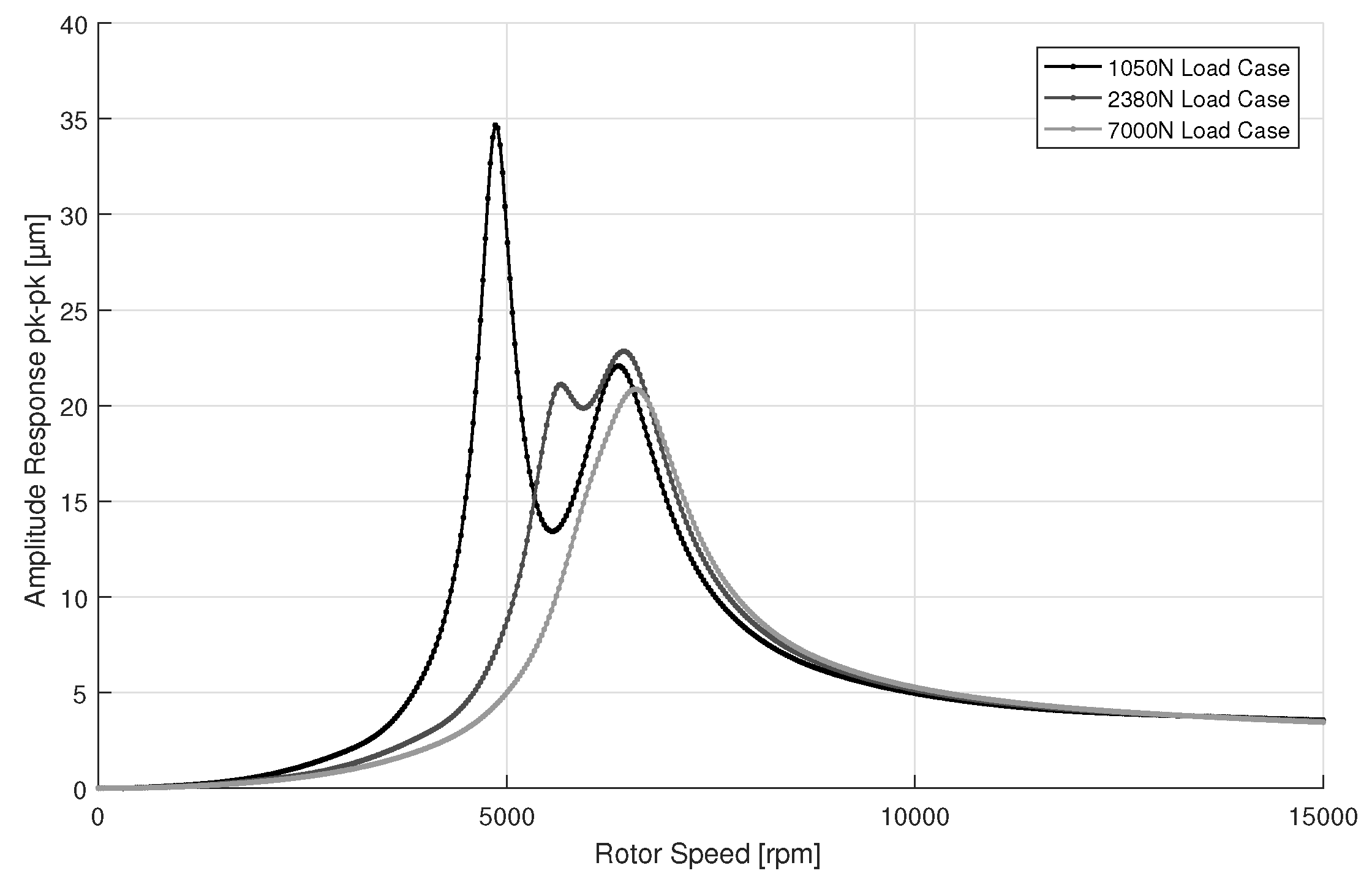
3.5. Forced Response Analysis
3.6. Concluding Remark
4. Experimental Work
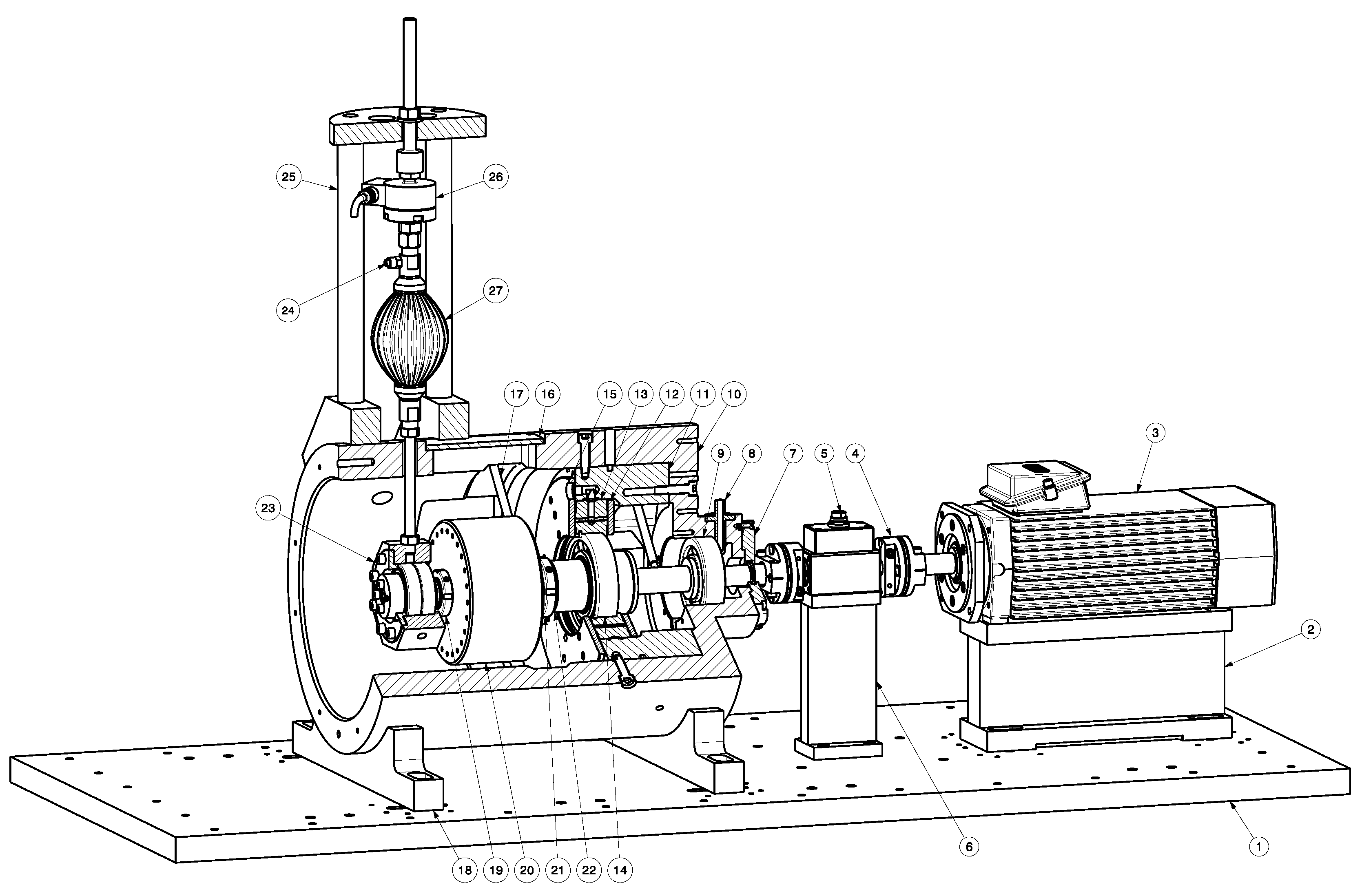
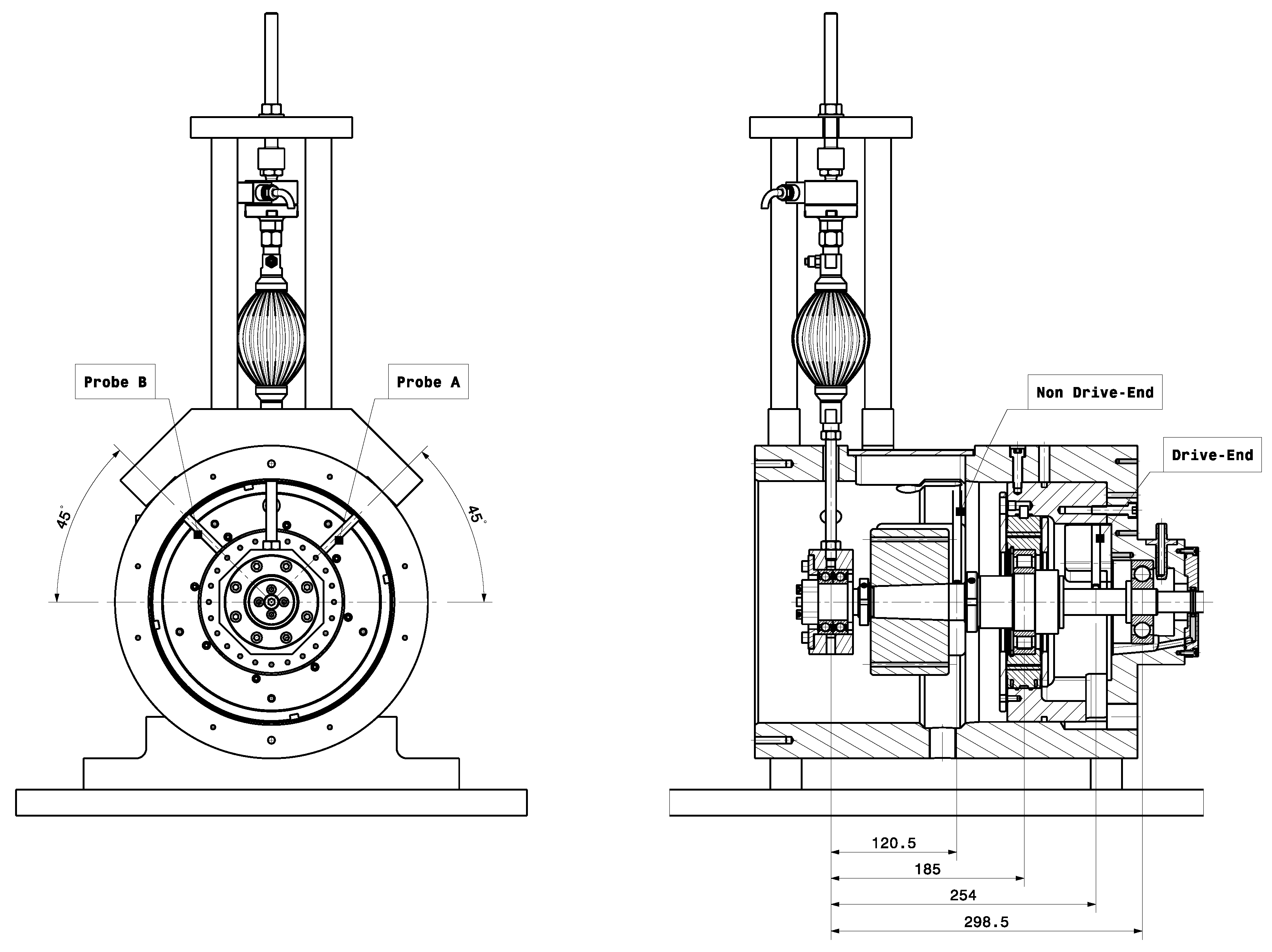
4.1. Test Rig Design
4.2. Measurement Procedure
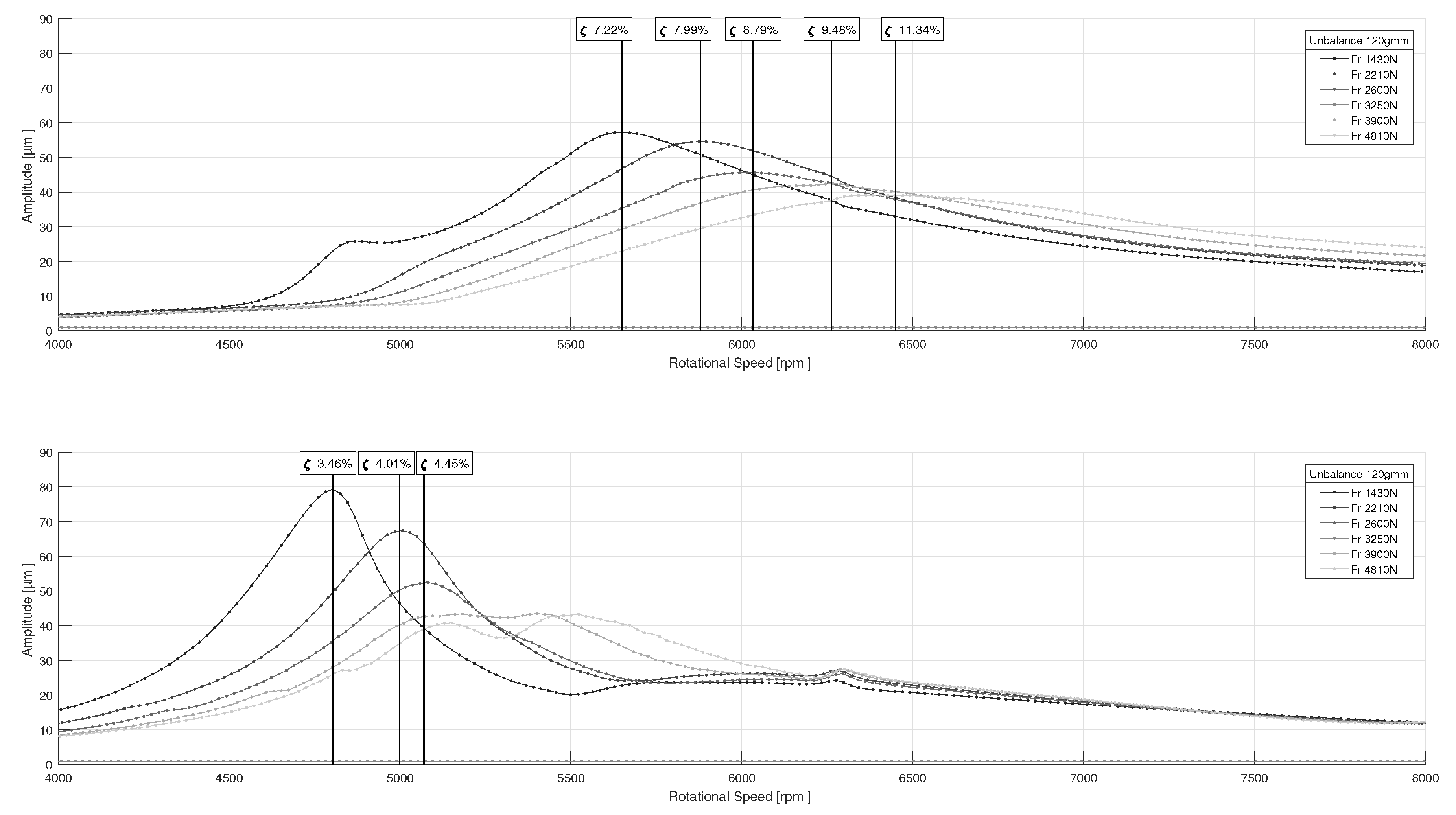
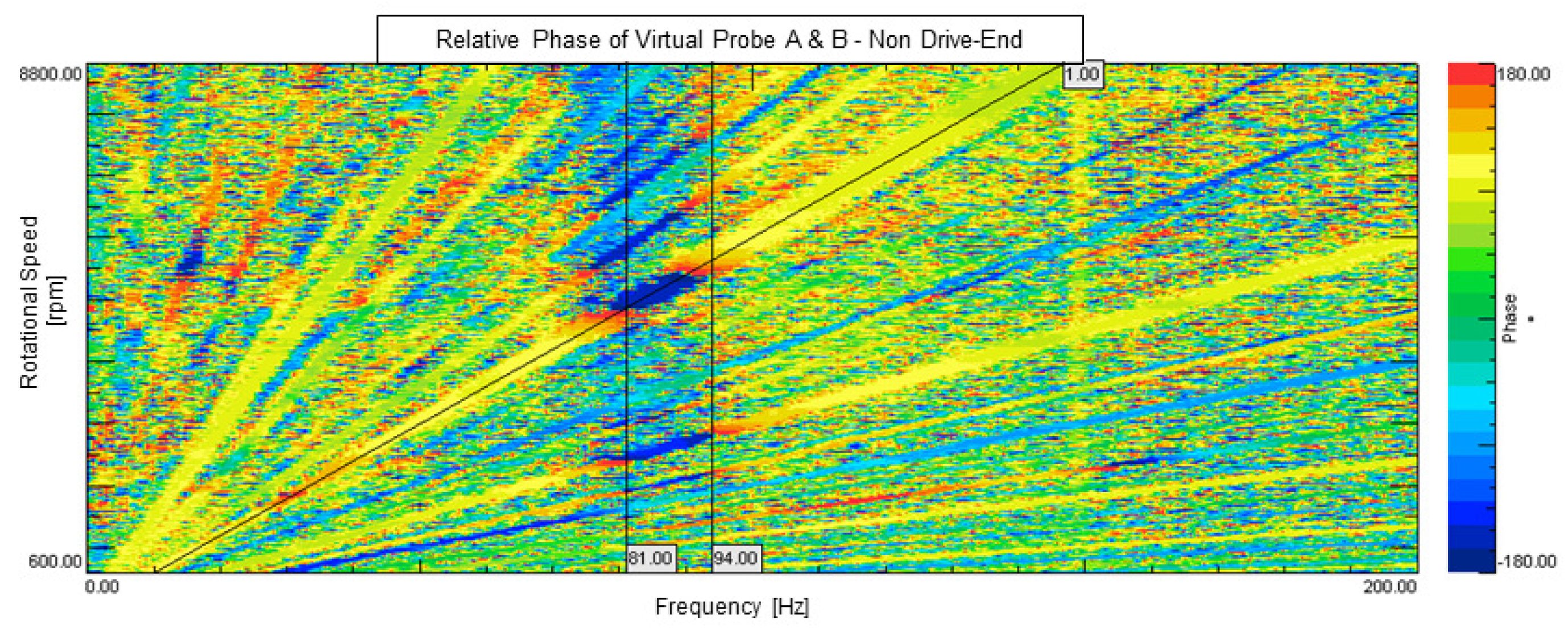
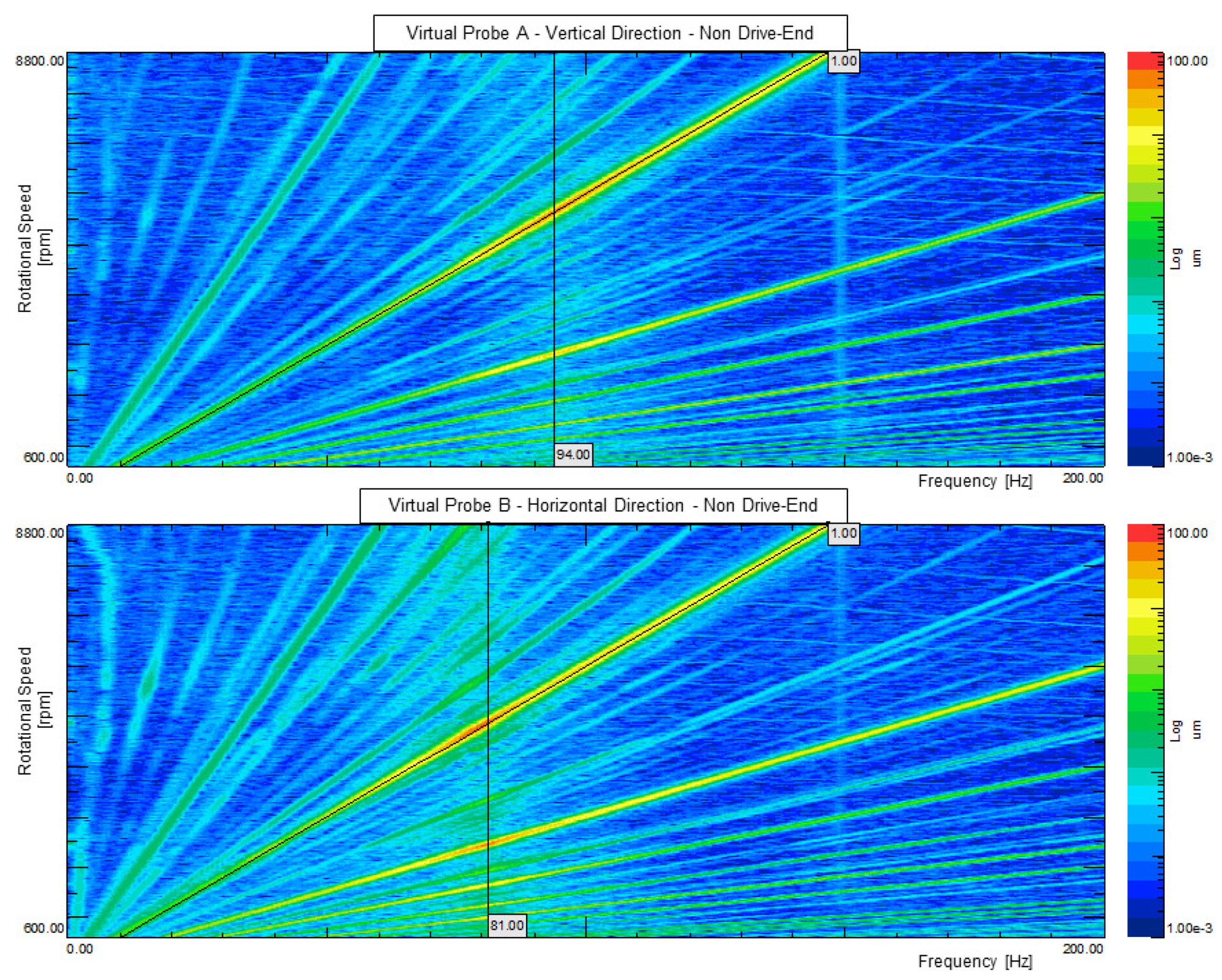
4.3. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACBB | Angular Contact Ball Bearing |
| CRB | Cylindrical Roller Bearing |
| DGBB | Deep Groove Ball Bearing |
| DOF | Degree-of-Freedom |
| ISFD | Integral Squeeze Film Damper |
| SFD | Squeeze Film Damper |
References
- Vance, J.; Zeidan, F.; Murphy, B. Machinery Vibration and Rotordynamics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bently, D.E.; Hatch, C.T. Fundamentals of Rotating Machinery Diagnostics; Bently Pressurized Bearing Company: Minden, LO, USA, 2002. [Google Scholar]
- Mitchell, C.; Schaefer, C.; Graf-Coller, O.; Solfrank, P.; Scheldt, M. Rolling Bearings in Turbochargers: A Real Bargain with Regard to CO2 Emissions. In Solving the Powertrain Puzzle: 10th Schaeffler Symposium; Schaeffler Technologies: Detroit, MI, USA, 2014. [Google Scholar]
- Müller, C.; Schuster, P.; Koch, O. Energy Efficiency by using Innovative Bearing Solutions. Power Transm. Eng. 2010, 4, 32–36. [Google Scholar]
- Zeidan, F.Y.; San Andrés, L.; Vance, J.M. Design and Application of Squeeze Film Dampers in Rotating Machinery. In Proceedings of the 25th Turbomachinery Symposium, Houston, TX, USA, 17–19 September 1996. [Google Scholar]
- Gunter, E.J. Rotor-Bearing Stability. In Proceedings of the First Turbomachinery Symposium, College Station, TX, USA, 24–26 October 1972. [Google Scholar]
- Ertas, B.; Cerny, V.; Kim, J.; Polreich, V. Stabilizing a 46MW Multi-Stage Utility Steam Turbine using Integral Squeeze Film Bearing Support Dampers. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Cooper, S. Preliminary Investigation of Oil Films for the Control of Vibration; Institution of Mechanical Engineers: London, UK, 1963. [Google Scholar]
- Jeung, S.H.; San Andrés, L.; Bradley, G. Forced Coefficients for a Short Length, Open Ends Squeeze Film Damper with End Grooves: Experiments and Predictions. J. Eng. Gas Turb. Power 2016, 138. [Google Scholar] [CrossRef]
- San Andrés, L.; Jeung, S.H. Experimental Performance of an Open Ends, Centrally Grooved, Squeeze Film Damper Operating with Large Amplitude Orbital Motions. J. Eng. Gas Turb. Power 2015, 137. [Google Scholar] [CrossRef]
- Della Pietra, L.; Adiletta, G. The Squeeze Film Damper over Four Decades of Investigations. Part I: Characteristics and Operating Features. Shock Vib. Dig. 2002, 34, 3–26. [Google Scholar]
- Della Pietra, L.; Adiletta, G. The Squeeze Film Damper over Four Decades of Investigations. Part II: Rotordynamic Analyses with Rigid and Flexible Rotors. Shock Vib. Dig. 2002, 34, 97–126. [Google Scholar]
- San Andrés, L. Squeeze Film Dampers: Operation, Models and Technical Issues; Turbomachinery Laboratory, Texas A&M University: College Station, TX, USA, 2010. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology, 5th ed.; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- De Mul, J.M.; Vree, J.M.; Maas, D.A. Equilibrium and Associated Load Distribution in Ball and Roller Bearings Loaded in Five Degrees of Freedom while Neglecting Friction—Part I: General Theory and Application to Ball Bearings. Trans. ASME Tribol. Conf. 1989, 111, 149–155. [Google Scholar] [CrossRef]
- Andréason, S. Load Distribution in a Taper Roller Bearing Arrangement considering Misalignment. Tribology 1973, 6, 84–92. [Google Scholar] [CrossRef]
- Jacobs, W. Experimental Analysis of the Dynamic Characteristics and Lubricant Film of a Ball Bearing under Combined Static and Dynamic Load. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2014. [Google Scholar]
- Verrelst, B. A Dynamic Walking Biped Actuated by Pleated Pneumatic Artificial Muscles: Basic Concepts and Control Issues. Ph.D. Thesis, Vrije Universiteit Brussel, Brussel, Belgium, 2005. [Google Scholar]


| m (kg) | Ip (kg m2) | Kxx (N/m) | Kyy (N/m) | |
|---|---|---|---|---|
| Radial Loading System | 2.26 | / | 8.29 | 8.29 |
| Unbalance Disc | 8.40 | 21.0 | / | / |
| Rotor Support—CRB | 0.70 | 74.6 | Section 3.3 | Section 3.3 |
| Rotor Support—SFD | 1.56 | / | Section 3.2 | Section 3.2 |
| Undamped Bearing | / | / | 1.00 | 1.00 |
| CRB | Type (-) | NU 211 | SFD | Type (-) | ISFD |
|---|---|---|---|---|---|
| Inner Diameter (mm) | 55 | Inner Diameter (mm) | 100 | ||
| Outer Diameter (mm) | 100 | Outer Diameter (mm) | 165 | ||
| Width (mm) | 21 | Width (mm) | 32 | ||
| Number of Damper Slots (-) | 3 | ||||
| Mean Damper Slot Diameter (mm) | 127 | ||||
| Damper Slot Thickness (mm) | 0.25 | ||||
| Damper Slot Span () | 330 |
| Load Case | Static Load (N) | Kxx (N/m) | Kxy (N/m) | Kyx (N/m) | Kyy (N/m) | Kyy/Kxx (-) |
|---|---|---|---|---|---|---|
| 1 | 1050 | 3.14 | 1.60 | 1.60 | 3.68 | 12 |
| 2 | 2380 | 7.47 | 1.42 | 1.42 | 5.39 | 7 |
| 3 | 7000 | 1.76 | 7.50 | 7.50 | 8.06 | 5 |
| Oil | Type (-) | ISO VG 68 |
| Temperature () | 50 | |
| Pressure (bar) | 2.3 | |
| Flow (L/min) | 2.5 | |
| Loading Conditions | Dynamic Unbalance (gmm) | 120 |
| ISO 1940 Balancing Class (-) | G9 | |
| Radial Load (kN) | 1.4–5.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meeus, H.; Fiszer, J.; Van De Velde, G.; Verrelst, B.; Desmet, W.; Guillaume, P.; Lefeber, D. Dynamic Performance of a Squeeze Film Damper with a Cylindrical Roller Bearing under a Large Static Radial Loading Range. Machines 2019, 7, 14. https://doi.org/10.3390/machines7010014
Meeus H, Fiszer J, Van De Velde G, Verrelst B, Desmet W, Guillaume P, Lefeber D. Dynamic Performance of a Squeeze Film Damper with a Cylindrical Roller Bearing under a Large Static Radial Loading Range. Machines. 2019; 7(1):14. https://doi.org/10.3390/machines7010014
Chicago/Turabian StyleMeeus, Hans, Jakob Fiszer, Gabriël Van De Velde, Björn Verrelst, Wim Desmet, Patrick Guillaume, and Dirk Lefeber. 2019. "Dynamic Performance of a Squeeze Film Damper with a Cylindrical Roller Bearing under a Large Static Radial Loading Range" Machines 7, no. 1: 14. https://doi.org/10.3390/machines7010014
APA StyleMeeus, H., Fiszer, J., Van De Velde, G., Verrelst, B., Desmet, W., Guillaume, P., & Lefeber, D. (2019). Dynamic Performance of a Squeeze Film Damper with a Cylindrical Roller Bearing under a Large Static Radial Loading Range. Machines, 7(1), 14. https://doi.org/10.3390/machines7010014





