Tuning and Feasibility Analysis of Classical First-Order MIMO Non-Linear Sliding Mode Control Design for Industrial Applications
Abstract
1. Introduction
- The classical first-order SM control for MIMO system feasibility conditions are deeply analyzed and correlated to the entity of the uncertainties affecting the real system.
- A straightforward procedure to obtain the majorant matrix of the errors introduced by the multiplicative uncertainties is given.
- A novel method to properly tune SM controllers exploiting the coefficients which guarantee the sliding condition to be verified is proposed.
2. Theoretical Remarks
2.1. Necessary Conditions for Non-Linear MIMO Sliding Mode Control
2.2. Procedure for Multiplicative Uncertainty Upper Bound Matrix Definition
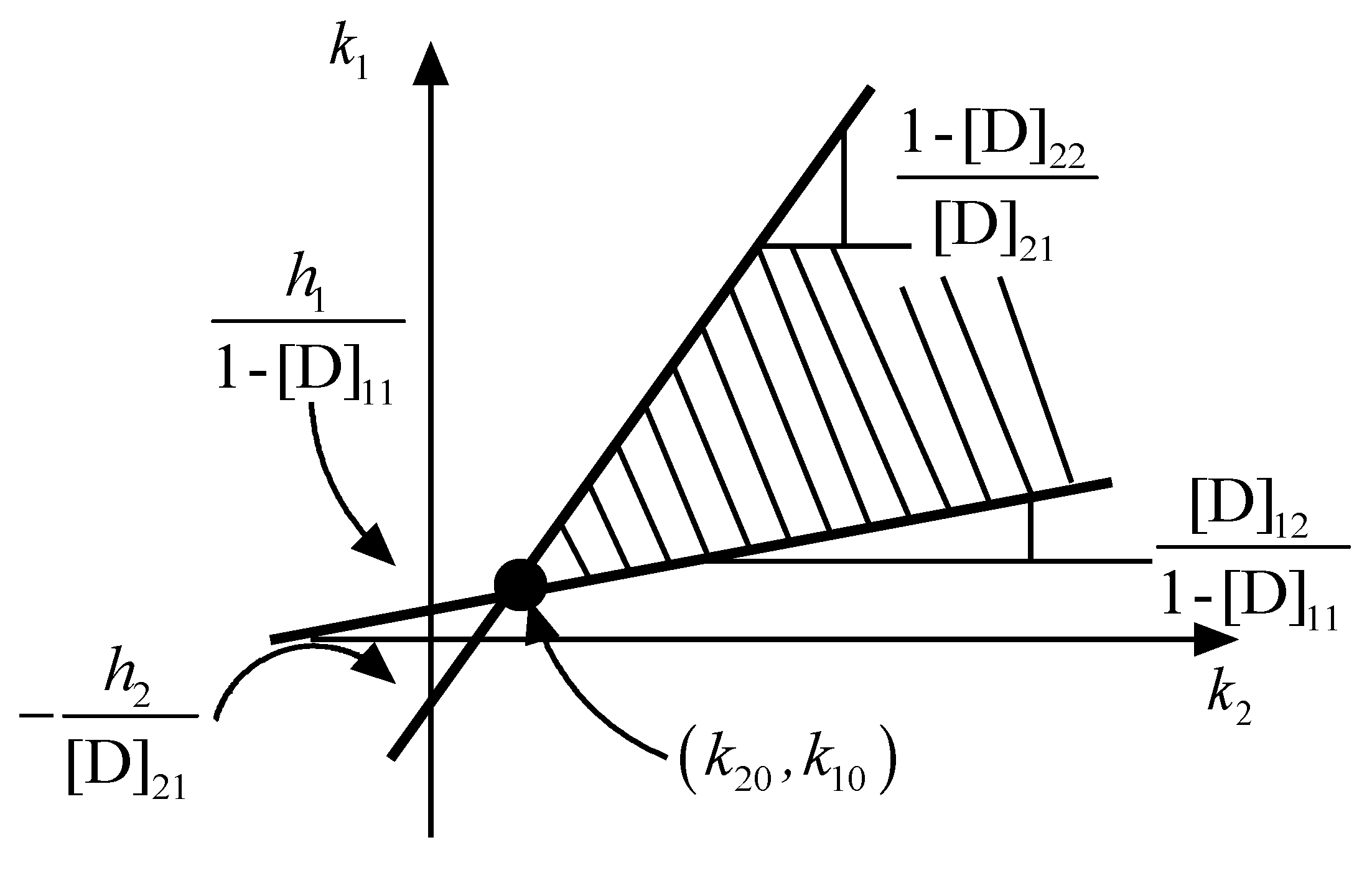
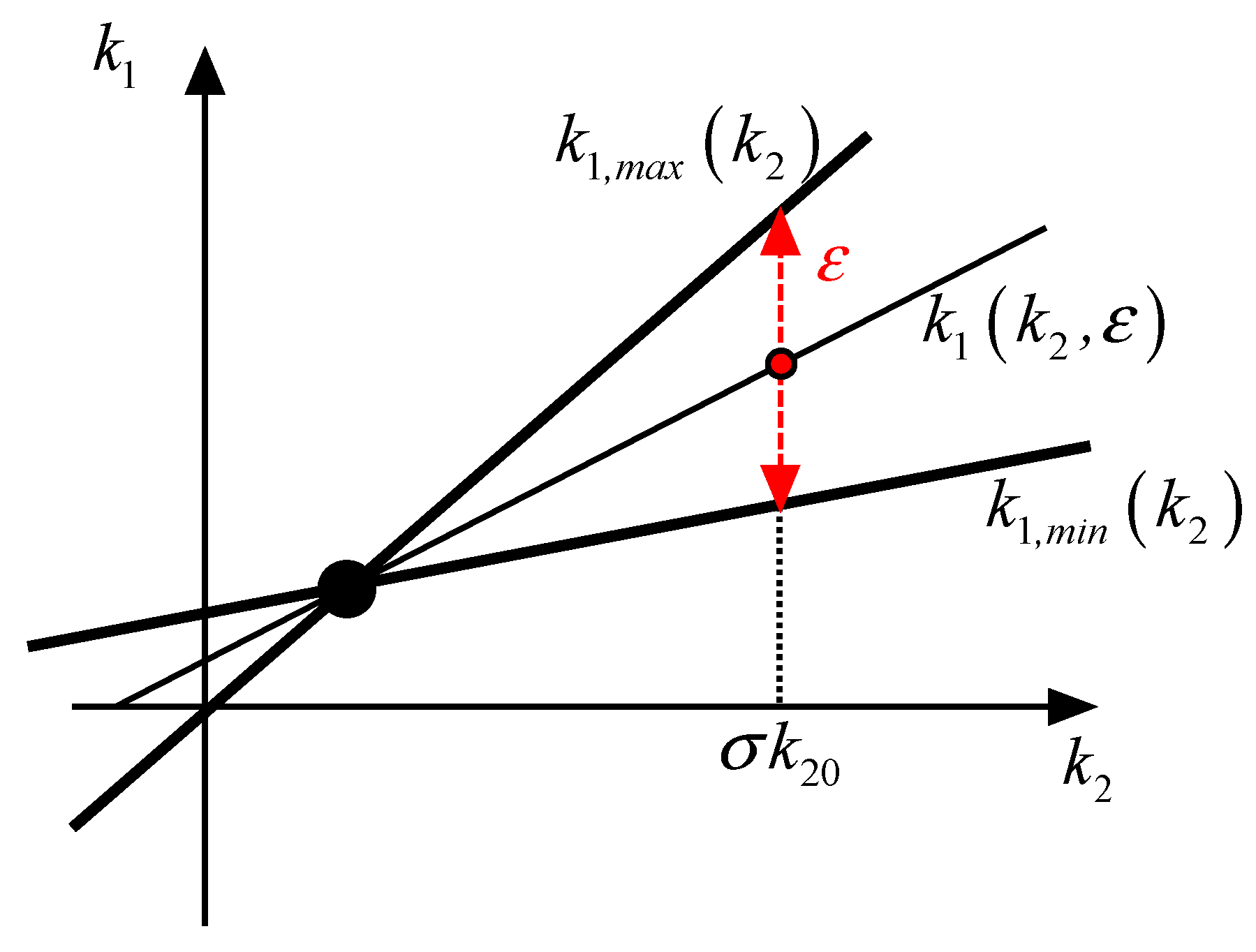
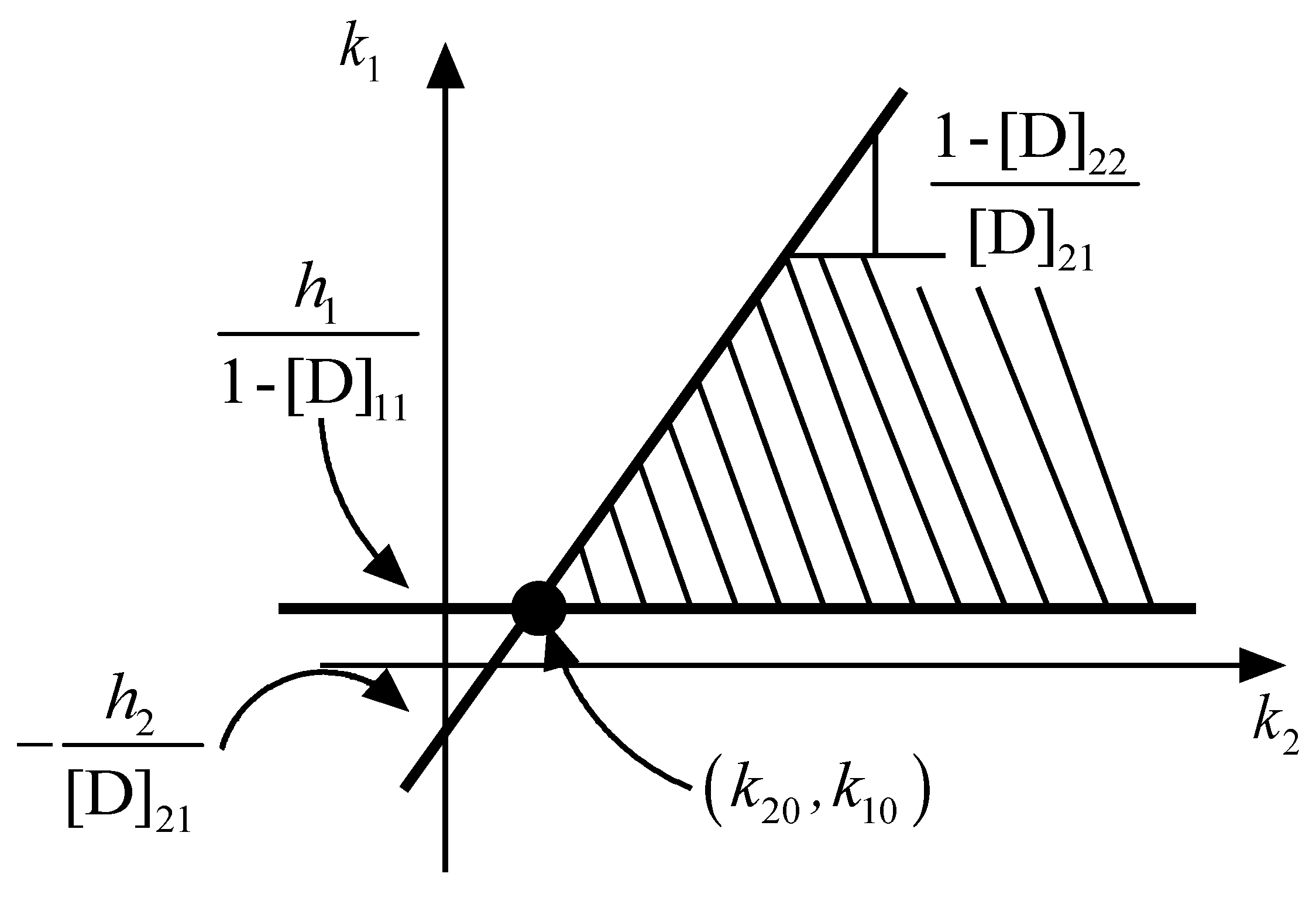
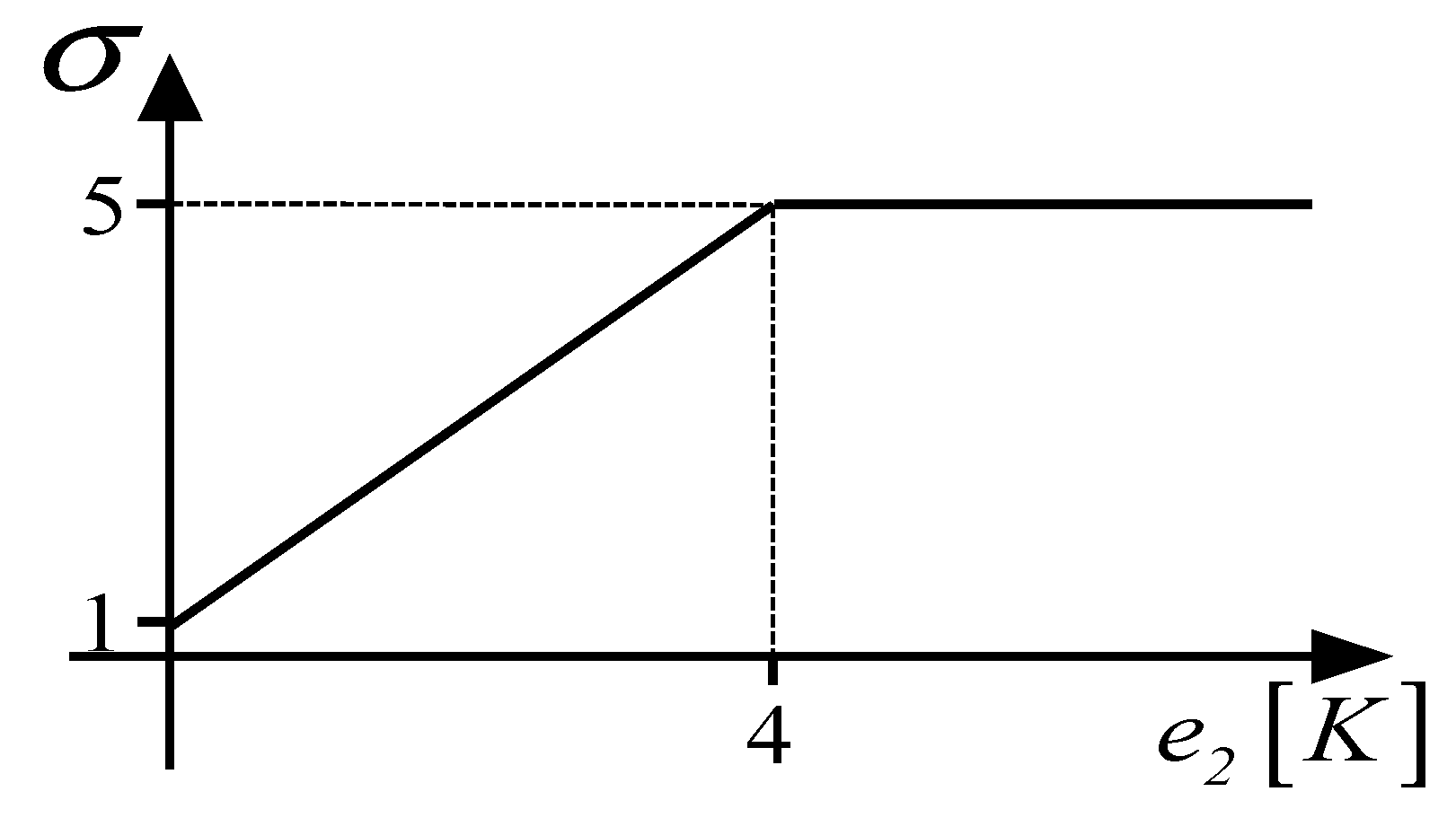
2.3. Controller Tuning Method for Systems with First-Order Channel
3. Test Case
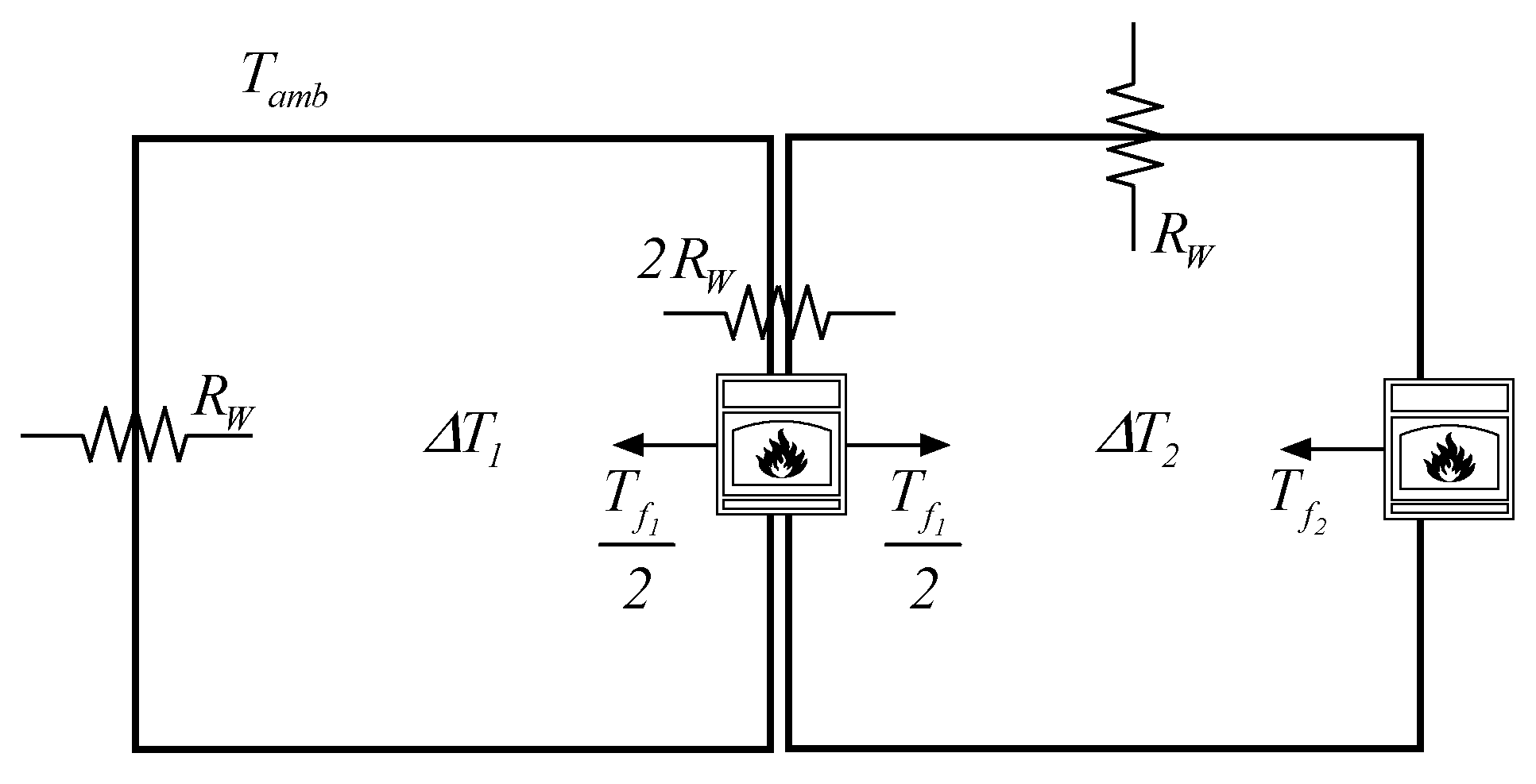
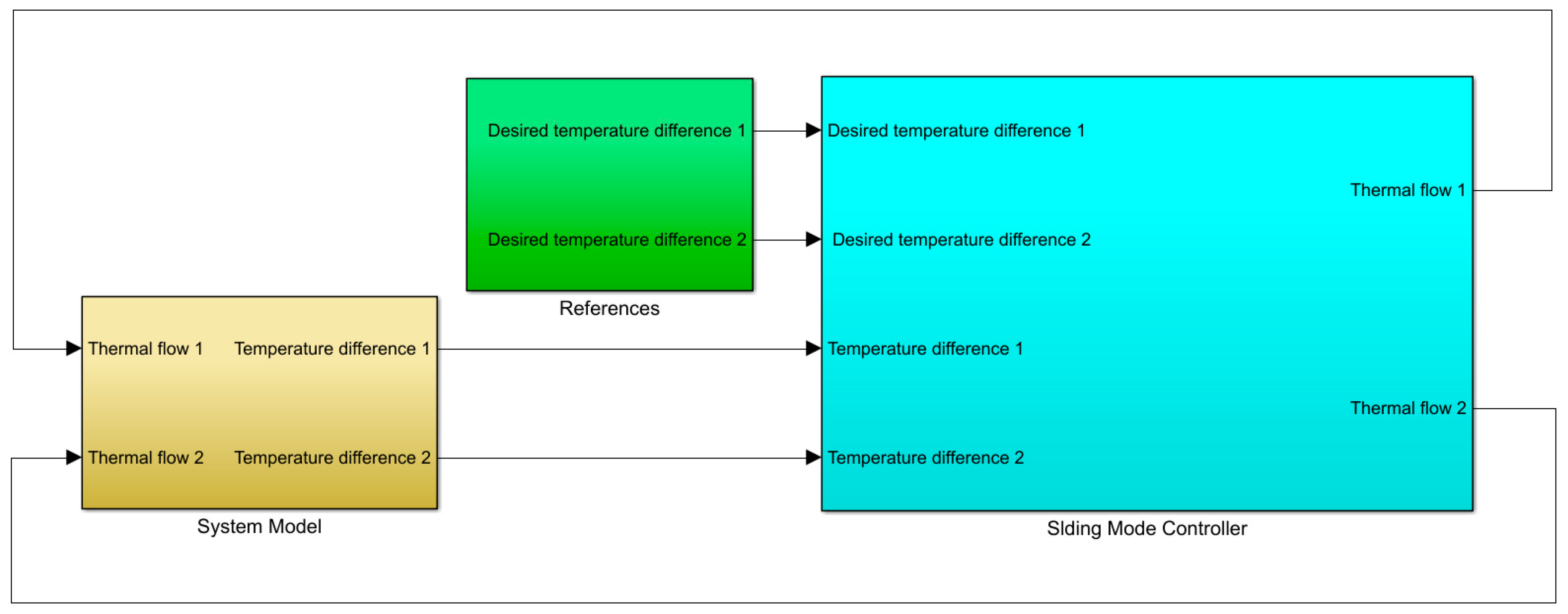
3.1. System Description and Modeling
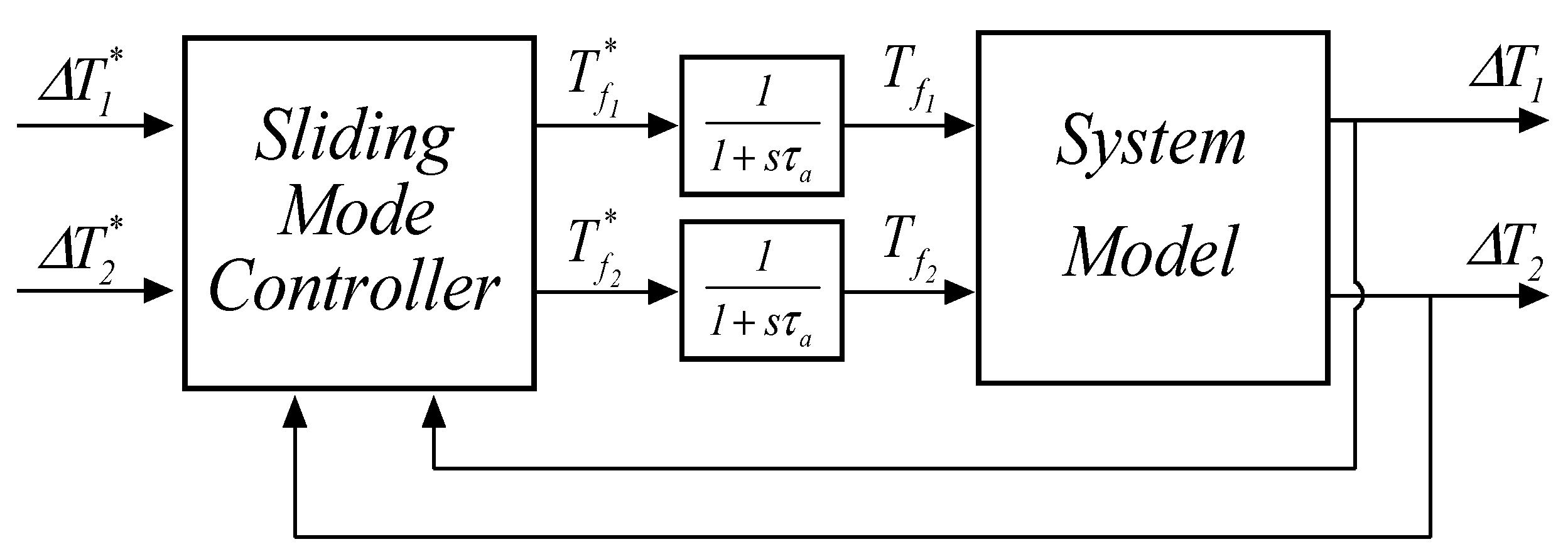
3.2. Sliding Mode Controller Design
3.3. Considerations on the Entity of Uncertainties
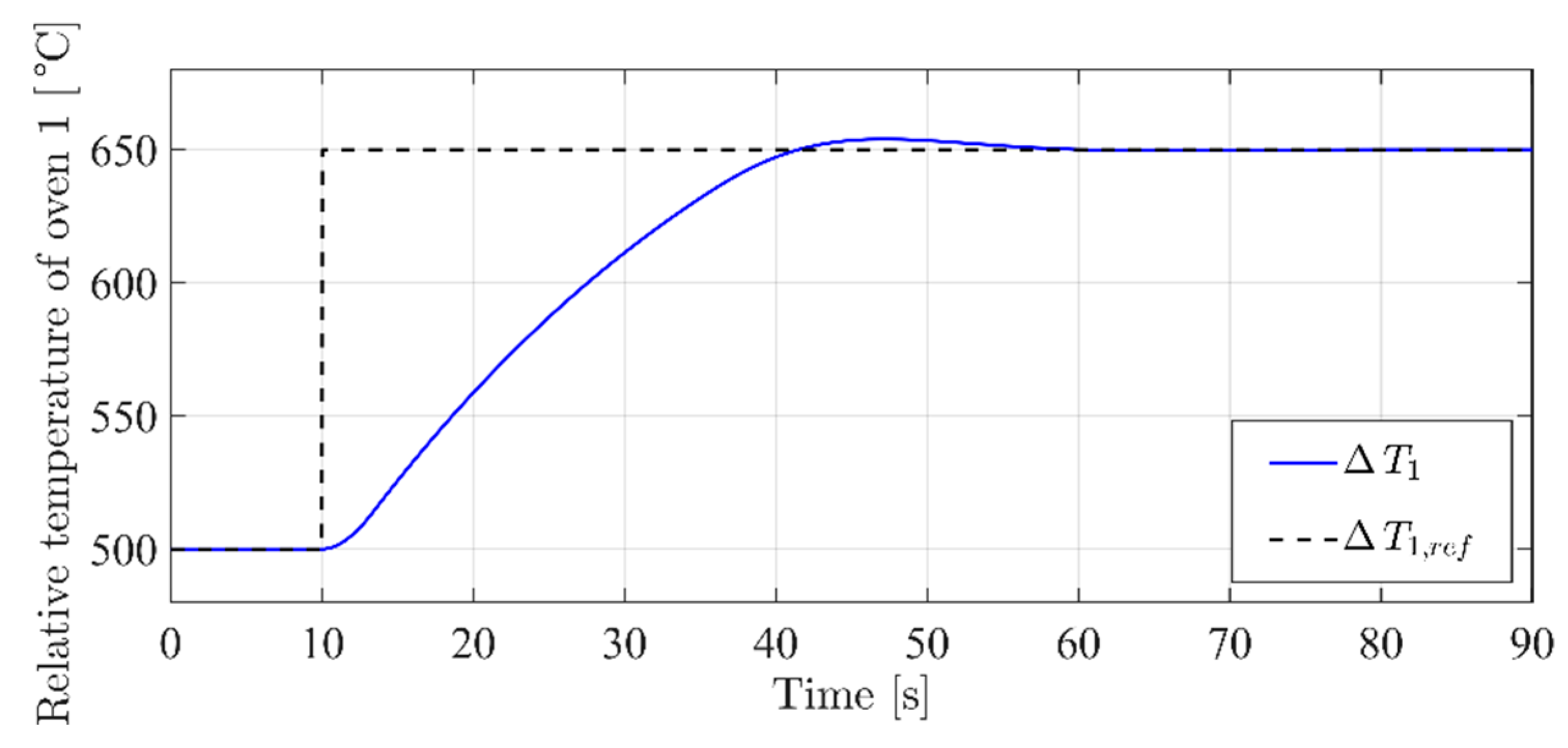
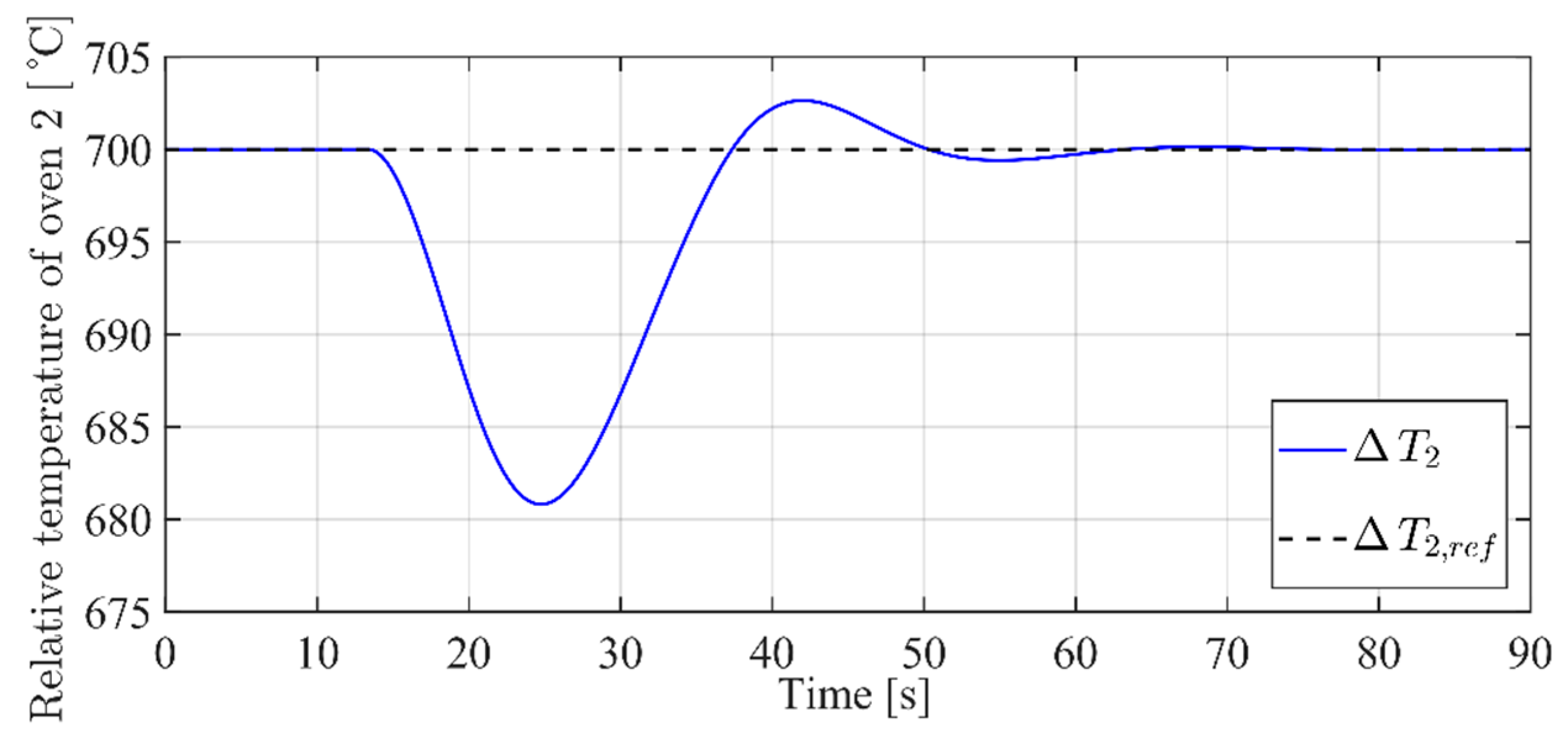
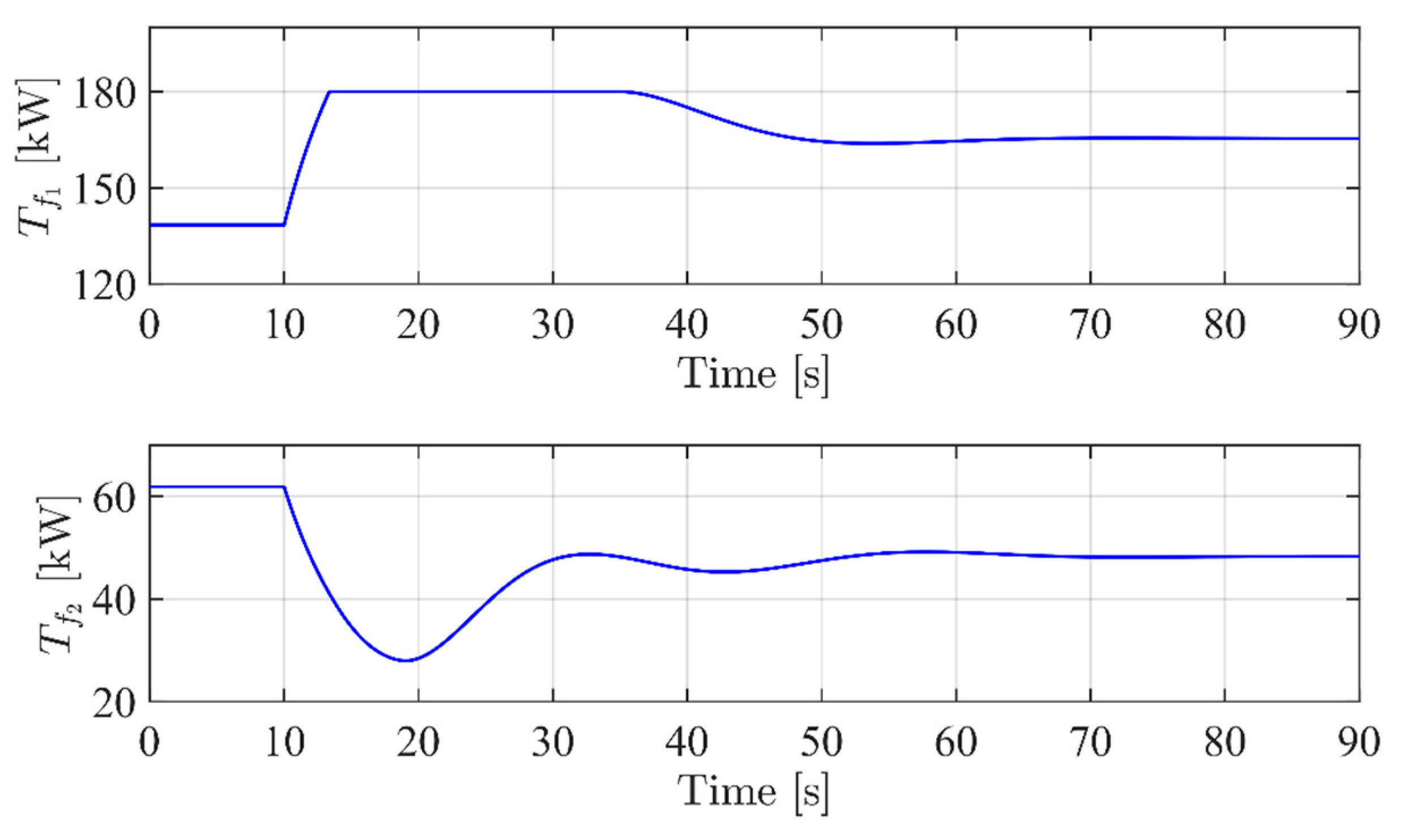
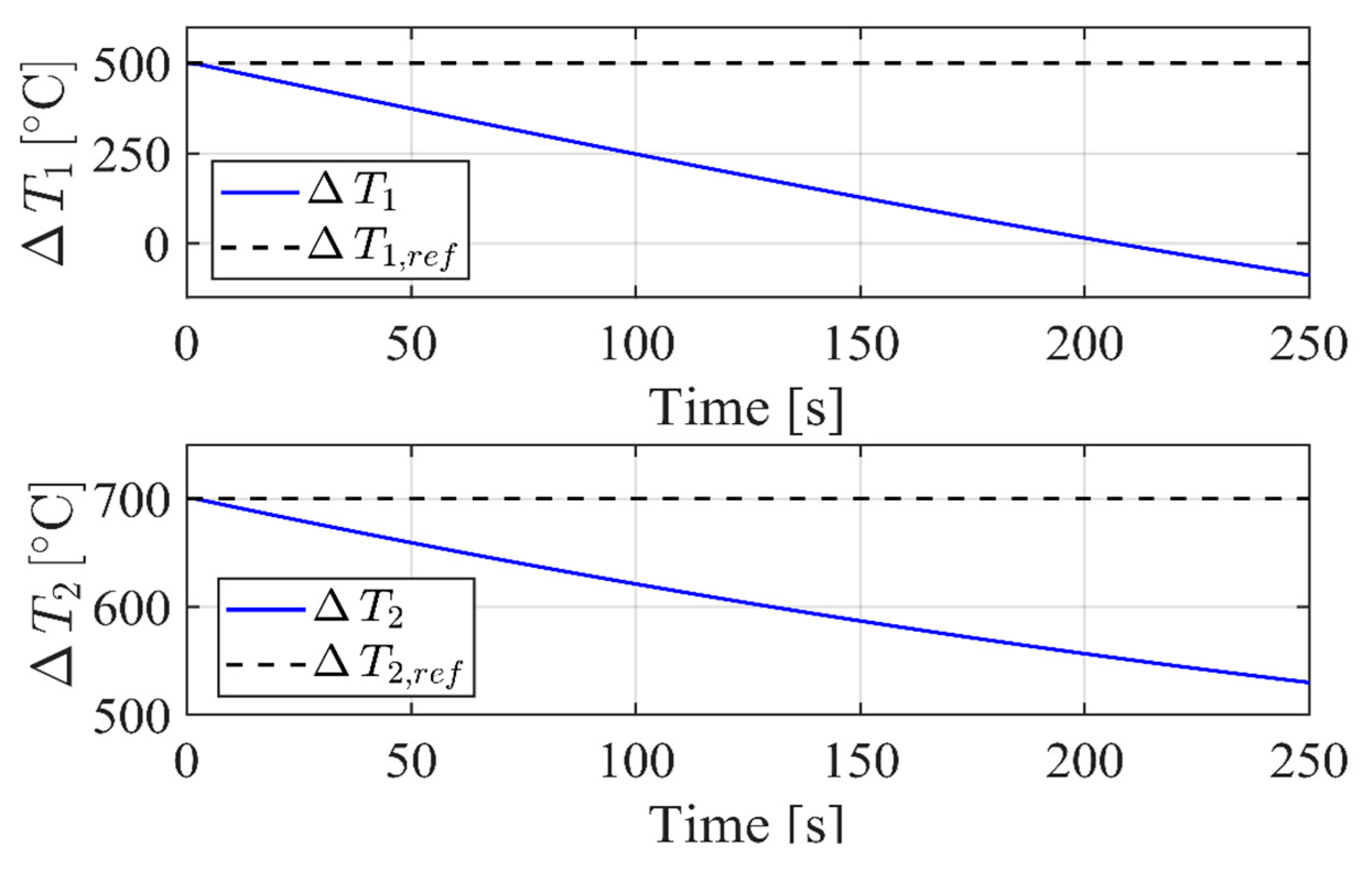
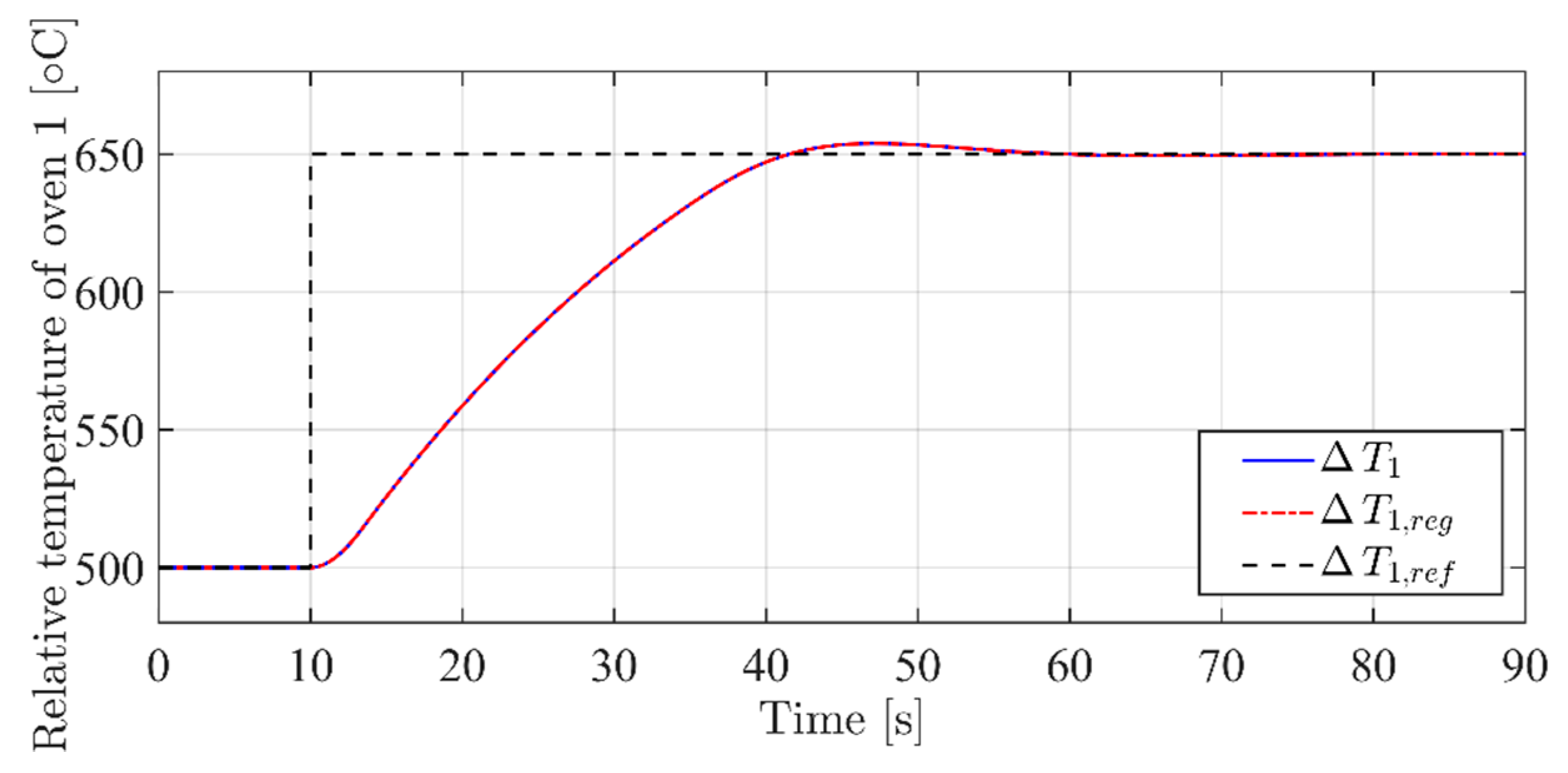
3.4. Simulation Set I
3.5. Simulation Set II
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Ubertini, S.; Facci, A.L.; Andreassi, L. Hybrid Hydrogen and Mechanical Distributed Energy Storage. Energies 2017, 10, 2035. [Google Scholar] [CrossRef]
- Bendato, I.; Bonfiglio, A.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R. A real-time Energy Management System for the integration of economical aspects and system operator requirements: Definition and validation. Renew. Energy 2017, 102, 406–416. [Google Scholar] [CrossRef]
- Higuchi, T.; Yokoi, Y.; Abe, T.; Sakimura, K. Design analysis of a novel synchronous generator for wind power generation. Machines 2014, 2, 202–218. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Barillari, L.; Bendato, I.; Bracco, S.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R.; Robba, M.; Rossi, M. Day ahead microgrid optimization: A comparison among different models. In Proceedings of the OPT-i 2014—1st International Conference on Engineering and Applied Sciences Optimization, Kos Island, Greece, 4–6 June 2014; pp. 1153–1165. [Google Scholar]
- Bonfiglio, A.; Lanzarotto, D.; Marchesoni, M.; Passalacqua, M.; Procopio, R.; Repetto, M. Electrical-Loss Analysis of Power-Split Hybrid Electric Vehicles. Energies 2017, 10, 2142. [Google Scholar] [CrossRef]
- Passalacqua, M.; Lanzarotto, D.; Repetto, M.; Marchesoni, M. Advantages of using supercapacitors and silicon carbide on hybrid vehicle series architecture. Energies 2017, 10, 920. [Google Scholar] [CrossRef]
- Lanzarotto, D.; Marchesoni, M.; Passalacqua, M.; Prato, A.P.; Repetto, M. Overview of different hybrid vehicle architectures. IFAC-PapersOnLine 2018, 51, 218–222. [Google Scholar] [CrossRef]
- Diao, W.; Jiang, J.; Liang, H.; Zhang, C.; Jiang, Y.; Wang, L.; Mu, B. Flexible grouping for enhanced energy utilization efficiency in battery energy storage systems. Energies 2016, 9, 498. [Google Scholar] [CrossRef]
- Yang, X.; Wen, P.; Xue, Y.; Zheng, T.Q.; Wang, Y. Super Capacitor Energy Storage Based MMC for Energy Harvesting in Mine Hoist Application. Energies 2017, 10, 1428. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Delfino, F.; Gonzalez-Longatt, F.; Procopio, R. Steady-state assessments of PMSGs in wind generating units. Int. J. Electr. Power Energy Syst. 2017, 90, 87–93. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Bonfiglio, A.; Procopio, R.; Bogdanov, D. Practical limit of synthetic inertia in full converter wind turbine generators: Simulation approach. In Proceedings of the 2016 19th International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 29 May–1 June 2016. [Google Scholar]
- Bonfiglio, A.; Delfino, F.; Invernizzi, M.; Procopio, R. Modeling and Maximum Power Point Tracking Control of Wind Generating Units Equipped with Permanent Magnet Synchronous Generators in Presence of Losses. Energies 2017, 10, 102. [Google Scholar] [CrossRef]
- Bemporad, A.; Borrelli, F.; Morari, M. Model predictive control based on linear programming—The explicit solution. IEEE Trans. Autom. Control 2002, 47, 1974–1985. [Google Scholar] [CrossRef]
- Guechi, E.-H.; Bouzoualegh, S.; Zennir, Y.; Blažič, S. MPC Control and LQ Optimal Control of A Two-Link Robot Arm: A Comparative Study. Machines 2018, 6, 37. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Oliveri, A.; Procopio, R.; Delfino, F.; Denegri, G.B.; Invernizzi, M.; Storace, M. Improving power grids transient stability via Model Predictive Control. In Proceedings of the 2014 Power Systems Computation Conference (PSCC), Wroclaw, Poland, 18–22 August 2014. [Google Scholar]
- Bonfiglio, A.; Delfino, F.; Invernizzi, M.; Perfumo, A.; Procopio, R. A feedback linearization scheme for the control of synchronous generators. Electr. Power Compon. Syst. 2012, 40, 1842–1869. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Cacciacarne, S.; Invernizzi, M.; Procopio, R.; Schiano, S.; Torre, I. Gas turbine generating units control via feedback linearization approach. Energy 2017, 121, 491–512. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer: Berlin, Germany, 2013. [Google Scholar]
- Utkin, V. First Stage of VSS: People and events. In Variable Structure Systems: Towards the 21st Century; Springer: Berlin, Germany, 2002; pp. 1–32. [Google Scholar]
- Meng, Z.; Shao, W.; Tang, J.; Zhou, H. Sliding-mode control based on index control law for MPPT in photovoltaic systems. CES Trans. Electr. Mach. Syst. 2018, 2, 303–311. [Google Scholar] [CrossRef]
- Farhadi, P.; Sedaghat, M.; Sharifi, S.; Taheri, B. Power point tracking in photovoltaic systems by sliding mode control. In Proceedings of the 2017 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2017; pp. 781–785. [Google Scholar]
- Bonfiglio, A.; Cacciacarne, S.; Invernizzi, M.; Lanzarotto, D.; Palmieri, A.; Procopio, R. A Sliding Mode Control Approach for Gas Turbine Power Generators. IEEE Trans. Energy Convers. 2018. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Invernizzi, M.; Lanzarotto, D.; Palmieri, A.; Procopio, R. Definition of a sliding mode controller accounting for a reduced order model of gas turbine set. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; pp. 1–6. [Google Scholar]
- Subudhi, B.; Ge, S.S. Sliding-Mode-Observer-Based Adaptive Slip Ratio Control for Electric and Hybrid Vehicles. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1617–1626. [Google Scholar] [CrossRef]
- Liu, Y.; Shao, C. A Torque Control Scheme of Induction Motor in Hybrid Electric Vehicle. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Korea, 18–21 October 2006; pp. 540–544. [Google Scholar]
- Emelyanov, S.; Korovin, S.; Levantovsky, L. Second order sliding modes in controlling uncertain systems. Sov. J. Comput. Syst. Sci. 1986, 24, 63–68. [Google Scholar]
- Levant, A. Universal single-input-single-output (SISO) sliding-mode controllers with finite-time convergence. IEEE Trans. Autom. Control 2001, 46, 1447–1451. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin, Germany, 2014; Volume 10. [Google Scholar]
- Man, Z.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; pp. 4619–4624. [Google Scholar]
- Veselić, B.; Draženović, B.; Milosavljević, Č. Integral sliding manifold design for linear systems with additive unmatched disturbances. IEEE Trans. Autom. Control 2016, 61, 2544–2549. [Google Scholar] [CrossRef]
- Incremona, G.P.; Cucuzzella, M.; Ferrara, A. Adaptive suboptimal second-order sliding mode control for microgrids. Int. J. Control 2016, 89, 1849–1867. [Google Scholar] [CrossRef]
- Precup, R.-E.; Radac, M.-B.; Roman, R.-C.; Petriu, E.M. Model-free sliding mode control of nonlinear systems: Algorithms and experiments. Inf. Sci. 2017, 381, 176–192. [Google Scholar] [CrossRef]
- Komurcugil, H.; Biricik, S. Time-varying and constant switching frequency-based sliding-mode control methods for transformerless DVR employing half-bridge VSI. IEEE Trans. Ind. Electron. 2017, 64, 2570–2579. [Google Scholar] [CrossRef]
- Slotine, J.-J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; Volume 199. [Google Scholar]
- Slotine, J.-J.E. The robust control of robot manipulators. Int. J. Robot. Res. 1985, 4, 49–64. [Google Scholar] [CrossRef]
- Slotine, J.-J.E. Sliding controller design for non-linear systems. Int. J. Control 1984, 40, 421–434. [Google Scholar] [CrossRef]
- Li, D.; Slotine, J.J.E. On Sliding Control for Multi-Input Multi-Output Nonlinear Systems. In Proceedings of the 1987 American Control Conference, Minneapolis, MN, USA, 10–12 June 1987; pp. 874–879. [Google Scholar]
- Slotine, J.J.E.; Hong, S. Two-time Scale Sliding Control of Manipulators with Flexible Joints. In Proceedings of the 1986 American Control Conference, Seattle, WA, USA, 18–20 June 1986; pp. 805–810. [Google Scholar]
- Johnson, C.R.; Smith, R.L. Inverse M-matrices, II. Linear Algebra Its Appl. 2011, 435, 953–983. [Google Scholar] [CrossRef]
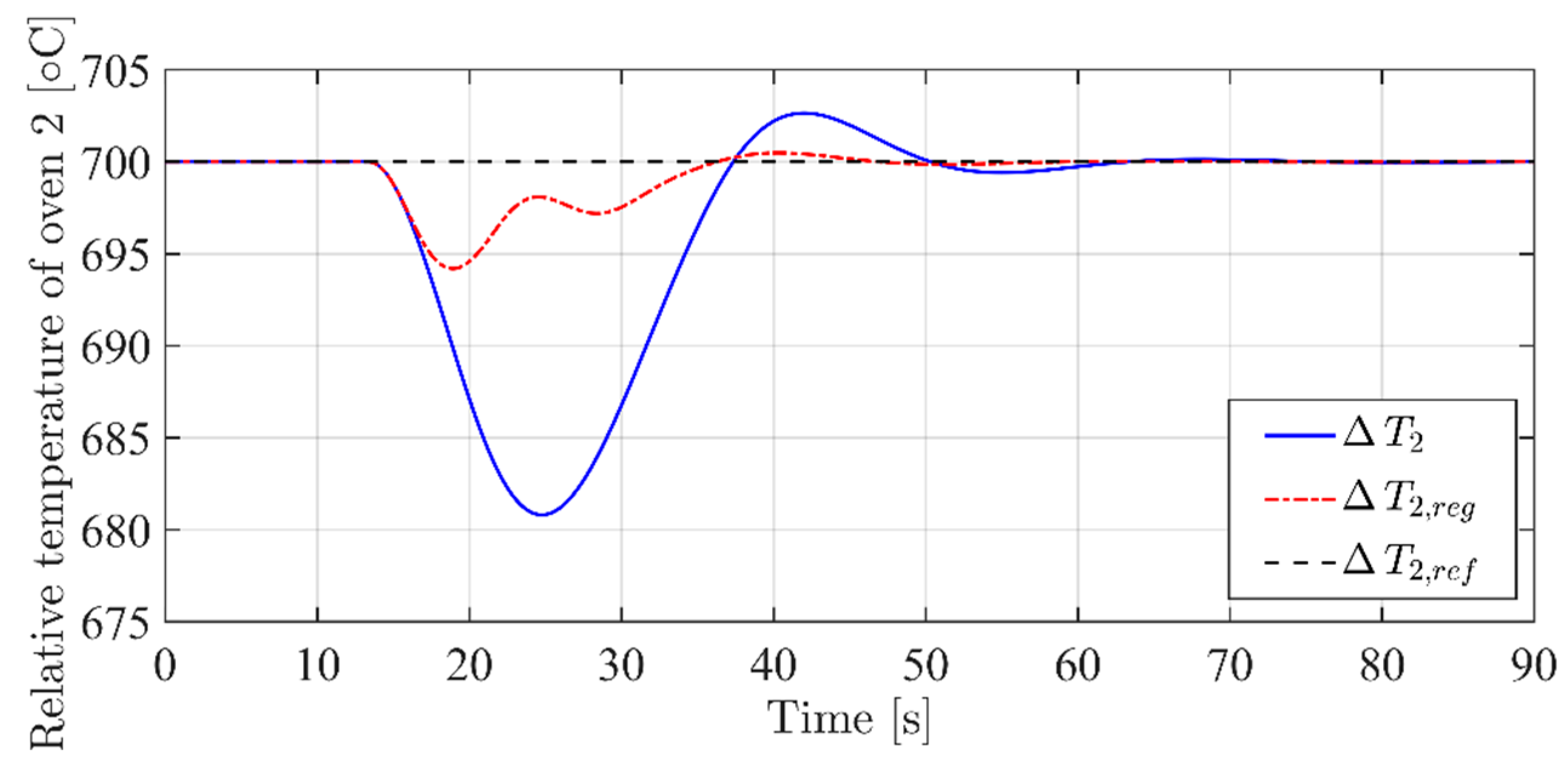
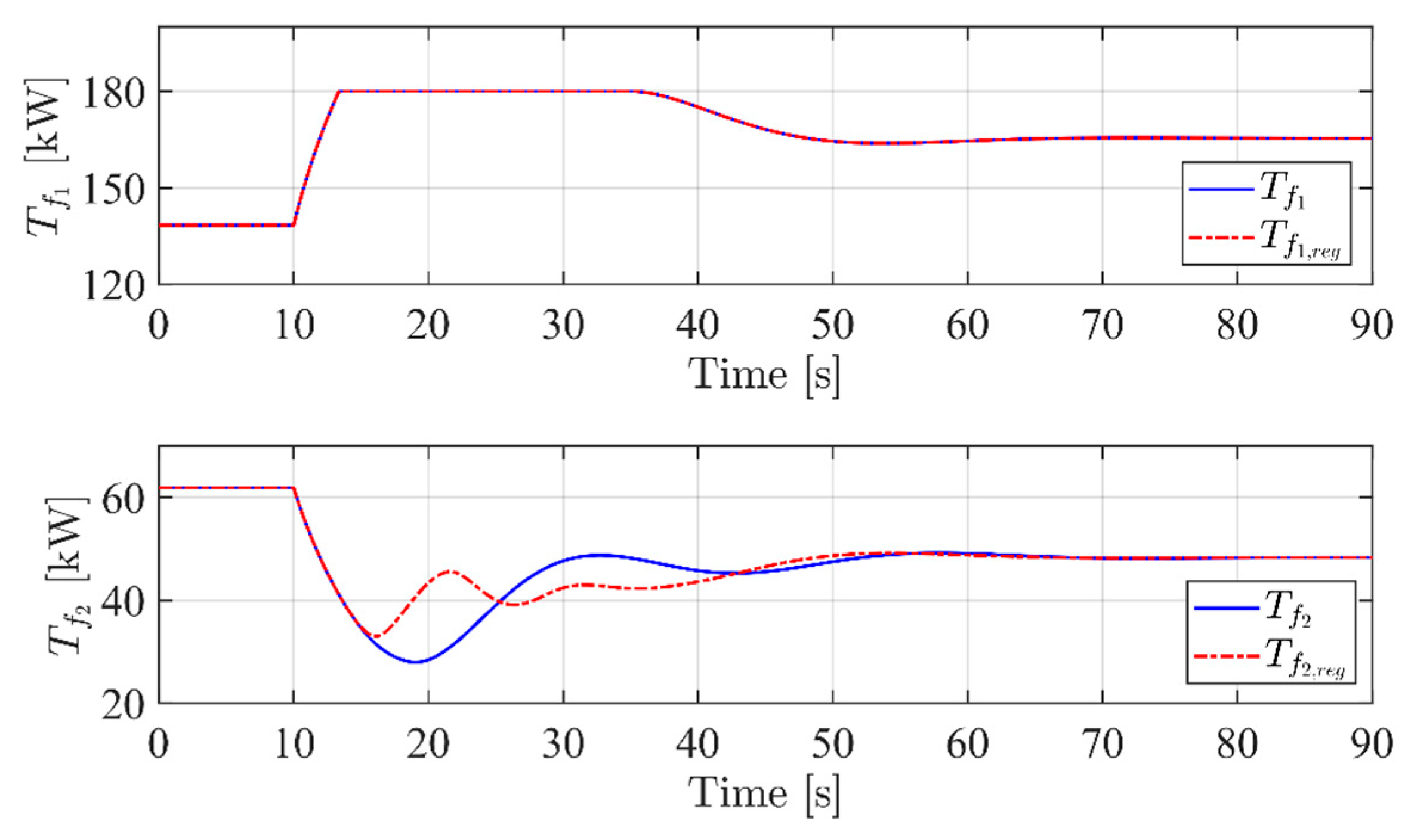
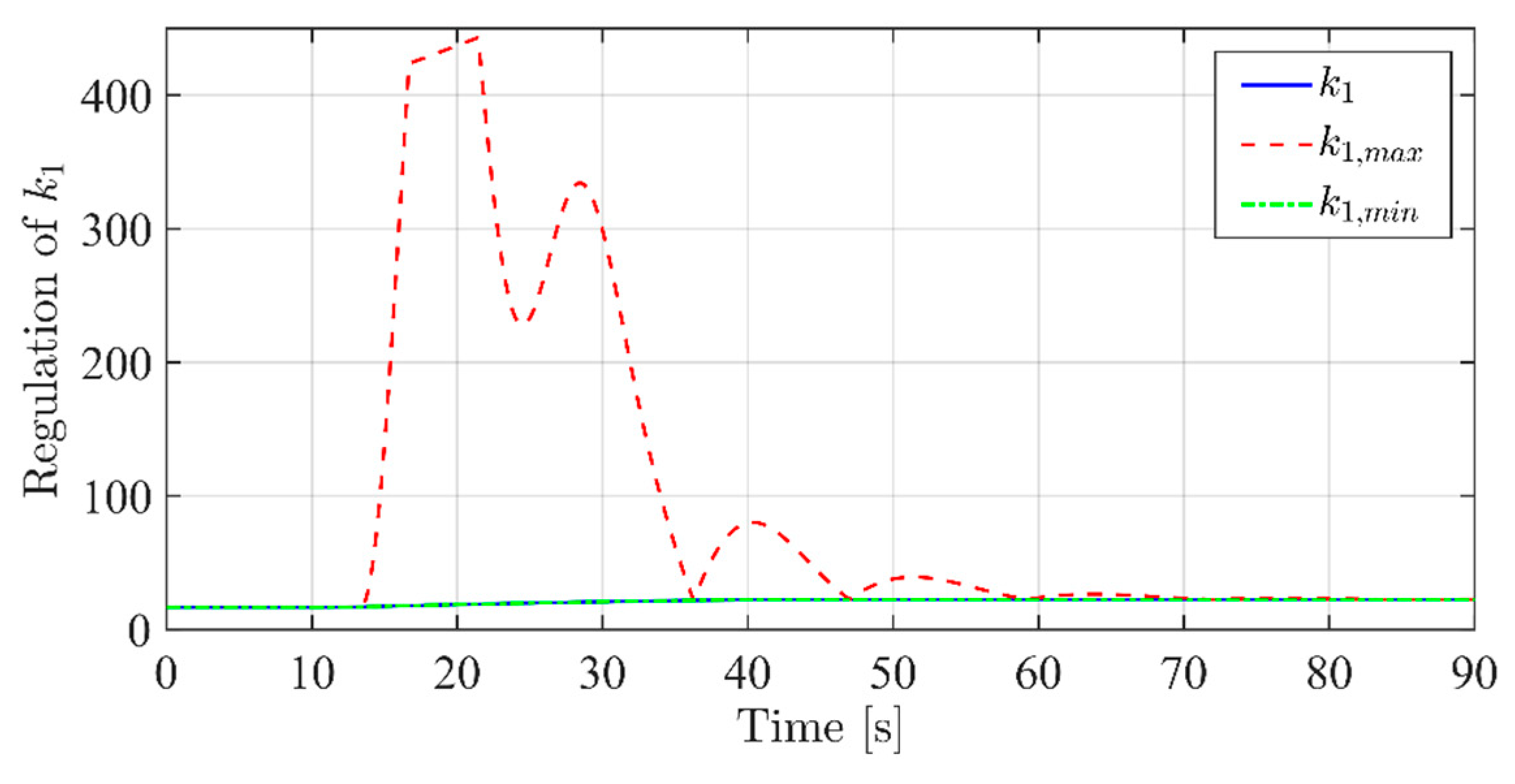
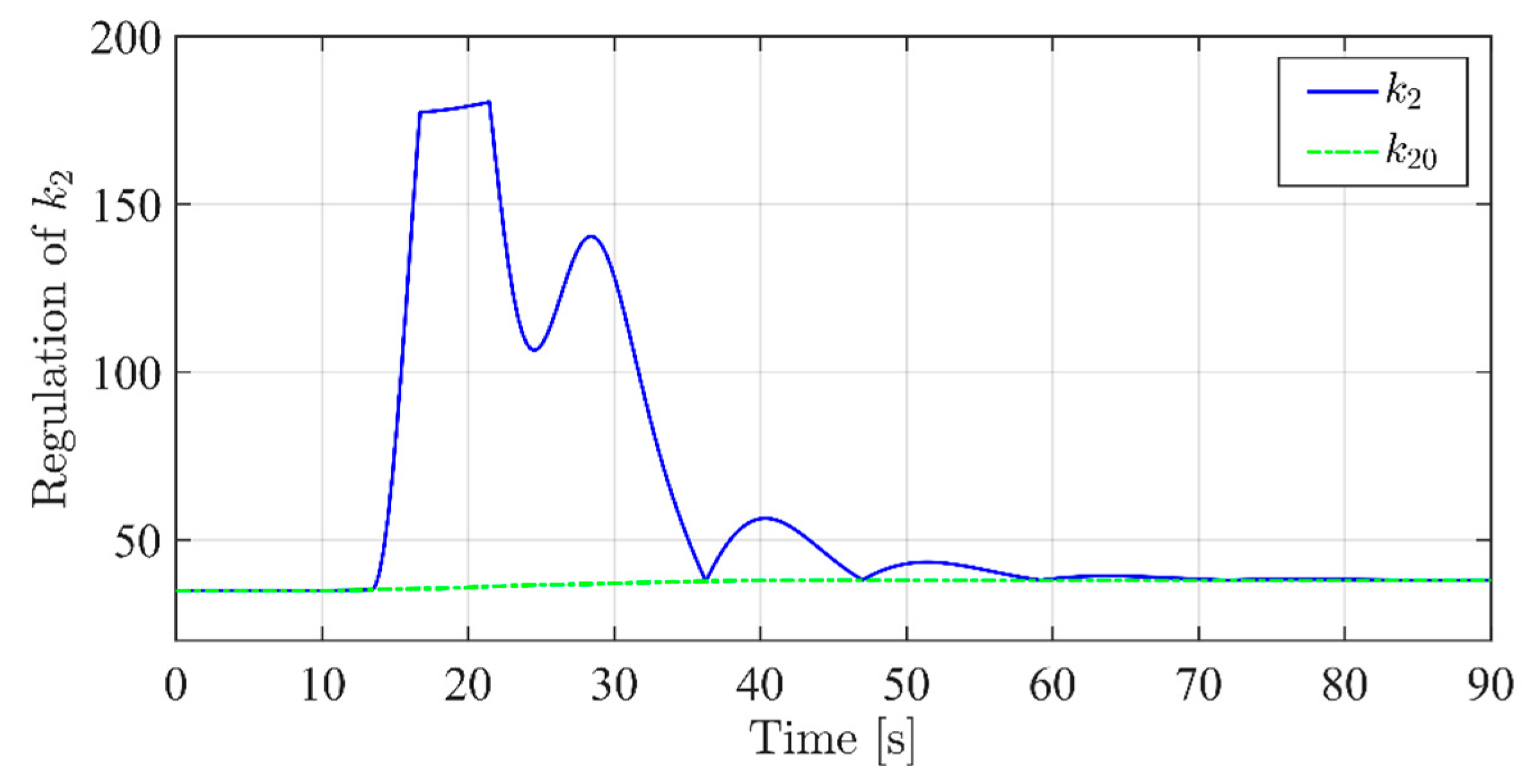
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 8 m3 | 15.6 m3 | ||
| 16 m2 | 25 m2 | ||
| 4 m2 | 15 °C | ||
| 1.225 kg/m3 | 1005 J/kg·K | ||
| 0.2 m2·K/W | 5 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmieri, A.; Procopio, R.; Bonfiglio, A.; Brignone, M.; Invernizzi, M.; Morini, A.; Veselic’, B. Tuning and Feasibility Analysis of Classical First-Order MIMO Non-Linear Sliding Mode Control Design for Industrial Applications. Machines 2019, 7, 10. https://doi.org/10.3390/machines7010010
Palmieri A, Procopio R, Bonfiglio A, Brignone M, Invernizzi M, Morini A, Veselic’ B. Tuning and Feasibility Analysis of Classical First-Order MIMO Non-Linear Sliding Mode Control Design for Industrial Applications. Machines. 2019; 7(1):10. https://doi.org/10.3390/machines7010010
Chicago/Turabian StylePalmieri, Alessandro, Renato Procopio, Andrea Bonfiglio, Massimo Brignone, Marco Invernizzi, Andrea Morini, and Boban Veselic’. 2019. "Tuning and Feasibility Analysis of Classical First-Order MIMO Non-Linear Sliding Mode Control Design for Industrial Applications" Machines 7, no. 1: 10. https://doi.org/10.3390/machines7010010
APA StylePalmieri, A., Procopio, R., Bonfiglio, A., Brignone, M., Invernizzi, M., Morini, A., & Veselic’, B. (2019). Tuning and Feasibility Analysis of Classical First-Order MIMO Non-Linear Sliding Mode Control Design for Industrial Applications. Machines, 7(1), 10. https://doi.org/10.3390/machines7010010








