Robot Coverage Path Planning under Uncertainty Using Knowledge Inference and Hedge Algebras
Abstract
1. Introduction
- How can a high-level probabilistic representation (a model) of the environment be created;
- How can understanding and reasoning about the environment be achieved to enable CPP with completion of the required task(s) while a robot is in motion.
2. Related Research
3. Problem Formulation
3.1. Awareness in CPP with Decision-Support
- is a collection of birth elements of linguistic variable;
- is a set of hedges; (and)
- is semantic relation on .
- Each element is either positive or negative for any part in including itself;
- The two elements and are independent. That is: are comparable with . are not comparable, are comparable;
- with ;
- where ;
Fuzzy Linguistic Representation
- : is a set of linguistic values for (dom();
- : is a set of primitive words - birth elements (true, false);
- : is a set of linguistic hedges (very, more, little);
- : is the semantic relation on “words" (a fuzzy concept). The semantic relations are the ordered relations derived from the natural language meaning, i.e., , , , , , ….
- is set of elements is resulting from
- Considering , , is positive and is negative is positive and is negative
- has exactly two fuzzy primitive elements and , then is called a positive birth element and is called a negative birth element and
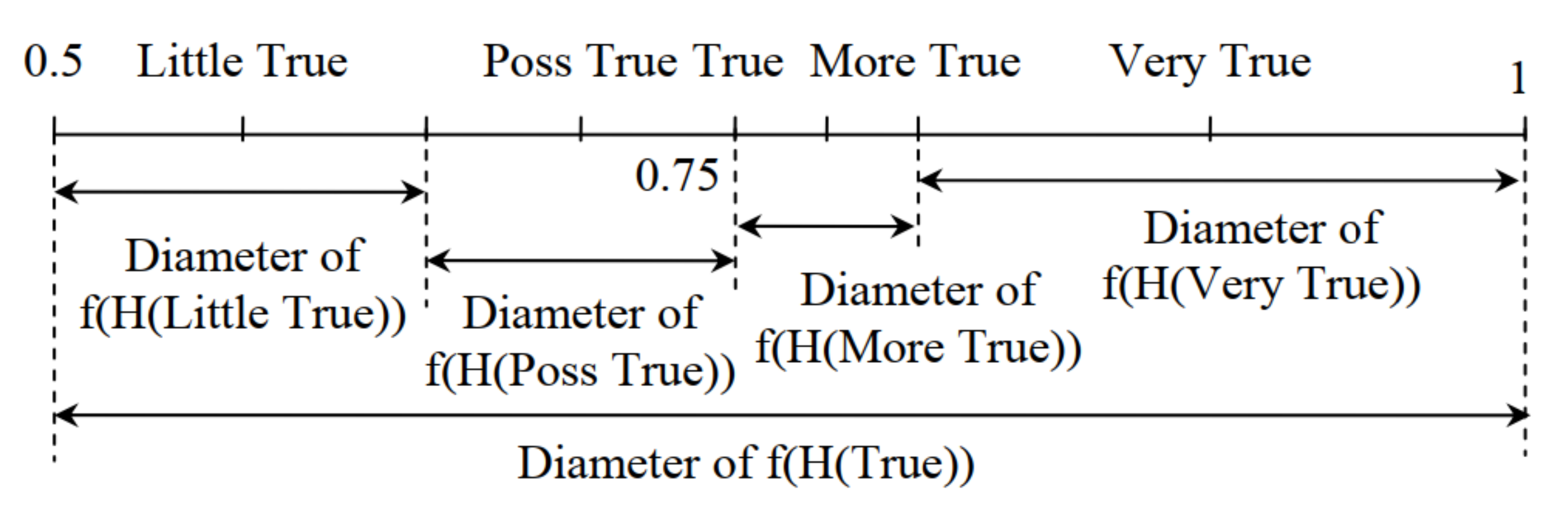
3.2. Quantitative Semantic Mapping
4. The Methodology
- Using the optimal path traverse the complete environment and visit all nodes without repeating or overlapping paths;
- Identify if the nodes (cells) are: (a) clear; (b) occupied by an obstacle (static or moving); or (c) are bounded by walls;
- Avoid all static and moving obstacles;
- Find the optimal CPP and traverse operating environment with multiple decision-making.
4.1. The Coverage Path Planning Problem
- Hedge_DSS_Robot: the objective optimisation function to maximise the operational efficiency of the robot in CPP and enable multiple robot decision-making objectives;
- : the weight which is representative of and . The weight is a value of the linguistic variable that can recognised as the value in range: important, very important, more important, little important, very little important, possibly important, ...;
- Based on quantitative semantic mapping of linguistic values for fall in the range and are used in multiple decision-making objectives for the Robot tasks where ;
- : the objective function for the multiple decision-making objective. recognises the linguistic value of the linguistic variable used in the quantitative semantics mapping of and transfers the linguistic value in the range ;
- The decision variable is binary and defines the tasks for the multiple decision- making objectives;
- Calculate the objective function value for .
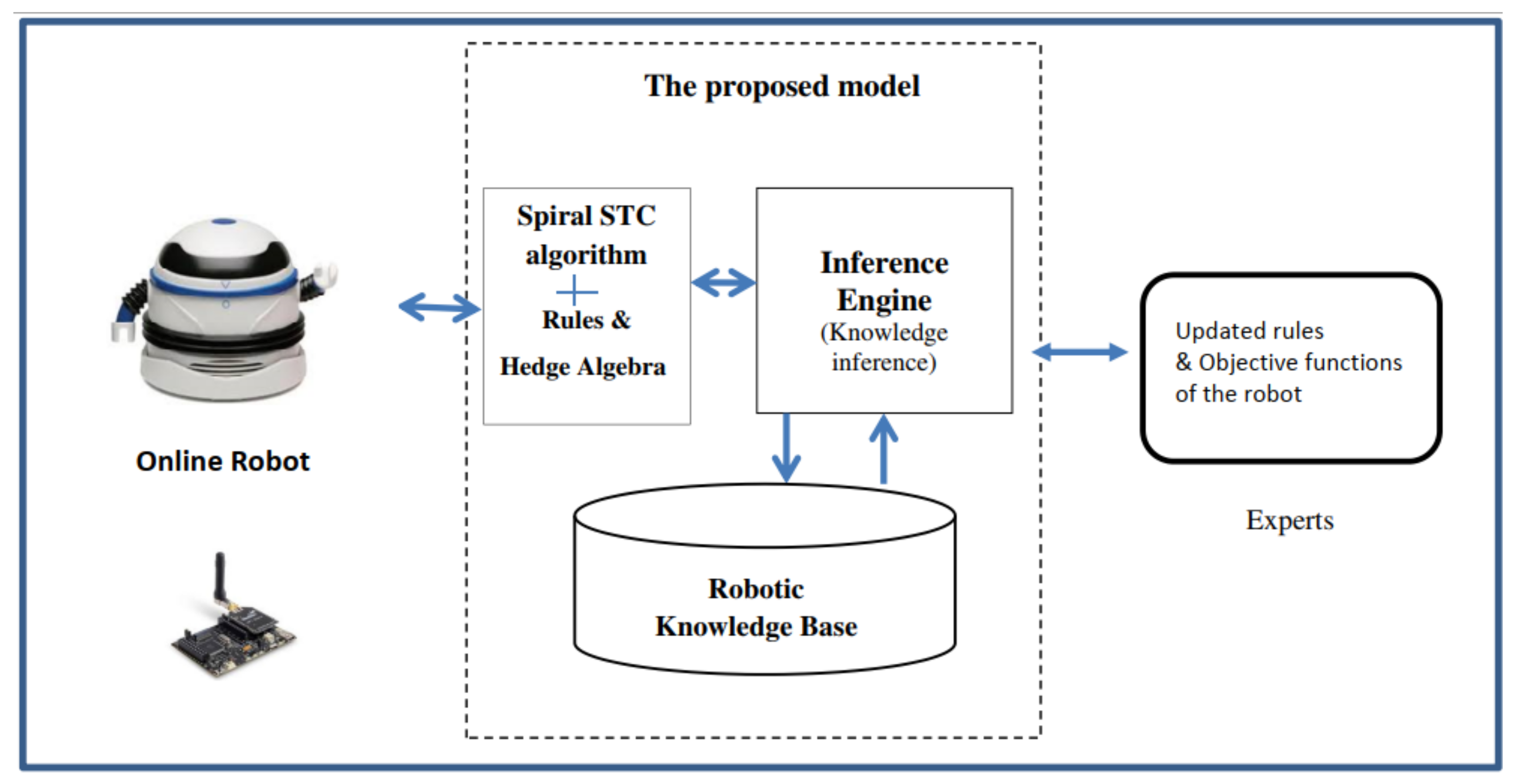
4.2. The Proposed Coverage Path Planning Algorithm
5. Evaluation
5.1. The Robot Case Study
- : Traverse the operating environment visiting all the nodes in the operating environment;
- : Identify if the nodes (cells) are: (a) clear, (b) occupied by an obstacle(s), or (c) bounded by wall(s);
- : Complete its traverse over the operating environment without repeating or overlapping paths;
- : Avoid all static and dynamic (independently moving) obstacles;
- : Apply CPP to find the “optimal path” to traverse operating environment with multiple decision-making;
- Simple cleaning function;
- Cleaning and picking up rubbish;
- Cleaning while avoiding objects;
- Intelligent cleaning with decision-support in selecting tasks;
- Heavy cleaning.
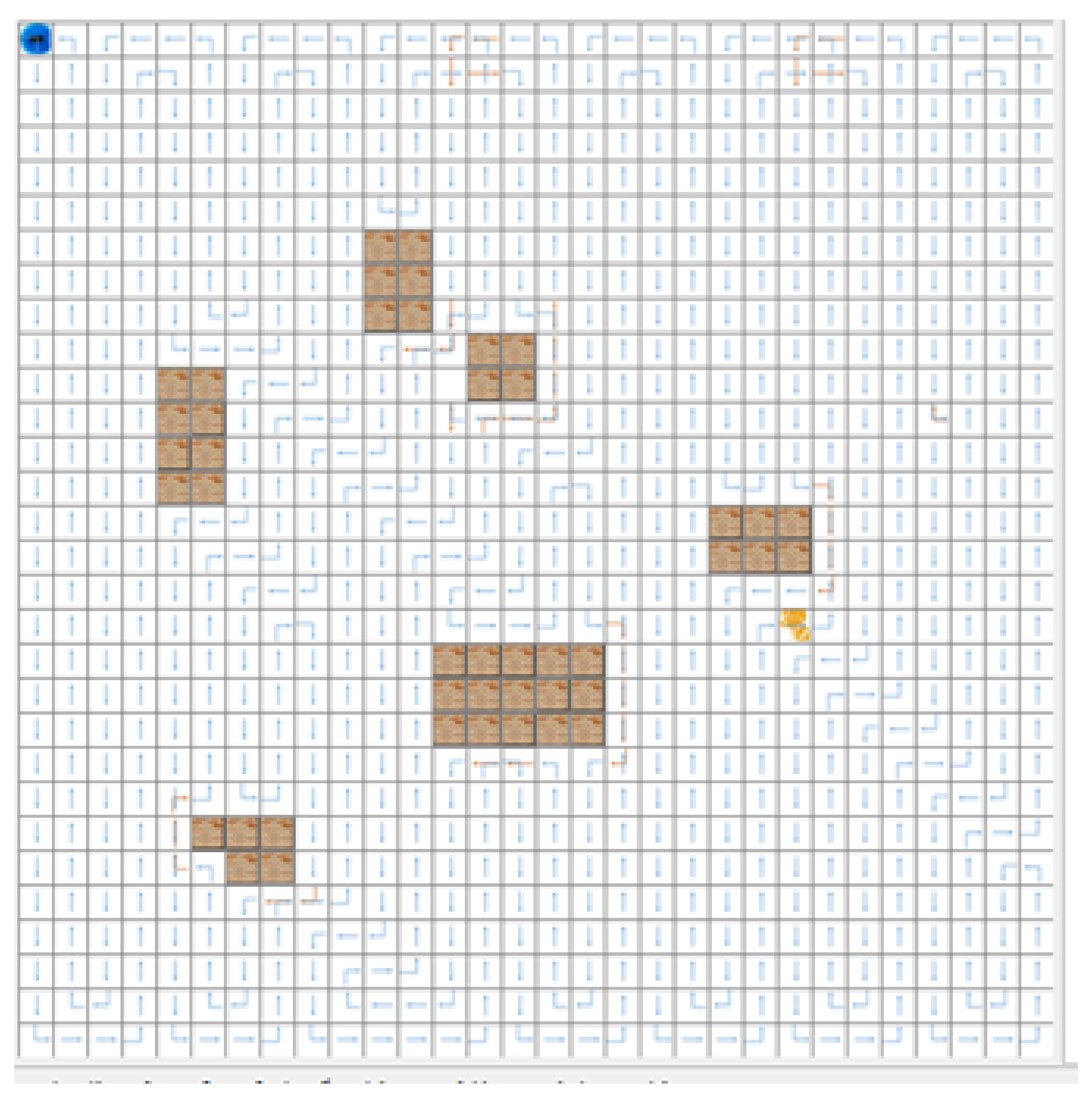
6. Experimental Testing and Comparative Analysis
6.1. The Experimental Results
6.2. A Comparative Analysis for Moving Obstacles
7. Discussion
7.1. The Concept of “Self”
7.2. Machine Cognition
7.3. Future Directions for Research
- Extending the proposed rule-based linguistic approach using semantics with kansei engineering in combination with hedge algebras forms an interesting research direction;
- A further potentially profitable direction for research (in computing terms) lies in the use of semiotics [20] and SC [60] to recognise the type and nature of obstacles or other robots operating in the environment. Semiotics employs both linguistics and images to create a representative model, their combined use in context-aware intelligent robotic systems is a potentially profitable direction for robotics research;
- There are potential use-cases where multiple mobile robots may operate collaboratively using for example “forward chaining” [62,63,64]; in such a use-case awareness of their environment and other robots operating in the same environment is required. For example, in a large search area multiple robots may be deployed to investigate an environment where efficient search requires both CPP for each robot while avoiding duplication in the search activity.
8. Concluding Observations
Author Contributions
Funding
Conflicts of Interest
References
- Martínez-Tenor, A.; Fernández-Madrigal, J.A.; Cruz-Martín, A.; González-Jiménez, J. Towards a common implementation of reinforcement learning for multiple robotic tasks. Expert Syst. Appl. 2018, 100, 246–259. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Bayat, F.; Najafinia, S.; Aliyari, M. Mobile robots path planning: Electrostatic potential field approach. Expert Syst. Appl. 2018, 100, 68–78. [Google Scholar] [CrossRef]
- Moore, P.T.; Pham, H.V. On Context and the Open World Assumption. In Proceedings of the 29th IEEE International Conference on Advanced Information Networking and Applications (AINA-2015), Gwangju, Korea, 25–27 March 2015; pp. 387–392. [Google Scholar]
- Moore, P. Do We Understand the Relationship between Affective Computing, Emotion and Context- Awareness? Machines 2017, 5, 16. [Google Scholar] [CrossRef]
- Bem, D.J. Self-perception: An alternative interpretation of cognitive dissonance phenomena. Psychol. Rev. 1967, 74, 183. [Google Scholar] [CrossRef] [PubMed]
- Brehm, J.W.; Cohen, A.R. Explorations in Cognitive Dissonance; John Wiley & Sons Inc: New Jersey, NJ, USA, 1962. [Google Scholar]
- Festinger, L. A Theory of Cognitive Dissonance; Stanford University Press: Palo Alto, CA, USA, 1957. [Google Scholar]
- Festinger, L. Cognitive dissonance. Sci. Am. 1962, 207, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Moore, P.; Pham, H.V. Personalization and rule strategies in human-centric data intensive intelligent context-aware systems. Knowl. Eng. Rev. 2015, 30, 140–156. [Google Scholar] [CrossRef]
- Moore, P.; Pham, H.V. On Wisdom and Rational Decision-Support in Context-Aware Systems. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC2017), Banff, AB, Canada, 5–8 October 2017; pp. 1982–1987. [Google Scholar]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1995; Volume 4. [Google Scholar]
- Pham, H.V.; Moore, P.; Tran, K.D. Context Matching with Reasoning and Decision Support using Hedge Algebra with Kansei Evaluation. In Proceedings of the Fifth Symposium on Information and Communication Technology (SoICT 2014), Hanoi, Vietnam, 4–5 December 2014; ACM: New York, NY, USA, 2014; pp. 202–210. [Google Scholar] [CrossRef]
- Berkan, R.C.; Trubatch, S. Fuzzy System Design Principles; Wiley-IEEE Press: New Jersey, NJ, USA, 1997. [Google Scholar]
- Nguyen, C.H.; Tran, T.S.; Pham, D.P. Modeling of a semantics core of linguistic terms based on an extension of hedge algebra semantics and its application. Knowl.-Based Syst. 2014, 67, 244–262. [Google Scholar] [CrossRef]
- Cetisli, B. Development of an adaptive neuro-fuzzy classifier using linguistic hedges: Part 1. Expert Syst. Appl. 2010, 37, 6093–6101. [Google Scholar] [CrossRef]
- Chatterjee, A.; Siarry, P. A PSO-aided neuro-fuzzy classifier employing linguistic hedge concepts. Expert Syst. Appl. 2007, 33, 1097–1109. [Google Scholar] [CrossRef]
- Ho, N.C.; Wechler, W. Hedge algebras: An algebraic approach to structure of sets of linguistic truth values. Fuzzy Sets Syst. 1990, 35, 281–293. [Google Scholar]
- Ho, N.C.; Long, N.V. Fuzziness measure on complete hedge algebras and quantifying semantics of terms in linear hedge algebras. Fuzzy Sets Syst. 2007, 158, 452–471. [Google Scholar] [CrossRef]
- Chandler, D. Semiotics: The Basics; Psychology Press: London, UK, 2002. [Google Scholar]
- Gabriely, Y.; Rimon, E. Spanning-tree based coverage of continuous areas by a mobile robot. In Proceedings of the 2001 IEEE International Conference on Robotics and Automation (ICRA) (Cat. No. 01CH37164), Seoul, Korea, 21–26 May 1999; Volume 2, pp. 1927–1933. [Google Scholar]
- Gabriely, Y.; Rimon, E. Spanning-tree based coverage of continuous areas by a mobile robot. Ann. Math. Artif. Intell. 2001, 31, 77–98. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Xie, J.; Du, P.; Chen, L. Robot needle-punching path planning for complex surface preforms. Robot. Comput.-Integr. Manuf. 2018, 52, 24–34. [Google Scholar] [CrossRef]
- Mac, T.T.; Copot, C.; Tran, D.T.; Keyser, R.D. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28. [Google Scholar] [CrossRef]
- Mohanan, M.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robot. Auton. Syst. 2018, 100, 171–185. [Google Scholar] [CrossRef]
- Laporte, G.; Asef-Vaziri, A.; Sriskandarajah, C. Some Applications of the Generalized Travelling Salesman Problem. J. Oper. Res. Soc. 1996, 47, 1461–1467. [Google Scholar] [CrossRef]
- Acar, E.U.; Choset, H.; Zhang, Y.; Schervish, M. Path planning for robotic demining: Robust sensor-based coverage of unstructured environments and probabilistic methods. Int. J. Robot. Res. 2003, 22, 441–466. [Google Scholar] [CrossRef]
- Han, J.; Seo, Y. Mobile robot path planning with surrounding point set and path improvement. Appl. Soft Comput. 2017, 57, 35–47. [Google Scholar] [CrossRef]
- Mac, T.T.; Copot, C.; Tran, D.T.; Keyser, R.D. A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization. Appl. Soft Comput. 2017, 59, 68–76. [Google Scholar] [CrossRef]
- Palacios-Gasós, J.M.; Talebpour, Z.; Montijano, E.; Sagüés, C.; Martinoli, A. Optimal path planning and coverage control for multi-robot persistent coverage in environments with obstacles. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1321–1327. [Google Scholar]
- Bouzid, Y.; Bestaoui, Y.; Siguerdidjane, H. Quadrotor-UAV optimal coverage path planning in cluttered environment with a limited onboard energy. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 979–984. [Google Scholar]
- Li, D.; Wang, X.; Sun, T. Energy-optimal coverage path planning on topographic map for environment survey with unmanned aerial vehicles. Electron. Lett. 2016, 52, 699–701. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Cheng, S.; Xie, Y. Double Heuristic Optimization Based on Hierarchical Partitioning for Coverage Path Planning of Robot Mowers. In Proceedings of the 2016 12th International Conference on Computational Intelligence and Security (CIS), Wuxi, China, 16–19 December 2016; pp. 186–189. [Google Scholar]
- Chen, K.; Liu, Y. Optimal complete coverage planning of wall-climbing robot using improved biologically inspired neural network. In Proceedings of the 2017 IEEE International Conference on Real-time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 587–592. [Google Scholar]
- Jin, L.; Li, S.; Yu, J.; He, J. Robot manipulator control using neural networks: A survey. Neurocomputing 2018, 285, 23–34. [Google Scholar] [CrossRef]
- Leottau, D.L.; del Solar, J.R.; Babuška, R. Decentralized Reinforcement Learning of Robot Behaviors. Artif. Intell. 2018, 256, 130–159. [Google Scholar] [CrossRef]
- Karapetyan, N.; Benson, K.; McKinney, C.; Taslakian, P.; Rekleitis, I. Efficient multi-robot coverage of a known environment. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1846–1852. [Google Scholar]
- Agostini, A.; Torras, C.; Wörgötter, F. Efficient interactive decision-making framework for robotic applications. Artif. Intell. 2017, 247, 187–212. [Google Scholar] [CrossRef]
- Patle, B.; Parhi, D.; Jagadeesh, A.; Kashyap, S.K. Matrix-Binary Codes based Genetic Algorithm for path planning of mobile robot. Comput. Electr. Eng. 2018, 67, 708–728. [Google Scholar] [CrossRef]
- Muñoz, P.; R-Moreno, M.D.; Barrero, D.F. Unified framework for path-planning and task-planning for autonomous robots. Robot. Auton. Syst. 2016, 82, 1–14. [Google Scholar] [CrossRef]
- Brooks, R.A. Intelligence without representation. Artif. Intell. 1991, 47, 139–159. [Google Scholar] [CrossRef]
- Fakoor, M.; Kosari, A.; Jafarzadeh, M. Humanoid robot path planning with fuzzy Markov decision processes. J. Appl. Res. Technol. 2016, 14, 300–310. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Ni, C.C.; Lei, N.; Gu, X.D.; Gao, J. Robot Coverage Path planning for general surfaces using quadratic differentials. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5005–5011. [Google Scholar]
- Cai, Z.; Li, S.; Gan, Y.; Zhang, R.; Zhang, Q. Research on complete coverage path planning algorithms based on a* algorithms. Open Cybern. Syst. J. 2014, 8, 418–426. [Google Scholar]
- Minsky, M.D.R. Computational Haptics: The Sandpaper System for Synthesizing Texture for a Force-Feedback Display. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Salisbury, K.; Conti, F.; Barbagli, F. Haptic rendering: introductory concepts. IEEE Comput. Graph. Appl. 2004, 24, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Reeve, R.; Webb, B.; Horchler, A.; Indiveri, G.; Quinn, R. New technologies for testing a model of cricket phonotaxis on an outdoor robot. Robot. Auton. Syst. 2005, 51, 41–54. [Google Scholar] [CrossRef]
- Copenhagen, D. Retinal Neurobiology and Visual Processing; Technical Report; Federation of American Societies for Experimental Biology: Bethesda, MD, USA, 1996. [Google Scholar]
- Grifantini, K. To See Anew: New Technologies Are Moving Rapidly Toward Restoring or Enabling Vision in the Blind. IEEE Pulse 2017, 8, 35–38. [Google Scholar] [CrossRef] [PubMed]
- Talan, J. BEHIND THE BENCH: What MacArthur Awardee Sheila Nirenberg Is Doing to Help Blind People See. Neurol. Today 2013, 13, 24–27. [Google Scholar] [CrossRef]
- Basu, A. IEEE SMC 2017 in Banff, Alberta, Canada [Conference Reports]. IEEE Syst. Man Cybern. Mag. 2018, 4, 36–39. [Google Scholar] [CrossRef]
- Nirenberg, S.; Carcieri, S.M.; Jacobs, A.L.; Latham, P.E. Retinal ganglion cells act largely as independent encoders. Nature 2001, 411, 698. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, S.; Pandarinath, C. Retinal prosthetic strategy with the capacity to restore normal vision. Proc. Natl. Acad. Sci. USA 2012, 109, 15012–15017. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, S. Philosophical conceptions of the self: Implications for cognitive science. Trends Cogn. Sci. 2000, 4, 14–21. [Google Scholar] [CrossRef]
- Moore, P.; Xhafa, F.; Barolli, L. Semantic valence modeling: Emotion recognition and affective states in context-aware systems. In Proceedings of the 28th International Conference on Advanced Information Networking and Applications Workshops (WAINA 2014), Victoria, BC, Canada, 13–16 May 2014; pp. 536–541. [Google Scholar] [CrossRef]
- Simon, H.A. Cognitive science: The newest science of the artificial. Cogn. Sci. 1980, 4, 33–46. [Google Scholar] [CrossRef]
- Simon, H.A. The sciences of the Artificial; Massachusetts Institute of Technology: Cambridge, MA, USA, 1969. [Google Scholar]
- Koelstra, S.; Muhl, C.; Soleymani, M.; Lee, J.S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. Deap: A database for emotion analysis; using physiological signals. IEEE Trans. Affect. Comput. 2012, 3, 18–31. [Google Scholar] [CrossRef]
- Chen, J.; Hu, B.; Moore, P.; Zhang, X. Ontology-Based Model for Mining User’s Emotions on the Wisdom Web. In Wisdom Web of Things; Zhong, N., Ma, J., Liu, J., Huang, R., Tao, X., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Chapter 6; pp. 121–153. [Google Scholar] [CrossRef]
- Mondal, P. Does Computation Reveal Machine Cognition? Biosemiotics 2014, 7, 97–110. [Google Scholar] [CrossRef]
- Tanaka-Ishii, K. Semiotics of Programming; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bell, G.; Weir, M. Forward Chaining for Robot and Agent Navigation Using Potential Fields. In Proceedings of the 27th Australasian Conference on Computer Science (ACSC ’04); Australian Computer Society, Inc.: Darlinghurst, Australia, 2004; Volume 26, pp. 265–274. [Google Scholar]
- Chen, C.L.; Lin, I.H. Location-Aware Dynamic Session-Key Management for Grid-Based Wireless Sensor Networks. Sensors 2010, 10, 7347–7370. [Google Scholar] [CrossRef] [PubMed]
- Apoorva, G.R.; Kala, R. Motion Planning for a Chain of Mobile Robots Using A* and Potential Field. Robotics 2018, 7, 20. [Google Scholar] [CrossRef]



| very high | very low | little very low | low | |
| low | very low | high | little low | |
| very low | little very low | little high | low | |
| little high | little little high | little low | little low | |
| high | very high | little very high | very high |
| imp | imp | unimp | very very imp | |
| unimp | unimp | imp | unimp | |
| unimp | unimp | unimp | unimp | |
| little imp | little imp | very unimp | little imp | |
| little imp | little imp | very imp | very very imp |
| 0.875 | 0.125 | 0.1875 | 0.25 | |
| 0.25 | 0.125 | 0.75 | 0.375 | |
| 0.125 | 0.1875 | 0.625 | 0.25 | |
| 0.625 | 0.6875 | 0.375 | 0.375 | |
| 0.75 | 0.1375 | 0.1125 | 0.875 |
| μ (very very unimportant) = 0.10985 | μ (very unimportant) = 0.169 |
| (little very unimportant) = 0.20085 | (unimportant) = 0.26 |
| (little little unimportant) = 0.29185 | (little unimportant) = 0.309 |
| (very little unimportant) = 0.34085 | (very little important) = 0.488725 |
| (little important) = 0.5365 | (little little important) = 0.562225 |
| (important) = 0.61 | (little very important) = 0.698725 |
| (very important) = 0.7465 | (very very important) = 0.835225 |
| 0.61 | 0.61 | 0.26 | 0.835225 | |
| 0.26 | 0.26 | 0.61 | 0.26 | |
| 0.26 | 0.26 | 0.26 | 0.26 | |
| 0.5365 | 0.5365 | 0.169 | 0.5365 | |
| 0.5365 | 0.5365 | 0.7465 | 0.15225 |
| Methods | Obstacles | Multiple Decision Making Objectives | |||
|---|---|---|---|---|---|
| Regular (%) | Irregular (%) | Multiple Regular (%) | Multiple Irregular (%) | Average (%) | |
| BFS | 4.00 | 3.10 | 36.50 | 32.50 | 50 |
| ISS | 7.00 | 20.50 | 19.50 | 26.10 | 53 |
| UAPP | 5.00 | 5.40 | 8.85 | 14.40 | 67 |
| CPP | 0.00 | 2.20 | 2.00 | 7.30 | 96 |
| Methods | Duration (s)/Obstacles | ||||
|---|---|---|---|---|---|
| Regular | Irregular | Multiple Regular | Multiple Irregular | Average | |
| BFS | 134 | 154 | 150 | 144 | 140 |
| ISS | 115 | 135 | 130 | 125 | 120 |
| UAPP | 95 | 115 | 95 | 110 | 100 |
| CPP | 66 | 78 | 79 | 74 | 82 |
| Methods | Repetition Rate (%)/Obstacles | Repetition Rate (%)/Multiple Decision Making | |||
|---|---|---|---|---|---|
| Regular (%) | Irregular (%) | Multiple Regular (%) | Multiple Irregular (%) | Average (%) | |
| BFS | 14 | 29 | 38.5 | 38 | 40 |
| ISS | 16 | 25 | 29.5 | 32 | 35 |
| UAPP | 8 | 12 | 15 | 25 | 29 |
| CPP | 3 | 4 | 3 | 11.3 | 13.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Pham, H.; Moore, P. Robot Coverage Path Planning under Uncertainty Using Knowledge Inference and Hedge Algebras. Machines 2018, 6, 46. https://doi.org/10.3390/machines6040046
Van Pham H, Moore P. Robot Coverage Path Planning under Uncertainty Using Knowledge Inference and Hedge Algebras. Machines. 2018; 6(4):46. https://doi.org/10.3390/machines6040046
Chicago/Turabian StyleVan Pham, Hai, and Philip Moore. 2018. "Robot Coverage Path Planning under Uncertainty Using Knowledge Inference and Hedge Algebras" Machines 6, no. 4: 46. https://doi.org/10.3390/machines6040046
APA StyleVan Pham, H., & Moore, P. (2018). Robot Coverage Path Planning under Uncertainty Using Knowledge Inference and Hedge Algebras. Machines, 6(4), 46. https://doi.org/10.3390/machines6040046





