Customized Knowledge Discovery in Databases methodology for the Control of Assembly Systems
Abstract
1. Introduction
- Poverty of well-defined and standardized data analysis procedures and guidelines for manufacturing datasets [8];
- Absence of a consolidated data analysis culture in the manufacturing field [9];
- Scarcity of well-established and appropriate data collection and saving systems; and
- Issues with data accessibility and sharing.
2. Research Statement and Objective
- Assembly datasets mainly focus on quality variables and process parameters, leading to the generation of discrete time series related to processed items instead of continuous signals coming from equipment. Therefore, the nature of available data, as deeply discussed in Section 3.2, prevents the creation of models based on signals coming from sensors and describing machines technical parameters such as temperatures, absorbed powers or vibrations. This concept explains why powerful and reliable techniques provided by ICPS, such as data-driven KPI estimators and predictors, based on real or soft sensors [4], are not completely applicable to this specific context.
- Techniques typical of the control theory [16,17], such as dynamic state space models or observers (e.g., Kalman filter), could not be used because the tracking of different and multiple issues, featured by different physical reasons, could not be reliable in case of single mathematical modeling. Moreover, even if these strategies would be able to identify a certain deviation with respect to the typical stable scenario, they are not able to identify the root cause of the problem, leading to a partial effectiveness of predictive action.
Research Objective
- Consistency. Each step will be motivated and justified from both a mathematical-analytical and a physical-industrial point of view.
- Generality. Even though the tool will be specifically designed and validated within the Bosch VHIT S.p.A. assembly system, it strives for being a standardized instrument, applicable by a manufacturing industry independently from nature and layout of performed assembly process. Moreover, it aims to be easily tunable and customizable, depending on the local field of application, so to optimize its performances for the specific case study.
3. Background
3.1. KDD Methodology
- Capability to reduce Big Data original size, decreasing computational cost and associated technical problems, by focusing on useful variables only.
- Capability to work in uncertain situations. Since the goal of KDD is to extract knowledge from raw data, it is naturally built to be flexible and to adapt its framework with respect to partial results obtained along its application.
- Popularity and generality. Academic literature suggests KDD as the most suitable methodology to be used for the sake of information extraction from raw Big Data [21,22]. The main reason is that it gives very general guidelines, leaving to the practitioner a sufficient number of degrees of freedom to develop and adapt it to the actual case.
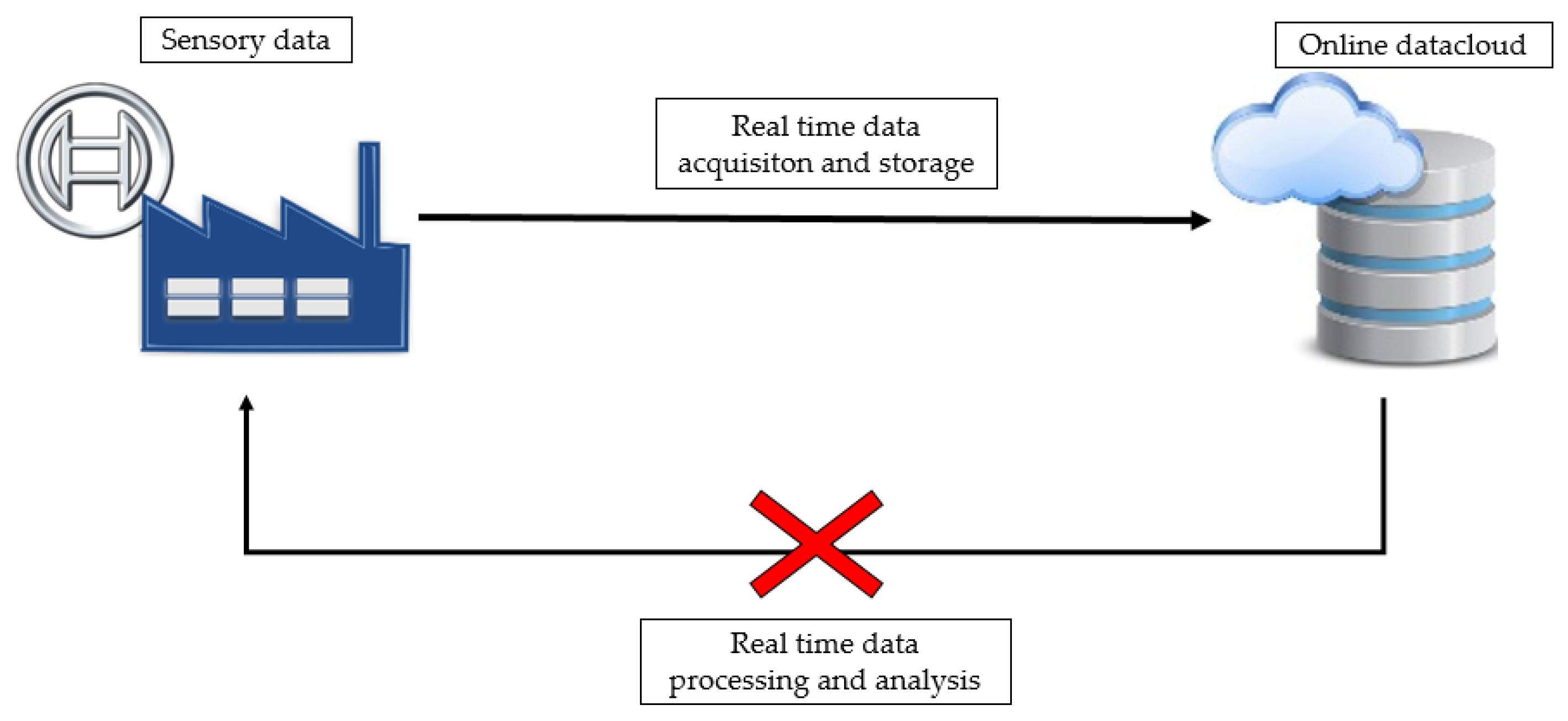
3.2. Bosch VHIT S.p.A. Assembly System
Collected Data
- General assembly layout information: codes for items’ traceability and model recognition, in case of multi-product lines; date and time of product processing; cycle time of each workstation.
- Single workstation information: physical variables referred to performed operation; station outcome (compliant or non-compliant piece).
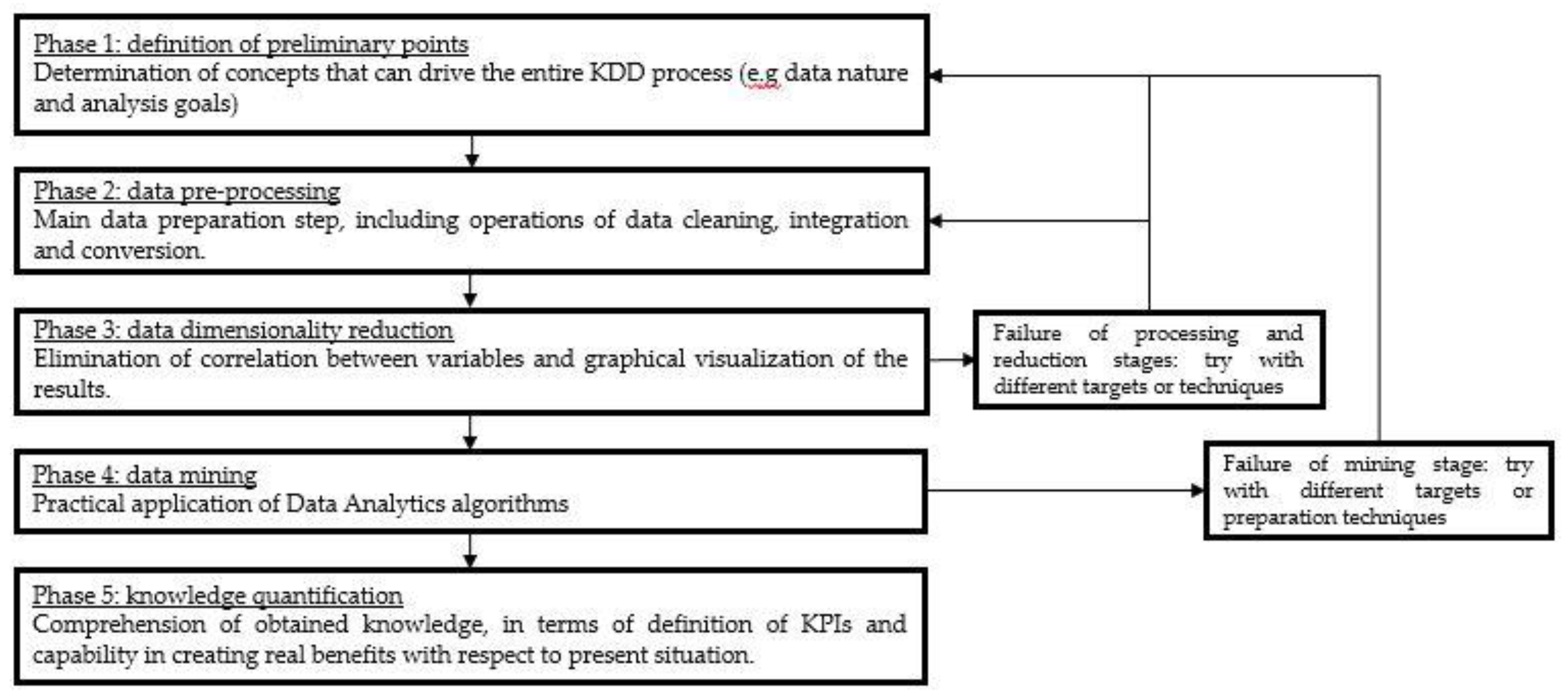
4. Customized KDD for Assembly System
4.1. Definition of Preliminary Points
4.2. Data Pre-processing
- Position data in a chronological order. These operations help future time-series analysis and forecasting activities.
- Consider the proper period only. The whole available history is not always the best choice, even though it may bring to a better validation of used stochastics models. For example, immediately after the assembly line installation, the series production will start only after properly equipment regulation and prototyped products, thus gathered data are highly affected by this extraordinary situation.
- Eliminate outliers. An outlier is defined as a measurement that results inconsistent with respect to the rest of the dataset. Its value can be generated by different causes such as poorly calibrated or faulty instruments, electrical issues, communication channels issues, and server issues. The management of outliers is particularly puzzling since outliers considered as normal measurements can contaminate data behavior, compromising the identification of patterns and the algorithms’ functioning; however, normal measurements considered as outliers can obstruct the capture of useful knowledge. If one removes them, a fundamental portion of the dataset is going to be removed, namely the non-compliant pieces. Since the final goal is to prevent issues, based on past knowledge, the exclusion of these values from the database seems inappropriate. To verify that data are not real outliers, a check if a candidate outlier corresponds to a compliant piece must be performed: if the answer is positive, the measurement is inconsistent and the point is discarded; if the answer is negative, it is not possible to neglect the point. Then, it is important to understand how to manage value of these points, which is completely different from the remaining portion of the dataset. Since the difference can be of several orders of magnitude too, a single anomaly can affect the entire dataset behavior and compromise prediction and regression analysis. Thus, their value is shifted to positions that lie immediately outside the admissible range to include these values in the analysis while keeping their original information (i.e. the piece is not compliant).
4.3. Data Dimensionality Reduction
4.4. Data Mining
4.5. Development of Algorithm’s Selection Criteria
- Selection layer one deals with the mathematical nature of the problem. When referring to statistical learning literature, two main objectives are usually faced: inference problems, which involve the research of relationships between different variables and the subdivision of individuals in specific categories basing on the values of parameters describing them; prediction problems, which involve the modeling of variables and the attempt of forecasting their future behavior [31]. First kind of problem should be faced with classification techniques while second one with regression algorithms. According to proposed analysis goal, focused on single process parameters, it is clear that the actual analysis should find a solution of a prediction problem.
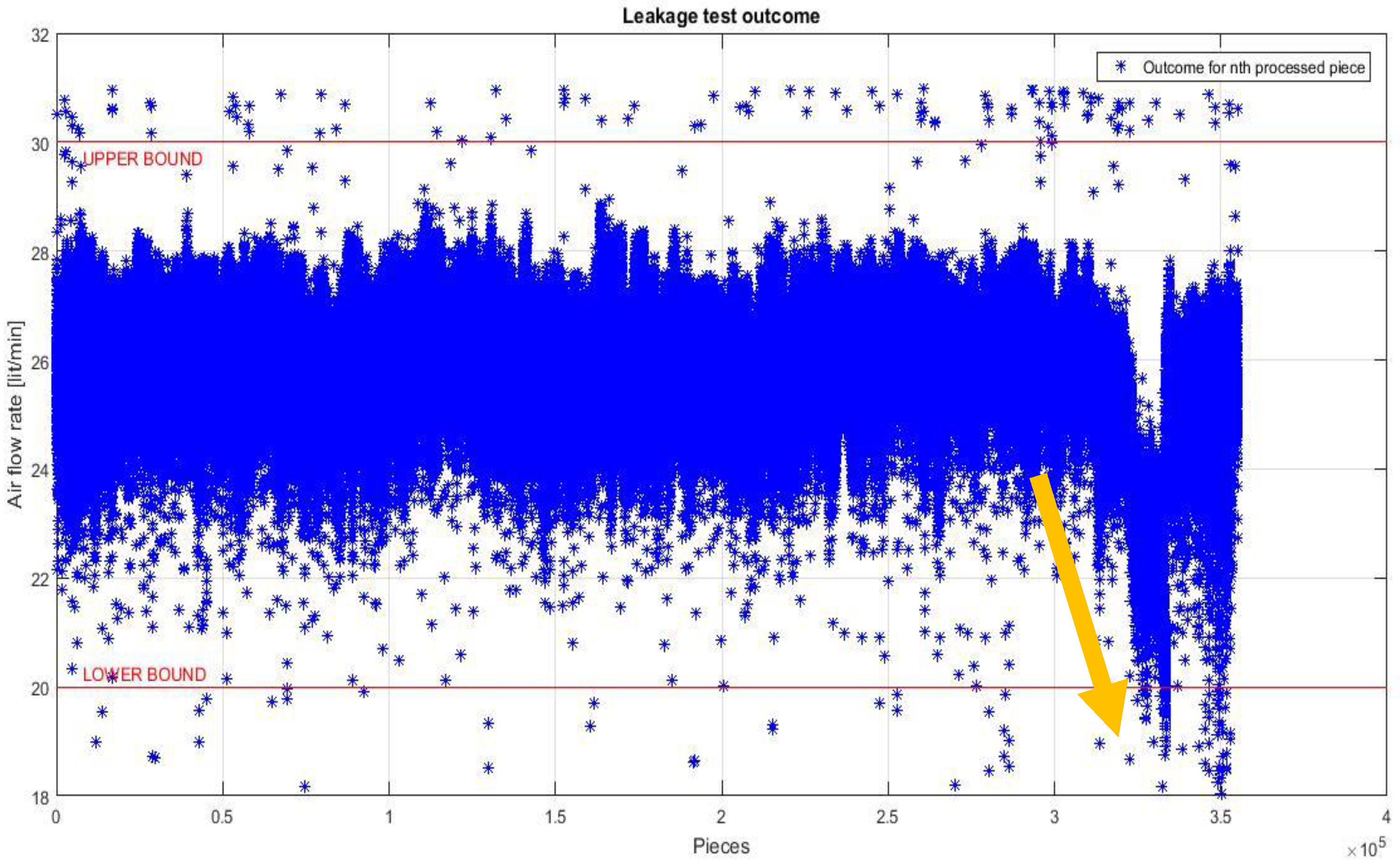
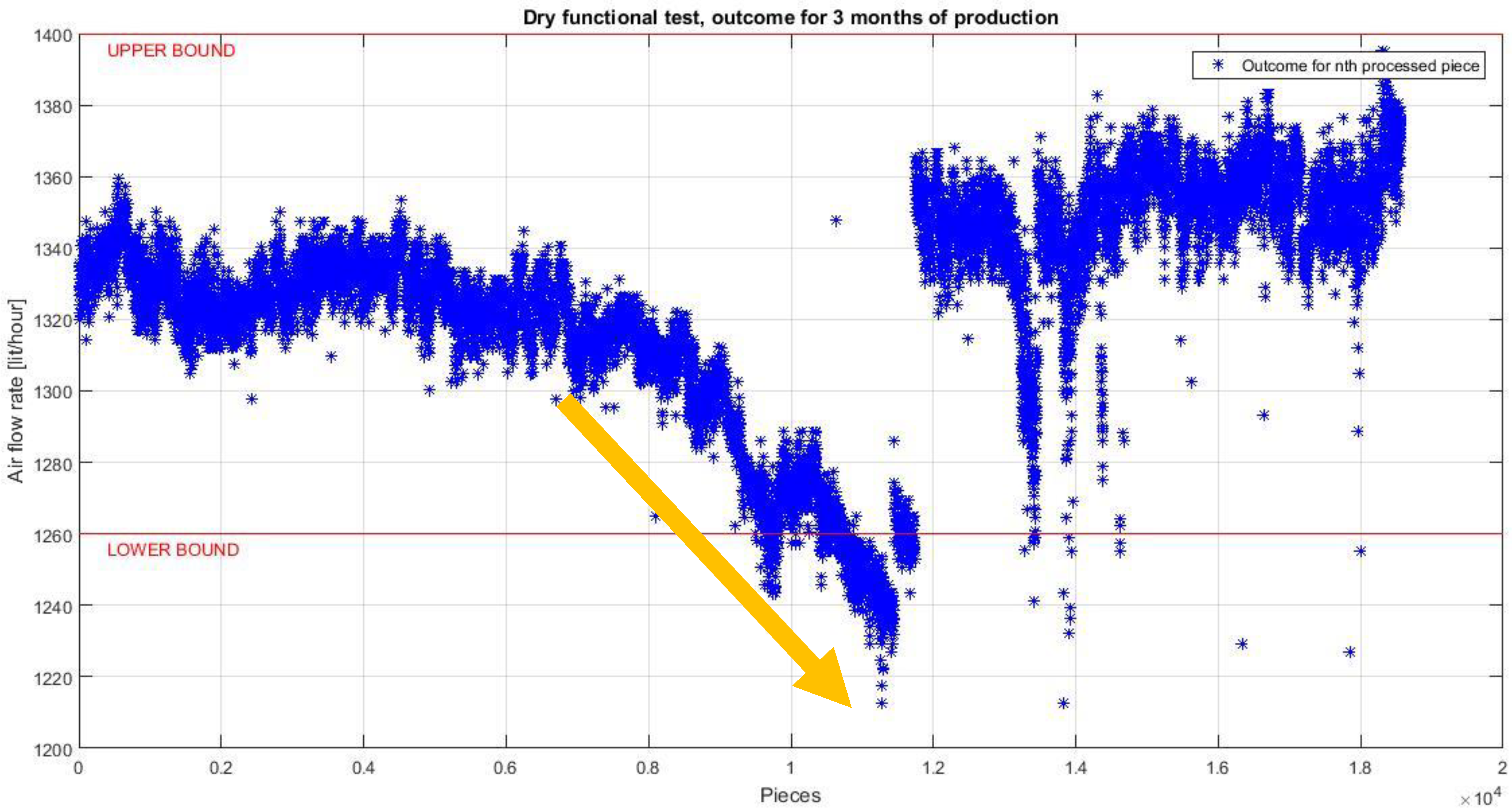
- Selection layer two deals with physical nature of the assembly system. Considering the very peculiar behavior of assembly systems, with the generation of almost non-repeatable technical or qualitative issues on different subgroups, data appear with a very particular shape. Process parameters sequences come with a general stable and planar behavior, spaced by local and isolated peaks caused by unique reasons. Each issue appears as an anomaly, namely a point in time where the behavior of the system is unusual and significantly different from previous and normal behavior. Figure 4, related to the time series of a process parameter collected in Bosch VHIT S.p.A., clearly shows this kind of behavior (see the area pointed by the arrow, highlighting the emerging behavior after 3,100,000 pieces).
5. Data Mining via ARIMA Modeling
5.1. Data Time Series Preparation
- Random fluctuations are absorbed within samples, solving to the aim of previously designed filters.
- The customized tuning of N allows freeing the algorithm from assembly’s production rate. The choice of N is postponed to the SA procedure, because no specific rules have been found to set it. The reason is that almost all literature is focused on sampling techniques for continuous-time signals more than discrete time series. When moving to time series of discrete measurements, namely referred to different individuals, literature focuses on sampling techniques of heterogeneous populations [36], while no specific criteria are provided in case of homogeneous measurements.
- The shift from physical process parameters to statistical moments allows freeing the algorithm from the physical nature of the problem. In this way, it is effective for all peculiarities appearing in the assembly system, not depending on their qualitative or technical causes and not depending on the involved process parameters.
- The inclusion of variables coming from Statistical Process Control (SPC) world allows freeing the algorithm from eventual modifications in the process limits. Even after a manual modification of boundaries, the algorithm is able to automatically adapt itself to new conditions.
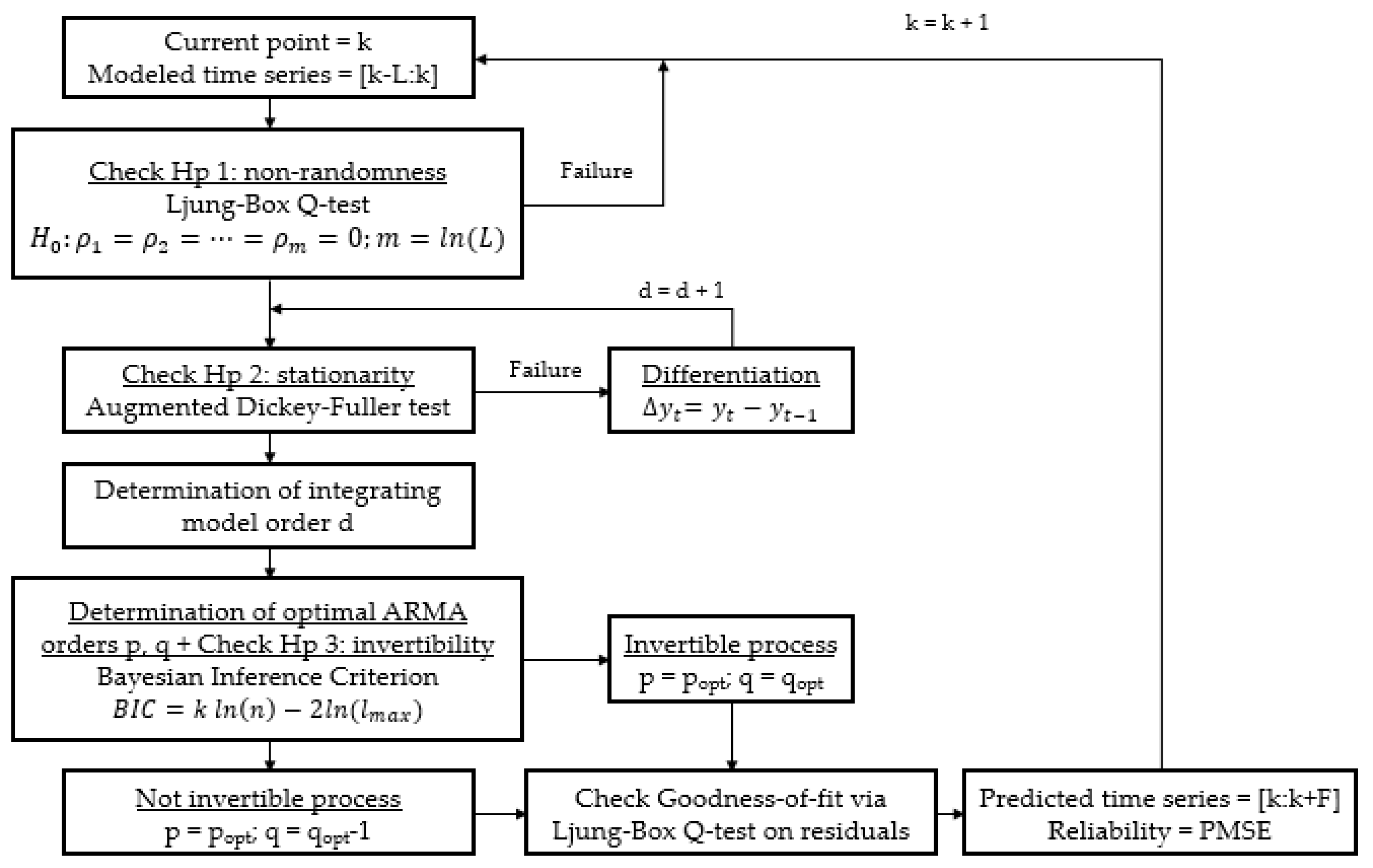
5.2. Application of Customized ARIMA Model
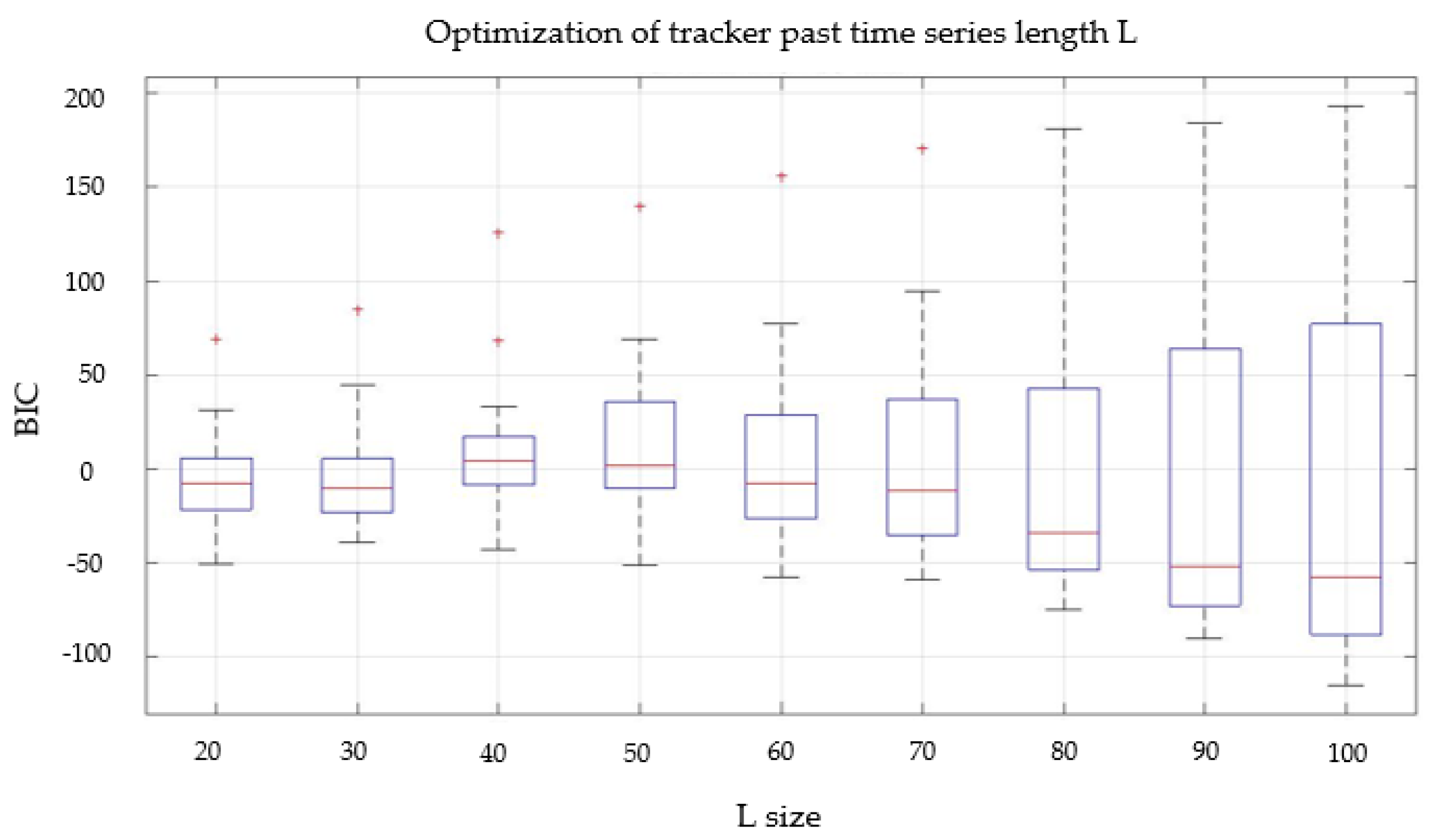
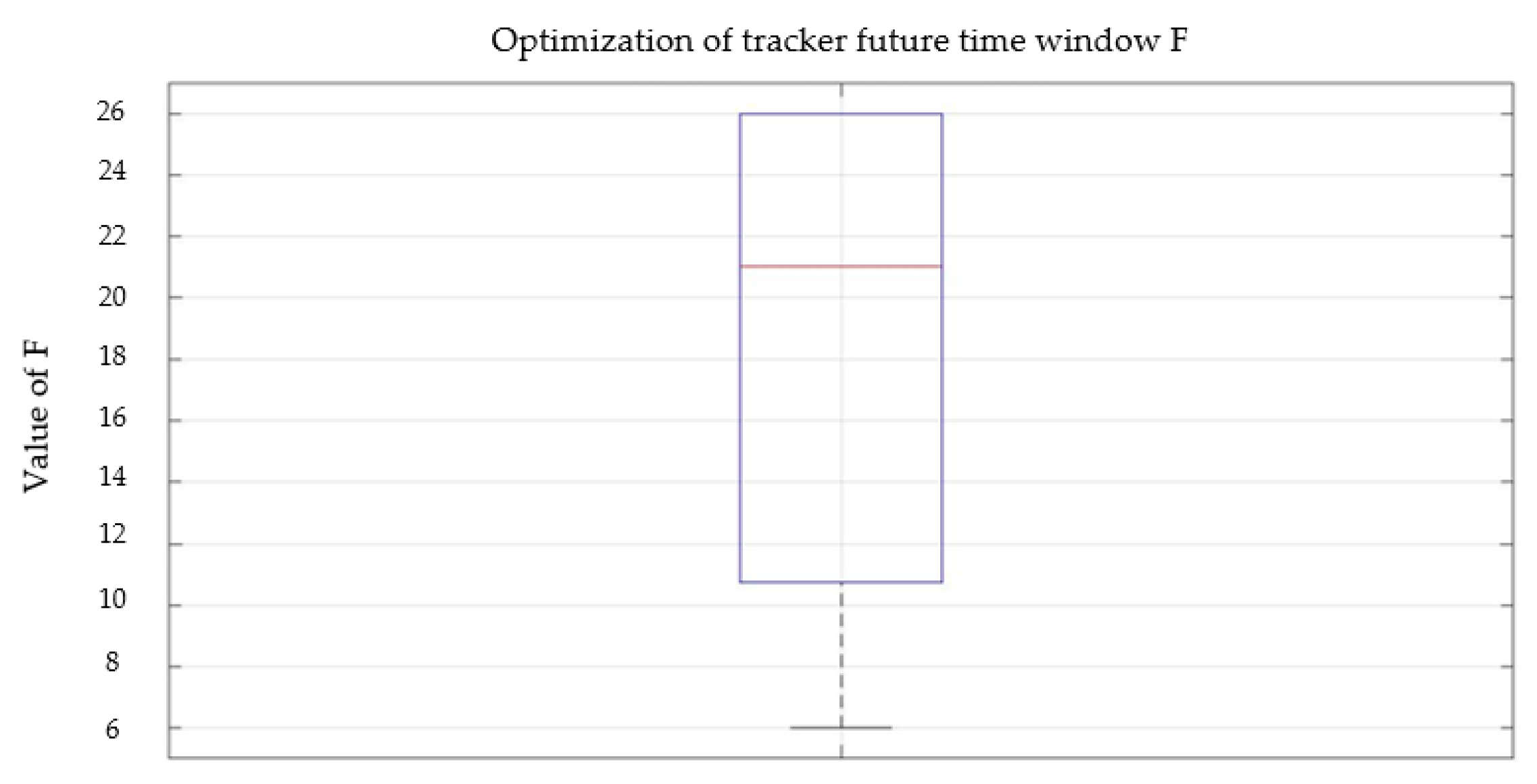
5.3. Parameters Optimization
6. Results
6.1. Customized KDD Application
6.2. Summary of Other Customized KDD Applications
7. Conclusions
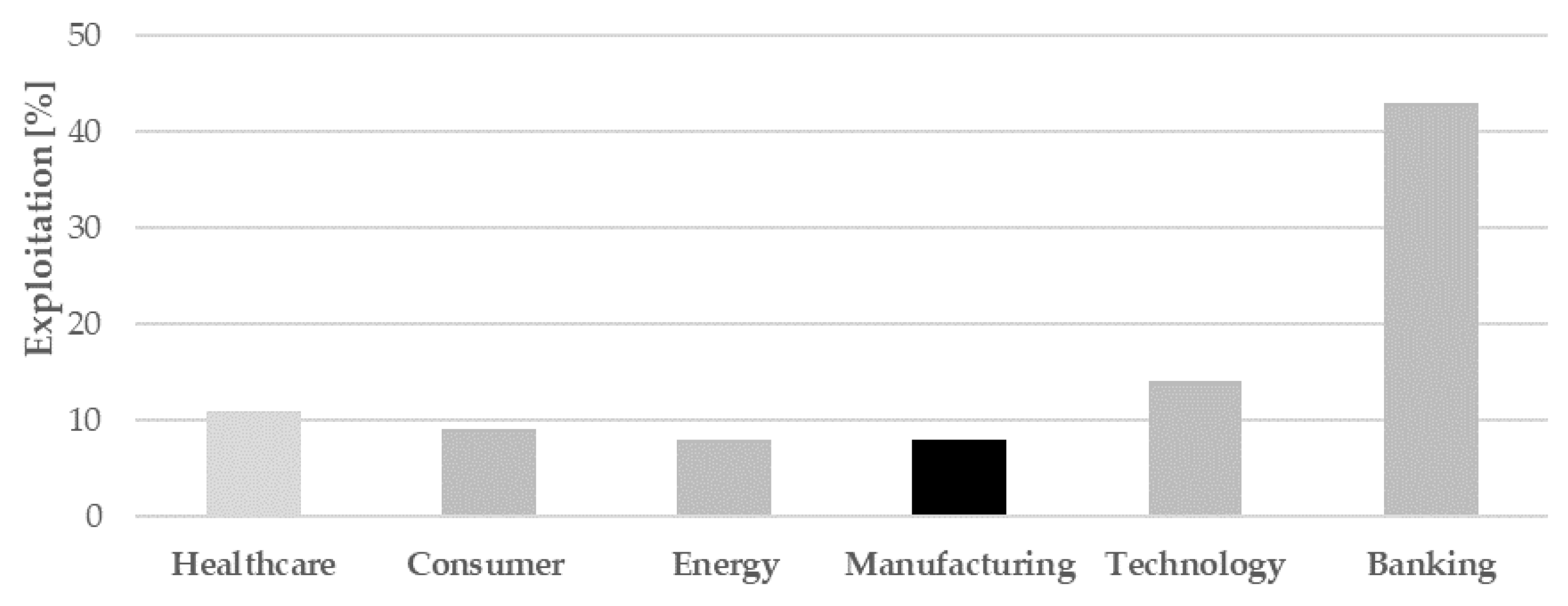
- Exploitation of data analysis in assembly environment. Literature research has revealed a high imbalance between research effort in studying machining data and assembly ones, in favor of the first category. This work could help in reducing this gap.
- Standardized and flexible framework of the presented procedure. The KDD-based backbone of the process, together with the systematic rules provided in each section of the process, gives it a standardized nature, fundamental to allow its full-scale implementation in the manufacturing world. On the other hand, the iterative and parametric policies adopted on different layers of the procedure leave some degrees of freedom with respect to its general architecture, allowing to customize it.
- Definition of rigorous and effective guidelines in data mining algorithms’ selection. The two-stage selection technique proposed in Section 4.5 appears as a powerful guideline devoted to the minimization of user’s effort in the choice and application of statistical learning algorithms.
Future Work
- Research for alternative algorithms satisfying the two-stage selection procedure discussed in Section 4.5. The target should be the comparison and the assessment of the proposed algorithm (ARIMA) with respect to alternative ones or its eventual replacement with more satisfactory solutions. This point is mainly driven by the extremely wide range of methods contained within novelty detection literature that must be investigated when applied to manufacturing environments.
- Research for tools able to work on entire assembly systems instead of single process parameters. Even though this work is focused on single variables, according to needs of the company and to physics of their processes, in other scenarios, relationships between different parameters may exist, pushing towards the identification of hidden patterns. A possible target for this kind of system could be the creation of a “Digital Check”, namely an instrument able to predict the outcome of a certain workstation by analyzing the outcomes of previous ones.
- Research for architectures able to industrialize the presented methodology in a structured way. Tools such as a Decision Support System (DSS), with high degrees of automation and easy implementation on company’s Manufacturing Execution System (MES), could be a reasonable solution for companies deciding to adopt implement the presented solution [43,44,45,46,47].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shin, J.H.; Jun, H.B. On condition based maintenance policy. J. Comput. Des. Eng. 2015, 2, 119–127. [Google Scholar] [CrossRef]
- Goel, P.; Datta, A.; Sam Mannan, M. Industrial alarm systems: Challenges and opportunities. J. Loss Prev. Process Ind. 2017, 50, 23–26. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S. Recursive total principle component regression based fault detection and its application to Vehicular Cyber-Physical Systems. IEEE Trans. Ind. Inf. 2018, 4, 1415–1423. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Kaynak, O. Data-driven Monitoring and Safety Control of Industrial Cyber-Physical Systems: Basics and Beyond. IEEE Access 2018, 6, 47374–47384. [Google Scholar] [CrossRef]
- Bumbaluskas, D.; Gemmill, D.; Igou, A.; Anzengruber, J. Smart Maintenance Decision Support System (SMDSS) based on corporate data analytics. Expert Syst. Appl. 2017, 90, 303–317. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Ding, D.X.; Haung, A.B. Data Mining and analytics in the process industry: The role of machine learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- Mourtzis, D.; Vlachou, K.; Milas, N. Industrial Big Data as a result of IoT adoption in manufacturing. Procedia CIRP 2016, 55, 290–295. [Google Scholar] [CrossRef]
- Kranz, M. Building the Internet of Things: Implement New Business Models, Disrupt Competitors, Transform Your Industry; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Tiwari, S.; Wee, H.M.; Daryanto, Y. Big data analytics in supply chain management between 2010 and 2016: Insights to industries. Comput. Ind. Eng. 2018, 115, 319–330. [Google Scholar] [CrossRef]
- Piateski, G.; Frawley, W. Knowledge Discovery in Databases; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Gamarra, C.; Guerrero, J.M.; Montero, E. A knowledge discovery in databases approach for industrial microgrid planning. Renew. Sustain. Energy Rev. 2016, 60, 615–630. [Google Scholar] [CrossRef]
- Cheng, G.Q.; Zhou, B.H.; Li, L. Integrated production, quality control and condition-based maintenance for imperfect production systems. Reliab. Eng. Syst. Saf. 2018, 175, 251–264. [Google Scholar] [CrossRef]
- Mourtzis, D.; Vlachou, E. A cloud-based cyber-physical system for adaptive shop-floor scheduling and condition-based maintenance. J. Manuf. Syst. 2018, 47, 179–198. [Google Scholar] [CrossRef]
- Kumar, S.; Goyal, D.; Dang, R.K.; Dhami, S.S.; Pabla, B.S. Condition based maintenance of bearings and gearsfor fault detection—A review. Mater. Today 2018, 5, 6128–6137. [Google Scholar] [CrossRef]
- Bengtsson, M.; Kurdve, M. Machining Equipment Life Cycle Costing Model with Dynamic Maintenance Cost. Procedia CIRP 2016, 48, 102–107. [Google Scholar] [CrossRef]
- Keliris, C.; Polycarpou, M.; Parisini, T. A distributed fault detection filtering approach for a class of interconnected continuous-time nonlinear systems. IEEE Trans. Autom. Control 2013, 58, 2032–2047. [Google Scholar] [CrossRef]
- Mahmoud, M.; Shi, P. Robust Kalman filtering for continuous time-lag systems with markovian jump parameters. IEEE Trans. Circuits Syst. 2003, 50, 98–105. [Google Scholar] [CrossRef]
- Nahmias, S.; Lennon Olsen, T. Production and Operations Analysis; Waveland Press Inc.: Long Grove, IL, USA, 2015. [Google Scholar]
- Fayyad, U.; Stolorz, P. Data mining and KDD: Promise and challenge. Future Gener. Comput. Syst. 1997, 13, 99–115. [Google Scholar] [CrossRef]
- Gullo, F. From Patterns in Data to Knowledge Discovery: What Data Mining can do. Phys. Procedia 2015, 62, 18–22. [Google Scholar] [CrossRef]
- Galar, D.; Kans, M.; Schmidt, B. Big Data in Asset Management: Knowledge Discovery in Asset Data by the Means of Data Mining. In Proceedings of the 10th World Congress on Engineering Asset Management, Tampere, Finland, 28–30 September 2015. [Google Scholar]
- Choudhary, A.K.; Harding, J.A.; Tiwari, M.K. Data Mining in manufacturing: a review based on the kind of knowledge. Adv. Eng. Inf. 2008, 33, 501. [Google Scholar] [CrossRef]
- Qu, Z.; Liu, J. A new method of power grid huge data pre-processing. Procedia Eng. 2011, 15, 3234–3239. [Google Scholar] [CrossRef]
- Bilalli, B.; Abellò, A.; Aluja–Banet, T.; Wrembel, R. Intelligent assistance for data pre-processing. Comput. Stand. Interfaces 2017, 57, 101–109. [Google Scholar] [CrossRef]
- Munson, M.A. A study on the importance of and time spent on different modeling steps. ACM SIGKDD Explor. Newsl. 2011, 13, 65–71. [Google Scholar] [CrossRef]
- Garces, H.; Sbarbaro, D. Outliers detection in industrial databases: An example sulphur recovery process. World Congr. 2011, 18, 1652–1657. [Google Scholar] [CrossRef]
- Nisbet, R.; Miner, G.; Yale, K. Handbook of Statistical Analysis and Data Mining Applications; Academic Press: Burlington, MA, USA, 2018. [Google Scholar]
- Gandomi, A.; Haider, M. Beyond the hype: Big Data concepts, methods and analytics. Int. J. Inf. Manag. 2014, 35, 137–144. [Google Scholar] [CrossRef]
- Saporta, G.; Niang, N. Data Analysis; ISTE Ltd.: London, UK, 2009; pp. 1–23. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The elements of Statistical Learning; Springer: New York, NY, USA, 2001. [Google Scholar]
- Pimentel, M.A.F.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Amhmad, S.; Lavin, A.; Purdy, S.; Agha, Z. Unsupervised real-time anomaly detection for streaming data. Neurocomputer 2017, 262, 134–147. [Google Scholar] [CrossRef]
- Baptista, M.; Sankararaman, S.; de Medeiros, I.P.; Nascimento, C.Jr; Prendiger, H.; Henriques, E.M.P. Forecasting fault events for predictive maintenance using data-driven techniques and ARMA modeling. Comput. Ind. Eng. 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Janouchová, E.; Kučerová, A. Competitive comparison of optimal designs of experiments for sampling-based sensitivity analysis. Comput. Struct. 2013, 124, 47–60. [Google Scholar] [CrossRef]
- Barreiro, P.L.; Albandoz, J.P. Population and sample. Sampling techniques. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwi9kez10ebdAhWOyKQKHXmvCVMQFjAAegQIBxAC&url=https%3A%2F%2Foptimierung.mathematik.uni-kl.de%2Fmamaeusch%2Fveroeffentlichungen%2Fver_texte%2Fsampling_en.pdf&usg=AOvVaw2btopZugJaU8jsfUXEfm2l (accessed on 2 October 2018).
- French, A.; Chess, S. Canonical Correlation Analysis & Principal Component Analysis. Available online: http://userwww.sfsu.edu/efc/classes/biol710/pca/CCandPCA2.htm (accessed on 2 October 2018).
- Chen, K.; Wang, J. Design of multivariate alarm systems based on online calculation of variational directions. Chem. Eng. Res. Des. 2017, 122, 11–21. [Google Scholar] [CrossRef]
- Neusser, K. Time Series Econometrics; Springer: New York, NY, USA, 1994. [Google Scholar]
- Model Selection. In Econometrics ToolboxTM User’s Guide; The MathWorks Inc.: Natick, MA, USA, 2001.
- Statistics ToolboxTM User’s Guide; The MathWorks Inc.: Natick, MA, USA, 2016.
- Woods, D.C.; McGree, J.M.; Lewis, S.M. Model selection via Bayesian information capacity designs for generalized linear models. Comput. Stat. Data Anal. 2016, 113, 226–238. [Google Scholar] [CrossRef]
- Prasad, D.; Ratna, S. Decision support systems in the metal casting industry: An academic review of research articles. Mater. Today Proc. 2018, 5, 1298–1312. [Google Scholar] [CrossRef]
- Krzywicki, D.; Faber, L.; Byrski, A.; Kisiel-Dorohinicki, M. Computing agents for decision support systems. Future Gener. Comput. Syst. 2014, 37, 390–400. [Google Scholar] [CrossRef]
- Li, H.; Pang, X.; Zheng, B.; Chai, T. The architecture of manufacturing execution system in iron & steel enterprise. IFAC Proc. Vol. 2005, 38, 181–186. [Google Scholar]
- Jiang, P.; Zhang, C.; Leng, J.; Zhang, J. Implementing a WebAPP-based Software Framework for Manufacturing Execution Systems. IPAC-Pap. Online 2015, 48, 388–393. [Google Scholar] [CrossRef]
- Itskovich, E.L. Fundamentals of Design and Operation of Manufacturing Executive Systems (MES) in Large Plants. IPAC Proc. Vol. 2013, 46, 313–318. [Google Scholar] [CrossRef]


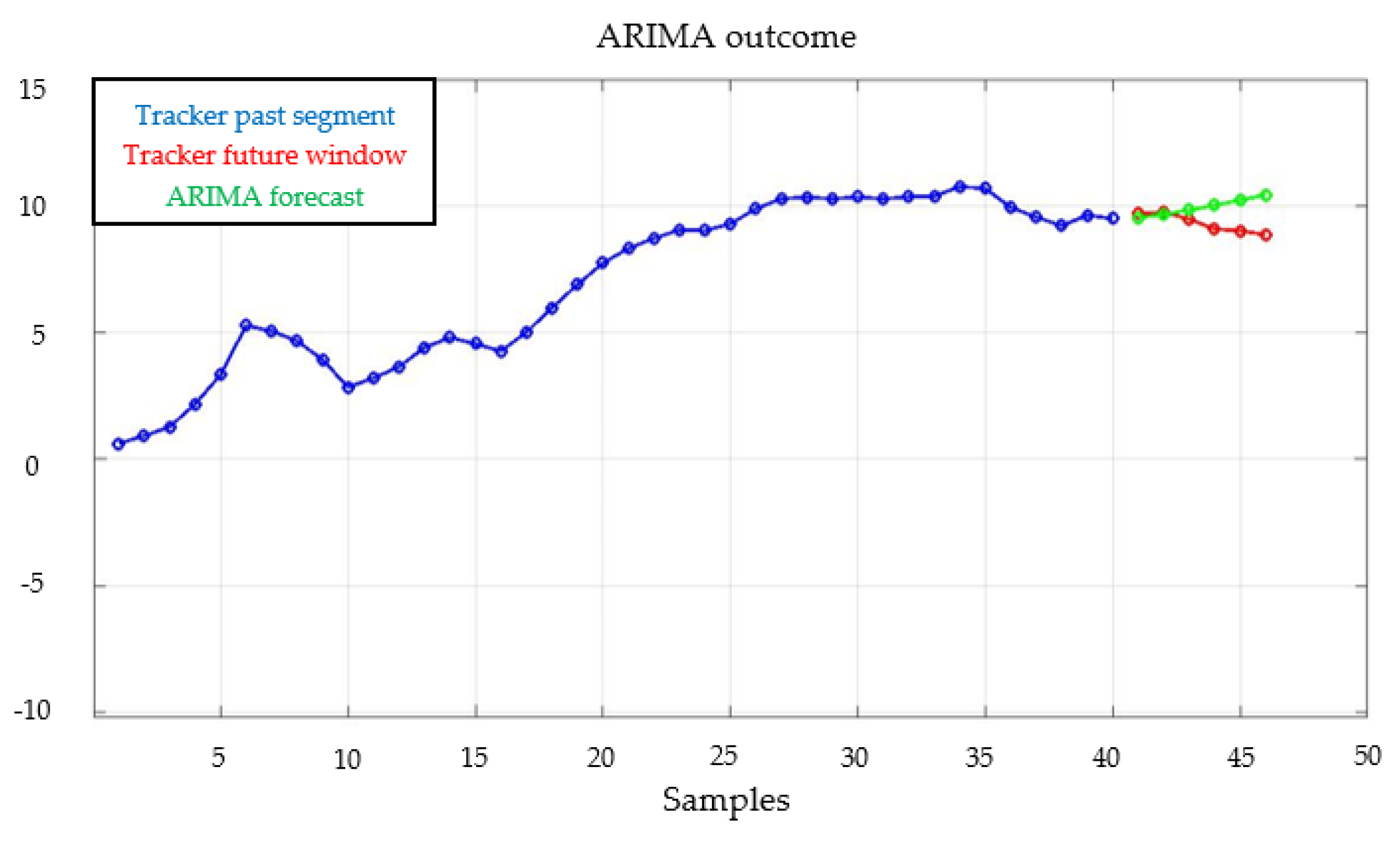
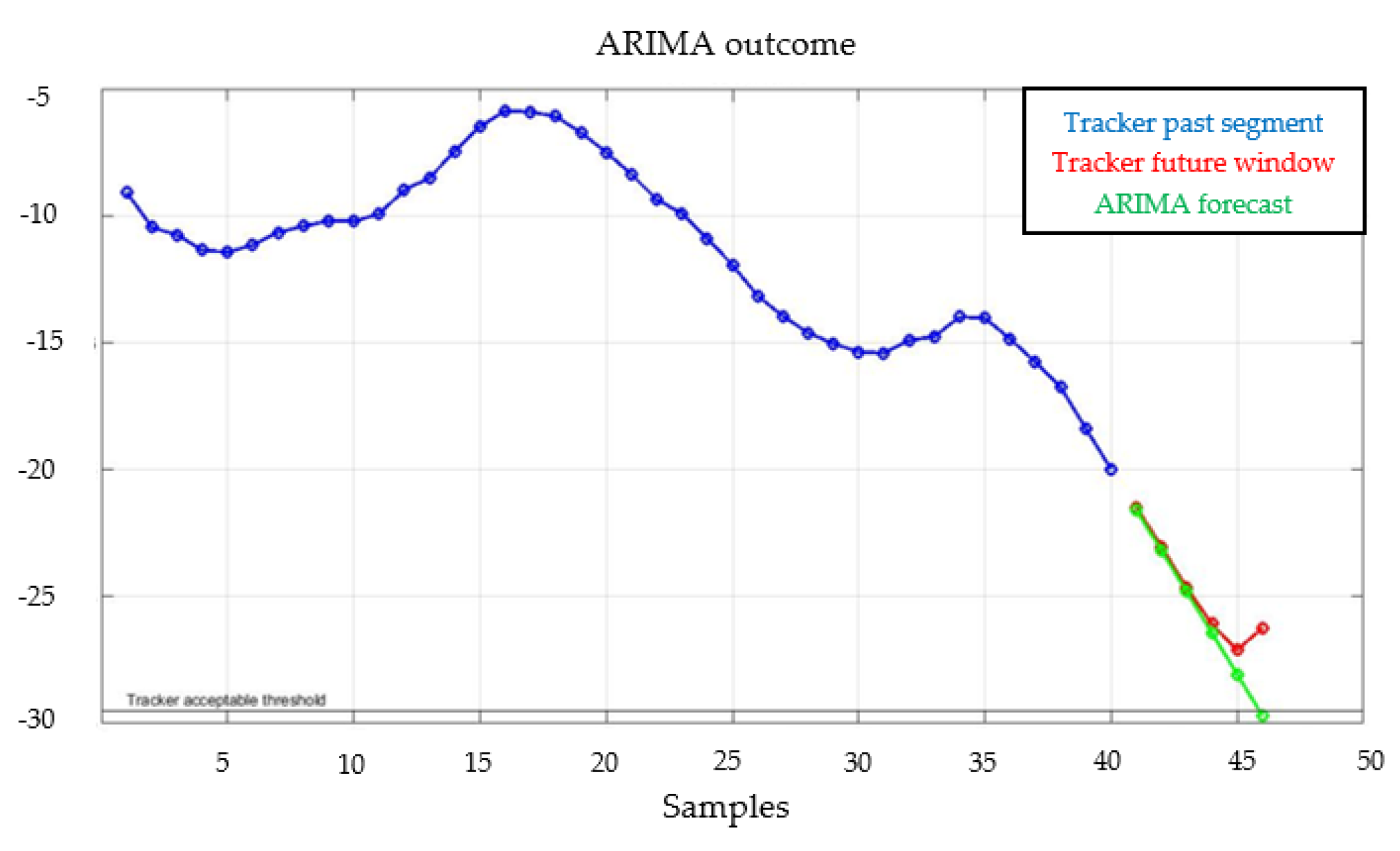
| Phase | Parameter | Nature | Description |
|---|---|---|---|
| 1—time series processing | N | OPT | Size of a sample of aggregated process parameters |
| 1—time series processing | M | OPT | Shift in between two consecutive samples |
| 1—time series processing | S | OPT | Set of main statistical magnitudes describing each sample |
| 1—time series processing | T | OPT | Tracker threshold: the system moves to a status of not-normality in case it is trespassed |
| 2—ARIMA modeling | L | OPT | Historical time window of time series used to fit ARIMA model |
| 2—ARIMA modeling | d | DET | Integrating model order |
| 2—ARIMA modeling | p | DET | Autoregressive model order |
| 2—ARIMA modeling | q | DET | Moving Average model order |
| 2—ARIMA modeling | F | OPT | Future time window of time series forecast by ARIMA model |
| Parameter | Description |
|---|---|
| μ | Mean value |
| σ | Standard deviation |
| Pu | Estimated probability of being above upper bound (Bup) |
| Pl | Estimated probability of being below lower bound (Blow) |
| Cpu | System capability of being below Bup: Bup − μ/3σ |
| Cpl | System capability of being above Blow: μ − Blow /3σ |
| θ | Linear regression slope |
| Δ | Difference between two consecutive linear regressions: θi – θi−1 |
| A+ | Number of pieces lying inside process parameters but above a confidence interval of 95%, assuming normal data distribution (μ + 3σ) |
| A− | Number of pieces lying inside process admissible range but below a confidence interval of 95%, assuming normal data distribution (μ − 3σ) |
| S+ | Number of pieces lying above process admissible range |
| S− | Number of pieces lying below process admissible range |
| Problem | Nature of the Issue | Affected Process Parameter | Algorithm’s Performance | N | M | L | F |
|---|---|---|---|---|---|---|---|
| Obstruction of a pipe due to engine oil drops | Technical | Air volumetric flow rate | Identification in advance of 61 h | 800 | 100 | 20 | 8 |
| Porosity in pump’s channels | Qualitative | Air volumetric flow rate | Identification in advance of 2.3 h | 100 | 10 | 40 | 4 |
| Wear and sliding of a spindle | Technical | Torque absorbed by the pump | Identification in advance of 16 h | 400 | 40 | 40 | 6 |
| Non-compliant material of screws | Qualitative | Screwing torque | Identification in advance of 1.3 h | 750 | 100 | 30 | 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Storti, E.; Cattaneo, L.; Polenghi, A.; Fumagalli, L. Customized Knowledge Discovery in Databases methodology for the Control of Assembly Systems. Machines 2018, 6, 45. https://doi.org/10.3390/machines6040045
Storti E, Cattaneo L, Polenghi A, Fumagalli L. Customized Knowledge Discovery in Databases methodology for the Control of Assembly Systems. Machines. 2018; 6(4):45. https://doi.org/10.3390/machines6040045
Chicago/Turabian StyleStorti, Edoardo, Laura Cattaneo, Adalberto Polenghi, and Luca Fumagalli. 2018. "Customized Knowledge Discovery in Databases methodology for the Control of Assembly Systems" Machines 6, no. 4: 45. https://doi.org/10.3390/machines6040045
APA StyleStorti, E., Cattaneo, L., Polenghi, A., & Fumagalli, L. (2018). Customized Knowledge Discovery in Databases methodology for the Control of Assembly Systems. Machines, 6(4), 45. https://doi.org/10.3390/machines6040045






