Homogeneous Continuous-Time, Finite-State Hidden Semi-Markov Modeling for Enhancing Empirical Classification System Diagnostics of Industrial Components
Abstract
1. Introduction
Methodology Snapshot
2. The Hybrid Diagnostic Approach
2.1. Development of the ECS within the Feature-Driven Approach
- (1)
- (2)
- The selection of an optimal subset of relevant features to be used for the classification [26] through the scheme proposed in our earlier work [22], i.e., the feature selector behaves as a wrapper around the specific learning algorithm used to construct the classifier [16]. The objective functions used for evaluating and comparing the feature subsets during the search are the recognition rate achieved by the ECS (to be maximized) and the number of features forming the subsets (to be minimized). This way, the feature selection problem is formulated as a multiobjective optimization problem [27]. As the large number of extracted features makes it infeasible for an exhaustive search, we use a binary differential evolution (BDE) [28], which has been shown to explore the decision space more efficiently compared to other multiobjective evolutionary algorithms [29] such as non-dominated sorting genetic algorithm II (NSGA-II) [30], strength Pareto evolutionary algorithm (SPEA2) [31], and indicator-based evolutionary algorithm (IBEA) [32].
- (3)
- The development of the empirical classifier. A k-nearest neighbors (KNN) is used as the classification algorithm [33,34]. This choice is justified by the following advantages: (1) KNN requires setting few parameters and (2) it does not require the classes to be linearly separable in the input space.
2.2. Degradation Modeling Based on Homogeneous Continuous-Time Finite State Semi-Markov Processes
- Markov models, in which the sojourn times in the states are exponentially distributed and the transition rates are constant.
- Semi-Markov models, where the transition rates depend on the time spent in the current state. In semi-Markov models, the transition occurrences depend on the sojourn times, which can follow arbitrary distributions. In this work, we assume that they are Weibull distributions, as these are the probability distributions most commonly used to describe the degradation processes of industrial components [3,36].
2.3. Hidden Semi-Markov Model for Degradation Assessment
2.4. HCTFSHSMM for Degradation Modeling
- Estimation of the model parameters, i.e., the parameters of the transition rate functions. This issue arises during the development of the hybrid diagnostic model.
- Estimation of the most likely degradation state at the current time , given the sequence of observations. This issue arises when the developed diagnostic model is used for assessing the degradation state of a test component of interest.
- At time the component is not degraded, i.e., it is in state 1.
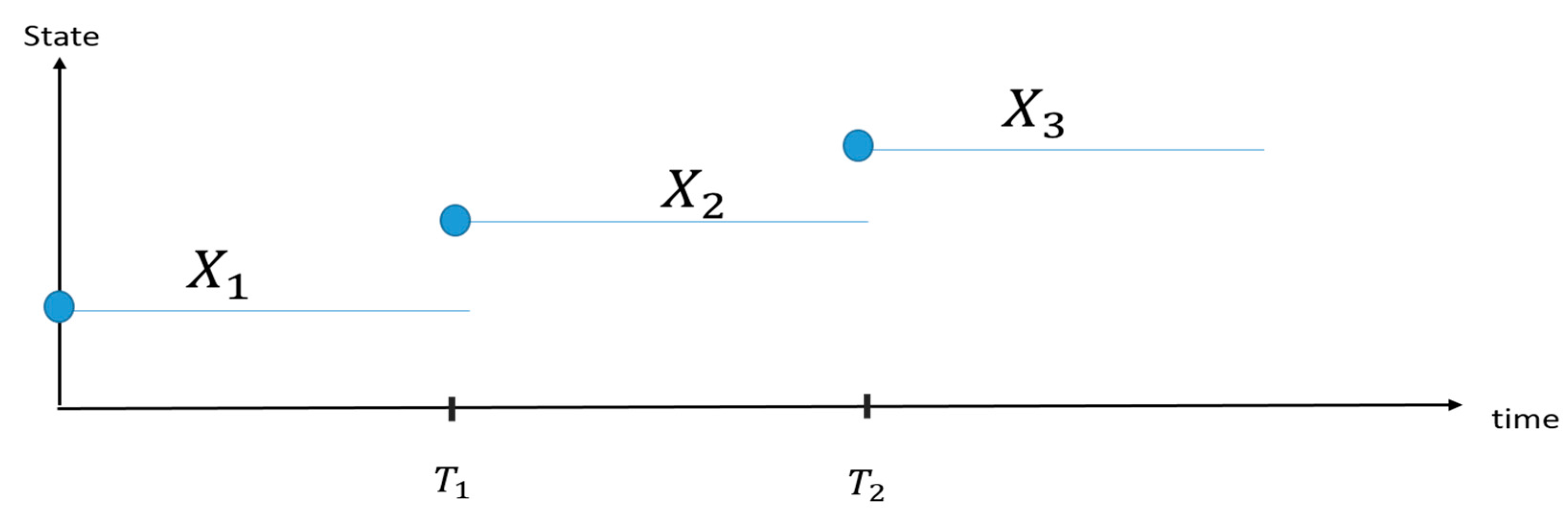
- The data available to estimate the model parameters are sequences of observations , which represent the outcomes of the KNN classifier taken at times , where the superscript refers to the sequence of observations, .
- The number of degradation states is known, .
- The acquisition time period is constant, and . For simplicity, but with no loss of generality, we suppose ; then, the equations presented in the next sections can be easily extended to the more general case.
- Just one transition can occur in the time interval .
- The last observation of each time series coincides with the failure of the component, which is directly observed.
- No maintenance and repair operations are considered; transitions only go left-to-right across the states.
- The ECS presented in Section 2.1 has been developed to assess the degradation state of the equipment. The misclassification probabilities of the KNN classification algorithm are estimated by testing the performance of the diagnostic system on degradation patterns for which the actual degradation state is known. The values of the probabilities are then considered as the entries of the observation matrix .
3. Maximum Likelihood Estimation of the Transition Function Rates
4. Assessment of the Degradation State
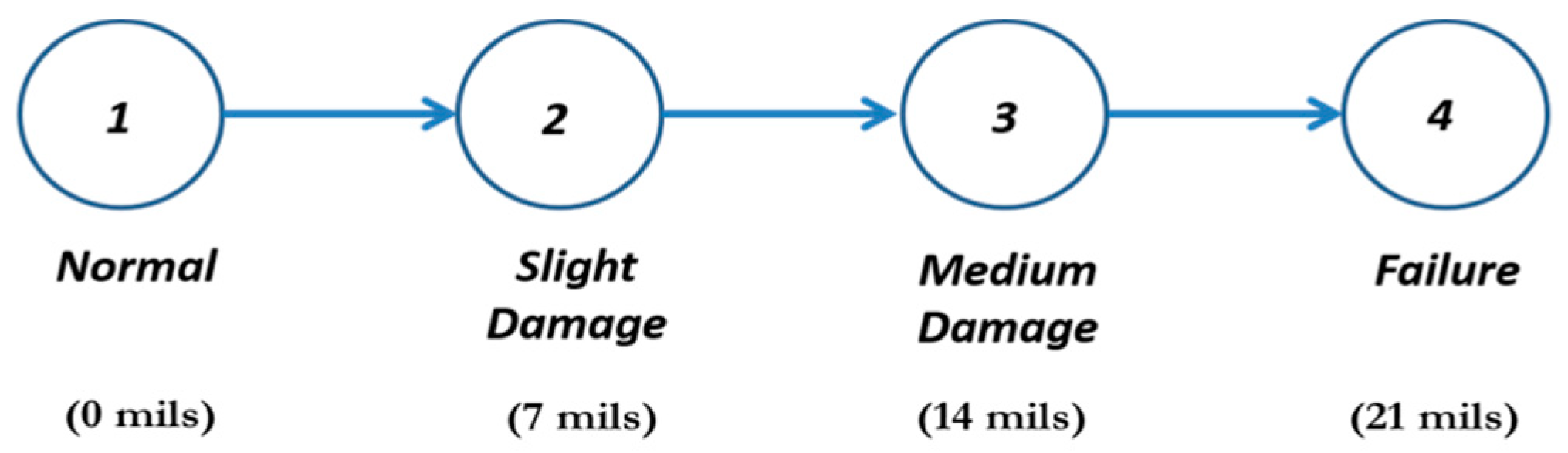
5. Case Study
5.1. Degradation Trajectory Simulation
5.2. Results
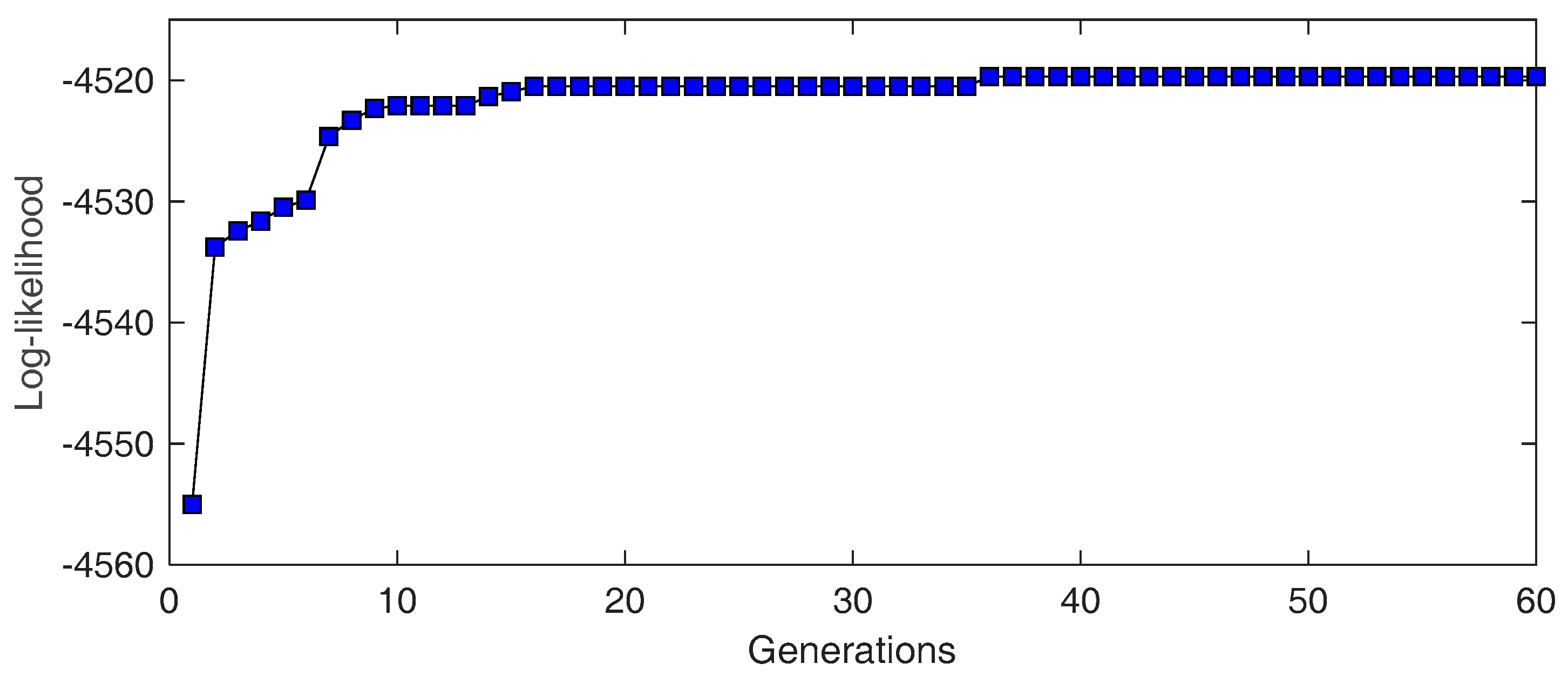
5.2.1. Parameter Optimization
5.2.2. Assessment of the Degradation State
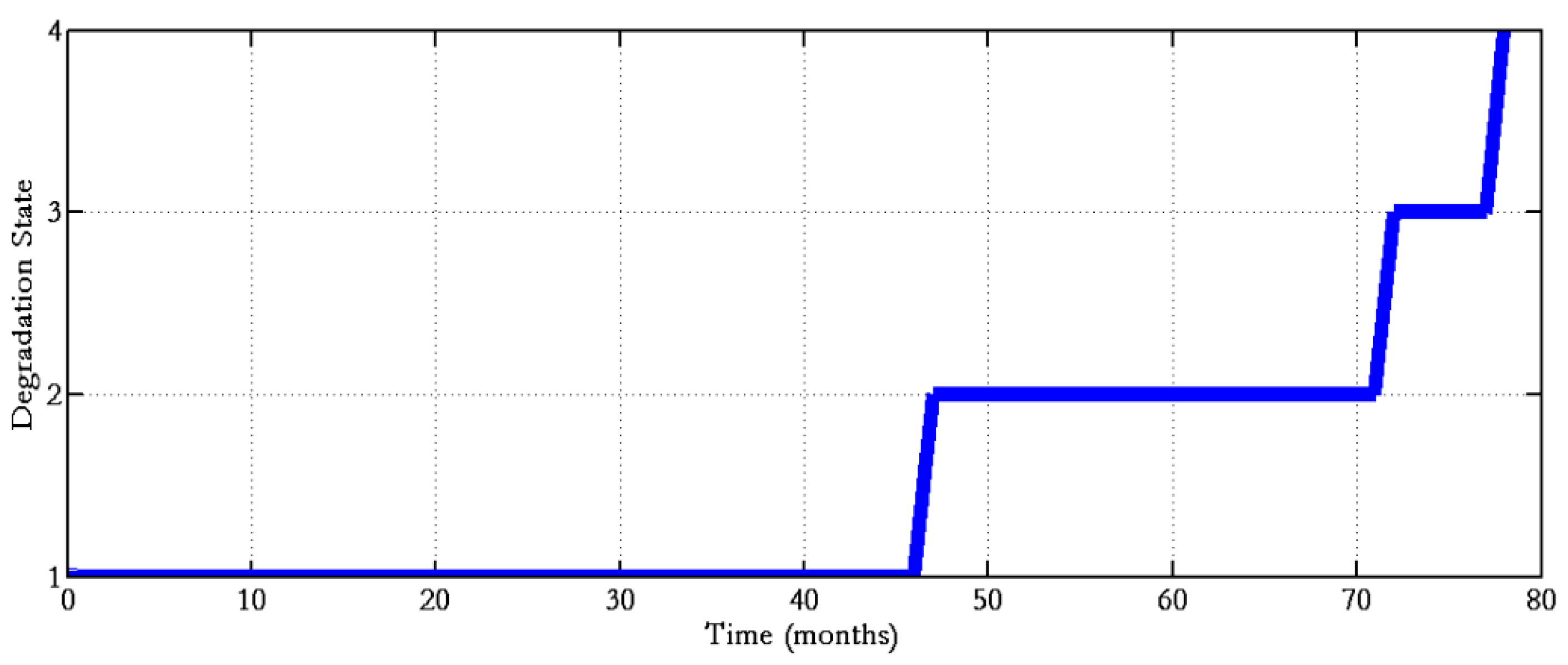
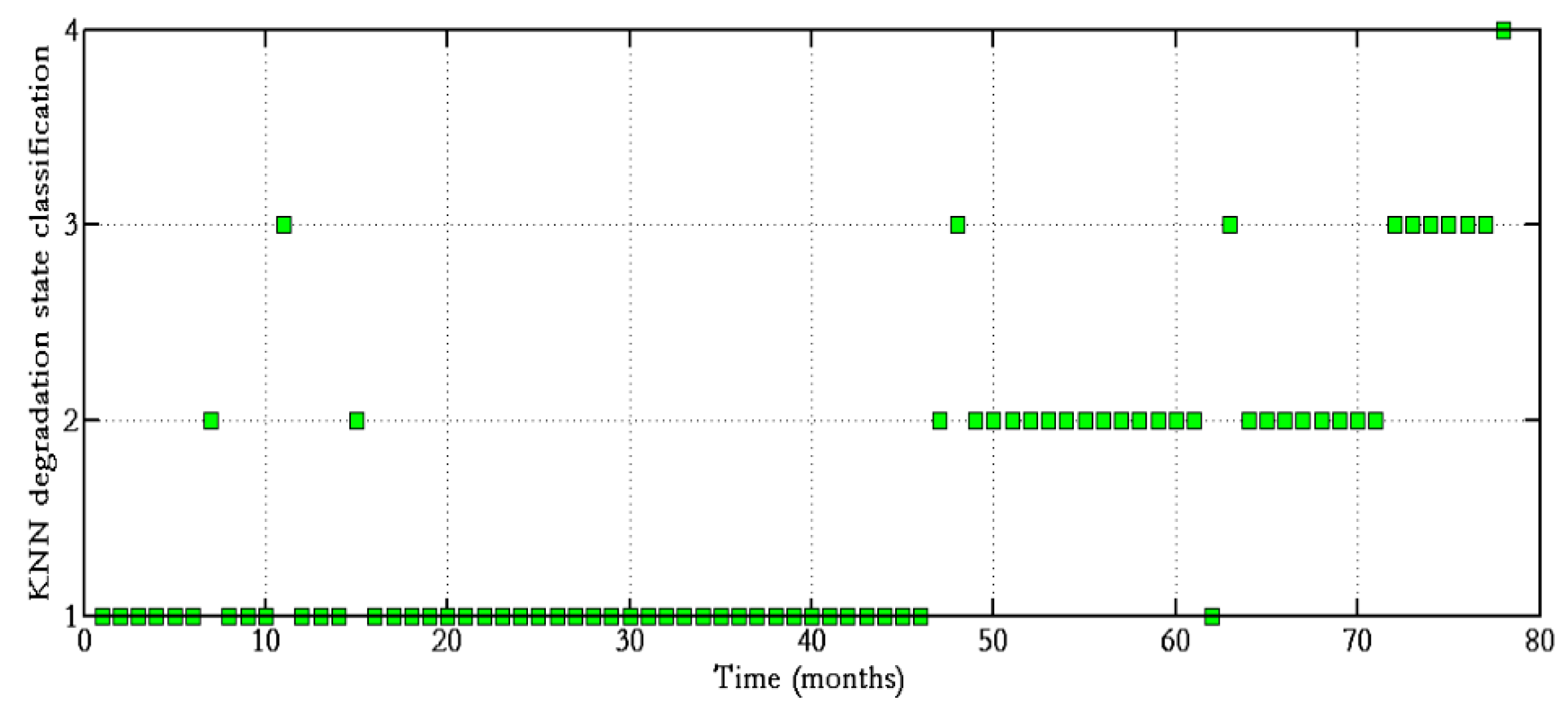
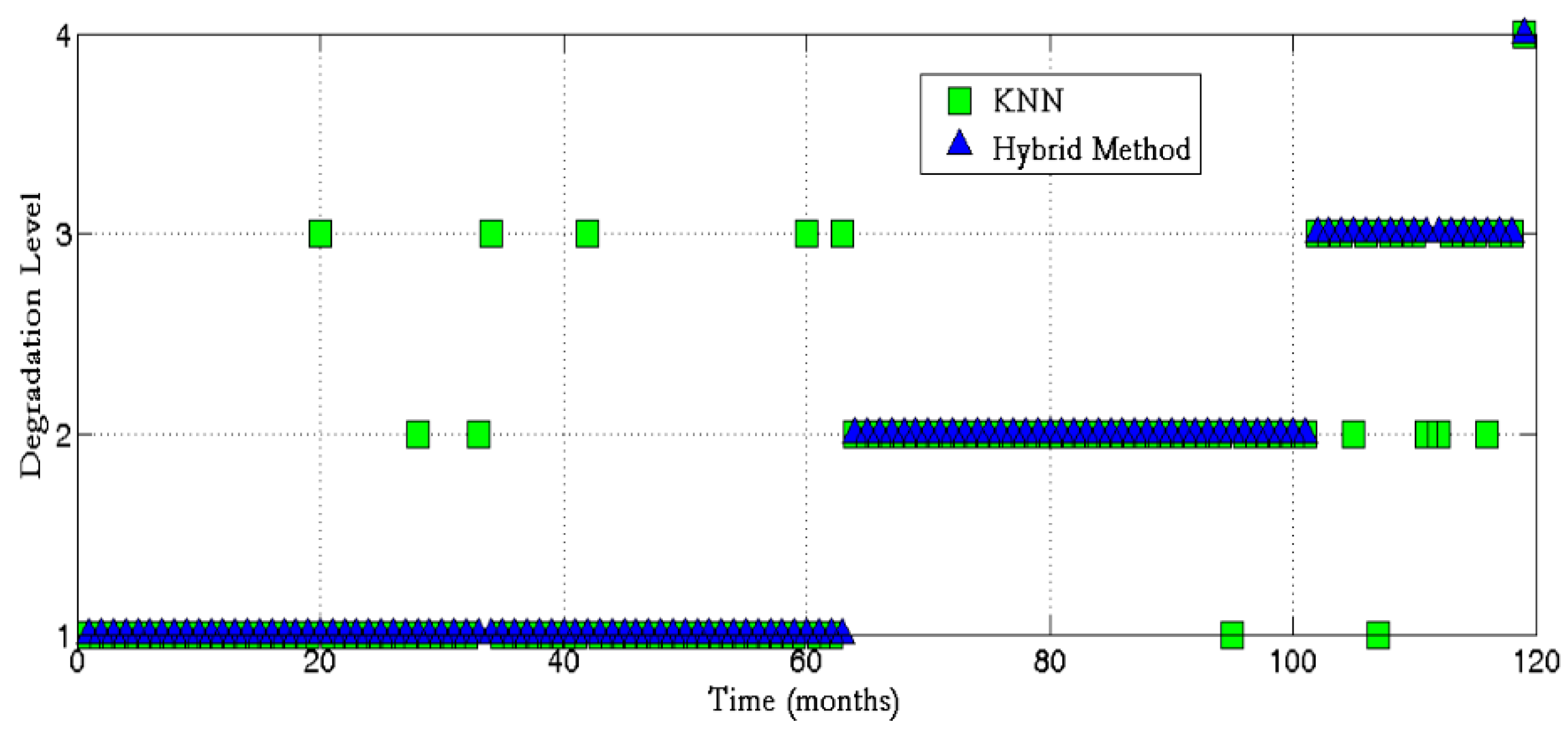
- Correction of the misclassifications of the KNN classifier. In particular, the decoded sequences are always increasing in monotone due to the fact that the underlying semi-Markov process allows only left-to-right transitions.
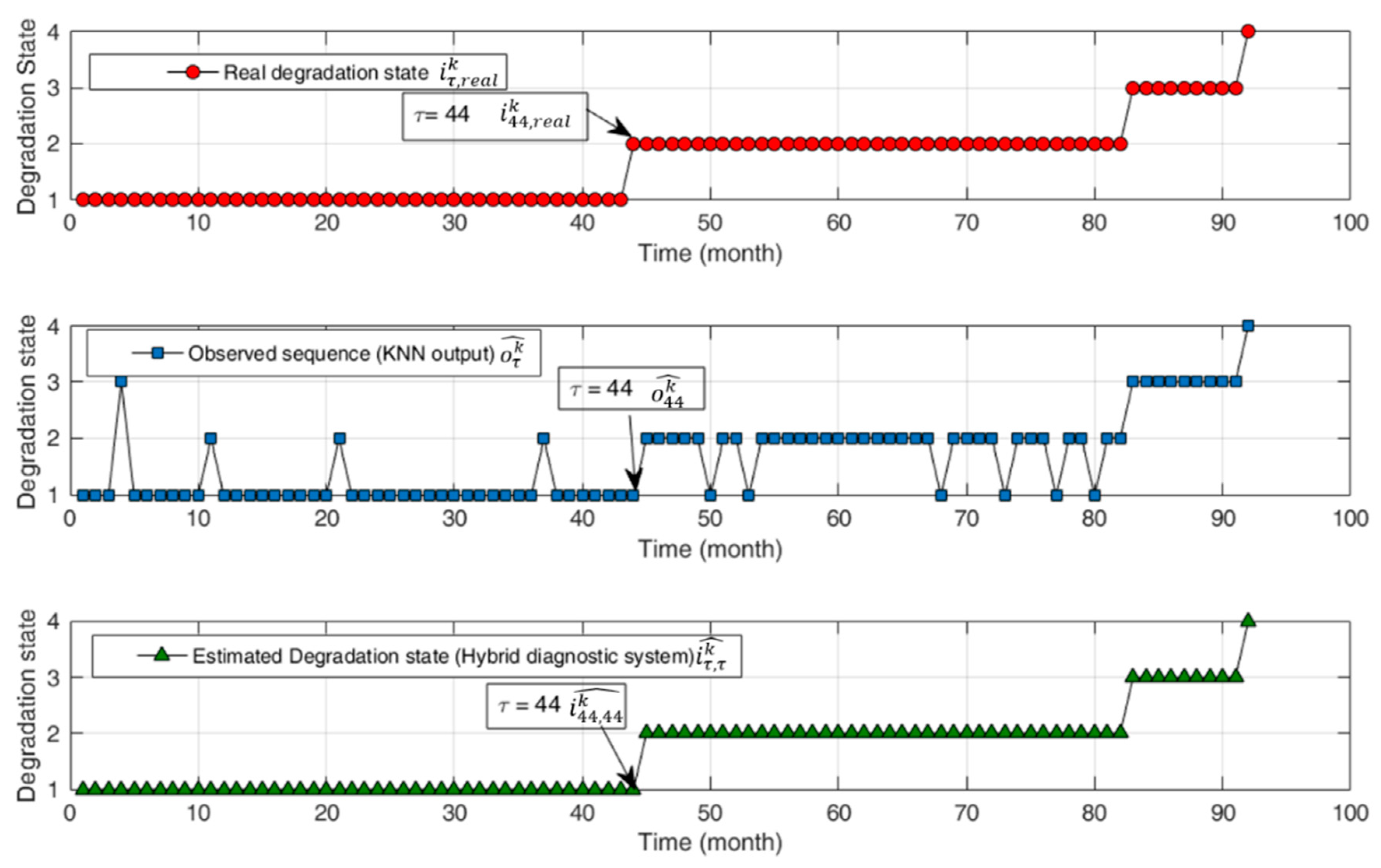
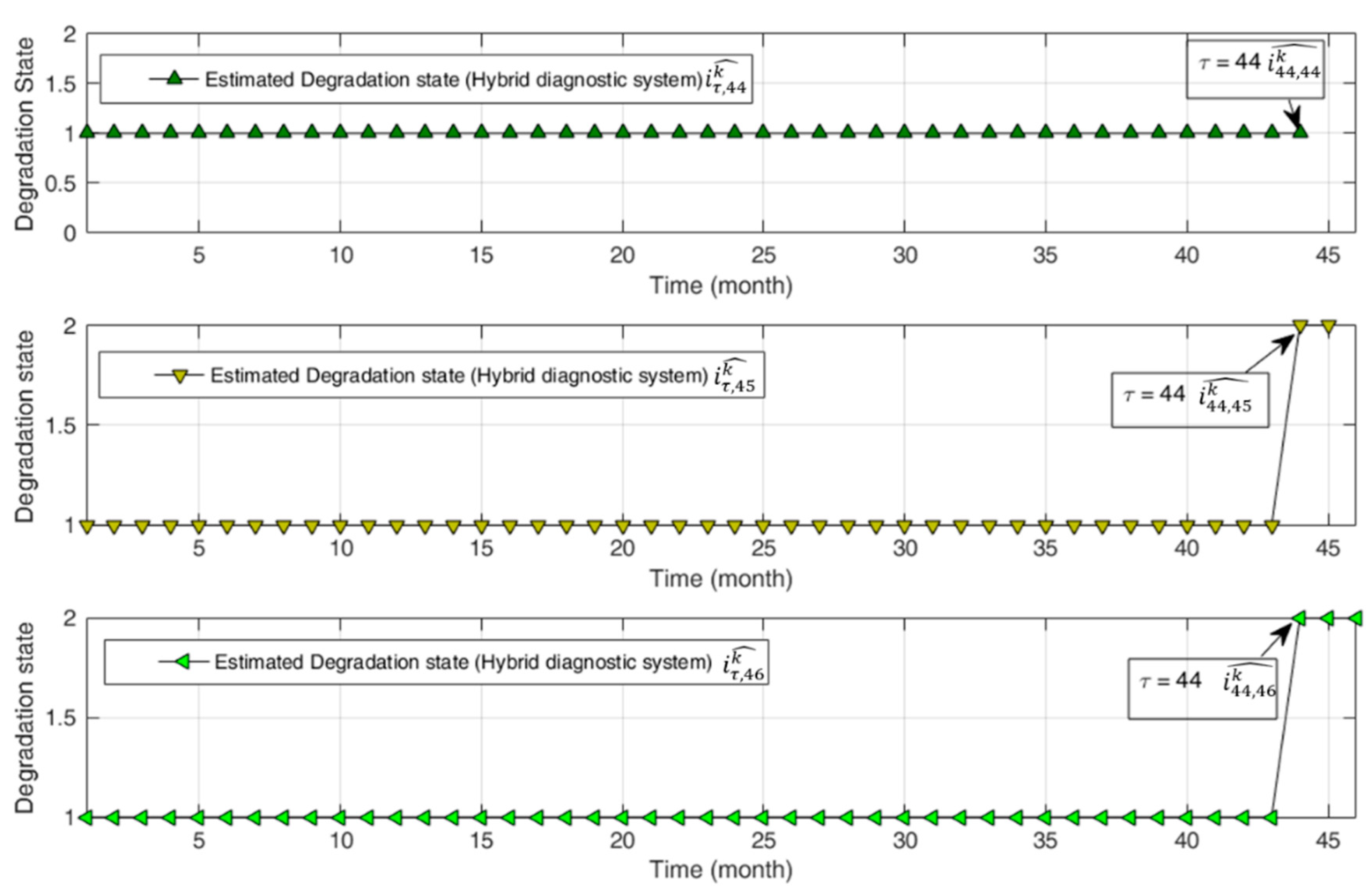
- Estimation, in an unambiguous way, of the time instant that the bearing entered for the first time in a given state. With reference to Figure 6, we can state that the bearing entered for the first time in states 2 and 3 at time instants 65 and 102 (months), respectively. Notice that this information cannot be retrieved by the KNN-based ECS only as it is pointwise static.
5.2.3. Computational Time for On-Line Degradation State Assessment
6. Discussion and Outlooks
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Homogenous Semi-Markov Model
References
- Baraldi, P.; Compare, M.; Zio, E. A practical analysis of the degradation of a nuclear component with field data. In Reliability and Risk Analysis: Beyond the Horizon; Steenbergen, R.D.J.M., van Gelder, P.H.A.J.M., Miraglia, S., Vrouwenvelder, A.C.W.M., Eds.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Giorgio, M.; Guida, M.; Pulcini, G. An age- and state-dependent Markov model for degradation processes. IIE Trans. 2011, 43, 621–632. [Google Scholar] [CrossRef]
- Moghaddass, R.; Zuo, M.J. A parameter estimation method for a condition-monitored device under multistate deterioration. Reliab. Eng. Syst. Saf. 2012, 106, 94–103. [Google Scholar] [CrossRef]
- Vrignat, P.; Avila, M.; Duculty, F.; Aupetit, S.; Slimane, M.; Kratz, F. Maintenance policy: Degradation laws versus Hidden Markov Model availability indicator. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2011, 226, 137–155. [Google Scholar] [CrossRef]
- Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Grall, A.; Blain, C.; Barros, A.; Lefebvre, Y.; Billy, F. Modeling of Stress Corrosion Cracking with Periodic Inspection. In Proceeding of the 32nd ESReDA Seminar on Italy Maintenance Modeling and Application, Alghero, Italy, 8–9 May 2007; Volume 1, pp. 253–260. [Google Scholar]
- Baraldi, P.; Compare, M.; Despujols, A.; Zio, E. Modelling the effects of maintenance on the degradation of a water-feeding turbo-pump of a nuclear power plant. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2011, 225, 169–183. [Google Scholar] [CrossRef]
- Compare, M.; Legnani, L.; Zio, E. MUSTADEPT: A tool for the analysis of industrial equipment degradation Safety and Reliability: Methodology and Applications. In Proceedings of the European Safety and Reliability Conference (ESREL 2014), Tri City, Poland, 27–30 June 2014; pp. 873–881. [Google Scholar]
- Baraldi, P.; Balestrero, A.; Compare, M.; Benetrix, L.; Despujols, A.; Zio, E. A modeling framework for maintenance optimization of electrical components based on fuzzy logic and effective age. Qual. Reliab. Eng. Int. 2013, 29, 385–405. [Google Scholar] [CrossRef]
- Baraldi, P.; Compare, M.; Zio, E. Uncertainty analysis in degradation modeling for maintenance policy assessment. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2013, 22, 267–278. [Google Scholar] [CrossRef]
- Giorgio, M.; Guida, M.; Pulcini, G. A state-dependent wear model with an application to marine engine cylinder liners. Technometrics 2010, 52, 172–187. [Google Scholar] [CrossRef]
- Cannarile, F.; Compare, M.; Rossi, E.; Zio, E. A fuzzy expectation maximization based method for estimating the parameters of a multi-state degradation model from imprecise maintenance outcomes. Ann. Nucl. Energy 2017, 110, 739–752. [Google Scholar] [CrossRef]
- Kwan, C.; Zhang, X.; Xu, R.; Haynes, L. A novel approach to fault diagnostics and prognostics. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 1, pp. 604–609. [Google Scholar]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Moghaddass, R.; Zuo, M.J. An integrated framework for online diagnostic and prognostic health monitoring using a multistate deterioration process. Reliab. Eng. Syst. Saf. 2014, 124, 92–104. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Ocak, H.; Loparo, K.A.; Discenzo, F.M. Online tracking of bearing wear using wavelet packet decomposition and probabilistic modeling: A method for bearing prognostics. J. Sound Vib. 2007, 302, 951–961. [Google Scholar] [CrossRef]
- Georgoulas, G.; Loutas, T.; Stylios, C.D.; Kostopoulos, V. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition. Mech. Syst. Signal Process. 2013, 41, 510–525. [Google Scholar] [CrossRef]
- Cannarile, F.; Baraldi, P.; Compare, M.; Borghi, D.; Capelli, L.; Cocconcelli, M.; Lahrache, A.; Zio, E. An unsupervised clustering method for assessing the degradation state of cutting tools in the packaging industry. In Safety and Reliability: Theory and Application, Proceedings of the European Safety and Reliability Conference (ESREL 2017), Portoroz, Slovenia, 18–22 June 2017; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Medjaher, K.; Tobon-Mejia, D.A.; Zerhouni, N. Remaining useful life estimation of critical components with application to bearings. IEEE Trans. Reliab. 2012, 61, 292–302. [Google Scholar] [CrossRef]
- Dong, M.; He, D.A. Hidden semi-Markov model-based methodology for multi-sensor equipment health diagnosis and prognosis. Eur. J. Oper. Res. 2007, 178, 858–878. [Google Scholar] [CrossRef]
- Baraldi, P.; Cannarile, F.; Di Maio, F.; Zio, E. Hierarchical k-nearest neighbours classification and binary differential evolution for fault diagnostics of automotive bearings operating under variable conditions. Eng. Appl. Artif. Intell. 2016, 56, 1–13. [Google Scholar] [CrossRef]
- Narasimhan, S.; Roychoudhury, I.; Balaban, E.; Saxena, A. Combining model-based and feature-driven approaches: A case study on electromechanical actuators. In Proceedings of the 21st International Workshop on Principles of Diagnosis, Portland, OR, USA, 13–16 October 2010. [Google Scholar]
- Caesarendra, W.; Tjahwowidodo, T. A review of feature extraction methods in vibration-based condition monitoring and its application for degradation trend estimation of low-speed slew bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Cannarile, F.; Compare, M.; Zio, E. A Fault Diagnostic tool based on a First Principle Model Simulator. In Model-Based Safety and Assessment, IMBSA 2017; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Bozzano, M., Papadopoulos, Y., Eds.; Springer: Cham, Switzerland, 2017; Volume 10437, pp. 179–193. [Google Scholar]
- Baraldi, P.; Pedroni, N.; Zio, E. Application of a niched Pareto genetic algorithm for selecting features for nuclear transients classification. Int. J. Intell. Syst. 2009, 24, 118–151. [Google Scholar] [CrossRef]
- Cordón, O.; Herrera-Viedma, E.; Luque, M. Improving the learning of Boolean queries by means of a multiobjective IQBE evolutionary algorithm. Inf. Process. Manag. 2006, 42, 615–632. [Google Scholar] [CrossRef]
- He, X.; Zhang, Q.; Sun, N.; Dong, Y. Feature selection with discrete binary differential evolution. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence (AICI 2009), Shanghai, China, 7–8 November 2019; Volume 4, pp. 327–330. [Google Scholar]
- Tušar, T.; Filipič, B. Differential evolution versus genetic algorithms in multiobjective optimization. In Evolutionary Multi-criterion Optimization, EMO 2007; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Obayashi, S., Deb, K., Poloni, C., Hiroyasu, T., Murata, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Performance of the Strength Pareto Evolutionary Algorithm; Technical Report 103; Computer Engineering and Communication Networks Lab (TIK), Swiss Federal Institute of Technology (ETH): Zurich, Switzerland, 2001. [Google Scholar]
- Zitzler, E.; Künzli, S. Indicator-based selection in multi-objective search. In Parallel Problem Solving fron Nature-PPSN VIII; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Yao, X., Burke, E.K., Lozano, J.A., Smith, J., Merelo-Guervós, J.J., Bullinaria, J.A., Rowe, J.E., Kabán, P.T., Schwefel, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Bang, S.L.; Yang, J.D.; Yang, H.J. Hierarchical document categorization with k-NN and concept-based thesauri. Inf. Process. Manag. 2006, 42, 387–406. [Google Scholar] [CrossRef]
- Wu, W.F.; Ni, C.C. A study of stochastic fatigue crack growth modeling through experimental data. Probab. Eng. Mech. 2003, 18, 107–118. [Google Scholar] [CrossRef]
- Boutros, T.; Liang, M. Detection and diagnosis of bearing and cutting tool faults using hidden Markov models. Mech. Syst. Signal Process. 2011, 25, 2102–2124. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T. Statistical Inference for Probabilistic Functions of Finite State Markov Chains. Ann. Math. Stat. 1966, 37, 1554–1563. [Google Scholar] [CrossRef]
- Baum, L.E.; Eagon, J.A. An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology. Bull. Am. Math. Soc. 1967, 73, 360–363. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T.; Soules, G.; Weiss, N. A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains. Ann. Math. Stat. 1970, 41, 164–171. [Google Scholar] [CrossRef]
- Barbu, V.S.; Limnios, N. Semi-Markov Chains and Hidden Semi-Markov Models towards Applications in Reliability and DNA Analysis; Lecture notes in Statistics; Springer: New York, NY, USA, 2008; Volume 191. [Google Scholar]
- Moghaddass, R.; Zuo, M.J.; Zhao, X. Modeling multi-state equipment degradation with non-homogeneous continuous-time hidden semi-markov process. In Diagnostics and Prognostics of Engineering Systems: Methods and Techniques; IGI Global: Hershey, PA, USA, 2012; pp. 51–181. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zio, E. An Introduction to the Basics of Reliability and Risk Analysis; World Scientific Publishing Company: Singapore, 2007. [Google Scholar]
- Yu, S.-Z. Hidden semi-Markov models. Artif. Intell. 2010, 174, 215–243. [Google Scholar] [CrossRef]
- O’Donnell, P.; Bell, R.N.; McWilliams, D.W.; Singh, C.; Wells, S.J. Report of large motor reliability survey of industrial and commercial installations. In Proceedings of the IEEE Conference Record of Industrial and Commercial Power Systems Technical Conference, Philadelphia, PA, USA, 10–13 May 1983; pp. 58–70. [Google Scholar]
- Jiang, L.; Xuan, J.; Shi, T. Feature extraction based on semi-supervised kernel Marginal Fisher analysis and its application in bearing fault diagnosis. Mech. Syst. Signal Process. 2013, 41, 113–126. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, H.; Bai, F. Classification of fault location and performance degradation of a roller bearing. Measurement 2013, 46, 1178–1189. [Google Scholar] [CrossRef]
- Zhu, K.; Song, X.; Xue, D. A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm. Measurement 2014, 47, 669–675. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T.; Kosasih, B.; Tieu, A.K. Integrated condition monitoring and prognosis method for incipient defect detection and remaining life prediction of low speed slew bearing. Machines 2017, 5, 11. [Google Scholar] [CrossRef]
- Alwadie, A. The decision making system for condition monitoring of induction motors based on vector control model. Machines 2018, 5, 27. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N.; Tripot, G. A data-driven failure prognostics method based on mixture of gaussians hidden markov models. IEEE Trans. Reliab. 2012, 61, 491–503. [Google Scholar] [CrossRef]
- Soualhi, A.; Razik, H.; Clerc, G.; Doan, D.D. Prognosis of bearing failures using hidden markov models and the adaptive neuro-fuzzy inference system. IEEE Trans. Ind. Electron. 2014, 61, 2864–2874. [Google Scholar] [CrossRef]
- Ioannides, E.; Harris, T.A. A new fatigue life model for rolling bearings. J. Tribol. 1985, 107, 367–377. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 20 January 2018).
- Pak, A.; Parham, G.A.; Saraj, M. Inference for the Weibull distribution based on fuzzy data. Rev. Colomb. Estad. 2013, 36, 339–358. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Limnios, N.; Oprisan, G. Semi-Markov Processes and Reliability; Birkhauser: Boston, MA, USA, 2001. [Google Scholar]

| Input Features Selected for the KNN Classifier of the Degradation State | Comments |
|---|---|
| Peak Value (DrE accelerometer) | Maximum of the acceleration signal |
| Minimum Haar wavelet coefficient (DrE accelerometer) | Minimum coefficient from 3-level Discrete Wavelet Transform (DWT) using Haar wavelet basis |
| Norm Node 5 Symlet 6 wavelet (DrE accelerometer) | Squared Energy from 3-level Wavelet Packet Transform (WPT) at node 5 using Symlet 6 wavelet basis |
| Norm Node 12 Symlet 6 wavelet (DrE accelerometer) | Squared Energy from 3-level Wavelet Packet Transform (WPT) at node 12 using Symlet 6 wavelet basis |
| Norm Node 11 Symlet 6 wavelet (FE accelerometer) | Squared Energy from 3-level Wavelet Packet Transform (WPT) at node 11 using Symlet 6 wavelet basis |
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0.887 | 0.082 | 0.031 | 0.000 |
| 2 | 0.081 | 0.865 | 0.054 | 0.000 |
| 3 | 0.025 | 0.102 | 0.873 | 0.000 |
| 4 | 0.000 | 0.000 | 0.000 | 1.000 |
| Expected Sojourn Time (Month) | |||
|---|---|---|---|
| 1 | 55 | 3.8 | 49.7083 |
| 2 | 33 | 4 | 29.9113 |
| 3 | 15 | 4.2 | 13.6341 |
| 1 | 54.7862 | 3.9610 |
| 2 | 31.5632 | 4.1578 |
| 3 | 13.7613 | 4.5585 |
| 1 | 0.39% | 4.24% |
| 2 | 4.35% | 3.94% |
| 3 | 8.26% | 8.54% |
| Mean Misclassification Rate | Maximum Misclassification Rate | |
|---|---|---|
| KNN ( | 0.1195 ± 0.0338 | 0.2388 |
| Hybrid Method ( | 0.0276 ± 0.0203 | 0.0960 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cannarile, F.; Compare, M.; Baraldi, P.; Di Maio, F.; Zio, E. Homogeneous Continuous-Time, Finite-State Hidden Semi-Markov Modeling for Enhancing Empirical Classification System Diagnostics of Industrial Components. Machines 2018, 6, 34. https://doi.org/10.3390/machines6030034
Cannarile F, Compare M, Baraldi P, Di Maio F, Zio E. Homogeneous Continuous-Time, Finite-State Hidden Semi-Markov Modeling for Enhancing Empirical Classification System Diagnostics of Industrial Components. Machines. 2018; 6(3):34. https://doi.org/10.3390/machines6030034
Chicago/Turabian StyleCannarile, Francesco, Michele Compare, Piero Baraldi, Francesco Di Maio, and Enrico Zio. 2018. "Homogeneous Continuous-Time, Finite-State Hidden Semi-Markov Modeling for Enhancing Empirical Classification System Diagnostics of Industrial Components" Machines 6, no. 3: 34. https://doi.org/10.3390/machines6030034
APA StyleCannarile, F., Compare, M., Baraldi, P., Di Maio, F., & Zio, E. (2018). Homogeneous Continuous-Time, Finite-State Hidden Semi-Markov Modeling for Enhancing Empirical Classification System Diagnostics of Industrial Components. Machines, 6(3), 34. https://doi.org/10.3390/machines6030034







