An Empirical Investigation on a Multiple Filters-Based Approach for Remaining Useful Life Prediction

Abstract

Feature construction is critical in data-driven remaining useful life (RUL) prediction of machinery systems, and most previous studies have attempted to find a best single-filter method. However, there is no best single filter that is appropriate for all machinery systems. In this work, we devise a straightforward but efficient approach for RUL prediction by combining multiple filters and then reducing the dimension through principal component analysis. We apply multilayer perceptron and random forest methods to learn the underlying model. We compare our approach with traditional single-filtering approaches using two benchmark datasets. The former approach is significantly better than the latter in terms of a scoring function with a penalty for late prediction. In particular, we note that selecting a best single filter over the training set is not efficient because of overfitting. Taken together, we validate that our multiple filters-based approach can be a robust solution for RUL prediction of various machinery systems.

1. Introduction

Prognostics has been applied to the field of machinery maintenance, allowing industries to better plan logistics and save costs by conducting maintenance only when it is needed. This can be thought of as predicting the time remaining before a likely system failure, which is referred to as the remaining useful life (RUL). In the literature [1,2,3,4,5], existing prognostics approaches can generally be divided into three categories: physics-based, data-driven, and hybrid-based approaches. Physics-based approaches incorporate prior knowledge of physical and/or analytical models with measured data to predict the future degradation behavior of a system and its RUL. Alternatively, data-driven approaches rely on historically collected data and attempt to derive RUL prediction models from the data. Hybrid-based approaches attempt to make use of the strengths of both approaches by combining knowledge related to the physical process and information obtained from the observed data to improve the prediction performance. However, physics-based and hybrid-based approaches are limited in practice because accurate underlying physical models are not available in most real systems. Therefore, data-driven approaches have become increasingly popular with recent advancements in modern sensor systems and data storage/analysis techniques.

In data-driven techniques [3,6], a filtering algorithm that preprocesses the original signal is required to filter out noise from the acquired data. As surveyed in previous reports [7,8], the most commonly used filtering algorithms for machinery prognostics are the moving average, exponential smoothing, linear Fourier smoothing, and wavelet smoothing methods. Moving average methods can be further classified into simple moving average (SMA), central moving average (CMA), and exponential moving average (EMA) methods. For example, SMA was used to eliminate high-frequency thermal noise from sensor data when predicting the RUL of blast furnaces [9], and was applied to smooth sensor measurements to predict the RUL of aircraft engines [10,11] and bearings [12]. In addition, CMA was utilized to smooth the fluctuation of time series data when predicting the RUL of bearings and a heat-resistant alloy [8], and EMA was combined with the Gaussian mixture model to predict the RUL of slow-speed bearings [13]. Exponential smoothing (ES), which is similar to EMA with additional constraints [7], was employed to reduce system noise and measurement noise for RUL prediction of a three-vessel water tank system [14] and bearings [15]. Linear Fourier smoothing (LFS) was used to suppress the high-frequency noise in sensor data to predict the RUL of aircraft systems [16] and battery systems [17]. Similarly, wavelet smoothing (WS) was used to remove high-frequency noise from sensor data for RUL prediction of bearings [18] and lithium-ion batteries [19]. We note that most previous studies employed a single specific filtering algorithm by focusing on development of a new filter or modification of an existing filter. This kind of approach is limited because the optimal filter varies depending on the characteristics of the testing dataset. Therefore, it is a challenge to develop an RUL prognostics system that is robust over various types of datasets.

In this regard, we propose a simple but efficient approach to predict the RUL in a more robust way by employing various filtering methods. Specifically, a set of various features are created from six well-known filter methods. These are then reduced into a smaller number of features by a principal component analysis together with the original variables. These reduced features are used as input variables in machine learning methods; herein the multilayer perceptron and the random forests methods are employed. To verify the usefulness of our approach, we compare it with traditional single-filtering approaches using two benchmark datasets of RUL prediction (i.e., the IEEE 2012 PHM challenge and NASA C-MAPSS datasets). We firstly show that it is difficult to select a proper single-filtering approach due to negative correlations between the training and test errors. Alternatively, our approach showed the best or near-best prediction performances for all of the tested datasets.

The remainder of this paper is structured as follows. Section 2 introduces some background information about traditional single-filtering approaches and the performance evaluation metrics, and then explains our approach. Section 3 presents the experimental results and discussion. We conclude with remarks and suggestions for future work in Section 4.

2. Backgrounds

Traditional Single-Filtering Approaches

Most previous approaches for RUL prediction have applied a single-filtering method to remove noise from the original observed signals to improve performance. In case that there are a lot of observed signals, the principal component analysis (PCA) is often applied to reduce the dimension of the feature space. We call this traditional approach a single-filtering approach with PCA (SF-PCA).

We surveyed six well-known filtering methods for RUL prediction as follows (Let $f_t$ is the value of feature $f$ at time $t$):

• Simple Moving Average (SMA)

SMA is the unweighted average of values over the previous time points (Equation (1)).

$$SMA\left(f_t\right)=\frac{f_t+f_{t-1}+\cdots +f_{t-n+1}}{n},$$

(1)

where $n$ is the number of previous time points.

• Central Moving Average (CMA)

SMA causes a shift in the trend because it considers only previous data. To overcome its tendency for lateness, CMA can be computed by averaging values over equal periods of past and future time points, as follows Equation (2):

$$CMA\left(f_t\right)=\frac{f_{t-\lfloor n/2\rfloor }+\cdots +f_{t-1}+f_t+f_{t+1}+\cdots +f_{t+\lfloor n/2\rfloor }}{n},$$

(2)

where $n$ is an odd number specifying the number of time points being averaged.

• Exponential Moving Average (EMA)

EMA, also known as an exponentially weighted moving average (EWMA), is a type of infinite impulse response filter with exponentially decreasing weighting factors. Here, we employ a variant EMA that uses non-constant weighting factors. The EMA of a time series of feature $f$ is calculated recursively, as follows Equation (3):

$$EMA\left(f_t\right)=\{\begin{array}{ll}{f}_t & \mathrm{if} t=1\\ \frac{\left(1-\alpha \right)·f_t+\alpha \left(1-{\alpha }^{t-1}\right)·EMA\left(f_{t-1}\right)}{1-{\alpha }^t}& \mathrm{if} t>1\end{array},$$

(3)

where $\alpha =e^{-1/N}$ is a constant given the total number of observations $N$.

• Exponential Smoothing (ES)

Similar to EMA, ES is another weighted recursive combination of signals where a constant weighting factor is employed, as follows Equation (4):

$$ES\left(f_t\right)=\{\begin{array}{ll}{f}_t& \mathrm{if} t=1\\ \left(1-\alpha \right)·f_t+\alpha ·ES\left(f_{t-1}\right)& \mathrm{if} t>1\end{array}.$$

(4)

• Linear Fourier Smoothing (LFS)

LFS is based on the well-known Fourier transform that decomposes a signal into its frequency components. By suppressing the high-frequency components, one can achieve a denoising effect (Equation (5)).

$$LFS\left(f\right)={\mathcal{F}}^{-1}\left({\chi }_{\left[-\lambda ,\lambda \right]}\mathcal{F}\left(f\right)\right),$$

(5)

where $\mathcal{F}\left(·\right)$ and ${\mathcal{F}}^{-1}\left(·\right)$ denote the forward and inverse Fourier transforms, respectively, and ${\chi }_A$ is the characteristic function of set $A$. The parameter $\lambda$ is the cut-off frequency. We used the standard Fast Fourier Transform algorithm to compute the one-dimensional discrete Fourier transform of a real-valued time series array of feature $f$.

• Wavelet Smoothing (WS)

Wavelets can be used to decompose a signal into a series of frequency coefficients. A WS method applies soft thresholding to the coefficients and then reconstructs the signal with the threshold coefficients (Equation (6)).

$$WS\left(f\right)={\mathcal{W}}^{-1}\left(\mathcal{D}\left( \mathcal{W}\left(f\right),\gamma \right)\right),$$

(6)

where $\mathcal{W}\left(·\right)$ and ${\mathcal{W}}^{-1}\left(·\right)$ denote the forward and inverse wavelet transform operators, respectively, and $\mathcal{D}\left(·, \gamma \right)$ denotes the denoising operator with the soft threshold $\gamma$. Given the threshold $\gamma$ for data $U$:

$$\mathcal{D}\left(U,\gamma \right)\equiv \mathrm{sgn}\left(U\right)\times \max \left(0,\left|U\right|-\gamma \right),$$

where $\mathrm{sgn}\left(U\right)$ denotes the sign of data $U$ (positive or negative). The threshold $\gamma$ is determined as a universal threshold:

$$\gamma =\widehat{\sigma }\times \sqrt{2\times \log N},$$

where $N$ is the number of data values in the time series of feature $f$ and $\widehat{\sigma }$ is the standardized median absolute deviation of the finest-level detail coefficients.

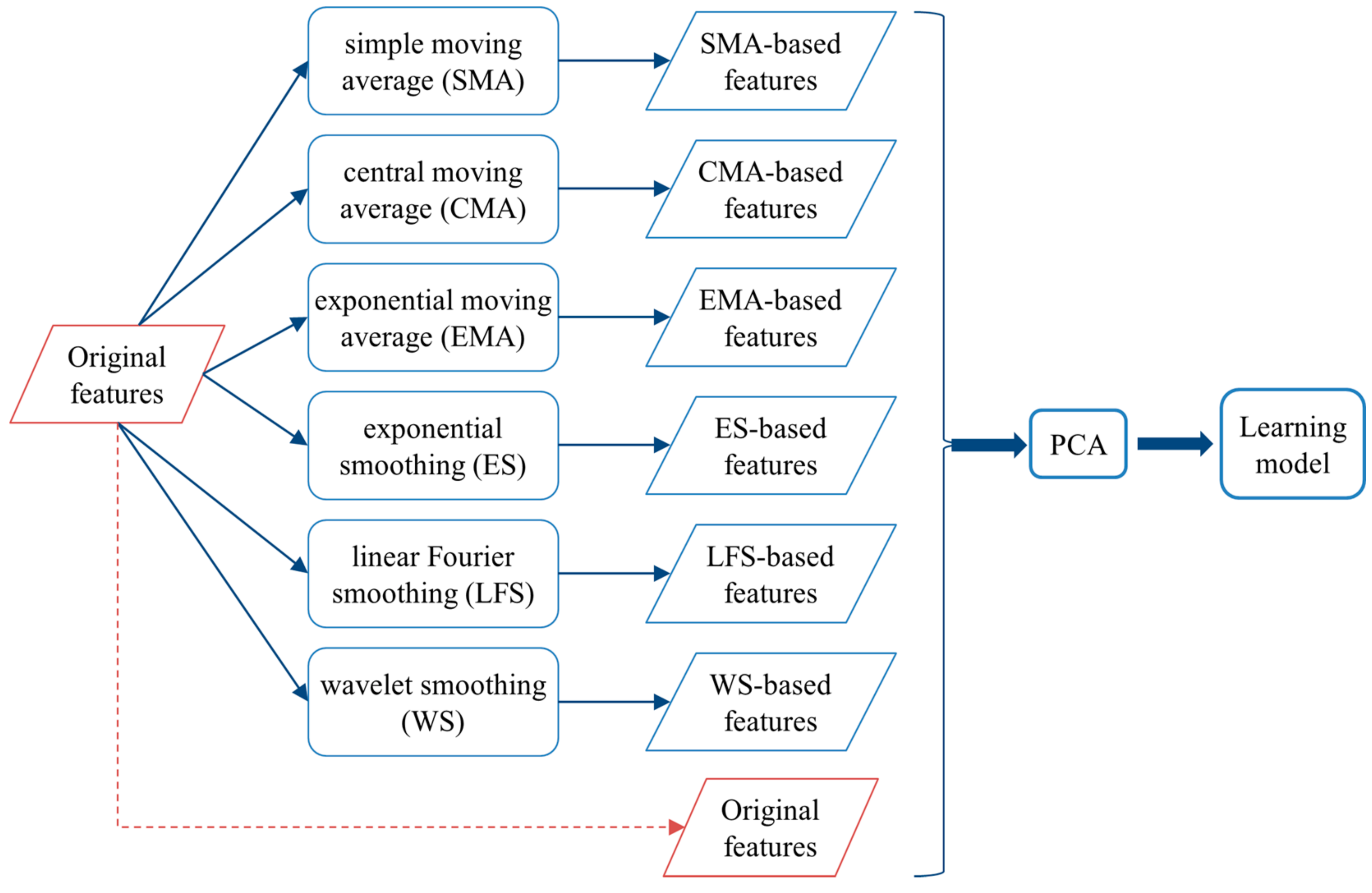
3. Our Proposed Approach

3.1. The Framework

In this work, we propose a robust approach to combine multiple filtering methods and a dimension reduction for the RUL prediction problem (Figure 1). Filtering methods are mainly concerned with reducing relatively high-frequency noise. However, selecting the most suitable filter is a challenge because the best filter varies depending on the characteristics of the signal and/or application. Moreover, keeping the original signal unfiltered can be useful in some prediction problems where it is difficult to realize the presence or absence of noise. To overcome this limitation, we first generate a set of noise-filtered features by using six representative filter methods as we surveyed in the Background section. In addition, the original signals were included to the candidate features so that they can be partially used for learning. This construction process can create a large number of features that can be considered as the input variables in learning. Since such a high-dimensional input space can cause the overfitting problem, we applied PCA to reduce the dimension of the input space. PCA reduces a system of $p$-features into $k$-principal components by using a linear transformation, while still maintaining most of the variability in the feature set. PCA is performed by using singular value decomposition of the data to project it to a lower dimensional space. Here, we choose the principal components, which account for more than 99% of the data variability. Finally, a learning technique can learn the underlying model between a set of features and the RUL variable. In this study, we employed two well-known methods: the multilayer perceptron and random forest methods. This approach is referred to as the multiple-filtering and PCA-based (MF-PCA) RUL prediction.

3.2. Performance Evaluation Metrics

In this study, we employ two metrics to evaluate the RUL prediction performance: the scoring function and the mean squared error (MSE). An RUL prediction is called a failed-safe prediction (FSP, or early prediction) and a failed-dangerous prediction (FDP, or late prediction) when the actual RUL is larger and smaller than the estimated RUL, respectively. The scoring function favors the FSP prediction more than the FDP prediction whereas the MSE gives an equal weight to both types of predictions. Considering that the recovery cost is extremely large in the FDP case, the former measure seems to be more reasonable. However, the score can be forced to be increased by underestimating the RUL. In this regard, it is necessary to assess the prediction performance using both two metrics together [12,15,20,21,22,23]. In the following, the definitions of the metrics are described.

3.2.1. Scoring Function

The scoring function used in this paper is identical to the one used in the IEEE PHM 2012 Data Challenge [24]. Let ${\widehat{RUL}}_i$ and $ActRU{L}_i$ be the estimated RUL and actual RUL of the $i$th sample, respectively (where $i\in \left[1, N\right]$ and $N$ is the number of samples). The percent error on the $i$th sample is then defined by Equation (7):

$$E{r}_i=100\times \frac{ActRU{L}_i-{\widehat{RUL}}_i}{ActRU{L}_i}.$$

(7)

Then, the score of each RUL prediction is defined by setting asymmetric penalties to late and early predictions, with late predictions penalized more (i.e., cases where $E{r}_i<0$):

$$S_i=\{\begin{array}{ll}ex{p}^{-ln\left(0.5\right)\times \left(E{r}_i/5\right)}& \mathrm{if} E{r}_i\le 0\\ ex{p}^{+ln\left(0.5\right)\times \left(E{r}_i/20\right)}& \mathrm{if} E{r}_i>0\end{array}.$$

(8)

The final score is then defined as the average over all samples (Equation (9)):

$$Score=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{S}_i.$$

(9)

3.2.2. Mean Squared Error (MSE)

In addition to the scoring function, we use the MSE is used as a performance measure in this study because it is a general metric for function regression problems. We note that it gives an equal weight to both early and late predictions (Equation (10)).

$$MSE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(ActRU{L}_i-{\widehat{RUL}}_i\right)}^2.$$

(10)

4. Results and Discussion

To validate our MF-PCA approach, we compared it with some traditional SF-PCA approaches. We tested these with two well-known benchmark datasets used for remaining useful life prediction: the IEEE PHM 2012 Prognostic Challenge and NASA C-MAPSS datasets.

4.1. Datasets

4.1.1. IEEE PHM 2012 Prognostic Challenge Dataset

The experimental dataset in the IEEE PHM 2012 Prognostic Challenge was provided by the FEMTO-ST Institute [24] to compete for the best RUL estimator of ball bearings under experimental loading conditions. It consists of six training sets obtained from run-to-failure experiments and eleven test sets showing truncated experimental data; three different loading conditions were considered in the experiments. Two accelerometers were mounted on the bearing housing to measure vibrations in the vertical and horizontal directions. Data sampling was conducted at 10 s intervals at a 25.6 kHz sampling rate and 0.1 s duration; hence, each observation contained 2560 points. The total observations of each case in the training and test sets are listed in

Table 1. Total numbers of observations in the IEEE PHM 2012 Challenge dataset.

Category	Index	Condition 1	Condition 2	Condition 3
Training set	1	2802	910	514
	2	870	796	1636
Test set	3	1801	1201	351
	4	1138	611	N/A
	5	2301	2001	N/A
	6	2301	571	N/A
	7	1501	171	N/A

.

We apply the Fast Fourier Transform (FFT) algorithm to every observation in order to achieve the frequency domain representation of the original observation. We then examine 128 frequency bands $\left[0, \frac{f_s}{256},\frac{2f_s}{256},\cdots \frac{126f_s}{256},\frac{127f_s}{256},\frac{f_s}{2}\right]$, where $f_s$ is the sampling frequency (25.6 kHz). For each frequency band, the energy value, peak existence indicator (true or false), and maximum peak value are extracted. Thus, 768 features are extracted for two vibration features ($2\times 128\times 3$); these are considered as the input variables for learning.

4.1.2. NASA C-MAPSS Dataset

The NASA commercial modular aero-propulsion system simulation (C-MAPSS) dataset contains simulated data produced using a model-based simulation program [25,26]. It is further divided into four sub-datasets, as shown in

Table 2. NASA C-MAPSS dataset details.

Sub-Dataset	C-MAPSS
	FD001	FD002	FD003	FD004
Train trajectories	100	260	100	248
Test trajectories	100	259	100	248
No. of operational modes	1	6	1	6

. Each trajectory within the train and test trajectories is assumed to be the life-cycle of an engine.

The data are arranged in an $n$-by-26 matrix, where $n$ corresponds to the number of data points in each dataset. Each row is a snapshot taken during a single operational cycle and each column represents a different variable. There are six operational modes (in sub-datasets FD002 and FD004) that have a substantial effect on engine performance [21,27,28]. Therefore, it is possible to include the operational mode history as a feature. This is done by adding six columns of data representing the number of cycles spent in their respective operational mode since the beginning of the series [21]. In addition, data normalization is also carried out based on operational modes, as was done in [21].

4.2. Performance Comparisons Between MF-PCA and SF-PCA

In this study, we employ two learning models: the multi-layer perceptron (MLP) and random forest (RF) models. For filtering parameters, the number of time points used to compute the moving average in SMA and CMA is set to five. In LFS, the top 75% high-frequency components of the Fourier transform are removed. For more stable performance analysis, the train-and-test process for each dataset was repeated over 100 trials. Average results and standard deviations are shown in

Table 3. Performance comparisons of MF-PCA and SF-PCA approaches. (a) IEEE 2012 PHM and (b) NASA C-MAPSS datasets. Averages and standard deviations are computed over 100 trials.

(a) IEEE 2012 PHM Dataset
Filtering		MLP			RF
		Train MSE	Test MSE	Test Score	Train MSE	Test MSE	Test Score
None		724 ± 103	744,198 ± 310,888	0.057 ± 0.033	2266 ± 137	103,123 ± 26,233	0.089 ± 0.044
Traditional SF-PCA	SMA	127 ± 97	1,158,819 ± 403,550	0.076 ± 0.032	651 ± 83	138,249 ± 6789	0.152 ± 0.047
	CMA	41 ± 16	1,439,890 ± 492,107	0.090 ± 0.041	421 ± 61	147,384 ± 10,721	0.116 ± 0.044
	EMA	711 ± 115	737,573 ± 295,667	0.049 ± 0.026	2261 ± 122	100,311 ± 24,294	0.083 ± 0.049
	ES	970 ± 2192	110,497 ± 19,777	0.095 ± 0.034	7 ± 2	63,471 ± 1919	0.118 ± 0.010
	LFS	595 ± 106	140,679 ± 110,303	0.100 ± 0.054	1906 ± 123	131,457 ± 13,699	0.128 ± 0.058
	WS	501 ± 430	4,225,192 ± 1,785,637	0.090 ± 0.032	1153 ± 106	179,486 ± 18,961	0.169 ± 0.037
MF-PCA		2593 ± 3720	143,238 ± 37,597	0.113 ± 0.032	375 ± 41	107,308 ± 938	0.182 ± 0.017
(b) NASA C-MAPSS Dataset
Filtering		MLP			RF
		Train MSE	Test MSE	Test Score	Train MSE	Test MSE	Test Score
None		2114 ± 757	1549 ± 320	0.258 ± 0.026	383 ± 158	1603 ± 315	0.250 ± 0.040
Traditional SF-PCA	SMA	2326 ± 707	1543 ± 240	0.248 ± 0.028	305 ± 102	1823 ± 209	0.237 ± 0.026
	CMA	2101 ± 684	2524 ± 1454	0.219 ± 0.077	206 ± 85	2897 ± 1530	0.203 ± 0.066
	EMA	1812 ± 896	3707 ± 2347	0.222 ± 0.017	345 ± 178	1926 ± 381	0.242 ± 0.038
	ES	436 ± 397	9485 ± 3210	0.095 ± 0.027	21 ± 20	3776 ± 1441	0.181 ± 0.033
	LFS	2383 ± 748	1512 ± 332	0.260 ± 0.018	399 ± 154	1941 ± 431	0.224 ± 0.024
	WS	1591 ± 465	3018 ± 1304	0.227 ± 0.035	120 ± 37	2011 ± 341	0.236 ± 0.020
MF-PCA		1064 ± 799	1211 ± 243	0.291 ± 0.031	210 ± 166	1496 ± 264	0.265 ± 0.042

Bold values denote the smallest MSE or the highest score in each column. All these values are significantly smaller or larger than the other values in each column (P-values < 0.05).

. In the table, “None” indicates that the original variables were used as input variables without applying any filtering method. With respect to the MSE in the training set, the ES or CMA filtering methods were best. In addition, the best single-filtering method also showed the best MSE in the test set in the case of the IEEE PHM dataset using the RF learning model. In the rest cases, however, the best method in the training set did not show relatively good MSE in the test set. Interestingly, the ES filtering method over the NASA C-MAPSS dataset showed the worst performance over the test set in both learning models. This implies that there exists an overfitting problem and therefore it is not robust to select a best filter based on the training set. To clarify this point, we further plot the relations between the training and test MSE values (Figure 2). As shown in the figure, the two MSE values do not show positive correlations. We observe negative correlations in Figure 2a,c,d, which imply that the better in the training MSE the worse in the test MSE. Alternatively, our approach was not best in terms of the training MSE but it showed the best test MSE over the NASA C-MAPSS dataset and a medium test MSE over the IEEE PHM dataset. More interestingly, MF-PCA showed the best performance in terms of the test score value in all cases. Considering that the assessment by the scoring function is meaningful in machinery prognostics because late predictions are most dangerous, MF-PCA is the most efficient approach in RUL prediction. In addition, it is notable that the test score of the RF method was considerably low in cases where it was best with respect to the test MSE. Finally, we note that the test score values of the IEEE 2012 PHM dataset are relatively small on average. This might be caused by insufficient amount of training data as mentioned in some previous studies [15,29] where the same dataset was investigated. Specifically, we note that the test score achieved in [15] was 0.0981, which is smaller than that of MF-PCA.

To visualize the prediction result of our approach, we plotted the actual and predicted RULs by MF-PCA (Figure 3). The points below (or above) the diagonal line mean early (resp. late) predictions. As shown in the figure, MF-PCA was likely to predict earlier RULs than the actual RULs. Specifically, the numbers of early predictions in the MLP and RF models were 10 and 6, respectively, among a total of 11 test cases in the IEEE PHM dataset (Figure 3a,b). In the case of the NASA C-MAPSS dataset, those numbers in the MLP and RF models were 468 and 513, respectively, among a total of 707 test cases (Figure 3c,d). This tendency led to a relatively high score values. Taken together, MF-PCA is a good approach for accurate and robust RUL prediction.

4.3. The Number of Components Selected by PCA

In the data-driven prognostics, a large number of features can overfit the training data and eventually reduce the general performance of the learning model. In this regard, we used the PCA to properly reduce the dimension of the input space and to enhance speed of the training phase. It is intended to retain the most important characteristics of the whole input space by using the principal components. In this study, the principal components that explain 99% of the data variance were selected.

Table 4. The numbers of principal components selected by PCA process in MF-PCA and SF-PCA approaches. The principal components that explain 99% of the data variance were selected. (a) IEEE 2012 PHM and (b) NASA C-MAPSS datasets. NuOF and NuPC stand for “the number of original features” and “the number of principal components selected”, respectively.

(a) IEEE 2012 PHM Dataset
Filtering		NuOF		NuPC
				Condition 1		Condition 2		Condition 3
None		768		435		436		338
Traditional SF-PCA	SMA			397		388		340
	CMA			317		315		296
	EMA			435		436		338
	ES			125		134		123
	LFS			449		445		349
	WS			320		352		289
MF-PCA		5376		709		700		609
(b) NASA C-MAPSS Dataset
Filtering		FD001		FD002		FD003		FD004
		NuOF	NuPC	NuOF	NuPC	NuOF	NuPC	NuOF	NuPC
None		21	14	30	22	21	12	30	21
Traditional SF-PCA	SMA		11		8		9		8
	CMA		10		9		8		8
	EMA		17		19		14		19
	ES		15		7		13		6
	LFS		15		9		13		8
	WS		5		14		7		14
MF-PCA		147	50	210	41	147	39	210	38

shows the numbers of principal components selected in MF-PCA and SF-PCA approaches. As shown in the table, the number of features is largely reduced by the PCA; specifically, at least 87% and 66% features were reduced in the IEEE PHM and NASA C-MAPSS datasets, respectively, by the MF-PCA process.

5. Conclusions

In this study, we proposed MF-PCA, which predicts the RUL in a more robust way by combining various filtering methods. We compared MF-PCA with none-filtered and six single-filtering approaches in two different learning models (MLP and RF), and over two benchmark datasets (the IEEE PHM 2012 and NASA C-MAPSS datasets). Results show that MF-PCA has a more robust and accurate performance than single-filtering approaches because it resolves the overfitting problem (Table 3). This is because MF-PCA not only keeps the original variables but also generates a large number of various features from different filtering methods. Because it is difficult to select a proper single-filtering approach due to the negative or unclear correlations between the training and test errors (Figure 2), MF-PCA is useful because it can be applied to other machinery systems without a priori knowledge. Finally, we note the limitations of the MF-PCA approach. As a pure date-driven approach, it is not applicable in early stage of real machine operation. In addition, the prediction performance is highly affected by the quality and the amount of training data. Moreover, PCA is a basically linear transformation so other nonlinear reduction process can be more efficient for more noisy data. Future studies will further focus on validating the usefulness of our approach by employing other learning models, such as support vector machines and k-nearest neighbors. Parameters of the filtering methods are also needed to be automatically determined by an optimization process, like a genetic algorithm. It is worth to investigate the optimal ratio between the training and the test datasets.